Investigation of Photovoltaic Grid System under Non-Uniform Irradiance Conditions

Abstract

Photovoltaic (PV) systems have recently been recognized as a leading way in the production of renewable electricity. Due to the unpredictable changes in environmental patterns, the amount of solar irradiation and cell operating temperature affect the power generated by the PV system. This paper, therefore, discusses the grid-integrated PV system to extract maximum power from the PV array to supply load requirements and the supply surplus power to the AC grid. The primary design is to have maximum power point tracking (MPPT) of the non-uniformly irradiated PV array, conversion efficiency maximization, and grid synchronization. This paper investigates various MPPT control algorithms using incremental conductance method, which effectively increased the performance and reduced error, hence helped to extract solar array’s power more efficiently. Additionally, other issues of PV grid-connected system such as network stability, power quality, and grid synchronization functions were implemented. The control of the voltage source converter is designed in such a way that PV power generated is synchronous to the grid. This paper also includes a comparative analysis of two MPPT techniques such as incremental conductance (INC) and perturb-and-observe (P&O). Extensive simulation of various controllers has been conducted to achieve enhanced efficient power extraction, grid synchronization and minimal performance loss due to dynamic tracking errors, particularly under fast-changing irradiation in Matlab/Simulink. The overall results favour INC algorithm and meet the required standards.

1. Introduction

Governments and public bodies are now worried about energy production with as clean technology as possible. Consequently, the requirements for future energy development are drawn up following the Kyoto Protocol, which encourages the European countries ‘2020’ plan. Solar, wind, photovoltaic, and geothermal energy-focused energy production systems are sustainable and renewable alternatives to non-clean traditional fossil-fuel and nuclear fission-based technologies.

Photovoltaic (PV) is one of the clean technologies that has grown significantly in recent years, almost 60 per cent in Europe. PV systems are no longer isolated from the grid but connected to it as part of electrical generation. Such plants are economically feasible, even without government subsidies for renewable energy, and the photovoltaic plant’s potential is growing considerably. As a result, the production of grid-connected PV plants continues to expand worldwide, exceeding hundreds of megawatts, making these plants a vital part of the future electrical energy system and smart grids.

Due to the abundant availability of solar radiant energy, the impact of photovoltaic (PV) energy on renewable energy sources can be considered as a vital and indispensable sustainable fuel. PV systems have recently been recognized as a leading way in the production of renewable electricity. This can produce direct energy when exposed to solar radiation without any environmental effects of pollution. The PV system is stationary, silent, free of mechanical parts, and has low running and manufacturing costs compared to other renewable resources. The use of photovoltaic as a source of electrical energy shows a growing trend both in the implementation of the global energy sector and in the performance of various industrial plants. This trend is motivated by many factors, such as the decrease in the cost of producing photovoltaic electricity per kW and the rise in fossil fuel prices and the development of effective photovoltaic energy conversion technology. With energy issues becoming increasingly urgent, the world needs to start developing new technology and related technologies. Today, large-scale photovoltaic generation and the size of renewable energy have become core components of the development plan, but the progress of the photovoltaic industry is the way ahead. However, due to its characteristics, which differ from conventional power generation, the grid-connected PV power plant and its performance and stability, a new challenge has emerged [1,2,3,4].

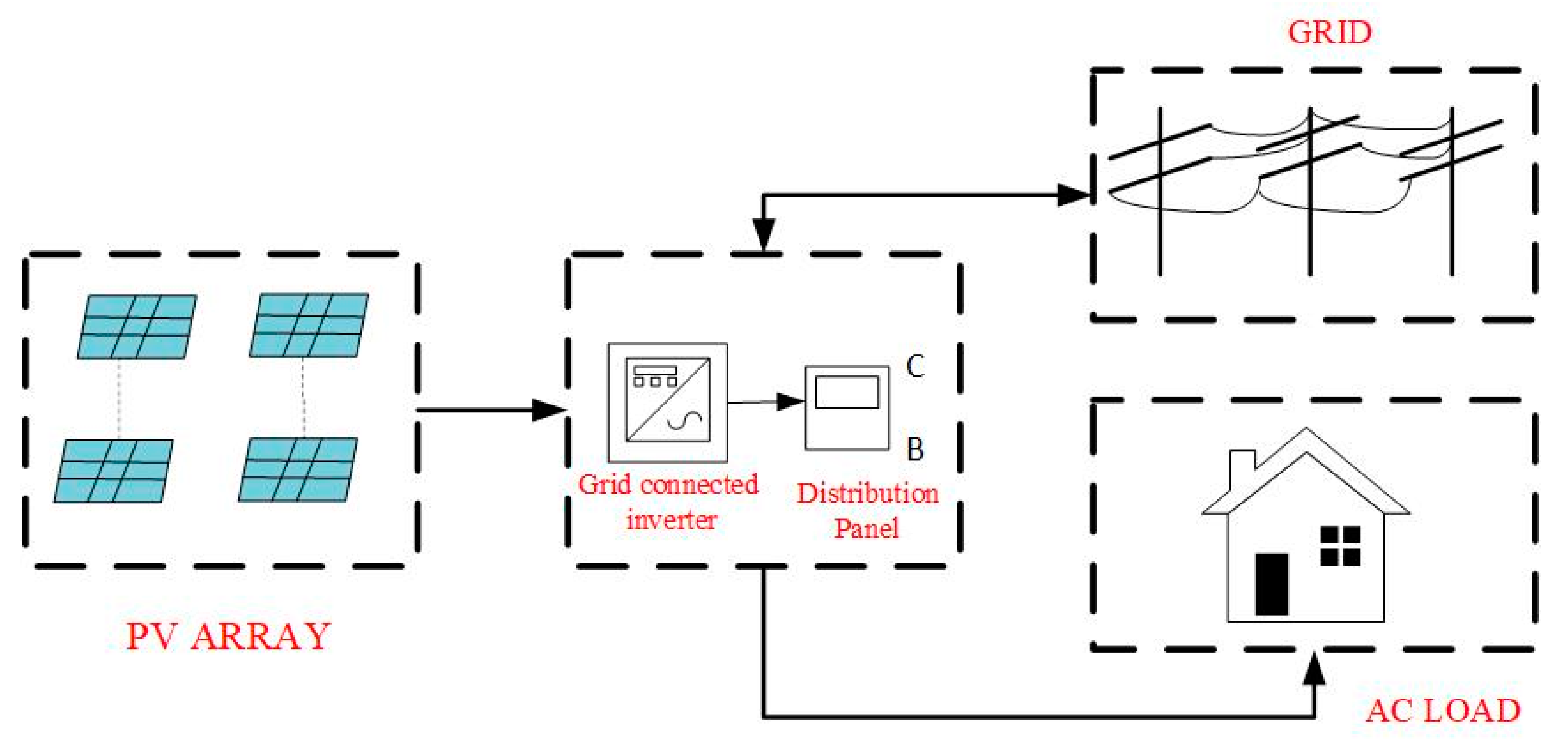
The grid-based PV systems are systems connected to a large, independent grid that usually provide direct power to the main grid. Such grid-connected systems can be used both for decentralized PV and central grid applications. Decentralized grid-connected photovoltaic applications include photovoltaic generators on apartment roofs and an integrated building network that incorporates photovoltaic systems into homes [3]. For PV networks connected to residential or commercial grids, the demand for commercial electricity is served by the PV network, and the excess is supplied to the grid, usually in lower kilowatt capacity. A typical hybrid grid-connected PV system, as shown in Figure 1, consisting of solar PV panels, power conditioner, net metering and an inverter.

When surplus power returns to the grid and is purchased from the grid when there is a power deficit through a net metering system, excess power is pumped into the electricity grid when PV generates more than the required demand. In reality, when this happens, the meter runs the other way round. As before, when the system does not generate enough energy, it can be drawn from the utility. The “back-and-forth” between the grid and your network means that surplus capacity is still being used and that shortages are being addressed.

Due to the changing nature of solar energy emitted as a consequence of unpredictable and unexpected variations in weather conditions that alter the rate of solar irradiation and the values of cell-operating temperature [5], the electrical device operated by solar arrays requires special design considerations during early days, PV systems were primarily used as power sources for special purposes, such as communications and satellites. With the development of the power electronics network, the role of the PV source in all domestic and few commercial sectors has been extended. Renewable energy, such as the PV network, is linked to the grid in a number of ways [6,7,8,9,10].

Maximum power point tracking controllers play an important role in photovoltaic power generation to extract maximum power from PV panels and help to run at their maximum power point (MPP) with environmental changes and varying irradiance patterns. In order to run the PV array at its maximum power point, the PV system implements the maximum power point tracking controller and thus requires MPPT algorithms as varying solar irradiance results PV arrays with non-linear voltage-current characteristics. These voltage-current characteristics have a particular point where the maximum output is achieved. That point depends on the various environmental conditions. Such conditions change during the day and differ depending on the season. Different MPPT control methods are used for solar PV systems, Incremental conductivity INC, P&O, constant voltage, constant, current fuzzy control, and neural network control. Incremental conductance and perturbation and observation approaches are widely used for their simplicity and popularity [11,12,13,14,15].

This paper presents a comparative analysis of perturb-and-observe and incremental conductance MPPT techniques using a boost converter, and the simulation model of the PV-based system with the MPPT algorithm is implemented in Matlab/Simulink 2020. The purpose of this comparative analysis is to determine which MPPT methods are better suited to MPPT in order to construct an optimal algorithm.

The PV power injected into the grid must comply with the regulations, such as EN61000-3-2 and IEEE 1547 [5]. If the AC output voltage from the interconnecting inverter has higher levels, the grid current injected contains less harmonic content. Multilevel and interleaved inverters can deliver enhanced waveform efficiency, smaller filter sizes, lower electromagnetic induction and lower harmonic distortion [6,7,8], which is ensured by power conditioning units. The power conditioning unit is the heart of PV grid-connected systems. It is used mainly to overcome the following issues:

• PV should be synchronized with the grid voltage in case of distortion or imbalance in grid voltage, or difference in grid frequency can affect the stability of the system [16].
• The DC/AC converter is connected to the grid through an RL reactor, an RLC series filter to smooth current harmonics [17] and a step-up Δ-Y transformer to insulate the PV farm from zero-sequence current faults that might occur on the grid side. The AC/DC converter controls the PV voltage via MPPT algorithm [18], as well as the reactive power injected to the grid [19].
• The unbalanced load injects zero and negative sequence currents into the distribution network. However, these sequence currents are mitigated by the VSC. Nonlinear loads inject the harmonics current at the point of common coupling which is compensated by the same VSC. Moreover, VSC integrates the stored energy to the three-phase AC grid [20].
• Multipulse VSCs such as 12-pulse, 24-pulse and 48-pulse converters are the solution for large scale solar PV grid interfaced power generating system to minimize harmonics in the line currents and operate with low frequency-based control with good power quality, high efficiency and reliability as compared with the conventional two-level topologies [21,22,23].
• In connecting photovoltaic installations to the grid, one essential problem is the ability to monitor reactive power in both transient and stable conditions. To inject or require a pre-established reactive power imposed by the electrical system operator or determined by the inverter itself, the inverter must regulate the operation of the currents, depending on the magnitudes measured from the grid.
• The connection of energy storage systems (ESS) with photovoltaic power plants is another important problem to address in the future. Considering the prices of the energy generated and used, and the optimization of the ESS power, it is important to determine when and how to charge and discharge the energy. This is called smart power storage.

PV-grid simulations have been performed using Matlab in this article. Matlab technology enhances incorporation with many new blocks that are readily available to minimize simulation time and ease the complexity of the simulation process, and this should be integrated into the existing system to ensure its continued growth. The significant contributions made to the research work presented are as follows.

• This paper investigates the performance of two MPPT techniques such as incremental conductance (INC) and perturb-and-observe (P&O) under parameter variations. The MPPT controllers for a PV-grid connected system has been designed to achieve the optimum and fast maximum power point tracking by varying temperatures and solar irradiance values. Extensive simulation has been conducted to achieve enhanced efficient power extraction, grid synchronization and minimal performance loss due to dynamic tracking errors, particularly under fast-changing irradiation using Matlab/Simulink. The INC algorithm was proved to be robust as compared to the P&O algorithm. This is discussed in Section 3 and Section 4. The authors are not aware of any such investigation carried out in the literature as per their best knowledge.
• The complete PV grid-connected system has been designed with a boost converter (DC-DC) and voltage source inverter (DC-AC). The control of the voltage source converter is designed in such a way that PV power generated is synchronous to the grid. The duty ratio of boost converter-based power conditioning was controlled using the MPPT controllers. The system-level approach has been considered by providing a detailed analysis of the designed controller and other electronic component.

2. System Modelling

Matlab/Simulink is used for PV-grid simulation. Simulink is an extremely versatile platform for simulation. In this analysis, several Matlab/Simulink toolboxes were used to build different components and to study the PV device under various conditions. Simulation in Matlab provided modelling and variations in input parameters like temperature and irradiance to generate output power from the PV module.

2.1. System Description

An integral part of the power conditioning unit in the PV-grid is the DC-DC converter where the duty cycle is controlled by the MPPT controllers to generate the maximum power from the irradiance at that time and the DC to the AC converter connected with the voltage source control (VSC) as shown in Figure 2. For simulation, the PV array is connected to the DC to DC boost converter, which boosts the DC value and in turn, is connected to the DC-AC inverter with the 25 kV AC grid.

2.2. PV Array

MATLAB has a build-in PV array block, even though the modelling of PV arrays can be done using Simulink simple components. The built-in Simulink Sun Power-305E-WHT-D module is considered for the simulation, with each module able to produce a power of 305.2 Watts power. Hence, a PV block for an output power of 12.5 KW from the PV array under standard test conditions (STC) requires 45 solar modules with nine parallel string connection and five series string connection, so the average power obtained from the PV system is 5 × 9 × (maximum power obtained from each PV panel) 305.2 W = 13.7 kW at a temperature of 25 °C or STC. Series and parallel connection of strings layout is shown in Figure 3.

2.3. Boost Converter (DC-DC Converter)

The boost converter is used to increase the output voltage of the PV module. The duty cycle of the converter determines the output voltage. The state of the transistor determines the output of the converter. The Matlab modelled boost converter is shown in Figure 4. The duty ratio is given by 1/1 − d, which depends on the output to input voltage ratio. The converter is a power transmission medium for energy absorption from the solar panel and for injection into the DC-link. 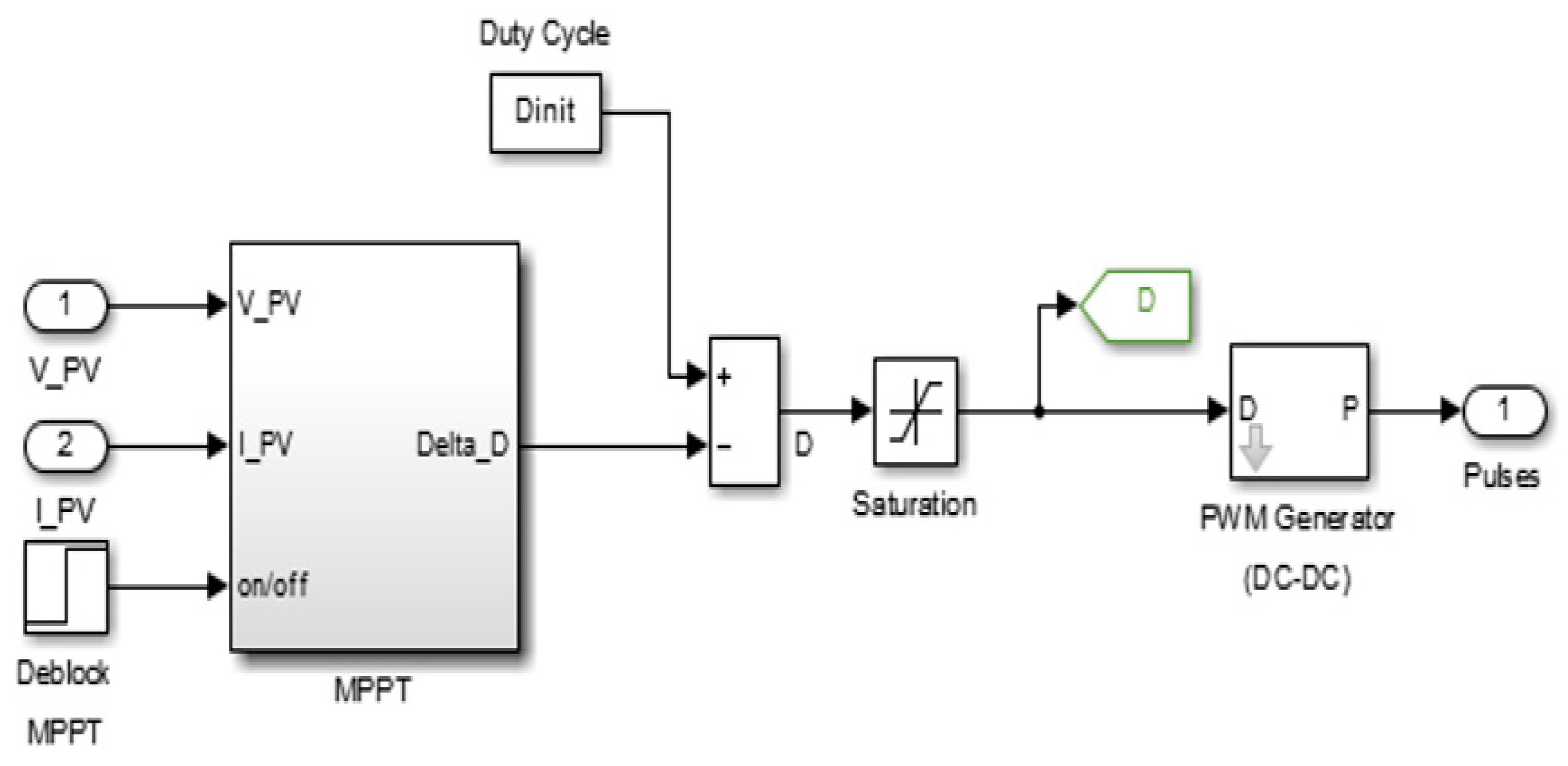Figure 5 shows the boost converter with MPPT controller to control the duty ratio of the DC-DC boost converter.

Proper switching frequency is considered to achieve less harmonics in output voltage. To determine minimum Inductor value denoted by L_min and minimum capacitance value is denoted by C_min for the converter and for continuous driving mode, the minimum, and maximum duty cycles can be obtained from Equations (1)–(4):

$$D_{\min }=1-\frac{V_{i\max }}{V_o}$$

(1)

$$D_{\max }=1-\frac{V_{i\min }}{V_o}$$

(2)

$$L_{\min }=\frac{2}{27}\times \frac{R{L}_{\max }}{f_s}$$

(3)

$$C_{\min }=\frac{D_{\max }{V}_0}{f_s{R}_{\min }{V}_r}$$

(4)

where V_r is the output voltage rip factor, V_imax and V_imin are the threshold values of the input voltage. Ripple element in the system is considered as 5% for designing the converter. The ratings selected for a PV side boost converter are 1 mH and 3500 μF depending on its minimum values of inductor and capacitor. These parameters apply to the simulation model, as in Figure 6. The duty cycle is varied from 0.71 to 0.5 and controlled the output of 600 volts to a constant DC output of at least 196 V to 250 V.

2.4. Maximum Power Point Tracking (MPPT)

Maximum power of PV is tracked with MPPT trackers, thus minimizing the size and number of the PV panels and maximizing the production of electricity. The energy that the PV panels can absorb is constant over time; variation in the irradiance angle of PV panels is caused due to the moving sun, which causes the change in the amount of irradiation in the panels. The I-V properties changes and the maximum power point (MPP) moves when this happens; hence a controlled outage with the same operation point and new conditions will most likely occur. MPPT has been developed to overcome this problem.

The output from the array varies with the intensity of incident sunlight, and for a given PV system, there is only one maximum power, and the technology used for tracking is MPPT algorithms. Most efficient and popular methods are perturbation and observation and incremental conductance strategies. The main feature of the P&O methodology is the comparison of current PV power with previous PV power. Maximum photovoltaic power is measured using a combination of current (I) and voltage (V). When the difference between the previous power and the current power is not 0, the purpose of this algorithm is to find an optimal position on the left or the right side of the last position. Maximum power is reached when ΔP is equal to 0 [9,10]. The P&O solution shall be applied to the buck-boost by changing the duty period of the PWM. When the current power is higher than the previous one, the duty period will be increased before the MPP has been established. The downside is that the steady-state oscillation is applied and the voltage deviation is large [11]. P&O approach has a long time of monitoring and a slow response to changes in irradiance and temperature.

2.4.1. Perturbation and Observation (P&O) Algorithm

The P&O algorithm is advantageous for simple software and hardware credit. The P&O algorithm perturbs the duty cycle of the power converter. The algorithm uses voltage and current measurements to calculate the change in power over the change in time (∆P) and the change in duty cycle (∆D) of the signal sent to the switch gate in the converter. Since ∆P and ∆D can be either positive or negative, there are four instances where the duty cycle of the gate signal will be increased or decreased. The flow chart for the Figure 7 clearly explains the P&O algorithm.

The P&O algorithm has a simple structure, low cost, ease of execution, reduced number of parameters, enhanced functionality, and may result in top-level performance. This algorithm depends on the relationship between the output power of the PV module and its voltage. The actions of the solar panel showing the MPP and the operating theory are shown in Figure 6 which implies that the resulting shift in PV power is observed as follows: when the PV operating point is on the left of the curve (ΔP/ΔV is positive), which implies the output power of the PV module is increased, the PV module voltage perturbation towards the MPP will be increased. If the module’s operating point was on the right side of the curve (ΔP/ΔV is negative), the PV module voltage perturbation should be reduced to the MPP.

Figure 7 displays the flowchart for the implementation of the P&O algorithm; first, the voltage and current from the PV array are calculated. The combination of voltage and current then gives the actual power of the PV module. Then, test the status as to whether ΔP = 0 or not. If this status is satisfied, the MPP will be the operating stage. If this is not sufficient, another status that is ΔP > 0 will be reviewed. When this status is fulfilled, the ΔV > 0 will be verified. If satisfied, it means that the operating point is on the left side of the MPP. When the ΔV > 0 condition is not achieved, it means that the operating point is on the right side of the MPP. The cycle is performed continuously until the MPP has been achieved. Therefore, there is often a balance between the fractions and the sampling rate in the P&O algorithm.

2.4.2. Incremental Conductance (INC) Algorithm

In the incremental conductivity method, the terminal voltage of the array is always adjusted according to the MPP voltage based on the incremental and instantaneous conductivity of the PV module. This algorithm was implemented in 1993 and was intended to fix some of the drawbacks of the P&O algorithm. The objective of INC is to increase monitoring time and generate more energy in a vast environment due to changes in irradiation [12]. The relationship between dI/dV and I/V is used to measure the MPP. If dP/dV is negative, MPPT will be on the right side of the new position, and if positive, the MPP will be on the left side. The IC-method equation is as follows:

$$\frac{\partial P}{\partial V}=\frac{\partial (VI)}{\partial V}=I\frac{\partial V}{\partial V}+V\frac{\partial I}{\partial V}=I+V\frac{\partial I}{\partial V}$$

(5)

MPP is reached when:

$$\frac{\partial P}{\partial V}=0$$

(6)

$$I+V\frac{\partial I}{\partial V}=0$$

(7)

Hence:

$$\frac{\partial I}{\partial V}=-\frac{I}{V}$$

(8)

$$\frac{\partial P}{\partial V}>0,V<Vmpp$$

(9)

$$\frac{\partial P}{\partial V}=0,V=Vmpp$$

(10)

$$\frac{\partial P}{\partial V}<0,V>Vmpp$$

(11)

The incremental conductivity flow chart is shown in Figure 8, MPP is shown on the right, dI/dV < −I/V, and then the PV voltage must be decreased to reach the MPP [13]. IC methods can be used to detect MPP, increase PV performance, reduce power losses and reduce device costs. The implementation of INC on a microcontroller resulted in more accurate performance than P&O [13]. Figure 9 demonstrates the incremental conductivity approach used in Simulink, where the controller output was optimized for the initial duty cycle, and the incremental conductivity algorithm was used.

Of the two methods, incremental conductivity measures more precisely than the P&O method and changes rapidly with the irradiation parameters. The oscillation around the MPP area can also be suppressed by the complexity of its implementation. Tracking time is still not quick because the increase and decrease of the voltage were chosen manually by trial and error.

MPPT used in this work is the gradual driving approach where the required variations are found in the current, voltage, instantaneous values of voltage and instantaneous values of current. The operation time is contrasted with a PWM producing triangle wave pulse. Therefore, the MPPT provides the control signal to the PWM generator, which provides a pulse to the boost converter hence controlling the duty ratio. This is applied to the simulation model in Figure 10, which controls a 600 V constant DC output range from a minimum of 196 V and a maximum of 250 V due to duty cycle variation of 0.71 to 0.5.

2.5. DC-AC Inverter

The inverter used for simulation is based on an insulated-gate bipolar transistor (IGBT). The conversion percentage determines the amount of DC converted to AC. The pulse width modulation (PWM) method for triggering the IGBT, thus convert DC to AC. Matlab/Simulink’s universal bridge was used as a 3-level IGBT in this project is in Figure 11.

The inverter of the proposed model is connected to the common DC connection. The interface mechanism of the DC bus and the three-stage AC grid, followed by the L filter, transfer electricity into the power supply grid. In the following equation, the value of the connecting DC tension and the grid line voltage is related in Equation (12). The grid management control option is meant to control both reactive and active power injected into the grid. Primary parameters for control are V_dc, V_abc grid voltage, I_abc grid current, and V_{dc_ref} is a DC-link voltage reference:

$$0.612m_a{V}_{dc}\ge \overline{){(V_{ac})}_{}^2+3\omega {(f{I}_{ac})}_{}^2)}$$

(12)

VSC converters are capable of controlling both reactive and active power separately. In the case of a renewable energy network as a PV system, the active power reference is changed to control the DC bus voltage in order to maintain the power balance. As a consequence, the energy pumped into the grid will be the same as the power produced.

The control system for the converter is shown in Figure 12. It’s based on a two-level cascaded control system. The inner level controller regulates the AC current in the reference current loop while the outer level controller regulates the DC bus voltage in the reference voltage loop.

Various controllers deal with current and voltages in the qd₀ rotating two-axis reference frame to change the electrical grid angle. As a result, a phase locked loop (PLL) is needed to monitor the grid angle.

IGBT turns on and off time at the inverter gate control signals. The inverter control loop produces these signals. The configuration of the inverter control consists of the following.

• Phase-locked loop (PLL): A phase-locked loop (PLL) is used to determine the frequency and phase of the grid in which the system is connected.
• DC voltage control loop: The voltage loop is used for DC bus voltage control and to ensure the power balance between PV and grid-injected power.
• Current control loop: Is programmed to evaluate the voltages to be used by the VSC to ensure that the currents flowing through the converter are the same as the voltages provided by the controller.
• Voltage Modulation: voltages computed from the current loop in the dq₀ reference frame are converted into the abc reference frame with the anti-park transformation block and are directly inserted into the regulated voltage sources modelled on the AC converter side.

The control system is made up of the voltage control unit and the current control unit. The control system output signal used as input for the PWM signal generator to control the grid end converter by the pulse. The grid voltage is calibrated for the correct voltage for each sampling period Vdc, and Vdc ref is compared to each sample. When modelling the PI controller for the voltage and current, Equations (13)–(16) are used.

$$V_{d{c}_{-}error}=V_{d{c}_{-}ref}-V_{dc}$$

(13)

$$I_{d_{-}ref}=K_p-V_{dc}(V_{d{c}_{-}error})+K_i-V_{dc}{\displaystyle \int (V_{d{c}_{-}error})dt}$$

(14)

$$I_{q_{-}ref}=0$$

(15)

$$I_{d_{-}error}=I_{d_{-}ref}-I_d$$

(16)

$${V^{\prime }}_d=V_d[K_p-CR(I_{d_{-}error})+K_i-CR{\displaystyle \int (I_{d_{-}error})dt]+L{I}_q}$$

(17)

$$I_{q_{-}error}=I_{q_{-}ref}-I_q$$

(18)

$${V^{\prime }}_q=-[K_p-CR(I_{q_{-}error})+K_i-CR{\displaystyle \int (I_{q_{-}error})dt]+L{I}_d}$$

(19)

where V_dc is DC-link tension, V_dc-ref, is DC-link tension of reference, and V_dc-error is DC-link tension error. The current components of I_dref, I_qref, is referencing d and q axis components. The proportional and integrated PI controller constant is K_{p_vdc}, K_{i_vdc}. For the development of the current regulator, Equations (17)–(19) are used. The current regulators PI controller K_{p_cr}, K_{i_cr} are 0.3 and 20 for V_d and V_q, respectively. For the three-phase grid current I_{abc_grid}, the d and q current components are the Id and the I_q, respectively. The control voltage V_{control_grid} used for PWM generation is obtained by applying a transformation to provide V_d and V_q.

The controller of the inverter is constructed, as shown in Figure 13, is grid-connected, which operates at grid voltage and frequency of the grid. At the transformer’s side, ABC coordination is used to measure current and voltage and pass by a step-by-step lock loop. This transformation is called an asynchronous framework, from the abc frame to dq frame transformation, and three-phased parameters are converted into two-phase parameters. The PLL is the phase angle. 3-stage VSC transforms the 500 V DC into 260 V AC in the simulation. A 10 KVAR condenser bank filter is used to minimize the harmonics generated by this VSC.

2.5.1. The Phase-Locked Loop (PLL) and the dq₀ Transformer

Converting the signals to the dq₀ frame gives accurate control. This inverter control portion converts voltage and currents to per-circuit values. PLL picks up the grid voltage and determines its frequency and angle. It plays an important role in equalizing the output and grid angles of the inverters. The dq₀ transformer converts the reference frame from three-phase voltages and currents from abc to dq₀.

PLL is shown in Figure 14 and is used to synchronize the inverter designed with the Grid Line. The PLL control reduces the difference in phase angle between the inverter voltage (V_inv) and the grid voltage (V_grid) to 0. By sensing grid voltage in a phase-locked loop, accurate synchronization control can be performed to demonstrate noise relative to the grid. The current angle of the grid voltage is the PLL output. Through managing δ, the actual and reactive power flux to the gridline can be obtained:

$$\begin{gathered} P=\frac{V_{inv}{V}_{grid}}{X_L}\sin \delta \\ Q=\frac{V_{inv}}{X_L}(V_{inv}-V_g\cos \delta ) \end{gathered}$$

(20)

Equation (20) shows the reactive and active power of the system. Here X_L is the impedance associated with the impedance and impedance of the transformer leakage, device reliability, and control efficiency are the main issues of the hybrid operation system. These issues can be significantly removed for the grid-connected option by improving the inverter pulse control and Synchronization process.

2.5.2. DC Voltage Control Loop

This loop controls the DC voltage at the inverter input and is also used to increase noise immunity ability of inverter. The gains from the PI controller were selected using Equations (21) and (22). The modelling and derivation of Equations (21) and (22) are similar to the referenced ones [24]. The other assumed parameters such as boost converter capacitor and switching frequency values are 3500 μF, and 4.5 kHz, respectively. Where Kp and K_I are the proportional and integral gains of the PI controller, and Ts is the switching time of the inverter switches, and it is 22 ms. The MATLAB auto-tuning function was used to tune proportional and integral gains, and the values were 2.3625 and 532.125 respectively. The other assumptions such as nonlinearities attached with the switches. Also, the resistance of inductor and capacitors were ignored and treated as ideal. Figure 15 shows how the DC link-controlled voltage block to obtain the voltage stable, voltage control, which have K_p value 7 and K_i value 800 of PI controller, regulate the inverter output voltage with the grid voltage:

$$K_p{}_{}=\frac{3C}{20T_s}$$

(21)

$$K_l=\frac{K_p}{20T_s}$$

(22)

2.5.3. Current Control Loop

This loop regulates the value of current in the dq₀ reference frame. The loop is shown in Figure 16.

2.6. Voltage Modulation

The VSC converter can use the referenced voltages by modulating them with pulse width modulation (PWM). Modulation determines IGBT switching cycle. Sinusoidal pulse width modulation (SPWM) is one of the simplest methods used to incorporate PWM.

SPWM distinguishes two signals: desired signal or a modulating signal, and a triangular signal considered as a carrier signal. The comparison of the two signals results in a square waveform signal containing a replica of the desired signal (Figure 17). The IGBT switching frequency will be the carrier signal frequency. This technique enables easy signal filtering with good results. Higher carrier frequency allows more accurate switching, but often implies a greater number of changes per cycle and thus increased power loss.

There are two parameters which have to be considered when designing the SPWM, the modulation index and the carrier is shown in Equation (23), and the relationship between the frequency of the modulation signal and the carrier is shown in Equation (24) [14]:

$$m=\frac{A_m}{A_C}\le 1$$

(23)

$$n=\frac{f_m}{f_c}=3k(k\in N)$$

(24)

It also regulates the amplitude of the applied output voltage by adjusting the modulation index. An index of modulation greater than one means overmodulation. Usually, switching frequencies within the range of 215 kHz are considered sufficient for power system applications [14].

3. Simulation Result

Electrical demand is increasingly growing, and renewable energy sources are crucial for the maintenance of the electrical grid and for the supply of isolated loads. This paper presents a simulation-based comparative analysis of the two most popular algorithms, perturb and observation and incremental conductivity techniques, to improve the energy conversion efficiency of the PV method. Simulation analysis and results of the PV module shall be conducted in order to obtain its characteristics.

The complete PV-grid system simulation is shown in Figure 18, with a total of 13.7 KW power with 45 solar modules under STC. The system has 9 parallel strings with five series strings of PV array.

3.1. Solar PV Array Characteristics

The irradiance and temperature of the system are varied for analysis of the system. Initially, irradiance is set at a value of 1000 W/m² when time = 0.6 s for the simulation. Then irradiance is decreased from thousand to two hundred and fifty (250 w/m²) from time = 0.6 to 1.1 s, from time t = 1.2 to 1.6 s, irradiance value is increased to 1000 w/m² and to study the effect of temperature in PV array the temperature is raised from 25 °C to 50 °C as shown in Figure 19.

The study of PV output voltage vs. current characteristics simulated for various irradiance is shown in Figure 20. The graphs show the behaviour of output current of the PV module is linear to the amount of irradiance.

The irradiance also has an impact on voltage vs. power of the PV module. It also varies with irradiance, as shown in Figure 21. The decrease in the amount of irradiance will reduce the overall performance.

Similarly, its analysis based on the temperature impacts on the PV array shown in Figure 22 and Figure 23. Temperature affects the voltage on the PV array. Temperature rise reduces the performance of PV panels.

3.2. PV Side Result Simulation for the P&O Algorithm and INC Algorithm

The simulation starts at t = 0 when irradiance is 1000 W/m², and the temperature is 25 °C as the irradiance 1000 W/m² is the systems maximum irradiance here the maximum output power 13.7 kW will be extracted from PV array. From t = 0.6 s, the solar irradiance reduces to 250; hence the incident solar energy reduces, and the output power reduces from 13.7 KW. Therefore, irradiance is directly proportional to power generated; hence reducing irradiance will reduce the performance of the system. The change in temperature also has a significant impact on the output voltage and output current from the PV array. The graphs clearly show the increase in temperature decreases the performance of the PV panels.

Figure 24a–d show the simulation results of P&O at the PV side and Figure 25a–d show the simulation results of INC at the PV side. The result shows the irradiance pattern applied to the PV module, the current and the voltage characteristics of the PV module and the active power output of the PV module, respectively.

3.3. Simulation Results of P&O and INC Algorithm at Grid Side

Figure 26a–e illustrates the simulation using P&O model on the grid side. Figure 27a–e illustrates the simulation using INC model on the grid side. This shows that the d-axis current component, the q-axis current component, active and reactive power on the grid side, the DC voltage input to the inverter and, injected PV voltage and current waveforms to the grid at the point of contact is in phase, respectively.

4. Comparison between P&O and INC MPPT Algorithms

The P&O and INC MPPT algorithms are simulated and compared using the same conditions. When atmospheric conditions are constant or change slowly, the P&O MPPT oscillates close to MPP, but INC finds the MPP accurately at changing atmospheric conditions also. Simulation tests with MATLAB/Simulink display PV and grid side output with varying time and irradiance. The INC algorithm tracks rapidly changing irradiation conditions more precisely than the P&O process. In P&O system, the voltage does not exceed the exact value but perturbs MPP value. Figure 25d and Figure 26d clearly demonstrate that the INC solution to the MPP is quicker and better than the P&O due to the lack of a drifting problem and was the most effective under rapidly changing conditions.

5. Conclusions

In order to improve the conventional system due to fast-changing irradiation, this paper suggested an improved MPPT controller without measuring the produced PV array capacity. The robust tracking capability of gradually rising and declining irradiance was demonstrated in simulation. The proposed MPPT allows the decoupling of the power shift caused by the simultaneous increase in disruption and variance in irradiation.

The output power losses caused by dynamic tracking errors are dramatically reduced, especially under fast-changing irradiation. The irradiation difference is calculated by an error in the PI DC voltage controller signal. The PI regulator is designed to ensure zero signal error when the ambient conditions are constant. The error of the signal, therefore, is just the difference in power induced by the variance of the irradiation. Previously, the d-axis grid current component is used to measure the total power shift in the PV array. The d-axis grid current component is then used to measure the overall shift in the power of the PV array. The feasibility of an engineered PV network capable of providing sufficient constant power to various AC loads with various environmental constraints, such as irradiance and temperature, has therefore been studied.

6. Future Prospects

In the process, it has been developed that the system can be made more effective by using the battery storage system parallel to the PV system to help produce more constant power and that the complexity of the system design compared to the stand-alone grid-connected system. The PV system with a battery storage system (BESS) can be tested for different environmental scenarios in the future.

Since the output power of the stand-alone PV system fluctuates due to various factors, or the provided power is insufficient to supply the load, and if the constant load power of the BESS system can be obtained by discharging the necessary amount of power from the battery.

In the stand-alone system, the excess power is fed to the dump load instead of being stored in the battery and used when the power demand is high and cannot be met by the power generated by the PV alone, so the excess power is absorbed in the BESS system.

The environmental conditions needed to be improved in this work have been quite elaborated; future work will involve more realistic irradiance and temperature predictions on the PV panel.