Max–Min Fairness Optimization for D2D Communications Coexisting with Cellular Networks
Abstract
:1. Introduction
- We formulate a max-min fairness optimization problem, which aims at providing a uniformly good QoS to everyone in the network where both cellular users and D2D users coexist, subject to the limited power budgets. In particular, a number of NOMA-based D2D device groups are allowed to reuse the bandwidth from that dedicated to the cellular users, which is controlled by a base station (BS). For a given QoS level, we then transfer the max–min fairness optimization problem into a minimum total transmit power consumption problem under the QoS requirements and the power constraints.
- We observe the quasilinear convexity of the proposed max-min fairness optimization problem and utilize the bisection method to obtain the global optimum. We rigorously find an upper bound on the QoSs that the system can provide to the cellular users and D2D devices. This upper bound offers a reduction of the computational complexity and also confirms that the proposed algorithm can be implemented in polynomial time. Our proposed algorithm balances between maximizing the worst spectral efficiency performance and minimizing the total transmit power consumption.
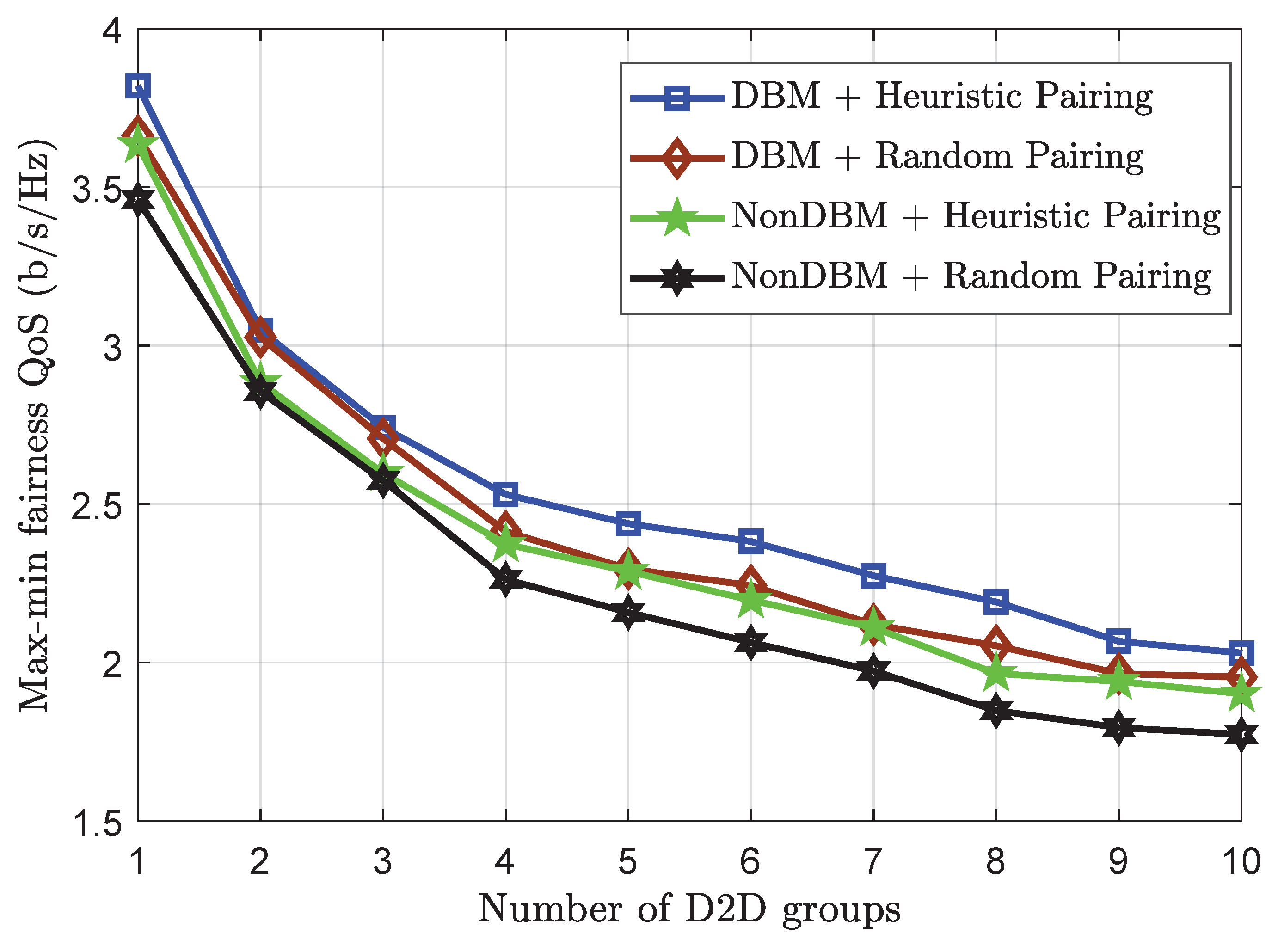
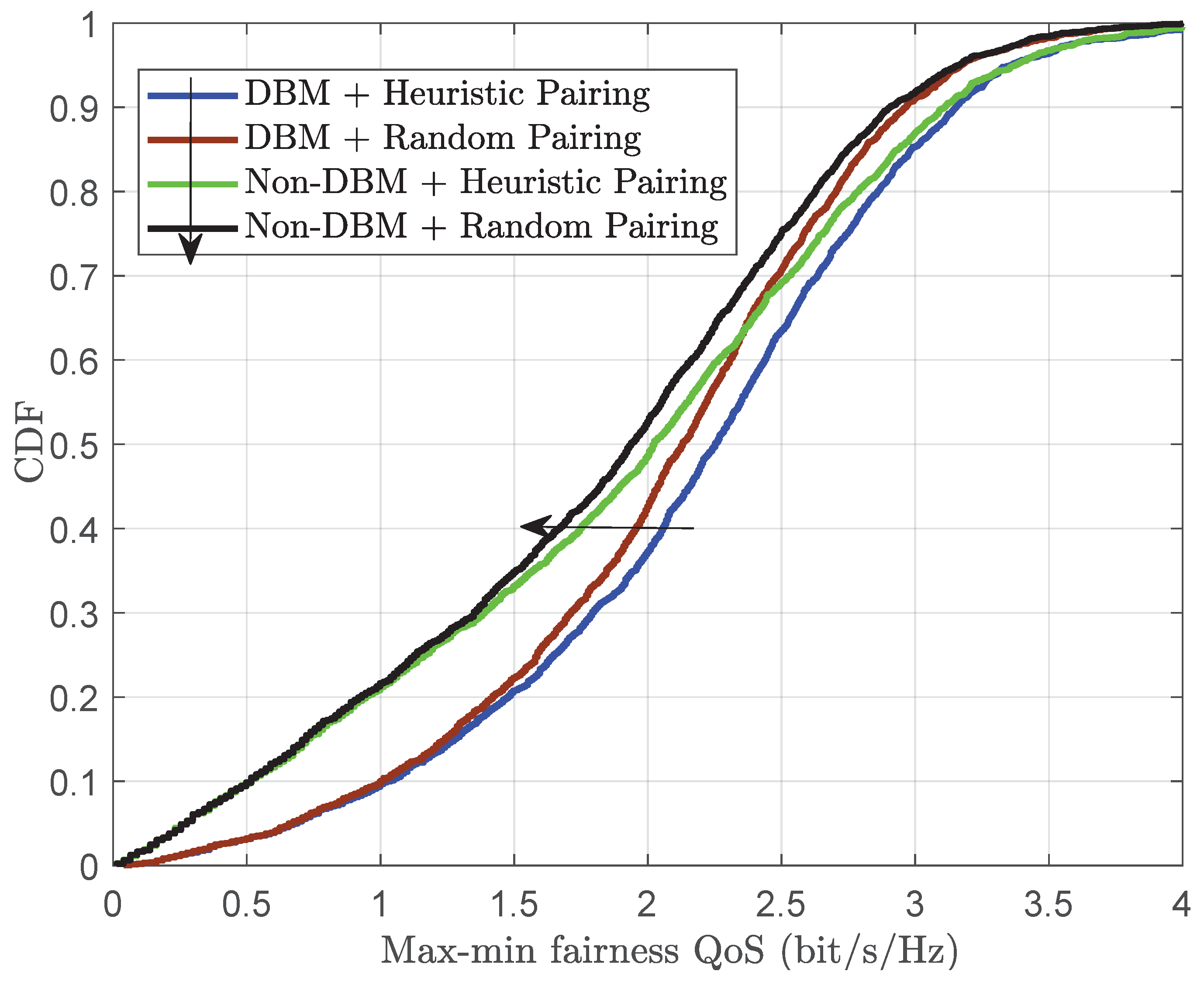
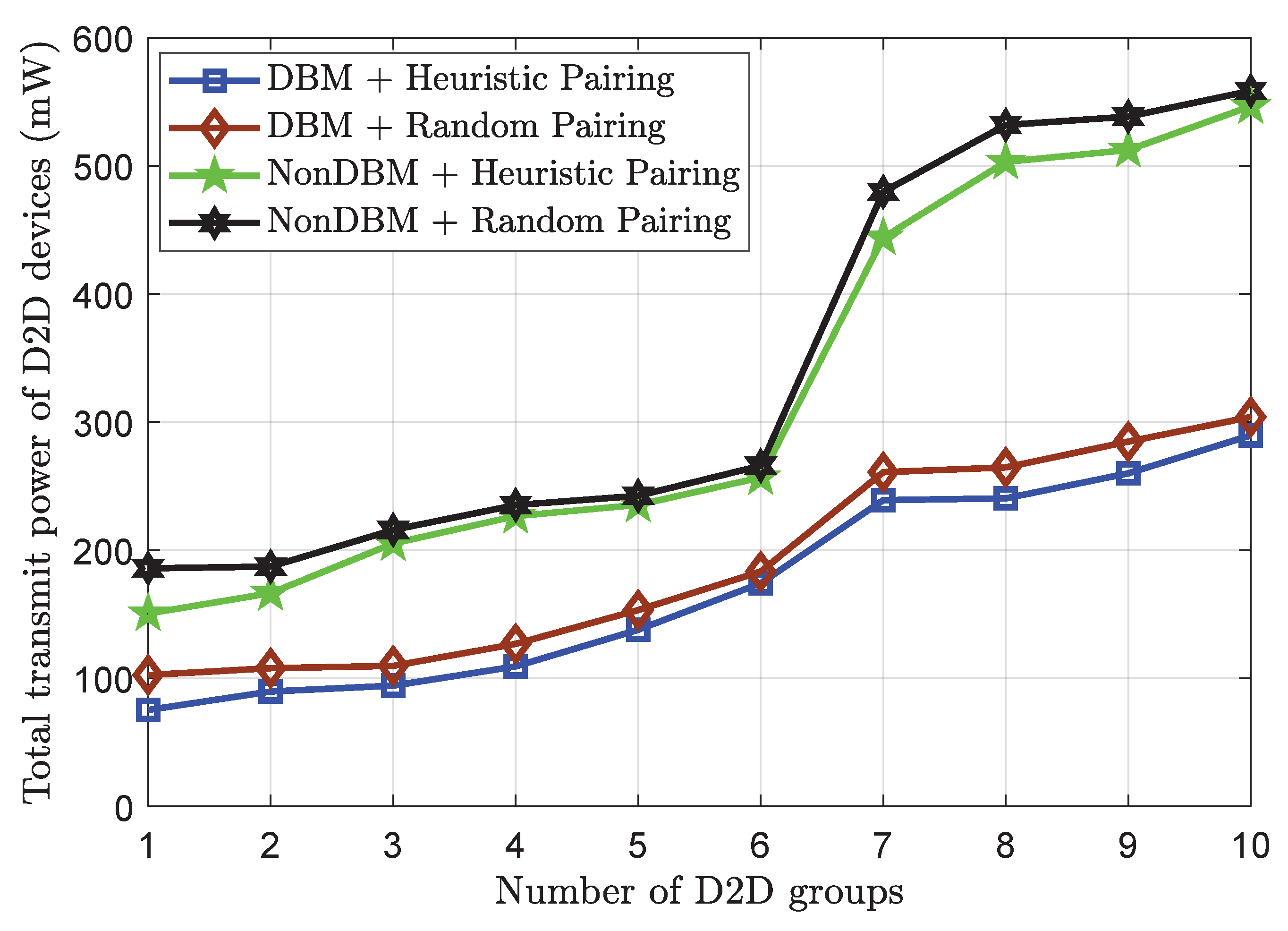
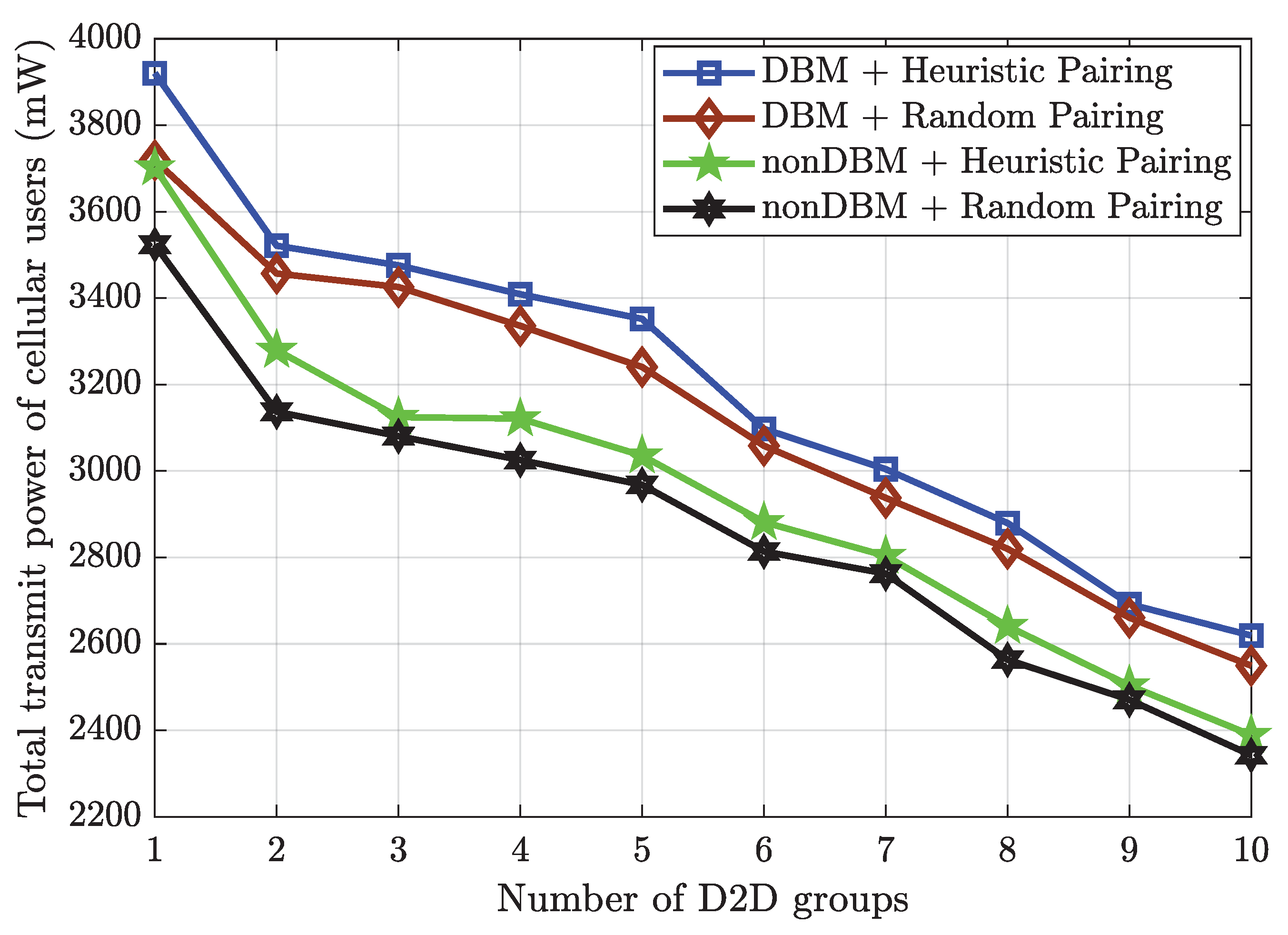
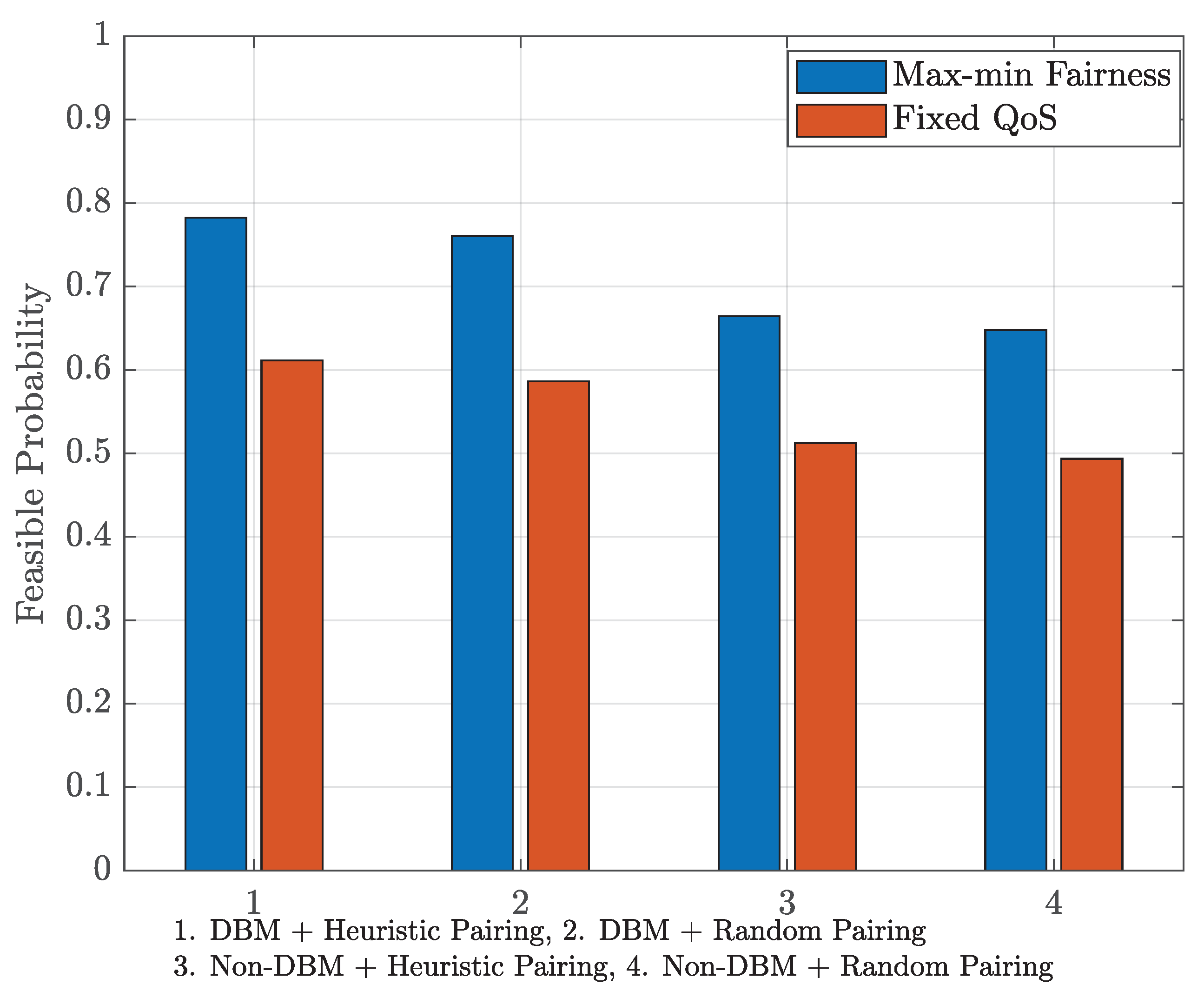
- The numerical results demonstrate the effectiveness of the proposed optimization framework in providing equally good QoS to all cellular users and D2D devices under the different subchannel assignments (either random assignment or a heuristic assignment that minimizes the mutual interference between cellular users and D2D devices), pairing techniques (either random paring or a heuristic pairing that reduces the total transmit power), and channel conditions.
2. System Model and Performance Analysis
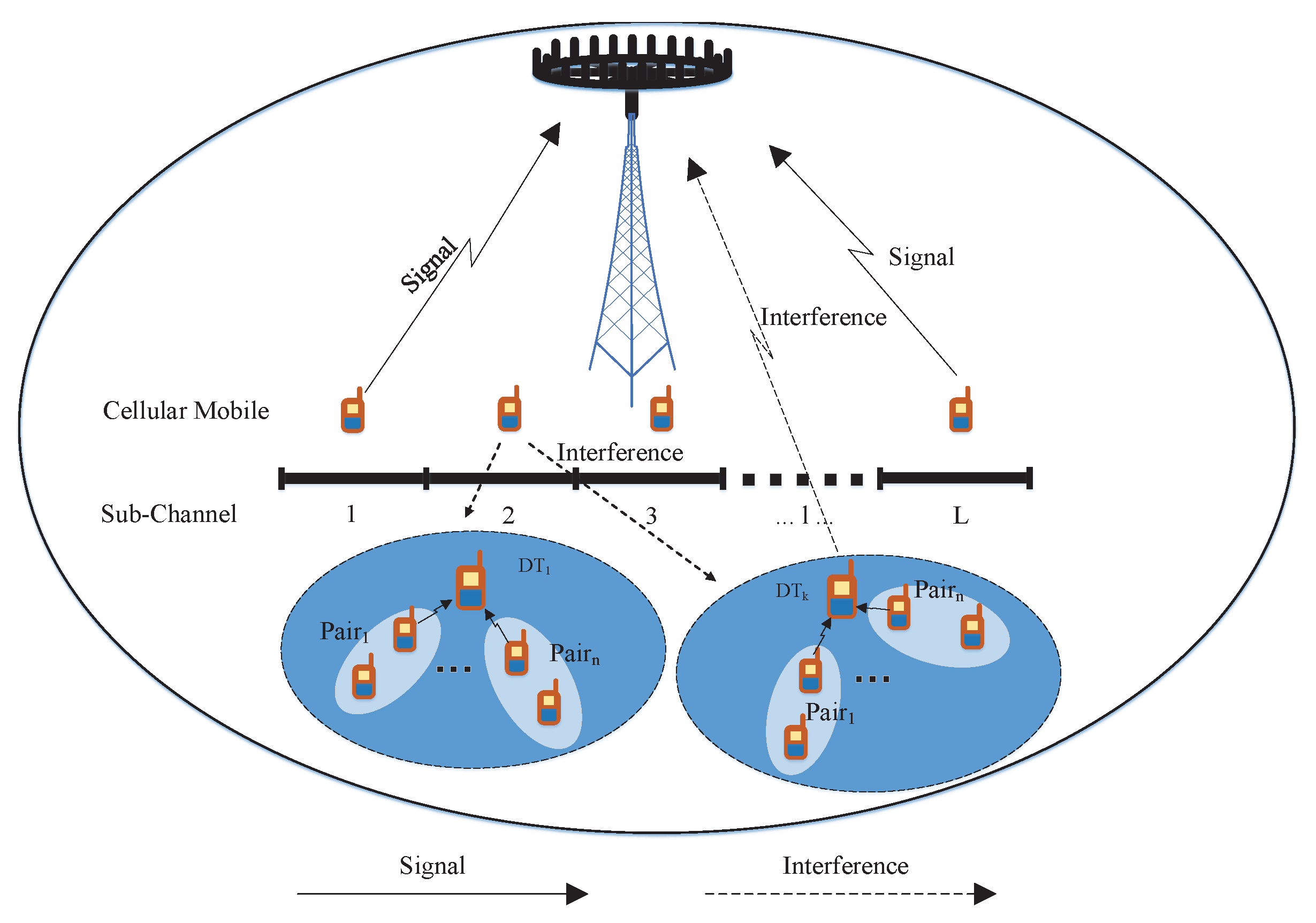
2.1. System Model and Assumptions
2.2. Channel Model
2.3. Channel Capacity of D2D Devices and Cellular Users
2.3.1. Uplink Cellular Network Transmission
2.3.2. Downlink D2D Transmission
3. Max–Min QoS Optimization
| Algorithm 1: Max–min quality of service (QoS) based on the bisection method. |
| 1Result: solve the optimization in (33). Input: Initial upper bound and line-search accuracy ; 2 Set ; ; 3 Calculate: 4 while do  13 Set and ; Output: Final interval and ; 14 final; |
4. Numerical Results
- (1)
- The diversity-based method (DBM) combined with heuristic pairing (denoted DBM + Heuristic Pairing in the figures): All cellular users have already been assigned to the subchannels. Subsequently, these subchannels are allocated to the D2D devices via channel diversity. In each D2D group, the devices are paired by the heuristic algorithm.
- (2)
- The DBM using random pairing (denoted DBM + Random Pairing in the figures): the system utilizes the heuristic algorithm to allocate the subchannels for the D2D groups; however, the devices in each group are paired randomly.
- (3)
- The random channel assignment using heuristic pairing (denoted NonDBM + Heuristic Pairing in the figures): the D2D groups are assigned randomly to the subchannels, and the devices in each group are paired by the heuristic algorithm.
- (4)
- The random channel assignment using heuristic pairing (denoted NonDBM + Random Pairing in the figures): the D2D groups are assigned randomly into subchannels, and the devices in each group are paired randomly.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jung, W.S.; Tu, L.T.; Van Chien, T.; Yoo, D.; Ro, S. Performance Analysis and Optimization of the Coverage Probability in Dual Hop LoRa Networks With Different Fading Channels. IEEE Access 2020, 8, 107087–107102. [Google Scholar] [CrossRef]
- Van Chien, T.; Canh, T.N.; Björnson, E.; Larsson, E.G. Power Control in Cellular Massive MIMO with Varying User Activity: A Deep Learning Solution. IEEE Trans. Wirel. Commun. 2020. [Google Scholar] [CrossRef]
- Zhu, L.; Xiao, Z.; Xia, X.; Oliver Wu, D. Millimeter-Wave Communications With Non-Orthogonal Multiple Access for B5G/6G. IEEE Access 2019, 7, 116123–116132. [Google Scholar] [CrossRef]
- Doppler, K.; Rinne, M.; Wijting, C.; Ribeiro, C.B.; Hugl, K. Device-to-Device Communication as an Underlay to LTE-advanced Networks. IEEE Commun. Mag. 2009, 47, 42–49. [Google Scholar] [CrossRef]
- Elouafadi, R.; Benjillali, M. Cooperative NOMA-based D2D Communications: A Survey in the 5G/IoT Context. In Proceedings of the 2018 19th IEEE Mediterranean Electrotechnical Conference (MELECON), Marrakech, Morocco, 2–8 May 2018; pp. 132–137. [Google Scholar]
- Lin, X.; Andrews, J.G.; Ghosh, A. Spectrum Sharing for Device-to-Device Communication in Cellular Networks. IEEE Trans. Wirel. Commun. 2014, 13, 6727–6740. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef] [Green Version]
- Van Chien, T.; Björnson, E.; Larsson, E.G. Joint Power Allocation and Load Balancing Optimization for Energy-Efficient Cell-Free Massive MIMO Networks. arXiv 2002, arXiv:2002.01504. [Google Scholar]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef] [Green Version]
- Yoon, T.; Nguyen, T.H.; Nguyen, X.T.; Yoo, D.; Jang, B. Resource Allocation for NOMA-based D2D Systems Coexisting with Cellular Networks. IEEE Access 2018, 6, 66293–66304. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 349–355. [Google Scholar] [CrossRef]
- Van Chien, T.; Dinh, K.Q.; Jeon, B.; Burger, M. Block Compressive Sensing of Image and Video with Nonlocal Lagrangian Multiplier and Patch-based Sparse Representation. Signal Process. Image Commun. 2017, 54, 93–106. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Chen, W.; Ng, D.W.K.; Schober, R. Spectral and Energy-Efficient Wireless Powered IoT Networks: NOMA or TDMA? IEEE Trans. Veh. Technol. 2018, 67, 6663–6667. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-Lin, I.; Wang, Z. Non-orthogonal Multiple Access for 5G: Solutions, Challenges, Opportunities, and Future Research Trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Z.; Fan, P.; Karagiannidis, G.K. On the Performance of Non-orthogonal Multiple Access Systems with Partial Channel Information. IEEE Trans. Commun. 2015, 64, 654–667. [Google Scholar] [CrossRef]
- Do, D.T.; Le, C.B. Application of NOMA in Wireless System with Wireless Power Transfer Scheme: Outage and Ergodic Capacity Performance Analysis. Sensors 2018, 18, 3501. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Truong, A.Q.; Nguyen, T.H. Power Control for Sum Spectral Efficiency Optimization in MIMO-NOMA Systems With Linear Beamforming. IEEE Access 2019, 7, 10593–10605. [Google Scholar] [CrossRef]
- Ali, M.S.; Tabassum, H.; Hossain, E. Dynamic User Clustering and Power Allocation for Uplink and Downlink Non-Orthogonal Multiple Access (NOMA) Systems. IEEE Access 2016, 4, 6325–6343. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Zeng, M.; Dobre, O.A.; Kwak, K. Resource Allocation for Downlink NOMA Systems: Key Techniques and Open Issues. IEEE Trans. Commun. 2018, 25, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Gau, R.H.; Chiu, H.T.; Liao, C.H. A Geometric Approach for Optimal Power Control and Relay Selection in NOMA Wireless Relay Networks. IEEE Trans. Commun. 2020, 68, 2032–2047. [Google Scholar] [CrossRef]
- Yoo, T.; Goldsmith, A. Capacity and power allocation for fading MIMO channels with channel estimation error. IEEE Trans. Inf. Theory 2006, 52, 2203–2214. [Google Scholar]
- Nguyen, B.C.; Hoang, T.M.; Tran, P.T.; Nguyen, T.N. Outage probability of NOMA system with wireless power transfer at source and full-duplex relay. AEU Int. J. Electron. Commun. 2020, 116, 152957. [Google Scholar] [CrossRef]
- Wei, Z.; Ng, D.W.K.; Yuan, J. Power-Efficient Resource Allocation for MC-NOMA with Statistical Channel State Information. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–7. [Google Scholar]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M. Joint subchannel and power allocation for NOMA enhanced D2D communications. IEEE Trans. Commun. 2017, 65, 5081–5094. [Google Scholar] [CrossRef]
- Zhang, Z.; Qu, H.; Wang, W.; Luan, Z.; Zhao, J. Joint User Association and Power Allocation for Max-Min Fairness in Downlink Multicell NOMA Networks. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 941–946. [Google Scholar]
- Kim, J.B.; Lee, I.H.; Lee, J. Capacity Scaling for D2D Aided Cooperative Relaying Systems Using NOMA. IEEE Wirel. Commun. Lett. 2017, 7, 42–45. [Google Scholar] [CrossRef]
- Kang, J.M.; Kim, I.M. Optimal user grouping for downlink NOMA. IEEE Wirel. Commun. Lett. 2018, 7, 724–727. [Google Scholar] [CrossRef]
- Su, N.; Zhu, Q.; Wang, Y. Resource Allocation Algorithm for NOMA-Enhanced D2D Communications with Energy Harvesting. Mob. Inf. Syst. 2020, 2020, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Van Chien, T.; Mollén, C.; Björnson, E. Large-Scale-Fading Decoding in Cellular Massive MIMO Systems with Spatially Correlated Channels. IEEE Trans. Wirel. Commun. 2019, 67, 2746–2762. [Google Scholar] [CrossRef] [Green Version]
- Andrade, C.B.; Hoefel, R.P.F. IEEE 802.11 WLANs: A Comparison on Indoor Coverage Models. In Proceedings of the Canadian Conference on Electrical and Computer Engineering (CCECE), Calgary, AB, Canada, 2–5 May 2010; pp. 1–6. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Van Chien, T.; Björnson, E.; Larsson, E.G. Joint Pilot Design and Uplink Power Allocation in Multi-cell Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2018, 17, 2000–2015. [Google Scholar] [CrossRef] [Green Version]
- CVX Research Inc. CVX: Matlab Software for Disciplined Convex Programming, Academic Users. 2015. Available online: http://cvxr.com/cvx (accessed on 24 June 2020).
- Chien, T.V.; Björnson, E.; Larsson, E.G. Joint Power Allocation and User Association Optimization for Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2016, 15, 6384–6399. [Google Scholar] [CrossRef] [Green Version]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
| Cellular radius | 250 (m) |
| Base station height | 6 (m) |
| Beamforming technology | Maximum Ratio Combining (MRC) |
| D2D group radius | 10 (m) |
| Device and cellular user height | 1.5 (m) |
| Operating frequency | 1.9 (GHz) |
| Maximum transmit power of devices and cellular users | 23 (dBm) |
| Noise power | −96 (dBm) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.G.; Nguyen, X.T.; Nguyen, V.S.; Chien, T.V.; Nguyen, T.H.; Ro, S. Max–Min Fairness Optimization for D2D Communications Coexisting with Cellular Networks. Electronics 2020, 9, 1422. https://doi.org/10.3390/electronics9091422
Nguyen HG, Nguyen XT, Nguyen VS, Chien TV, Nguyen TH, Ro S. Max–Min Fairness Optimization for D2D Communications Coexisting with Cellular Networks. Electronics. 2020; 9(9):1422. https://doi.org/10.3390/electronics9091422
Chicago/Turabian StyleNguyen, Hoai Giang, Xuan Tung Nguyen, Van Son Nguyen, Trinh Van Chien, Tien Hoa Nguyen, and Soonghwan Ro. 2020. "Max–Min Fairness Optimization for D2D Communications Coexisting with Cellular Networks" Electronics 9, no. 9: 1422. https://doi.org/10.3390/electronics9091422
APA StyleNguyen, H. G., Nguyen, X. T., Nguyen, V. S., Chien, T. V., Nguyen, T. H., & Ro, S. (2020). Max–Min Fairness Optimization for D2D Communications Coexisting with Cellular Networks. Electronics, 9(9), 1422. https://doi.org/10.3390/electronics9091422






