Meminductor Emulator Based on a Modified Antoniou’s Gyrator Circuit
Abstract
:1. Introduction
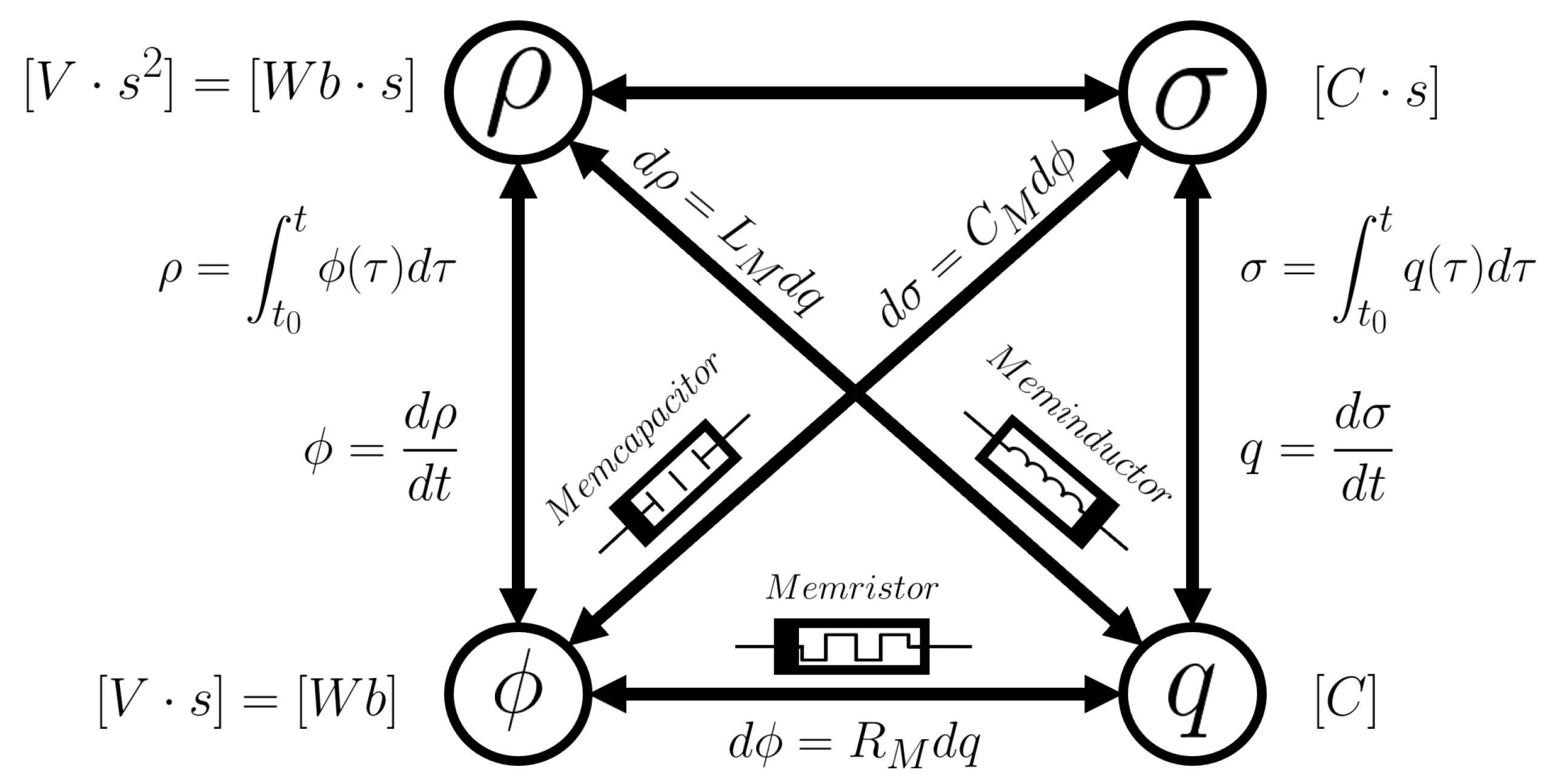
2. Meminductance and Antoniou’s Circuit
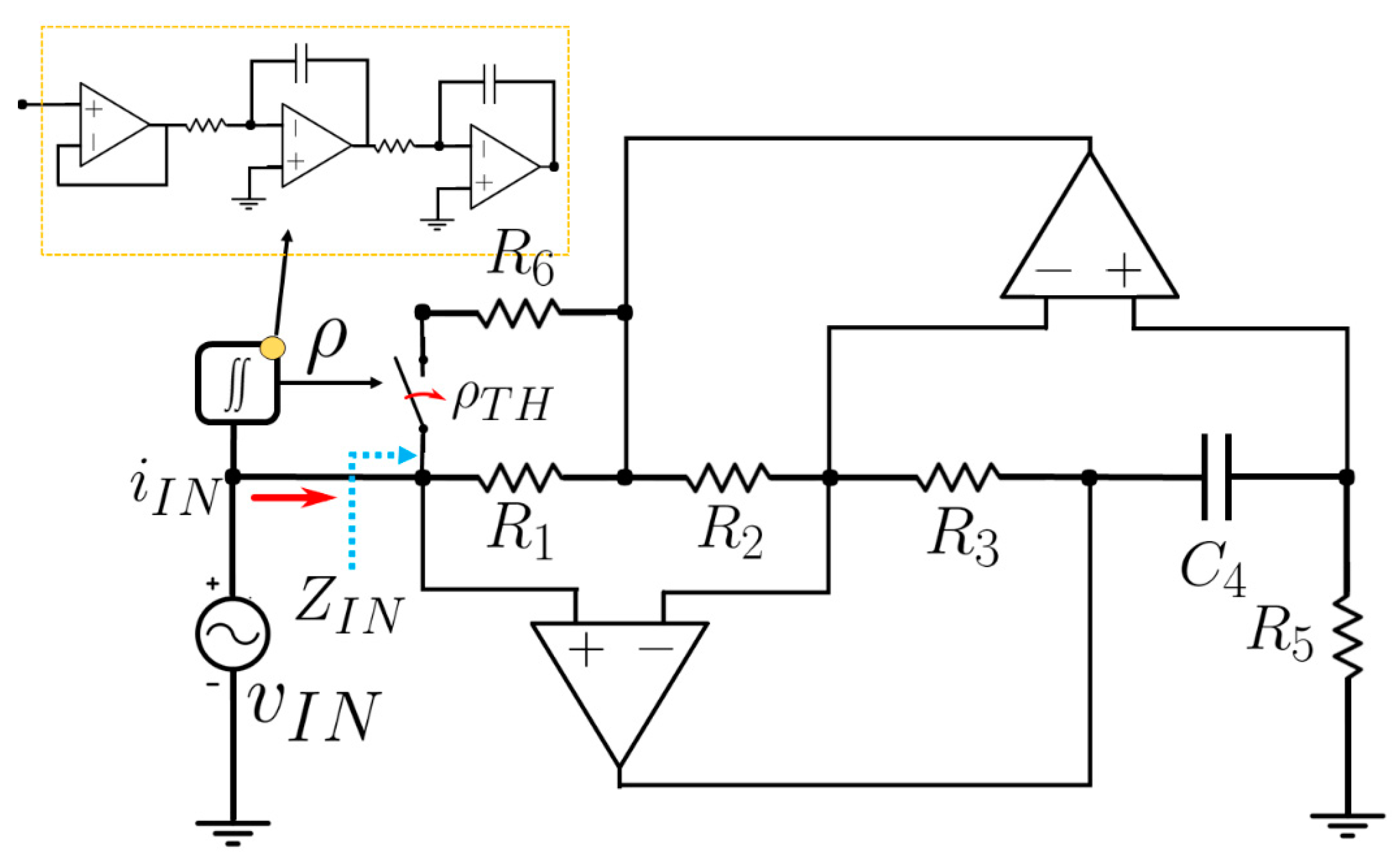
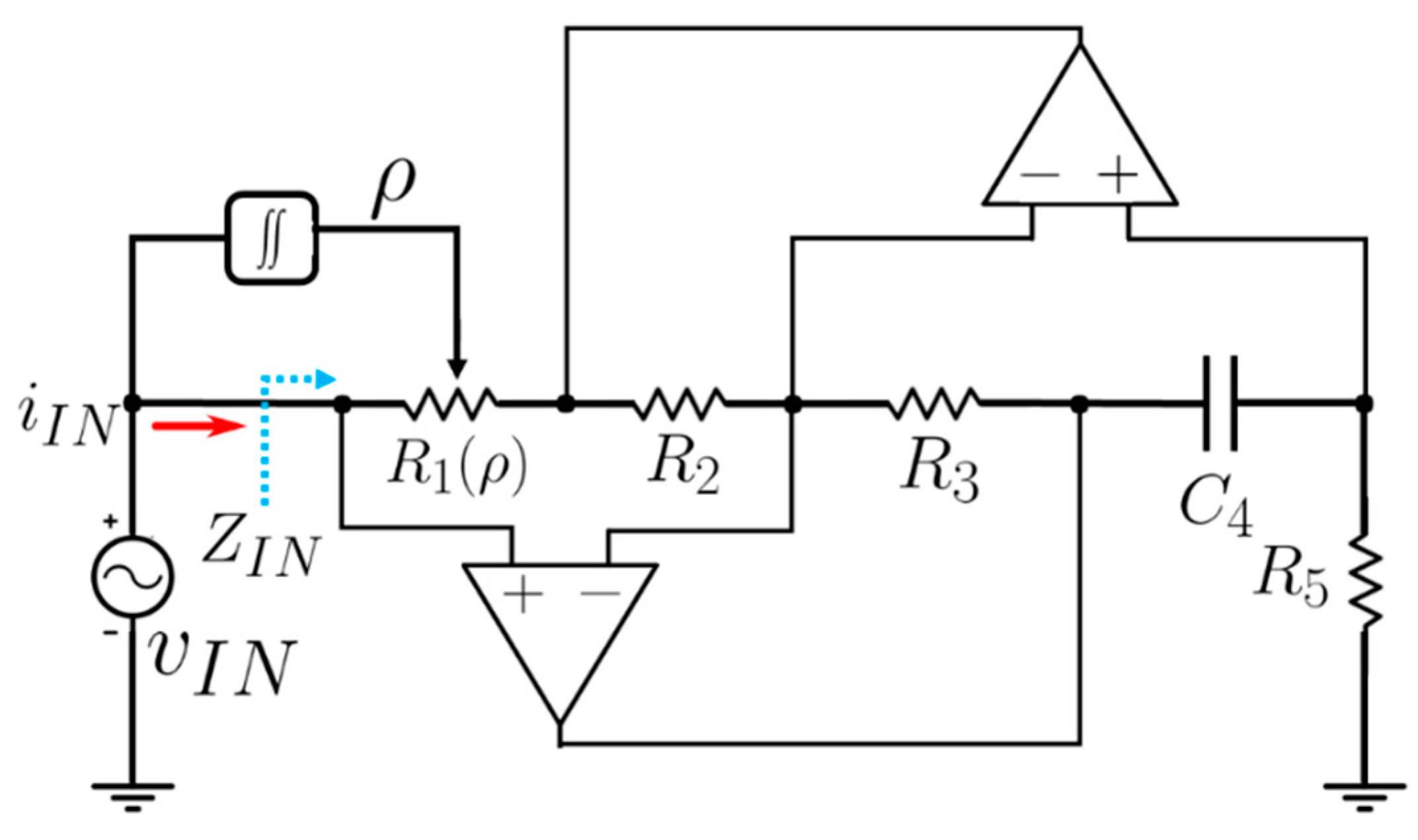
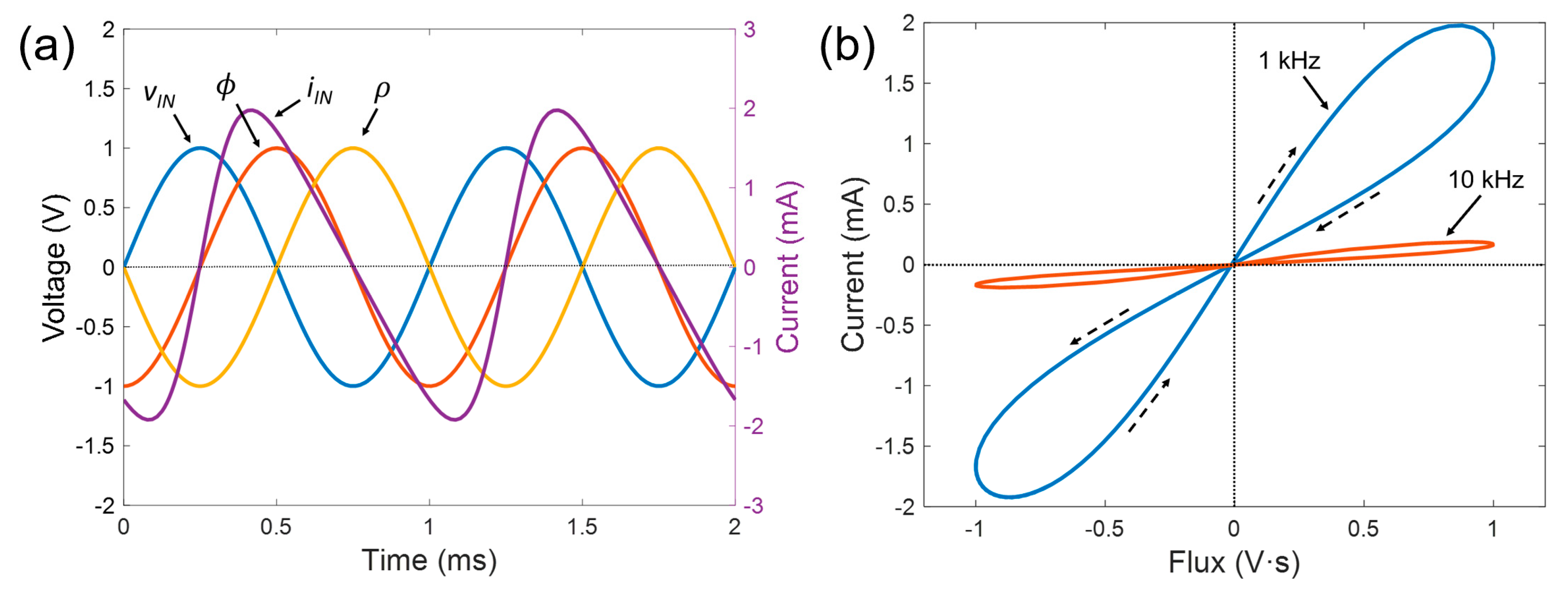
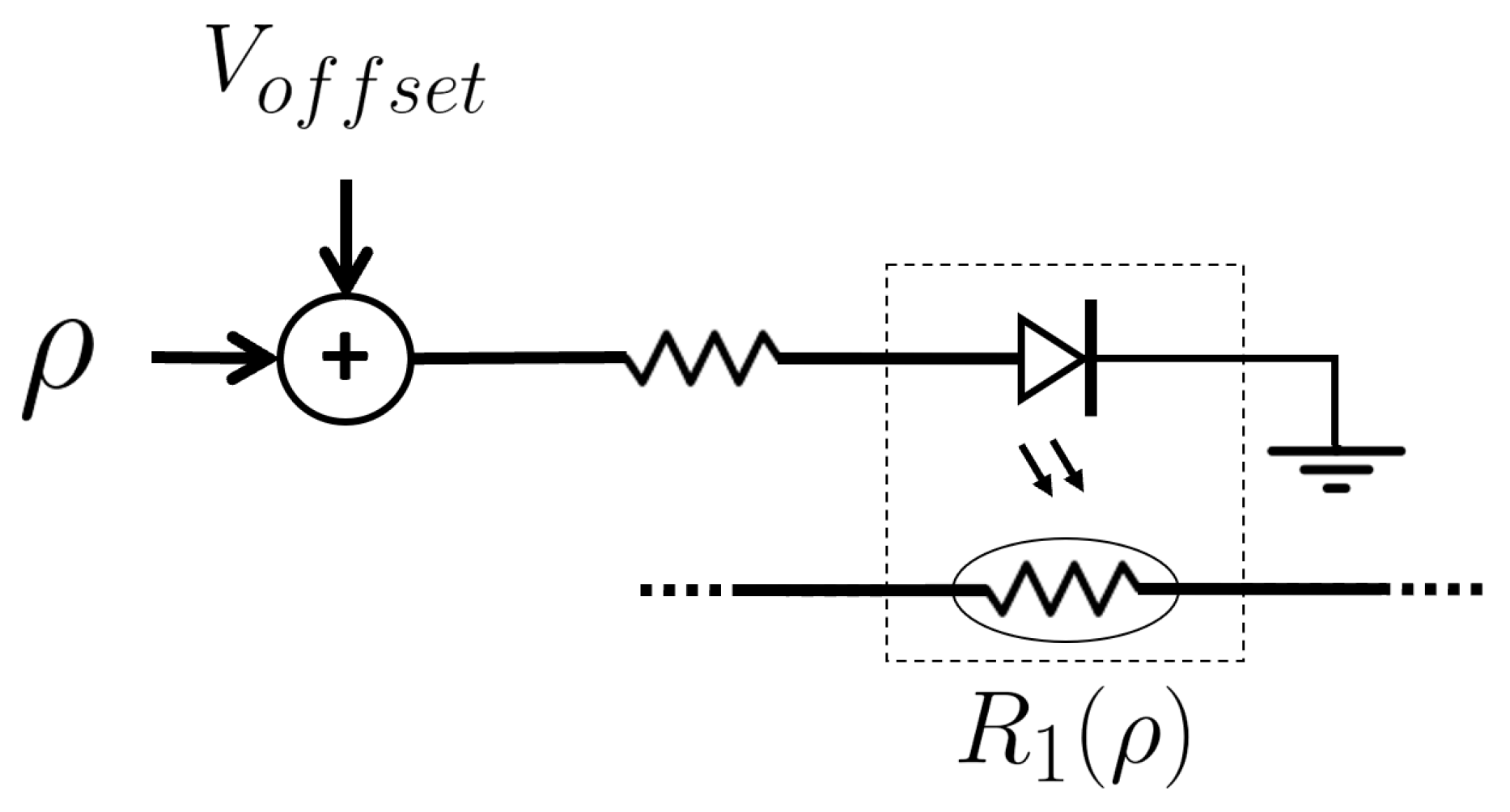
3. Meminductor Circuit Demonstrator
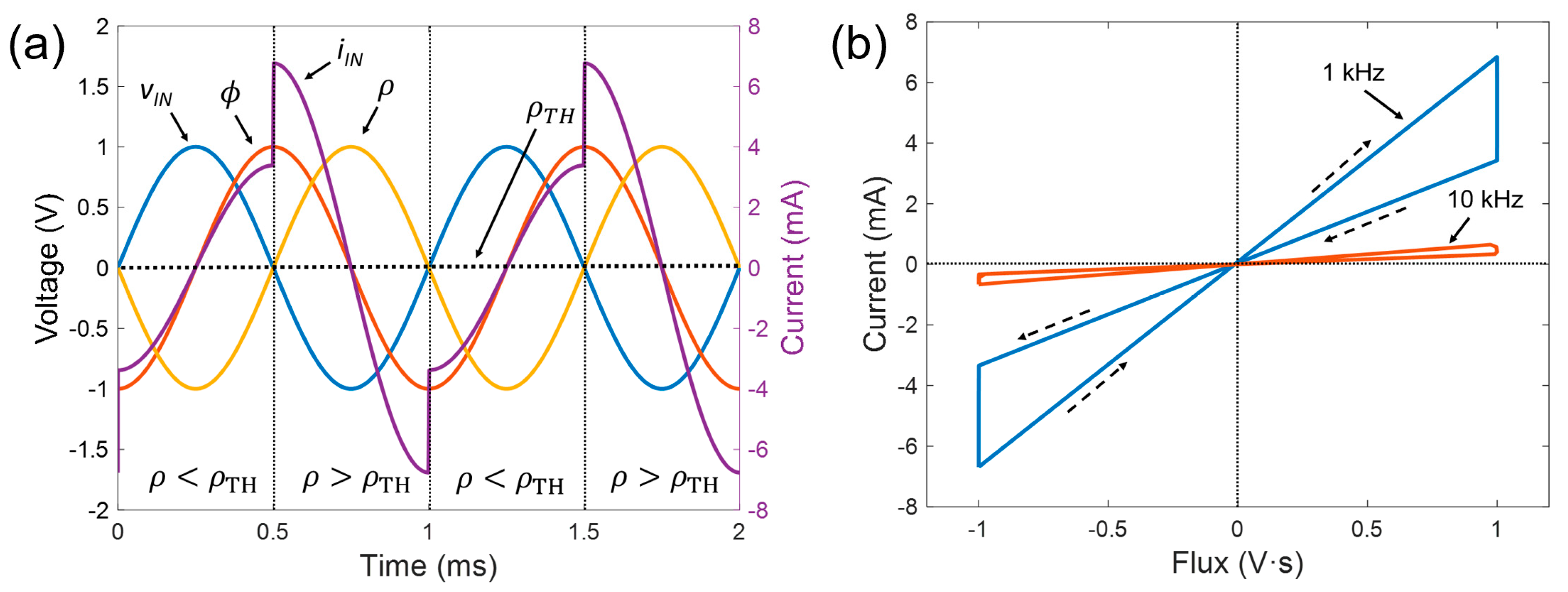
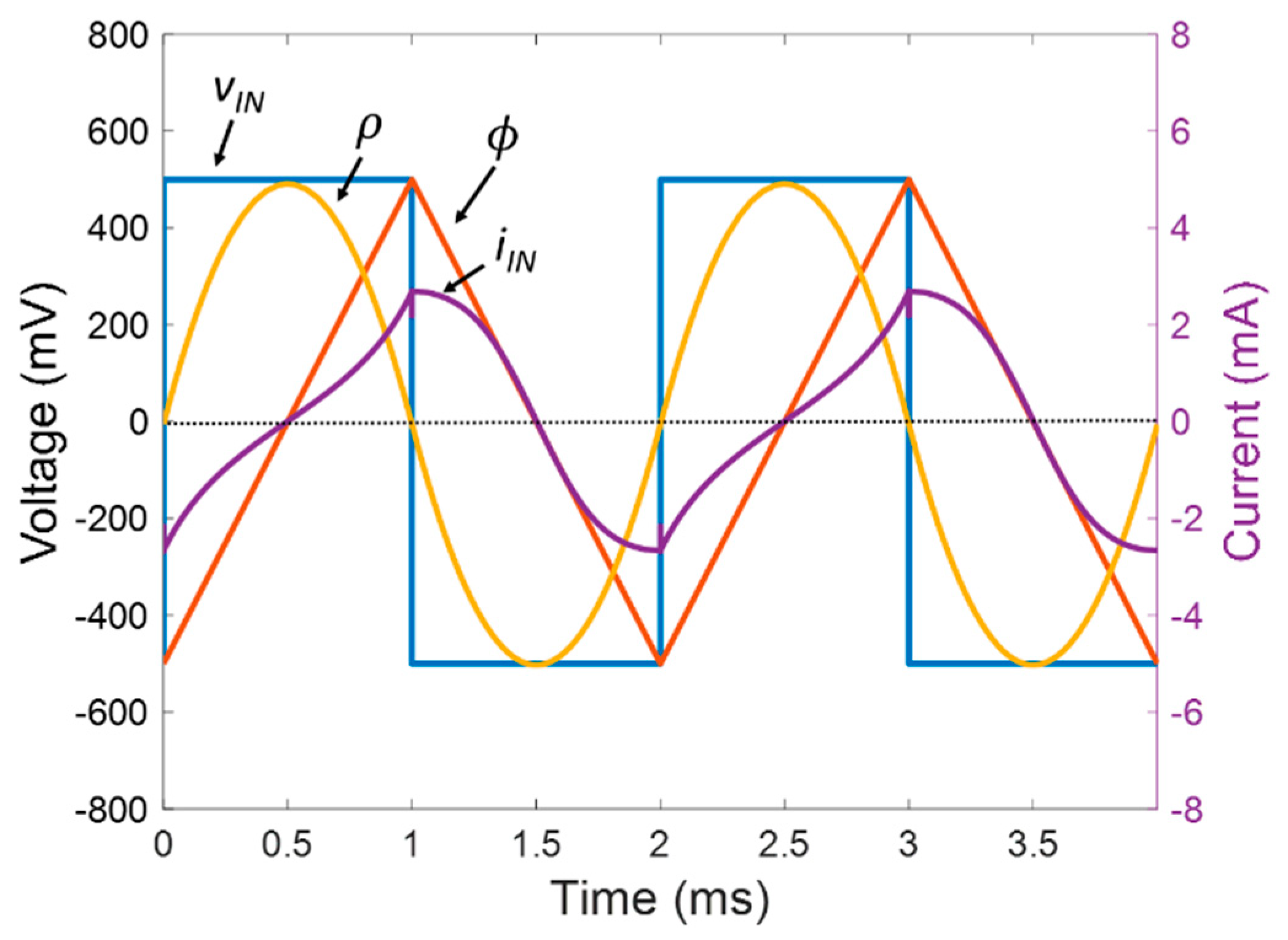
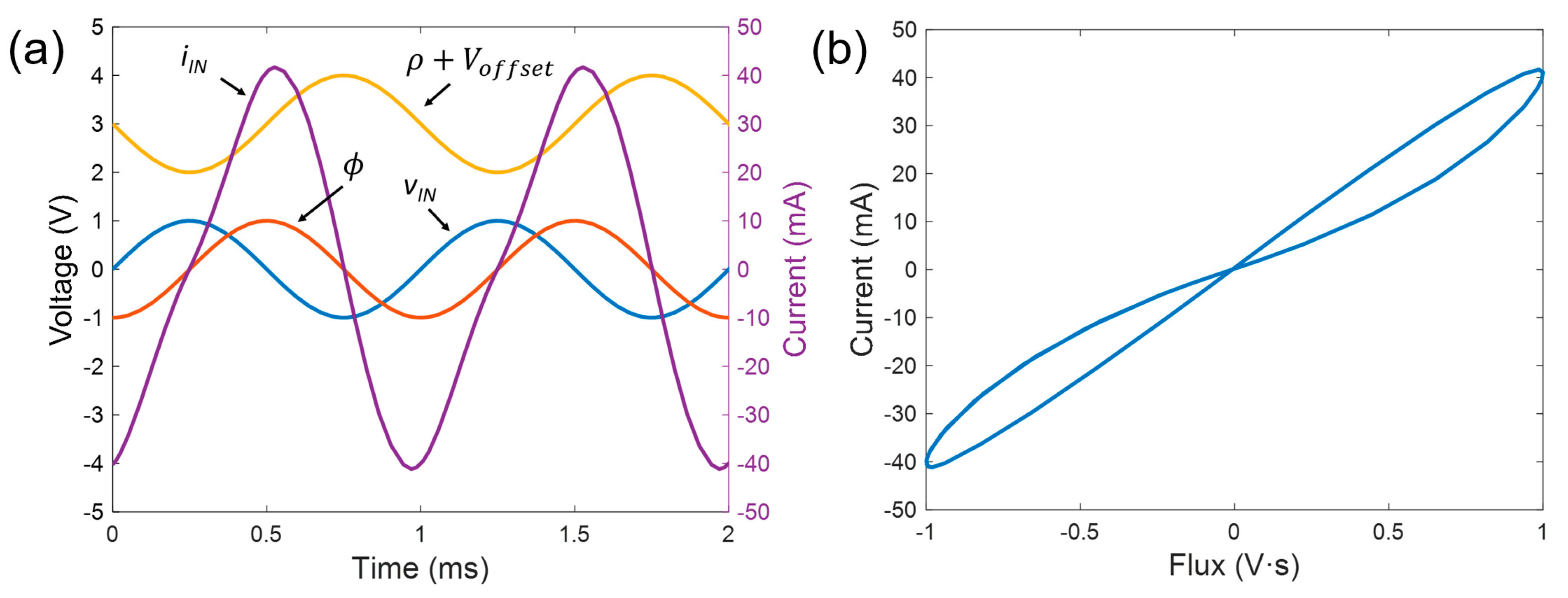
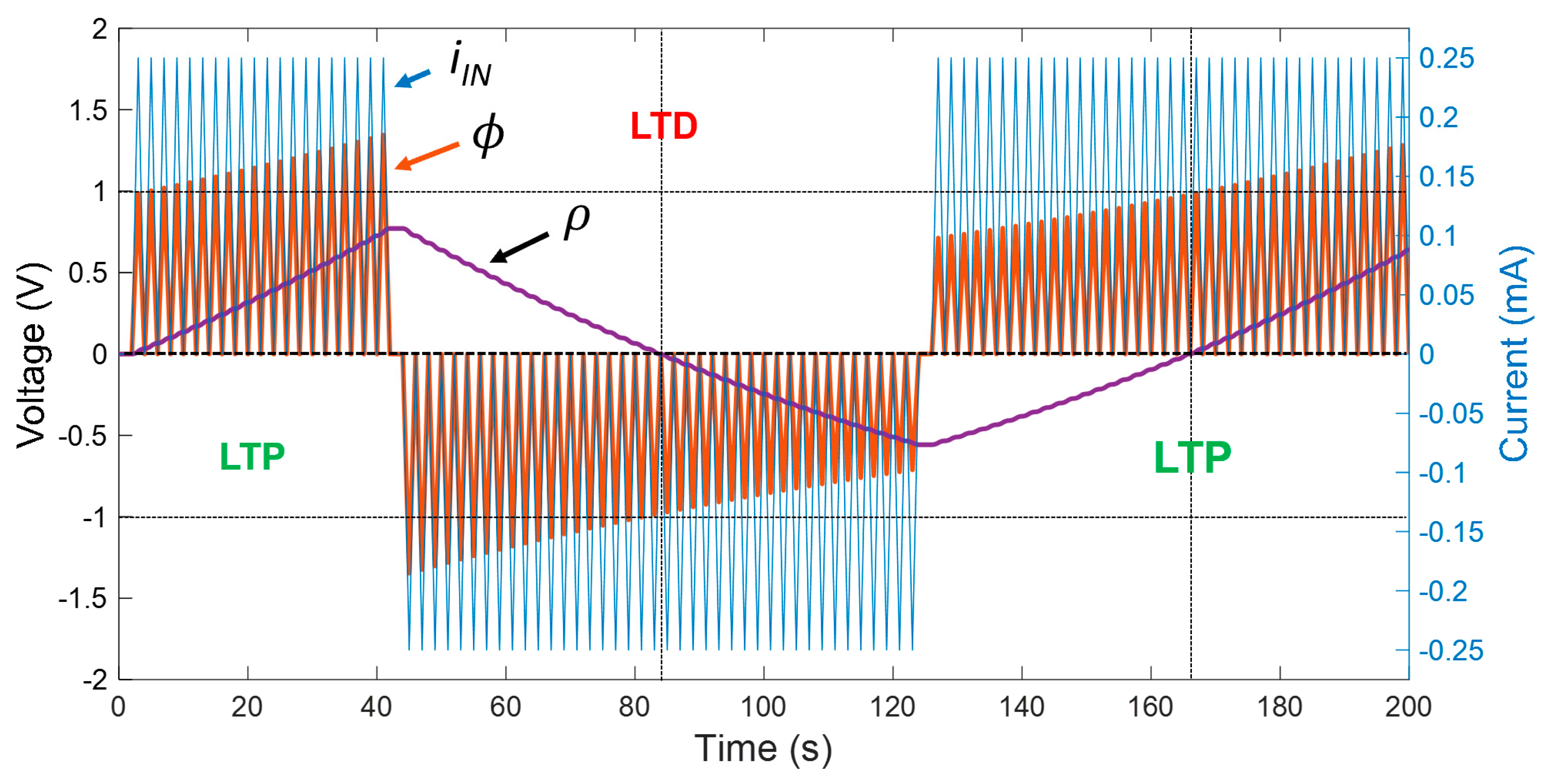
4. Long-Term Potentiation Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Romero, F.J.; Toral-Lopez, A.; Ohata, A.; Morales, D.P.; Ruiz, F.G.; Godoy, A.; Rodriguez, N. Laser-Fabricated Reduced Graphene Oxide Memristors. Nanomaterials 2019, 9, 897. [Google Scholar] [CrossRef] [Green Version]
- Villena, M.A.; Hui, F.; Liang, X.; Shi, Y.; Yuan, B.; Jing, X.; Zhu, K.; Chen, S.; Lanza, M. Variability of metal/h-BN/metal memristors grown via chemical vapor deposition on different materials. Microelectron. Reliab. 2019, 102, 113410. [Google Scholar] [CrossRef]
- Zhu, K.; Liang, X.; Yuan, B.; Villena, M.A.; Wen, C.; Wang, T.; Chen, S.; Hui, F.; Shi, Y.; Lanza, M. Graphene-Boron Nitride-Graphene Cross-Point Memristors with Three Stable Resistive States. ACS Appl. Mater. Interfaces 2019, 11, 37999–38005. [Google Scholar] [CrossRef]
- Iu, H.H.C.; Yu, D.S.; Fitch, A.L.; Sreeram, V.; Chen, H. Controlling Chaos in a Memristor Based Circuit Using a Twin-T Notch Filter. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1337–1344. [Google Scholar] [CrossRef]
- Xia, Q.; Robinett, W.; Cumbie, M.W.; Banerjee, N.; Cardinali, T.J.; Yang, J.J.; Wu, W.; Li, X.; Tong, W.M.; Strukov, D.B.; et al. Memristor−CMOS Hybrid Integrated Circuits for Reconfigurable Logic. Nano Lett. 2009, 9, 3640–3645. [Google Scholar] [CrossRef]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.D.; Adam, G.; Likharev, K.K.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Azghadi, M.R.; Linares-Barranco, B.; Abbott, D.; Leong, P.H.W. A Hybrid CMOS-Memristor Neuromorphic Synapse. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 434–445. [Google Scholar] [CrossRef] [Green Version]
- Di Ventra, M.; Pershin, Y.V.; Chua, L.O. Circuit Elements With Memory: Memristors, Memcapacitors, and Meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.-Y.; Jin, P.-P.; Wang, X.-W.; Shen, Y.; Yuan, F.; Wang, X.-Y. A flux-controlled model of meminductor and its application in chaotic oscillator. Chin. Phys. B 2016, 25, 090502. [Google Scholar] [CrossRef]
- Driscoll, T.; Quinn, J.; Klein, S.; Kim, H.T.; Kim, B.J.; Pershin, Y.V.; Di Ventra, M.; Basov, D.N. Memristive adaptive filters. Appl. Phys. Lett. 2010, 97, 93502. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Wang, G.; Jin, P.; Wang, X.; Ma, G. Chaos in a Meminductor-Based Circuit. Int. J. Bifurc. Chaos 2016, 26, 1650130. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Di Ventra, M. Neuromorphic, Digital, and Quantum Computation with Memory Circuit Elements. Proc. IEEE 2011, 100, 2071–2080. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.S.; Liang, Y.; Chen, H.; Iu, H.H.C. Design of a Practical Memcapacitor Emulator without Grounded Restriction. IEEE Trans. Circuits Syst. II: Express Briefs 2013, 60, 207–211. [Google Scholar] [CrossRef]
- Romero, F.J.; Morales, D.P.; Godoy, A.; Ruiz, F.G.; Tienda-Luna, I.M.; Ohata, A.; Rodriguez, N. Memcapacitor emulator based on the Miller effect. Int. J. Circuit Theory Appl. 2019, 47, 572–579. [Google Scholar] [CrossRef]
- Sah, M.P.; Yang, C.; Budhathoki, R.K.; Kim, H.; Yoo, H.J. Implementation of a Memcapacitor Emulator with Off-the-Shelf Devices. Elektronika ir Elektrotechnika 2013, 19, 54–58. [Google Scholar] [CrossRef]
- Sah, M.P.; Budhathoki, R.K.; Yang, C.; Kim, H. A mutator-based meminductor emulator circuit. In Proceeding of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014; pp. 2249–2252. [Google Scholar] [CrossRef]
- Yu, D.; Zhao, X.; Sun, T.; Iu, H.H.C.; Fernando, T. A Simple Floating Mutator for Emulating Memristor, Memcapacitor, and Meminductor. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1334–1338. [Google Scholar] [CrossRef]
- Sozen, H.; Cam, U. A Novel Floating/Grounded Meminductor Emulator. J. Circuits Syst. Comput. 2020, 2050247. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Zhang, X. A universal emulator for memristor, memcapacitor, and meminductor and its chaotic circuit. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013141. [Google Scholar] [CrossRef]
- Kumar, U.; Shukla, S.K.; Amiete. Analytical Study of Inductor Simulation Circuits. Act. Passiv. Electron. Compon. 1989, 13, 211–227. [Google Scholar] [CrossRef]
- Torres, L.A.B.; Aguirre, L.A. Inductorless Chua’s circuit. Electron. Lett. 2000, 36, 1915–1916. [Google Scholar] [CrossRef]
- Sedra, A.S.; Smith, K.C. Microelectronic Circuits; The Oxford Series in Electrical and Computer Engineering, 5th ed.; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Yuan, F.; Deng, Y.; Li, Y.; Wang, G. The amplitude, frequency and parameter space boosting in a memristor–meminductor-based circuit. Nonlinear Dyn. 2019, 96, 389–405. [Google Scholar] [CrossRef]
- Fouda, M.E.; Radwan, A.G. Meminductor Response Under Periodic Current Excitations. Circuits Syst. Signal Process. 2013, 33, 1573–1583. [Google Scholar] [CrossRef]
- NSL-32 Optoisolator Datasheet. Available online: https://lunainc.com/wp-content/uploads/2016/06/NSL-32.pdf (accessed on 27 August 2020).
- Wang, X.-Y.; Fitch, A.L.; Iu, H.H.C.; Sreeram, V.; Qi, W.-G. Implementation of an analogue model of a memristor based on a light-dependent resistor. Chin. Phys. B 2012, 21, 108501. [Google Scholar] [CrossRef]
- Majumdar, S.; Tan, H.; Qin, Q.H.; Van Dijken, S. Energy-Efficient Organic Ferroelectric Tunnel Junction Memristors for Neuromorphic Computing. Adv. Electron. Mater. 2019, 5, 1800795. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero, F.J.; Escudero, M.; Medina-Garcia, A.; Morales, D.P.; Rodriguez, N. Meminductor Emulator Based on a Modified Antoniou’s Gyrator Circuit. Electronics 2020, 9, 1407. https://doi.org/10.3390/electronics9091407
Romero FJ, Escudero M, Medina-Garcia A, Morales DP, Rodriguez N. Meminductor Emulator Based on a Modified Antoniou’s Gyrator Circuit. Electronics. 2020; 9(9):1407. https://doi.org/10.3390/electronics9091407
Chicago/Turabian StyleRomero, Francisco J., Manuel Escudero, Alfredo Medina-Garcia, Diego P. Morales, and Noel Rodriguez. 2020. "Meminductor Emulator Based on a Modified Antoniou’s Gyrator Circuit" Electronics 9, no. 9: 1407. https://doi.org/10.3390/electronics9091407
APA StyleRomero, F. J., Escudero, M., Medina-Garcia, A., Morales, D. P., & Rodriguez, N. (2020). Meminductor Emulator Based on a Modified Antoniou’s Gyrator Circuit. Electronics, 9(9), 1407. https://doi.org/10.3390/electronics9091407







