Toward Blockchain-Enabled Privacy-Preserving Data Transmission in Cluster-Based Vehicular Networks
Abstract
:1. Introduction
2. Related Works
3. The Proposed ROAC-B Technique
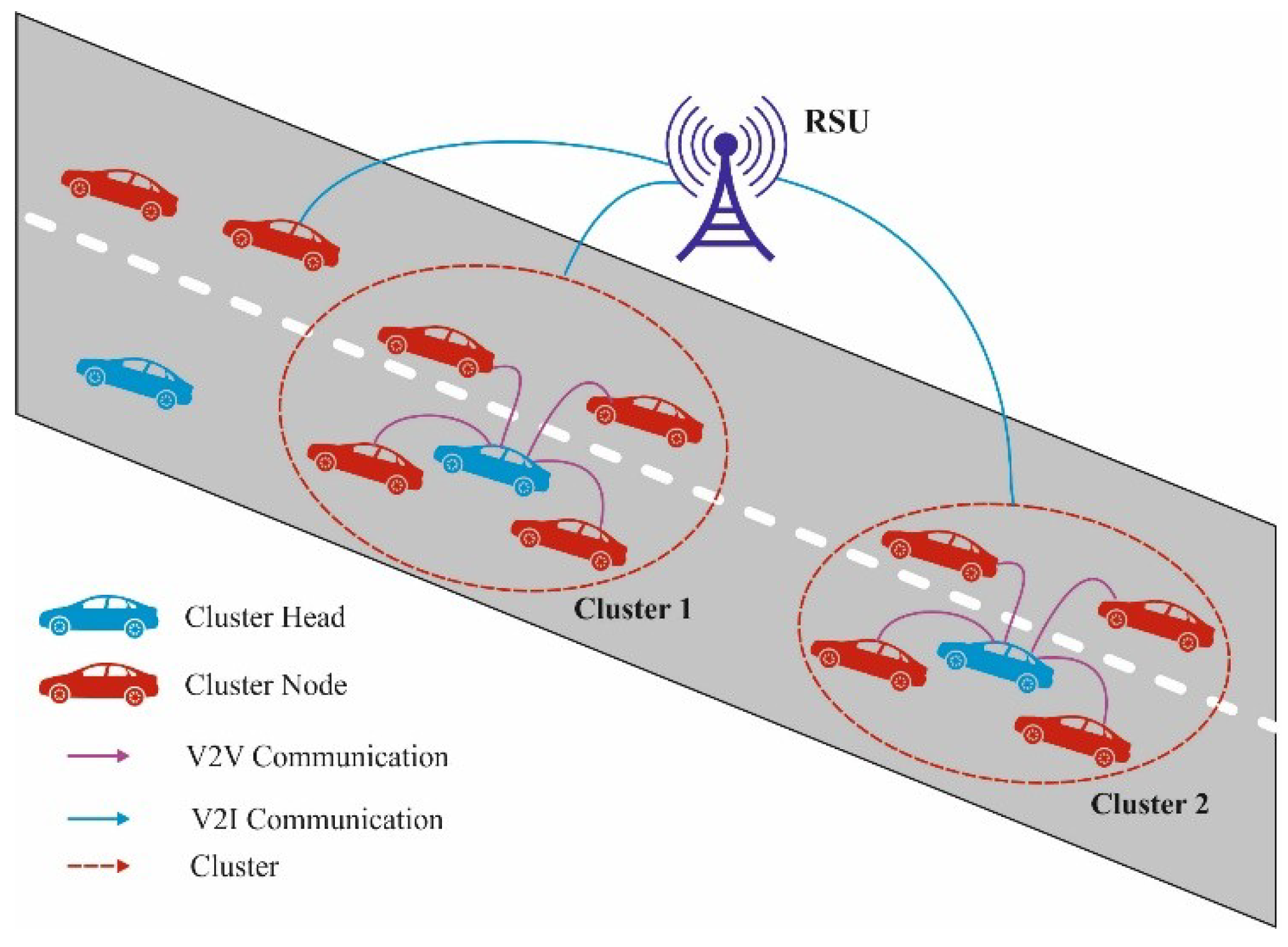
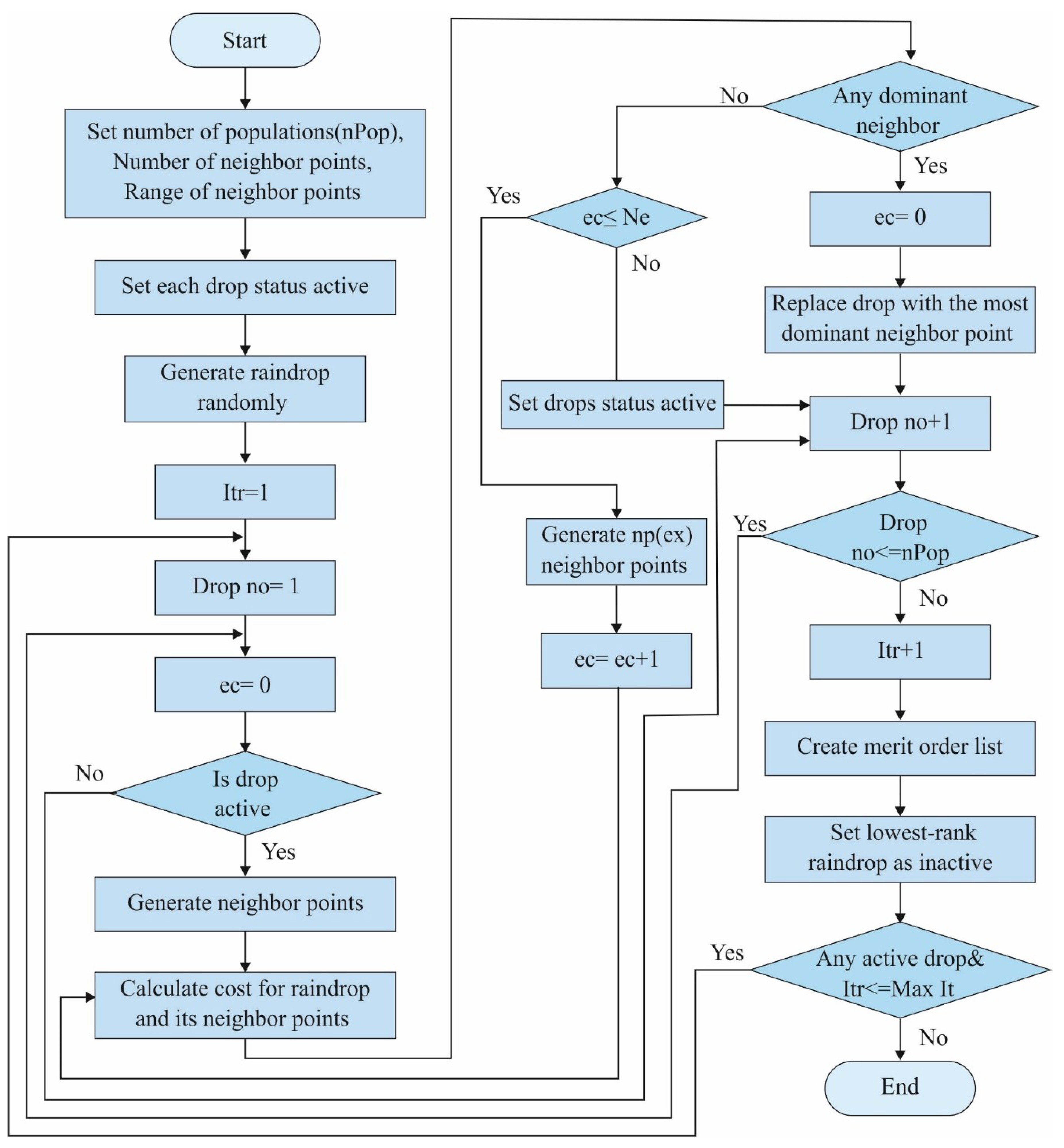
3.1. ROA for Clustering in VANET
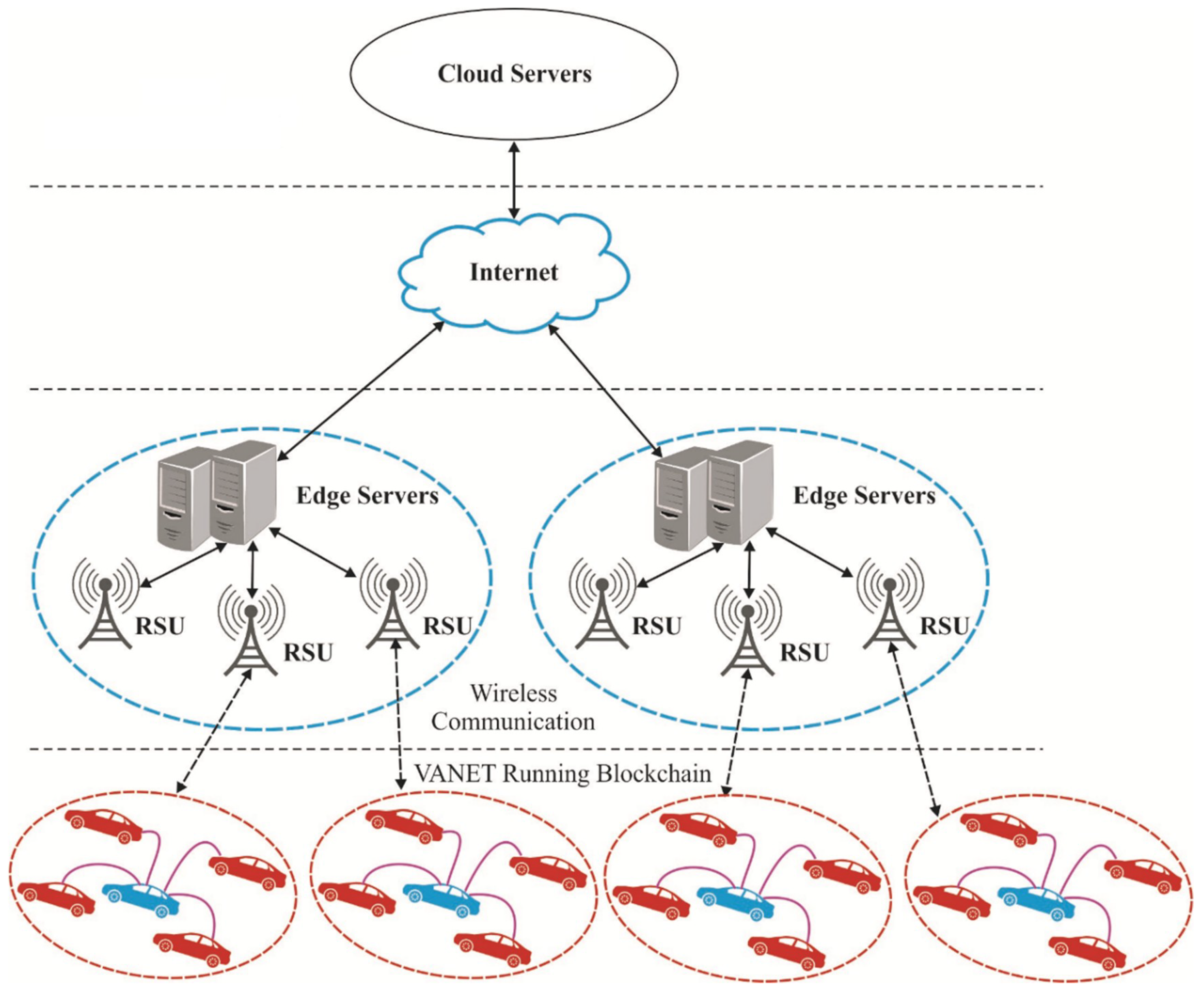
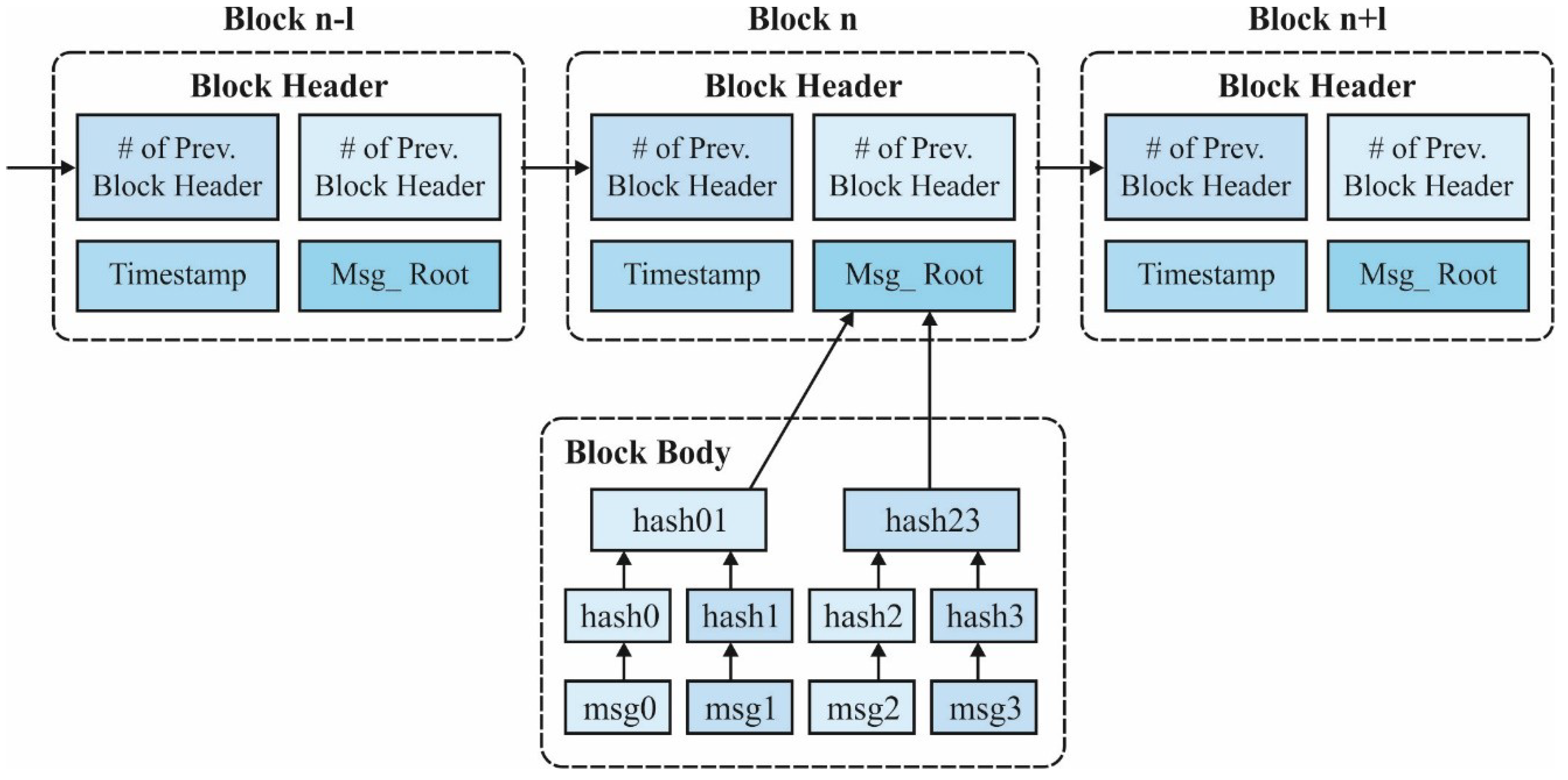
3.2. Blockchain-Based Secure Transmission
4. Performance Validation
4.1. Parameter Settings
4.2. Analysis of the ROAC-B Technique at Various Grid Sizes
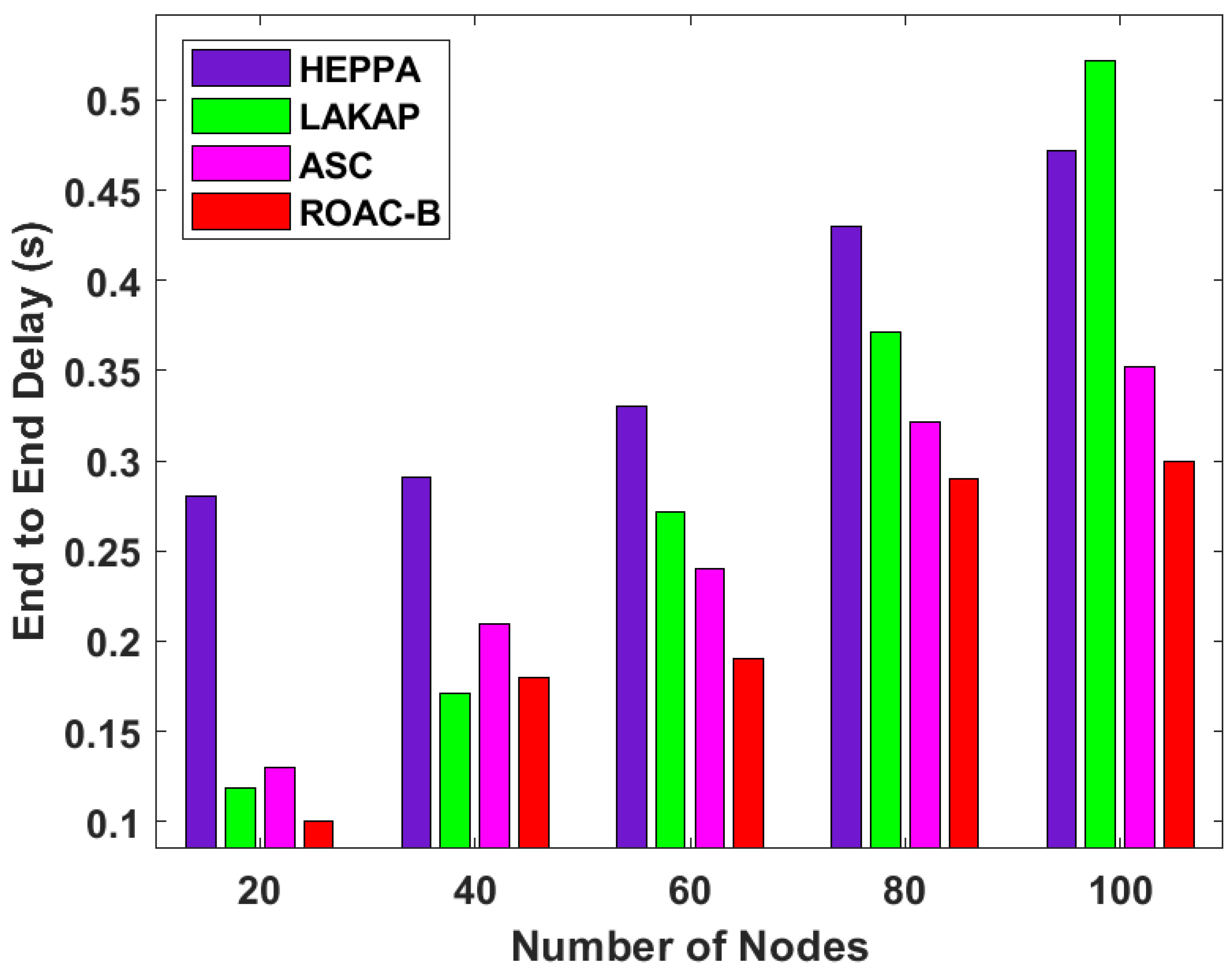
4.3. Analysis of the ROAC-B Technique in Terms of PDR
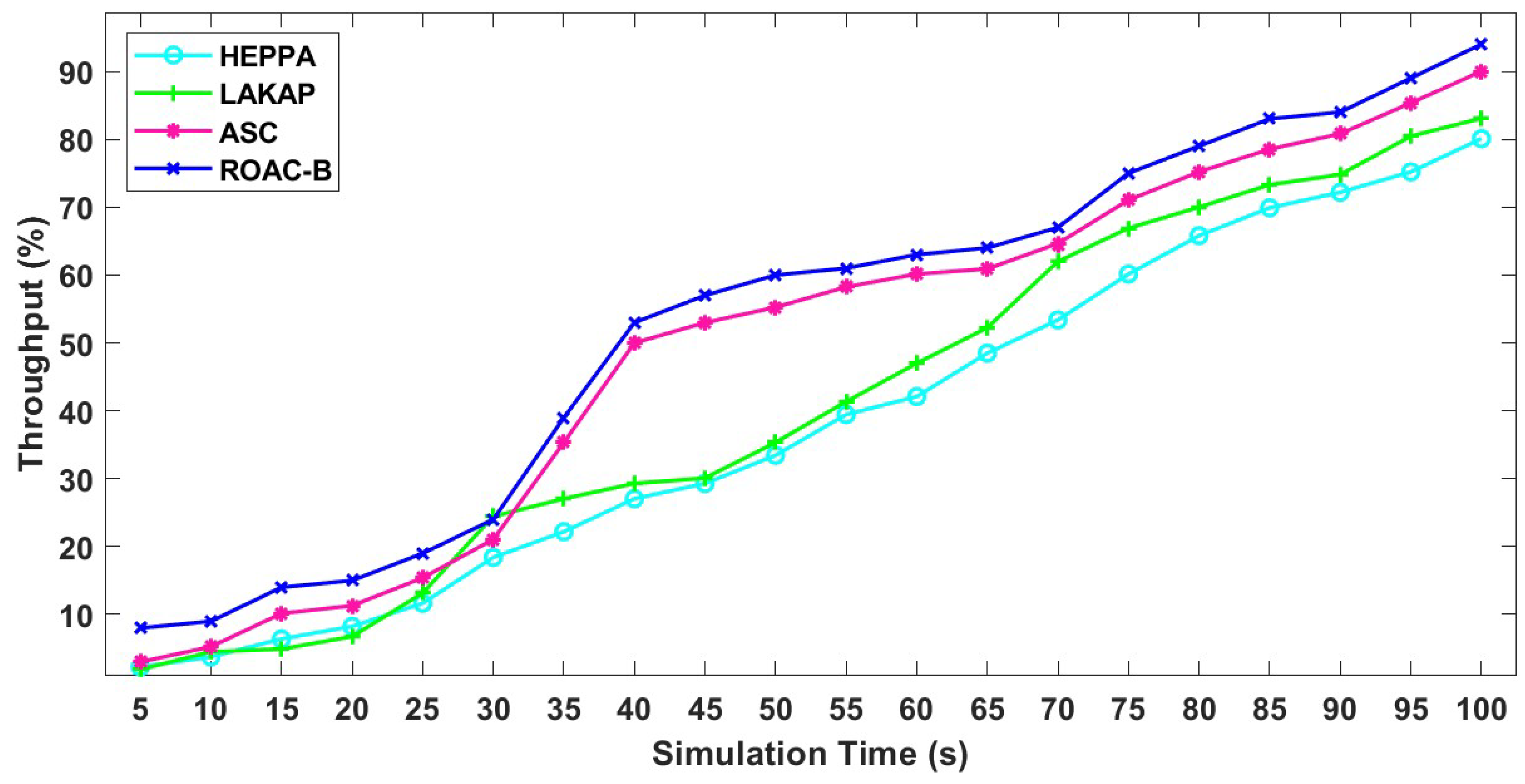
4.4. Analysis of the ROAC-B Technique in Terms of Throughput
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghori, M.R.; Zamli, K.Z.; Quosthoni, N.; Hisyam, M.; Montaser, M. Vehicular ad-hoc network (VANET): Review. In Proceedings of the 2018 IEEE International Conference on Innovative Research and Development ICIRD, Bangkok, Thailand, 11–12 May 2018. [Google Scholar]
- Abbasi, I.A.; Khan, A.S. A review of vehicle to vehicle communication protocols for VANETs in the urban environment. Future Int. 2018, 10, 14. [Google Scholar] [CrossRef] [Green Version]
- Zeadally, S.; Hunt, R.; Chen, Y.S.; Irwin, A.; Hassan, A. Vehicular ad hoc networks (VANETS): Status, results, and challenges. Telecommun. Syst. 2012, 50, 217–241. [Google Scholar] [CrossRef]
- Qu, F.; Wu, Z.; Wang, F.Y.; Cho, W. A security and privacy review of VANETs. IEEE Trans. Intell. Transp. Syst. 2015, 10, 2985–2996. [Google Scholar] [CrossRef]
- Engoulou, R.G.; Bellaïche, M.; Pierre, S.; Quintero, A. VANET security surveys. Comput. Commun. 2014, 44, 1–13. [Google Scholar] [CrossRef]
- Patel, N.J.; Jhaveri, R.H. Trust based approaches for secure routing in VANET: A survey. Procedia Comput. Sci. 2015, 45, 592–601. [Google Scholar] [CrossRef] [Green Version]
- Xi, Y.; Sha, K.; Shi, W.; Schwiebert, L.; Zhang, T. Enforcing privacy using symmetric random key-set in vehicular networks. In Proceedings of the Eighth International Symposium on Autonomous Decentralized Systems, Phoenix, AZ, USA, 21–23 March 2007. [Google Scholar]
- Defrawy, K.E.; Tsudik, G. ALARM: Anonymous location-aided routing in suspicious MANETs. IEEE Trans. Mob. Comput. 2016, 10, 1345–1358. [Google Scholar] [CrossRef] [Green Version]
- Prashar, D.; Jha, N.; Jha, S.; Joshi, G.P.; Seo, C. Integrating IoT and Blockchain for Ensuring Road Safety: An Unconventional Approach. Sensors 2020, 20, 3296. [Google Scholar] [CrossRef]
- Dai, H.-N.; Zheng, Z.; Zhang, Y. Blockchain for Internet of Things: A Survey. IEEE Internet Things J. 2019, 6, 8076–8094. [Google Scholar] [CrossRef] [Green Version]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://nakamotoinstitute.org/bitcoin/ (accessed on 20 April 2020).
- Ostermaier, B.; Dotzer, F.; Strassberger, M. Enhancing the security of local dangerwarnings in vanets—A simulative analysis of voting schemes. In Proceedings of the 2nd International Conference on Availability, Reliability and Security, Vienna, Austria, 10–13 April 2007; pp. 422–431. [Google Scholar]
- Ying, B.; Nayak, A. Anonymous and lightweight authentication for secure vehicular networks. IEEE Trans. Veh. Technol. 2017, 66, 10626–10636. [Google Scholar] [CrossRef]
- Wazid, M.; Das, A.K.; Kumar, N.; Odelu, V.; Reddy, A.G.; Park, K.; Park, Y. Design of lightweight authentication and key agreement protocol for vehicular ad hoc networks. IEEE Access 2017, 5, 14966–14980. [Google Scholar] [CrossRef]
- Rajput, U.; Abbas, F.; Eun, H.; Oh, H. A hybrid approach for efficient privacy-preserving authentication in VANET. IEEE Access 2017, 5, 12014–12030. [Google Scholar] [CrossRef]
- Tangade, S.; Manvi, S.S. Scalable and privacy-preserving authentication protocol for secure vehicular communications. In Proceedings of the 2016 IEEE International Conference on Advanced Networks and Telecommunications Systems, Bangalore, India, 6–9 November 2016. [Google Scholar]
- Cui, J.; Zhang, J.; Zhong, H.; Xu, Y. SPACF: A secure privacy-preserving authentication scheme for VANET with CUCKOO Filter. IEEE Trans. Veh. Technol. 2017, 66, 10283–10295. [Google Scholar] [CrossRef]
- Lei, A.; Ogah, C.; Al, E. A Secure Key Management Scheme for Heterogeneous Secure Vehicular Communication Systems. Zte Commun. Mag. 2016, 111. [Google Scholar] [CrossRef]
- Leiding, B.; Memarmoshrefi, P.; Hogrefe, D. Self-managed and blockchain-based vehicular ad-hoc networks. In Proceedings of the 2016 ACM Int. Jt. Conf. Pervasive Ubiquitous Comput. Adjun—UbiComp, Heidelberg, Germany, 12–16 September 2016; Volume 16, p. 137140. [Google Scholar]
- Dorri, A. BlockChain: A Distributed Solution to Automotive Security and Privacy. IEEE Commun. Mag. 2017, 55, 119–125. [Google Scholar] [CrossRef] [Green Version]
- Rowan, S.; Clear, M.; Gerla, M.; Huggard, M.; Goldrick, C.M. Securing Vehicle to Vehicle Communications using Blockchain through Visible Light and Acoustic Side-Channels. arXiv 2017, arXiv:1704.02553. [Google Scholar]
- Song, F.; Zhu, M.; Zhou, Y.; You, I.; Zhang, H. Smart collaborative tracking for ubiquitous power IoT in edge-cloud interplay domain. IEEE Int. Things J. 2019. [Google Scholar] [CrossRef]
- Guo, S.; Hu, X.; Zhou, Z.; Wang, X.; Qi, F.; Gao, L. Trust access authentication in vehicular network based on blockchain. China Commun. 2019, 16, 18–30. [Google Scholar] [CrossRef]
- Sherazi, H.H.R.; Iqbal, R.; Ahmad, F.; Khan, Z.A.; Chaudary, M.H. DDoS attack detection: A key enabler for sustainable communication in internet of vehicles. Sustain. Comput. Inf. Syst. 2019, 23, 13–20. [Google Scholar] [CrossRef]
- Yang, Y.T.; Chou, L.D.; Tseng, C.W.; Tseng, F.H.; Liu, C.C. Blockchain-based traffic event validation and trust verification for VANETs. IEEE Access 2019, 7, 30868–30877. [Google Scholar] [CrossRef]
- Sherazi, H.H.R.; Khan, Z.A.; Iqbal, R.; Rizwan, S.; Imran, M.A.; Awan, K. A heterogeneous IoV architecture for data forwarding in vehicle to infrastructure communication. Mob. Inf. Syst. 2019. [Google Scholar] [CrossRef] [Green Version]
- Moazzeni, A.R.; Khamehchi, E. Rain optimization algorithm (ROA): A new metaheuristic method for drilling optimization solutions. J. Pet. Sci. Eng. 2020, 107512. [Google Scholar] [CrossRef]
- Shrestha, R.; Bajracharya, R.; Shrestha, A.P.; Nam, S.Y. A new type of blockchain for secure message exchange in VANET. Digit. Commun. Netw. 2020, 6, 177–186. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Node Count | 100 |
| Max. Vehicle Speed | 33 m/s |
| Max. Acceleration | 2.6 m/s2 |
| Max. Deceleration | 4.5 m/s2 |
| Number of RSUs | 10 |
| RSU Coverage | 1 km |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joshi, G.P.; Perumal, E.; Shankar, K.; Tariq, U.; Ahmad, T.; Ibrahim, A. Toward Blockchain-Enabled Privacy-Preserving Data Transmission in Cluster-Based Vehicular Networks. Electronics 2020, 9, 1358. https://doi.org/10.3390/electronics9091358
Joshi GP, Perumal E, Shankar K, Tariq U, Ahmad T, Ibrahim A. Toward Blockchain-Enabled Privacy-Preserving Data Transmission in Cluster-Based Vehicular Networks. Electronics. 2020; 9(9):1358. https://doi.org/10.3390/electronics9091358
Chicago/Turabian StyleJoshi, Gyanendra Prasad, Eswaran Perumal, K. Shankar, Usman Tariq, Tariq Ahmad, and Atef Ibrahim. 2020. "Toward Blockchain-Enabled Privacy-Preserving Data Transmission in Cluster-Based Vehicular Networks" Electronics 9, no. 9: 1358. https://doi.org/10.3390/electronics9091358
APA StyleJoshi, G. P., Perumal, E., Shankar, K., Tariq, U., Ahmad, T., & Ibrahim, A. (2020). Toward Blockchain-Enabled Privacy-Preserving Data Transmission in Cluster-Based Vehicular Networks. Electronics, 9(9), 1358. https://doi.org/10.3390/electronics9091358







