Output Feedback Control via Linear Extended State Observer for an Uncertain Manipulator with Output Constraints and Input Dead-Zone
Abstract
:1. Introduction
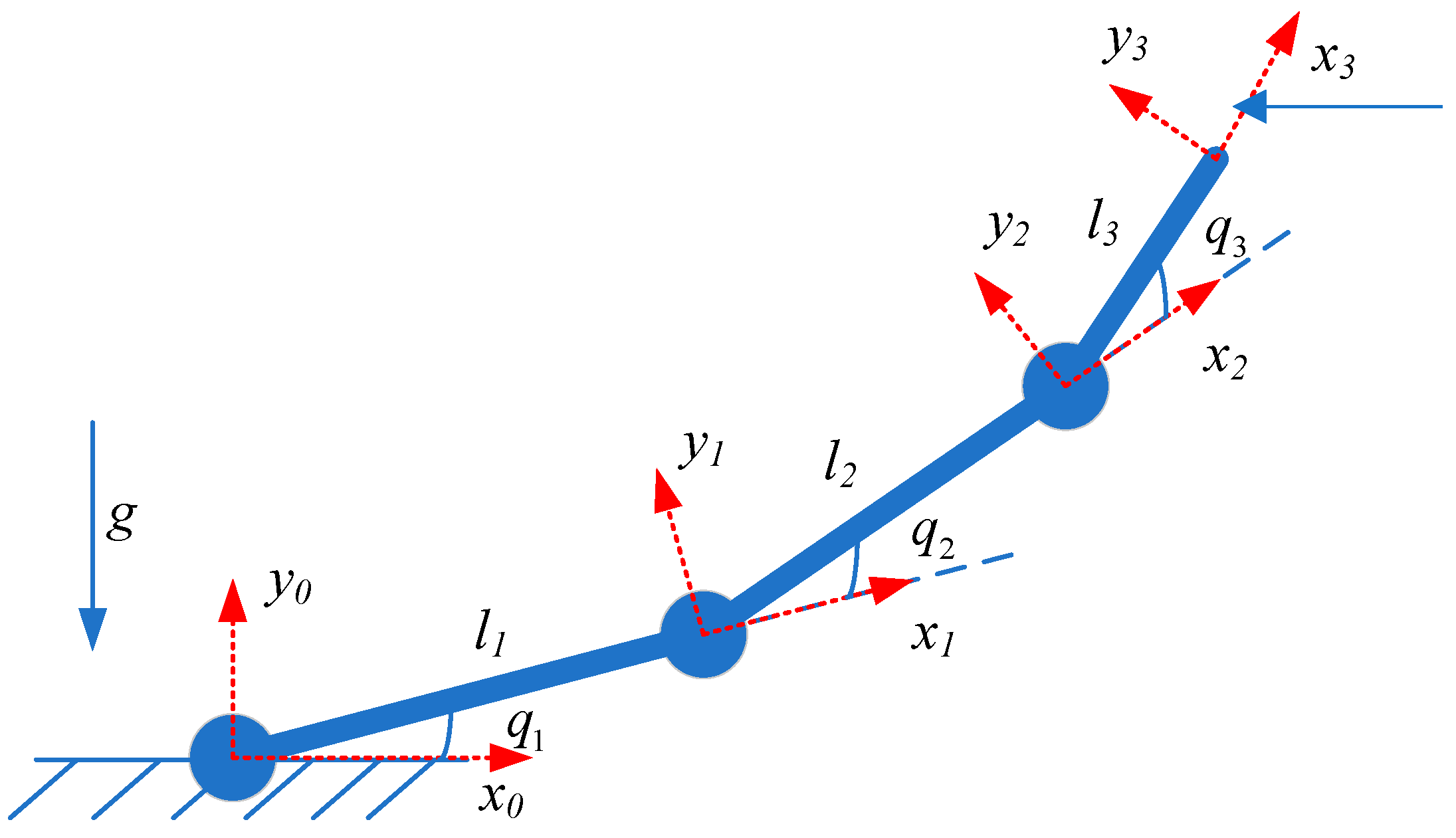
2. Robotic Manipulator Dynamics
3. Control Design
3.1. Linear Extended State Observer Design
3.2. Proposed Control Design
3.3. Stability Analysis
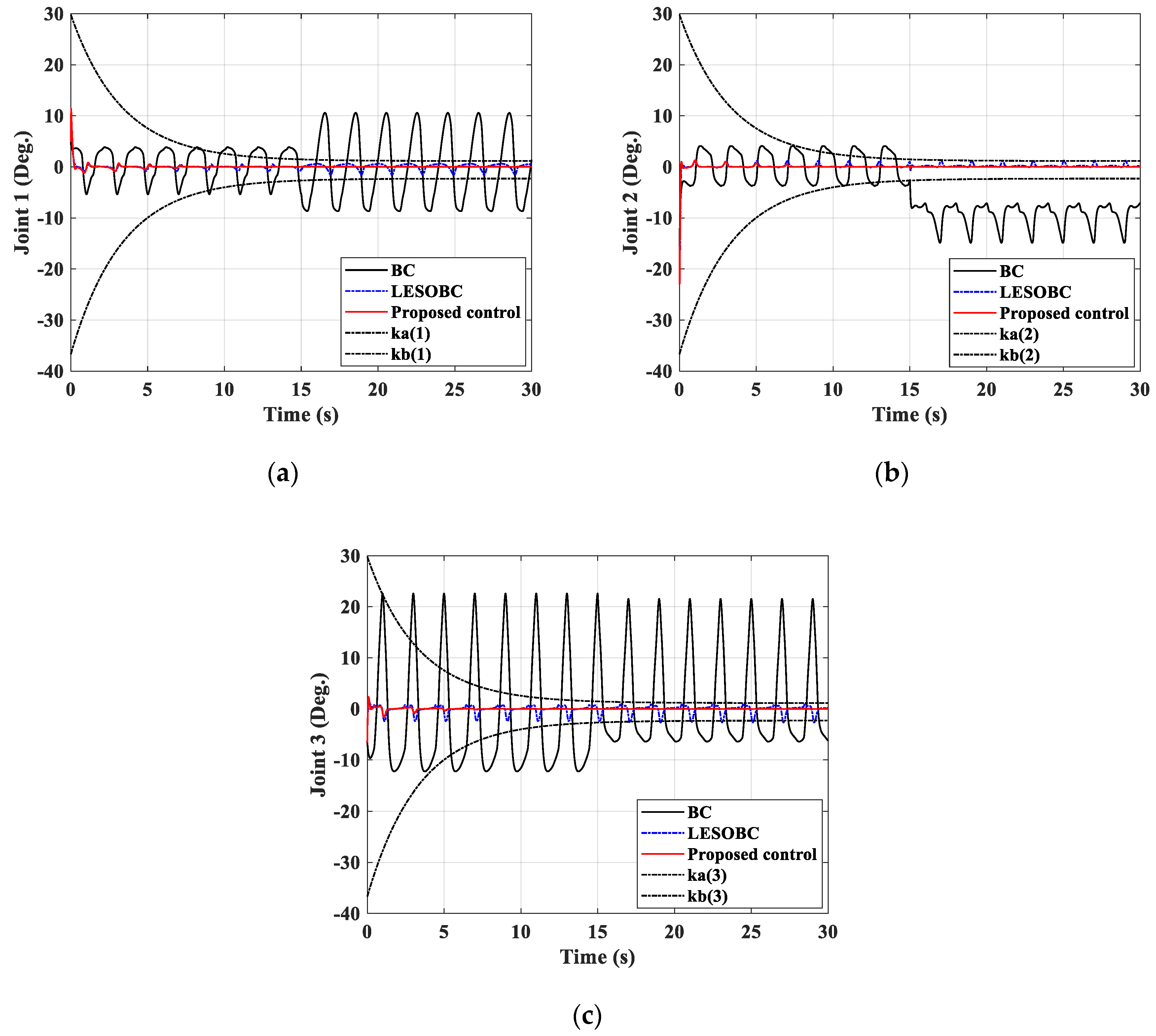
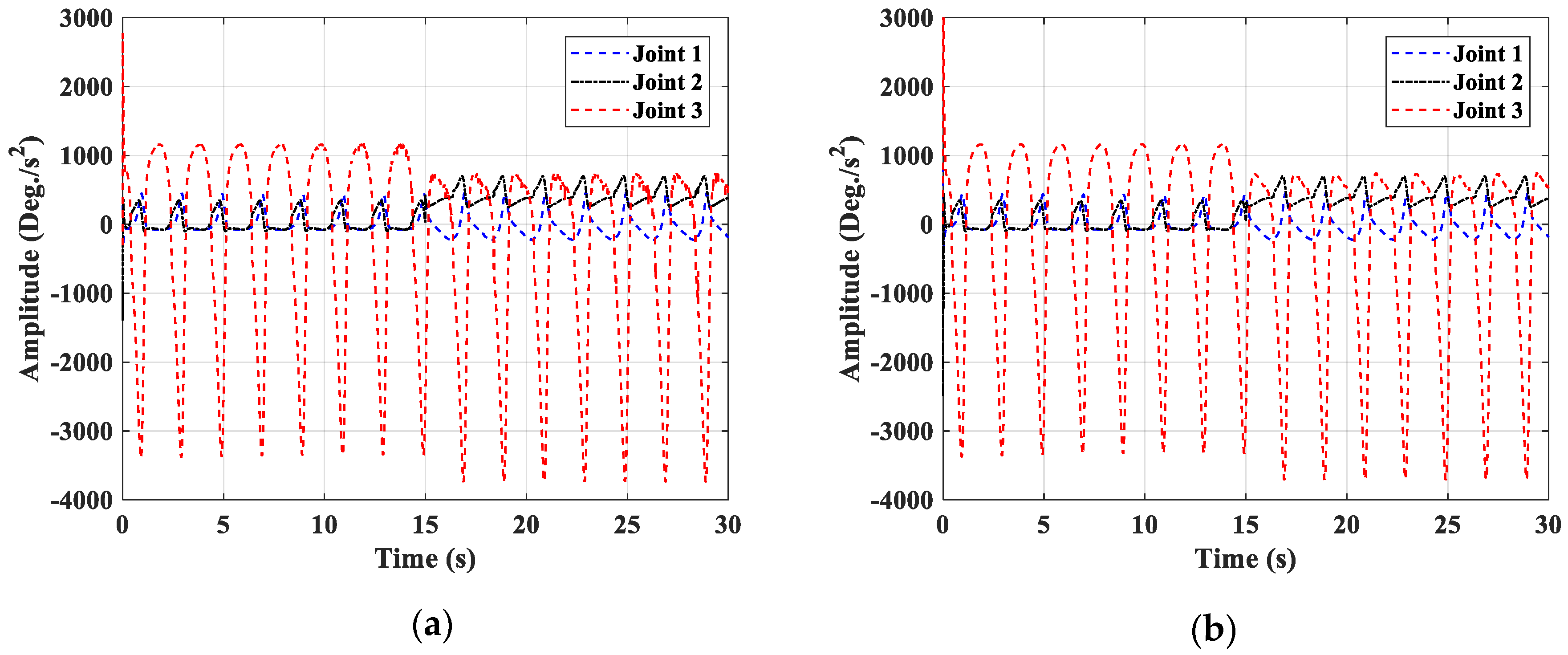
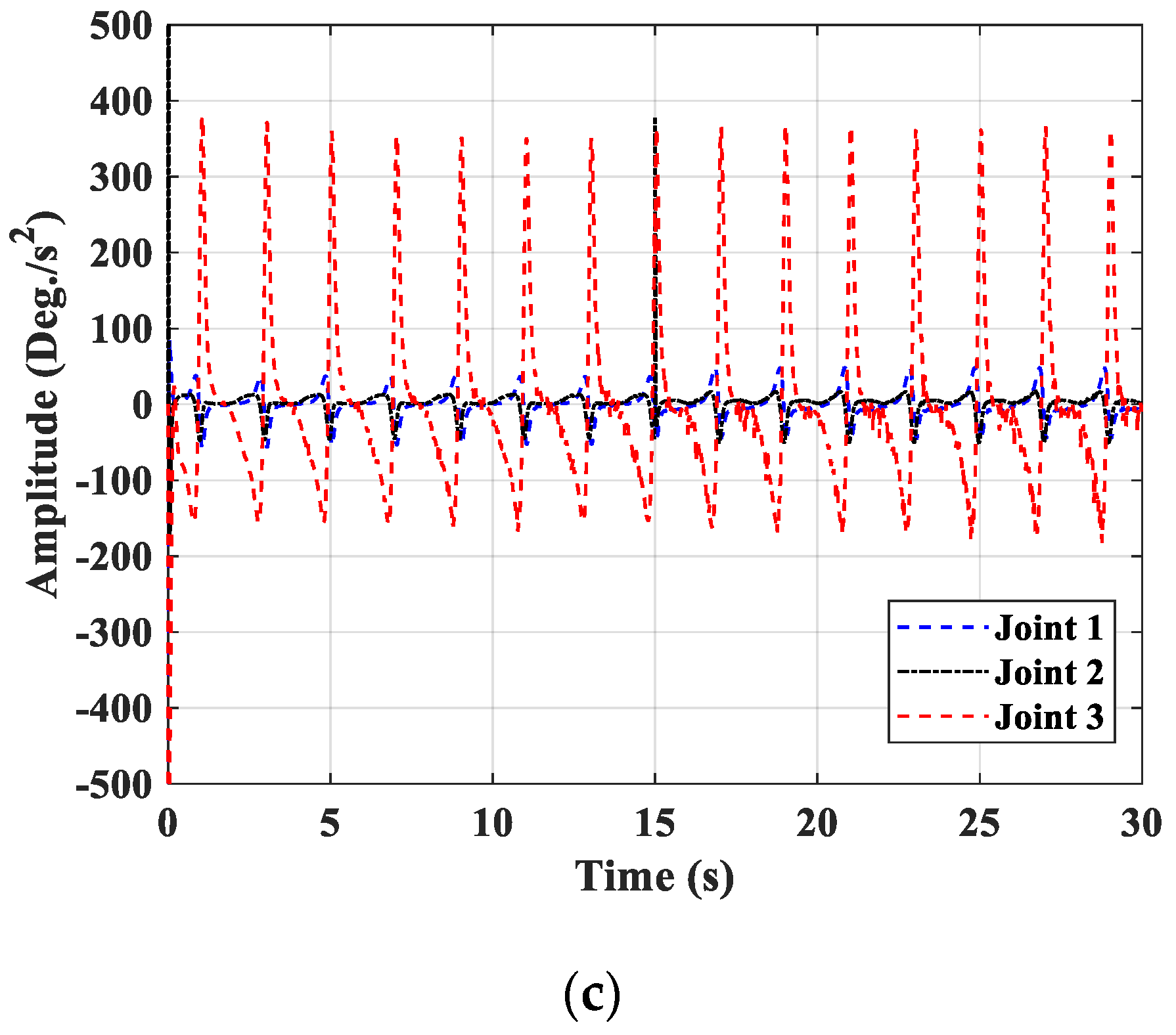
4. Numerical Simulations
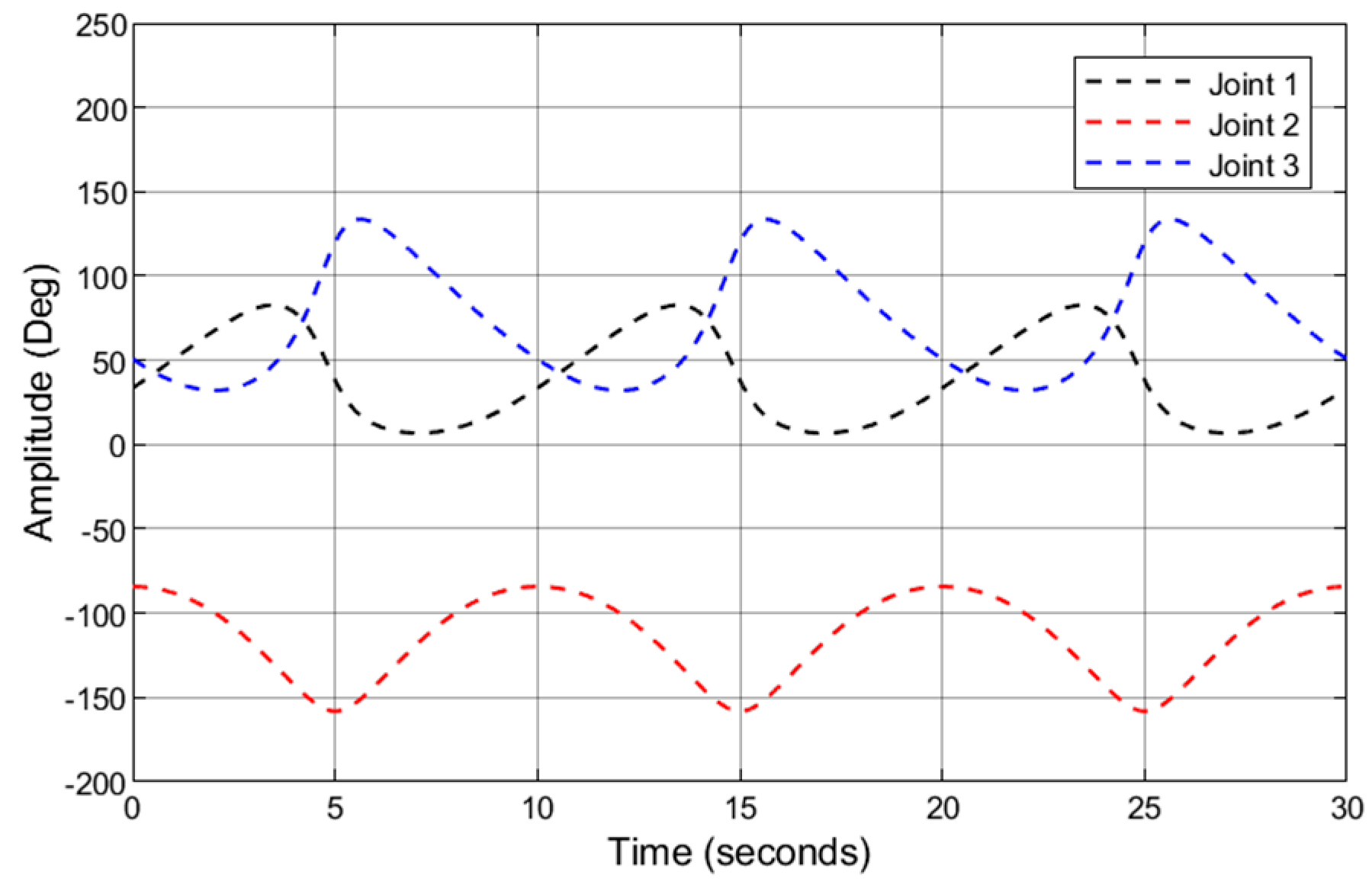
4.1. Simulation Descriptions
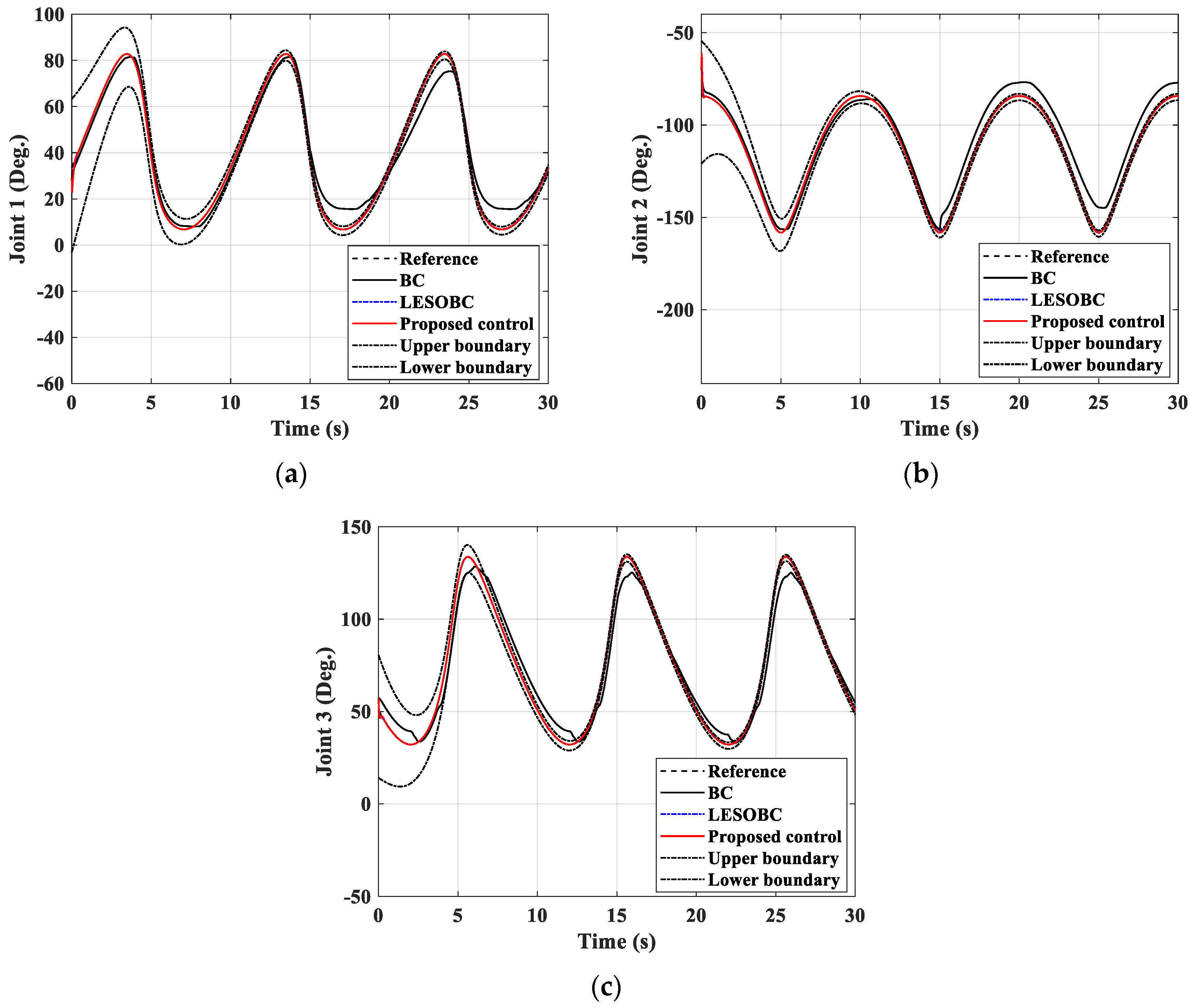
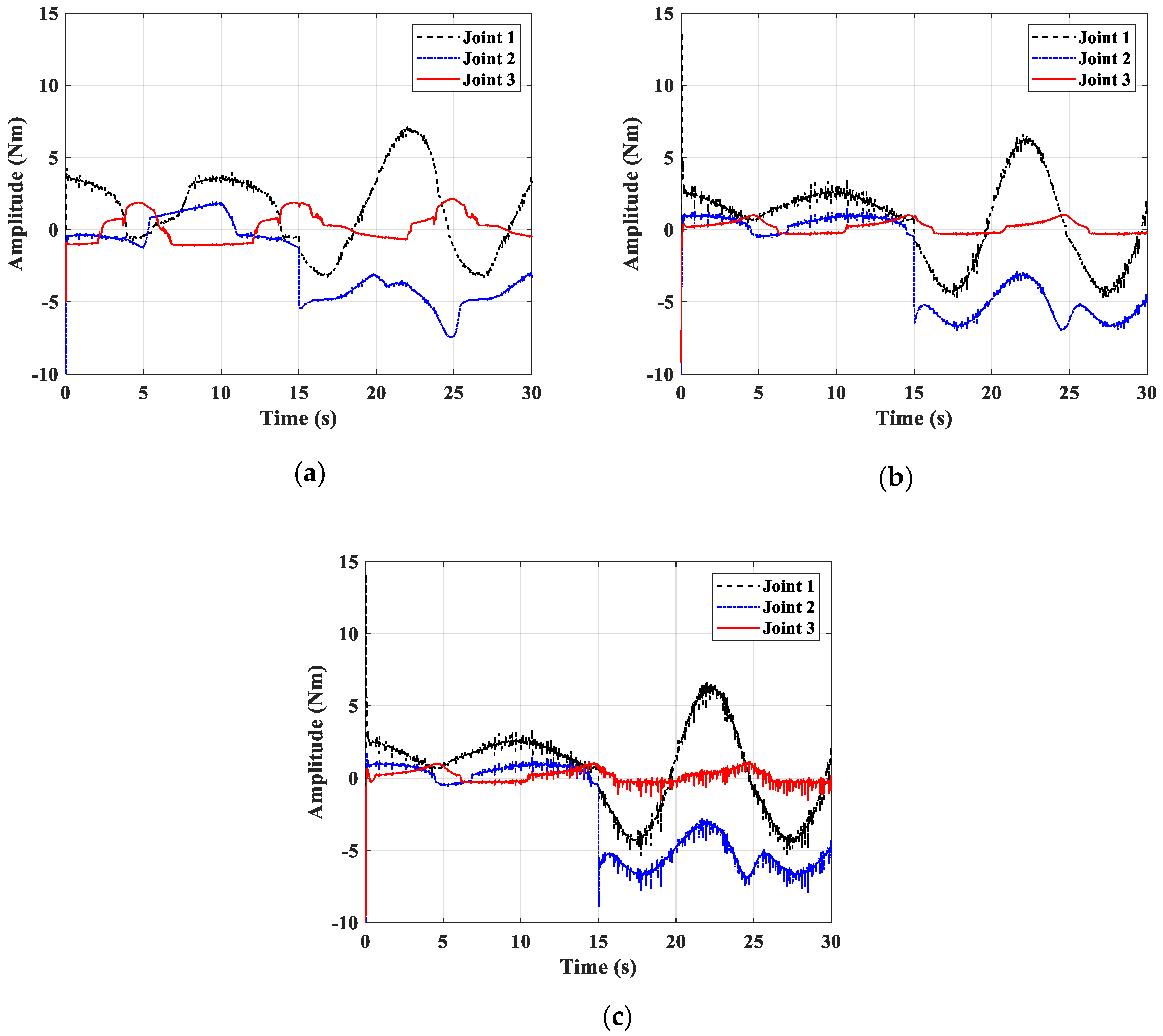
4.2. Simulation Results
- The backstepping control (BC):
- The linear extended state observer via backstepping control (LESOBC):where is the estimated lumped disturbance. This estimated lumped disturbance is approximated by the LESO in (9).
4.2.1. The First Simulation Case
4.2.2. The Second Simulation Case
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Baek, J.; Kwon, W.; Kim, B.; Han, S. A Widely adaptive time-delayed control and its application to robot manipulators. IEEE Trans. Ind. Electron. 2018, 66, 5332–5342. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005; Volume 3. [Google Scholar]
- Tran, D.T.; Truong, H.V.A.; Ahn, K.K. Adaptive backstepping sliding mode control based rbfnn for a hydraulic manipulator including actuator dynamics. Appl. Sci. 2019, 9, 1265. [Google Scholar] [CrossRef] [Green Version]
- Truong, H.V.A.; Tran, D.T.; To, X.D.; Ahn, K.K.; Jin, M. Adaptive fuzzy backstepping sliding mode control for a 3-DOF hydraulic manipulator with nonlinear disturbance observer for large payload variation. Appl. Sci. 2019, 9, 3290. [Google Scholar] [CrossRef] [Green Version]
- Tran, D.T.; Ba, D.X.; Ahn, K.K.; Thien, T.D. Adaptive backstepping sliding mode control for equilibrium position tracking of an electrohydraulic elastic manipulator. IEEE Trans. Ind. Electron. 2020, 67, 3860–3869. [Google Scholar] [CrossRef]
- Duc-Thien, T. Adaptive sliding mode control with backstepping technique for hydraulic manipulator. In Proceedings of the 33rd Institute of Control Robotics and Systems, Buan, Korea, 17 May 2018. [Google Scholar]
- Jung, S. Improvement of tracking control of a sliding mode controller for robot manipulators by a neural network. Int. J. Control. Autom. Syst. 2018, 16, 937–943. [Google Scholar] [CrossRef]
- Chen, K.Y. Robust Optimal Adaptive Sliding Mode Control with the Disturbance Observer for a Manipulator Robot System. Int. J. Control. Autom. Syst. 2018, 16, 1701–1715. [Google Scholar] [CrossRef]
- Nikdel, N.; Badamchizadeh, M.; Azimirad, V.; Nazari, M. Adaptive backstepping control for an n-degree of freedom robotic manipulator based on combined state augmentation. Robot. Comput. Manuf. 2017, 44, 129–143. [Google Scholar] [CrossRef]
- Chang, W.; Li, Y.; Tong, S. Adaptive fuzzy backstepping tracking control for flexible robotic manipulator. IEEE/CAA J. Autom. Sin. 2018, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Lee, H.; Han, S.; Lee, J. Adaptive Fuzzy Super-twisting Backstepping Control Design for MIMO Nonlinear Strict Feedback Systems. Int. J. Control. Autom. Syst. 2018, 16, 1165–1178. [Google Scholar] [CrossRef]
- Lv, W.; Wang, F.; Zhang, L. Adaptive fuzzy finite-time control for uncertain nonlinear systems with dead-zone input. Int. J. Control. Autom. Syst. 2018, 16, 2549–2558. [Google Scholar] [CrossRef]
- He, W.; Huang, B.; Dong, Y.; Li, Z.; Su, C.Y. Adaptive neural network control for robotic manipulators with unknown deadzone. IEEE Trans. Cybern. 2017, 48, 2670–2682. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.H. Nonlinear backstepping control design of LSM drive system using adaptive modified recurrent laguerre orthogonal polynomial neural network. Int. J. Control. Autom. Syst. 2017, 42, 494–917. [Google Scholar] [CrossRef]
- Lin, C.H.; Ting, J.C. Novel nonlinear backstepping control of synchronous reluctance motor drive system for position tracking of periodic reference inputs with torque ripple consideration. Int. J. Control. Autom. Syst. 2019, 17, 1–17. [Google Scholar] [CrossRef]
- Yi, G.; Mao, J.; Wang, Y.; Guo, S.; Miao, Z. Adaptive tracking control of nonholonomic mobile manipulators using recurrent neural networks. Int. J. Control. Autom. Syst. 2018, 16, 1390–1403. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. Extended-state-observer-based output feedback nonlinear robust control of hydraulic systems with backstepping. IEEE Trans. Ind. Electron. 2014, 61, 6285–6293. [Google Scholar] [CrossRef]
- Liu, J.; Gai, W.; Zhang, J.; Li, Y. Nonlinear adaptive backstepping with ESO for the quadrotor trajectory tracking control in the multiple disturbances. Int. J. Control. Autom. Syst. 2019, 17, 2754–2768. [Google Scholar] [CrossRef]
- Wang, J.; Hung, J.Y. Adaptive Backstepping Control for an Underwater Vehicle Manipulator System Using Fuzzy Logic. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Wu, Y.; Huang, R.; Li, X.; Liu, S. Adaptive neural network control of uncertain robotic manipulators with external disturbance and time-varying output constraints. Neurocomputing 2019, 323, 108–116. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Tran, D.T.; Do, T.C.; Ahn, K.K. Extended high gain observer-based sliding mode control for an electro-hydraulic system with a variant payload. Int. J. Precis. Eng. Manuf. 2019, 20, 2089–2100. [Google Scholar] [CrossRef]
- Jun, G.H.; Ahn, K.K. Extended-state-observer-based nonlinear servo control of an electro-hydrostatic actuator. J. Drive Control 2017, 14, 61–70. [Google Scholar]
- Chen, H.T.; Song, S.M.; Zhu, Z.B. Robust Finite-time Attitude Tracking Control of Rigid Spacecraft Under Actuator Saturation. Int. J. Control. Autom. Syst. 2018, 16, 1–15. [Google Scholar] [CrossRef]
- Mario, R.N.; Hebertt, S.R.; Rubén, G.M.; Alberto, L.J. Active Disturbance Rejection Control of the Inertia Wheel Pendulum through a Tangent Linearization Approach. Int. J. Control. Autom. Syst. 2019, 17, 18–28. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, J.; Tian, J. Robust output tracking control for a class of uncertain nonlinear systems using extended state observer. Int. J. Control. Autom. Syst. 2017, 15, 1227–1235. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive neural control for output feedback nonlinear systems using a barrier lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.G.; Yan, W.; Cui, R.; Annamalai, A. Admittance-based adaptive cooperative control for multiple manipulators with output constraints. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3621–3632. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Wu, Y.; Yu, J. Barrier Lyapunov functions-based adaptive control for nonlinear pure-feedback systems with time-varying full state constraints. Int. J. Control. Autom. Syst. 2017, 15, 2714–2722. [Google Scholar] [CrossRef]
- He, W.; David, A.O.; Yin, Z.; Sun, C. Neural network control of a robotic manipulator with input deadzone and output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 759–770. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Y.; Wang, Q.; Jiang, D. Adaptive neural network control of Two-DOF robotic arm driven by electro-hydraulic actuator with output constraint. In Proceedings of the IET Conference, Guiyang, China, 19–22 June 2018; p. 7. [Google Scholar]
- Zhou, Q.; Wang, L.; Wu, C.; Li, H.; Du, H. Adaptive fuzzy control for nonstrict-feedback systems with input saturation and output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1–12. [Google Scholar] [CrossRef]
- Edalati, L.; Sedigh, A.K.; Shooredeli, M.A.; Moarefianpour, A. Adaptive fuzzy dynamic surface control of nonlinear systems with input saturation and time-varying output constraints. Mech. Syst. Signal. Process. 2018, 100, 311–329. [Google Scholar] [CrossRef]
- Mien, V.; Mavrovouniotis, M.; Ge, S.S. An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1448–1458. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Sun, J.; Xia, Y.; Zhao, L. Position control for magnetic rodless cylinders with strong static friction. IEEE Trans. Ind. Electron. 2018, 65, 5806–5815. [Google Scholar] [CrossRef]
- Tran, D.T.; Jin, M.; Ahn, K.K. Nonlinear extended state observer based on output feedback control for a manipulator with time-varying output constraints and external disturbance. IEEE Access 2019, 7, 156860–156870. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S. Backstepping control of electro-hydraulic system based on extended-state-observer with plant dynamics largely unknown. IEEE Trans. Ind. Electron. 2016, 63, 6909–6920. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, L.; Yu, H.; Lin, C. Barrier Lyapunov functions-based command filtered output feedback control for full-state constrained nonlinear systems. Automatica 2019, 105, 71–79. [Google Scholar] [CrossRef]
- Huang, A.C.; Chien, M.C. Adaptive Control of Robot Manipulators: A Unified Regressor-Free Approach; World Scientific: Singapore, 2010. [Google Scholar]







| Symbol | Description | Symbol | Description |
|---|---|---|---|
| l1 = 0.35 m | Length of 1st link | m1 = 0.23 kg | Mass of 1st link |
| l2 = 0.3 m | Length of 2nd link | m2 = 0.2 kg | Mass of 2nd link |
| l3 = 0.15 m | Length of 3rd link | m3 = 0.1 kg | Mass of 3rd link |
| g = 9.81 ms−2 | Gravity constant | - | - |
| Controllers | Parameters |
|---|---|
| Backstepping control | , ; |
| LESOBC | , ; |
| Proposed control | , ; , , |
| Controllers | 1st Joint (Deg) | 2nd Joint (Deg) | 3rd Joint (Deg) |
|---|---|---|---|
| Backstepping control | 24.5205 | 47.3142 | 43.4415 |
| LESOBC | 0.0055 | 0.008 | 0.0038 |
| Proposed control | 0.0001 | 0.0001 | 0.0001 |
| Controllers | 1st Joint (Deg) | 2nd Joint (Deg) | 3rd Joint (Deg) |
|---|---|---|---|
| Backstepping control | 30.4138 | 52.7901 | 115.0904 |
| ESOBC | 0.2315 | 0.1260 | 0.6836 |
| Proposed control | 0.0159 | 0.0179 | 0.0197 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, D.T.; Dao, H.V.; Dinh, T.Q.; Ahn, K.K. Output Feedback Control via Linear Extended State Observer for an Uncertain Manipulator with Output Constraints and Input Dead-Zone. Electronics 2020, 9, 1355. https://doi.org/10.3390/electronics9091355
Tran DT, Dao HV, Dinh TQ, Ahn KK. Output Feedback Control via Linear Extended State Observer for an Uncertain Manipulator with Output Constraints and Input Dead-Zone. Electronics. 2020; 9(9):1355. https://doi.org/10.3390/electronics9091355
Chicago/Turabian StyleTran, Duc Thien, Hoang Vu Dao, Truong Quang Dinh, and Kyoung Kwan Ahn. 2020. "Output Feedback Control via Linear Extended State Observer for an Uncertain Manipulator with Output Constraints and Input Dead-Zone" Electronics 9, no. 9: 1355. https://doi.org/10.3390/electronics9091355






