The k-means Algorithm: A Comprehensive Survey and Performance Evaluation
Abstract
1. Introduction
- Existing solutions of the k-means algorithm along with a taxonomy are outlined and discussed in order to augment the understanding of these variants and their relationships.
- This research frames the problems, analyses their solutions and presents a concrete study on advances in the development of the k-means algorithm.
- Experiments are performed using the improved k-means algorithms to find out their effectiveness using six benchmark datasets.
Paper Roadmap
2. k-means Variants for Solving the Problem of Initialization
3. k-means Variants for Solving the Problem of Data Issue
4. Performance Evaluation of k-means Representative Variants
4.1. Metrics Used for Experimental Analysis
- Accuracy: This measure outlines the extent to which the predicted labels are in agreement with the true labels. The predicted labels correspond to the class labels where new instances are clustered. The accuracy is calculated by Equation (1).
- Adjusted rand index (ARI): Provides a score of similarity between two different clustering results of the same dataset. For a given set S consisting of elements and r subsets and two partitions and , the overlap between the two partitions can be summarized as follows:The adjusted rand index (ARI) is then calculated by Equation (2):The ARI score is adjusted to have values between 0 and 1 to represent scores for random and perfect clustering, respectively.
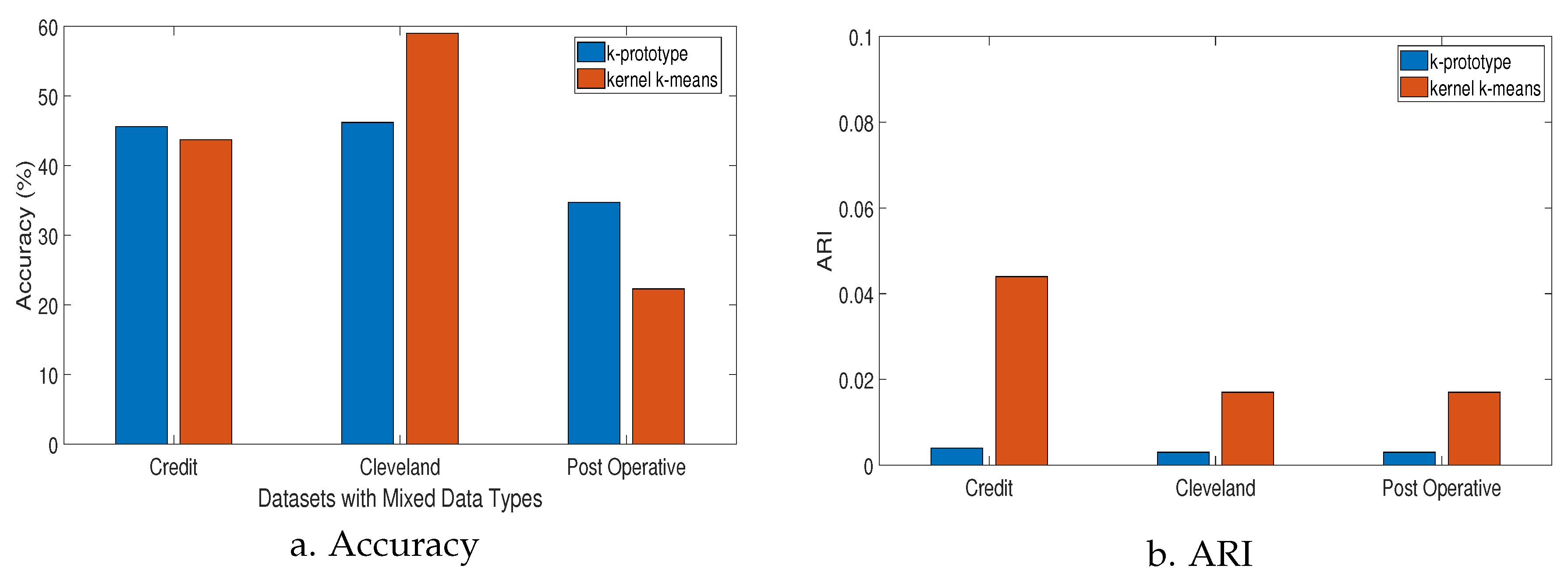
4.2. Results
4.3. Computational Complexity Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Ahmed, M.; Choudhury, V.; Uddin, S. Anomaly detection on big data in financial markets. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Sydney, Australia, 31 July–3 August 2017; pp. 998–1001. [Google Scholar]
- Ahmed, M. An unsupervised approach of knowledge discovery from big data in social network. EAI Endorsed Trans. Scalable Inf. Syst. 2017, 4, 9. [Google Scholar] [CrossRef][Green Version]
- Ahmed, M. Collective anomaly detection techniques for network traffic Analysis. Ann. Data Sci. 2018, 5, 497–512. [Google Scholar] [CrossRef]
- Tondini, S.; Castellan, C.; Medina, M.A.; Pavesi, L. Automatic initialization methods for photonic components on a silicon-based optical switch. Appl. Sci. 2019, 9, 1843. [Google Scholar] [CrossRef]
- Ahmed, M.; Mahmood, A.N.; Islam, M.R. A survey of anomaly detection techniques in financial domain. Future Gener. Comput. Syst. 2016, 55, 278–288. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 1 January 1967; pp. 281–297. [Google Scholar]
- Su, M.C.; Chou, C.H. A modified version of the k-means algorithm with a distance based on cluster symmetry. IEEE Trans. Patternanal. Mach. Intell. 2001, 23, 674–680. [Google Scholar]
- Cabria, I.; Gondra, I. Potential-k-means for load balancing and cost minimization in mobile recycling network. IEEE Syst. J. 2014, 11, 242–249. [Google Scholar] [CrossRef]
- Xu, T.S.; Chiang, H.D.; Liu, G.Y.; Tan, C.W. Hierarchical k-means method for clustering large-scale advanced metering infrastructure data. IEEE Trans. Power Deliv. 2015, 32, 609–616. [Google Scholar] [CrossRef]
- Qin, J.; Fu, W.; Gao, H.; Zheng, W.X. Distributed k-means algorithm and fuzzy c-means algorithm for sensor networks based on multiagent consensus theory. IEEE Trans. Cybern. 2016, 47, 772–783. [Google Scholar] [CrossRef]
- Liu, H.; Wu, J.; Liu, T.; Tao, D.; Fu, Y. Spectral ensemble clustering via weighted k-means: Theoretical and practical evidence. IEEE Trans. Knowl. Data Eng. 2017, 29, 1129–1143. [Google Scholar] [CrossRef]
- Adapa, B.; Biswas, D.; Bhardwaj, S.; Raghuraman, S.; Acharyya, A.; Maharatna, K. Coordinate rotation-based low complexity k-means clustering Architecture. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 1568–1572. [Google Scholar] [CrossRef]
- Jang, H.; Lee, H.; Lee, H.; Kim, C.K.; Chae, H. Sensitivity enhancement of dielectric plasma etching endpoint detection by optical emission spectra with modified k-means cluster analysis. IEEE Trans. Semicond. Manuf. 2017, 30, 17–22. [Google Scholar] [CrossRef]
- Yuan, J.; Tian, Y. Practical privacy-preserving mapreduce based k-means clustering over large-scale dataset. IEEE Trans. Cloud Comput. 2017, 7, 568–579. [Google Scholar]
- Xu, J.; Han, J.; Nie, F.; Li, X. Re-weighted discriminatively embedded k-means for multi-view clustering. IEEE Trans. Image Process. 2017, 26, 3016–3027. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Peng, M. A data mining approach combining k-means clustering with bagging neural network for short-term wind power forecasting. IEEE Internet Things J. 2017, 4, 979–986. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J. Tag clustering algorithm lmmsk: Improved k-means algorithm based on latent semantic analysis. J. Syst. Electron. 2017, 28, 374–384. [Google Scholar]
- Zeng, X.; Li, Z.; Gao, W.; Ren, M.; Zhang, J.; Li, Z.; Zhang, B. A novel virtual sensing with artificial neural network and k-means clustering for igbt current measuring. IEEE Trans. Ind. Electron. 2018, 65, 7343–7352. [Google Scholar] [CrossRef]
- He, L.; Zhang, H. Kernel k-means sampling for nyström approximation. IEEE Trans. Image Process. 2018, 27, 2108–2120. [Google Scholar] [CrossRef]
- Manju, V.N.; Fred, A.L. Ac coefficient and k-means cuckoo optimisation algorithm-based segmentation and compression of compound images. IET Image Process. 2017, 12, 218–225. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Sun, Y.; Long, T.; Sarkar, T.K. Fast and robust rbf neural network based on global k-means clustering with adaptive selection radius for sound source angle estimation. IEEE Trans. Antennas Propag. 2018, 66, 3097–3107. [Google Scholar] [CrossRef]
- Bai, L.; Liang, J.; Guo, Y. An ensemble clusterer of multiple fuzzy k-means clusterings to recognize arbitrarily shaped clusters. IEEE Trans. Fuzzy Syst. 2018, 26, 3524–3533. [Google Scholar] [CrossRef]
- Schellekens, V.; Jacques, L. Quantized compressive k-means. IEEE Signal. Process. Lett. 2018, 25, 1211–1215. [Google Scholar]
- Alhawarat, M.; Hegazi, M. Revisiting k-means and topic modeling, a comparison study to cluster arabic documents. IEEE Access 2018, 6, 740–749. [Google Scholar] [CrossRef]
- Wang, X.D.; Chen, R.C.; Yan, F.; Zeng, Z.Q.; Hong, C.Q. Fast adaptive k-means subspace clustering for high-dimensional data. IEEE Access 2019, 7, 639–651. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, E.; Hu, J.; Li, M.; Zhao, K.; Hu, N.; Liu, X. Efficient multiple kernel k-means clustering with late fusion. IEEE Access 2019, 7, 109–120. [Google Scholar] [CrossRef]
- Kwedlo, W.; Czochanski, P.J. A hybrid mpi/openmp parallelization of k-means algorithms accelerated using the triangle inequality. IEEE Access 2019, 7, 280–297. [Google Scholar] [CrossRef]
- Karlekar, A.; Seal, A.; Krejcar, O.; Gonzalo-Martin, C. Fuzzy k-means using non-linear s-distance. IEEE Access 2019, 7, 121–131. [Google Scholar] [CrossRef]
- Gu, Y.; Li, K.; Guo, Z.; Wang, Y. Semi-supervised k-means ddos detection method using hybrid feature selection algorithm. IEEE Access 2019, 7, 351–365. [Google Scholar] [CrossRef]
- Lee, M. Non-alternating stochastic k-means based on probabilistic representation of solution space. Electron. Lett. 2019, 55, 605–607. [Google Scholar] [CrossRef]
- Ahmed, M. Data summarization: A survey. Knowl. Inf. Syst. 2019, 58, 249–273. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Philip, S.Y.; et al. Top 10 algorithms in data Mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Tian, K.; Zhou, S.; Guan, J. Deepcluster: A general clustering framework based on deep learning. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Skopje, Macedonia, 18–22 September 2017; pp. 809–825. [Google Scholar]
- He, B.; Qiao, F.; Chen, W.; Wen, Y. Fully convolution neural network combined with k-means clustering algorithm for image segmentation. In Proceedings of the Tenth International Conference on Digital Image Processing (ICDIP 2018), Shanghai, China, 11–14 May 2018; Volume 10806, pp. 1–7. [Google Scholar]
- Yang, M.S. A survey of fuzzy clustering. Math. Comput. 1993, 18, 1–16. [Google Scholar] [CrossRef]
- Filippone, M.; Camastra, F.; Masulli, F.; Rovetta, S. A survey of kernel and spectral methods for clustering. Pattern Recognit. 2008, 41, 176–190. [Google Scholar] [CrossRef]
- Rai, P.; Singh, S. A survey of clustering techniques. Int. Comput. Appl. 2010, 7, 1–5. [Google Scholar] [CrossRef]
- Yu, H.; Wen, G.; Gan, J.; Zheng, W.; Lei, C. Self-paced learning for k-means clustering algorithm. Pattern Recognit. Lett. 2018. [Google Scholar] [CrossRef]
- Ye, S.; Huang, X.; Teng, Y.; Li, Y. K-means clustering algorithm based on improved cuckoo search algorithm and its application. In Proceedings of the 2018 IEEE 3rd International Conference on Big Data Analysis (ICBDA), Shanghai, China, 9–12 March 2018; pp. 422–426. [Google Scholar]
- Ben-David, S.; Von Luxburg, U.; Pál, D. A sober look at clustering stability. In Proceedings of the International Conference on Computational Learning Theory, San Diego, CA, USA, 13–15 June 2006; pp. 5–19. [Google Scholar]
- Bubeck, S.; Meilă, M.; von Luxburg, U. How the initialization affects the stability of the k-means algorithm. ESAIM Probab. Stat. 2012, 16, 436–452. [Google Scholar] [CrossRef]
- Melnykov, I.; Melnykov, V. On k-means algorithm with the use of mahalanobis Distances. Stat. Probab. Lett. 2014, 84, 88–95. [Google Scholar] [CrossRef]
- Ball, G.H.; Hall, D.J. A clustering technique for summarizing multivariate data. Syst. Res. Behav. Sci. 1967, 12, 153–155. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S. A massively parallel architecture for a self-organizing neural pattern recognition machine. Comput. Vis. Graph. Image Process. 1987, 37, 54–115. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Clustering; Wiley-IEEE Press: Piscataway, NJ, USA, 2009. [Google Scholar]
- Pelleg, D.; Moore, A.W. X-means: Extending k-means with efficient estimation of the number of clusters. In Proceedings of the 17th International Conference on Machine Learning, Stanford, CA, USA, 29 June–2 July 2000; Volume 1, pp. 727–734. [Google Scholar]
- Bozdogan, H. Model selection and akaike’s information criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Ahmed, M.; Barkat Ullah, A.S.S.M. Infrequent pattern mining in smart healthcare environment using data summarization. J. Supercomput. 2018, 74, 5041–5059. [Google Scholar] [CrossRef]
- Ahmed, M.; Mahmood, A. Network traffic analysis based on collective anomaly Detection. In Proceedings of the 9th IEEE International Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2004; pp. 1141–1146. [Google Scholar]
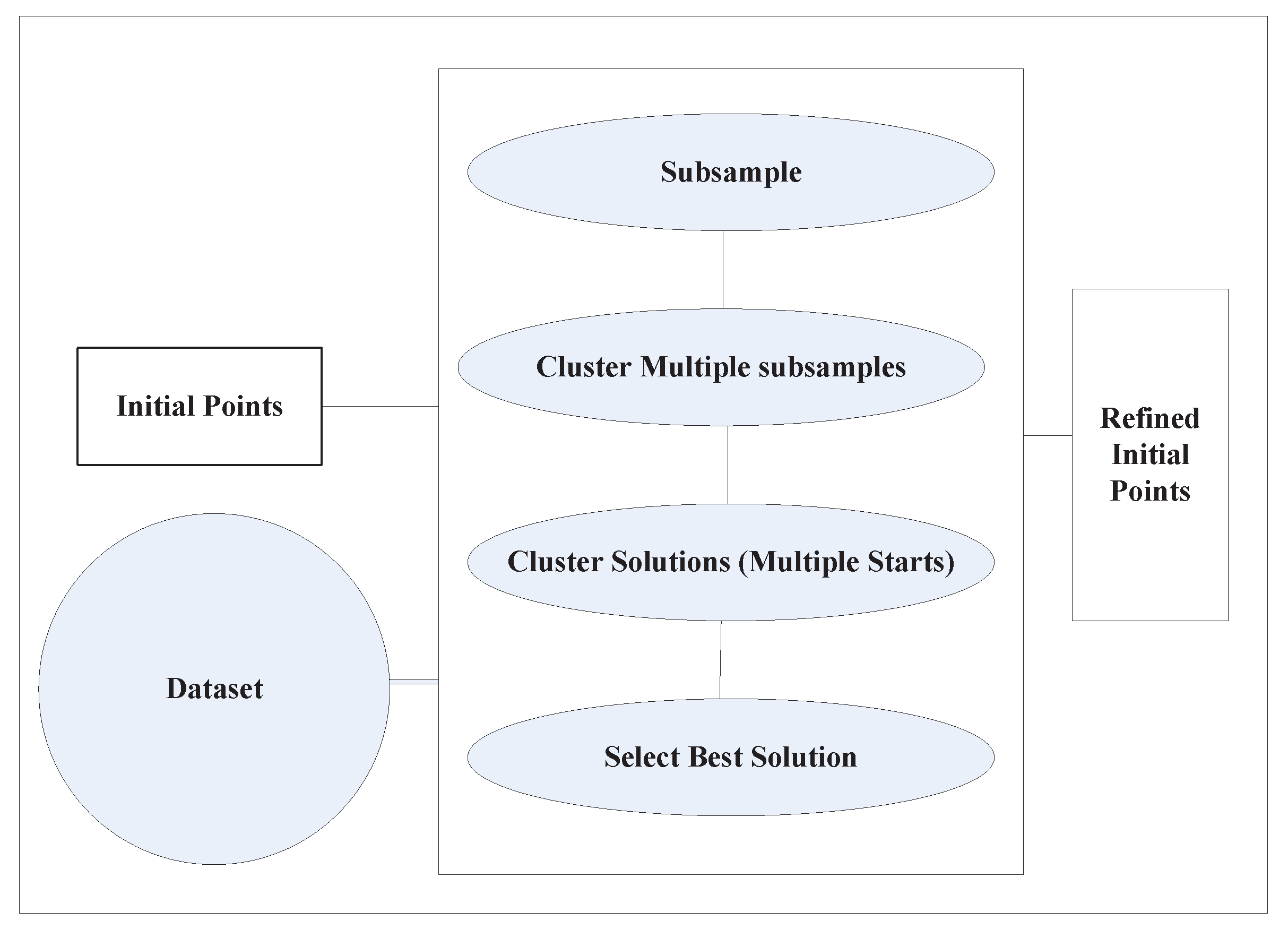
- Bradley, P.S.; Fayyad, U.M. Refining initial points for k-means Clustering. ICML 1998, 98, 91–99. [Google Scholar]
- Pena, J.M.; Lozano, J.A.; Larranaga, P. An empirical comparison of four initialization methods for the k-means algorithm. Pattern Recognit. Lett. 1999, 20, 1027–1040. [Google Scholar] [CrossRef]
- Forgy, E.W. Cluster analysis of multivariate data: Efficiency versus interpretability of classifications. Biometrics 1965, 21, 768–769. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]
- Hussain, S.F.; Haris, M. A k-means based co-clustering (kcc) algorithm for sparse, high dimensional data. Expert Syst. Appl. 2019, 118, 20–34. [Google Scholar] [CrossRef]
- Gupta, S.; Rao, K.S.; Bhatnagar, V. K-means clustering algorithm for categorical attributes. In Proceedings of the International Conference on Data Warehousing and Knowledge Discovery, Florence, Italy, 30 August–1 September 1999; pp. 203–208. [Google Scholar]
- Jiacai, W.; Ruijun, G. An extended fuzzy k-means algorithm for clustering categorical valued data. In Proceedings of the 2010 International Conference on Artificial Intelligence and Computational Intelligence (AICI), Sanya, China, 23–24 October 2010; Volume 2, pp. 504–507. [Google Scholar]
- Ahmad, A.; Dey, L. A k-mean clustering algorithm for mixed numeric and categorical data. Data Knowl. Eng. 2007, 63, 503–527. [Google Scholar] [CrossRef]
- Couto, J. Kernel k-means for categorical data. In International Symposium on Intelligent Data Analysis; Springer: Berlin, Germany, 2005; pp. 46–56. [Google Scholar]
- Huang, Z. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Bai, L.; Liang, J.; Dang, C.; Cao, F. The impact of cluster representatives on the convergence of the k-modes type clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1509–1522. [Google Scholar] [CrossRef]
- Dzogang, F.; Marsala, C.; Lesot, M.; Rifqi, M. An ellipsoidal k-means for document clustering. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining (ICDM), Brussels, Belgium, 10–13 December 2012; pp. 221–230. [Google Scholar]
- Jing, L.; Ng, M.K.; Huang, J.Z. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data. IEEE Trans. Knowl. Data Eng. 2007, 19, 1026–1041. [Google Scholar] [CrossRef]
- Cramér, H. The Elements of Probability Theory and Some of Its Applications; John Wiley & Sons: New York, NY, USA, 1954. [Google Scholar]
- Maung, K. Measurement of association in a contingency table with special reference to the pigmentation of hair and eye colours of scottish school children. Ann. Eugen. 1941, 11, 189–223. [Google Scholar] [CrossRef]
- Pearson, K. On the general theory of multiple contingency with special reference to partial contingency. Biometrika 1916, 11, 145–158. [Google Scholar] [CrossRef]
- Stanfill, C.; Waltz, D. Toward memory-based reasoning. Commun. ACM 1986, 29, 1213–1228. [Google Scholar] [CrossRef]
- Boriah, S.; Chandola, V.; Kumar, V. Similarity measures for categorical data: A comparative evaluation. In Proceedings of the SIAM International Conference on Data Mining, Atlanta, GA, USA, 24–26 April 2008; pp. 243–254. [Google Scholar]
- Ahmed, M. Detecting Rare and Collective Anomalies in Network Traffic Data Using Summarization. 2016. Available online: http://handle.unsw.edu.au/1959.4/56990 (accessed on 29 May 2020).
- Dheeru, D.; Karra Taniskidou, E. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml (accessed on 29 May 2020).
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering Algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Pakhira, M.K. A linear time-complexity k-means algorithm using cluster Shifting. In Proceedings of the 2014 International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 14–16 November 2014; pp. 1047–1051. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and Implementation. IEEE Trans. Pattern Anal. Mach. 2002, 7, 881–892. [Google Scholar] [CrossRef]
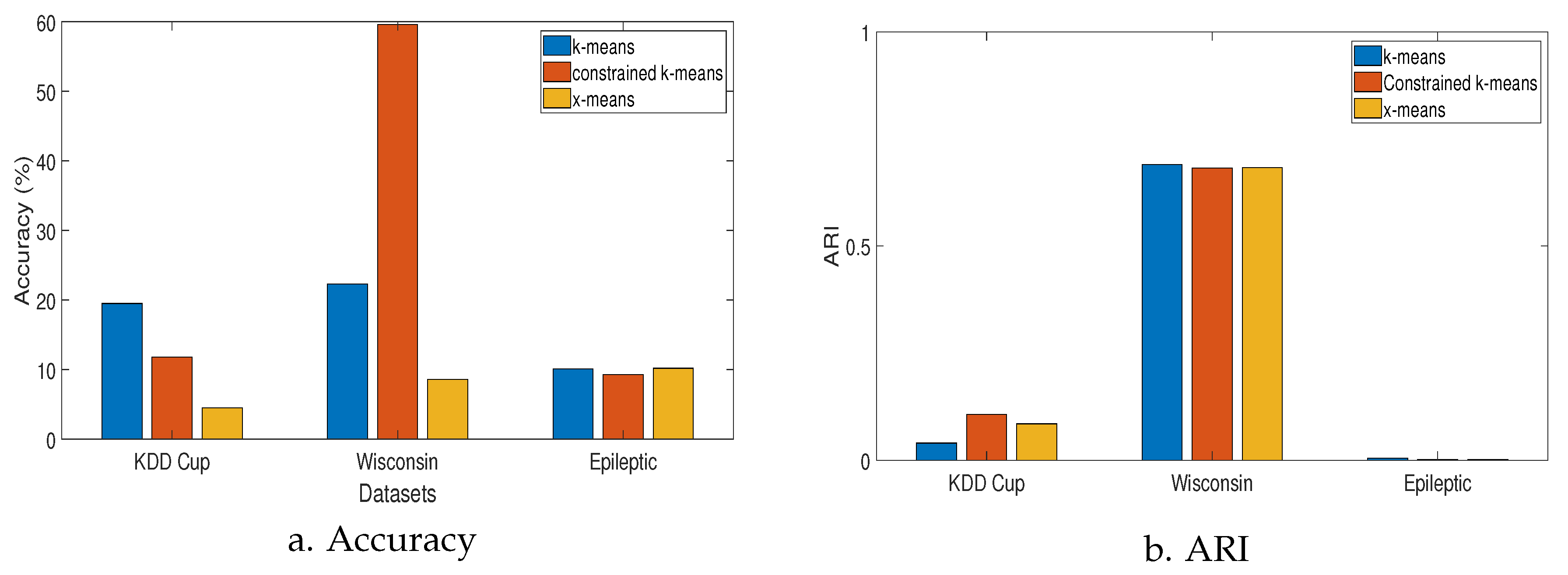
| Reference | Application | Algorithm |
|---|---|---|
| [10] | Face detection | Symmetry-based version of k-means (SBKM). |
| [11] | Mobile storage positioning | Potential k-means. |
| [12] | Load pattern | Hierarchical k-means (H-Kmeans). |
| [13] | Wireless sensor networks | Distributed k-means and fuzzy c-means. |
| [14] | Partial multiview data | Weighted k-means. |
| [15] | Mobile health | k-means implemented with CORDIC. |
| [16] | Endpoint detection | k-means for realtime detection. |
| [17] | Big data | Privacy preserving k-means. |
| [18] | Multiview data | k-means. |
| [19] | Wind power forecasting | k-means with bagging neural network. |
| [20] | Social tags | k-means based on latent semantic analysis. |
| [21] | Sensing for IGBT current | k-means with neural network. |
| [22] | Image segmentation. | Kernel k-means Nystrom approximation. |
| [23] | Image compression | k-means cuckoo optimization. |
| [24] | Sound source angle estimation. | Neural network based on global k-means. |
| [25] | Shape recognition | Fuzzy k-means clustering ensemble (FKMCE). |
| [26] | Signal processing | Compressive k-means clustering (CKM). |
| [27] | Text processing | Vanilla k-means. |
| [28] | High dimensional data processing | Fast adaptive k-means (FAKM). |
| [29] | Computational complexity | Multiple kernel k-means with late fusion. |
| [30] | Image processing | A hybrid parallelization of k-means algorithm. |
| [31] | Adaptive clustering | Fuzzy k-means with S-distance. |
| [32] | DDoS detection | Semi-supervised k-means algorithm with hybrid feature. |
| [33] | Optimization | Non alternating stochastic k-means. |
| [34] | Data Summarization | Modified x-means. |
| Survey | Initialization | Data Types | Applications | Experiments |
|---|---|---|---|---|
| Yang [38] | ✓ | × | × | × |
| Filippone [39] | ✓ | × | × | × |
| Rai [40] | ✓ | × | × | × |
| This paper | ✓ | ✓ | ✓ | ✓ |
| Dataset | Summary |
|---|---|
| Cleveland Heart Disease | Widely used by machine learning researchers. The goal is to detect the presence of heart disease in a patient. |
| KDD-Cup 1999(10%) | Contains standard network traffic that contains different types of cyber attacks simulated in a military network. |
| Wisconsin Diagnostic Breast Cancer | Includes features calculated from the images of fine needle aspirate of breast mass. |
| Epileptic Seizure Recognition | Commonly used for feature epileptic seizure prediction. |
| Credit Approval | Contains a mix of attributes, which makes it interesting to be used with k-means for mixed attributes. |
| Postoperative | Contains both categorical and integer values. The missing values are replaced with an average. |
| Metric | k-means | Constrained k-means | x-means |
|---|---|---|---|
| Wisconsin Diagnostic Breast Cancer | |||
| Accuracy | |||
| ARI | |||
| KDD Cup 1999 | |||
| Accuracy | |||
| ARI | |||
| Epileptic Seizure | |||
| Accuracy | |||
| ARI | |||
| Metric | k-prototype | Kernel-k-means |
|---|---|---|
| Credit Approval | ||
| Accuracy | ||
| ARI | ||
| Cleveland Heart Disease | ||
| Accuracy | ||
| ARI | ||
| Post Operative | ||
| Accuracy | ||
| ARI | ||
| Complexity | k-means | Constrained-k-means | x-means |
|---|---|---|---|
| Time | |||
| Space |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. https://doi.org/10.3390/electronics9081295
Ahmed M, Seraj R, Islam SMS. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics. 2020; 9(8):1295. https://doi.org/10.3390/electronics9081295
Chicago/Turabian StyleAhmed, Mohiuddin, Raihan Seraj, and Syed Mohammed Shamsul Islam. 2020. "The k-means Algorithm: A Comprehensive Survey and Performance Evaluation" Electronics 9, no. 8: 1295. https://doi.org/10.3390/electronics9081295
APA StyleAhmed, M., Seraj, R., & Islam, S. M. S. (2020). The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics, 9(8), 1295. https://doi.org/10.3390/electronics9081295







