Simplified Modal-Cancellation Approach for Substrate-Integrated-Waveguide Narrow-Band Filter Design
Abstract
1. Introduction
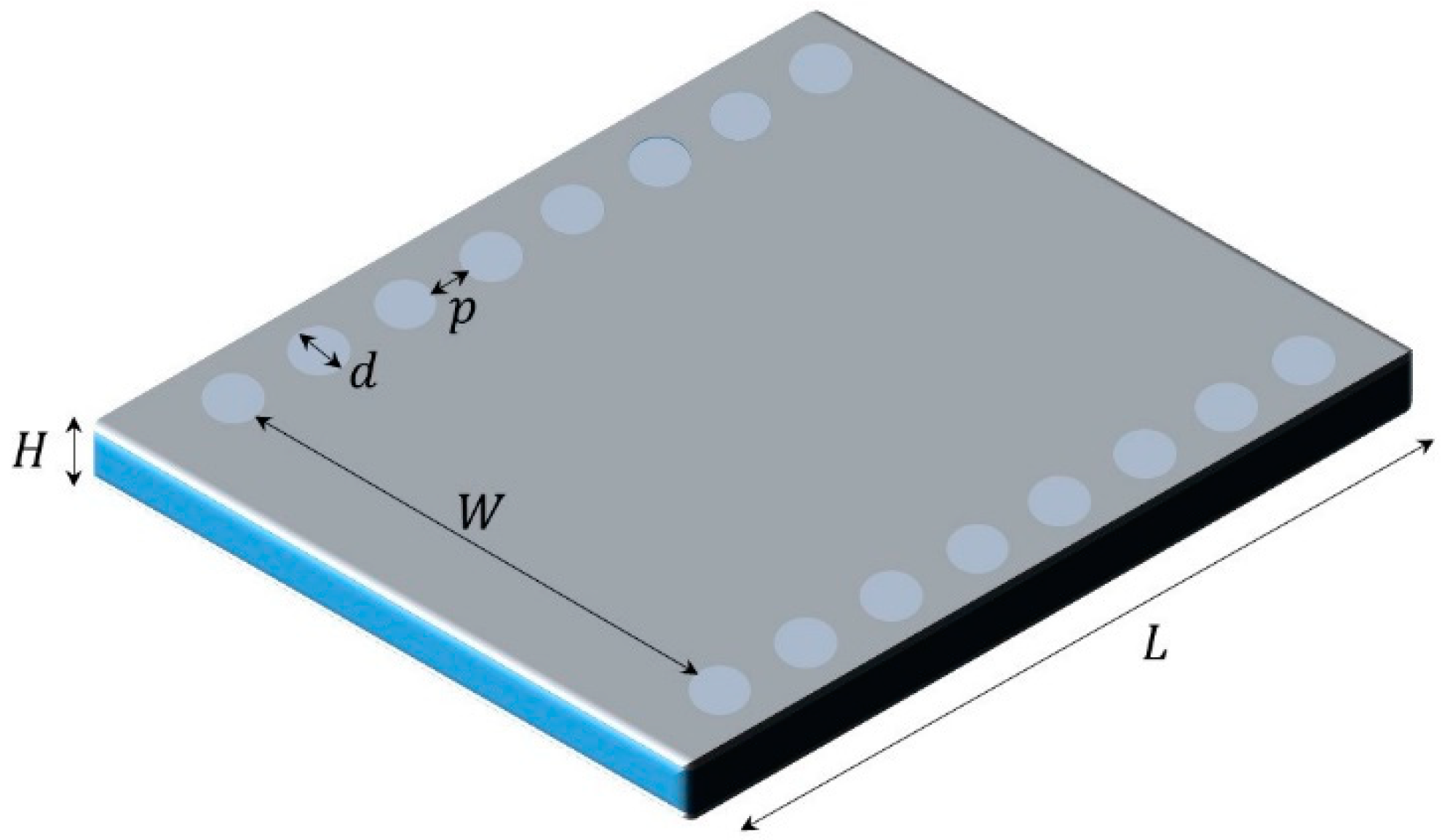
2. Materials and Methods
2.1. Mode Selection
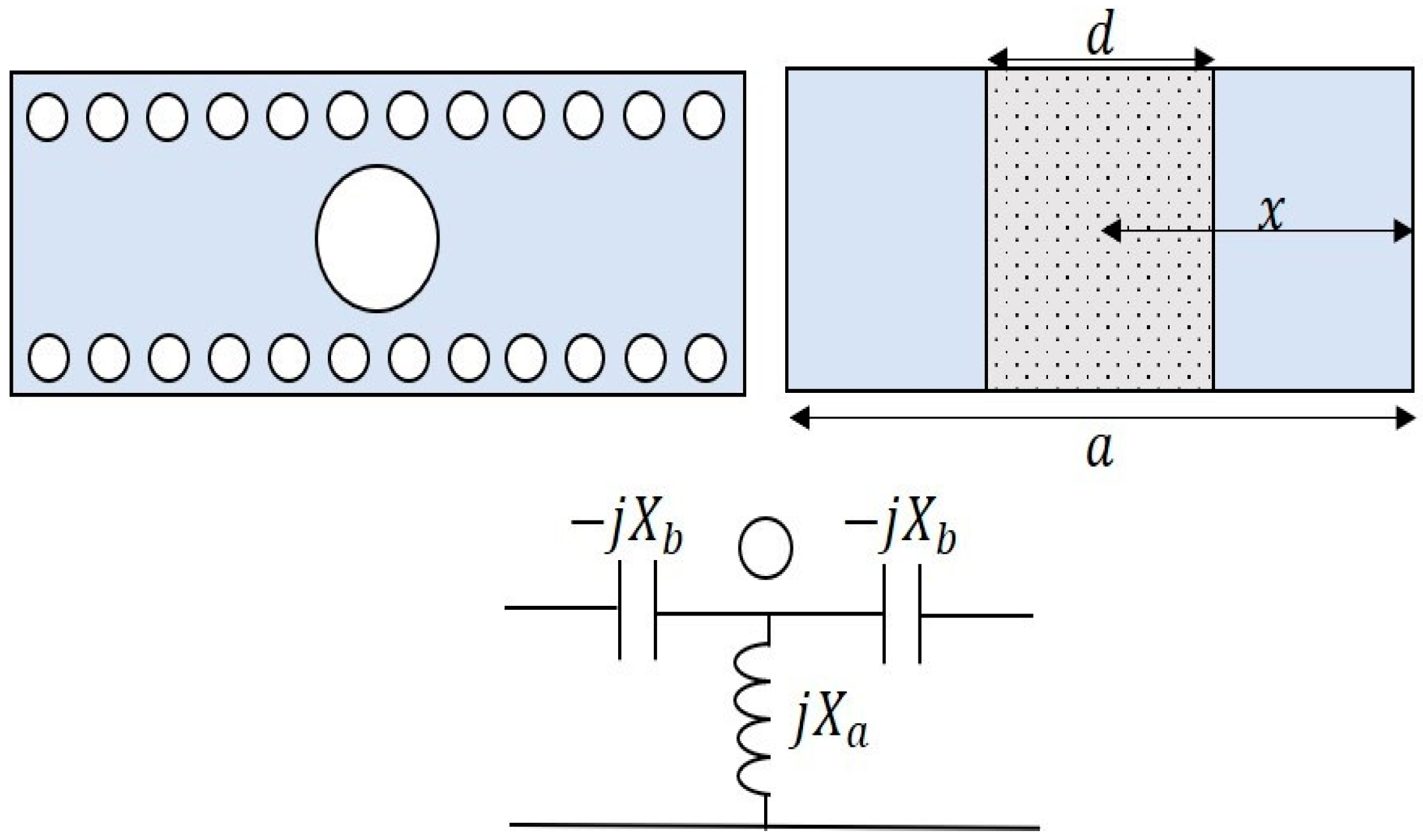
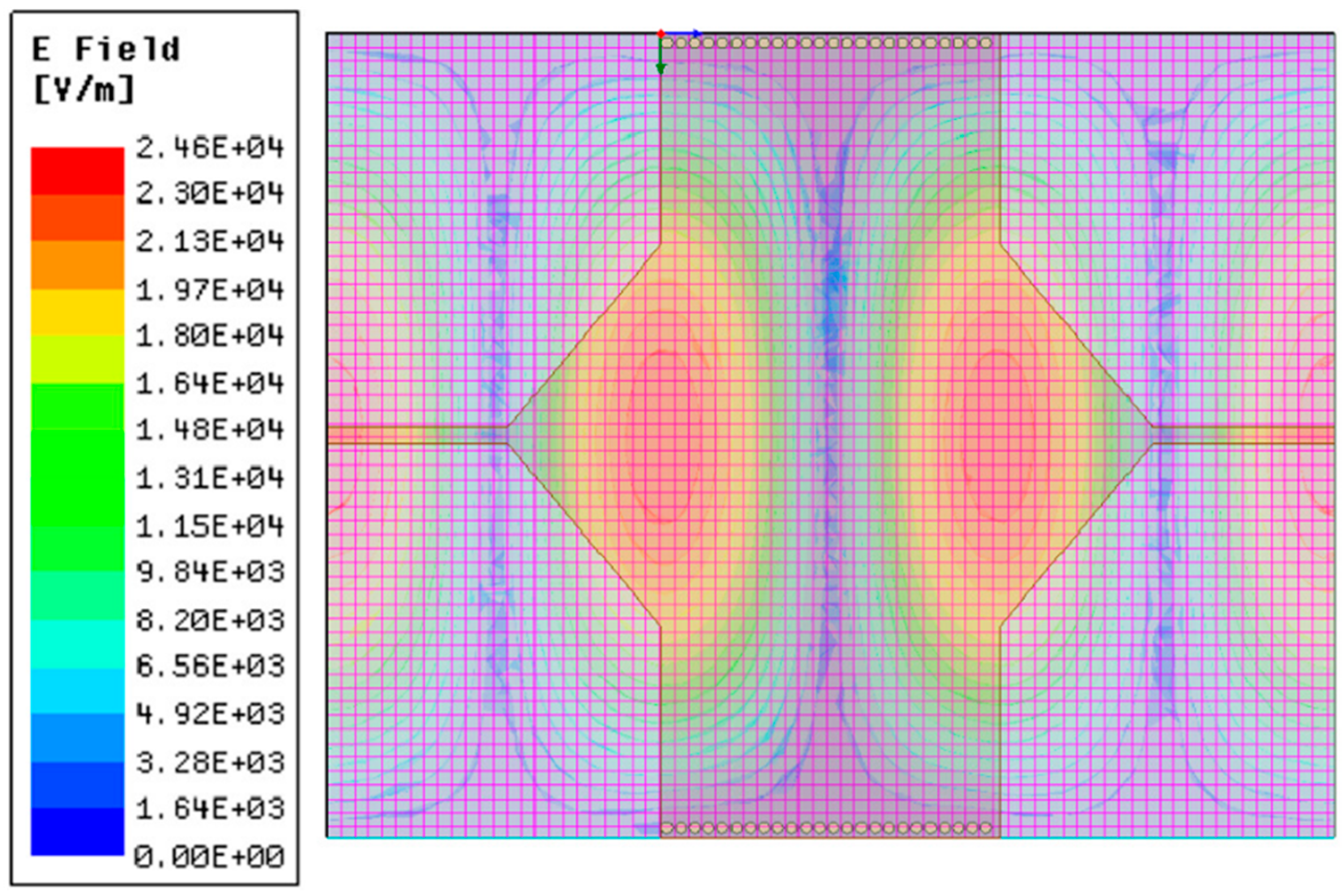
2.2. Mode Cancellation Using Inductive Obstacles
| Algorithm 1 Defining frequency-selective obstacles. |
 |
3. Results
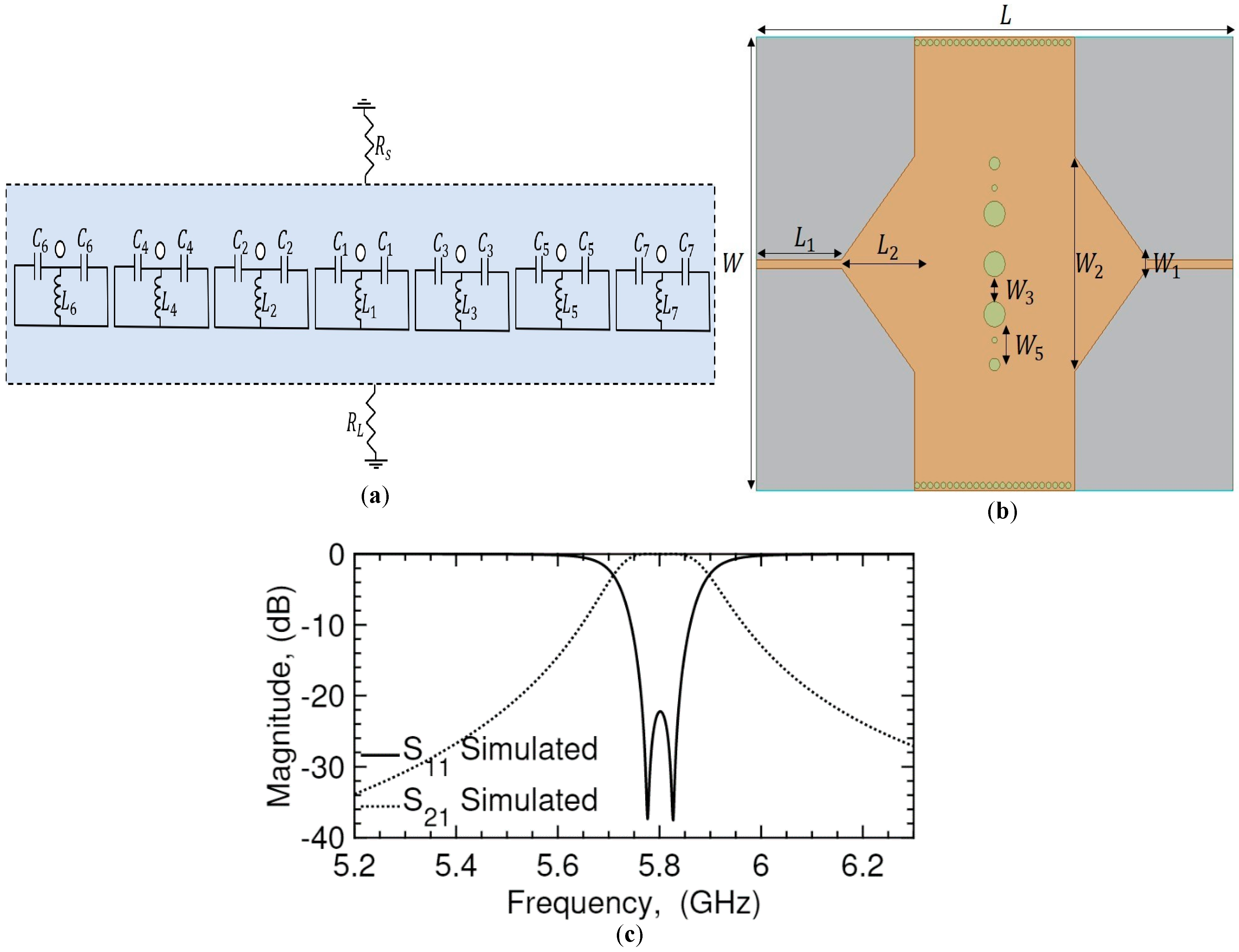
3.1. Narrow-Band Filter Design
- Multiple transverse electromagnetic modes should be tested.
- Verify the effect of the microstrip–SIW transition for different modes. For the sake of simplicity, the first filter was modeled as a no tapered SIW–microstrip transition.
- Different materials were tested using the proposed methodology. Complementary-metal-oxide-semiconductor (CMOS) integration requires the use of silicon (undoped silicon with ) as the substrate of the SIW devices, while traditional radio-frequency (RF) circuitry uses common FR4 and Rogers substrates.
- Devices with minimal sizes are always desired; for this, varying thicknesses of silicon were tested for different frequency ranges.
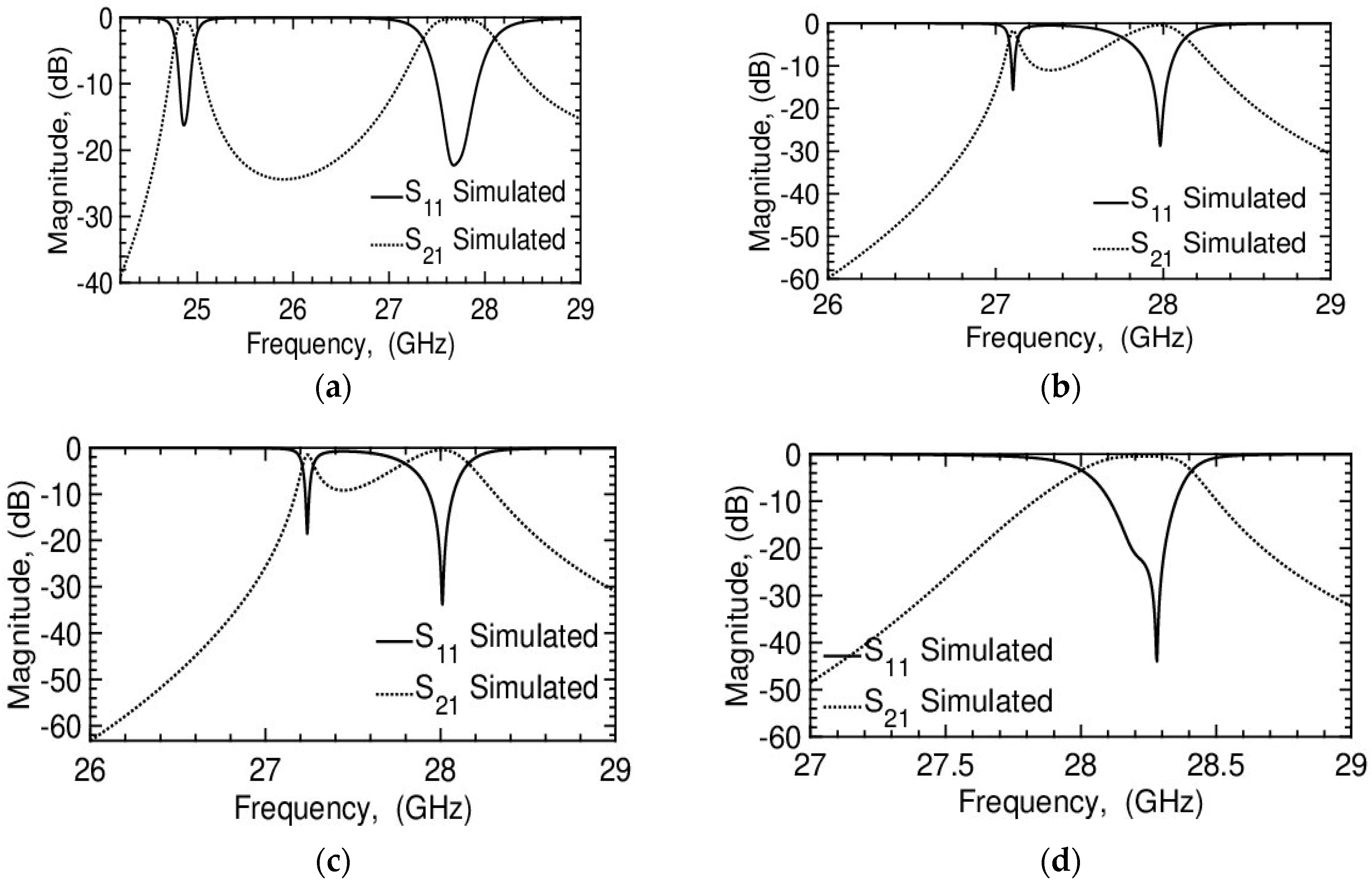
3.1.1. 28 GHz Filter Based on Smart Modal Selection
| Algorithm 2: Application of Algorithm 1 on the design of 28 GHz narrow-band filter. |
 |
3.1.2. 5.8 GHz Filter Based on Smart Modal Selection
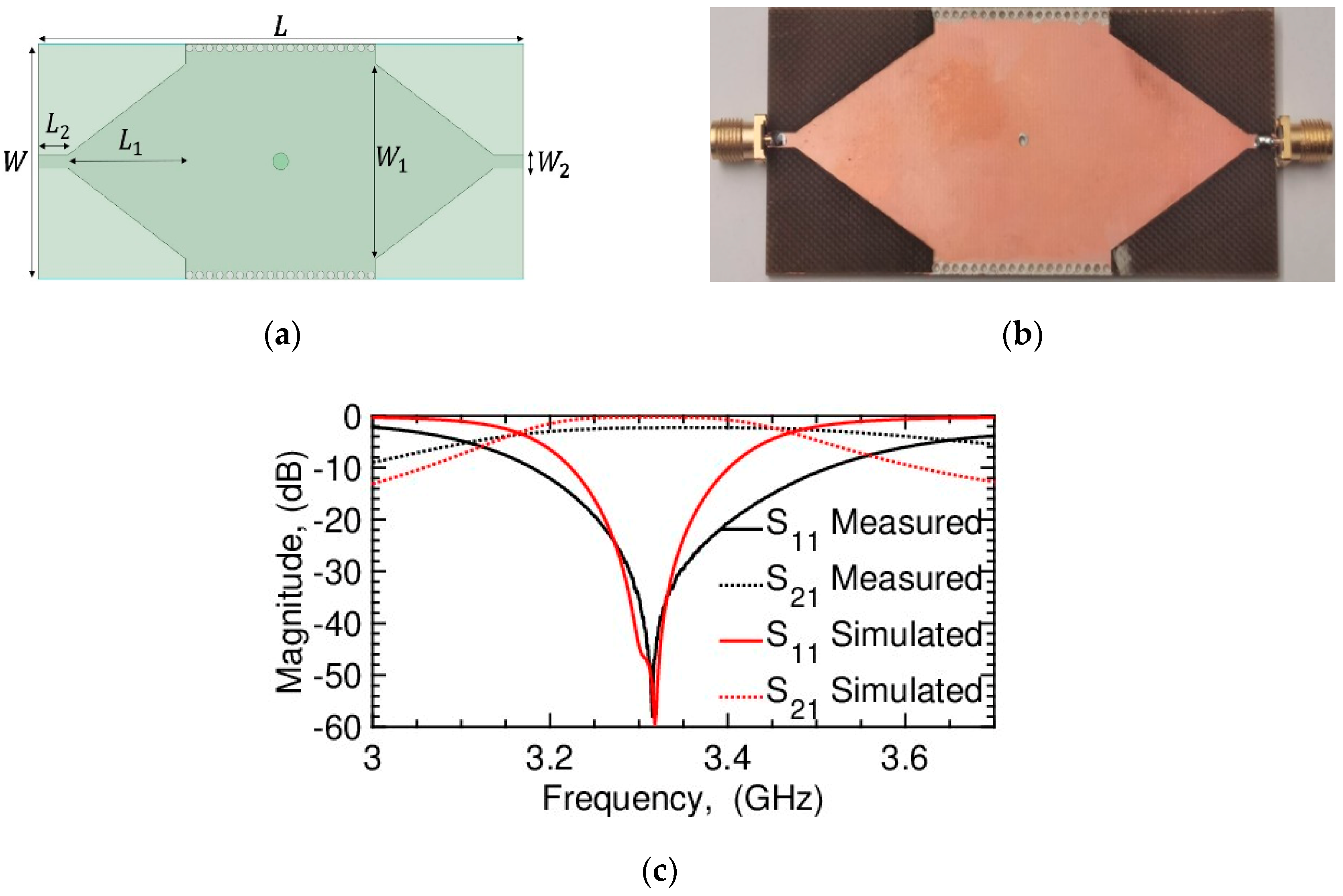
3.2. Fabrication and Proof of Concept for 3.2 GHz Filter
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Mahon, S. The 5G Effect on RF Filter Technologies. IEEE Trans. Semicond. Manuf. 2017, 30, 494–499. [Google Scholar] [CrossRef]
- List of Mobile Frequencies by Country (GSM, CDMA, UMTS, LTE, 5G). Available online: https://www.spectrummonitoring.com/frequencies/ (accessed on 7 April 2020).
- Chen, X.; Wu, K. Substrate integrated waveguide filters: Design techniques and structure innovations. IEEE Microw. Mag. 2014, 15, 121–133. [Google Scholar] [CrossRef]
- Teberio, F.; Percaz, J.M.; Arregui, I.; Martin-Iglesias, P.; Lopetegi, T.; Laso, M.A.G.; Arnedo, I. Rectangular Waveguide Filters with Meandered Topology. IEEE Trans. Microw. Theory Tech. 2018, 66, 3632–3643. [Google Scholar] [CrossRef]
- Krivovitca, A.; Shah, U.; Glubokov, O.; Oberhammer, J. Micromachined Silicon-core Substrate-integrated Waveguides with Co-planarprobe Transitions at 220–330 GHz. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium—MS, Philadelphia, PA, USA, 10–15 June 2018; pp. 190–193. [Google Scholar]
- Ding, Y.; Wu, K. Substrate Integrated Waveguide-to-Microstrip Transition in Multilayer Substrate. In Proceedings of the 2007 IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 3–8 June 2007; pp. 1555–1558. [Google Scholar]
- Hyeon, I.-J.; Baek, C.-W. Millimeter-Wave Substrate Integrated Waveguide Using Micromachined Tungsten-Coated Through Glass Silicon Via Structures. Micromachines 2018, 9, 172. [Google Scholar] [CrossRef] [PubMed]
- Isapour, A.; Kouki, A.B. Empty LTCC Integrated Waveguide with Compact Transitions for Ultra-low Loss Millimeter-wave Applications. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 144–146. [Google Scholar] [CrossRef]
- Wyndrum, R.W. Microwave filters, impedance-matching networks, and coupling structures. Proc. IEEE 1965, 53, 766. [Google Scholar] [CrossRef]
- Diaz-Caballero, E.; Belenguer, Á.; Esteban, H.; Boria, V.E.; Bachiller, C.; Morro, J.V. Analysis and design of passive microwave components in substrate integrated waveguide technology. In Proceedings of the 2015 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Ottawa, ON, Canada, 11–14 August 2015; pp. 1–3. [Google Scholar]
- Rhbanou, A.; Sabbane, M.; Bri, S. Design of K-Band Substrate Integrated Waveguide Band-Pass Filter with High Rejection. J. Microw. Optoelectron. Electromagn. Appl. 2015, 14, 155–169. [Google Scholar] [CrossRef]
- Wang, K.; Wong, S.; Sun, G.; Chen, Z.N.; Zhu, L.; Chu, Q. Synthesis Method for Substrate-Integrated Waveguide Bandpass Filter with Even-Order Chebyshev Response. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 126–135. [Google Scholar] [CrossRef]
- Cogollos, S.; Brumos, M.; Boria, V.E.; Vicente, C.; Gil, J.; Gimeno, B.; Guglielmi, M. A Systematic Design Procedure of Classical Dual-Mode Circular Waveguide Filters Using an Equivalent Distributed Model. IEEE Trans. Microw. Theory Tech. 2012, 60, 1006–1017. [Google Scholar] [CrossRef]
- Koziel, S.; Cheng, Q.S.; Bandler, J.W. Space mapping. IEEE Microw. Mag. 2008, 9, 105–122. [Google Scholar] [CrossRef]
- Dhwaj, K.; Li, X.; Shen, Z.; Qin, S. Cavity Resonators Do the Trick: A Packaged Substrate Integrated Waveguide, Dual-Band Filter. IEEE Microw. Mag. 2016, 17, 58–64. [Google Scholar] [CrossRef]
- Cassivi, Y.; Wu, K. Low cost microwave oscillator using substrate integrated waveguide cavity. IEEE Microw. Wirel. Compon. Lett. 2003, 13, 48–50. [Google Scholar] [CrossRef]
- Pant, M.; Ray, K.; Sharma, T.K.; Rawat, S.; Bandyopadhyay, A. Soft Computing: Theories and Applications: Proceedings of SoCTA 2016; Springer: Berlin/Heidelberg, Germany, 2017; Volume 2, ISBN 978-981-10-5699-4. [Google Scholar]
- Tang, Y.F.; Wu, K.; Mallat, N.K. Development of Substrate-Integrated Waveguide Filters for Low-Cost High-Density RF and Microwave Circuit Integration: Direct-Coupled Cavity Bandpass Filters with Chebyshev Response. IEEE Access 2015, 3, 1313–1325. [Google Scholar] [CrossRef]
- Marcuvitz, N.; Massachusetts Institute of Technology Radiation Laboratory. Waveguide Handbook; IET: London, UK, 1951; ISBN 978-0-86341-058-1. [Google Scholar]
- Jedrzejewski, A.; Leszczynska, N.; Szydlowski, L.; Mrozowski, M. Zero-Pole Approach to Computer Aided Design of in-Line SIW Filters with Transmission Zeros. Prog. Electromagn. Res. 2012, 131, 517–533. [Google Scholar] [CrossRef]
- Ben Romdhan Hajri, J.; Hrizi, H.; Sboui, N. Accurate and efficient study of substrate-integrated waveguide devices using iterative wave method. Int. J. Microw. Wirel. Technol. 2017, 9, 85–91. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Parment, F.; Ghiotto, A.; Wu, K.; Vuong, T.P. A fifth-order air-filled SIW filter for future 5G applications. In Proceedings of the 2017 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Pavia, Italy, 20–22 September 2017; pp. 1–3. [Google Scholar]
- Hu, S.; Hu, Y.; Zheng, H.; Zhu, W.; Gao, Y.; Zhang, X. A Compact 3.3–3.5 GHz Filter Based on Modified Composite Right-/Left-Handed Resonator Units. Electronics 2020, 9, 1. [Google Scholar] [CrossRef]
- Karim, M.F.; Ong, L.C.; Luo, B.; Chiam, T.M. A compact SIW bandpass filter based on modified CRLH. In Proceedings of the 2012 Asia Pacific Microwave Conference Proceedings, Kaohsiung, Taiwan, 4–7 December 2012; pp. 1133–1135. [Google Scholar]
- Abdalla, M.A.; Mahmoud, K.S. A compact SIW metamaterial coupled gap zeroth order bandpass filter with two transmission zeros. In Proceedings of the 2016 10th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (METAMATERIALS), Chania, Greece, 19–22 September 2016; pp. 4–6. [Google Scholar]
- Khan, A.A.; Mandal, M.K. Narrowband Substrate Integrated Waveguide Bandpass Filter with High Selectivity. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 416–418. [Google Scholar] [CrossRef]
- Shen, M.; Shao, Z.; Du, X.; He, Z.; Li, X. Ka-band multilayered substrate integrated waveguide narrowband filter for system-in-package applications. Microw. Opt. Technol. Lett. 2016, 58, 1395–1398. [Google Scholar] [CrossRef]
- Deslandes, D. Design equations for tapered microstrip-to-Substrate Integrated Waveguide transitions. In Proceedings of the 2010 IEEE MTT-S International Microwave Symposium, Anaheim, CA, USA, 23–28 May 2010; pp. 704–707. [Google Scholar]



| Ref. | Center Frequency | Bandwidth | Topology SIW | Number of Reported Variables | Size |
|---|---|---|---|---|---|
| 28 GHz filter using smartly positioned obstacles | 28 GHz | 0.27 GHz | Single layer—seven inner vias | 7 | |
| 5.8 GHz filter using smartly positioned obstacles | 5.8 GHz | 0.2 GHz | Single layer—seven inner vias | 11 | |
| 3.2 GHz filter using smartly positioned obstacles | 3.2 GHz | 0.28 GHz | Single layer—one inner via | 8 | |
| [23] | 3.35 GHz | 0.2 GHz | Two sawtooth CRLH | >10 | |
| [24] | 5 GHz | 0.7 GHz | Modified CRLH | >10 | |
| [25] | 6.8 GHz | 0.2 GHz | CRLH | >10 | |
| [26] | 8.25 GHz | 0.33 GHz | Single layer—multiple cavities | >10 | |
| [27] | 34.5 GHz | 0.86 GHz | Multilayered—multiple slots | >15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Celis, S.; Farhat, M.; Almansouri, A.S.; Bagci, H.; Salama, K.N. Simplified Modal-Cancellation Approach for Substrate-Integrated-Waveguide Narrow-Band Filter Design. Electronics 2020, 9, 962. https://doi.org/10.3390/electronics9060962
Celis S, Farhat M, Almansouri AS, Bagci H, Salama KN. Simplified Modal-Cancellation Approach for Substrate-Integrated-Waveguide Narrow-Band Filter Design. Electronics. 2020; 9(6):962. https://doi.org/10.3390/electronics9060962
Chicago/Turabian StyleCelis, Sebastian, Mohamed Farhat, Abdullah S. Almansouri, Hakan Bagci, and Khaled N. Salama. 2020. "Simplified Modal-Cancellation Approach for Substrate-Integrated-Waveguide Narrow-Band Filter Design" Electronics 9, no. 6: 962. https://doi.org/10.3390/electronics9060962
APA StyleCelis, S., Farhat, M., Almansouri, A. S., Bagci, H., & Salama, K. N. (2020). Simplified Modal-Cancellation Approach for Substrate-Integrated-Waveguide Narrow-Band Filter Design. Electronics, 9(6), 962. https://doi.org/10.3390/electronics9060962







