Combining Machine Learning Analysis and Incentive-Based Genetic Algorithms to Optimise Energy District Renewable Self-Consumption in Demand-Response Programs
Abstract
1. Introduction
2. Methods
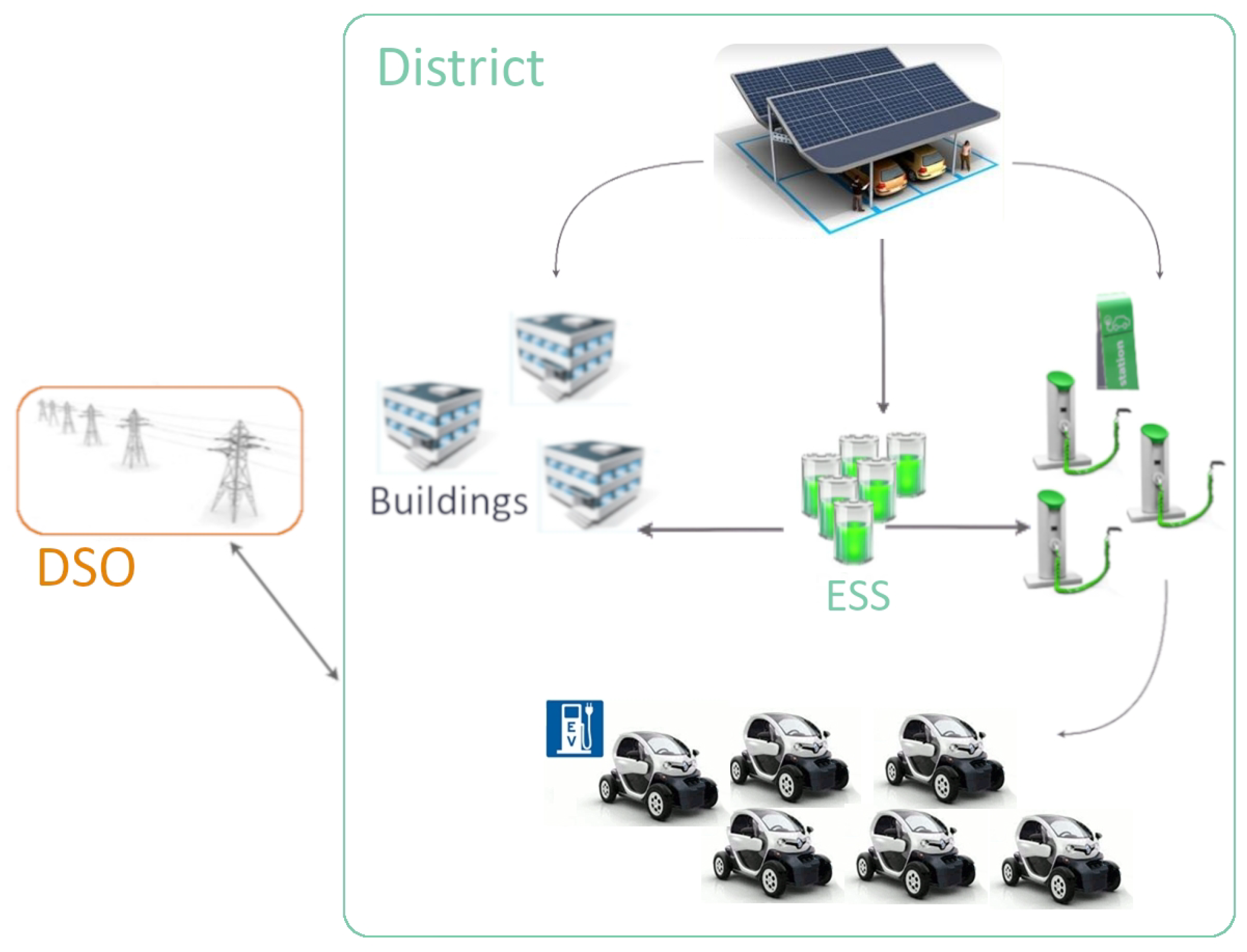
2.1. Case Study
2.2. Architecture
Smart Meters
2.3. Forecast
2.4. Optimization of the Forecast
2.5. Power Profile Optimization
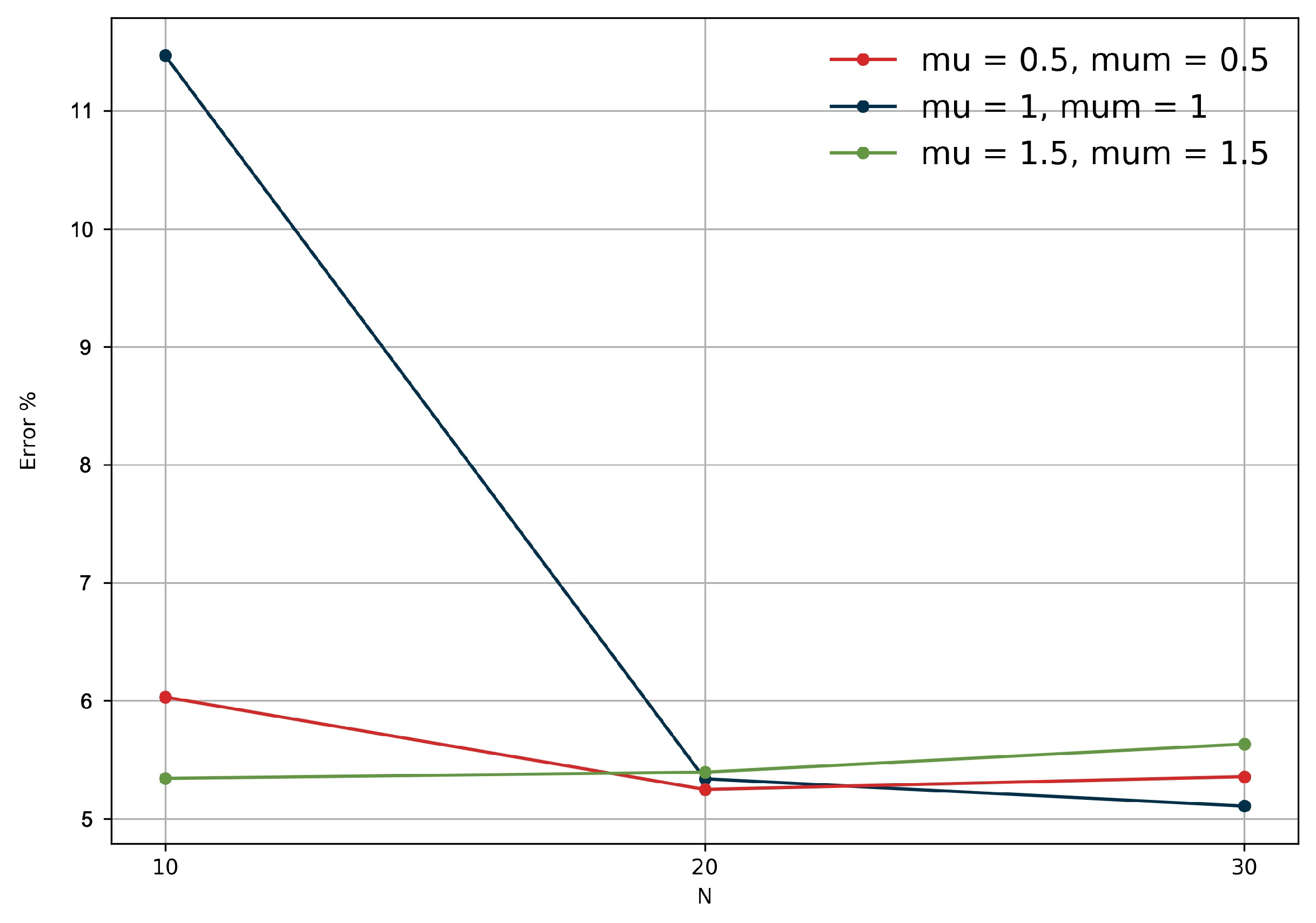
2.6. Calibration of NSGA-II Parameters
3. Results and Discussion
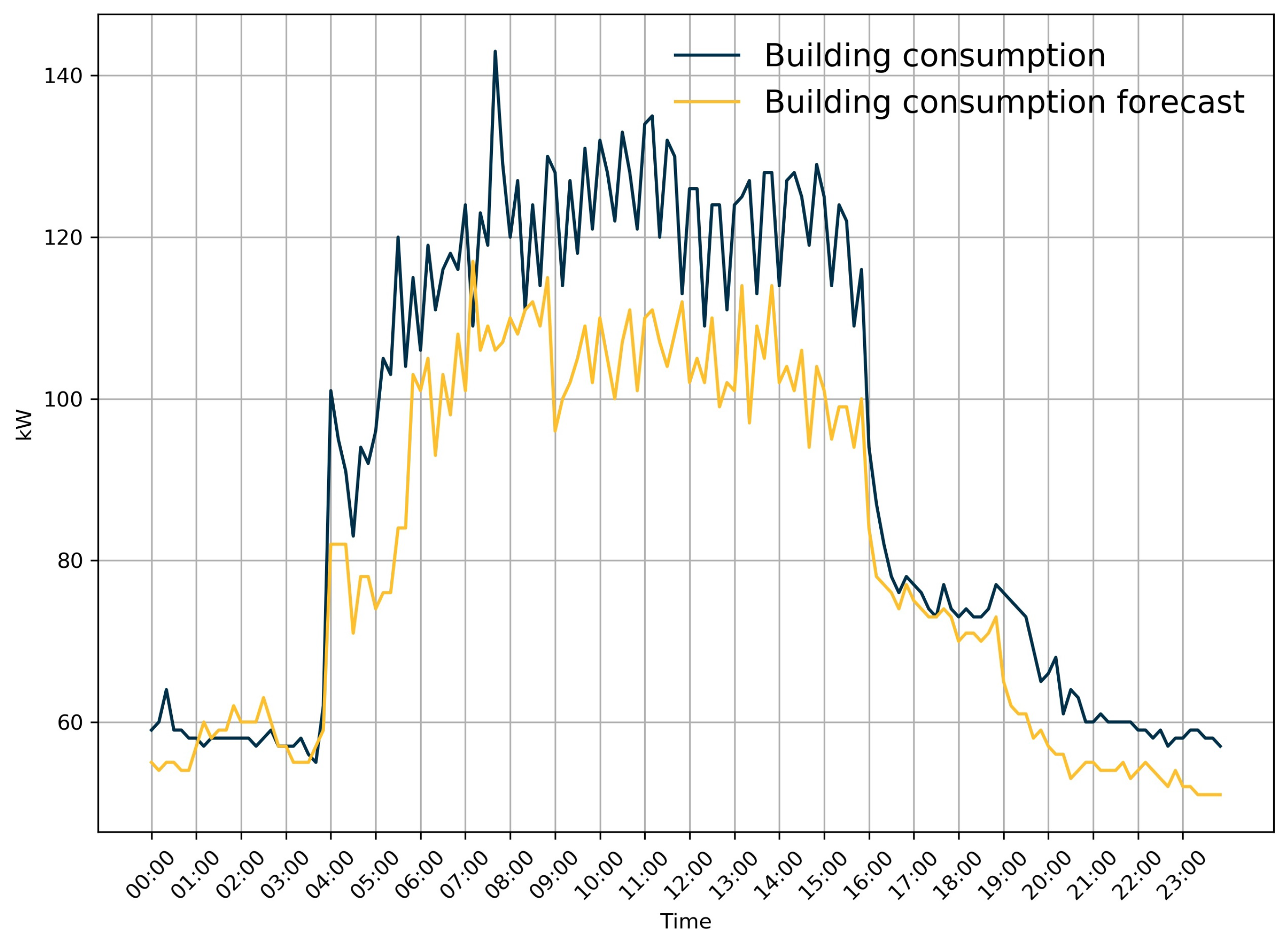
3.1. Optimization of the Forecast for Building Consumption
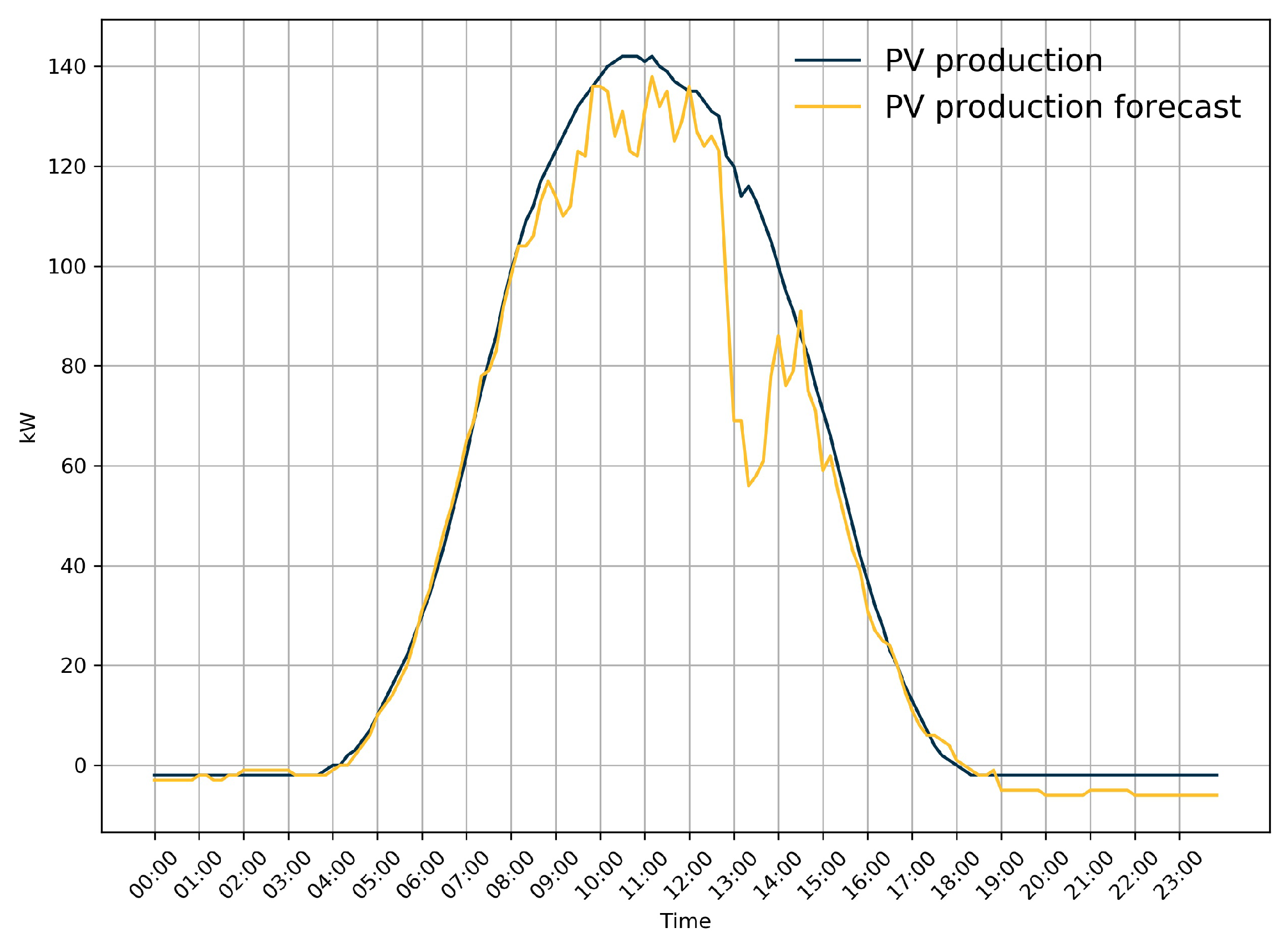
3.2. Optimization of the Forecast for PV Production
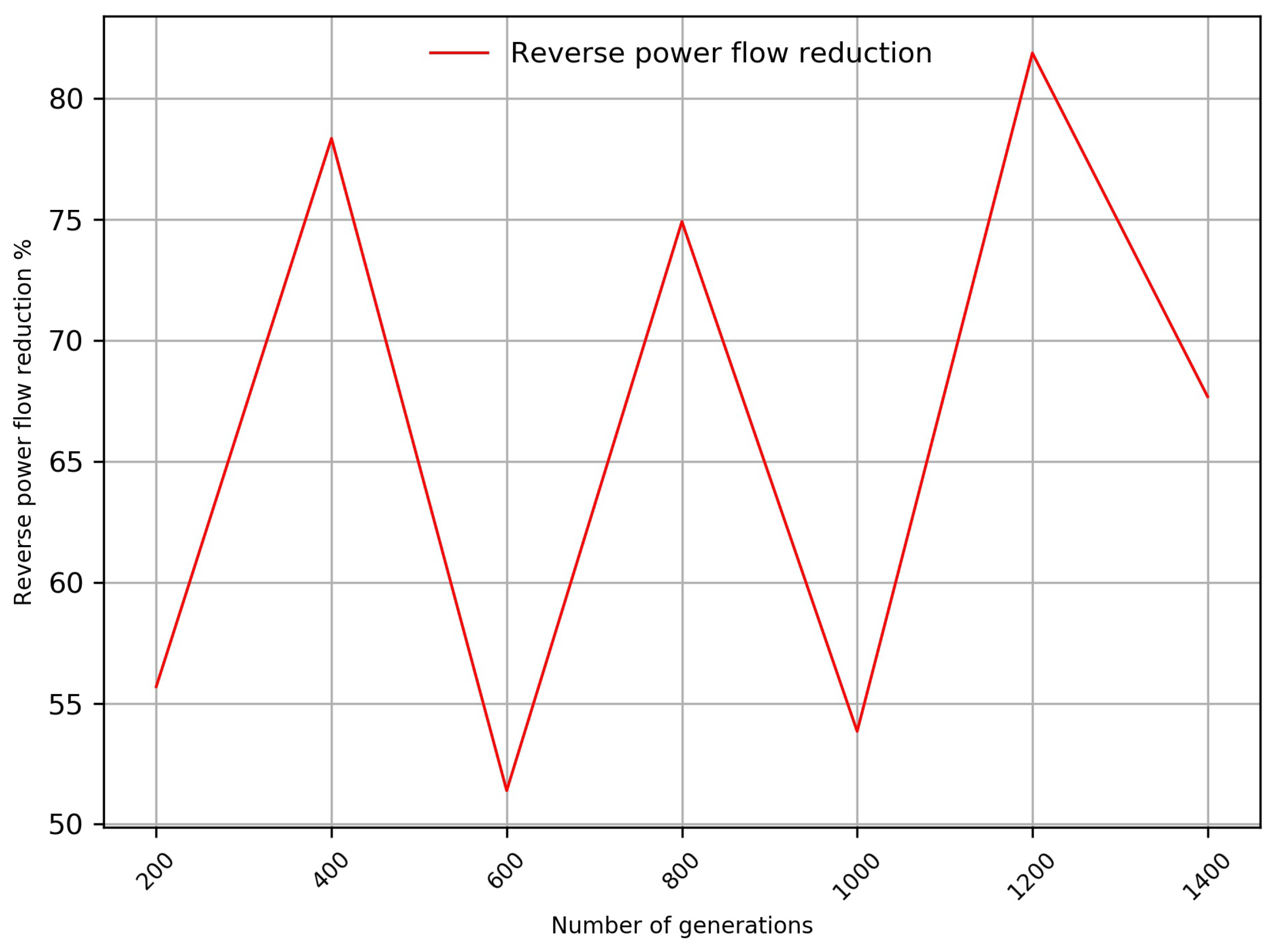
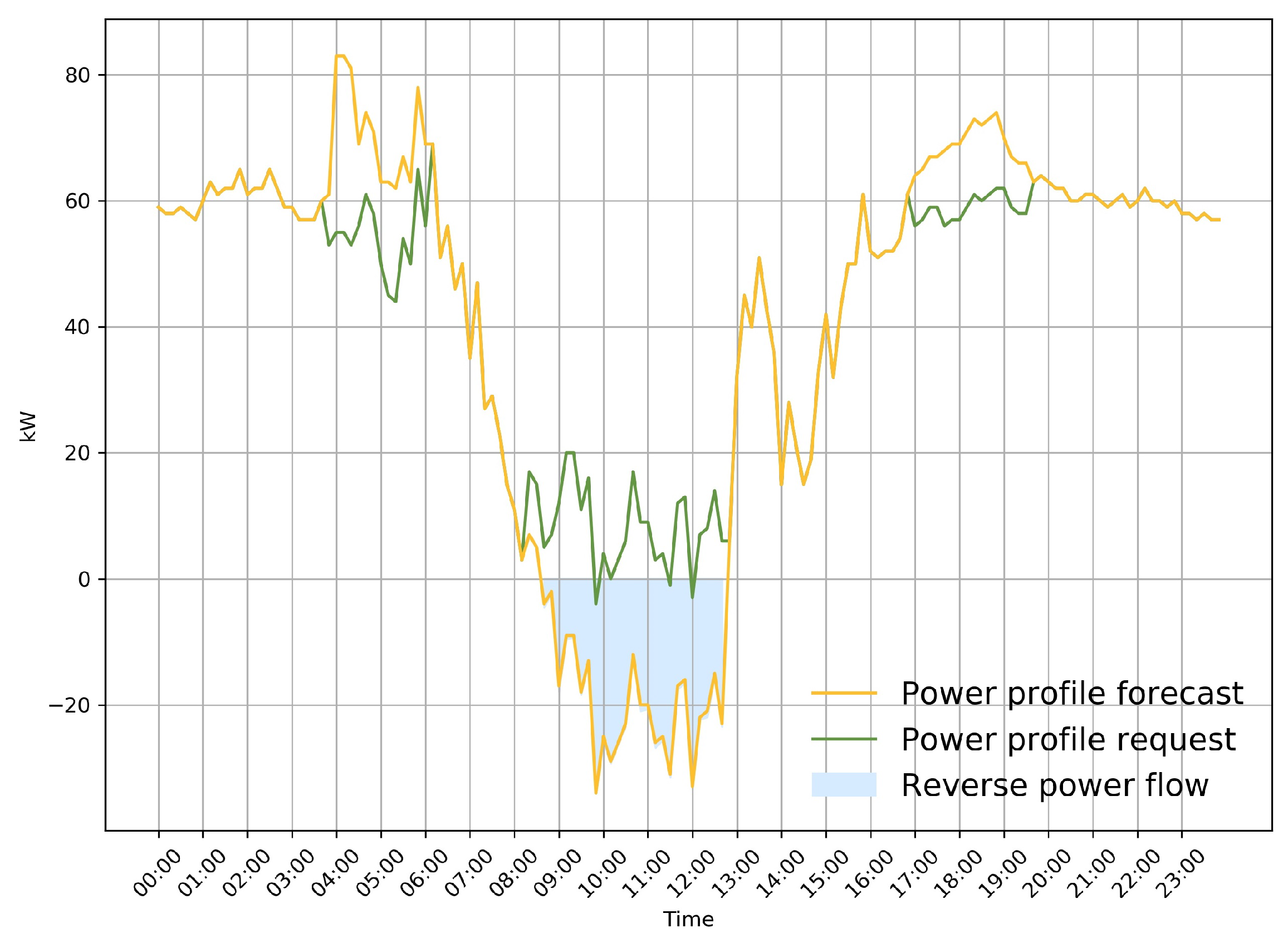
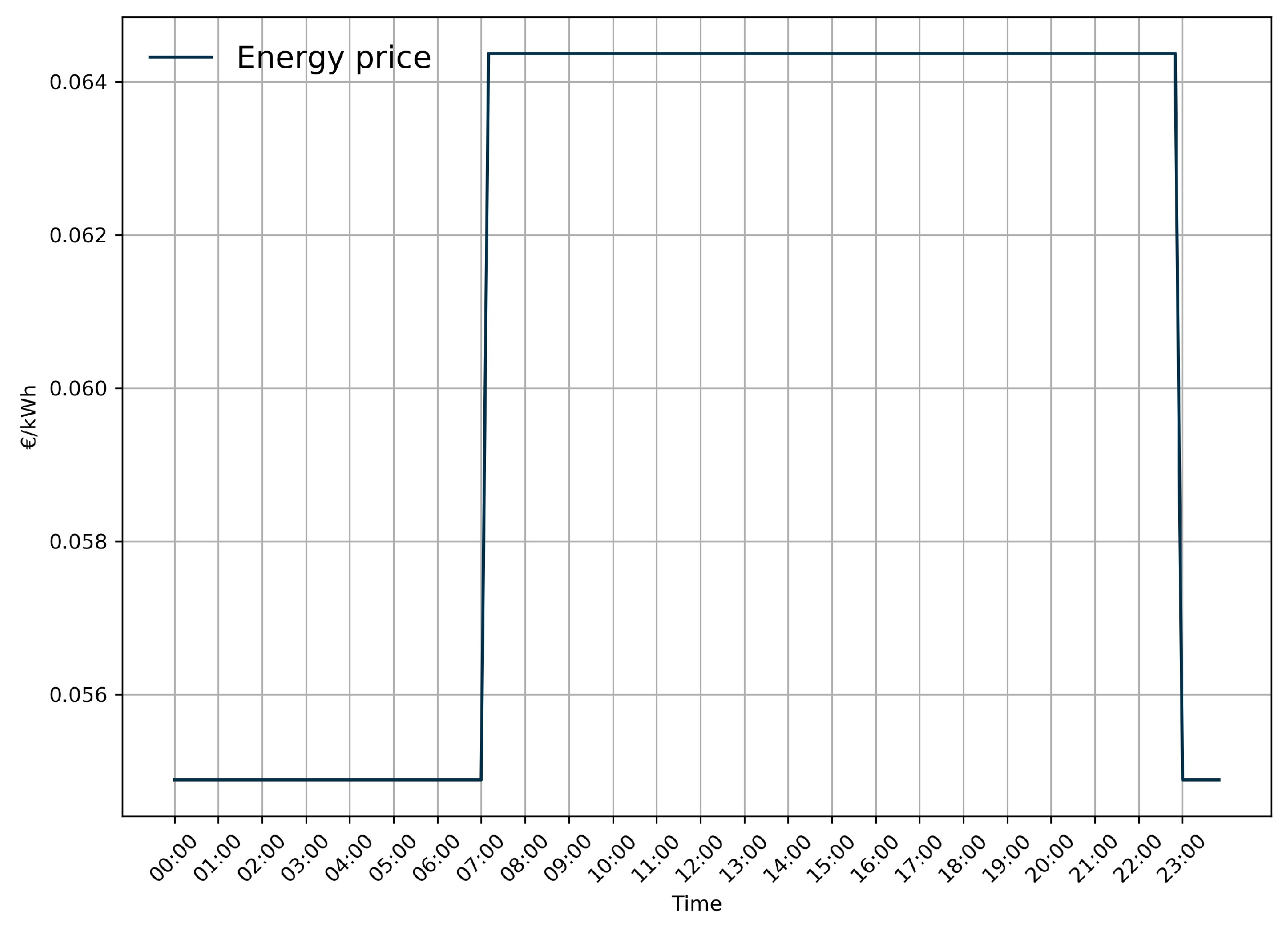
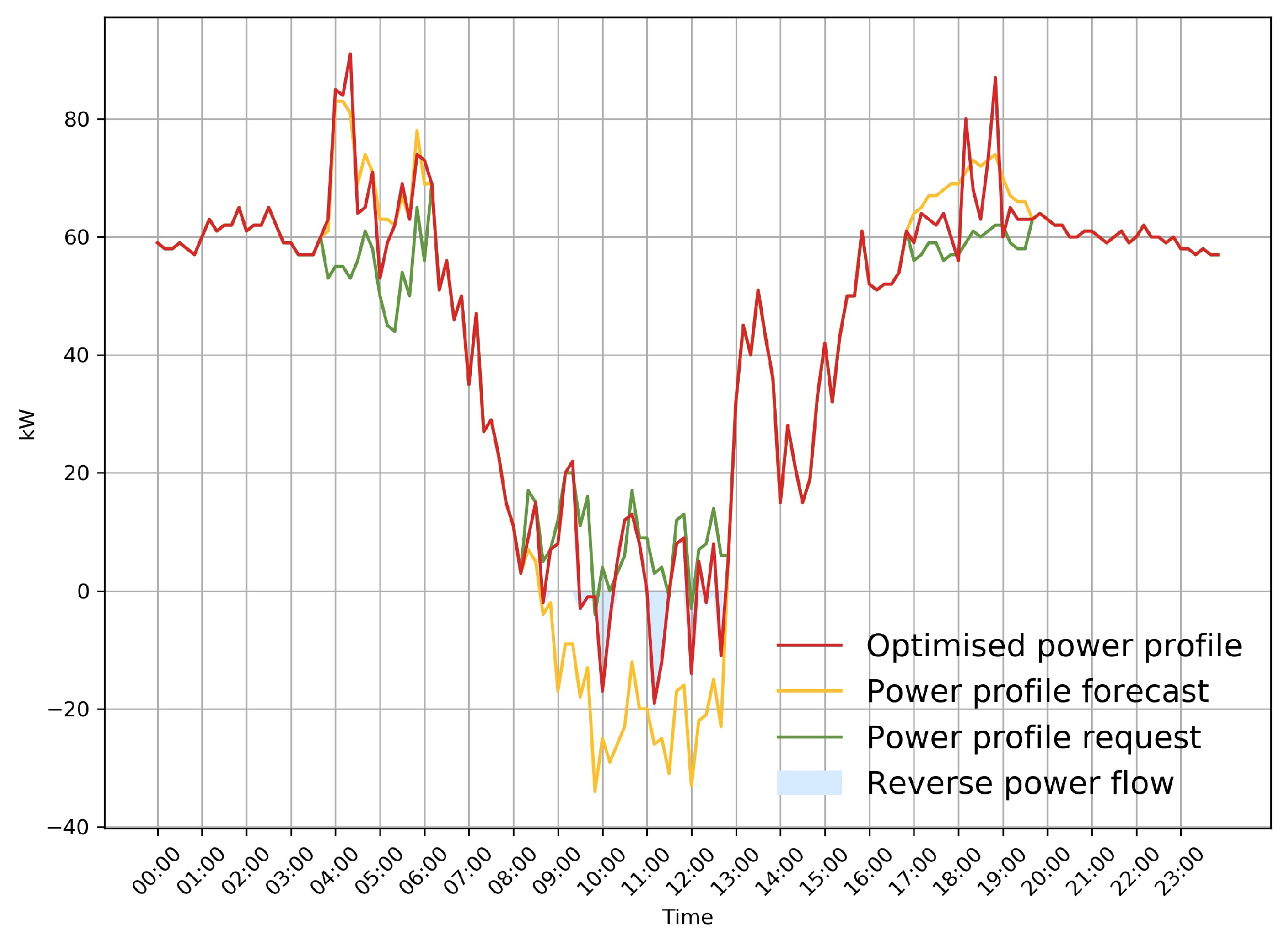
3.3. DSO District Profile Optimization
3.4. Managerial Implications of the Research
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BSS | Battery Storage System |
| DR | Demand Response |
| DSO | Distribution System Operator |
| ELM | Extreme Learning Machine |
| EMS | Energy Management System |
| E-NSGA | Extreme Nondominated Sorting Genetic Algorithm |
| IoT | Internet of Things |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MOGA | Multi-Objective Genetic Algorithm |
| MSE | Mean Squared Error |
| NPGA | Niched Pareto Genetic Algorithm |
| NRMSD | Normalized Root Mean Squared Deviation |
| MQTT | Message Queue Telemetry Transport |
| NSGA | Nondominated Sorting Genetic Algorithm |
| PAES | Pareto Archived Evolution Strategy |
| PV | Photovoltaics |
| RF | Random Forest |
| RMSD | Root Mean Squared Deviation |
| RMSD | Root Mean Squared Deviation |
| RPF | Reverse Power Flow |
| UPMSP | Unrelated Parallel Machines Scheduling Problem |
| WDN | Water Distribution Network |
Appendix A. Definitions
References
- Prettico, G.; Flammini, M.G.; Andreadou, N.; Vitiello, S.; Fulli, G.; Masera, M. Distribution System Operators Observatory 2018-Overview of the Electricity Distribution System in Europe; Technical Report EUR 29615EN; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar] [CrossRef]
- Shoreh, M.H.; Siano, P.; Shafie-khah, M.; Loia, V.; Catalão, J.P. A survey of industrial applications of Demand Response. Electr. Power Syst. Res. 2016, 141, 31–49. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Hosseinian Yengejeh, H.; Shahnia, F.; Islam, S. Contributions of single-phase rooftop PVs on short circuits faults in residential feeders. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Sarailoo, M.; Akhlaghi, S.; Rezaeiahari, M.; Sangrody, H. Residential solar panel performance improvement based on optimal intervals and optimal tilt angle. In Proceedings of the 2017 IEEE Power Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Li, Y.; Wang, C.; Li, G.; Wang, J.; Zhao, D.; Chen, C. Improving operational flexibility of integrated energy system with uncertain renewable generations considering thermal inertia of buildings. Energy Convers. Manag. 2020, 207, 112526. [Google Scholar] [CrossRef]
- Ghasemi, A.; Enayatzare, M. Optimal energy management of a renewable-based isolated microgrid with pumped-storage unit and demand response. Renew. Energy 2018, 123, 460–474. [Google Scholar] [CrossRef]
- Gils, H. Balancing of Intermittent Renewable Power Generation by Demand Response and Thermal Energy Storage. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2015. [Google Scholar]
- Lorenzi, G.; Silva, C.A.S. Comparing demand response and battery storage to optimize self-consumption in PV systems. Appl. Energy 2016, 180, 524–535. [Google Scholar] [CrossRef]
- Knezovic, K.; Marinelli, M.; Perez, y.; Codani, P. Distribution Grid Services and Flexibility Provision by Electric Vehicles: a Review of Options. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Bragatto, T.; Cresta, M.; Croce, V.; Paulucci, M.; Santori, F.; Ziu, D. A real-life experience on 2nd life batteries services for Distribution System Operator. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Luca de Tena, D. Large Scale Renewable Power Integration with Electric Vehicles: Long Term Analysis for Germany with a Renewable Based Power Supply. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2014. [Google Scholar]
- Cheng, C.; Pourhejazy, P.; Ying, K.; Li, S.; Chang, C. Learning-Based Metaheuristic for Scheduling Unrelated Parallel Machines With Uncertain Setup Times. IEEE Access 2020, 8, 74065–74082. [Google Scholar] [CrossRef]
- Sofia, A.; GaneshKumar, P. Multi-objective Task Scheduling to Minimize Energy Consumption and Makespan of Cloud Computing Using NSGA-II. J. Netw. Syst. Manag. 2017, 26, 1–23. [Google Scholar] [CrossRef]
- Nascimento, Z.; Sadok, D.; Fernandes, S.; Kelner, J. Multi-objective optimization of a hybrid model for network traffic classification by combining machine learning techniques. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2116–2122. [Google Scholar]
- Mellit, A.; Kalogirou, S.A. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Pour Rahimian, F.; Glesk, I.; Roper, M. Machine learning for estimation of building energy consumption and performance: A review. Vis. Eng. 2018, 6. [Google Scholar] [CrossRef]
- Bogner, K.; Pappenberger, F.; Zappa, M. Machine Learning Techniques for Predicting the Energy Consumption/Production and Its Uncertainties Driven by Meteorological Observations and Forecasts. Sustainability 2019, 11, 3328. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Mathematics 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Junior, B.; Cossi, A.; Mantovani, J. Multiobjective Short-Term Planning of Electric Power Distribution Systems Using NSGA-II. J. Control. Autom. Electr. Syst. 2013, 24. [Google Scholar] [CrossRef]
- Attari, S.; Shakarami, M.; Pour, E. Pareto optimal reconfiguration of power distribution systems with load uncertainty and recloser placement simultaneously using a genetic algorithm based on NSGA-II. In Proceedings of the 2016 21st Conference on Electrical Power Distribution Networks Conference (EPDC), Karaj, Iran, 26–27 April 2016; pp. 46–53. [Google Scholar] [CrossRef]
- Buoro, D.; Casisi, M.; Nardi, A.D.; Pinamonti, P.; Reini, M. Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 2013, 58, 128–137. [Google Scholar] [CrossRef]
- Ippolito, M.; Silvestre, M.D.; Sanseverino, E.R.; Zizzo, G.; Graditi, G. Multi-objective optimized management of electrical energy storage systems in an islanded network with renewable energy sources under different design scenarios. Energy 2014, 64, 648–662. [Google Scholar] [CrossRef]
- FIWARE. Available online: https://www.fiware.org (accessed on 20 April 2020).
- Amber, K.; Aslam, M.; Hussain, S. Electricity consumption forecasting models for administration buildings of the UK higher education sector. Energy Build. 2015, 90, 127–136. [Google Scholar] [CrossRef]
- Braun, M.; Altan, H.; Beck, S. Using regression analysis to predict the future energy consumption of a supermarket in the UK. Appl. Energy 2014, 130, 305–313. [Google Scholar] [CrossRef]
- Al-Garni, A.Z.; Zubair, S.M.; Nizami, J.S. A regression model for electric-energy-consumption forecasting in Eastern Saudi Arabia. Energy 1994, 19, 1043–1049. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Solar Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Nguyen, D.; Lehman, B.; Kamarthi, S. Performance evaluation of solar photovoltaic arrays including shadow effects using neural network. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3357–3362. [Google Scholar] [CrossRef]
- Hiyama, T.; Kitabayashi, K. Neural network based estimation of maximum power generation from PV module using environmental information. IEEE Trans. Energy Convers. 1997, 12, 241–247. [Google Scholar] [CrossRef]
- World Weather Online. Available online: https://www.worldweatheronline.com (accessed on 16 April 2020).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. Performance comparison of NSGA-II and NSGA-III on various many-objective test problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3045–3052. [Google Scholar]
- Farmani, R.; Savic, D.; Walters, G. Multi-objective optimization of water system: a comparative study. Pumps Electromech. Devices Syst. Appl. Urban Water Manag. 2003, 1, 247–256. [Google Scholar]
- D’Oriano, L.; Mastandrea, G.; Rana, G.; Raveduto, G.; Croce, V.; Verber, M.; Bertoncini, M. Decentralized blockchain flexibility system for Smart Grids: Requirements engineering and use cases. In Proceedings of the 2018 International IEEE Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 20–21 November 2018; pp. 39–44. [Google Scholar]




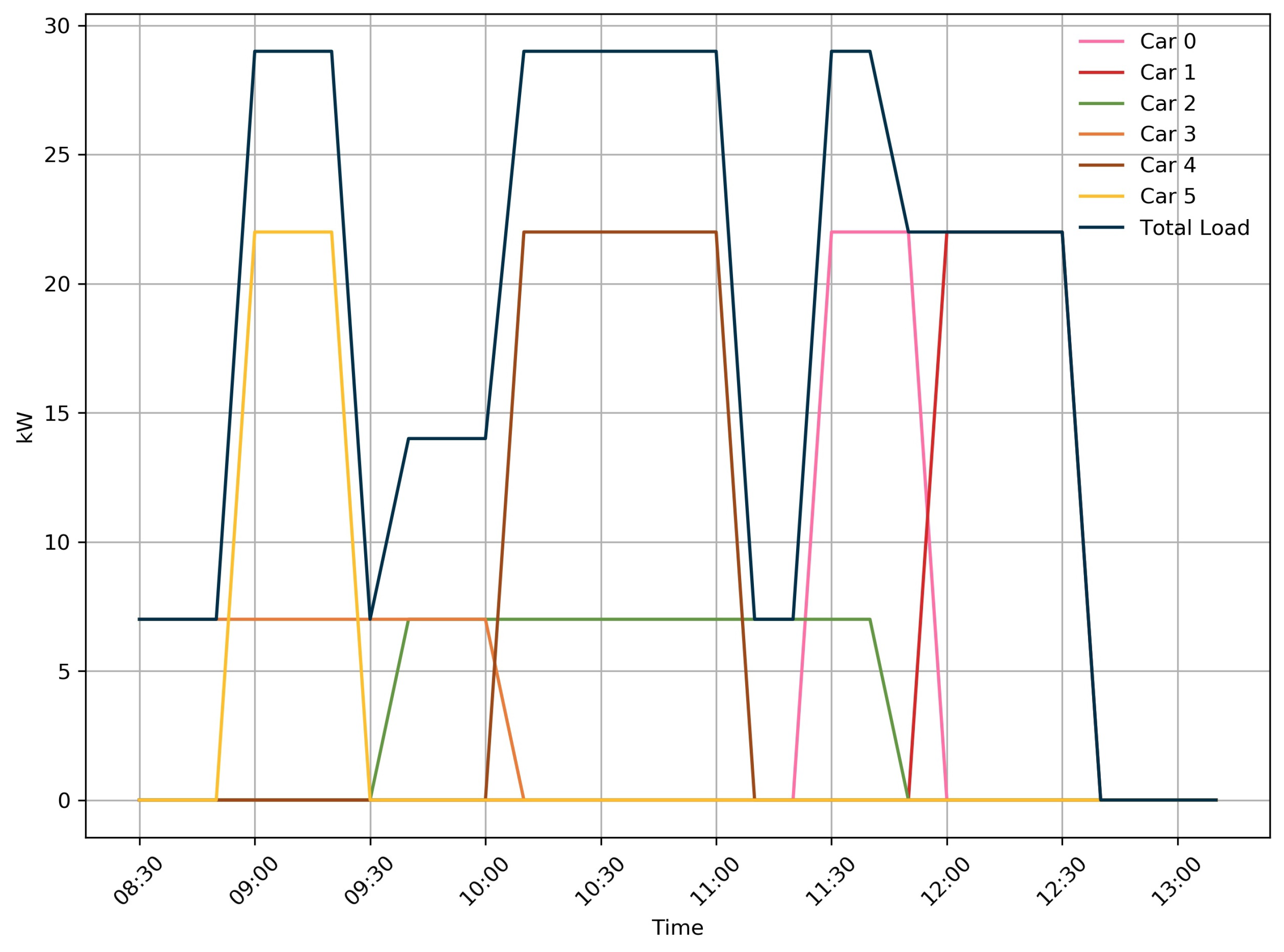
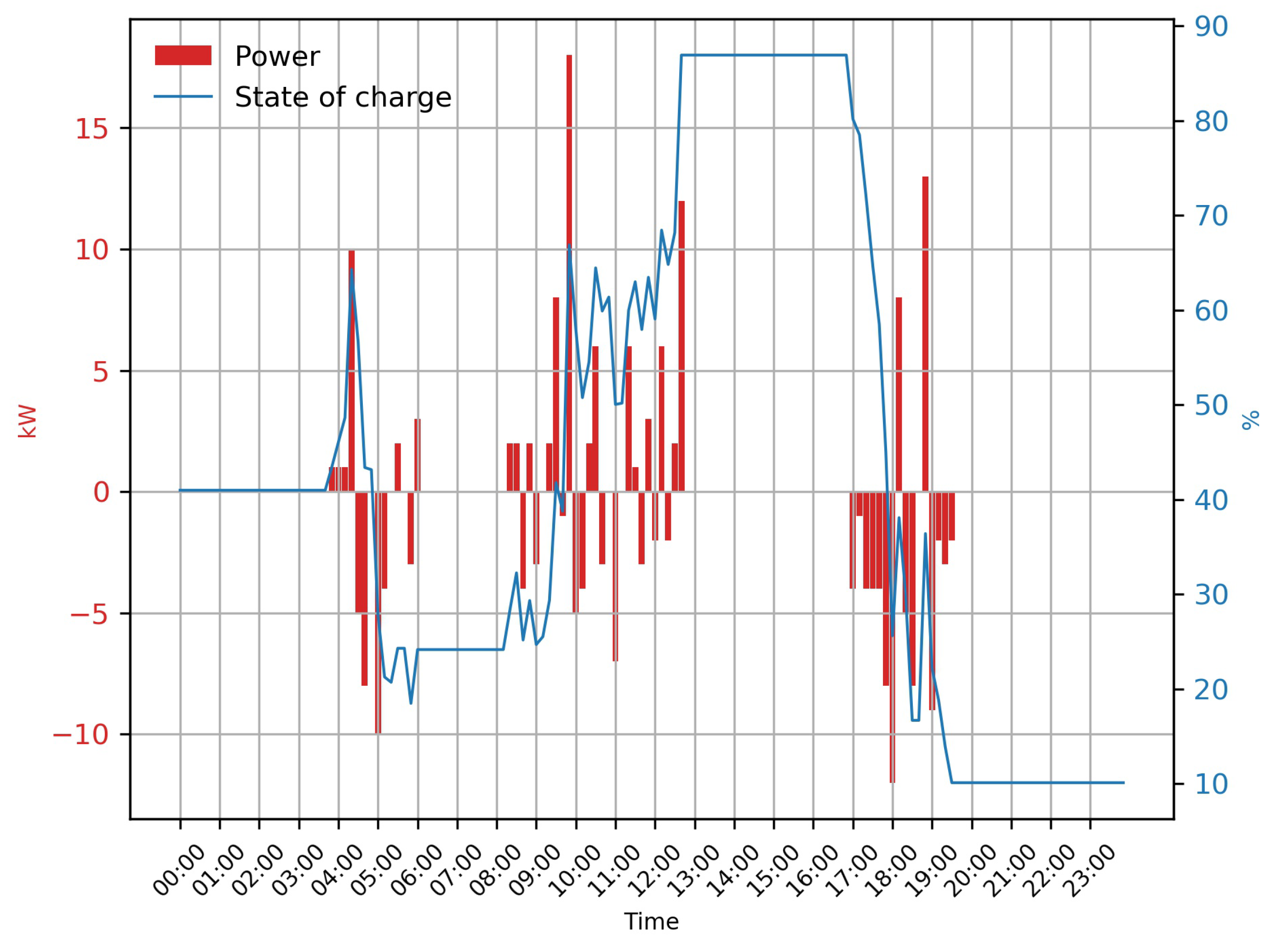
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Minutes | 0 | 0 | 0 | 0 | 0 | 50 |
| Hours | 0 | 0 | 0 | 0 | 0 | 4 |
| Day | 1 | 7 | 8 | 14 | 15 | 49 |
| 1st | |
| 2nd | |
| 3rd | |
| 4th | |
| 5th |
| Decision Variable | Coefficients | |
|---|---|---|
| 1st variable | ||
| 2nd variable | ||
| 3rd variable | ||
| 4th variable | ||
| 5th variable | ||
| 6th variable | ||
| Temperature | ||
| Wind speed | ||
| Humidity | ||
| Visibility | ||
| Pressure | ||
| Cloud cover | ||
| Dew point | ||
| UV index |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Minutes | 0 | 10 | 0 | 0 | 0 | 0 |
| Hours | 0 | 0 | 0 | 0 | 0 | 13 |
| Day | 1 | 1 | 2 | 3 | 5 | 5 |
| 1st | |
| 2nd | |
| 3rd | |
| 4th | |
| 5th |
| Decision Variable | Coefficients | |
|---|---|---|
| 1st variable | ||
| 2nd variable | ||
| 3rd variable | ||
| 4th variable | ||
| 5th variable | ||
| 6th variable | ||
| Temperature | ||
| Wind speed | ||
| Humidity | ||
| Visibility | ||
| Pressure | ||
| Cloud cover | ||
| Dew point | ||
| UV index |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croce, V.; Raveduto, G.; Verber, M.; Ziu, D. Combining Machine Learning Analysis and Incentive-Based Genetic Algorithms to Optimise Energy District Renewable Self-Consumption in Demand-Response Programs. Electronics 2020, 9, 945. https://doi.org/10.3390/electronics9060945
Croce V, Raveduto G, Verber M, Ziu D. Combining Machine Learning Analysis and Incentive-Based Genetic Algorithms to Optimise Energy District Renewable Self-Consumption in Demand-Response Programs. Electronics. 2020; 9(6):945. https://doi.org/10.3390/electronics9060945
Chicago/Turabian StyleCroce, Vincenzo, Giuseppe Raveduto, Matteo Verber, and Denisa Ziu. 2020. "Combining Machine Learning Analysis and Incentive-Based Genetic Algorithms to Optimise Energy District Renewable Self-Consumption in Demand-Response Programs" Electronics 9, no. 6: 945. https://doi.org/10.3390/electronics9060945
APA StyleCroce, V., Raveduto, G., Verber, M., & Ziu, D. (2020). Combining Machine Learning Analysis and Incentive-Based Genetic Algorithms to Optimise Energy District Renewable Self-Consumption in Demand-Response Programs. Electronics, 9(6), 945. https://doi.org/10.3390/electronics9060945




