Joint Scheduling and Power Allocation Using Non-Orthogonal Multiple Access in Multi-Cell Beamforming Networks
Abstract
1. Introduction
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Joint Scheduling and Power Allocation with NOMA
3.1. Optimality Conditions and Approximations
3.2. Heuristic Iterative Water-Filling
| Algorithm 1 Heuristic iterative water-filling algorithm for multi-cell WLAN |
| (1) Initialization |
| Initialize where where . |
| Repeat |
| (2) Beam allocation |
| Allocate beam based on initialized according to (10) |
| for = to do |
| for b = 1 to B do |
| Select schedule according to (18) |
| Allocate beam b to schedule |
| end |
| end |
| (3) Power allocation |
| Allocate beam power p based on allocated |
| Find according to (23) by using the bisection method |
| for = to do |
| for b = 1 to B do |
| Compute according to (20) |
| end |
| end |
| Until |
4. Performance Evaluation
4.1. Parameter for System Level Performance Evaluation
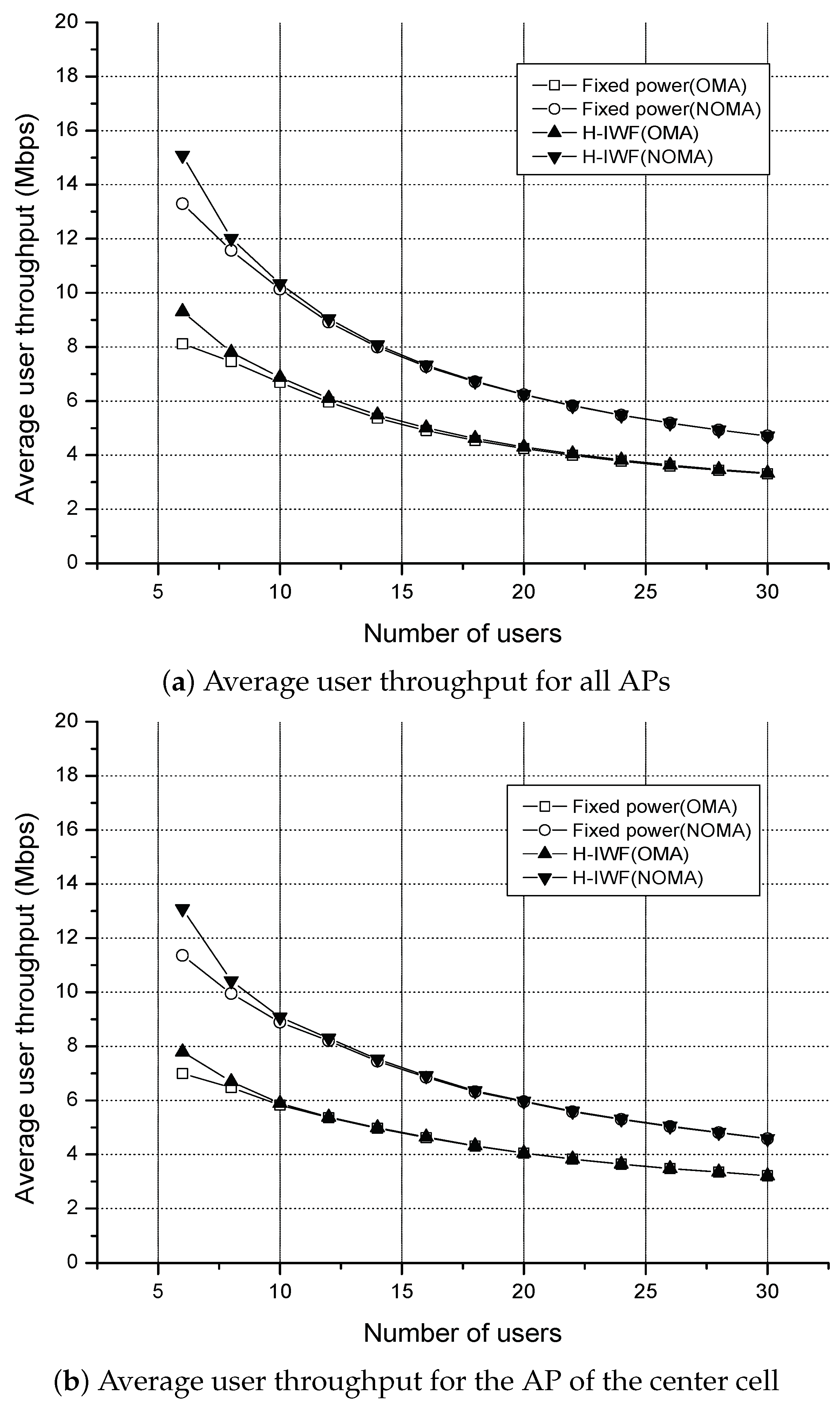
4.2. Simulation Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Otao, N.; Kishiyama, Y.; Higuchi, K. Performance of non-orthogonal access with SIC in cellular downlink using proportional fair-based resource allocation. In Proceedings of the International Symposium on Wireless Communication Systems (ISWCS) 2012, Paris, France, 28–31 August 2012; pp. 476–480. [Google Scholar]
- Takeda, T.; Higuchi, K. Enhanced User Fairness Using Non-Orthogonal Access with SIC in Cellular Uplink. In Proceedings of the IEEE Vehicular Technology Conference (VTC Fall) 2011, San Fracisco, CA, USA, 5–8 September 2011. [Google Scholar]
- Jo, O.; Hong, W.; Choi, S.; Chag, S.; Kweon, C.; Oh, J.; Cheun, K. Holistic design considerations for environmentally adaptive 60 GHz beamforming technology. IEEE Commun. Mag. 2014, 52, 30–38. [Google Scholar] [CrossRef]
- Jo, O.; Yoon, J. Spatial reuse algorithm using interference graph in millimeter wave beamforming systems. Etri J. 2017, 39, 255–263. [Google Scholar] [CrossRef]
- Zhao, N.; Li, D.; Liu, M.; Cao, Y.; Chen, Y.; Ding, Z.; Wang, X. Secure transmission via joint precoding optimization for downlink MISO NOMA. IEEE Trans. Veh. Technol. 2019, 68, 7603–7615. [Google Scholar] [CrossRef]
- Felici-Castell, S.; Navarro, A.; Pérez-Solano, J.; Segura-García, J.; García-Pineda, M. Practical considerations in the implementation of collaborative beamforming on wireless sensor networks. Sensors 2017, 17, 237. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Camba, A.; Felici-Castell, S.; Segura-García, J.; García-Pineda, M.; Pérez-Solano, J. Feasibility of a Stochastic Collaborative Beamforming for Long Range Communications in Wireless Sensor Networks. Electronics 2018, 7, 417. [Google Scholar] [CrossRef]
- Jo, O.; Shin, K. Joint scheduling and power allocation using non-orthogonal multiple access in directional beam-based WLAN systems. IEEE Wirel. Commun. Lett. 2017, 6, 482–485. [Google Scholar]
- Zhang, J.; Andrews, J. Adaptive Spatial Intercell Interference Cancellation in Multicell Wireless Networks. IEEE J. Sel. Areas Commun. 2010, 28, 1455–1468. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, C.; Ni, K.; Qian, L.; Huang, L.; Zhu, W. Optimal Resource Allocation for Uplink Data Collection in Nonorthogonal Multiple Access Networks. Sensors 2018, 18, 2542. [Google Scholar] [CrossRef] [PubMed]
- Selvaprabhu, P.; Chinnadurai, S.; Sarker, M.; Lee, M. Joint Interference Alignment and Power Allocation for K-User Multicell MIMO Channel through Staggered Antenna Switching. Sensors 2018, 18, 380. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.; Kim, Y.; Kim, R. A Novel WLAN Vehicle-To-Anything (V2X) Channel Access Scheme for IEEE 802.11p-Based Next-Generation Connected Car Networks. Appl. Sci. 2018, 8, 2112. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, H.; Wang, D. Channel and Bit Adaptive Power Control Strategy for Uplink NOMA VLC Systems. Appl. Sci. 2019, 9, 220. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, V. Random beamforming in millimeter-wave NOMA networks. IEEE Access 2017, 5, 7667–7681. [Google Scholar] [CrossRef]
- IEEE 802.11-2012. Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; IEEE: Piscataway, NJ, USA, 2012.
- Vanka, S.; Srinivasa, S.; Gong, Z.; Vizi, P.; Stamatiou, K.; Haenggi, M. Superposition coding strategies: Design and experimental evaluation. IEEE Trans. Wirel. Commun. 2012, 11, 2628–2639. [Google Scholar] [CrossRef]
- Kelly, F.; Maulloo, A.; Tan, D. Rate control for communication networks: Shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 1998, 49, 237–252. [Google Scholar] [CrossRef]
- IEEE Standard 802.11-14/0980r1, TGax Simulation Scenarios; IEEE: Piscataway, NJ, USA, 2015.
- ETSI. Spatial Channel Model for MIMO Simulations; Tech. Rep. 125.996 V11.0.0; ETSI: Darmstadt, Germany, 2012. [Google Scholar]
- Baum, D.; Hansen, J.; Salo, J. An interim channel model for beyond-3G systems: Extending the 3GPP spatial channel model (SCM). In Proceedings of the IEEE Vehicular Technology Conference (VTC Spring) 2005, Stockholm, Sweden, 30 May–1 June 2005; pp. 3132–3136. [Google Scholar]
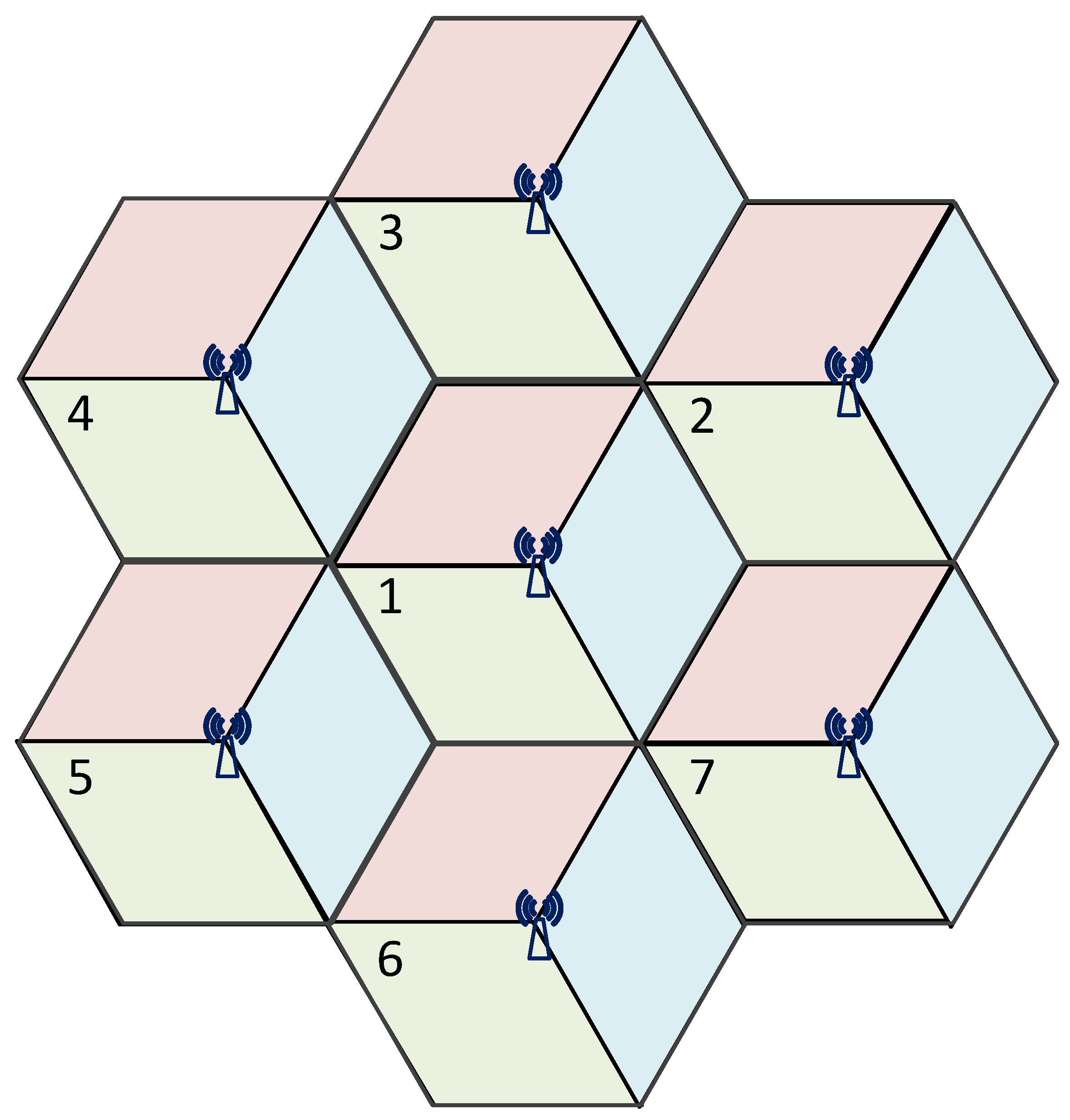

| Parameter | Value |
|---|---|
| Cell radius | 10 m |
| Distance between two cells | 34.6 m/17.3 m |
| Maximum number of users in a cell | 30 |
| Number of beams in a cell | 3 |
| Carrier frequency | 2.4 GHz |
| Channel bandwidth | 20 MHz |
| Noise spectral density | −174 dBm/Hz |
| Scheduling interval | 1 ms |
| Throughput averaging interval () | 1024 ms |
| Maximum transmittable power of AP () | 20 dBm |
| Path-loss (dB) [20] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, K.; Jo, O. Joint Scheduling and Power Allocation Using Non-Orthogonal Multiple Access in Multi-Cell Beamforming Networks. Electronics 2020, 9, 896. https://doi.org/10.3390/electronics9060896
Shin K, Jo O. Joint Scheduling and Power Allocation Using Non-Orthogonal Multiple Access in Multi-Cell Beamforming Networks. Electronics. 2020; 9(6):896. https://doi.org/10.3390/electronics9060896
Chicago/Turabian StyleShin, Kyungseop, and Ohyun Jo. 2020. "Joint Scheduling and Power Allocation Using Non-Orthogonal Multiple Access in Multi-Cell Beamforming Networks" Electronics 9, no. 6: 896. https://doi.org/10.3390/electronics9060896
APA StyleShin, K., & Jo, O. (2020). Joint Scheduling and Power Allocation Using Non-Orthogonal Multiple Access in Multi-Cell Beamforming Networks. Electronics, 9(6), 896. https://doi.org/10.3390/electronics9060896






