1. Introduction
As computing power has increased dramatically and the degree of integration has improved significantly owing to the development of nanoscale semiconductor processes in recent decades, the requirements in mobile devices are constantly evolving to satisfy the user experience. For example, a mobile chip that can acquire an image frame from 200 million pixels, perform 8K high dynamic range (HDR) recording, and display previews at 144 fps while maximizing the image quality for whole paths has emerged [
1]. However, the bandwidth and capacity of cutting-edge dynamic random-access memory (DRAM) have not made much progress in terms of thermal design power (TDP) to meet the aggressive market demands [
2,
3]. Therefore, it is essential to minimize power consumption by significantly reducing the DRAM bandwidth in high-end multimedia applications by introducing a method to resolve thermal problems and extend battery life. Consequently, several proprietary power reduction features such as ARM (Advanced RISC Machine) frame buffer compression (AFBC), adaptive scalable texture compression (ASTC), and transaction elimination (TE) have been introduced [
4].
Among these techniques, lossless embedded compression (LEC) has become essential such that it loses its competitiveness in the mobile chipset market if it is not actually used. In this regard, several related studies on LEC have surveyed the cache and memory compression methods, compression algorithms for various types of data, and interactions with other approaches.
Although lossy compression guarantees constant bandwidth gain, the image quality is inevitably deteriorated, which can be fatal in multimedia cases. For example, image details obtained through several painful tuning operations may vanish due to lossy compression, and it is more probable that image quality would be more deteriorated after repeated memory operations. Therefore, lossy compression is adaptable in minimal cases where quality is not a high priority.
In high-end mobile devices, the camera and display subsystems, as well as video codecs, are usually integrated into the same die and compete to occupy more memory bandwidth. However, they all operate in association with other subsystems even in extreme cases of 8K HDR recordings and 8K video conference calls via LTE (Long-Term Evolution) or 5G networks, and a given application task will be distributed in a heterogeneous computing environment to achieve minimum execution time.
In this situation, it is essential to use a unified bandwidth compression that all the necessary system components, including processors, can decompress. For example, in camera encoding, the neural processing unit (NPU) can be engaged to manage specific recognitions such as face detection and lane detection. However, the image data cannot be compressed when acquired from an image sensor if the processor cannot decompress. As another example, the graphics processing unit (GPU) fallback occurs whenever the display controller cannot perform even one of the input frames. In this case, if the GPU cannot decompress, the LEC algorithm is completely ineffective for display paths. As a final example, a digital signal processor (DSP) can enhance image quality when a movie is decoded via the video codec standard. Likewise, if a DSP does not know how to decompress the frame, the codec should write the decoded video frame in a raw format.
The contemporary memory system in mobile chips uses more ranks and banks to maximize the total bandwidth, with a minimum access size to mitigate the utilization loss of hardware resources such as bus, cache, and main memory [
5,
6]. Thus, the achievable compression ratio (CR) is inevitably quantized in real multimedia applications by burst lengths for a single access. For example, if the block size is 256 bytes and the bus width of a system is 16 bytes, the actual CR is quantized to 6.25% for each block. As another example, if the block size is the same and the minimum burst length of a system for high memory utilization is 64 bytes, the actual CR is quantized to 25% for each block. Therefore, the best CR of an LEC algorithm does not entirely guarantee the maximum bandwidth gain, and an efficient LEC algorithm can be affected by other parameters in the mobile chip design.
An optimized and unified LEC for mobile chips should satisfy not only high CR but also many other metrics, which is a trade-off with CR. In this paper, we suggest some metrics to assess LEC performance to consider the realistic factors in this dark silicon era [
7,
8] and propose an optimized LEC algorithm for mobile multimedia scenarios based on the metrics. With the proposed LEC implementation, we achieved up to 9.2% enhanced CR on average while satisfying the target frequency up to 1.4 GHz. The contributions of this paper are summarized as follows:
We propose realistic metrics to assess LEC performance that help to evaluate what is needed in the design of cutting-edge high-performance mobile devices.
We develop an efficient encoding method, according to the realistic characteristics of the residual distribution.
We present an efficient metadata structure to minimize the access overhead optionally.
We implement an optimized LEC for high-end mobile multimedia based on the metrics, which is used not only for video codec, but for the entire multimedia scenario in modern mobile devices.
2. Related Works
2.1. Data Compression for Cache and Memory Systems
Several data compression techniques were introduced to accomplish the aims of different approaches [
9,
10,
11]. Particularly, Mittal et al. [
11] summarized the current data compression techniques for memory systems, including cache. The authors classified the techniques based on the processor component in which compression is applied using the compression algorithm and the objective. In addition, the authors explained factors and trade-offs in compression, to which we referred to make our performance metrics. Although Mittal et al. mentioned that smartphones are used for data-intensive applications such as multimedia, they did not focus on multimedia data compression itself.
However, in mobile chipsets, memory bandwidth for multimedia applications such as camera, video codec, and display accounts for most of the total bandwidth. For example, a 200-megapixel camera and UHD (Ultra High-Definition) (3840 × 2160) 144 Hz display require a few tens of gigabytes per second, which generally accounts for most of the total memory bandwidth in a mobile system, and seamless operation is not possible without an efficient data compression algorithm.
In modern computing systems, if hardware accelerators cannot perform some multimedia jobs, then a GPU or central processing unit (CPU) should be engaged to process them, which is known as GPU fallback or CPU fallback [
12,
13]. In a similar vein, if there is no hardware accelerator for some specific functions, then the associated software task should process them using a DSP or NPU. In cases where the processors cannot manage compressed data in memory, the data compression for memory bandwidth is applicable to minimal cases in which the GPU is never involved. In other words, an LEC algorithm for mobile multimedia should be interpreted by processors such as CPU, DSP, and GPU for software solutions.
2.2. Lossy Compression for Bandwidth and Footprint Reduction
Lossy compression can be a very efficient way to save bandwidth and memory footprint. Efficient lossy compression algorithms and implementations are proposed previous studies [
14,
15,
16]. Data loss can cause significant image quality issues in multimedia applications, thus they are not appropriate approaches in general. Since the tolerance for image quality loss due to data compression is not allowed in most cases, this study does not deal with lossy compression. However, as future work, we plan to develop an optimized lossy compression only for specific cases, which tolerate some image quality loss to prioritize the sustainable battery time.
2.3. Lossless Compression for Bandwidth Reduction in Multimedia Environments
The LEC algorithms for the video codec system were previously proposed [
17,
18,
19,
20,
21]. However, the algorithms mainly enhance CR in video codec applications and use a much more complex addressing mode, which is not applicable to general multimedia scenarios, including camera, display, and associated software tasks in processors. The authors proposed efficient LEC algorithms that can save not only memory bandwidth but also memory footprint by using partition group and used finer-grained prediction and dynamic
k-order unary exponential Golomb (EG) code as entropy encoding or improved variable length coding (VLC). However, because only the video codec system is targeted, the LEC algorithms are too complex to obtain frequency higher than 1 GHz and throughput higher than 16 bytes/clock or 32 bytes/clock; therefore, other architectural alternatives need to be considered for high-performance mobile devices.
This study is different from previous studies on LEC algorithms and implementations in that we concentrate on searching for an LEC algorithm supported by all processors with high throughput and frequency as well as multimedia hardware accelerators. To accomplish the goal, we analyze the trade-off between algorithm complexity and hardware cost and search for an optimal point with evaluation metrics to assess an LEC.
3. Metrics for LEC Evaluation
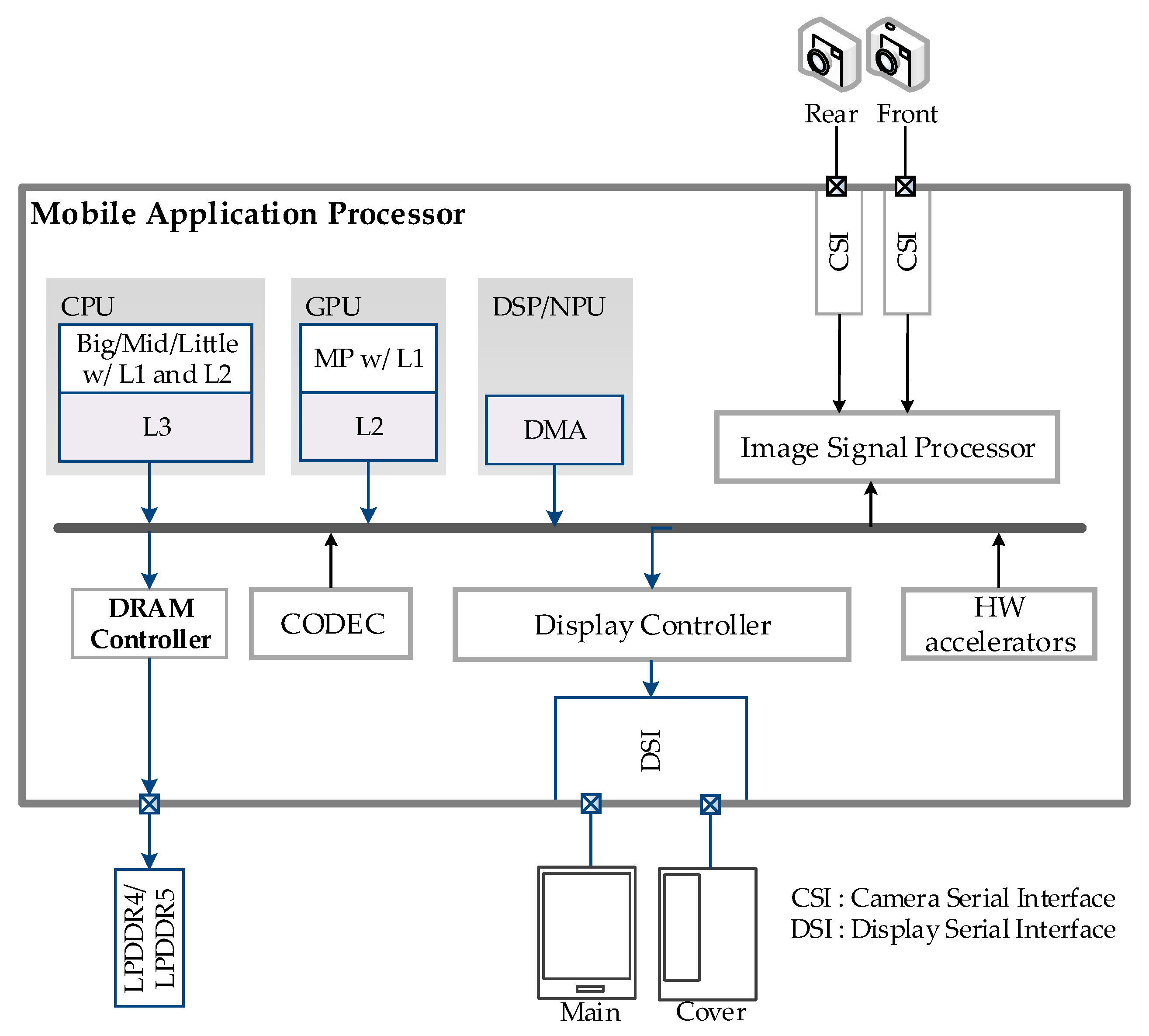
In leading-edge mobile application processors, various hardware accelerators for multimedia applications, and heterogeneous processors such as CPU, GPU, DSP, and NPU share unified system memory, as shown in
Figure 1. It is totally different from high-performance computing systems in which the GPU has a dedicated high-bandwidth memory. In addition, GPU, NPU, and DSP play critical roles in mobile multimedia scenarios as various artificial intelligence (AI)-based applications have emerged. Therefore, bandwidth compression for system memory can provide an appropriate gain only when the compression algorithm is feasible for the processors. However, according to our survey, researchers have not realized that the processors should understand the compression algorithm to obtain the maximum gain from expensive investment in compression and decompression.
As mentioned above, previous studies on LEC for multimedia concentrated on achieving the highest CR by improving their prediction and entropy encoding methods. However, because functions that require random access, such as motion estimation and geometric distortion compensation, are more often needed in modern mobile chips, the requirement for random access is mandatory with minimum overhead. In addition, because modern memory systems support a group of banks and have a minimum burst to increase DRAM utilization, the final CR is inevitably quantized at a minimum burst without a huge temporal buffer. This implies that a certain amount of compression gain can be sacrificed to increase the maximum throughput or random accessibility.
The complexity of a compression algorithm generally increases the hardware cost by increasing the area or reducing the feasibility of parallelism. Furthermore, random accessibility is crucial in some multimedia scenarios; however, it affects the actual CR because of metadata information and redundant access. Likewise, hardware area and performance such as throughput and maximum frequency, are the main factors to consider. In this section, we define four main metrics used to evaluate the performance of an LEC.
Table 1 shows the list of concerns to consider in an LEC algorithm.
3.1. Compression Ratio (CR)
The CR is the most crucial metric for the LEC algorithm, since a higher CR provides a greater chance to reduce memory bandwidth and power. The bigger the block size, the more complicated the prediction algorithm, and more adaptive entropy encoding generally helps to achieve high CR. In addition, efficient entropy encoding with residual values is one of the key factors for high CR.
A square block such as 16 × 16 generally shows the best CR due to high spatial locality, but higher blocks cost more area for line memories in real-time subsystems such as camera and display. In addition, a loop filter in video codec such as high efficiency video codec (HEVC) requires a read-and-write operation for the below four lines by re-reading the compression result of the above block. In this case, a 16 × 16 block shape is inefficient for the read-modify operation, thus twice accessing the whole compressed region. Therefore, in the case of multimedia operations involving camera, display, and codec, selecting a long horizontal block shape, such as 64 × 4, is a better choice when considering the overall system.
Numerous prediction algorithms for image compression have been reported [
22,
23,
24]. As a more sophisticated prediction algorithm refers to more neighborhood pixels, it becomes difficult to reach the maximum target frequency and process it in parallel. Meanwhile, a simple prediction algorithm cannot guarantee that it can satisfy the target CR because it refers to very few pixels. In this study, CR is defined as the equation below; a low number implies better performance from the compression perspective. In addition, to conduct experiments with various types of real images, we purchased test images from NHK (Nippon Hikikomori Kyokai) [
25] and categorized them into five groups according to their characteristics, as shown in
Table 2.
3.2. Metadata Overhead (MO)
Compressed data can be divided into payloads for encoded data and metadata for compression information. Metadata provides information to efficiently access compressed data, which is essential for random access. However, if the metadata is too large, even if the compression rate is large, the overall CR may drop due to the metadata overhead. Therefore, metadata should contain concise and essential information. The metadata overhead is defined as follows:
For example, if the size of metadata is 16 bytes for each 16 × 16 block with an 8-bit pixel component, the overall CR is likely to increase; however, the metadata overhead accounts for 6.25%. The reason why large metadata size can cause higher CR is that it contains as much information as possible to compress the data, for example, uniform color in graphic user interface (GUI) images. Meanwhile, if the metadata is only 1 byte, then the overhead is only 0.4%. This study proposes a method to increase random accessibility with only 0.4% of metadata overhead.
3.3. Achievable Frequency (AF)
A modern mobile CPU operates at almost 3 GHz, and a GPU operates at 1.4 GHz; NPU and DSP usually require a frequency higher than 1 GHz. For such processors to be able to compress and decompress the same algorithm to other multimedia accelerators, the algorithm should be as simple as possible to meet the maximum frequency of the processors. Alternatively, other architectural designs, such as a parallel operation for multiple blocks should also be considered, but this is not always possible for the processors. Therefore, the achievable frequency should be 1 if the LEC algorithm is to be applied to a specific system. In other words, if the AF metric is 0, it means that the compression algorithm is not appropriate for the system.
3.4. Area Overhead (AO)
The total area overhead (AO) is an important metric to assess an LEC algorithm. In general, larger block size and complexity of the algorithm provide a better CR, but this has a high cost in terms of huge area overhead due to register slices, temporal buffers, number of reference pixels, etc. Therefore, the unit area of an encoder and decoder engine affects the total area overhead of an LEC implementation. In addition, the height of the block is tightly coupled to area overhead in real-time operations such as camera and display subsystems. As the resolution increases, the number of line memories due to the height of the LEC block significantly affects the chip area. The area overhead can be calculated as the percentage of the total area increased by LEC support.
4. Proposed LEC
The aim of the proposed design is that all hardware accelerators are related to entire multimedia scenarios, and general processors such as GPU and DSP support the proposed LEC algorithm. Alternatively, very restricted paths can be used for compression, because the software cannot distinguish whether the frame buffer is compressed or not and hence cannot reach the total memory bandwidth requirement. The maximum target frequency is 1.4 GHz at nominal voltage, and the maximum throughput is 64 bytes/cycle for compression and 32 bytes/cycle for decompression.
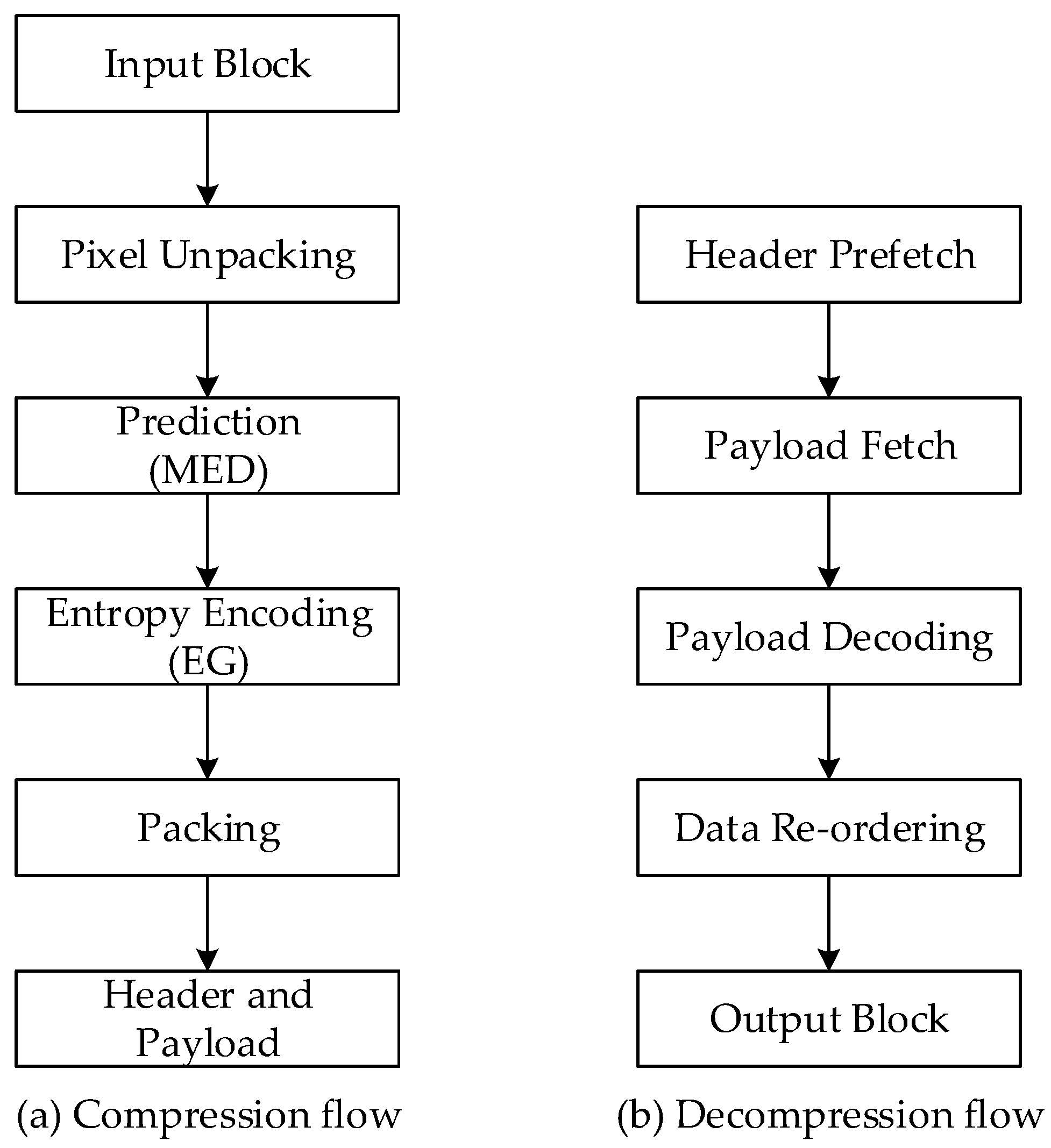
Figure 2 shows the compression and decompression flows in the proposed LEC.
4.1. Prediction
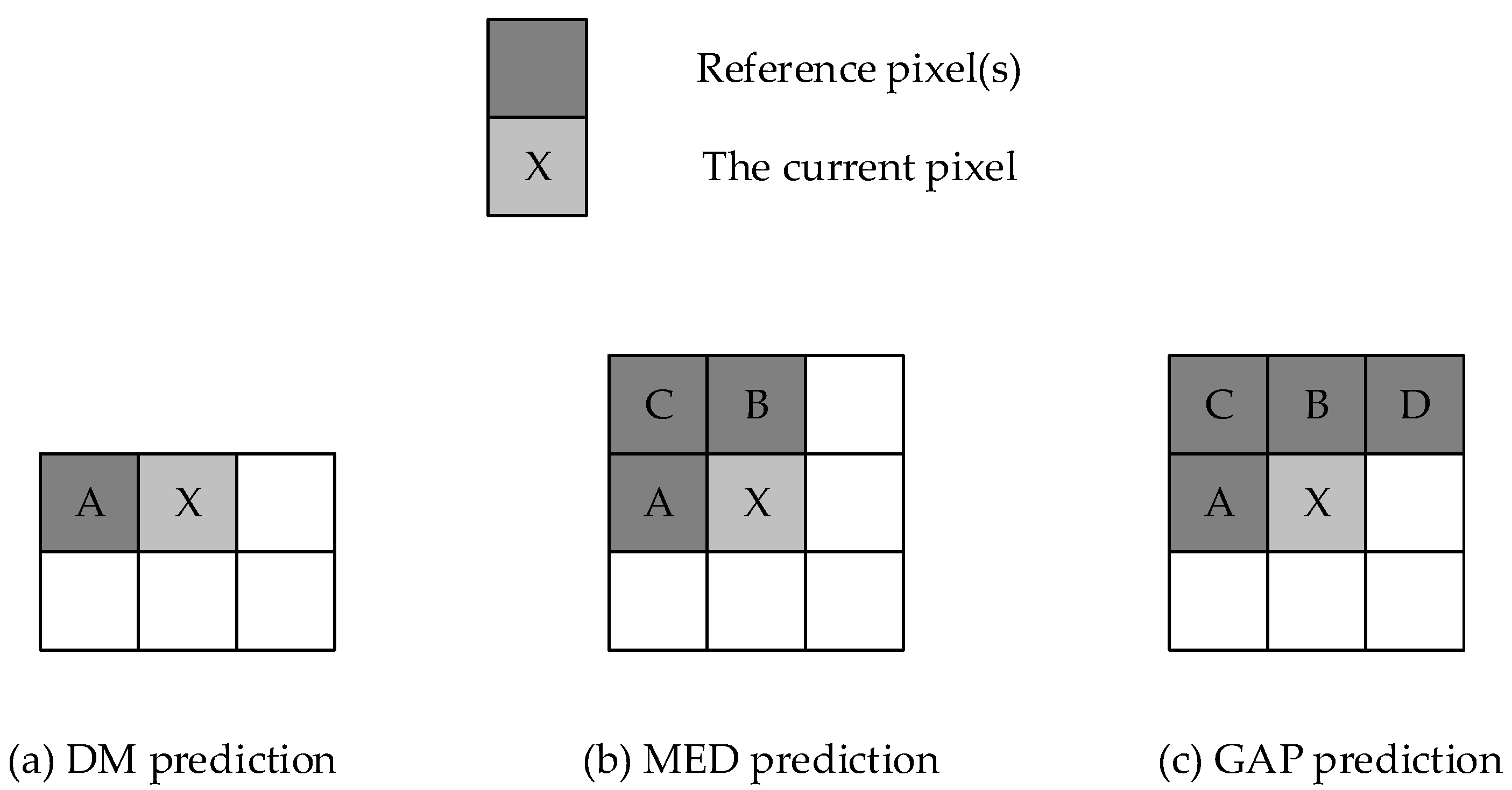
Gradient adaptive prediction (GAP) [
22] tends to show higher performance than delta modulation and median edge detection (MED) prediction [
23], but its maximum frequency is limited to a certain extent because of the number of reference neighborhood pixels, as shown in
Figure 3. According to our evaluation result, MED with LOCO-I (Low Complexity Lossless Compression for Images) algorithm shows a similar CR as GAP and provides a better chance to enhance the critical path by removing dependencies of neighborhood pixels. In addition, the max frequency of GAP is under 1 GHz (actually around 800 MHz) according to our implementation. The MED algorithm refers to four neighborhood pixels, but the prediction stage can be pipelined by grouping input pixels and changing the order of reference pixels. With the parallelization, we can enhance the critical path and total throughput. Therefore, we adapted the parallelized MED with LOCO-I algorithm as a prediction method.
Given a value X in MED prediction, and its left, upper, and upper-left neighbors A, B, and C, respectively, the prediction value is determined based on the following equation:
If C is greater than the maximum value out of A and B, the prediction value for X is the minimum value out of A and B.
If C is smaller than or equal to the minimum value out of A and B, the prediction value for X is the maximum value out of A and B.
Otherwise, the prediction value for X is A + B – C.
For boundary pixels that do not have a neighbor, MED prediction is the same as delta modulation.
Table 3 shows the CR comparison of four prediction algorithms with the same entropy encoding and data packing; that is, the MED and GAP with test image classes shown in
Table 2.
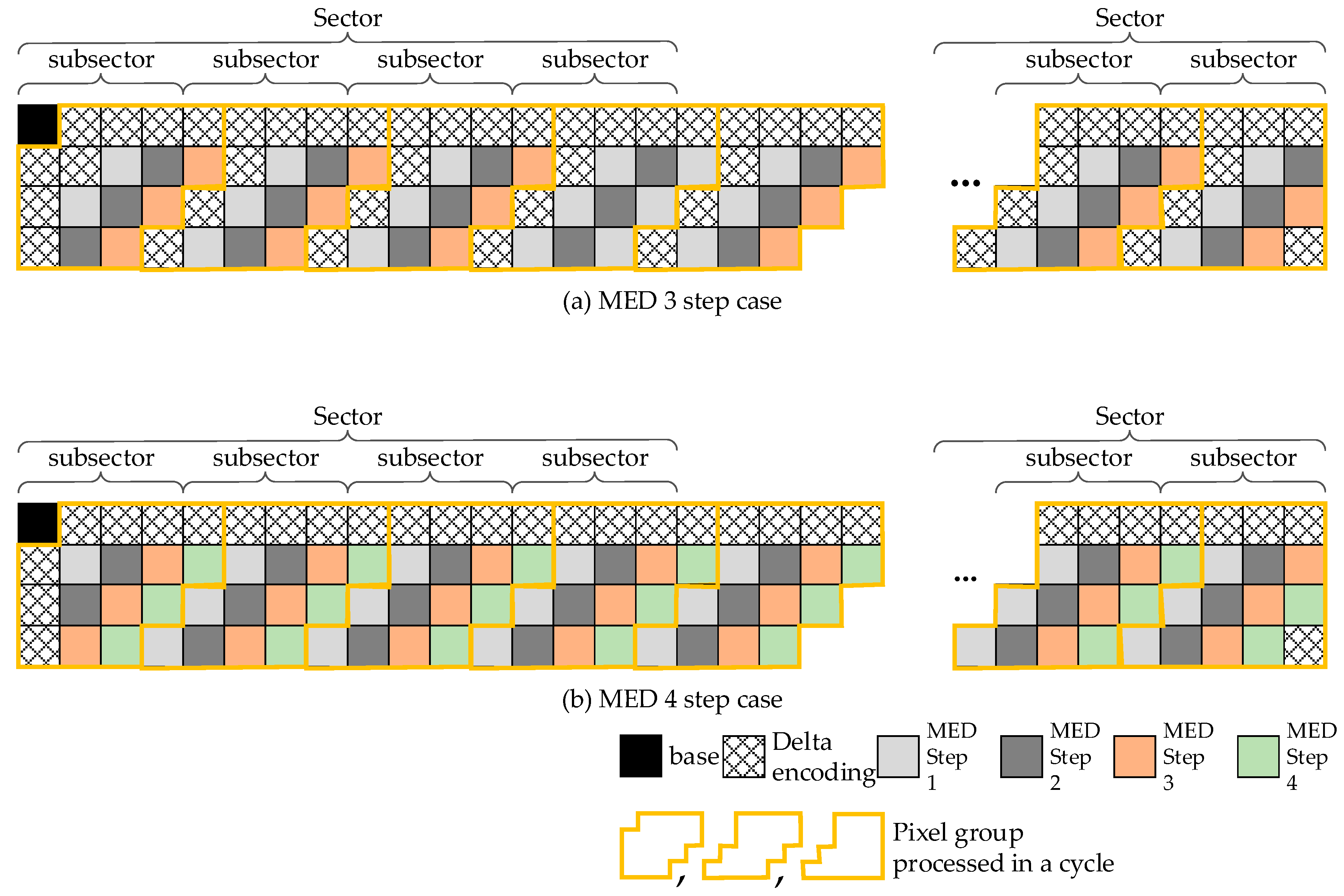
To increase the throughput of MED processing, we propose a per-sector decompression method that requires three or four independent MED decompressions in a cycle, as shown in
Figure 4. Due to the shape of the block, some pixels need to be processed through delta modulation instead of MED. By grouping up to 16 pixels and changing the order of pixels, we can achieve the desirable throughput for MED processing. With the synthesis results shown in
Table 4, we decided to use the three-step MED because implementation of the four-step MED cannot satisfy the AF metric, even though it might show slightly higher prediction performance because of the minimum delta modulation (DM) predictions.
4.2. Entropy Encoding
After prediction using an enhanced MED, the residual values of pixels are derived from the prediction engine. First, because an 8-bit input pixel is between 0 and 255, the residual value is between −255 and 255. To avoid the case that small residual value is encoded with a long code, we adapted the following residual transform. For example, let us consider that the current pixel is 0x00 (0 in decimal) and, the previous one is 0xff (255 in decimal). If we predict the current pixel using DM, the residual becomes −255. The transformed residual is 0x01, and the decompressed pixel value is obtained by adding 0x01 (the transformed residual) and the previous pixel value (0xff) and then removing the most significant byte (MSB), which is the same as 0x00.
To encode the transformed residual values, we considered run-length, quad-tree, EG [
26], and Golomb–Rice (GR) coding [
27]. Out of these, run-length and quad-tree coding showed insufficient performance, and we excluded them from our entropy encoding. However, we considered that run-length coding can be used to encode zero values separately in MSB of the residual values, because zero values significantly account for the MSB part of the transformed residuals as shown in
Table 5. EG encoding uses a nonnegative integer parameter
k to encode more significant numbers in fewer bits. Parameter
k indicates the order of EG, and the EG algorithm exhaustively searches for the optimal
k value after encoding with several
k values.
In EG encoding, the number of codes is the number of leading zeros plus 1 plus
k, and the number of bits for encoding is the number of leading zeros plus the number of codes.
Table 6 shows an EG encoding example according to
k values.
For lossless compression, it is assumed that the size of the compressed data is smaller than, or at least equal to, that of the original data for a block. Therefore, if the number of payload bits for a block is higher than the original bits, then it should be written with the uncompressed data. Otherwise, random accessibility is not guaranteed, and the metadata should contain more information to identify it because the block size varies. Based on this fact, if a long codeword is allocated and encoded, the probability that a block will be processed as uncompressed data increases. Instead, by initially restricting the type of codeword within the same k value, encoding only the least significant byte (LSB), and processing larger values as uncompressed data, the overall CR is similar to the full codeword case. Therefore, we decided to use restricted codeword-types with the same k value. This restriction makes the hardware implementation much simpler than rigid implementation, which helps to increase the overall pixel throughput.
Table 7,
Table 8,
Table 9 and
Table 10 show CR results with different
k and codewords for 8-bit and 10-bit images with GR and EG. Although the CR results seem similar, the complexity of GR is higher than EG because more lengths of codewords are possible. According to our analysis, EG has the following advantages compared to GR:
If we use a single k value, hardware encoding and decoding become simpler, and the hardware latency gets shorter because it does not need to parse the k value. In this regard, we adapted EG for entropy encoding with a predefined but configurable k value.
4.3. Metadata/Payload Structure
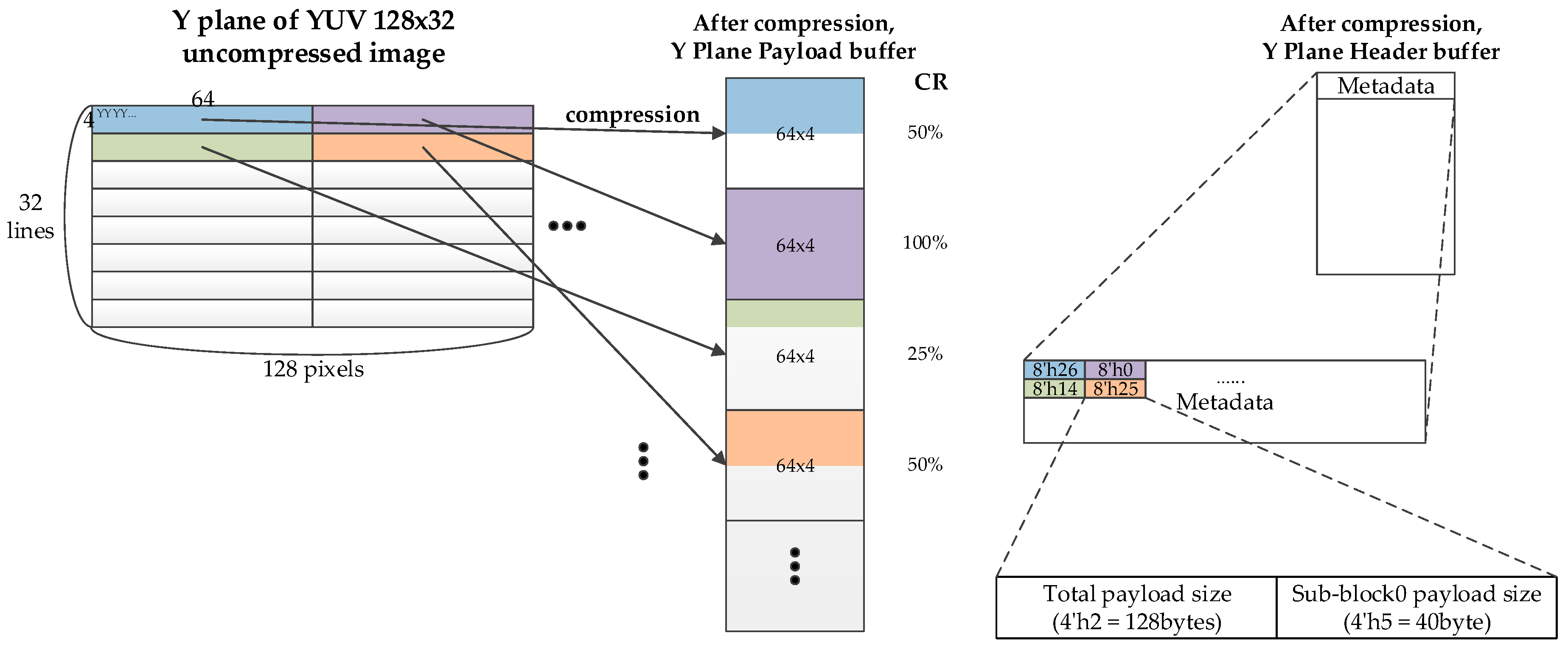
To minimize the metadata overhead, we propose 1-byte metadata that contains only the amount of data for the compressed block. The metadata indicates how many bytes the compressed data occupies. For example, if metadata is 1, then the compressed data is 32 bytes after compression when the basic unit is 32 bytes. If metadata is 0, then the block is not compressed.
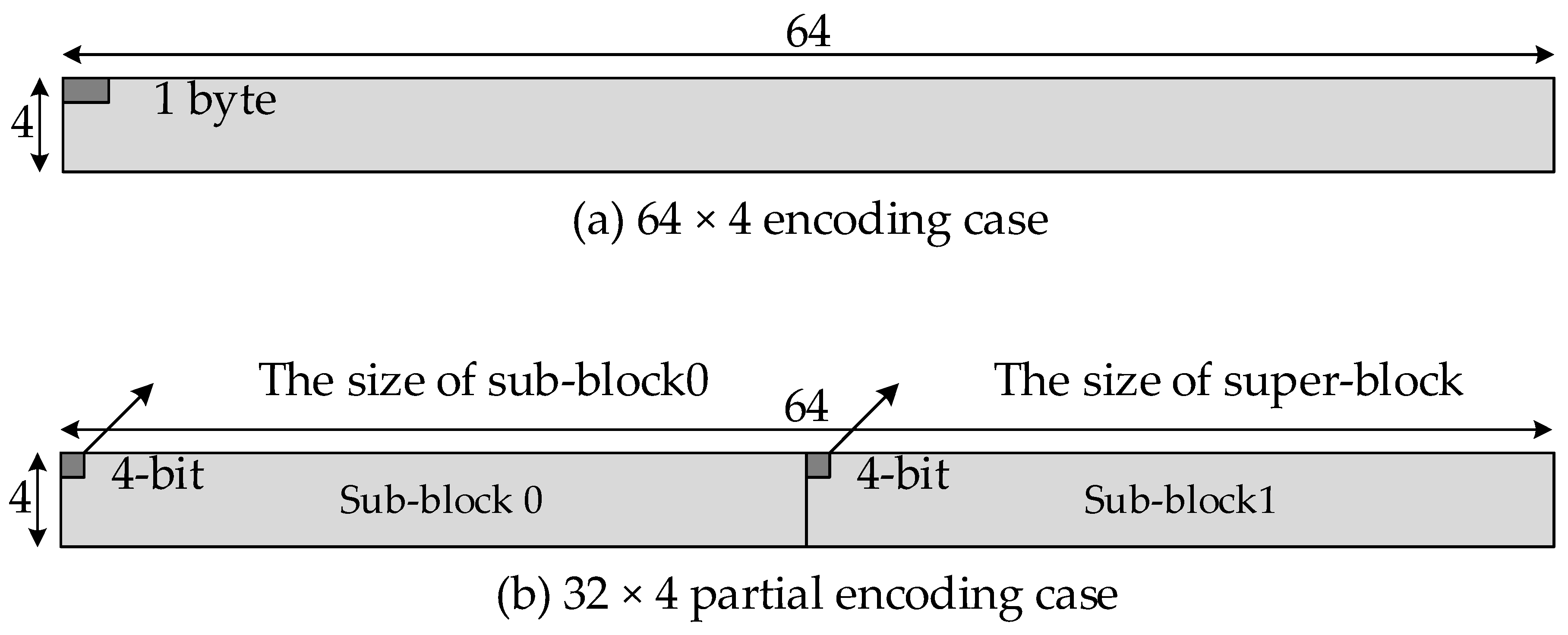
For random access, a block size of 64 × 4 is too large to reduce the access overhead. Therefore, we define a partial encoding to minimize the access overhead during random access, as shown in
Figure 5b. In partial mode, the superblock is 64 × 4 in size, whereas the subblock is 32 × 4 and the whole superblock is composed of two subblocks. The LSB 4-bit and MSB 4-bit metadata identify the sizes of subblock0 and superblock, respectively. The size of subblock1 can be calculated by subtracting LSB 4-bit from MSB 4-bit.
Figure 6 illustrates the payload structure. It contains a
k value and EG encoded data. As mentioned above, if the encoded data exceeds the original size, it is marked as an uncompressed block, and the original data is written as is. In addition, if a partial update is necessary, some specific blocks can be written in uncompressed data, which is very useful for boundary processing.
Figure 7 shows the metadata and payload layout of the proposed LEC algorithm. Since the positions of the metadata and payload are deterministic, the metadata can be pre-fetched into a buffer and the payload can also be pre-fetched when the metadata is not available, but the IP (Intellectual Property) is sensitive to latency immunity. However, the payload should generally be fetched according to the metadata information to reduce memory bandwidth.
5. Performance Evaluation and Implementation
5.1. Performance Evaluation with the Proposed Metrics
For the performance evaluation, we compared three LEC algorithms in commercial AP products with the performance metrics shown in
Section 3. Due to confidentiality issues, we cannot expose exactly. The first commercial LEC algorithm shows the best performance in area overhead; however, it cannot reach the achievable frequency metric and shows the worst CR. The second commercial LEC algorithm satisfies AF, but CR and AO are not competent. The proposed LEC algorithm shows better performance in every metric, except area overhead. The pipelined MED algorithm and two encoding methods according to MSB and LSB partitioning, enhance overall CR, keeping hardware reasonably simple. Moreover, the efficient metadata information shows the lower metadata overhead. As the minimum access unit is 32 bytes or 64 bytes in modern mobile chips due to multi-rank memory systems with high bandwidth, we calculated CR in the 64-byte minimum access case.
As shown in
Table 11, the proposed LEC algorithm has the best performance in CR and metadata overhead. In addition, it meets the achievable frequency that targets 1.4 GHz. Even though the area overhead is worse than algorithm 1, algorithm 1 is not feasible for the target system, because the achievable frequency metric is not satisfied.
5.2. Implementation Results
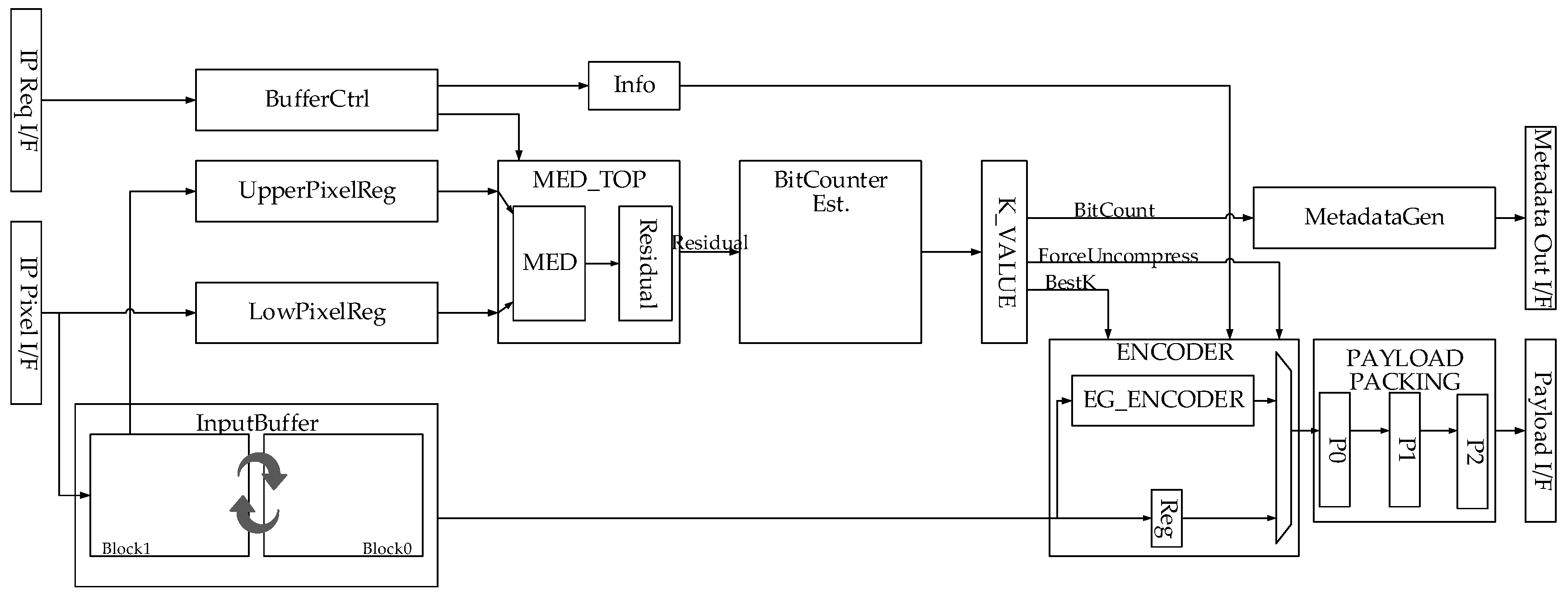
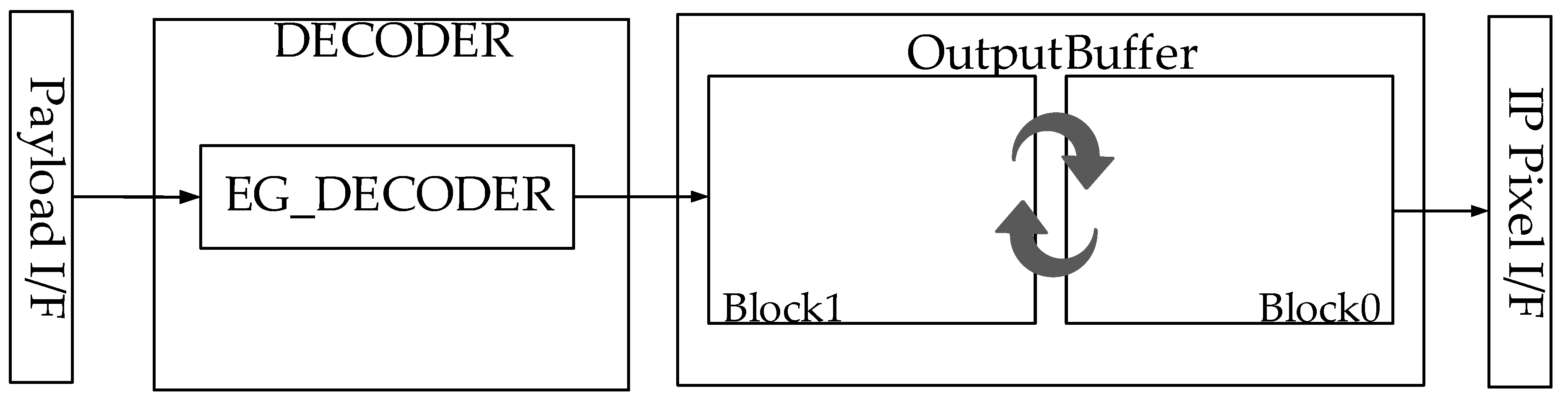
Figure 8 and
Figure 9 show the proposed LEC compression and decompression engines. Each hardware accelerator uses them in its way. For example, as the scan order is fixed in the display panel side, a display controller and a camera interface, which are representative real-time IPs, need four-line memories to decompress and a huge metadata buffer to pre-fetch metadata. As another example, codec utilizes random access to perform motion estimation and is very sensitive to memory latency; therefore, it should sometimes pre-fetch the payload data even when the metadata is not ready. It has huge metadata and payload caches to reuse them.
For the decompression side, each hardware accelerator can have metadata and payload access patterns as well as memory structure for the dedicated efficient storage to pre-fetch them. After pre-fetching the metadata, the hardware decides how many bursts it should request according to the metadata value. Furthermore, it reads the exact amount of payload data from memory and feeds the payload to the decompression engine.
Table 12 shows the implementation result of the compression and decompression engines. The pipelined MED prediction (
Figure 4) and a simplified encoding method achieve the target frequency of 1.4 GHz. The compression and decompression engines are integrated with each hardware accelerator and processor, so that the total area overhead is about 4.05%, as shown in
Table 12.
6. Conclusions
We present essential metrics to assess the LEC algorithm, show efficient encoding for metadata and payload, and propose an optimized LEC implementation for the most recent mobile multimedia scenarios. For GPU and DSP to support the same LEC algorithm in software IP, the algorithm should reach the target frequency and throughput. In addition, since the latest memory systems usually have a minimum burst length due to multiple bank structures to maximize utilization, the CR value is inevitably quantized to the minimum burst length. In this regard, the adequately simplified LEC algorithm can show improved performance over the complicated algorithm only for the best CR in the realistic metrics presented in this paper. The proposed algorithm enhances the actual CR of the LEC algorithm in a commercial chip up to 9.2% on average, while being able to keep the complexity to meet the timing closure condition.
For future work, a centralized LEC implementation is an exciting topic of research. After the memory management unit, since the address exists in the physical address space and the block data should be gathered to a certain point, the centralized LEC implementation does not seem to be beneficial. However, from an area perspective, the centralized LEC can give a better option than the distributed LEC implementation if the above-mentioned issues are resolved.
7. Patents
Jun, S.H. and Lim, Y.H., Samsung Electronics Co. Ltd. 2019. Image processing device and method for operating image processing device. U.S. Patent Application 16/205,900.
Jun, S.H., Park, C.S., Song, M.K., Lee, K.K., Lee, K.W., Jang, H.J., and Jeong, K.A., Samsung Electronics Co. Ltd. 2019. Image processing device. U.S. Patent Application 16/252,806.
Jun, S.H. and Lim, Y.H., Samsung Electronics Co. Ltd. 2019. Image processing device. U.S. Patent Application 16/252,796.