Sinusoidal Oscillators Operating at Frequencies Exceeding Unity-Gain Bandwidth of Operational Amplifiers
Abstract
1. Introduction
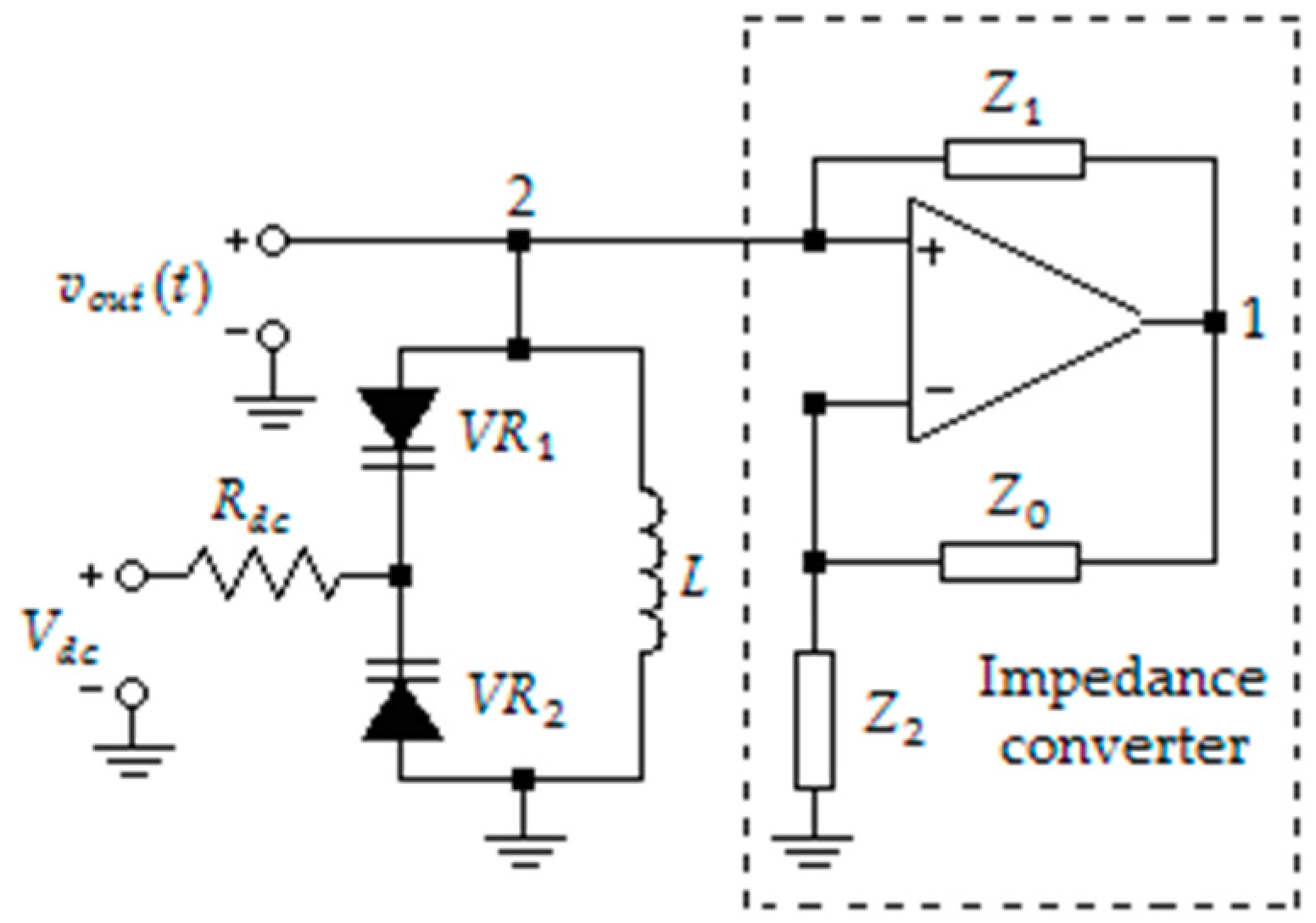
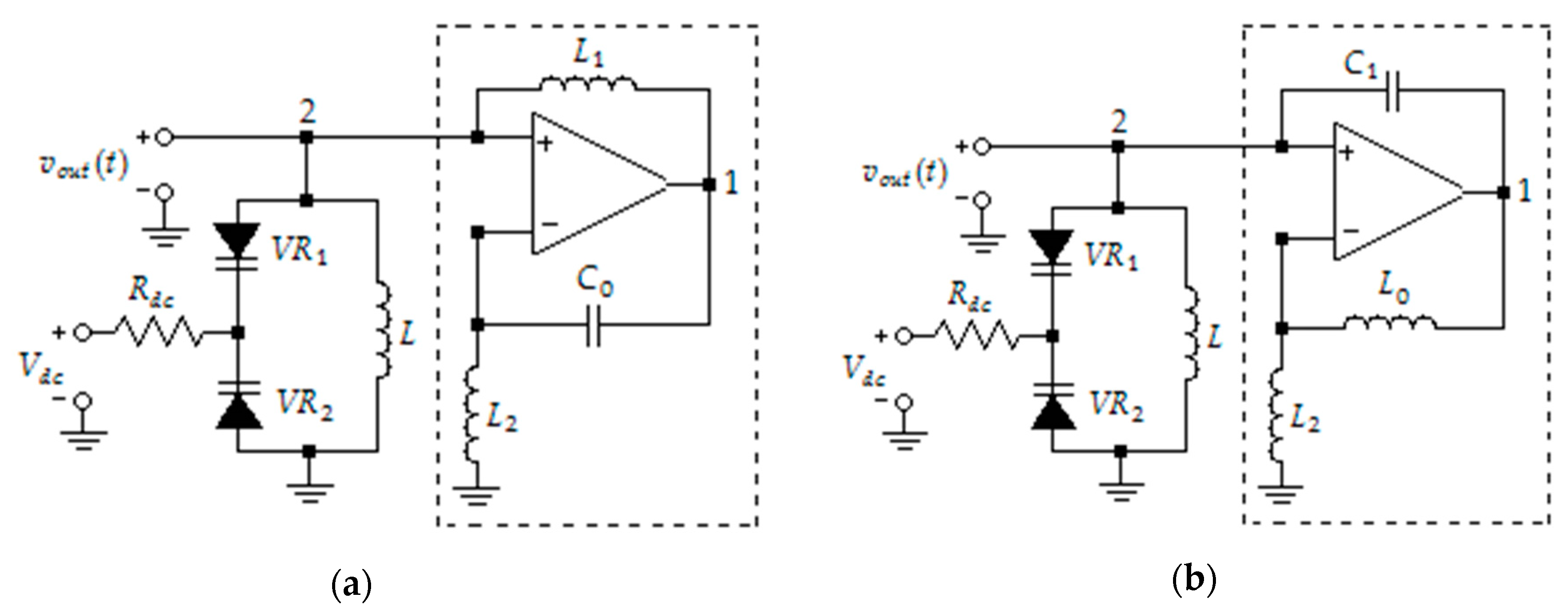
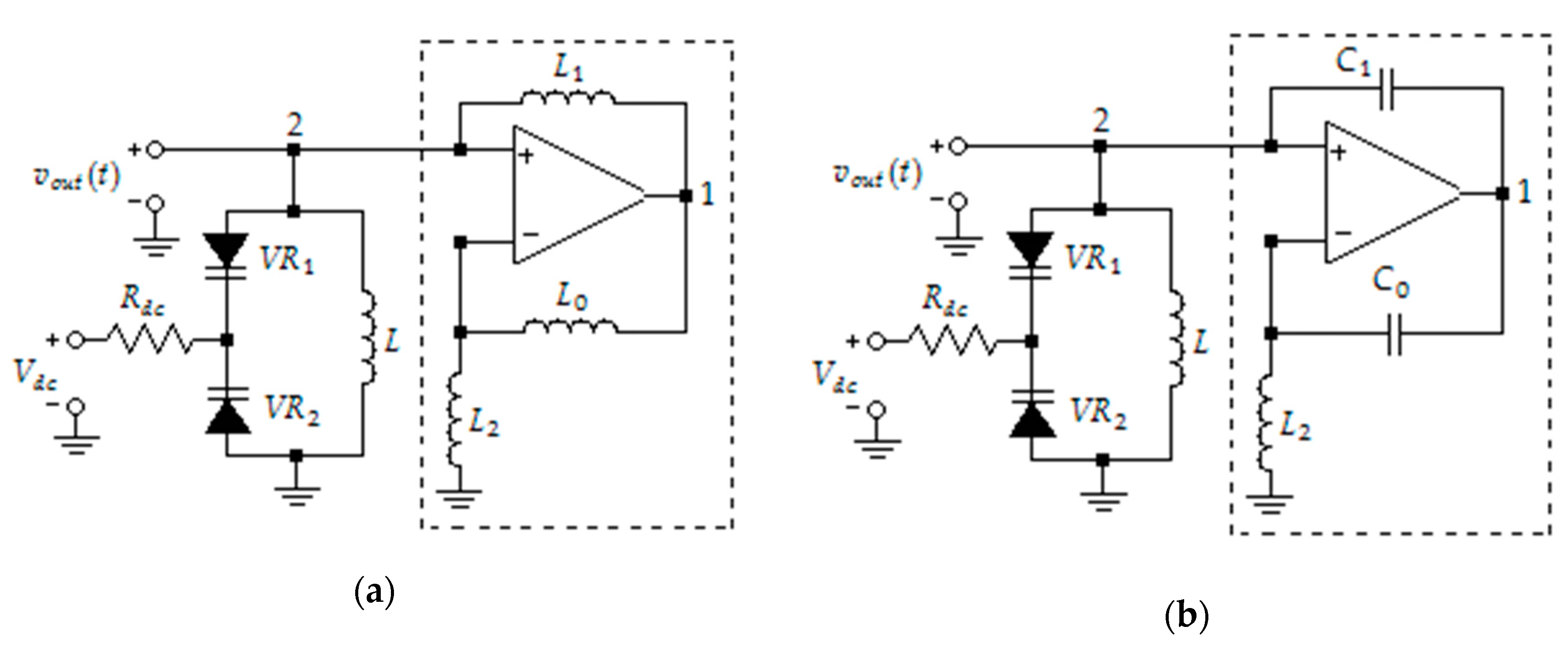
2. Architecture of Oscillators
3. Converter Analysis
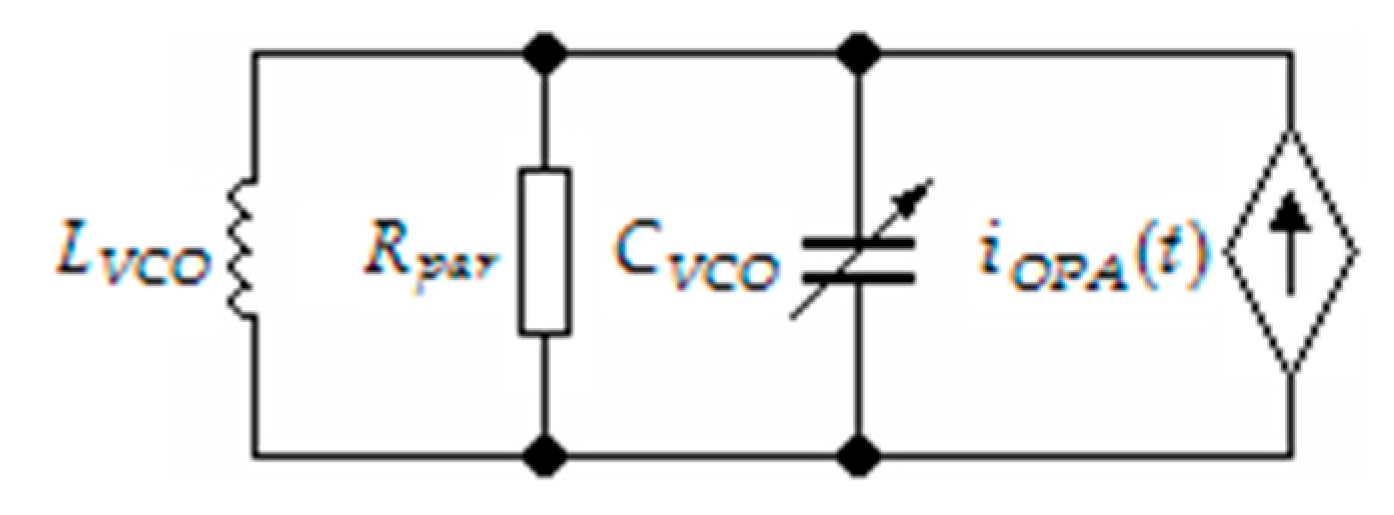
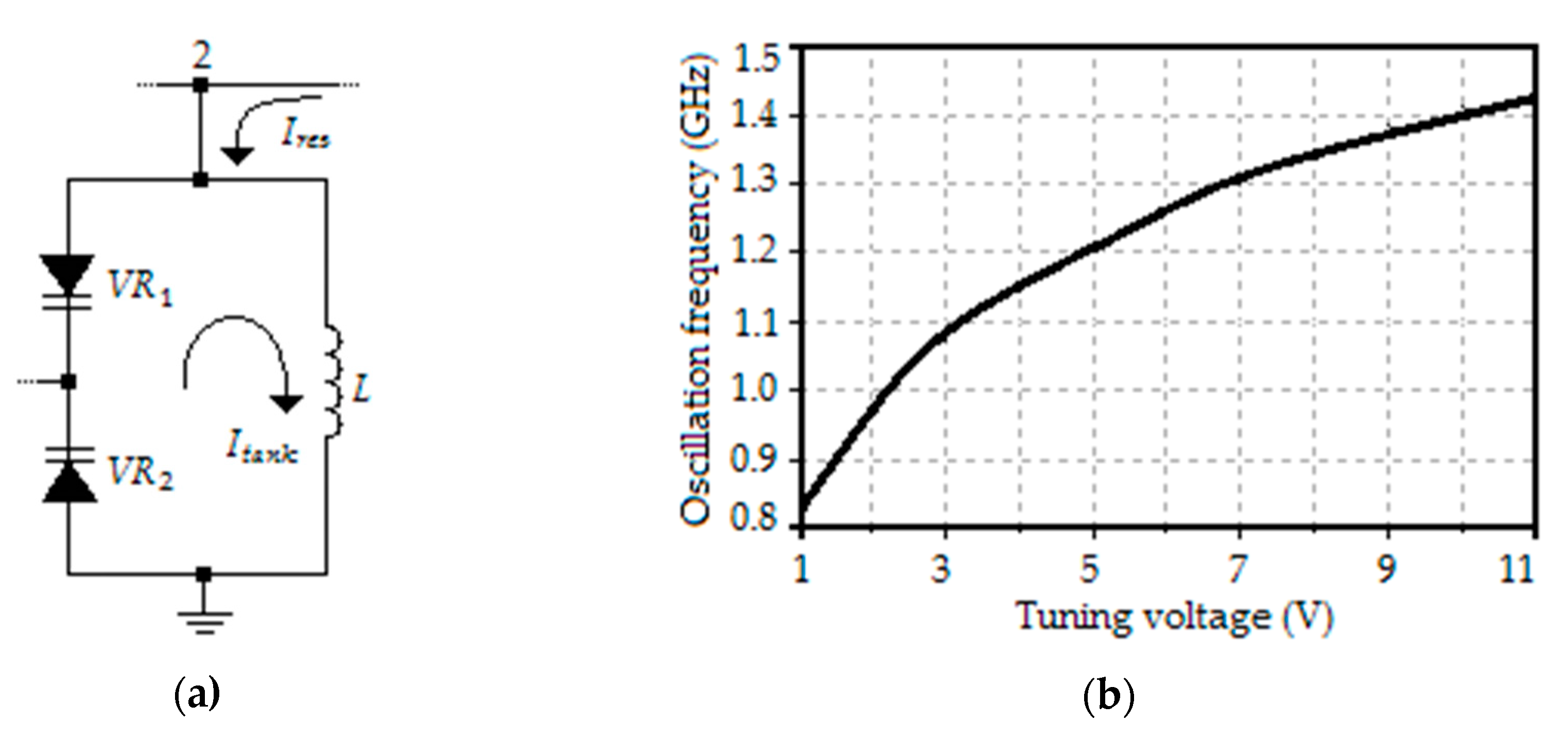
4. VCO Analysis
5. Amplitude of Oscillations
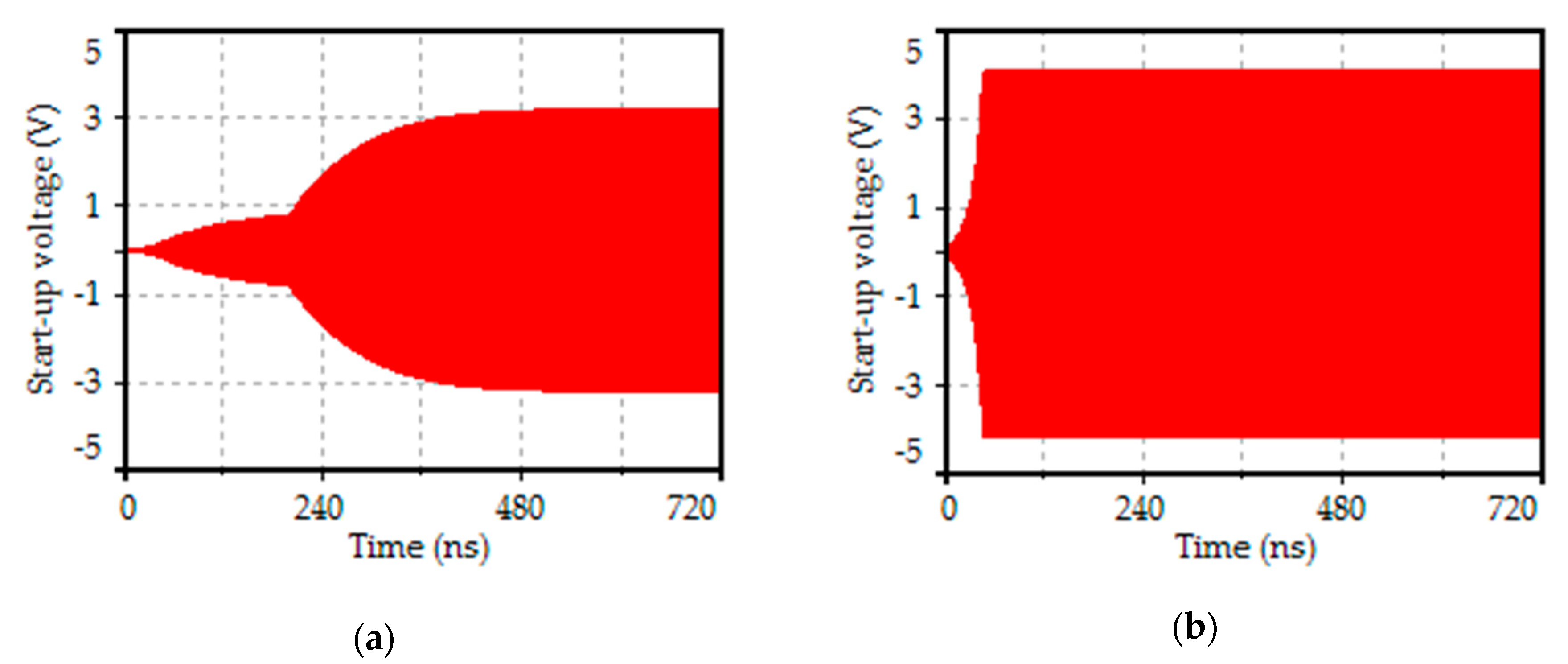
6. VCO Start-Up Conditions
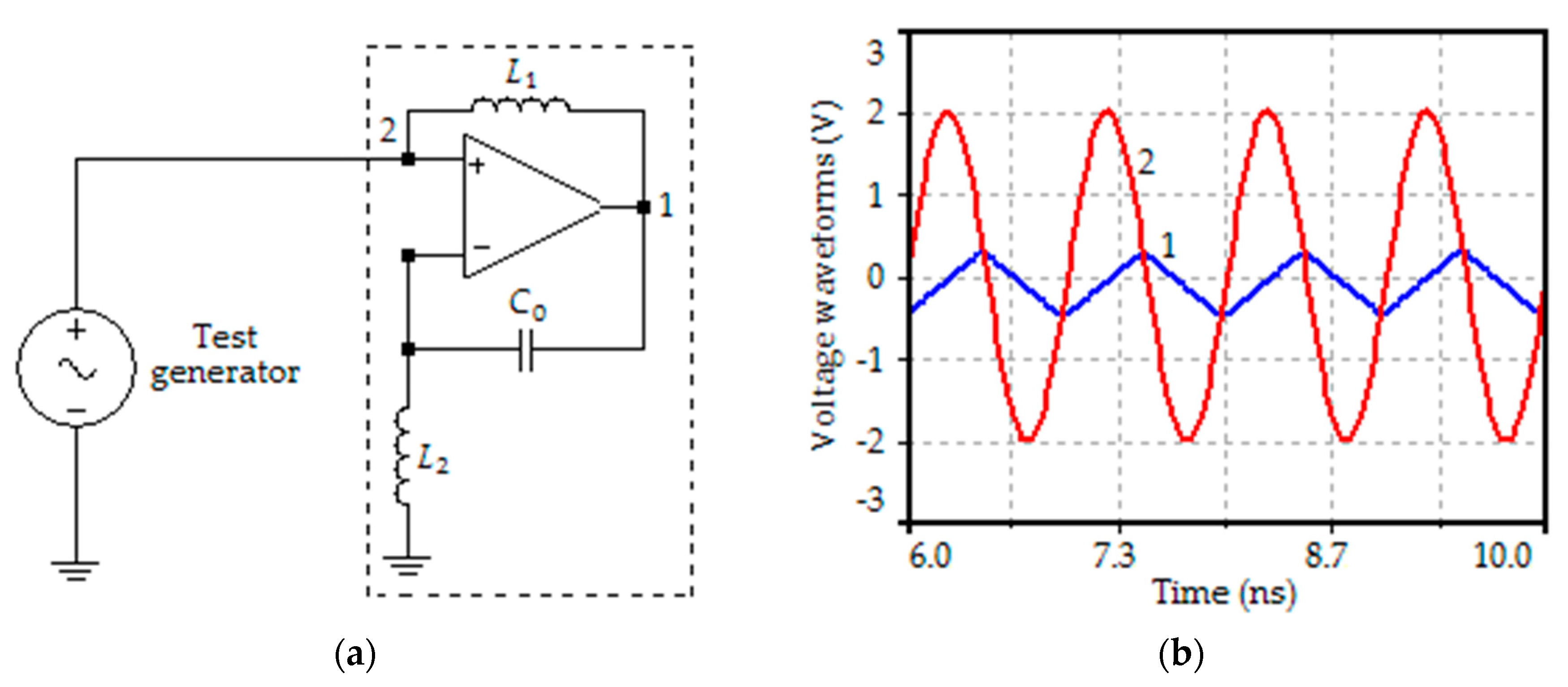
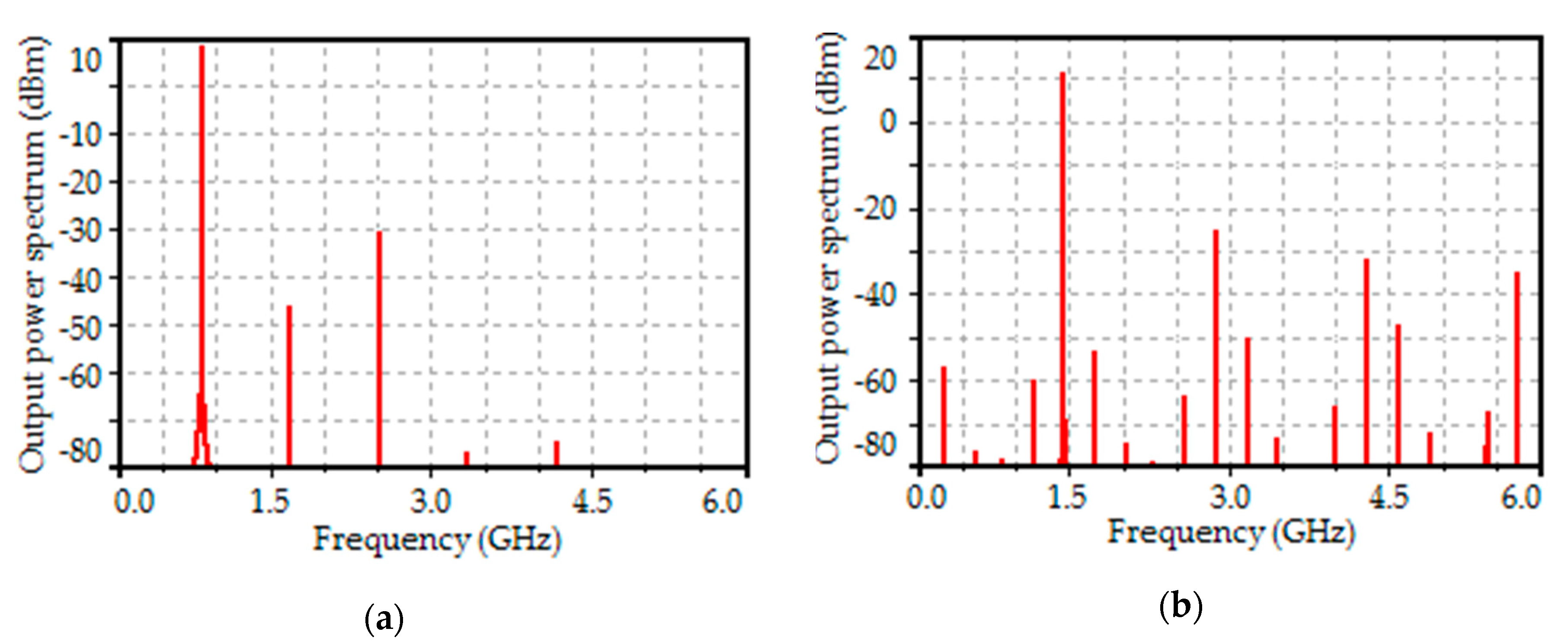
7. Simulation and Discussion
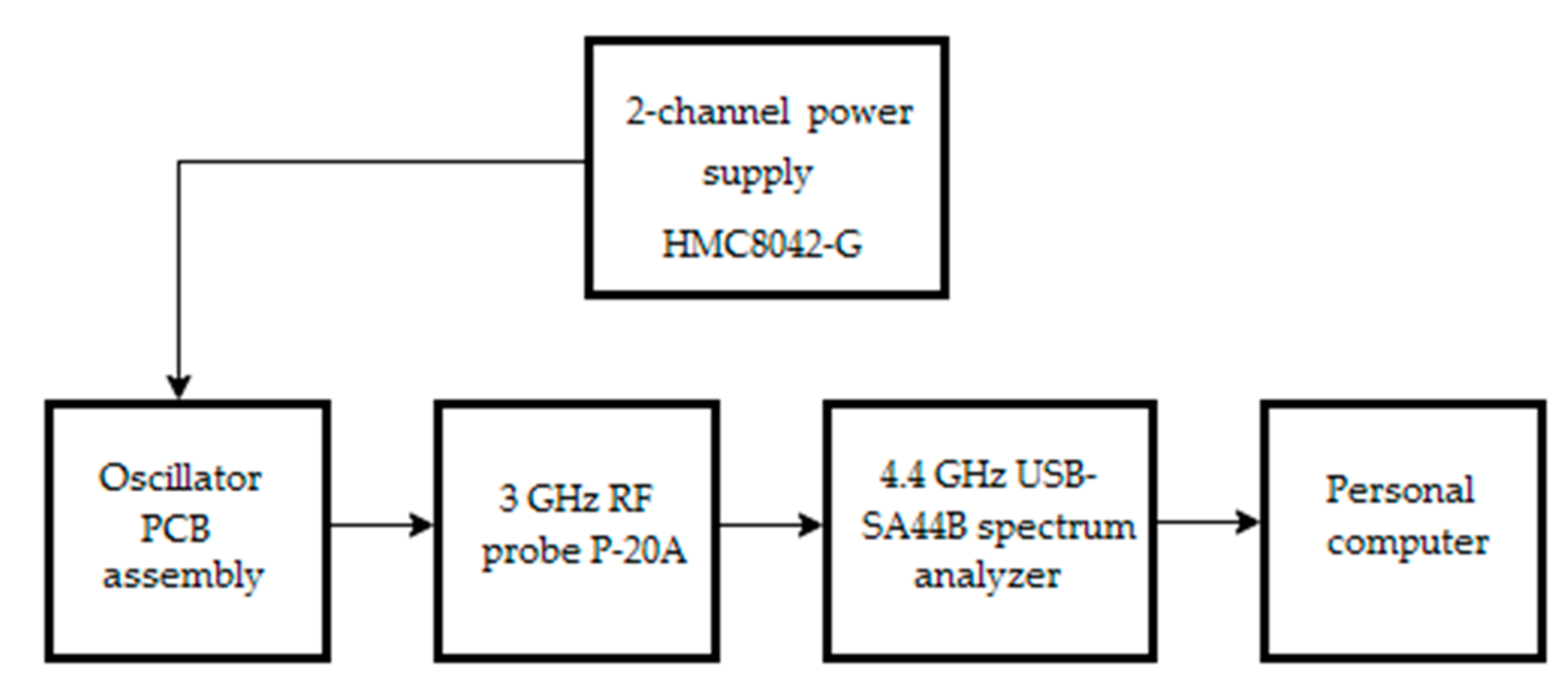
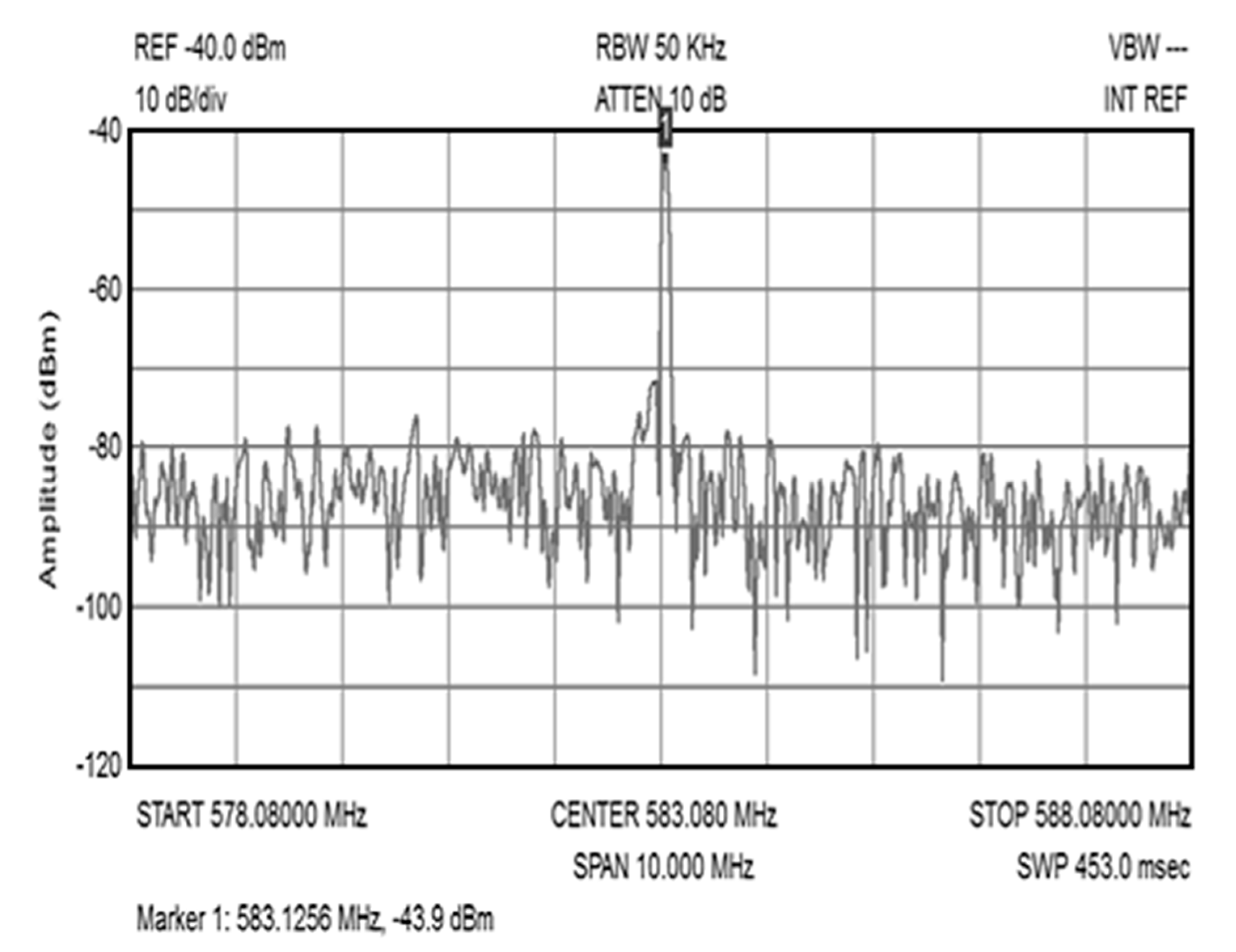
8. Experimental Results
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Zin | Input impedance seen by the noninverting terminal of OPA |
| Z0 | Impedance between the inverting input and output of OPA |
| Z1 | Impedance between the noninverting input and output of OPA |
| Z2 | Impedance between the inverting input of OPA and ground |
| L | Inductor of the tank circuit |
| VR1 and VR2 | Varactors of the tank circuit |
| Rdc | Resistor isolating the dc control voltage line from the VCO tank |
| L1 | Positive feedback inductor |
| C1 | Positive feedback capacitor |
| L0 | Negative feedback inductor |
| C0 | Negative feedback capacitor |
| L2 | Inductor between inverting terminal of OPA and ground |
| CVCO | VCO total capacitance |
| LVCO | VCO total inductance |
| COPA | Input capacitance of OPA |
| CPCB | Parasitic capacitance of PCB |
| CVR1 | Capacitance of varactor VR1 |
| CVR2 | Capacitance of varactor VR2 |
| y11 | Input admittance of feedback network |
| iOPA(t) | Feedback current flowing through impedance Z1 |
| vout(t) | Output voltage of VCO |
| IOPA,1 | Complex amplitude of the first harmonic of current iOPA(t) |
| ωfun | Angular frequency of the first (fundamental) harmonic of current iOPA(t) |
| φ1 | Phase of the first harmonic of current iOPA(t) |
| Rpar | Equivalent parallel resistance of the tank circuit at the fundamental frequency |
| Vsat | Saturation voltage of OPA |
| RC | Load resistor connected between OPA output and tank circuit in the Colpitts and Hartley oscillators |
| vOPA(t) | Voltage at the output of OPA (node 1) |
| Vμ | Complex amplitude of harmonic number μ of voltage vOPA(t) |
| |Vμ| | Amplitude of harmonic number μ of voltage vOPA(t) |
| θμ | Phase of harmonic number μ of voltage vOPA(t) |
| Vtriangle | Amplitude of triangular voltage at OPA output |
| IOPA,μ | Complex amplitude of current harmonic number μ |
| |IOPA,μ| | Amplitude of current harmonic number μ |
| φμ | Phase of current harmonic number μ |
| ρ | Tank circuit characteristic impedance |
| rs | Series loss resistance of the tank circuit |
| Q | Quality factor of the parallel tank circuit |
| QL | Quality factor of the loaded parallel tank circuit |
| |A| | Gain of impedance converter |
| |β| | Gain of feedback network |
| φA | Initial phase of impedance converter |
| φβ | Initial phase of feedback network |
| |V1| | Voltage amplitude of the first harmonic of triangular voltage at the output of OPA (node 1) |
| Itank | Current circulating in the tank circuit at resonance |
| Ires | External current entering the tank circuit at resonance |
| FoM | Figure of merit |
| Pc | Power consumption of oscillator |
| PN | Phase noise |
| Pout | Oscillator output power |
| F | Noise figure |
| k | Boltzmann constant |
| T | Temperature in Kelvin |
| fc | 1/f corner frequency |
| fm | Offset frequency |
| ffun | Frequency of oscillations in Hz |
Abbreviations
| AC | Alternating current |
| BJT | Bipolar junction transistor |
| CMOS | Complementary metal-oxide-semiconductor |
| FoM | Figure of merit |
| GaAs | Gallium arsenide |
| GaN | Gallium nitride |
| HBT | Heterojunction bipolar transistor |
| HEMT | High-electron-mobility transistor |
| OPA | Operational amplifier |
| PCB | Printed circuit board |
| pHEMT | Pseudomorphic high-electron-mobility transistor |
| RF | Radio frequency |
| SiGe | Silicon germanium |
| SPICE | Simulation program with integrated circuit emphasis |
| THD | Total harmonic distortion |
| VCO | Voltage controlled oscillator |
References
- Schulz:, M.; Strobel, A.; Ellinger, F. System considerations and VCO design for a local positioning system at 2.4 GHz for rescue of people on ships and in sea. In Proceedings of the IEEE 10th Workshop on Positioning, Navigation and Communication (WPNC), Dresden, Germany, 20–21 March 2013. [Google Scholar] [CrossRef]
- Carlowitz, C.; Esswein, A.; Weigel, R.; Vossiek, M. A low power pulse frequency modulated UWB radar transmitter concept based on switched injection-locked harmonic sampling. In Proceedings of the 7th German Microwave Conference, Ilmenau, Germany, 12–14 March 2012. [Google Scholar]
- Scherbina, K.A.; Pechenin, V.V.; Vonsovitch, M.A. Phase-locked loop combined system of voltage controlled oscillator. In Proceedings of the IEEE 9th International Kharkiv Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (MSMW), Kharkiv, Ukraine, 20–24 June 2016. [Google Scholar] [CrossRef]
- Grebennikov, A. RF and Microwave Transistor Oscillator Design; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar] [CrossRef]
- Gonzalez, G. Foundations of Oscillator Circuit Design; Artech House: Boston, MA, USA, 2007. [Google Scholar]
- Everard, J. Fundamentals of RF Circuit Design: With Low Noise Oscillators; John Wiley& Sons, Ltd.: Chichester, UK, 2001. [Google Scholar] [CrossRef]
- LMH6629 Ultra-Low Noise, High-Speed Operational Amplifier with Shutdown Datasheet (Rev. I). Available online: http://www.ti.com/lit/ds/symlink/lmh6629.pdf (accessed on 1 December 2014).
- Ulansky, V.; Machalin, I.; Tkalich, O. Analysis and design of voltage-controlled oscillators using high-speed operational amplifiers. Proc. Natl. Aviat. Univ. 2002, 3, 171–178. [Google Scholar] [CrossRef]
- Ulansky, V.V.; Kolesnik, A.A.; Elsherif, H.M. A new high-performance OPA based VCO for microwave applications. In Proceedings of the 2014 IEEE Microwaves, Radar and Remote Sensing Symposium, Kiev, Ukraine, 23–25 September 2014. [Google Scholar] [CrossRef]
- Rashid, M.H. Microelectronic Circuits. Analysis and Design; Cengage Learning: Stamford, CT, USA, 2011; p. 883. [Google Scholar]
- Jacas, M.M.; Llopis, F. LC sine-wave oscillators using general-purpose voltage operational-amplifiers. Int. J. Electr. Eng. Educ. 2007, 44, 244–248. [Google Scholar] [CrossRef]
- Boylestad, R.; Nashelsky, L. Electronic Devices and Circuit Theory, 11th ed.; Pearson: Boston, MA, USA, 2011; p. 619. [Google Scholar]
- Ulansky, V.V.; Elsherif, H.M. A voltage-controlled oscillator based on negative inductance converter. In Proceedings of the IEEE 35th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 21–24 April 2015. [Google Scholar] [CrossRef]
- Chen, W.K. The Circuits and Filters Handbook; CRC Press: New York, NY, USA, 2003; pp. 396–397. [Google Scholar]
- Horowitz, P.; Hill, W. The Art of Electronics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1989; pp. 266–267. [Google Scholar] [CrossRef]
- Beck, B.S.; Cunefare, K.A.; Collet, M. The power output and efficiency of a negative capacitance shunt for vibration control of a flexural system. Smart Mater. Struct. 2013, 22, 1–10. [Google Scholar] [CrossRef]
- Negative Impedance Converter. Available online: https://en.wikipedia.org/wiki/Negative_impedance_converter (accessed on 13 April 2020).
- Savant, C.J.; Roden, M.S.; Carpenter, G.L. Electronic Design. Circuits and Systems, 2nd ed.; The Benjamin/Cummings Publishing Company, Inc.: Redwood City, CA, USA, 1991. [Google Scholar]
- Johnson, J.B. Thermal agitation of electricity in conductors. Phys. Rev. 1928, 32, 97. [Google Scholar] [CrossRef]
- Nilson, J.W.; Riedel, S.A. Electric Circuits, 5th ed.; Addison Wesley: New York, NY, USA, 1996; pp. 791, 806–809. [Google Scholar]
- Boylestad, R.L. Introductory Circuit Analysis, 10th ed.; Pearson Education: London, UK, 2002. [Google Scholar]
- Jaeger, R.C.; Blalock, T.N. Microelectronic Circuit Design, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2010; p. 1449. [Google Scholar]
- Rhea, R.W. Oscillator Design and Computer Simulation; Noble Publishing Corp.: Atlanta, GA, USA, 1996. [Google Scholar] [CrossRef]
- Advanced XTAL Products. Available online: https://www.axtal.com/cms/docs/doc101437.pdf (accessed on 19 August 2016).
- Rohde, U.L.; Poddar, A.K.; Bock, G. The Design of Modern Microwave Oscillators for Wireless Applications: Theory and Optimization; John Wiley & Sons, Inc.: New Jersey, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Hegazi, E.; Sjoland, H.; Abidi, A. A filtering technique to lower LC oscillator phase noise. IEEE J. Sol.-St. Circ. 2001, 36, 1921–1930. [Google Scholar] [CrossRef]
- Jang, S.-L.; Su, Y.-J.; Lin, K.J.; Wang, B.-J. An 4.7 GHz low power cross-coupled GaN HEMT oscillator. Microw. Opt. Technol. Lett. 2018, 60, 2442–2447. [Google Scholar] [CrossRef]
- Hollmann, A.; Jirovec, D.; Kucharski, M.; Kissinger, D.G.; Fischer, G.; Schreiber, L.R. 30 GHz-voltage controlled oscillator operating at 4 K. Rev. Sci. Instrum. 2018, 89. [Google Scholar] [CrossRef] [PubMed]
- Matheoud, A.V.; Solmaz, N.S.; Boero, G. A low-power microwave HEMT LC oscillator operating down to 1.4 K. IEEE Trans. Microw. Theory Tech. 2019, 67, 2782–2792. [Google Scholar] [CrossRef]
- Drechsel, T.; Joram, N.; Ellinger, F. A 6.5 to 15.1 GHz ultra-wideband SiGe LC VCO with 80% continuous tuning range. In Proceedings of the Eur. Conf. Circuit Theory Design (ECCTD), Catania, Italy, 4–6 September 2017. [Google Scholar] [CrossRef]
- Kong, C.; Li, H.; Chen, X.; Jiang, S.; Zhou, J.; Chen, C. A monolithic AlGaN/GaN HEMT VCO using BST thin-film varactor. IEEE Trans. Microw. Theory Tech. 2012, 60, 3413–3419. [Google Scholar]
- Jang, S.L.; Chang, Y.-H.; Chiou, J.-S.; Lai, W.-C. A single GaN HEMT oscillator with four-path inductors. In Proceedings of the 2018 7th International Symposium on Next Generation Electronics (ISNE), Taipei, Taiwan, 7–9 May 2018. [Google Scholar] [CrossRef]
- Jang, S.-L.; Chang, Y.-H.; Lai, W.-C. A feedback GaN HEMT oscillator. In Proceedings of the 2018 IEEE International Conference on Microwave and Millimeter Wave Technology (ICMMT), Chengdu, China, 7–11 May 2018. [Google Scholar] [CrossRef]
- Lai, S.; Kuylenstierna, D.; Ozen, M.; Horberg, M.; Rorsman, N.; Angelov, I.; Zirath, H. Low phase noise GaN HEMT oscillators with excellent figures of merit. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 412–414. [Google Scholar] [CrossRef]
- Lai, W.-C.; Jang, S.-L.; Chen, Y.-W. Dual-feedback GaN HEMT oscillator. In Proceedings of the 2019 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Nanjing, China, 28–30 August 2019. [Google Scholar] [CrossRef]
- Chang, C.-L.; Tseng, C.-H.; Chang, H.-Y. A new monolithic Ka-band filter-based voltage-controlled oscillator using 0.15 μm GaAs pHEMT technology. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 111–113. [Google Scholar] [CrossRef]
- Lai, P.W.; Dobos, L.; Long, S. A 2.4 GHz SiGe low phase-noise VCO using on chip tapped inductor. In Proceedings of the 29th European Solid-State Circuits Conference, Estoril, Portugal, 16–18 September 2003. [Google Scholar] [CrossRef]
- Fu, Y.; Li, L.; Wang, D.; Wang, X.; He, L. 28-GHz CMOS VCO with capacitive splitting and transformer feedback techniques for 5G communication. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 2088–2095. [Google Scholar] [CrossRef]
- Cai, H.L.; Yang, Y.; Qi, N.; Chen, X.; Tian, H.; Song, Z.; Xu, Y.; Zhou, C.; Zhan, J.; Wang, A.; et al. A 2.7-mW 1.36–1.86-GHz LC-VCO with a FOM of 202 dBc/Hz enabled by a 26%-size-reduced nano-particle-magnetic-enhanced inductor. IEEE Trans. Microw. Theory Tech. 2014, 62, 1221–1228. [Google Scholar] [CrossRef]
- Kim, S.J.; Seo, D.I.; Kim, J.S.; Song, R.; Kim, B.S. Compact CMOS LiT VCO achieving 198.6 dBc/Hz FoM. Electron. Lett. 2018, 54, 175–177. [Google Scholar] [CrossRef]
- Zailer, E.; Belostotski, L.; Plume, R. 8-GHz, 6.6-mW LC-VCO with small die area and FOM of 204 dBc/Hz at 1-MHz offset. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 936–938. [Google Scholar] [CrossRef]






| VCO | Technology | Frequency GHz | Frequency Offset MHz | Phase Noise dBc/Hz | Power Consumption MW | FoM dBc/Hz |
|---|---|---|---|---|---|---|
| [27] | GaN HEMT | 4.7 | 1 | −121.7 | 2.7 | −190 |
| [28] | SiGe | 29.8 | 1 | −115 | 37 | −185 |
| [29] | HEMT | 11.2 | 1 | −97 | 0.09 | −188 |
| [30] | SiGe | 6.5 ÷ 15.1 | 1 | −110 | 19 | −177 |
| [31] | GaN HEMT | 6.5 ÷ 7.5 | 1 | −110 | 50 | −170 |
| [32] | GaN HEMT | 8.82 | 1 | −124.95 | 21.6 | −190.5 |
| [33] | GaN HEMT | 7.26 | 1 | −122.48 | 18.33 | −187 |
| [34] | GaN HEMT | 1.95 | 1 | −149 | 400 | −189 |
| [35] | GaN HEMT | 5.2 | 1 | −125.7 | 16 | −188 |
| [36] | GaAs pHEMT | 37.608 | 1 | −112.31 | 130 | −182.7 |
| [37] | SiGe BJT | 2.4 | 1 | −128 | 41 | −179.5 |
| [38] | CMOS | 26.5 | 1 | −105.8 | 10.8 | −183.9 |
| [39] | CMOS | 1.61 | 0.1 | −121 | 2.7 | −202 |
| [40] | CMOS | 11.58 | 1 | −112.62 | 6 | −198.6 |
| [41] | CMOS | 8 | 1 | −134.3 | 6.6 | −204 |
| This work | SiGe (LMH6629MF) | 1.429 | 0.1 | −139.3 | 240 | −198.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulansky, V.; Raza, A. Sinusoidal Oscillators Operating at Frequencies Exceeding Unity-Gain Bandwidth of Operational Amplifiers. Electronics 2020, 9, 845. https://doi.org/10.3390/electronics9050845
Ulansky V, Raza A. Sinusoidal Oscillators Operating at Frequencies Exceeding Unity-Gain Bandwidth of Operational Amplifiers. Electronics. 2020; 9(5):845. https://doi.org/10.3390/electronics9050845
Chicago/Turabian StyleUlansky, Vladimir, and Ahmed Raza. 2020. "Sinusoidal Oscillators Operating at Frequencies Exceeding Unity-Gain Bandwidth of Operational Amplifiers" Electronics 9, no. 5: 845. https://doi.org/10.3390/electronics9050845
APA StyleUlansky, V., & Raza, A. (2020). Sinusoidal Oscillators Operating at Frequencies Exceeding Unity-Gain Bandwidth of Operational Amplifiers. Electronics, 9(5), 845. https://doi.org/10.3390/electronics9050845






