1. Introduction
Finding a parking space is one of the main concerns of urban mobility, as it is well recognised that a significant fraction of the traffic in crowded urban areas is originated by drivers cruising in search of a parking space [
1]. The motivation behind this problem lies in that drivers have no knowledge about where there could be a free parking space matching their expectations. Thus, they have to roam, with significant consequences in terms of additional traffic, pollution, and drivers’ wasted time [
1,
2]. Moreover, parking search also affects road safety, since drivers cruising for parking are distracted, and thus more likely to hit other road users [
3].
Among the various types of Intelligent Transportation Systems, the
Parking Guidance and Information (PGI) solutions, integrated within in-vehicle navigation systems or intended as mobile apps, aim at significantly reduce this problem, by guiding drivers directly towards streets (or parking facilities) with current or future higher availability of free spaces. To this aim, PGIs require parking availability information to work. When dealing with on-street parking, this information can be collected from stationary sensors, or by means of participatory or opportunistic crowd-sensing solutions from mobile apps [
4,
5] or probe vehicles [
6,
7,
8]. The collected availability information is then aggregated on a remote back-end, to get a dynamic map of the parking infrastructure. This up-to-date map can be either pushed to the interested PGI users, or used to feed some prediction algorithms, to forecast the parking availability at the Estimated Time of Arrival (ETA) of a PGI user [
9,
10], to allow drivers to better organise their transport before their departures or during their trips [
2].
In the last years, the availability of sensor techniques to collect real on-street parking availability data triggered many researches on proposing solutions to predict parking availability (e.g., References [
9,
10,
11,
12,
13]), mostly using advanced machine/deep learning approaches. Results are encouraging, with prediction errors of available stalls in the range of 10–15%, on a city-wide scale (e.g., References [
9,
10]). Nevertheless, most of these approaches require to train one model for each road segment with parking stalls, with significant scalability issues when dealing with large urban maps, which can likely comprise hundreds of thousands of them. The problem was firstly highlighted by Zheng et al., who investigated the effectiveness and the computational requirements of three Machine Learning techniques, being even unable to obtain results for some settings
“due to the long computation time [...]” [
13], p. 5). To the best of our knowledge, only one paper introduced a preliminary solution to reduce the computational requirements for a service of on-street parking availability prediction [
14], based on simple clustering solutions.
To fill this gap, in this paper we present the results of an investigation meant to devise a pre-processing technique, leveraging the recurring patterns found in the dataset, to reduce the computational load required by an on-street parking prediction system, by minimising the prediction models and the training examples. More in detail, as a starting point we analysed the availability trends in a real on-street parking dataset from the municipality of San Francisco (USA), and we found that each road segment has a high temporal auto-correlation over itself, and a high cross-correlation among different trends. From this finding, we propose a pre-processing pipeline for parking prediction system where we firstly group together road segments showing a high similarity in parking availability trends, by means of a hierarchical clustering technique. The next step should be to train a shared prediction model on each of these clusters, to forecast future parking availability, but, as each of these clusters might include hundreds of road segments, with a potentially overwhelming number of training examples, we propose the use of the
Kennard-Stone algorithm [
15], to prune the training set, by maintaining only the most representative examples. Only after this training set filtering, on top of these reduced examples, we train a regressor, like for instance an SVR or a Deep Neural Network (DNN). As an additional observation, we found that on-street parking dynamics can be very fast: since each road segment has a limited number of parking spaces (for instance, over 500 road segments in San Francisco (USA) downtown, the most frequent number of parking stalls per road segment is 6), each change in the sensed availability has a deep impact on the occupancy percentage. Therefore, a misreading leads to abrupt changes in sensed availability, that are not related to the actual state. This is a common scenario, as current state-of-the art on-street sensing technologies suffer of an intrinsic amount of misreadings, quantifiable in at least 10% probability [
16,
17,
18]. Thus, this kind of data is challenging for machine learning techniques, both for model training and performance evaluation, since these time series exhibiting strong, abrupt and frequent changes from one sampling instant to the other. To cope with this
noise in the data, masking the general trend underlying the measurements, which is the real information [
12], in our pre-processing pipe-line we propose also the use of an optional filtering step, performed by means of specifically configured Kalman filters [
19].
To assess the effectiveness of the proposed solution, we conducted an empirical evaluation on a real dataset of five weeks of on-street parking data from the SFPark project in San Francisco [
20], covering 321 road segments, available at Reference [
21]. We evaluated the prediction performances of a Support Vector Regressor, with an horizon of 30 min, considering the solution with and without Kalman filters, in combination with three different filtering levels of the Kennard-Stone algorithm. Let us note that more advanced prediction techniques might provide better prediction performances, but the focus of this investigation is to understand and quantify the impact of the proposed pipeline to prune the dataset, rather than achieving the best possible predictions. Results show that the proposed on-street parking availability prediction solution performs in a way that is comparable with state-of-the-art techniques based on a model per segment, while requiring a fraction of the computational efforts. Indeed, by grouping the 321 segments in just five clusters, each with 4000 training examples of filtered data, provided practically the same prediction error (in terms of RMSE) of a model for each of the 321 models, each with more than 6000 examples, thus reducing by almost two orders of magnitude the required training efforts.
The main contributions of the paper are:
We provide the first analysis, to the best of our knowledge, on the temporal auto-correlation phenomenon for on-street parking availability.
We propose a technique to highly reduce the computational requirements of a parking availability prediction service, making it potentially scalable to a city-wide level, providing empirical evidence that it is able to provide parking predictions whose error is comparable with state-of-the-art solutions, based on one model per segment, at a fraction of their training costs.
We provide empirical evidence that, by applying a fast filtering step, the computational requirements for training can be further reduced.
The remainder of this paper is structured as follows—in
Section 2 we present the related work on data-driven parking space prediction. In
Section 3 we provide a detailed analysis on the temporal dynamics of parking availability. In
Section 4 we present the approaches to predict the parking availability based on training data reduction. In
Section 5 we describe the experiment design to assess the proposed approach, with the results we obtained. Finally, in
Section 6 some conclusions are outlined, together with some future research directions.
3. An Analysis of an On-Street Parking Availability Dataset
Recurring dynamics, in time series, present an important opportunity to be exploited for prediction systems. Indeed, even if machine learning algorithms are capable of capturing these dynamics, by knowing in advance the existence of significant temporal regularities in the data, a system designer may develop more efficient processing pipelines. More in detail, in this scenario, many techniques are available in the literature to help reduce the size of the training sets and/or the number of needed prediction models, thus reducing the computational requirements of the processing pipeline. These techniques are often employed for traffic predictions (e.g., References [
37,
38]), but, to the best of our knowledge, they have been applied to on-street parking predictions only in one preliminary paper [
14], also due to the lack of investigations focused on qualitative analyses of parking dynamics. Specifically, in Reference [
14], the presence of day-by-day, and weekdays/weekend recurring patterns was highlighted.
As a consequence, in this paper we start by providing an analysis on real data about on-street parking availability dynamics, to verify and quantify the presence of recurring temporal patterns in the data. In the following, we describe the dataset we collected about on-street parking availability from the Municipality of San Francisco (USA). We made available a part of the which is an extension of the one provided in Reference [
21]. Then we discuss the analysis of these data, that allowed us to get some insights on parking dynamics, motivating the proposal presented in this paper.
3.1. The Considered Dataset
A common problem when conducting experimental evaluations for approaches dealing with the on-street parking domain is the lack of suitable datasets. Indeed, while many smart cities are collecting parking data (e.g., Santander (Spain) [
39] or Los Angeles (USA) [
9]), usually these data are not publicly available. For our study, on-street parking availability data was collected from the
SFpark project [
27]. In 2011 the San Francisco Municipal Transportation Agency started a large experimental smart parking project, called
SFpark. The main focus of this project, whose costs exceeded
$46 million, was the improvement of on-street parking management in San Francisco, mostly by means of demand-responsive price adjustments [
27].
One of the key points of the project was the collection of information about parking availability in six districts in San Francisco between 2011 and 2014. To this aim, about 8000 parking spaces were equipped with specific sensors embedded in the asphalt of some pilot and control areas, periodically broadcasting availability information. Even though 8000 equipped stalls is a remarkable number, this is less than 3% of the total number of on-street legal parking spaces in San Francisco [
27]. These numbers make clear the problems and the costs to scale the instrumentation of on-street parking stalls to a city-wide dimension.
The SFpark project made available a public REST API, returning the number of free parking spaces and total number of provided parking spaces, for each involved street segment in the pilot areas. By exploiting those APIs, we collected parking availability data from middle of June 2013 to end of December 2013. In some cases, due to malfunctions in the collection procedure, we lost some weeks, giving rise to three trunks of data. Thus, the final dataset we used in our investigation consists of three subsets of data including, respectively, 5 weeks (Period 1), 6 weeks (Period 2) and 14 weeks (Period 3). Only road segments having at least 4 parking spaces are considered, in this work. Also, road segments that were never occupied for more than 85% of their capacity or showed missing/constant readings for more than 3 days were removed from the dataset, as we assumed that sensors were severely malfunctioning. The final number of considered segments is 321.
As for the distribution of provided parking spaces per road segment, the most frequent number of parking stalls per road segment is six, (8.8% of the total), while the average is about 7.9. Let us note that in the context of the SFpark project, a road segment (also named block face) is defined as one side of a road between two intersections. These numbers show that long parking lanes seldom exist in the evaluation regions and therefore each parking/leaving event has a relevant impact on the parking availability rate, which is defined as the ratio between the free and total stalls.
The reader interested in further statistical details on the distribution of available/free parking spaces per segment is referred to our previous work [
21].
3.2. Recurring Patterns in the Dataset
Starting from the observations in Reference [
14], we looked for temporal regularities in the data considering a temporal granularity at a day level. More in detail, we used the
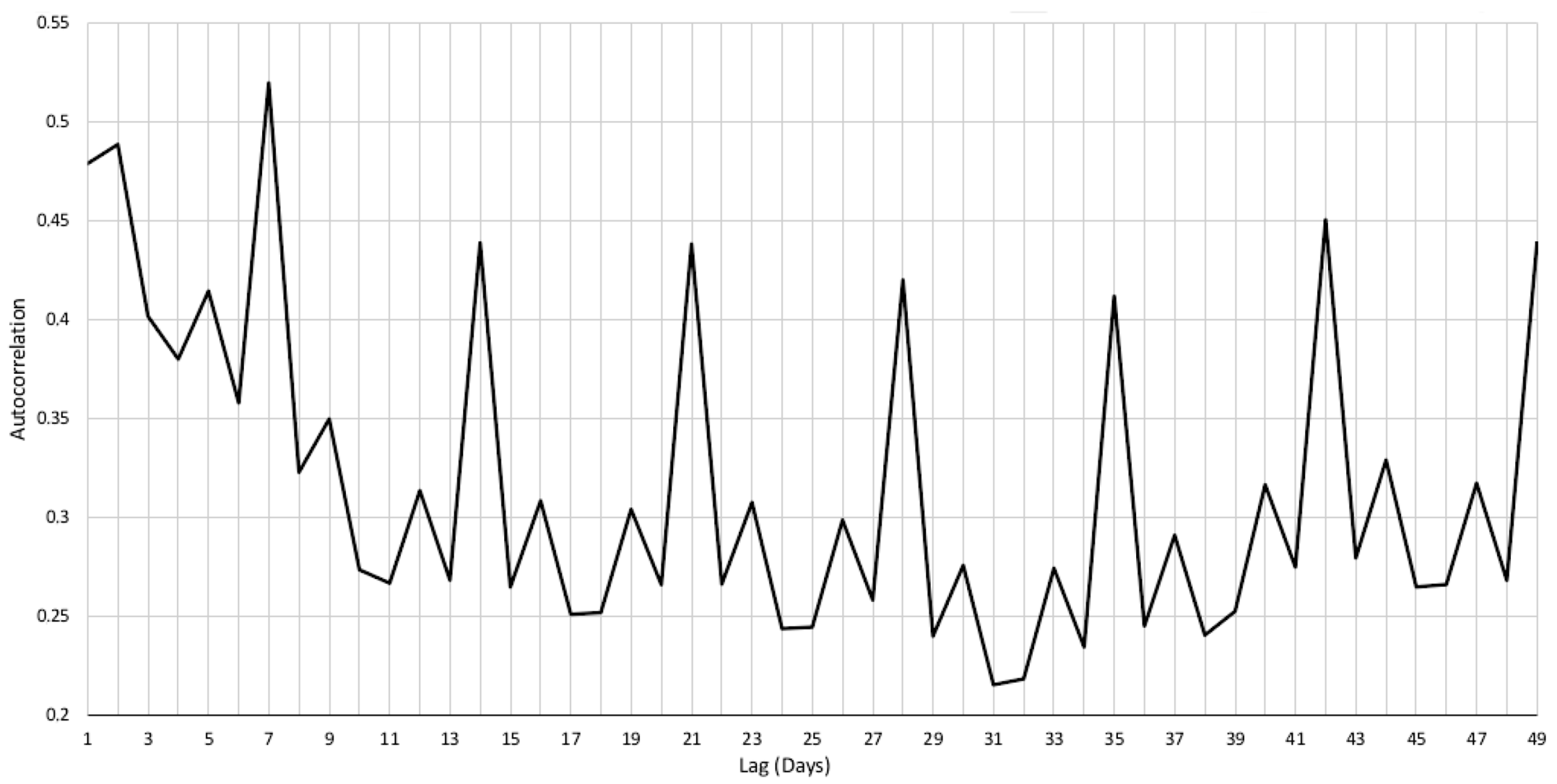
autocorrelation operator to detect recurring patterns for each road segment. This operator is used to evaluate at which lag a signal is maximally similar to itself. In presence of periodic dynamics, the autocorrelation plot will show strong local peaks, corresponding to lags at which the signal has a high recurrence. In our analysis, we searched for lags in a range from one day up to half the days available in each considered data collection period. This is to keep the number of superimposing samples sufficiently high to obtain reliable autocorrelation values. As an example,
Figure 1 shows the plot of the average autocorrelation values for all road segments in San Francisco during Period 3. The spikes due to the recurring patterns at 7 days lag are clearly visible in the autocorrelation curve, indicating that the on-street parking phenomenon has a recurring dynamic with a period of one week.
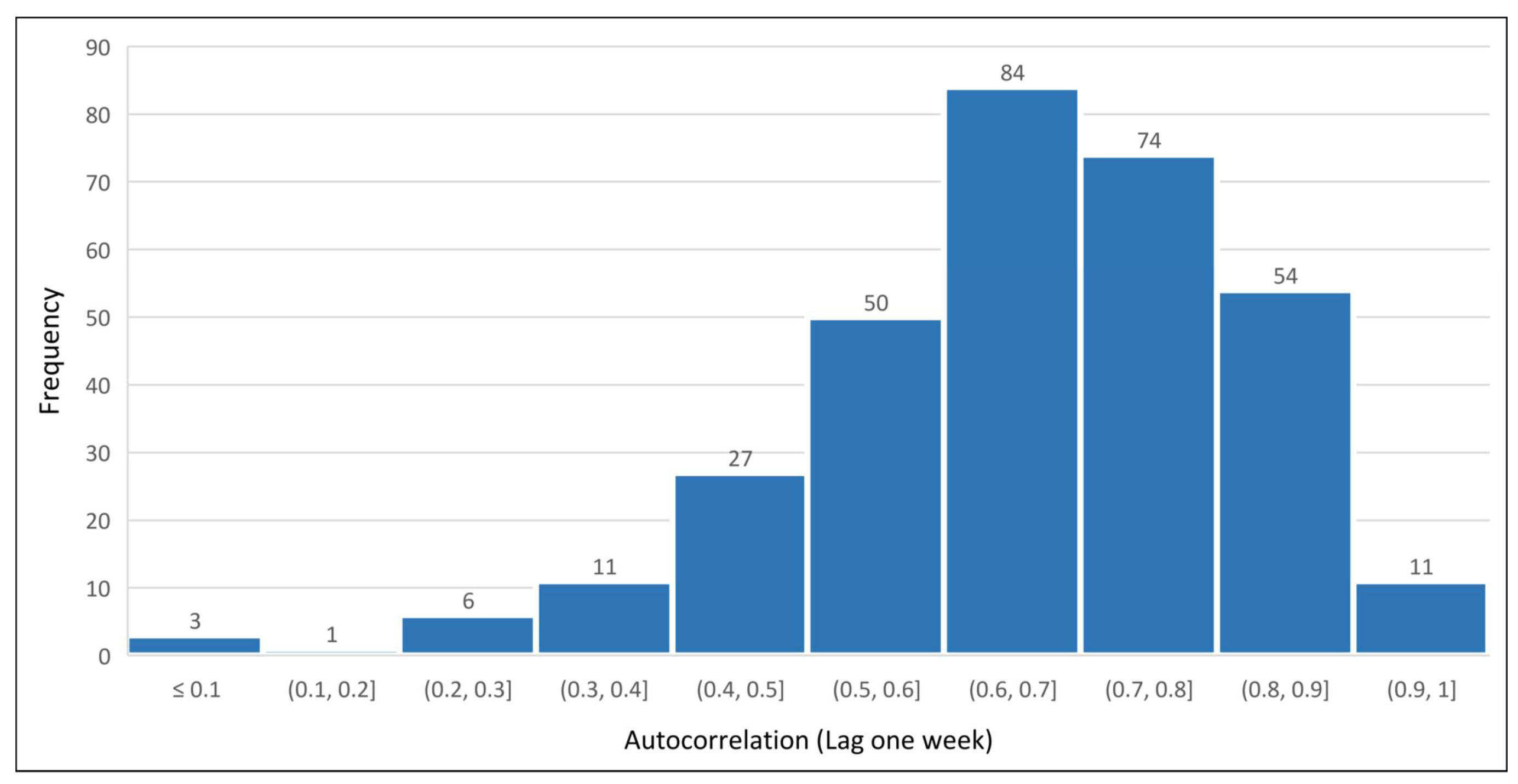
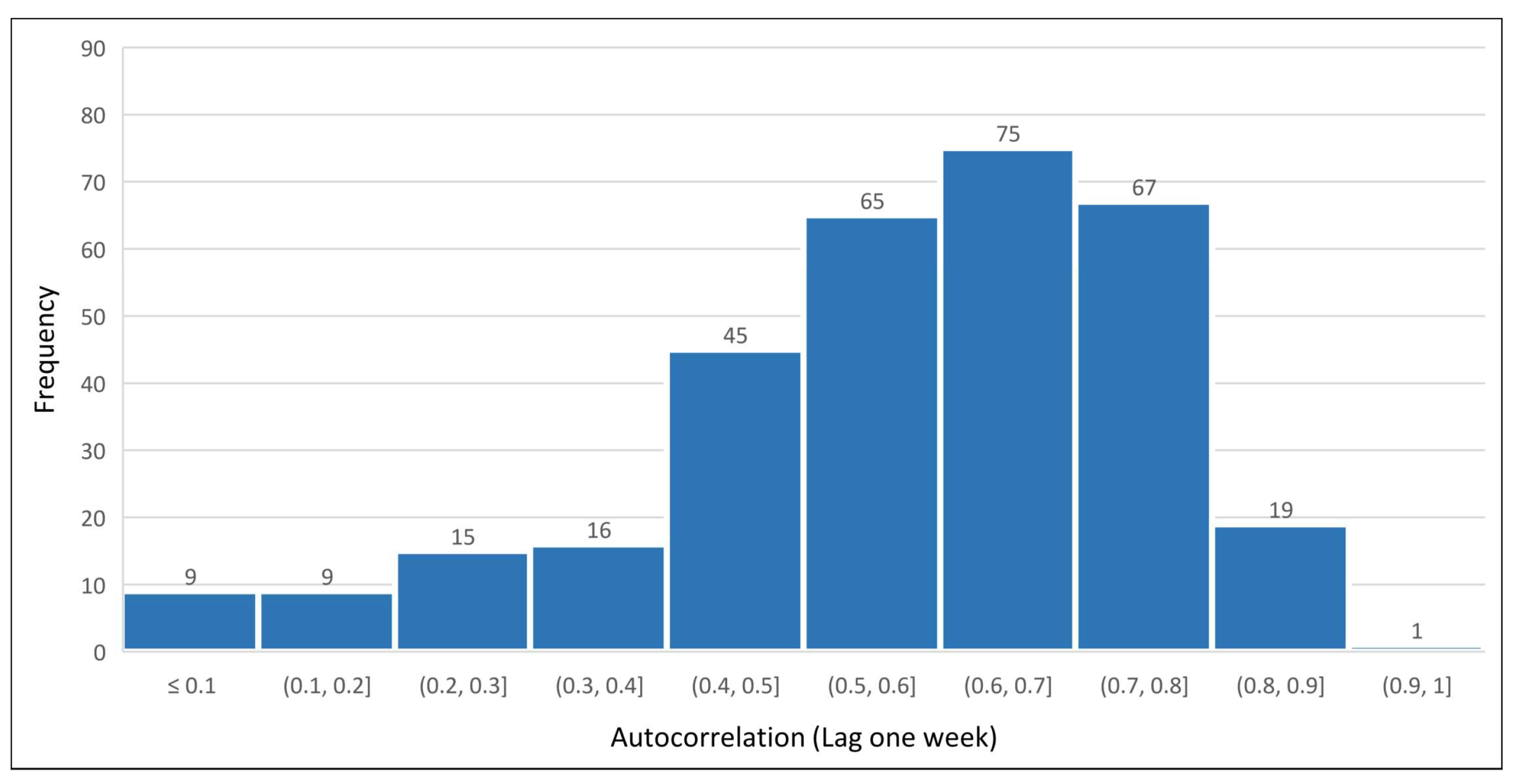
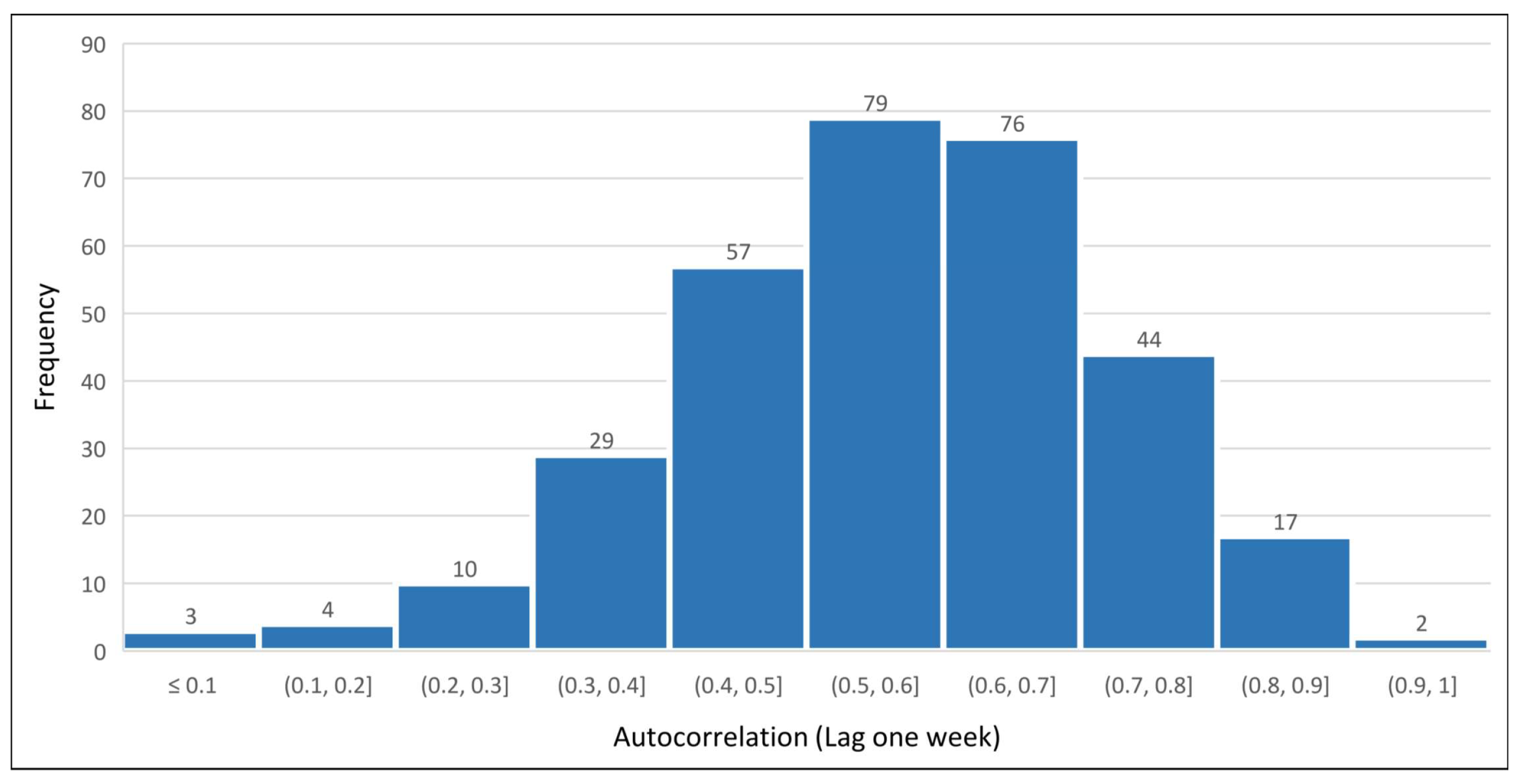
Considering the whole set of segments in the dataset and a 7 days lag, histograms shown in
Figure 2,
Figure 3 and
Figure 4 highlight that the majority of the road segments present a consistent pattern repeating itself at 1 week period.
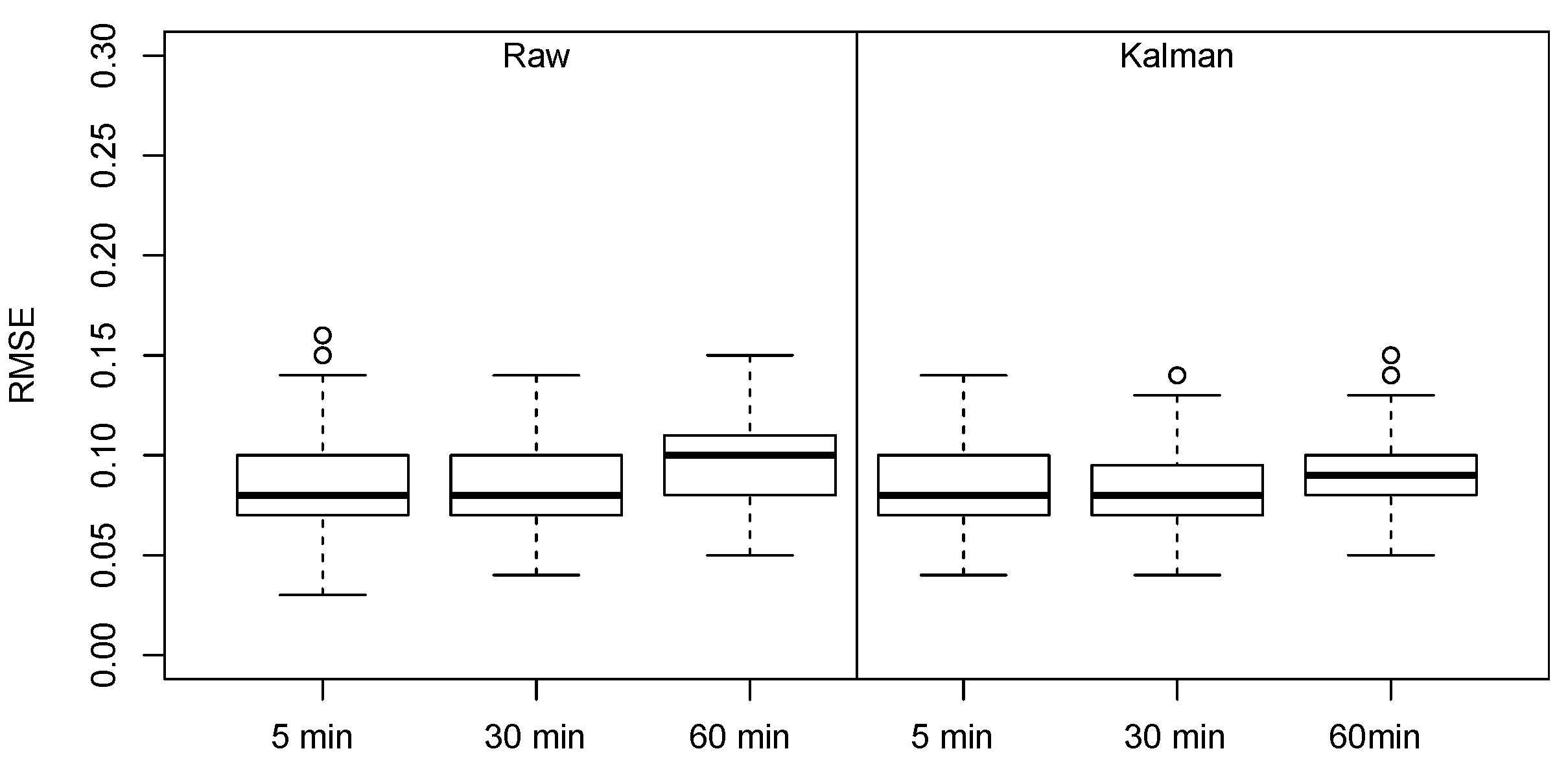
Having confirmed that the most of the road segment has a recurring pattern over a 1 week lag, an immediate conclusion that may be derived from this analysis is that it could be possible to predict the occupancy value for the current time and day by replicating the observation collected at the same time during the same day of the preceding week. Should this strategy pay off, it would be useless to proceed with machine learning at all. A simple preliminary experiment testing this hypothesis was, therefore, conducted to assess the possibility that the
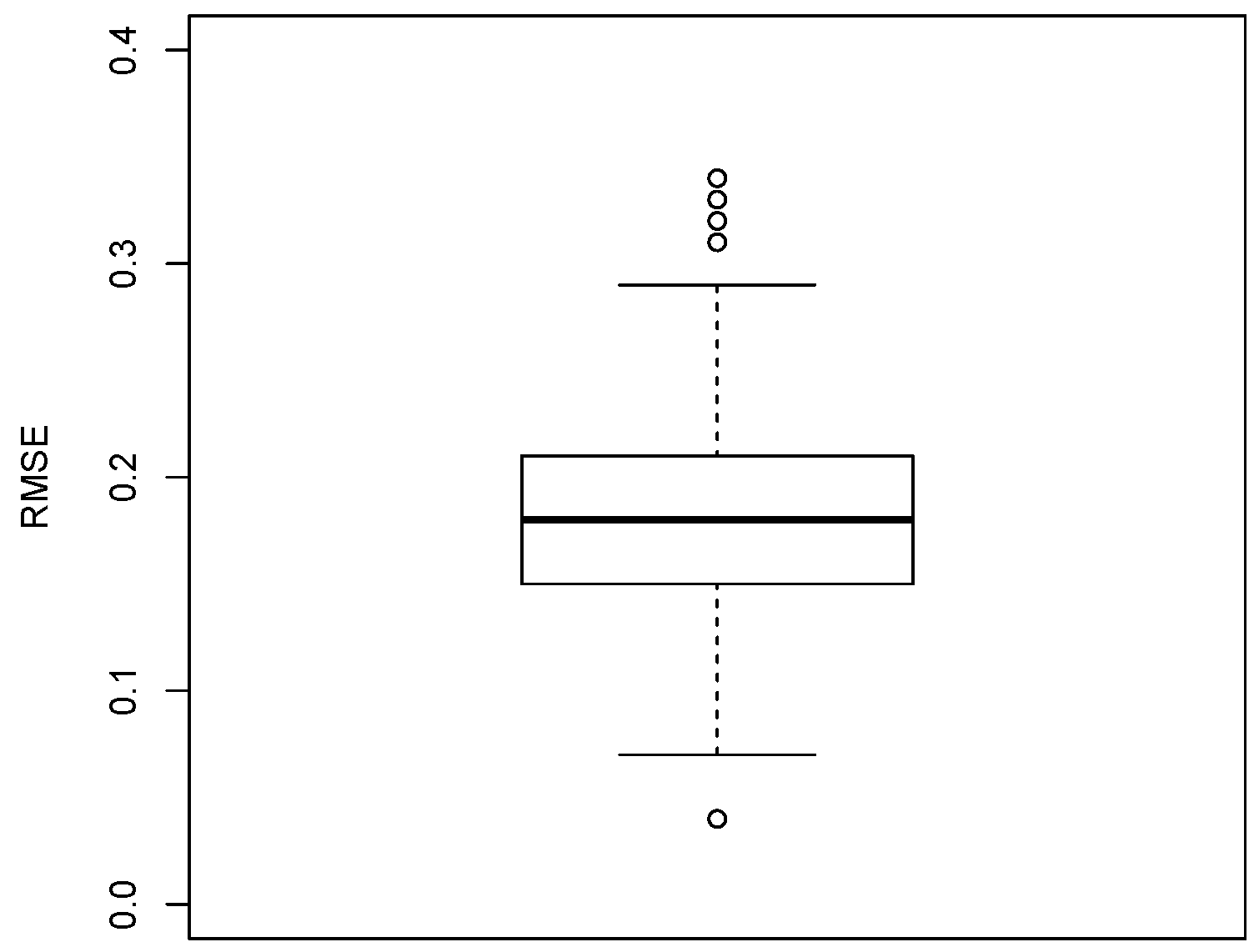
naive strategy is adequate to predict occupancy rate. The boxplot of the RMSE value obtained using this strategy is shown in
Figure 5 and it highlights that the prediction error, is more than two times the one found in Reference [
36], which used the same dataset. Moreover, also the distribution of the RMSE value is very large, making the predictions unreliable. As a consequence, even if recurring trends are present, there is still the need for more advanced prediction approaches. In the following we propose a parking availability prediction technique meant to exploit this characteristic, in terms of a strategy aimed at significantly reducing computational requirements.
4. The Proposed Processing Pipeline
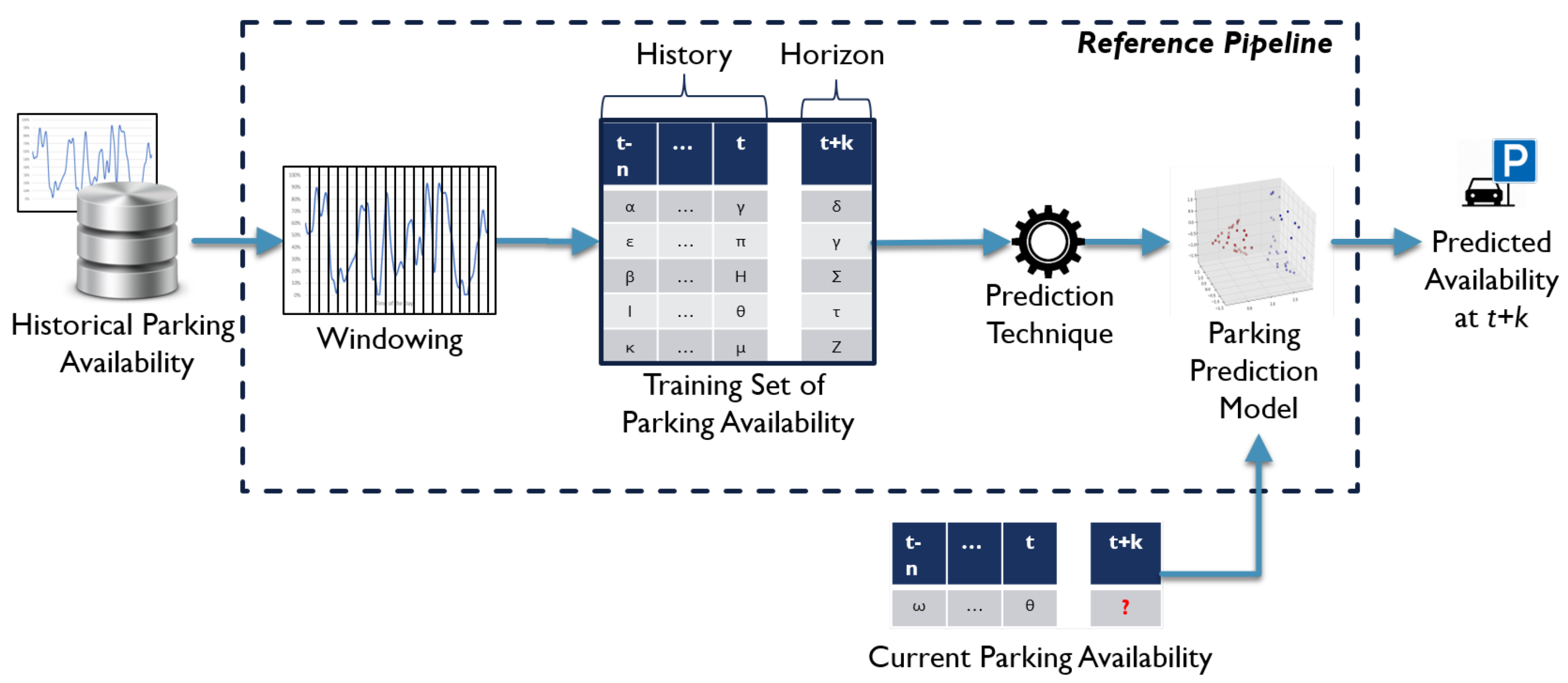
Many solutions presented in the on-street parking prediction literature use a pipeline like the one shown in
Figure 6 [
9,
10,
13,
35]. In detail, a dataset of historical parking availability contains the examples to train a supervised predictive model. Depending on the employed prediction technique, for each road segment, the dataset is windowed to generate a set of records, that is, the
features for the regressor, containing a sequence of parking availability information in the time interval
,
, referred to as
history in the rest of the paper.
A further point
in the record represent the observed availability at
, which is the target value for regressor, referred to as
prediction horizon. The regression technique is thus trained to learn, for each road segment, a
model representing the relationship between the parking history
and the prediction horizon
on these examples. Specifically, the historical data can be windowed at the desired length (for example using a history of 60 min in the past and predict availability at 30 min in the future), to generate the examples (i.e., the training set) on top of which a regressor can be trained, as proposed by Zheng et al. [
13]. Once a PGI user requests a prediction of parking availability at a given time
in the future for a given road segment, the PGI queries the prediction model with the parking data collected from sensors in the last
n time frames for that segment, and obtains as output the availability prediction for
. Let us note that training data in this scenario can be either raw or smoothed. In the rest of the paper, this
Reference Pipeline will be referred to as RP.
The key limitation of RP is that a model is required for each segment to be monitored. Most of the related papers deal with a few hundred road segments, still highlighting computational issues (e.g., Reference [
13]). To give a reference, the map of the urban area of San Francisco from OpenStreetMap includes more than 200,000 road segments, making it very hard for the solutions proposed in the literature to scale up to a city-wide dimension. To face this issue, we propose a strategy, intended as an evolution of RP, by adding two pre-processing steps:
Reduce the number of models, by clustering road segments with similar parking availability dynamics;
Reduce the number of training examples, for each cluster, by selecting the n most informative ones.
The key advantage of using a clustering technique is that the number of models to train grows sub-linearly with the number of road segments to monitor, with clear computational advantages. Thus, the final solution will be more likely to be able to scale to a city-wide level.
As in Reference [
36], this pipeline can include also an optional step to smooth data, to compensate the potential presence of strong noise caused by the sensing solution.
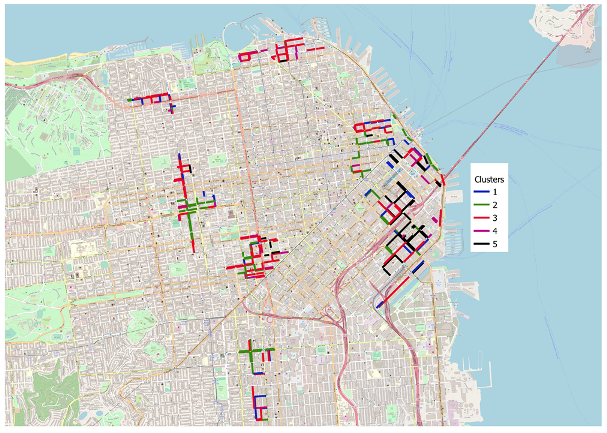
4.1. Clustering Road Segments
The first step to exploit recurrent temporal dynamics in the data consists in aggregating road segments based on the correlations among their occupancy rate curves. Specifically, a cross-correlation matrix
C is computed considering the smoothed occupancy rate curves among all segments in the dataset. Being
the cross-correlation value between the
i-th and the
j-th road segments, the
Pairwise Distance MatrixD is obtained by computing
, so that the higher the correlation, the lower the distance among the considered segments. On the basis of the data contained in
D, the hierarchical clustering
Ward Variance Minimization Algorithm is used to obtain the segments clusters. A Hierarchical clustering approach was selected as the number of clusters is not known
a priori. The algorithm is used to iteratively group the road segments, by minimising the internal variance of each cluster [
40], where the distance between two clusters
u and
v is defined as follows:
where
u is the new cluster generated by merging two clusters
s and
t,
v is every other cluster different from
u, on which we compute the distance from
u, and
.
The output of the hierarchical clustering algorithm is a dendrogram, which can be cut at different levels of similarity, to get different groupings, where the higher the cutting value, the lower is the number of obtained clusters. Many strategies are described in the literature to select the cutting threshold, often being domain-dependent [
41]. In our case, we adopted a simple criterion, using the default strategy implemented by both
SciPy and
Matlab, where the cutting threshold is computed as
of the maximum linkage distance among clusters.
Given the considered problem, through this clustering, we are able to group road segments that behave in a similar way, from an on-street parking dynamics point of view. The subsequent problem is how to train a single parking prediction model for each cluster, representative for all the segments in that cluster. Indeed, for a single cluster, if we simply merge together all the windowed examples from all the road segments belonging to that cluster, we will obtain a very large training set, containing a lot of very similar examples, as the road segments were grouped together on the basis of the similarity between their temporal dynamics: this will lead to very redundant datasets. While machine learning algorithms are, of course, designed to manage this situation, computational requirements can be greatly reduced if redundant information is filtered out of the dataset before the training phase. This is what we propose in the subsequent step.
4.2. Training Set Reduction
To obtain a sub-sample of the dataset in each cluster, that prioritises diversity with respect to the amount of data, we propose the use of the Kennard-Stone [
15] algorithm. This is a widely used technique, designed to select the set of
n most different examples from a given dataset, using the Euclidean distance as a reference measure. The rationale behind the use of the Kennard-Stone algorithm is to obtain a set of examples that is maximally informative for each cluster, rather than uniformly distributed like the set that could have been achieved by random sub-sampling. Indeed, this is also in line with the way Support Vector Machines represent prediction models, through the identification of informative support vectors.
Thus, the procedure followed by the algorithm can be summarised as follows, for each cluster:
Find the two most separated points in the original training set;
For each candidate point, find the smallest distance to any already selected object;
Select the point which has the largest of these smallest distances.
In this paper, we considered different values for n in order to evaluate how much the dataset used to train the model dedicated to each cluster can be reduced while limiting performance drops.
4.3. Kalman Filters
As reported in the SFPark description, data provided by the sensors were affected by noise due to multiple factors. In our previous works, we considered, for evaluation purposes, the trend line, computed as an SVR model fitting the raw data, as a target for predictions [
12]. This is because, at the decision level, it is more important to understand the underlying behaviour of the temporal series rather than predicting the exact occupancy of parking slots in a specific road segment. This is particularly important in the considered case, as the reported number of parking slots is affected by noise so that, by considering the occupancy rate, strong jumps in the series may be caused by random events. The SVR model representing the underlying trend, however, is computed using the full curve so that, while it is possible to use it as a prediction target, it is not possible to use it to provide features to machine learning algorithms. In order to approximate the trend line and filter out as much noise as possible, the proposed technique makes use of online Kalman filters.
Kalman filters are a well-known unsupervised approach to estimate systems’ states in presence of missing and noisy observations [
19]. While being relatively simple in their formulation, they possess a number of practical advantages. First of all, Kalman filters can be trained in a fast way without assuming the use of big data. Also, once the model is trained, it does not require significant memory space nor computational power to be queried and response time is fast. It is often useful, in the field, as it can handle missing observations and it can be continuously updated as data arrives. Kalman filters estimate the state of a system in terms of affine functions of state transitions and observations. A Kalman filter is entirely defined by its initial transition matrix
A and by its covariance matrix
Q. Optionally, in the case of noisy observations, a covariance matrix
R can be provided to describe Gaussian noise in the observations. These matrices are continuously updated as more data arrive and represent the model by themselves. It is therefore important to use domain knowledge, when designing Kalman filters, to provide an initial state that reasonably approximates the behaviour of the system, leaving fine tuning to training.
In this work, we use the same configuration of the Kalman filters we described in Reference [
36] to compensate the problem that, in the case of on-street parking, raw observations are affected by random events that end up
masking the underlying dynamics of street segments. The filter uses, for each road segment, the total number of parking spaces to estimate the Gaussian falloff of the true state probability space, centred on the last observation. To estimate the transition covariance matrix using the dynamics of each road segment, as observed in the training set, we introduce use the Expectation-Maximisation approach. The parameters are then used, using a sliding windows approach, to simulate online state estimation with a Kalman filter on each road segment. The reader is referred to Reference [
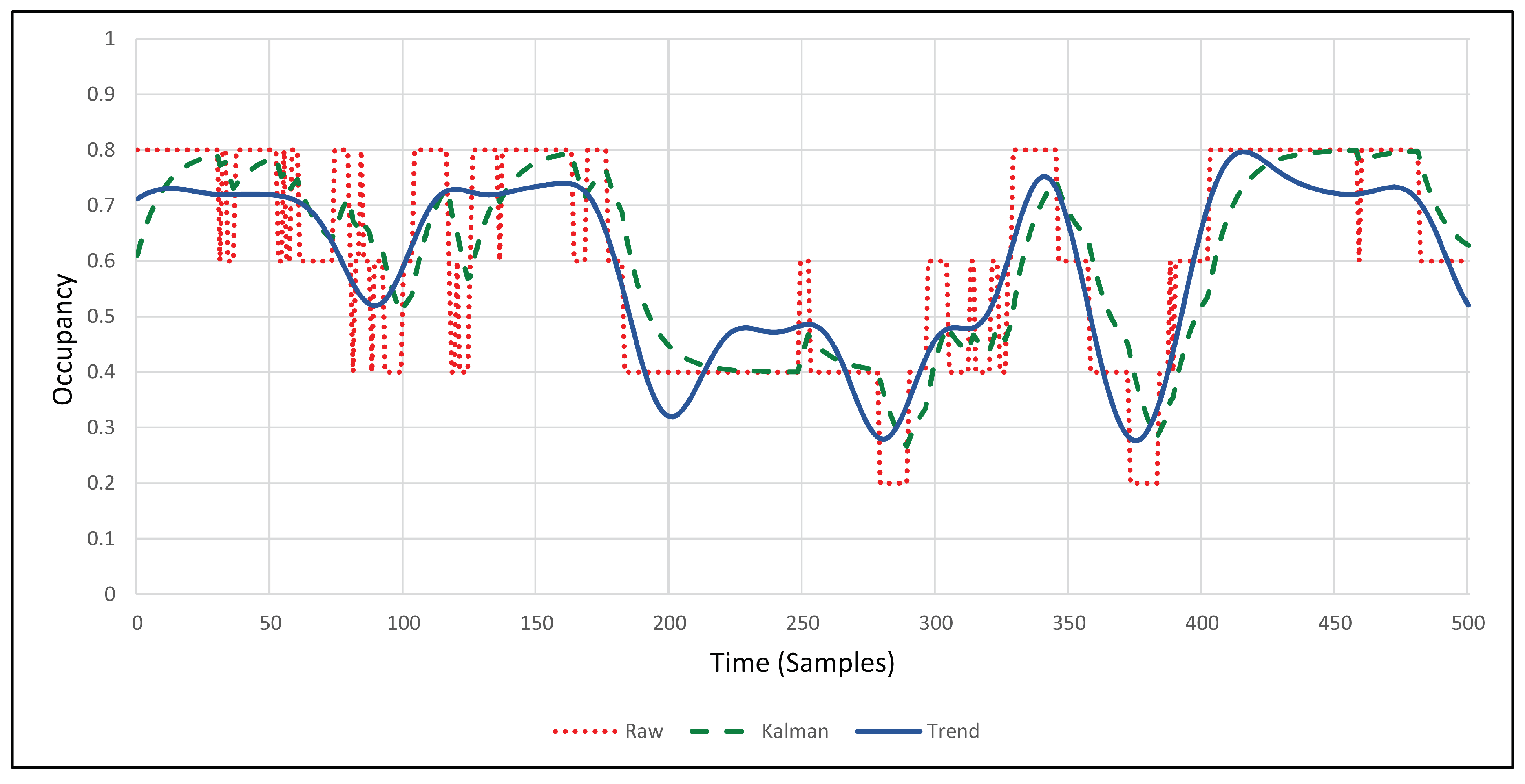
36] for more details about the Kalman filters configuration. An average RMSE of 0.05 between the Kalman curve and the trend curve was obtained on the dataset and an example comparison of the three curves is presented in
Figure 7.
6. Discussion and Conclusions
Improving the effectiveness of on-street parking availability predictions is a key issue for Parking Guidance and Information (PGI) systems. The most of on-street parking availability prediction solutions presented in the literature are characterised by significant computational requirements, by learning a model for each road segment offering parking spaces, with considerable scalability issues.
The investigation we presented in this paper aims at evaluating if and how recurrent temporal patterns may be exploited to reduce the computational requirements of predictive approaches for on-street parking availability. Firstly, we have provided a quantitative and qualitative analysis of recurring patterns in the data collected from stationary sensors employed in a large experimental project in the Municipality of San Francisco (USA). This analysis highlighted that there are notable temporal recurrences in on-street parking availability dynamics, with an evident recurring pattern at 7 days lags. Anyhow, a naive replication strategy, where the parking availability prediction is obtained by repeating the situation sensed 7 days before, is not sufficient to obtain an adequate quality of the predictions.
We have, therefore, presented a processing pipeline to predict parking availability, meant to exploit these recurrences to lower computational requirements, by including clustering and training set reduction techniques. In particular, the clustering step is designed to group together segments with the similar temporal dynamics so that a shared model could be trained to predict parking availability for all the segments in the cluster. This implies that, in comparison with the strategy employed in similar works, training one model for each road segment, the number of models needed to cover the area of interest does not increase linearly with the number of segments, reaching volumes that may become hard to manage when large cities are considered. This provides important advantages from the scalability point of view: indeed, using temporal clustering allows to group together road segments that, although possibly far from a spatial point of view, exhibit similar dynamic occupancy patterns. This may be caused, for example, by qualitatively similar contextual situations, like the presence of residential or commercial areas.
Grouping road segments having similar (recurrent) occupancy patterns has the consequence that, when considering the windowed samples from all the segments included in a cluster, to form a single training set, many of these samples will be very similar to each other. To reduce the computational complexity of the training step, given a large dataset with redundant information, we applied a data reduction approach, using the Kennard-Stone algorithm, and investigated at which size the considered configurations of our system reach comparable performances with the ones obtained with the baseline approach.
The Kennard-Stone algorithm and the prediction quality can be significantly influenced by the amount of noise in the features. For this reason, we introduced an online Kalman filter to smooth the raw curve and reduce the influence of random events causing strong changes in the raw curve. The results we presented show that, with the Kalman-filtered data, the number of samples to be selected with the Kennard-Stone algorithm to reach the performance of the baseline is lower than the number needed using the raw features. This combination of temporal clustering, online filtering and data reduction techniques, therefore, allows to reach performances comparable to the ones obtained with the baseline approach while using a significantly lower number of models.
We conducted an experimental evaluation on a real on-street parking availability dataset from 321 road segments, in San Francisco, comparing our pipeline against a baseline where we trained a SVR model for each segment over 6048 time frames, both for raw and filtered data. We had 5 clusters, and thus 5 models vs. 321 of the baseline. Result shown that performances comparable with the baseline approach can be reached, when raw features are used, by selecting, using the Kennard-Stone algorithm, 16,000 examples from the dataset obtained by merging all the data samples from all the roads included in a single cluster. Baseline performances, using Kalman-filtered features, can be reached by selecting 4000 examples, suggesting that a limited number of samples that are less affected by noise is sufficient to train supervised models when recurring patterns are present and shared among road segments. This means that we had 4000 × 5 = 20,000 training examples vs. 6048 × 321 = 1,941,408 of the original dataset, thus significantly reducing the computational complexity.
The limitations of this study are related to the dataset representing the specific situation of the San Francisco urban area, which may exhibit characteristics not found in other cities. The preliminary step of the procedure we followed here, using the autocorrelation operator to check the presence of recurring temporal dynamics in the considered road segments, remains necessary to deploy the approach in other situations. Potential differences may emerge due to different extensions of the considered urban areas or to specific geographical characteristics, as well as to the socio-economical background of the considered city, which may cause non-periodic recurrences that would not be detected through autocorrelation. Also, the temporal extension of the data available through the SFPark project is relatively limited and does not allow us to take into account possible changes due to seasonal variations through the whole year. Future work will, therefore, consist of re-applying the procedure to datasets collected from different cities and covering longer time periods, in order to evaluate, for example, if new clusters and/or new models should be trained to cover different times of the year, how long these time spans should be, and for how long a recurring pattern is present in the series.
We believe that the results of this work can be exploited for further replications/evolutions of the proposed pipeline. Indeed, as future work, we foresee the possibility that the obtained results can be improved by employing more advanced machine learning techniques, like CNN or LSTM on top of the proposed pipeline. Moreover, it would be interesting to replicate the experiment on other parking availability datasets, to understand if and how these recurrent patterns are common in other urban areas.