OCT Image Restoration Using Non-Local Deep Image Prior
Abstract
1. Introduction
2. Non-Local Deep Image Prior
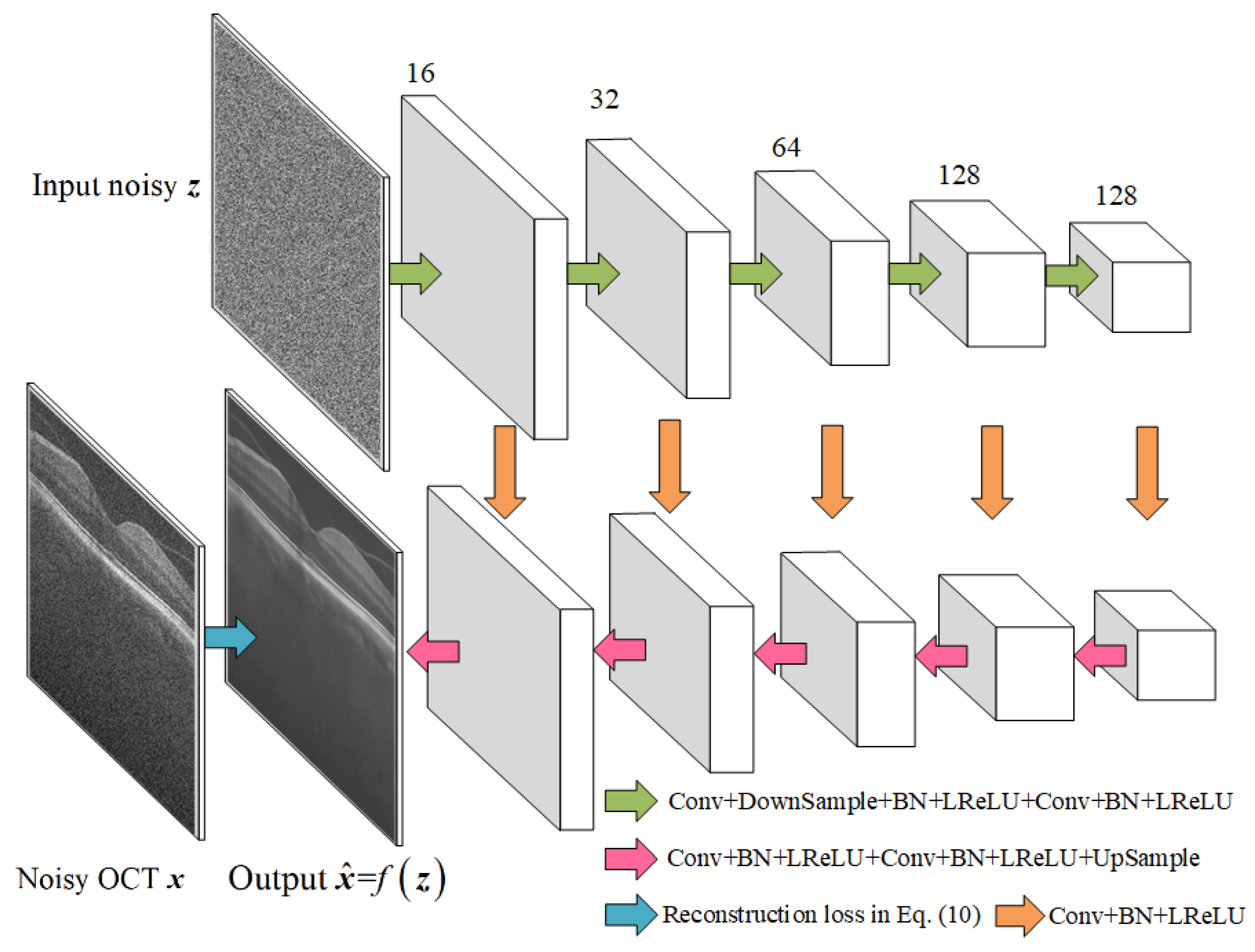
2.1. Deep Image Prior Model
2.2. Non-Local Deep Image Prior Model
2.3. Network Structure and the NLM-DIP Algorithm
| Algorithm NLM-DIP |
| Input: Maximum iteration number MaxIt, network initialization , noisy image and the network input (random noise). For to MaxIt do Calculate the signal uncorrelation of the differences using (9). Calculate the reconstruction loss using (10). Train the network using (11). End For Return . |
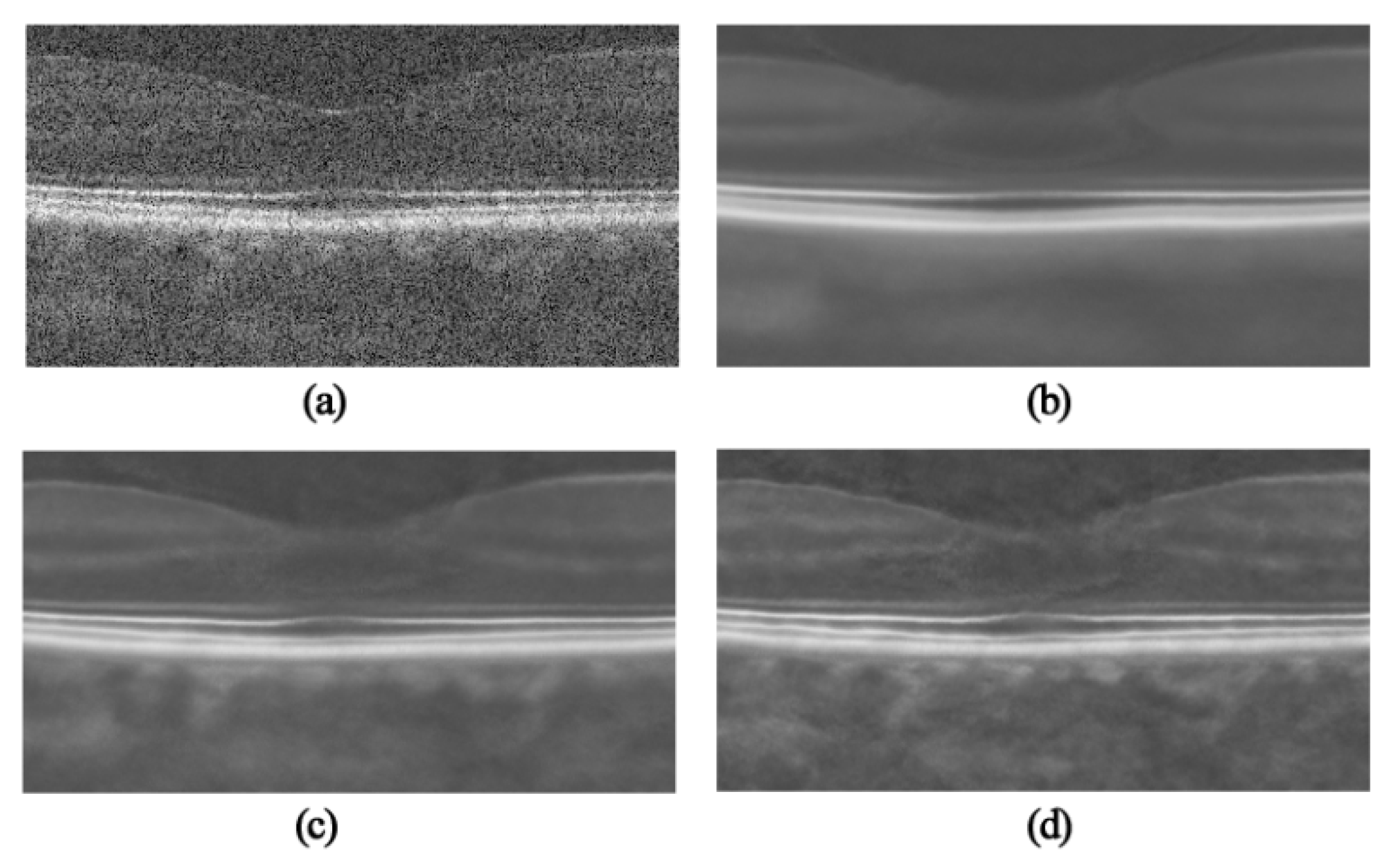
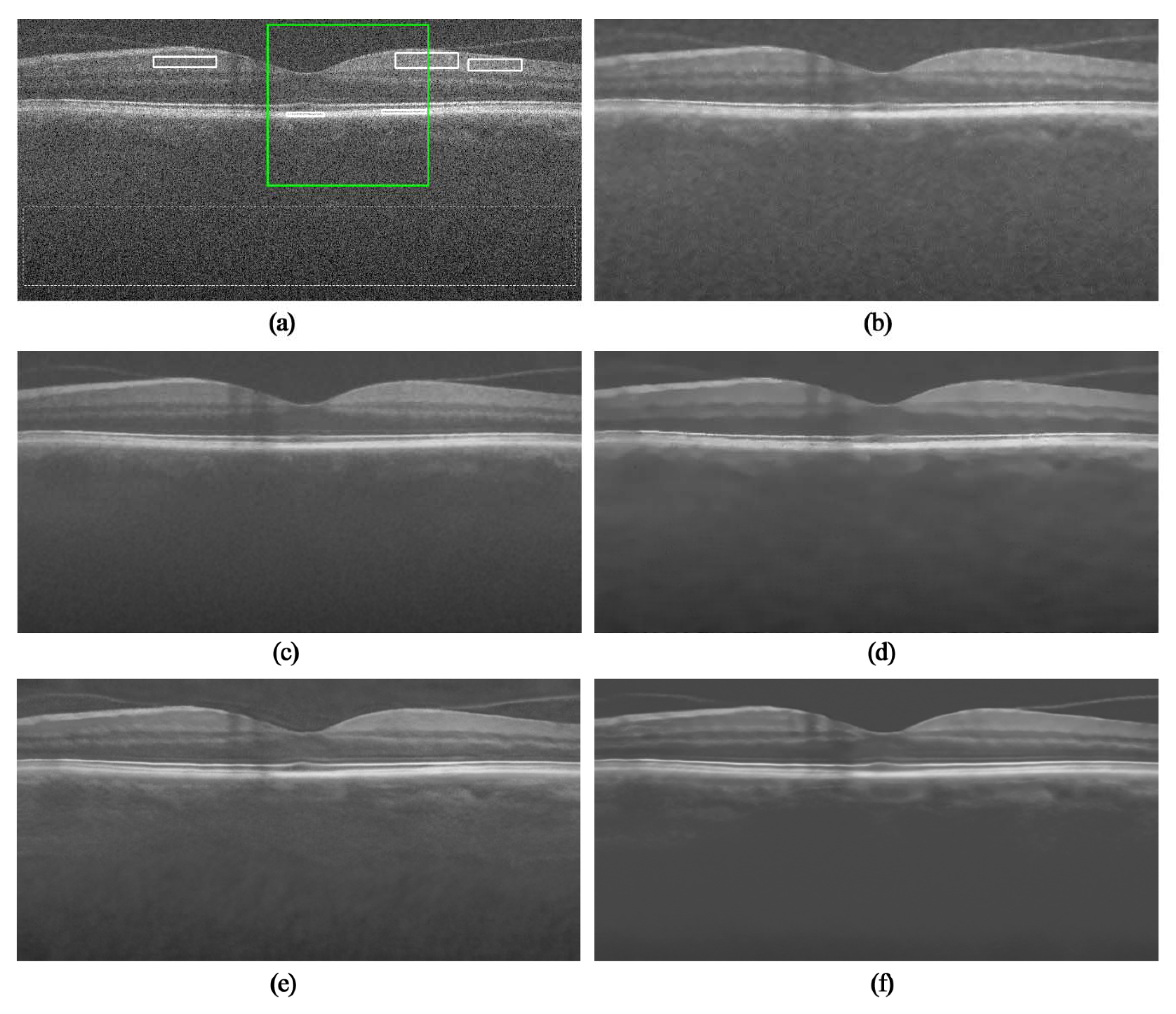
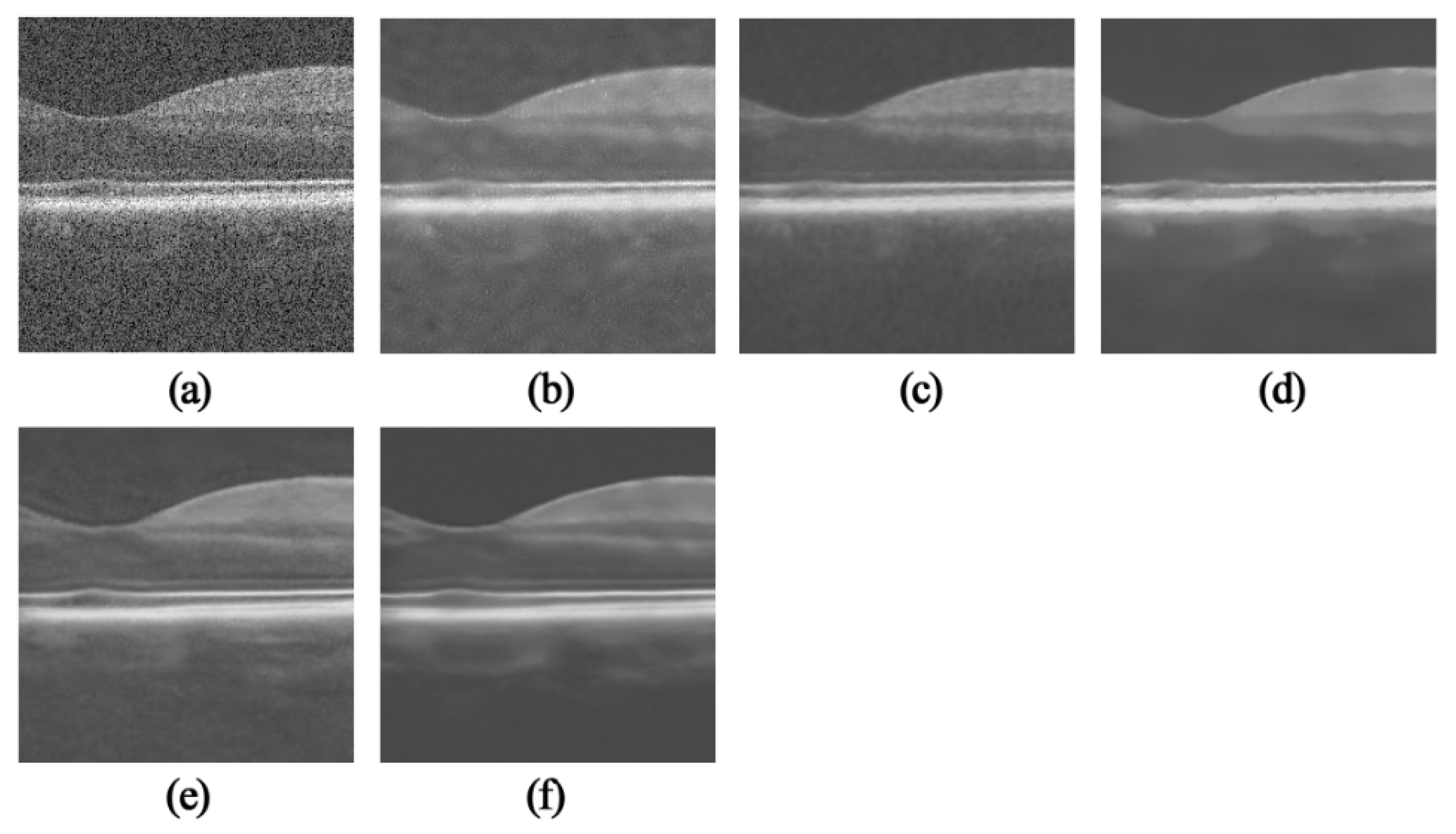
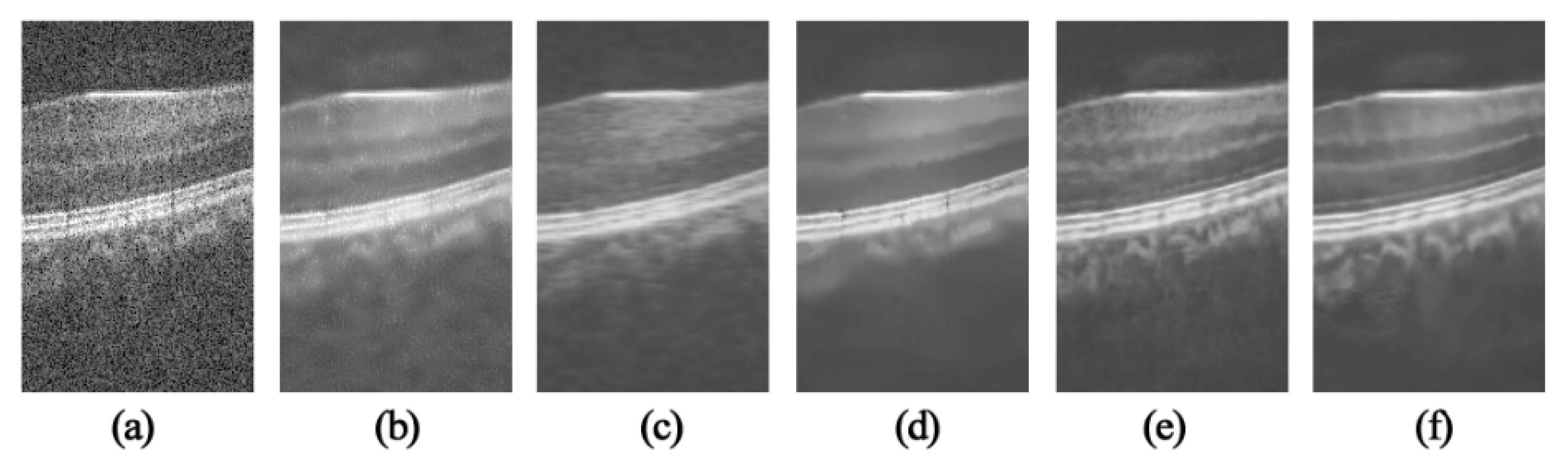
3. Experimental Results
3.1. OCT Despeckling Results
3.2. Image Quality Metrics
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Choma, M.; Sarunic, M.; Yang, C.; Izatt, J. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Opt. Express 2003, 18, 2183–2189. [Google Scholar] [CrossRef]
- Farsiu, S.; Chiu, S.; O’Connell, J.; Folgar, F.; Yuan, E.; Izatt, A.J.; Toth, C. Quantitative classification of eyes with and without intermediate age-related macular degeneration using optical coherence tomography. Ophthalmology 2014, 121, 162–172. [Google Scholar] [CrossRef]
- Karamata, B.; Hassler, K.; Laubscher, M.; Lasser, T. Speckle statistics in optical coherence tomography. J. Opt. Soc. Am. A 2005, 22, 593–596. [Google Scholar] [CrossRef]
- Mayer, M.A.; Borsdorf, A.; Wagner, M.; Hornegger, J.; Mardin, C.Y.; Tornow, P.R. Wavelet denoising of multiframe optical coherence tomography data. Biomed. Opt. Express 2012, 3, 572–589. [Google Scholar] [CrossRef]
- Zaki, F.; Wang, Y.; Su, H.; Yuan, X.; Liu, X. Noise adaptive wavelet thresholding for speckle noise removal in optical coherence tomography. Biomed. Opt. Express 2017, 8, 2720–2731. [Google Scholar] [CrossRef] [PubMed]
- Jian, Z.; Yu, Z.; Yu, L.; Rao, B.; Chen, Z.; Tromberg, B.J. Speckle attenuation in optical coherence tomography by curvelet shrinkage. Opt. Lett. 2009, 34, 1516–1520. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Ou, H.; Lam, E.Y.; Chui, P.C.; Wong, K.Y. Speckle reduction of retinal optical coherence tomography based on contourlet shrinkage. Opt. Lett. 2013, 38, 2900–2903. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Aum, J.; Kim, J.; Jeong, J. Effective speckle noise suppression in optical coherence tomography images using nonlocal means denoising filter with double Gaussian anisotropic kernels. Appl. Opt. 2015, 54, D43–D50. [Google Scholar] [CrossRef]
- Yu, H.; Gao, J.; Li, A. Probability-based non-local means filter for speckle noise suppression in optical coherence tomography images. Opt. Lett. 2016, 41, 994–998. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Chen, T.; Xu, M.; Qiu, Y.; Lei, Z. BM3D-based total variation algorithm for speckle removal with structure-preserving in OCT images. Appl. Opt. 2019, 58, 6233–6243. [Google Scholar] [CrossRef] [PubMed]
- Carlos, C.V.; René, R.; Bouma, B.E.; Néstor, U.P. Volumetric non-local-means based speckle reduction for optical coherence tomography. Biomed. Opt. Express 2018, 9, 3354–3372. [Google Scholar]
- Qi, G.; Zhang, Q.; Zeng, F.; Wan, J.; Zhu, Z. Multi-focus image fusion via morphological similarity-based dictionary construction and sparse representation. CAAI Trans. Intell. Technol. 2018, 3, 83–94. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Nie, Q.; Izatt, J.A.; Toth, C.A.; Farsiu, S. Sparsity based denoising of spectral domain optical coherence tomography images. Biomed. Opt. Express 2012, 3, 927–942. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Li, S.; McNabb, R.P.; Nie, Q.; Kuo, A.N.; Toth, C.A.; Izatt, J.A.; Farsiu, S. Fast acquisition and reconstruction of optical coherence tomography images via sparse representation. IEEE Trans. Med. Imaging Process. 2013, 32, 2034–2049. [Google Scholar] [CrossRef] [PubMed]
- Le, N.Q.K.; Ho, Q.T.; Ou, Y.Y. Incorporating deep learning with convolutional neural networks and position specific scoring matrices for identifying electron transport proteins. J. Comput. Chem. 2017, 38, 2000–2006. [Google Scholar] [CrossRef] [PubMed]
- Le, N.Q.K. Fertility-GRU: Identifying Fertility-Related Proteins by Incorporating Deep-Gated Recurrent Units and Original Position-Specific Scoring Matrix Profiles. J. Proteome Res. 2019, 18, 3503–3511. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Yapp, E.K.Y.; Yeh, H.Y. ET-GRU: Using multi-layer gated recurrent units to identify electron transport proteins. BMC Bioinform. 2019, 20, 377. [Google Scholar] [CrossRef]
- Halupka, K.J.; Antony, B.J.; Lee, M.H.; Lucy, K.A.; Rai, R.S.; Ishikawa, H.; Wollstein, G.; Schuman, J.S.; Garnavi, R. Retinal optical coherence tomography image enhancement via deep learning. Biomed. Opt. Express 2018, 9, 6205–6221. [Google Scholar] [CrossRef]
- Qiu, B.; Huang, Z.; Liu, X.; Meng, X.; You, Y.; Liu, G.; Yang, K.; Maier, A.; Ren, Q.; Lu, Y. Noise reduction in optical coherence tomography images using a deep neural network with perceptually-sensitive loss function. Biomed. Opt. Express 2020, 11, 817–830. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Priyanka, S.; Wang, Y.K. Fully symmetric convolutional network for effective image denoising. Appl. Sci. 2019, 9, 778. [Google Scholar] [CrossRef]
- Dong, W.; Wang, P.; Yin, W.; Shi, G. Denoising Prior Driven Deep Neural Network for Image Restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2305–2318. [Google Scholar] [CrossRef] [PubMed]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep Image Piror. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Lecture Notes in Computer Science, Proceedings of International Conference Medical Image Computing and Computer-Assisted Intervention, MICCAI, Athens, Greece, 17–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar]


| TNode | SBSDI | PNLM | DIP | NLM-DIP | |
|---|---|---|---|---|---|
| CNR(dB) | 8.67 | 10.72 | 10.25 | 10.32 | 11.17 |
| ENL | 544 | 1267 | 1420 | 1012 | 1468 |
| TNode | SBSDI | PNLM | DIP | NLM-DIP | |
|---|---|---|---|---|---|
| CNR(dB) | 9.92 | 11.28 | 11.12 | 11.14 | 11.65 |
| ENL | 596 | 740 | 793 | 595 | 1306 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, W.; Yu, H.; Chen, T.; Ji, S. OCT Image Restoration Using Non-Local Deep Image Prior. Electronics 2020, 9, 784. https://doi.org/10.3390/electronics9050784
Fan W, Yu H, Chen T, Ji S. OCT Image Restoration Using Non-Local Deep Image Prior. Electronics. 2020; 9(5):784. https://doi.org/10.3390/electronics9050784
Chicago/Turabian StyleFan, Wenshi, Hancheng Yu, Tianming Chen, and Sheng Ji. 2020. "OCT Image Restoration Using Non-Local Deep Image Prior" Electronics 9, no. 5: 784. https://doi.org/10.3390/electronics9050784
APA StyleFan, W., Yu, H., Chen, T., & Ji, S. (2020). OCT Image Restoration Using Non-Local Deep Image Prior. Electronics, 9(5), 784. https://doi.org/10.3390/electronics9050784





