1. Introduction
The low-power wide-area network (LPWAN) is a promising wireless platform to meet three key requirements of IoT applications distributed over wide areas; i.e., low cost, large scale deployment, and high energy efficiency. Most of all, it can be supported on battery-powered electronic devices for 10-years while communicating at low data-rates to gateways several kilometers away. It is conceived as an appealing technology to realize smart cities, smart farms, and smart buildings. In recent times, LPWAN has been actively researched in relation to sustainable and fully-connected IoT for ongoing 5G and towards 6G; i.e., long-term evolution (LTE) machine-type-communications (LTE-MTC), narrow band-IoT (NB-IoT), LoRa (long range), and Bluetooth low energy (BLE). LTE-MTC is an LPWA technology standard published by the 3GPP, which can achieve a much higher data rate. NB-IoT is an evolution form regular MTC to massive MTC (mMTC) which was a 3GPP standard in 2016 [
1]. They all work over the licensed spectrum. LoRa operates over an unlicensed spectrum; that is, 433 MHz, 868 MHz (Europe), 915 MHz (Australia and North America), and 923 MHz (Asia). As the chip spread spectrum technology is defined by the LoRa Alliance in 2015 [
2], it allows the cost of each LoRa device to be lowered with the usage of the cheap oscillator. BLE was released in 2010 as part of the Bluetooth 4.0 server’s specifications [
3], which works over the unlicensed 2.4 GHz band, and the transmission range can be up to 100 m. As supported by different standards organizations and alliances, each piece of LPWA technology shows different practical deployment potential. LTE-MTC and NB-IoT may be favored by cellular network operators due to high compatibility with existing cellular networks, while LoRa and BLE are supported by IoT operators with specific applications due to their good network scalability [
4]. Among the IoT networks, LPWAN is certainly becoming the main technique envisioned to be part of the cooperative distributed networks in IoT network connectivity in the ongoing 5G and towards 6G.
Recent studies have been conducted to address and analyze the performance of the LPWAN. In [
5], they assess the performance of LoRaWAN—which is one of the main LPWA technology available—in terms of network performance metrics, such as range, coverage, latency, and packet delivery ratio. In [
6], they derive the uplink throughput and data transmission time of a single LoRaWAN end device and analyze the maximum number of end devices which can be served by a single LoRaWAN base station. In [
7], they analyze the flexibility of LoRa and propose various strategies to adapt its radio parameters to different deployment scenarios and compute the energy consumption of LoRa transceivers. In [
8], they analyze the coverages and the capacities of four types of LPWAN using a real site deployment assuming traffic growth. They all explain that the LPWAN possess the ability to offer low-cost connections for a huge number of low-power devices distributed over large areas [
9].
Nevertheless, the LPWAN still has several challenges to be addressed effectively, including interference management, the massive access scheme, the optimal coexistence scheme, and energy efficient schemes, which are presented with overall knowledge about LPWAN in [
10].
Most of all, despite LPWAN wireless protocols enabling long-range communications (up to 10–15 km in rural zones and 2–5 km in urban zones [
11]) between connected devices with minimal energy requirements (battery can last up to 10 years for low data usage cases), communications are not always guaranteed. Because it depends on data rage, availability, range, noise, and required throughput [
12]. Actually, devices located in urban spaces deep inside buildings will experience severe drain in the battery, as their signals are highly attenuated, even at the closest gateway (GW) [
13]. In [
13], the decoding weak transmission solution is presented with the use of the
coherent combining technique, which enhances both the battery lives of client devices and the coverage of LPWANs in major urban deployments. It allows multiple LoRa wide-area network (LoRaWAN) GWs to pool their received signals in the
cloud, coherently combining them in order to detect weak signals that are not decodable at any individual GW. It was implemented as a service running on a campus-wide LoRaWAN network installed at Carnegie Mellon University and evaluated through proof-of-concept experiments and a large-scale, trace-driven simulation. That is a coherent combining technique, which is similar to the macro-diversity technique in the cellular network. They evaluated it over a test network and through a simulation using traces from a LoRaWan deployment. However, the performance analysis is not presented in the literature.
Actually, it is not trivial to attain tractable exact performance analysis for networks with multiple antennas. In [
14], the cloud-radio access network with remote radio heads (RRHs) is analyzed in term of outage probability, for which RRHs are equipped with multiple antennas. The exact closed-form expression for the outage probability is obtained. However, It is derived from using the moment generating function approach with the approximation. With the finite limiting factor, it does not match well with the simulation result in the low signal-to-noise ratio (SNR) regime. This paper aims to exactly address the error performance analysis of the cooperative uplink LPWAN with multiple antennas GWs. The exact closed-form expressions for the performance analysis are derived using the exact channel distribution information (CDI) (
hyper-Erlang distribution) [
15]. LPWAN is basically based on the low power transmission. It is certainly needed to analyze the performance exactly in the low SNR regime. The exact closed-form expressions of bit error rate (BER) and outage probability performances are obtained. Furthermore, the diversity order is obtained from the derived BER expression, which is the first theoretical result in the literature. Finally, the asymptotic expression of BER is addressed with the numerical results.
The rest of the paper is organized as follows. The system model is explained in
Section 2. In
Section 3, the novel channel distribution is introduced and the analytical expressions for the error performances are derived. The numerical results are presented in
Section 4. Finally, we draw conclusions in
Section 5.
2. System Model
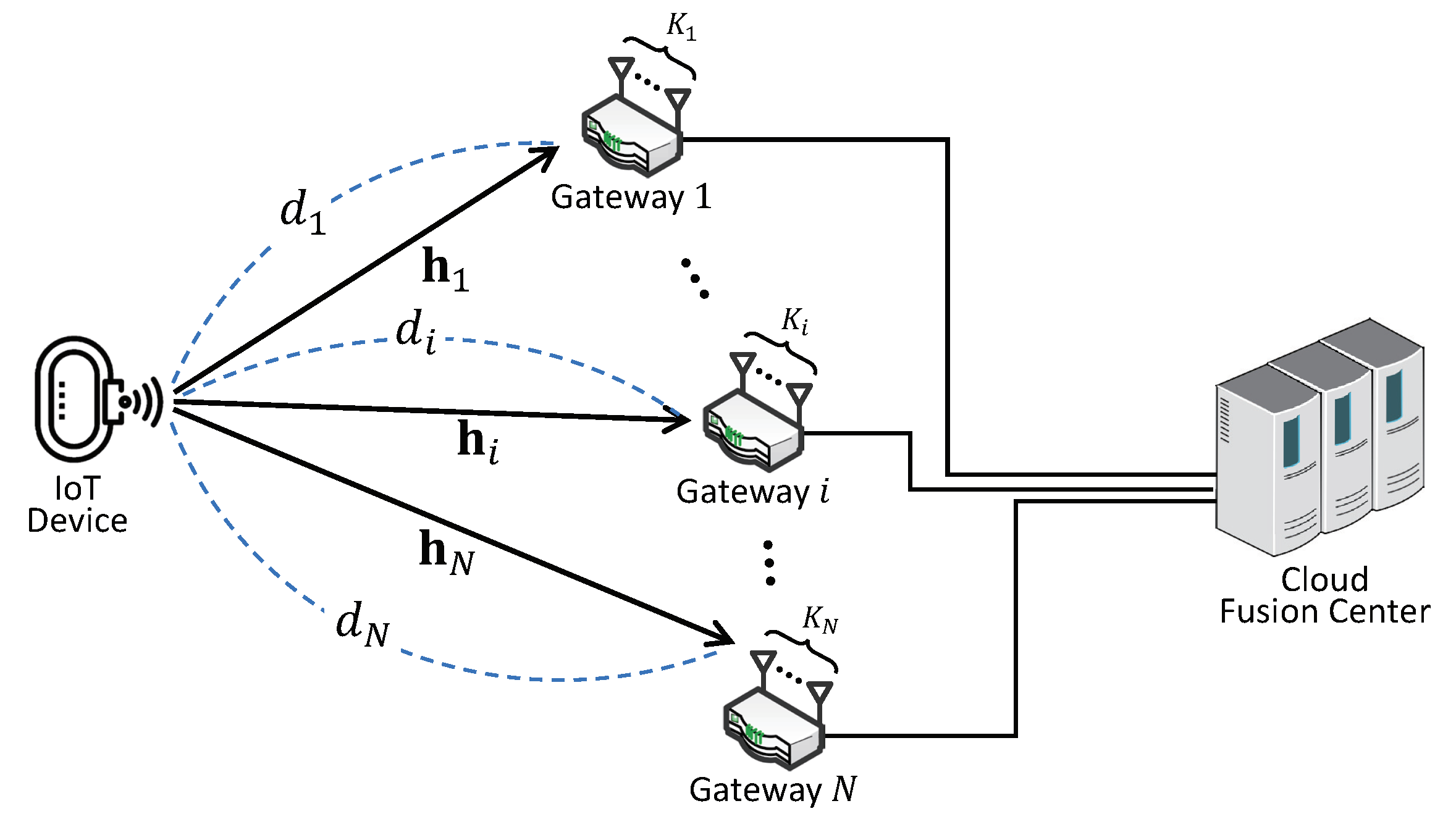
In this paper, we consider the uplink cooperative system in the LPWAN with multiple GWs. Considering a real situation and a simplification of analysis, the system consists of
N GWs, which are equipped with
(
) multiple antennas in each and an IoT device (ID) with a single antenna, as shown in
Figure 1. Then, the received signal at
i-th GW,
(
), is given by
where
P denotes the transmission power of the ID and
denotes the distance between the ID and the
i-th GW. The term
denotes the path-loss exponent and
x is a signal of the ID, which has a unit power; i.e.,
. In this paper, it is assumed that the small-scale fading channel between the ID and each GW follows a Rayleigh fading model, such as [
16]. Thus, the fading channel vector from the ID to
i-th GW is represented as
and follows the identically and independently distributed (i.i.d.) complex Gaussian distribution with zero mean and unit variance; i.e.,
. The additive white Gaussian noise (AWGN) at
i-th GW is represented as
, each element of which is identically and independently distributed complex Gaussian random variable with zero mean and variable of
. It is assumed that each ID knows the local channel state information by a pilot signal from the ID. At each GW, the maximum ratio combining (MRC) is operated in order to maximize the SNR, and the minimal essential information, a real-valued combining signal, is derived to the cloud server.
where
is related to the additive white Gaussian noise term. The cloud server receives the essential information from multiple GWs and then combines them as follows:
where
.
3. Error Performance Analysis
In order to derive the error probabilities, we first should know a distribution of effective channel gain for a signal at the cloud server. The effective channel gain,
Z, is equal to
where
(
). Since the fact is that
follows the Erlang distribution with
mean and
variance represented as following probability density function (p.d.f.):
the distribution of the effective channel gain
Z is the same as the distribution of the sum of
N non-identical and independent random variables, which follows Erlang distribution. It is known as hyper-Erlang distribution [
15] which is the mixture of
N mutually independent Erlang distribution and parallel
N-phase Erlang distribution weighted with probabilities. Therefore, the p.d.f. of
Z is given by
The coefficient
is iteratively obtained by the recursive method [
15]. See
Appendix A.
3.1. Outage Probability
From the definition of outage probability, it is straightforward to calculate the outage probability. Generally, an outage occurs when the channel capacity defined
is below the target rate
R [
17].
In non-cooperative LPWAN, the outage probability at the GW
i is given from (
2) as follows.
where
denotes the SNR and
is the outage channel threshold related to the target rate. Note that the cumulative distribution function (c.d.f.) of Erlang distribution
for all
i is given as
. Therefore, the outage probability
is derived as
Considering the effective channel gain of the uplink cooperation, the outage probability of that is given as follows
Since the hyper-Erlang distribution is given as the sum of
N polynomials, which are the
polynomials of the product of the coefficient
and the p.d.f. of each Erlang distributions as
j is the antenna index, the cumulative distribution function (c.d.f.) of hyper-Erlang distribution is obtained from the summation of
N Erlang distributions c.d.f as follows.
Therefore, the outage probability of the uplink cooperative system in LPWAN is exactly derived as follows:
3.2. Bit Error Rate (BER)
In this subsection, we derive the BER of the uplink cooperative technique in LPWAN. First, we assume that the transmit signal of the ID is modulated to quadrature phase-shift keying (QPSK) modulation. The BER of QPSK modulation is known as .
From (
2), the conditional BER for given channel gain
at the GW
i in non-cooperative LPWAN is given as
where
dedicates the bit-error event at GW
i. We easily can derive the non-cooperative BER of the
i-th GW with
antennas as follows:
where
is given in [
18].
Now, we analyze the BER of the uplink cooperative technique. As in Equation (
12), The conditional BER for given all channel gains,
at the cloud server is given as
where
dedicates the bit-error event at the cloud server.
Finally, we can obtain the exact closed-form BER performance of the uplink cooperative technique in the presence of the cloud server connected with them as follows.
3.3. Diversity Order
In this section, we analyze the diversity order of the uplink cooperative technique with the exact BER expression (Equation (
15)), which is defined as:
which is used to verify the tendency of BER performance; i.e., the slope of BER curve, in high SNR regime [
17]. The diversity order is obtained through Taylor series expansion for (
15), of which the first-order coefficient shows how the system parameters affect the performance in high SNR regime; e.g., the distances between ID and GWs, the number of antennas, pass-loss factor, and so on. An asymptotic expression is given by
where
,
, and
denotes the first coefficient of Taylor series expansion for the BER. It varies according to the total number of antennas of all GWs that participate in cooperative communication. It also depends on the distances between the ID and the GWs. Plugging (
17) into (
16) shows that the diversity order of uplink cooperative LPWAN system with
N GWs equipped with multiple antennas
is equal to
K; i.e.,
4. Numerical Results
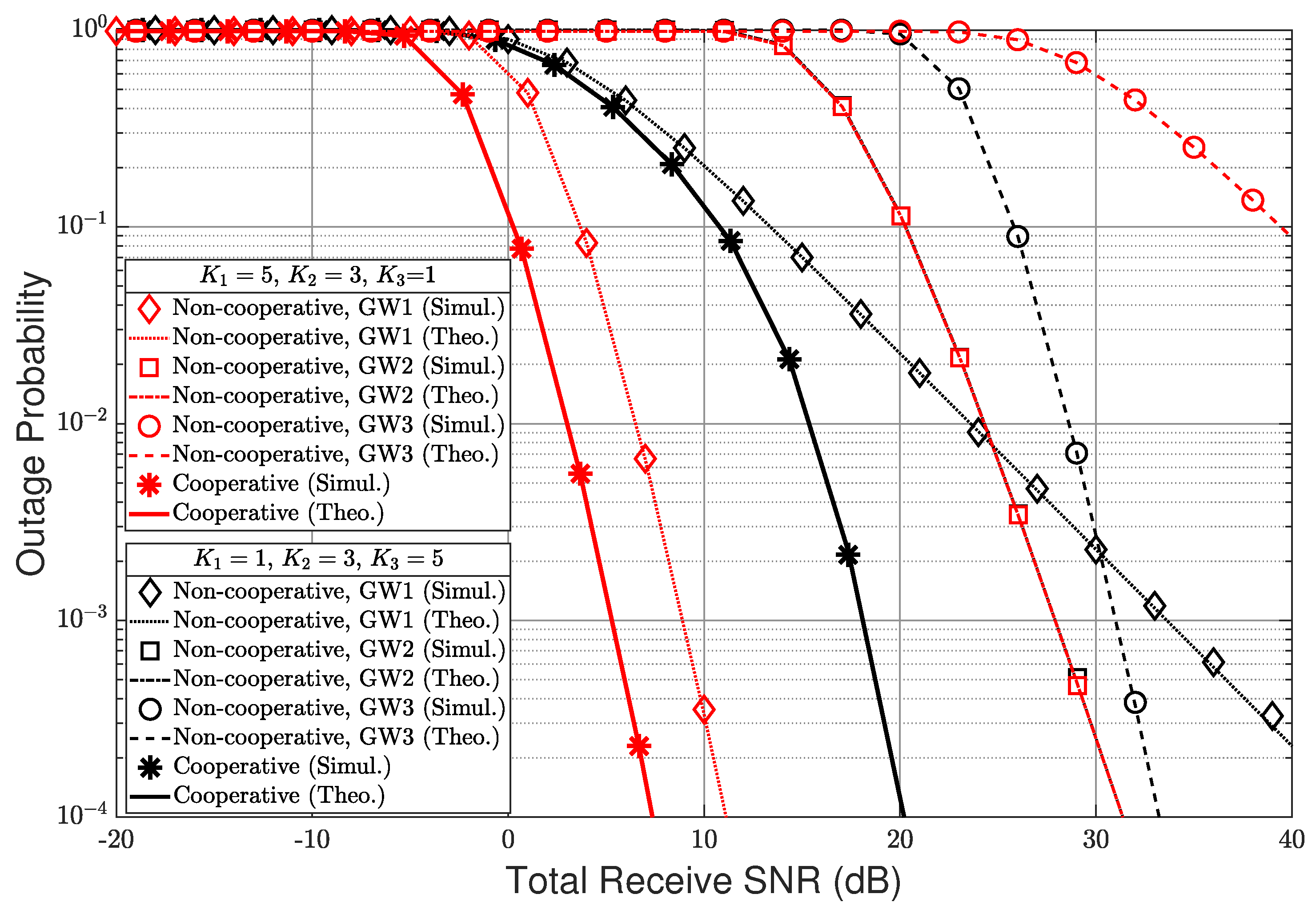
We show the performance of the uplink cooperative system in LPWAN while varying the total received SNR (the effective SNR at the cloud server), which has three GWs (), each with the different number of the antennas. We also generalize for a distance from ID to each GW; i.e., , , and .
Figure 2 shows the outage performances of uplink LPWAN with non-cooperative and cooperative techniques when
,
,
,
,
, and
. In this figure, the analytic results derived from Equations (
8) and (
11), are exactly matched with the Monte-Carlo simulation results for all cases of antenna combination. They show that the cooperative technique always outperforms the non-cooperative technique. It also has better performances when the number of antennas of the near GW from the ID is more than the number of antennas of the far GW.
Figure 3 shows the BER performances on the same system as the simulation environment in
Figure 2. The analyzed BER performances in this paper, Equation (
13) and (
15), are verified to match well with the simulation results by Monte-Carlo. The detailed interpretation of the results is omitted because it is the same as the interpretation of the result of outage probability.
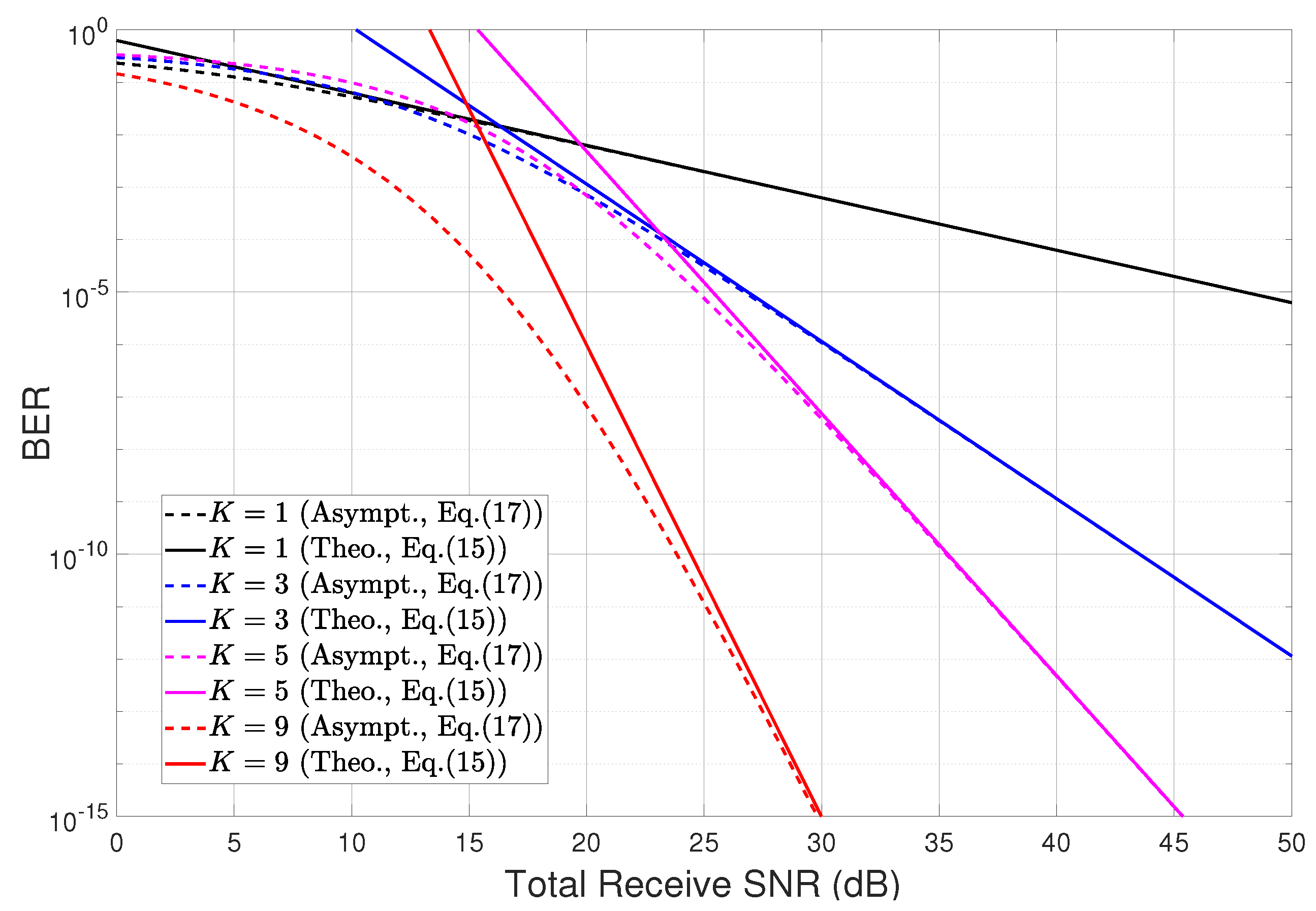
Figure 4 validates the diversity order analysis of the uplink cooperative technique in LPWAN when
; i.e.,
. As expected in
Section 3.3, the asymptotic analysis results (
17) are matched well with the exact analysis results in the form of an upper boundary curve as the SNR increases.