Secure Information Transmission with Self Jamming SWIPT

Abstract

This article is focused on implementing simultaneous wireless information and power transmission as a physical layer security measure by using artificial noise. A series of high energy precoded symbols is simultaneously transmitted along with the information symbols over a Rayleigh frequency selective fading channel. The high energy precoded symbols act as an artificial noise for the eavesdroppers. The energy symbols are precoded on the basis of a legitimate user’s channel matrix to form a null space vector, which eliminates the interference of energy symbols at the information symbol receiver antennas, while allowing the rectenna to harvest energy from the superimposed information and energy symbols. We analyze the secrecy rate and error rate performance at the receiver under different circumstances, and we show that the performance of the legitimate user can be improved by using the iterative block decision feedback equalization method at the receiver.

1. Introduction

In a dense wireless communication network (WCN), both the energy and security reliability need to be assured. This represents a challenge in the case of a network with a huge number of nodes [1]. Thus, in order to keep up with the energy demands of the increasing number of network nodes, new radio frequency energy harvesting (EH) techniques like simultaneous wireless information and power transmission (SWIPT) are investigated for 5G networks [1,2,3]. Apart from harvesting energy by using SWIPT techniques, many other signal processing applications like channel estimation with SWIPT [4] and physical layer security (PLS) measures with the help of SWIPT technique were investigated in [5]. One of the most important techniques in improving PLS in a wiretap channel is using artificial noise (AN) in the communication channel to degrade the signal-to-noise plus interference ratio (SINR) of eavesdroppers; thereby improving the security of legitimate users [6]. The high energy signal that is used for harvesting energy in SWIPT can also be adopted for creating AN to improve PLS, as in [7]. The secrecy rate of legitimate users in a wiretap channel can be improved with the SINR degradation of eavesdroppers as in [8,9]. Furthermore, the secrecy rate for the multiple-input and multiple-output (MIMO) system model was established in [10]. To avoid the impact of AN on the legitimate receiver, AN is introduced in the null space of the legitimate receiver’s channel matrix. Thereby, AN degrades the SINR of eavesdroppers without compromising the quality of the legitimate users’ signal [11]. However, the successful negation of AN is dependent on the channel state information (CSI) of the receiver at the legitimate transmitter and can be effectively used against very robust eavesdroppers as in [12,13]. This is considered as a challenge in the imperfect CSI condition [14,15]. Another challenge in using AN against eavesdroppers lies in the fact that a jamming attack depends on the channel correlation between the eavesdroppers and legitimate receiver; if the channel correlation is very high, then AN can be partially canceled out by the eavesdropper [16,17].

In this article, we use energy signals as a source of AN for secure communication, but also to harvest energy at the receiver. We consider the conventional MIMO system model with separate antennas for data and energy signal transmission and reception. AN is created by the transmitter by using channel precoding based on the CSI of the receiver. In this paper, we analyze the impact on channel precoding based on imperfect CSI. Furthermore, we also consider high channel correlation between eavesdroppers and the legitimate receiver as one of the challenges in the analysis. Our main contribution in this paper involves improving the error rate and secrecy rate performance of the legitimate receiver using iterative block decision feedback equalization (IB-DFE). IB-DFE is an efficient low complex receiver and performs better than non-iterative methods [18]. IB-DFE is effectively used with the single carrier frequency-division multiple access (SC-FDMA) transmission technique, and its performance was studied in detail [19,20,21]. IB-DFE can also be used to improve channel estimation at the transmitter side against imperfect CSI by using the robust superimposed pilot signal method for accurate channel estimation, as in [4,22]. For a fair comparison between the legitimate user and eavesdroppers, we also analyze the impact of imperfect CSI on the legitimate user’s performance.

Throughout this article, matrices or vectors are denoted by bold letters, and scalar variables are denoted by italic letters. The variables associated with the frequency domain and time domain are denoted by capital letters and small letters, respectively. ${(.)}^{*}$, ${(.)}^T$, ${(.)}^H$, $\left|\right|.\left|\right|$, and $\mathbb{E}[.]$ denote the conjugate, transpose, Hermitian, trace, and expectation operation, respectively.

2. System Model

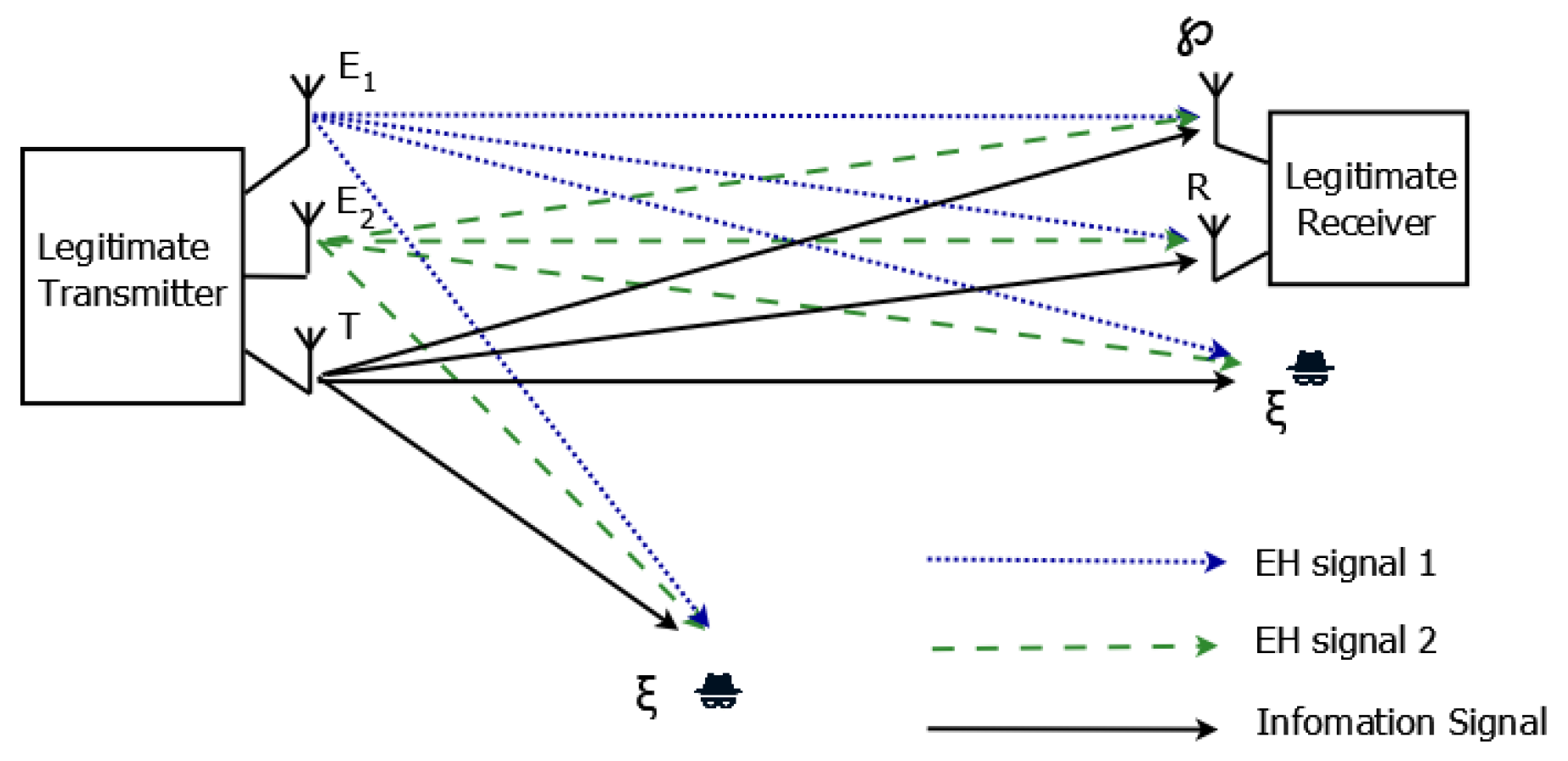
The MIMO system model is shown in Figure 1. It is composed of three transmitting antennas and two receiving antennas, with a dedicated transmitting antenna and a receiving antenna for information transmission, denoted as $\mathcal{T}$ and R, respectively. The other two transmitting antennas, $E1$ and $E2$, are used for energy transmission, and the rectenna ℘ is used to harvest energy from the physical layer network coded (PLNC) signal. The eavesdropper is denoted as $\xi$. It is assumed that $E1$, $E2$, and $\mathcal{T}$ are not spatially correlated. In Figure 1, based on the location of $\xi$, if $\xi$ is very close to R, $\xi$ is considered to have high channel correlation with R [16]. The system adopts the quadrature amplitude modulation (QAM) signal over the Rayleigh frequency selective fading channel by using SC-FDMA for simultaneously transferring information from $\mathcal{T}$ and the high energy signal from $E1$ and $E2$ to both R and ℘. 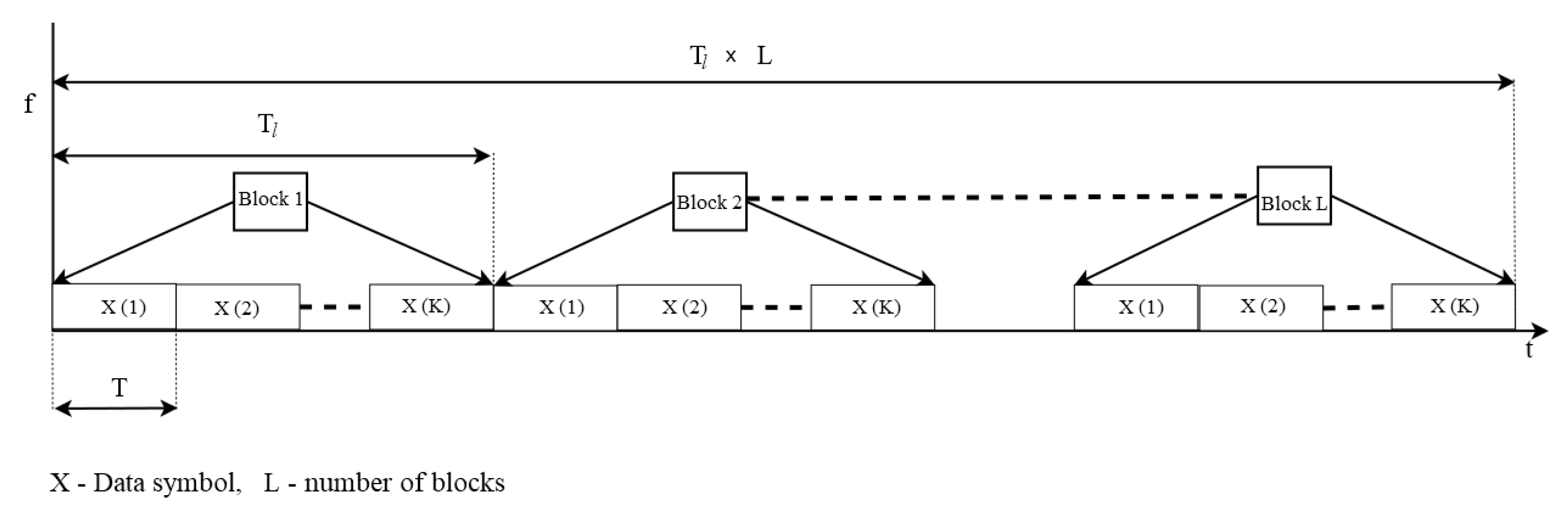The frequency domain signals transmitted from $\mathcal{T}$, $E1$, and $E2$ are denoted as $X_I^{\left(k\right)}$, $X_{E1}^{\left(k\right)}$, and $X_{E2}^{\left(k\right)}$, respectively, where k represents the index of the symbol with $k=0,1,\dots K$ and K is the total number of symbols in the respective signal stream. The frame structure of ${\mathbf{X}}_I$, ${\mathbf{X}}_{E1}$, and ${\mathbf{X}}_{E2}$ is illustrated in Figure 2, where the time duration per symbol, block duration, and total time for all the blocks are denoted as $T,T_l$, and $T_{l}L$, respectively. A frame consists of L signal blocks where each signal block contains N symbols. The signal blocks are denoted as l, where $l=0,1,\dots L$. We assume that $X_I^{\left(k\right)}$, $X_{E1}^{\left(k\right)}$, and $X_{E2}^{\left(k\right)}$ are transmitted with perfect time synchronization and in equal block size. The following system of equations is considered for a single block, and therefore, we set $l=1$.

$S_{E1}$, $S_{E2}$, and $S_I$ are the unamplified versions of ${\mathbf{X}}_{E1}$, ${\mathbf{X}}_{E2}$, and ${\mathbf{X}}_I$, respectively, and the power amplification levels of energy symbols and information symbols are at different levels. $P_{E1}$, $P_{E2}$, and $P_I$ denote the transmit powers of ${\mathbf{X}}_{E1}$, ${\mathbf{X}}_{E2}$, and ${\mathbf{X}}_I$, respectively. For the sake of simplicity, without loss of generality, we assume that $P_{E1}=P_{E2}$. The relationship between the power levels of energy and information symbols is given as:

$$\begin{array}{c}{X}_I^{\left(k\right)}=S_I^{\left(k\right)}{P}_I;X_{E1}^{\left(k\right)}=S_{E1}^{\left(k\right)}{P}_{E1};X_{E2}^{\left(k\right)}=S_{E2}^{\left(k\right)}{P}_{E2};\hfill \\ \beta =\frac{2P_{E1}}{P_I},\hfill \end{array}$$

(1)

where $\beta$ is the ratio between the transmit power of the energy and information signal.

Throughout this paper, the channel coefficient for the channel link between two nodes, i.e., for example, nodes $\mathcal{T}$ and R, is denoted as $H_{TR}^{\left(k\right)}$, where k represents the index of channel coefficient with respect to the transmitted symbol in the signal stream. Then, $H_{TR}^{\left(k\right)}$ is characterized as $H_{TR}^{\left(k\right)}\sim \mathcal{CN}(0,{\sigma }_{H,TR}^2)$, and its channel gain is given as $|{\left(H_{TR}^{\left(k\right)}\right)}^2|\sim \mathrm{Exp}\left\{{\sigma }_{H,TR}^2\right\}$, where ${\sigma }_{H,TR}^2$ is the variance of $H_{TR}^{\left(k\right)}$. Since all the channel links between the nodes are Rayleigh frequency selective fading channels, they follow similar notation and channel characterization as $H_{TR}^{\left(k\right)}$. Similarly, the channel coefficients corresponding to the channel link between $E1$ and R, $E2$ and R, $\mathcal{T}$ and ℘, $E1$ and ℘, $E2$ and ℘, $\mathcal{T}$ and $\xi$, $E1$ and $\xi$, and $E2$ and $\xi$ are denoted as $H_{E1R}^{\left(k\right)}$, $H_{E2R}^{\left(k\right)}$, $H_{T\wp }^{\left(k\right)}$, $H_{E1\wp }^{\left(k\right)}$, $H_{E2\wp }^{\left(k\right)}$, $H_{T\xi }^{\left(k\right)}$, $H_{E1\xi }^{\left(k\right)}$, and $H_{E2\xi }^{\left(k\right)}$, respectively. The received signals at R, ℘, and $\xi$ experience additive white Gaussian noise (AWGN) modeled as a zero mean complex Gaussian random variable, and their respective AWGNs are given as $N^{\left(k\right)}\sim \mathcal{CN}(0,{\sigma }_N^2)$, $W^{\left(k\right)}\sim \mathcal{CN}(0,{\sigma }_W^2)$, and $J^{\left(k\right)}\sim \mathcal{CN}(0,{\sigma }_J^2)$, respectively.

The system model exploits the CSI of $H_{E2R}^{\left(k\right)}$ and $H_{E1R}^{\left(k\right)}$, to cancel the interference of the energy signals to the information signal at R. $X_{E1}^{\left(k\right)}$ and $X_{E2}^{\left(k\right)}$ will be precoded to equalize $H_{E2R}^{\left(k\right)}$ and $H_{E1R}^{\left(k\right)}$, respectively. Unlike R, the eavesdropper $\xi$ receives a highly distorted signal, which makes the decoding process difficult. In general, $\xi$ can decode the information based on the estimated value of $X_{E1}^{\left(k\right)}$, $X_{E2}^{\left(k\right)}$, $H_{E2R}^{\left(k\right)}$, and $H_{E1R}^{\left(k\right)}$. Furthermore, to reduce the accuracy of these estimated values at $\xi$, the EH signal should act as AN. Similar to $\xi$, ℘ will receive the combination of all the transmitted signals as a PLNC signal. Furthermore, ℘ can effectively take advantage of the PLNC signal for harvesting energy, and the received PLNC signal at ℘ is given as:

$$\begin{array}{cc}\hfill & Y_{\wp }^{\left(k\right)}=H_{E1\wp }^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2\wp }^{\left(k\right)}{X}_{E2}^{\left(k\right)}+H_{T\wp }^{\left(k\right)}{X}_I^{\left(k\right)}+W^{\left(k\right)}.\hfill \end{array}$$

(2)

The performance of this secure self jamming SWIPT technique is analyzed based on the secrecy rate and the bit error rate (BER). Here, three different scenarios are considered, and in all the scenarios, R and $\xi$ are considered to have a CSI of ${\mathbf{H}}_{TR}$ and ${\mathbf{H}}_{T\xi }$, respectively. Here, both R and $\xi$ do not have a CSI of ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$. The assumptions behind the three scenarios are explained as follows:

A

Scenario A: $\mathcal{T}$ has the CSI of ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$. $\xi$ is assumed to be far away from R, and $\xi$ does not have channel correlation. In this scenario, $\xi$ is denoted as $\xi \left(a\right)$, and R is denoted as $R\left(a\right)$.

B

Scenario B: $\mathcal{T}$ does not have the CSI of ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$, and $\mathcal{T}$ estimates ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$. $\xi$ is assumed to be very close to R, and their channel correlation is very high. In this scenario, $\xi$ is denoted as $\xi \left(b\right)$, and R is denoted as $R\left(b\right)$.

C

Scenario C: This scenario is similar to A where $\mathcal{T}$ has the CSI of ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$, but here, $\xi$ is assumed to be very close to R, and their channel correlation is very high. In this scenario, $\xi$ is denoted as $\xi \left(c\right)$. Based on the perfect CSI condition, R is the same in Scenario A and Scenario C.

Then, the received signal at $R\left(a\right)$ is given as:

$$\begin{array}{c}\hfill Y_{R\left(a\right)}^{\left(k\right)}=\left\{\begin{array}{cc}{H}_{TR}^{\left(k\right)}{X}_I^{\left(k\right)}+N^{\left(k\right)};\hfill & \mathrm{if}\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)=0,\hfill \\ H_{TR}^{\left(k\right)}{X}_I^{\left(k\right)}+N^{\left(k\right)}+H_{E1R}^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2R}^{\left(k\right)}{X}_{E2}^{\left(k\right)};\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(3)

where $\mathcal{L}(.)$ denotes the linear subspace of a vector and ${\mathcal{V}}^{\left(k\right)}=H_{E1R}^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2R}^{\left(k\right)}{X}_{E2}^{\left(k\right)}$. Here, $H_{E1R}^{\left(k\right)}{X}_{E1}^{\left(k\right)}$ is the additive inverse of $H_{E2R}^{\left(k\right)}{X}_{E2}^{\left(k\right)}$, and this allows $\mathcal{T}$ to nullify the interference of $X_{E1}^{\left(k\right)}$ and $X_{E2}^{\left(k\right)}$. To achieve $\mathcal{L}(H_{E1R}^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2R}^{\left(k\right)}{X}_{E2}^{\left(k\right)})=0$, both $X_{E1}^{\left(k\right)}$ and $X_{E2}^{\left(k\right)}$ should be precoded based on the CSI of the EH signals; thereby, the inference of EH signals to $X_I^{\left(k\right)}$ can be reduced to a negligible level as in (3). The precoded $X_{E1}^{\left(k\right)}$ and $X_{E2}^{\left(k\right)}$ are given in Appendix A.1. Therefore, due to precoding, the SINR of ${\mathbf{Y}}_{R\left(a\right)}$ at $R\left(a\right)$ does not experience any interference from EH signals, which is given as:

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{R\left(a\right)}=\frac{\mathbb{E}\left[\right|{\mathbf{X}}_I^T{\mathbf{H}}_{TR}{|}^2]}{\mathbb{E}\left[\right|\left|\mathbf{N}\right|{|}^2]}=\frac{{\sigma }_{X,I}^2{\sigma }_{H,TR}^2}{{\sigma }_N^2},\hfill \end{array}$$

(4)

where $\mathbb{E}\left[\right|{\mathbf{X}}_I{|}^2]={\sigma }_{X,I}^2$. Thus, under the perfect channel condition, the EH signal does not affect the performance of the legitimate receiver R.

Irrespective of its location, $\xi$ receives the signal with low SINR due to the EH signal interference. The received signal at $\xi \left(a\right)$ is given as:

$$\begin{array}{cc}\hfill & Y_{\xi }^{\left(k\right)}\left(a\right)=H_{T\xi }^{\left(k\right)}{X}_I^{\left(k\right)}+H_{E1\xi }^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2\xi }^{\left(k\right)}{X}_{E2}^{\left(k\right)}+J^{\left(k\right)},\hfill \end{array}$$

(5)

where $Y_{\xi }^{\left(k\right)}\left(a\right)$ is the PLNC signal, $H_{T\xi }^{\left(k\right)}{X}_I^{\left(k\right)}$ is the useful information component, and the EH signal components ($H_{E1\xi }^{\left(k\right)}{X}_{E1}^{\left(k\right)}$ and $H_{E2\xi }^{\left(k\right)}{X}_{E2}^{\left(k\right)}$) are considered as interference to $X_I^{\left(k\right)}$. Hence, the SINR of ${\mathbf{Y}}_{\xi }\left(a\right)$ at $\xi \left(a\right)$ is given as:

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{\xi \left(a\right)}=\frac{\mathbb{E}\left[\right|{\mathbf{X}}_I^T{\mathbf{H}}_{T\xi }{|}^2]}{\mathbb{E}\left[\right|{\mathbf{X}}_{E1}^T{\mathbf{H}}_{E1\xi }{|}^2]+\mathbb{E}[|{\mathbf{X}}_{E2}^T{\mathbf{H}}_{E2\xi }{|}^2{]+\mathbb{E}[\left|\right|\mathbf{J}\left|\right|}^{\mathbf{2}}]}=\frac{{\sigma }_{X,I}^2{\sigma }_{H,T\xi }^2}{{\sigma }_{H,E1\xi }^2{\sigma }_{X,E1}^2+{\sigma }_{H,E2\xi }^2{\sigma }_{X,E2}^2+{\sigma }_J^2}.\hfill \end{array}$$

(6)

Note that the performance of the legitimate user is dependent on the perfect channel condition, which allows $E1$ and $E2$ to perform signal precoding using CSI. With the imperfect channel condition, the performance of R is dependent on a robust channel estimation technique as in [2,4]. The channel estimates of ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$ are obtained by using training symbols from R to $E1$ and $E2$, respectively. The channel estimates of $H_{E1R}^{\left(k\right)}$ and $H_{E2R}^{\left(k\right)}$, respectively, are given as ${\widehat{H}}_{E1R}^{\left(k\right)}=H_{E1R}^{\left(k\right)}+{ϵ}_{E1R}^{\left(k\right)}$ and ${\widehat{H}}_{E2R}^{\left(k\right)}=H_{E2R}^{\left(k\right)}+{ϵ}_{E1R}^{\left(k\right)}$. Here, ${ϵ}_{E1R}^{\left(k\right)}$ and ${ϵ}_{E2R}^{\left(k\right)}$ are the channel estimation errors of $H_{E1R}^{\left(k\right)}$ and $H_{E2R}^{\left(k\right)}$, respectively. Then, the new precoded EH signals denoted as ${X^{\prime }}_{E1}^{\left(k\right)}$ and ${X^{\prime }}_{E2}^{\left(k\right)}$ are expressed in Appendix A.2. ${ϵ}_{A,E1}^{\left(k\right)}$ and ${ϵ}_{A,E2}^{\left(k\right)}$ are the precoding errors due to channel estimation error at ${ϵ}_{E2R}^{\left(k\right)}{A}_{E1}^{\left(k\right)}$ and ${ϵ}_{E1R}^{\left(k\right)}{A}_{E2}^{\left(k\right)}$, respectively.

Similarly, the received signal at $R\left(b\right)$ based on the impact of ${\widehat{H}}_{E1R}^{\left(k\right)}$ and ${\widehat{H}}_{E2R}^{\left(k\right)}$ is given as:

$$\begin{array}{c}\hfill Y_{R\left(b\right)}^{\left(k\right)}=\left\{\begin{array}{cc}{H}_{TR}^{\left(k\right)}{X}_I^{\left(k\right)}+N^{\left(k\right)}+{\epsilon }_{R\left(b\right),E1}^{\left(k\right)}+{\epsilon }_{R\left(b\right),E2}^{\left(k\right)};\hfill & \mathrm{if}\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)={\epsilon }_{R\left(b\right)}^{\left(k\right)},\hfill \\ H_{TR}^{\left(k\right)}{X}_I^{\left(k\right)}+N^{\left(k\right)}+H_{E1R}^{\left(k\right)}{X^{\prime }}_{E1}^{\left(k\right)}+H_{E2R}^{\left(k\right)}{X^{\prime }}_{E2}^{\left(k\right)};\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(7)

where ${\epsilon }_{R\left(b\right),E1}^{\left(k\right)}=H_{E1R}^{\left(k\right)}{ϵ}_{A,E2}^{\left(k\right)}$, ${\epsilon }_{R\left(b\right),E2}^{\left(k\right)}=H_{E2R}^{\left(k\right)}{ϵ}_{A,E1}^{\left(k\right)}$, and ${\epsilon }_{R\left(b\right),E1}^{\left(k\right)}$ and ${\epsilon }_{R\left(b\right),E2}^{\left(k\right)}$ are the additional noise components of $Y_{R\left(b\right)}^{\left(k\right)}$ due to precoding error. Then, $\mathcal{L}(H_{E1R}^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2R}^{\left(k\right)}{X}_{E2}^{\left(k\right)})={\epsilon }_{R\left(b\right)}^{\left(k\right)}$, where ${\epsilon }_{R\left(b\right)}^{\left(k\right)}={\epsilon }_{R\left(b\right),E1}^{\left(k\right)}+{\epsilon }_{R\left(b\right),E2}^{\left(k\right)}$. The SINR of ${\mathbf{Y}}_{R\left(b\right)}$ for the condition $\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)={\epsilon }_{R\left(b\right)}^{\left(k\right)}$ is given as:

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{R\left(b\right)}=\frac{\mathbb{E}\left[\right|{\mathbf{X}}_I^T{\mathbf{H}}_{TR}{|}^2]}{\mathbb{E}\left[\right({\sum }_{k=0}^{K-1}|{\epsilon }_{R\left(b\right),E1}^{\left(k\right)}{\left|\right)}^2]+\mathbb{E}[({\sum }_{k=0}^{K-1}|{\epsilon }_{R\left(b\right),E2}^{\left(k\right)}{\left|\right)}^2{]+\mathbb{E}[\left|\right|\mathbf{N}\left|\right|}^{\mathbf{2}}]}=\frac{{\sigma }_{X,I}^2{\sigma }_{H,TR}^2}{{\sigma }_{\epsilon ,R\left(b\right),E1}^2+{\sigma }_{\epsilon ,R\left(b\right),E2}^2+{\sigma }_N^2}.\hfill \end{array}$$

(8)

Note that, since R does not need to equalize $H_{E1R}^{\left(k\right)}$ and $H_{E2R}^{\left(k\right)}$, their respective channel estimation errors ${ϵ}_{E1R}^{\left(k\right)}$ and ${ϵ}_{E2R}^{\left(k\right)}$ are neglected in Equation (8).

The performance of $\xi \left(b\right)$ is better than $\xi \left(a\right)$ due to high channel correlations between ${\mathbf{H}}_{E1\xi }$ and ${\mathbf{H}}_{E1R}$ and also between ${\mathbf{H}}_{E2\xi }$ and ${\mathbf{H}}_{E2R}$. Let us denote the channel correlation between ${\mathbf{H}}_{E1\xi }$ and ${\mathbf{H}}_{E1R}$ as ${\rho }_{E1}$. Furthermore, let us denote the channel correlation between between ${\mathbf{H}}_{E2\xi }$ and ${\mathbf{H}}_{E2R}$ as ${\rho }_{E2}$. ${\rho }_{E1}$ and ${\rho }_{E2}$ are expressed in Appendix B. The error due to ${\rho }_{E1}$ and ${\rho }_{E2}$ is denoted as ${ϵ}_{\rho ,E1}$ and ${ϵ}_{\rho ,E2}$, respectively. The channel precodings at $E1$ and $E2$ from the perspective of $\xi \left(b\right)$, respectively, are given as:

$$\begin{array}{cc}\hfill & {X^{\prime }}_{E1}^{\left(k\right)}(1+{ϵ}_{\rho ,E2})=(X_{E1}^{\left(k\right)}+{ϵ}_{A,E1}^{\left(k\right)})(1+{ϵ}_{\rho ,E2})=A_{E1}^{\left(k\right)}(H_{E2R}^{\left(k\right)}+{ϵ}_{E2R}^{\left(k\right)})(1+{ϵ}_{\rho ,E2}),\hfill \\ \hfill & {X^{\prime }}_{E2}^{\left(k\right)}(1+{ϵ}_{\rho ,E1})=(X_{E2}^{\left(k\right)}+{ϵ}_{A,E2}^{\left(k\right)})(1+{ϵ}_{\rho ,E1})=A_{E2}^{\left(k\right)}(H_{E1R}^{\left(k\right)}+{ϵ}_{E1R}^{\left(k\right)})(1+{ϵ}_{\rho ,E1}).\hfill \end{array}$$

(9)

From the perspective of $\xi$, $(1+{ϵ}_{\rho ,E2})$ and $(1+{ϵ}_{\rho ,E2})$ are the impacts on ${X^{\prime }}_{E1}^{\left(k\right)}$ and ${X^{\prime }}_{E2}^{\left(k\right)}$, respectively, which degrade the precoded EH signals and increase the precoding errors.

The received signal at $\xi \left(b\right)$ is given as:

$$\begin{array}{c}\hfill Y_{\xi \left(b\right)}^{\left(k\right)}=\left\{\begin{array}{cc}{H}_{T\xi }^{\left(k\right)}{X}_I^{\left(k\right)}+J^{\left(k\right)}+{\epsilon }_{\xi \left(b\right),E1}^{\left(k\right)}+{\epsilon }_{\xi \left(b\right),E2}^{\left(k\right)};\hfill & \mathrm{if}\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)={\epsilon }_{\xi \left(b\right)}^{\left(k\right)},\hfill \\ H_{T\xi }^{\left(k\right)}{X}_I^{\left(k\right)}+J^{\left(k\right)}+H_{E1R}^{\left(k\right)}{X^{\prime }}_{E1}^{\left(k\right)}(1+{ϵ}_{\rho ,E2})+H_{E2R}^{\left(k\right)}{X^{\prime }}_{E2}^{\left(k\right)}(1+{ϵ}_{\rho ,E1});\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(10)

where ${\epsilon }_{\xi \left(b\right),E1}^{\left(k\right)}=\frac{H_{E1R}^{\left(k\right)}(X_{E1}^{\left(k\right)}+{ϵ}_{A,E1}^{\left(k\right)})(1+{ϵ}_{\rho ,E2})}{X_{E2}^{\left(k\right)}}$, ${\epsilon }_{\xi \left(b\right),E2}^{\left(k\right)}=\frac{H_{E2R}^{\left(k\right)}(X_{E2}^{\left(k\right)}+{ϵ}_{A,E2}^{\left(k\right)})(1+{ϵ}_{\rho ,E2})}{X_{E1}^{\left(k\right)}}$, and ${\epsilon }_{\xi \left(b\right),E1}^{\left(k\right)}$ and ${\epsilon }_{\xi \left(b\right),E2}^{\left(k\right)}$ are the additional noise components to $Y_{\xi \left(b\right)}^{\left(k\right)}$. Then, $\mathcal{L}(H_{E1\xi }^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2\xi }^{\left(k\right)}{X}_{E2}^{\left(k\right)})={\epsilon }_{\xi \left(b\right)}^{\left(k\right)}$, where ${\epsilon }_{\xi \left(b\right)}^{\left(k\right)}={\epsilon }_{\xi \left(b\right),E1}^{\left(k\right)}+{\epsilon }_{\xi \left(b\right),E2}^{\left(k\right)}$. The SINR of ${\mathbf{Y}}_{\xi \left(b\right)}$ for the condition $\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)={\epsilon }_{\xi \left(b\right)}^{\left(k\right)}$ is given as:

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{\xi \left(b\right)}=\frac{\mathbb{E}\left[\right|{\mathbf{X}}_I^T{\mathbf{H}}_{T\xi }{|}^2]}{\mathbb{E}\left[\right({\sum }_{k=0}^{K-1}|{\epsilon }_{\xi \left(b\right),E1}^{\left(k\right)}{\left|\right)}^2]+\mathbb{E}[({\sum }_{k=0}^{K-1}|{\epsilon }_{\xi \left(b\right),E2}^{\left(k\right)}{\left|\right)}^2{]+\mathbb{E}[\left|\right|\mathbf{J}\left|\right|}^{\mathbf{2}}]}=\frac{{\sigma }_{X,I}^2{\sigma }_{H,T\xi }^2}{{\sigma }_{\epsilon ,\xi \left(b\right),E1}^2+{\sigma }_{\epsilon ,\xi \left(b\right),E2}^2+{\sigma }_J^2}.\hfill \end{array}$$

(11)

The best scenario for $\xi$ is $\xi \left(c\right)$, where, the precoding errors due to the channel estimation errors can be avoided at $\mathcal{T}$. However, there will be a precoding error due to $H_{E1R}^{\left(k\right)}(1+{ϵ}_{\rho ,E1})$ and $H_{E2R}^{\left(k\right)}(1+{ϵ}_{\rho ,E2})$. Hence, the precoded EH signals can be written as:

$$\begin{array}{cc}\hfill & X_{E1}^{\left(k\right)}(1+{ϵ}_{\rho ,E2})=A_{E1}^{\left(k\right)}{H}_{E2R}^{\left(k\right)}(1+{ϵ}_{\rho ,E2}),\hfill \\ \hfill & X_{E2}^{\left(k\right)}(1+{ϵ}_{\rho ,E1})=A_{E2}^{\left(k\right)}{H}_{E1R}^{\left(k\right)}(1+{ϵ}_{\rho ,E1}).\hfill \end{array}$$

(12)

Then, the received signal at $\xi \left(c\right)$ is given as:

$$\begin{array}{c}\hfill Y_{\xi \left(c\right)}^{\left(k\right)}=\left\{\begin{array}{cc}{H}_{T\xi }^{\left(k\right)}{X}_I^{\left(k\right)}+N^{\left(k\right)}+{\epsilon }_{\xi \left(c\right),E1}^{\left(k\right)}+{\epsilon }_{\xi \left(c\right),E2}^{\left(k\right)};\hfill & \mathrm{if}\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)={\epsilon }_{\xi \left(c\right)}^{\left(k\right)},\hfill \\ H_{T\xi }^{\left(k\right)}{X}_I^{\left(k\right)}+N^{\left(k\right)}+H_{E1R}^{\left(k\right)}{X}_{E1}^{\left(k\right)}(1+{ϵ}_{\rho ,E2})+H_{E2R}^{\left(k\right)}{X}_{E2}^{\left(k\right)}(1+{ϵ}_{\rho ,E1});\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(13)

where ${\epsilon }_{\xi \left(c\right),E1}^{\left(k\right)}=H_{E1R}^{\left(k\right)}(1+{ϵ}_{\rho ,E2})$ and ${\epsilon }_{\xi \left(c\right),E2}^{\left(k\right)}=H_{E2R}^{\left(k\right)}(1+{ϵ}_{\rho ,E1})$. Then, $\mathcal{L}(H_{E1\xi }^{\left(k\right)}{X}_{E1}^{\left(k\right)}+H_{E2\xi }^{\left(k\right)}{X}_{E2}^{\left(k\right)})={\epsilon }_{\xi \left(c\right)}^{\left(k\right)}$, where ${\epsilon }_{\xi \left(c\right)}^{\left(k\right)}={\epsilon }_{\xi \left(c\right),E1}^{\left(k\right)}+{\epsilon }_{\xi \left(c\right),E2}^{\left(k\right)}$. The SINR of ${\mathbf{Y}}_{\xi \left(c\right)}$ for the condition $\mathcal{L}\left({\mathcal{V}}^{\left(k\right)}\right)={\epsilon }_{\xi \left(c\right)}^{\left(k\right)}$ is given as:

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{\xi \left(c\right)}=\frac{\mathbb{E}\left[\right|{\mathbf{X}}_I^T{\mathbf{H}}_{T\xi }{|}^2]}{\mathbb{E}\left[\right({\sum }_{k=0}^{K-1}|{\epsilon }_{\xi \left(c\right),E1}^{\left(k\right)}{\left|\right)}^2]+\mathbb{E}[({\sum }_{k=0}^{K-1}|{\epsilon }_{\xi \left(c\right),E2}^{\left(k\right)}{\left|\right)}^2{]+\mathbb{E}[\left|\right|\mathbf{J}\left|\right|}^{\mathbf{2}}]}=\frac{{\sigma }_{X,I}^2{\sigma }_{H,T\xi }^2}{{\sigma }_{\epsilon ,\xi \left(c\right),E1}^2+{\sigma }_{\epsilon ,\xi \left(c\right),E2}^2+{\sigma }_J^2}.\hfill \end{array}$$

(14)

For all the scenarios of $\xi$ and $R\left(b\right)$, the channel precoding error is denoted as ${ϵ}_A$, and its variance is denoted as ${\sigma }_A^2$. In this system model, both the channel estimate errors and the channel correlation errors are considered to be the sole contributors of ${ϵ}_A$, and ${ϵ}_A$ proportionally increases with the increase in $\beta$. To form the generalized SINR equation, ${\sigma }_{H,TR}^2$ and ${\sigma }_{H,T\xi }^2$ are assumed as one; then, the SINR of the received signal at R and $\xi$ can be written as:

$$\begin{array}{cc}\hfill & \mathsf{\Gamma }=\frac{{\sigma }_{X,I}^2}{{\sigma }_N^2+\beta {\sigma }_A^2},\hfill \end{array}$$

(15)

At a very high SINR of the information signal, ${\sigma }_N^2$ can be neglected. Then, Equation (15) can be written as:

$$\begin{array}{cc}\hfill & \mathsf{\Gamma }\approx \frac{{\sigma }_{X,I}^2}{\beta {\sigma }_A^2}.\hfill \end{array}$$

(16)

Therefore, even at a very high SINR condition, $\beta {\sigma }_A^2$ can be used to degrade the performance of $\xi$. The secrecy of ${\mathbf{X}}_I$ can be improved at $R\left(a\right)$ and $R\left(b\right)$ by increasing $\beta$ under the condition that the ${\sigma }_A^2$ value in ${\mathbf{Y}}_{R\left(a\right)}$ and ${\mathbf{Y}}_{R\left(b\right)}$ is lesser than the ${\sigma }_A^2$ value in ${\mathbf{Y}}_{\xi \left(a\right)}$, ${\mathbf{Y}}_{\xi \left(b\right)}$, and ${\mathbf{Y}}_{\xi \left(c\right)}$. Another observation from Equation (15) indicates that, if $\beta \ge 1$, then $\xi \left(a\right)$ will always be in the negative SINR region.

2.1. Secrecy Rate Analysis

The secrecy rate analysis of this system model is based on the Gaussian wiretap channel secrecy capacity, which deduces the difference between Shannon’s capacity of R and $\xi$. The maximum achievable secrecy rate is the secrecy capacity of R [8,9]. The secrecy capacity of $R\left(a\right)$ with respect to $\xi \left(a\right)$ and the secrecy capacity of $R\left(a\right)$ with respect to $\xi \left(c\right)$, respectively, are given (The notation for the secrecy rate of $R\left(a\right)$ with respect to $\xi \left(c\right)$ is given as ${\mathbb{C}}_{\left(c\right),A}$, where $\left(c\right)$ denotes $\xi \left(c\right)$ and A denotes $R\left(a\right)$. A similar rule is followed for the other three secrecy rate notions.) as:

$$\begin{array}{c}{\mathbb{C}}_{\left(a\right),A}=\frac{\Delta f}{k}\sum _{k=0}^{K-1}\left(log\left(\frac{1+|H_{TR}^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{R\left(a\right)}}{1+|H_{T\xi }^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{\xi \left(a\right)}}\right)\right),\hfill \\ {\mathbb{C}}_{\left(c\right),A}=\frac{\Delta f}{k}\sum _{k=0}^{K-1}\left(log\left(\frac{1+|H_{TR}^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{R\left(a\right)}}{1+|H_{T\xi }^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{\xi \left(c\right)}}\right)\right),\hfill \end{array}$$

(17)

where $2\Delta f$ is the bandwidth and $\Delta f$ is the peak frequency deviation. The secrecy capacity of $R\left(b\right)$ with respect to $\xi \left(a\right)$ and the secrecy capacity of $R\left(b\right)$ with respect to $\xi \left(b\right)$, respectively, are given as:

$$\begin{array}{cc}\hfill & {\mathbb{C}}_{\left(a\right),B}=\frac{\Delta f}{k}\sum _{k=0}^{K-1}\left(log\left(\frac{1+|H_{TR}^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{R\left(b\right)}}{1+|H_{T\xi }^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{\xi \left(a\right)}}\right)\right),\hfill \\ \hfill & {\mathbb{C}}_{\left(b\right),B}=\frac{\Delta f}{k}\sum _{k=0}^{K-1}\left(log\left(\frac{1+|H_{TR}^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{R\left(b\right)}}{1+|H_{T\xi }^{\left(k\right)}{|}^2{\mathsf{\Gamma }}_{\xi \left(b\right)}}\right)\right).\hfill \end{array}$$

(18)

Here, the interference of the EH signals is used as the external noise to improve the maximum achievable secrecy rate of R, and by increasing $\beta$, the secrecy capacity can be improved in all scenarios. Even though $\beta$ can reduce the capacity of $R\left(b\right)$ due to the amplification of channel estimation errors, since $\xi \left(b\right)$ also has channel correlation error in addition to the channel estimate errors, $\beta$ will improve R’s secrecy capacity.

2.2. Iterative Block Decision Feedback Equalization Receiver

In this system model, it is assumed that both R and $\xi$ employ IB-DFE to improve the accuracy of the information estimate as proposed in [18]. The IB-DFE based estimate for $X_I^{\left(k\right)}$ at R is given as:

$$\begin{array}{cc}\hfill & {\tilde{X}}_I^{(j,k)}=Y_I^{\left(k\right)}{F}^{(j,k)}-{\tilde{X}}_I^{(j-1,k)}{B}^{(j,k)},\hfill \end{array}$$

(19)

where $j=0,1,\dots ,J$, j is the number of iterations followed in the IB-DFE receiver, ${\tilde{X}}_I^{(j-1,k)}$ is the previous iteration value of ${\tilde{X}}_I^{(j,k)}$, and $F^{(j,k)}$ is the iteration of the feedforward coefficient, given as:

$$\begin{array}{cc}\hfill & F^{(j,k)}=\frac{{\tilde{F}}^{(j,k)}}{\frac{1}{K}{\sum }_{k=0}^{K-1}\left({\tilde{F}}^{(j,k)}{H}_{TR}^{(j,k)}\right)},\hfill \end{array}$$

(20)

where ${\tilde{F}}^{(j,k)}$ is written as:

$$\begin{array}{cc}\hfill & {\tilde{F}}^{(j,k)}=\frac{H_{TR}^{(j,k)*}}{\left(\frac{{\sigma }_N^2}{{\sigma }_{X,I}^2}\right)+{|H_{TR}^{(j,k)}|}^2\left(1-{\left({\rho }^{(j-1)}\right)}^2\right)},\hfill \end{array}$$

(21)

and the correlation factor ${\rho }^{(j-1)}=\frac{\mathbb{E}\left[{\widehat{x}}_i^{(j,n)}{x}_i^{(j,n*)}\right]}{\mathbb{E}\left[\right|{x_i^{(j,n)}}^2\left|\right]}$, where $x_i^{(j,n)}$ is time domain equivalent of $X_I^{(j,k)}$ and ${\widehat{x}}_i^{(j,n)}$ is the extrinsic information of $x_i^{(j,n)}$. Furthermore, $\{X_I^{(j,k)};k=0,1,\dots ,K-1\}=$ DFT $\{x_i^{(j,n)}{g}_n;n=0,1,\dots ,N-1\}$, and if the $n^{\mathrm{th}}$ time domain is inside the cycle prefix, then $g_n$ is either one or zero. The feedback co-efficient $B^{(j,k)}$ is written as:

$$\begin{array}{cc}\hfill & B^{(j,k)}=F^{(j,k)}\widetilde{H_{TR}^{(j,k)}}-1.\hfill \end{array}$$

(22)

In fact, the accuracy of ${\tilde{X}}_I^{(j,k)}$ increases with each iteration up to its saturation point. Similarly, the accuracy of the information estimate can be improved at R and $\xi$ for all the scenarios except $\xi \left(a\right)$. For $\xi \left(a\right)$, ${\tilde{X}}_I^{(j,k)}$ is completely distorted by EH signals.

The performance of the IB-DFE receiver can be improved at $R\left(b\right)$ with improved feedforward input in the iteration. The feedforward estimate, ${\tilde{F}}^{(j,k)}$, is derived in Equation (21), and this estimate can be improved by including the impact of $\beta {\sigma }_A^2$ in the SINR of the information signal. Therefore, by using Equation (15) in (21), we get:

$$\begin{array}{cc}\hfill & {\tilde{F}}^{(j,k)}=\frac{H_{TR}^{(j,k)*}}{\left(\frac{{\sigma }_N^2+\beta {\sigma }_A^2}{{\sigma }_{X,I}^2}\right)+{|H_{TR}^{(j,k)}|}^2\left(1-{\left({\rho }^{(j-1)}\right)}^2\right)}.\hfill \end{array}$$

(23)

Here, unlike the eavesdropper, $R\left(b\right)$ can take advantage of the available knowledge from the legitimate transmitter and improve the performance of $R\left(b\right)$; therefore, $R\left(b\right)$ with the improved feedback estimate can perform better than $\xi$.

3. Numerical Results

In this section, the BER performance of the legitimate user and eavesdropper in the system model is analyzed by using Monte Carlo simulations. The signal used the 2.4 GHz frequency band, $T=4\times {10}^{-6}$, and it was considered that all the communication nodes including the eavesdroppers were operating in the non-line-of-sight channel condition. The secrecy rate was another performance metric of the legitimate user in the presence of the eavesdropper at various conditions and was analyzed through simulations. In the following simulations, the system adopted the 4-QAM signal with $K=256$ and $L=200$, and the IB-DFE receiver was used in R and $\xi$ to improve their error rate performance. The channel estimate errors of the ${\mathbf{H}}_{E1R}$ and ${\mathbf{H}}_{E2R}$ links, i.e., ${ϵ}_{E1R}$ and ${ϵ}_{E2R}$, respectively were assumed to be equal, i.e., ${ϵ}_{E1R}={ϵ}_{E2R}$, and ${ϵ}_{E1R}$ was either $0.02$ or $0.1$. We assumed that, under an exceptionally favorable circumstance, ${\rho }_{E1}={\rho }_{E2}=0.99$ and $0.98$; this allowed $\xi \left(b\right)$ and $\xi \left(c\right)$ to perform better than $\xi \left(a\right)$. In the following figures, the BER performance results by default illustrate the fourth iteration of the IB-DFE decoder unless it is specified as zero-forcing (ZF) decoding.

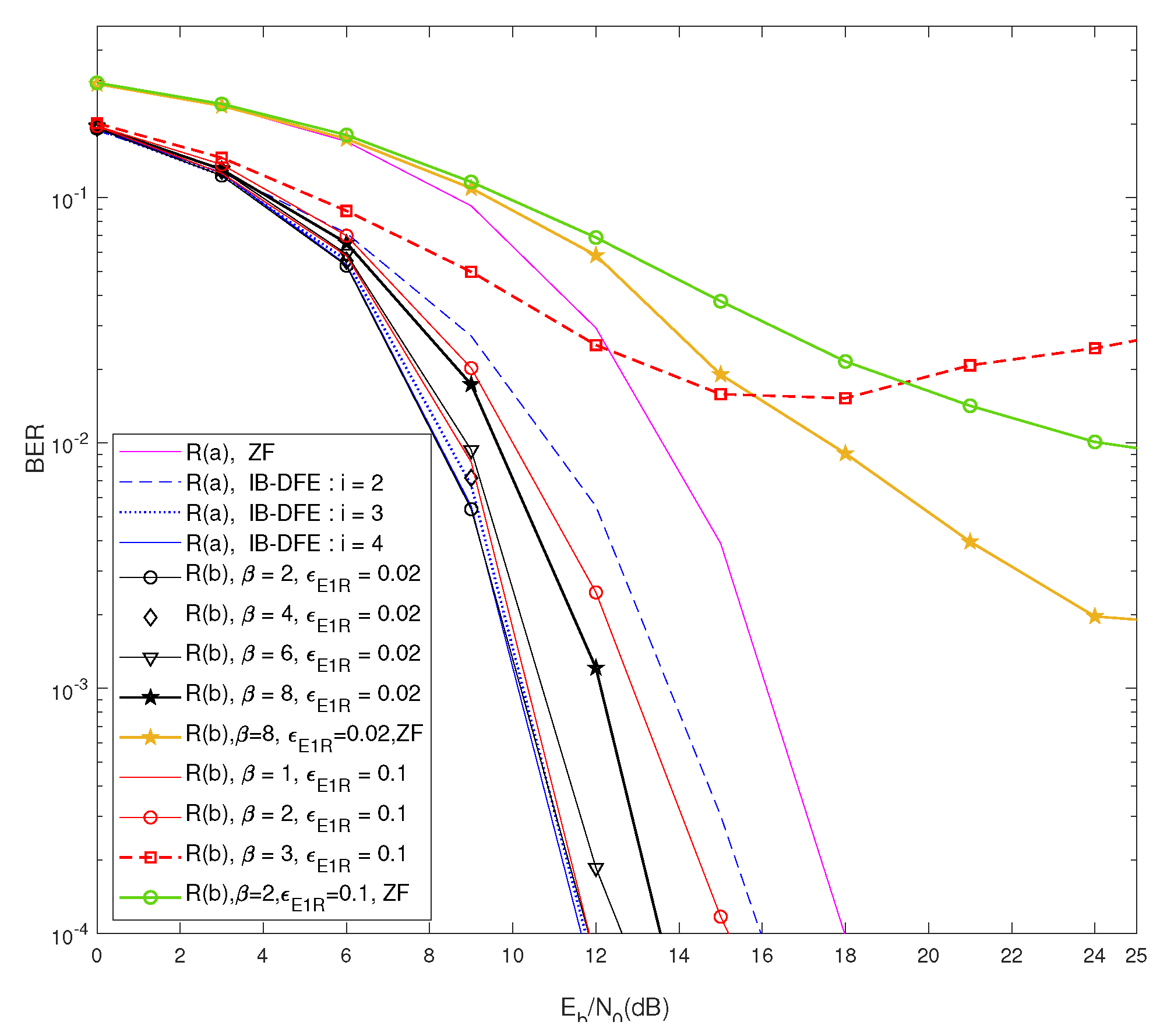
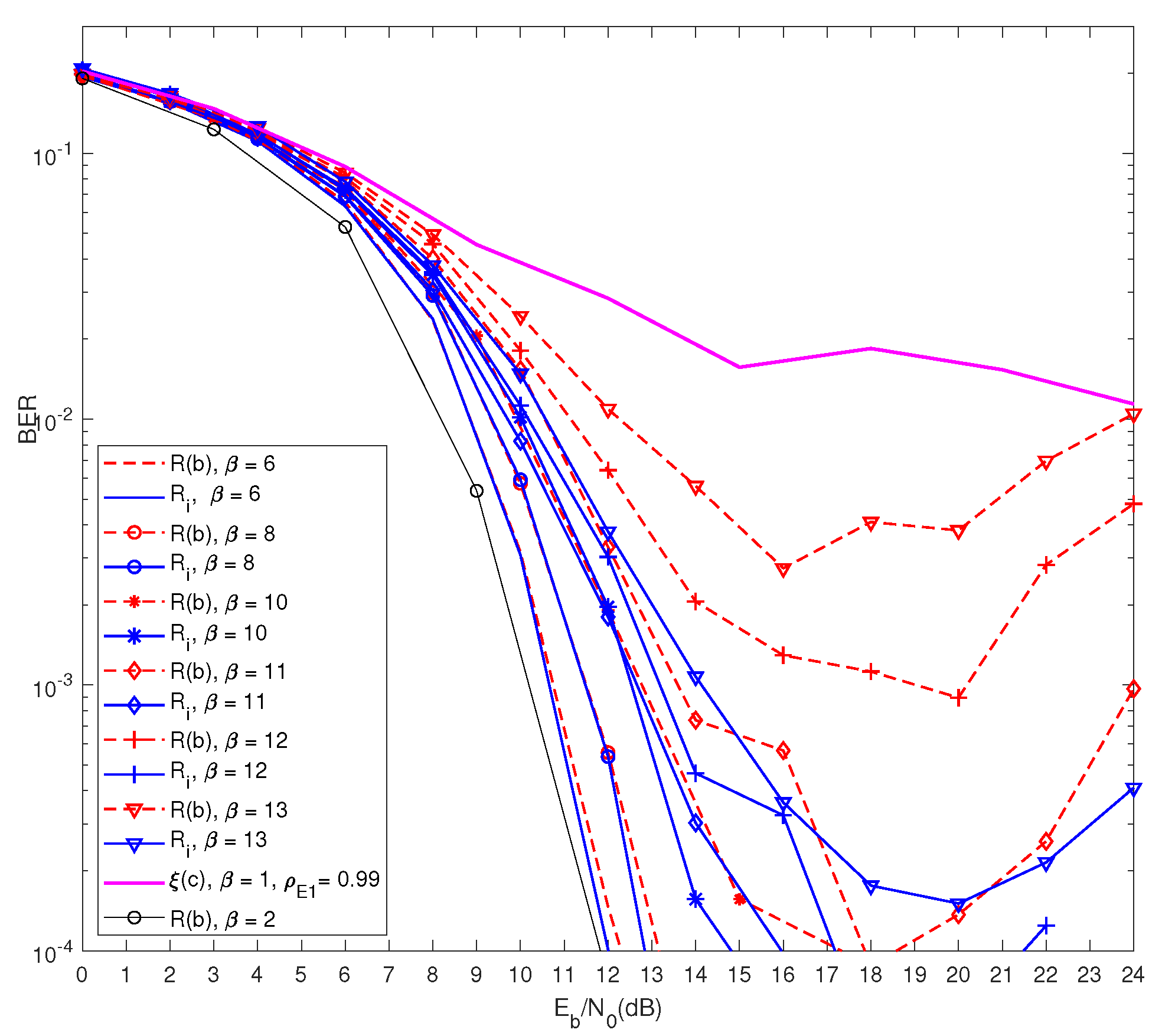
Figure 3 demonstrates the BER performance of $R\left(a\right)$ and $R\left(b\right)$. We see that the BER performance of $R\left(a\right)$ did not vary with the change in $\beta$, due to the successful channel precoding, which was based on the complete CSI of the EH signals, i.e., jamming signals. Furthermore, the results of $R\left(a\right)$ demonstrated that the performance of IB-DFE receiver and BER improved up to the fourth iteration. In the first iteration, without any feedforward and feedback values, the resultant BER of the first iteration was equal to the ZF decoding. For $R\left(b\right)$, the channel precoding error occurred due to ${ϵ}_{E1R}$, where ${ϵ}_{E1R}=0.02$ and $0.1$, and the results demonstrated that due to the precoding error at the transmitter, the BER performance of $R\left(b\right)$ was poorer as compared to $R\left(a\right)$. When ${ϵ}_{E1R}=0.2$, up to $\beta =4$, the performance of $R\left(b\right)$ was equivalent to that of $R\left(a\right)$, whereas for $\beta >4$, the performance of $R\left(b\right)$ degraded with the increase in $\beta$. The precoding error increased proportionally with the increase in ${ϵ}_{E1R}$, and $\beta$ acted as a multiplication factor in increasing the precoding error.

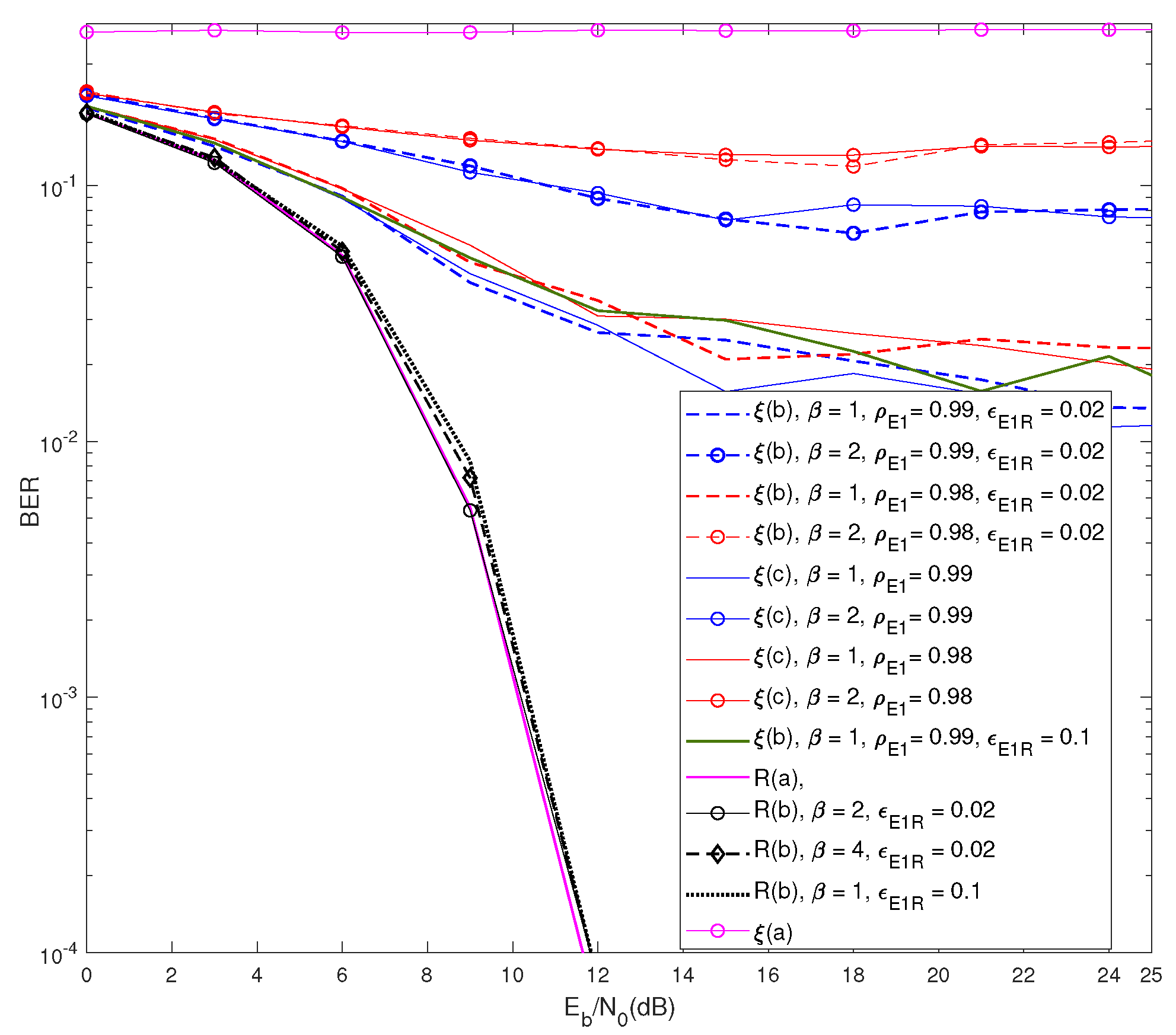
Figure 4 demonstrates the BER performance of $\xi$ in all the scenarios with the comparison to BER of R, and $\xi \left(a\right)$ received an incompatible signal for decoding the information. Unlike $\xi \left(a\right)$, with ${\rho }_{E1}={\rho }_{E2}=0.99$ and $0.98$, $\xi \left(b\right)$ and $\xi \left(c\right)$ could partially decode the signal, and their performance degraded with the decrease in ${\rho }_{E1}$ as the precoding errors increased in turn. Due to high channel correlation between ${\mathbf{H}}_{E1\xi }$ and ${\mathbf{H}}_{E1R}$ and similarly between ${\mathbf{H}}_{E1\xi }$ and ${\mathbf{H}}_{E1R}$, the jamming EH signals were partially canceled out in $\xi \left(b\right)$ and $\xi \left(c\right)$, allowing them to perform better than $\xi \left(a\right)$. With ${ϵ}_{E1R}=0.02$, $\xi \left(b\right)$ performed slightly more poorly as compared to $\xi \left(c\right)$. Even though $\xi \left(b\right)$ and $\xi \left(c\right)$ could decode information in the high channel correlation condition, the BER results of R demonstrated that, by increasing $\beta$, the jamming signals could degrade the performance of $\xi$, while R suffered a negligible loss.

Figure 5 demonstrates the impact of the inclusion of $\beta {\sigma }_A^2$ in the IB-DFE receiver, and the results validated the advantage of using (23) over (21) in the iterative loop. $R_i$ had significant SINR gain over $R\left(b\right)$ with the increase in $\beta$. At $\beta =10$, $R_i$ had $0.5$ dBm SINR gain over $R\left(b\right)$, and when $\beta >12$, $R_i$ had more than 6 dBm SINR gain over $R\left(b\right)$. The results also illustrated the BER difference between the best performance of $\xi \left(c\right)$, i.e., $\xi \left(c\right)$ with $\beta =1$ and ${\rho }_{E1}={\rho }_{E2}=0.99$ versus the performance of $R_i$ with $\beta =13$.

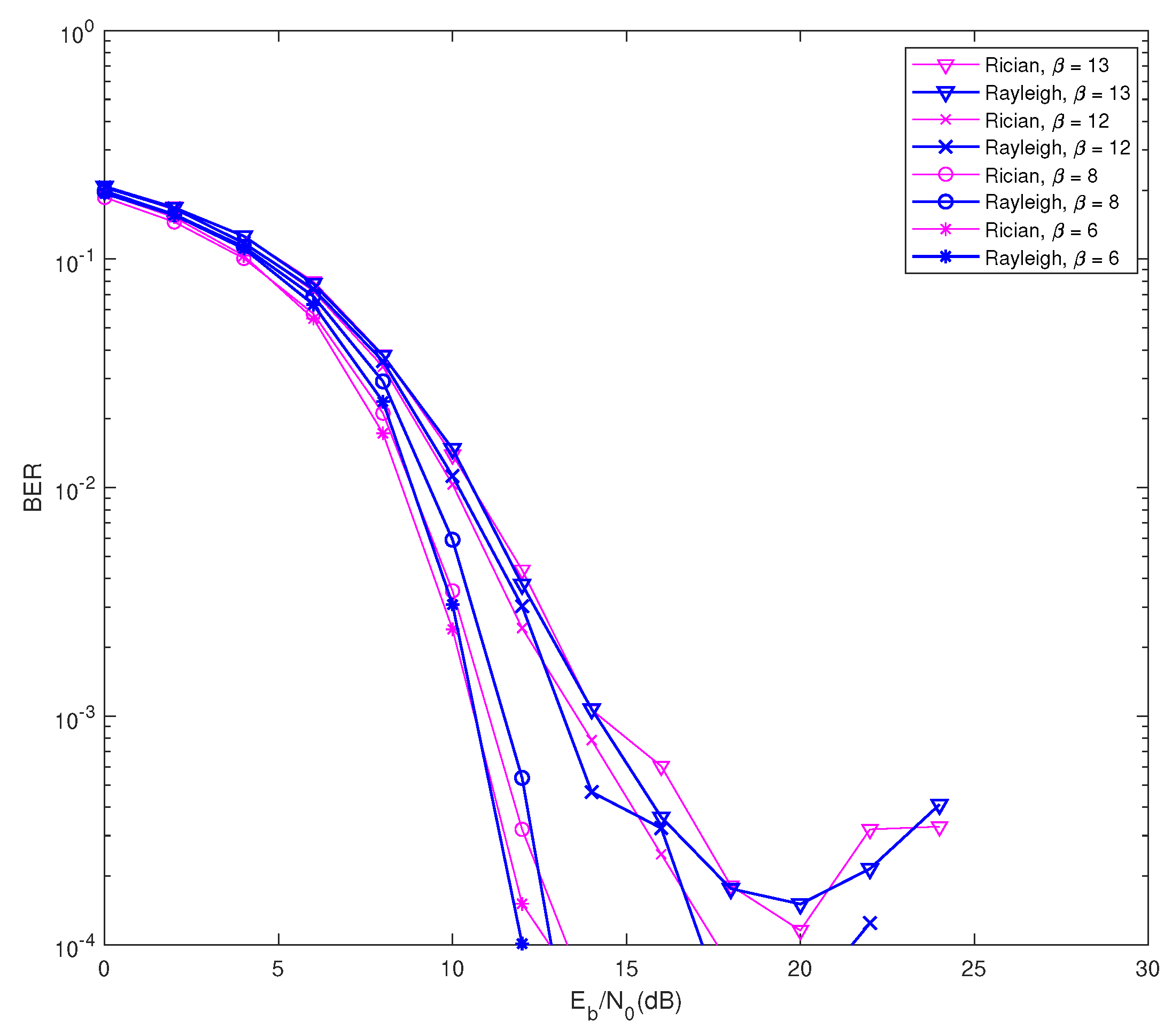
In Figure 6, we compare the BER performance of $R_i$ in Rician fading and Rayleigh frequency flat fading channel conditions. For the simulation of Rician fading, we set $T=4\times {10}^{-6}$ for 256 symbols; the multipath gain range was $0:-3:-45$; the Doppler shift was 50; and the kfactor was 10. The results of Figure 6 demonstrate that the BER performance of $R_i$ under both fading conditions had similar effects on the signal performance. The fading effects were relatively low due to the application of SC-FDMA, and the BER performance improved with the IB-DFE receiver.

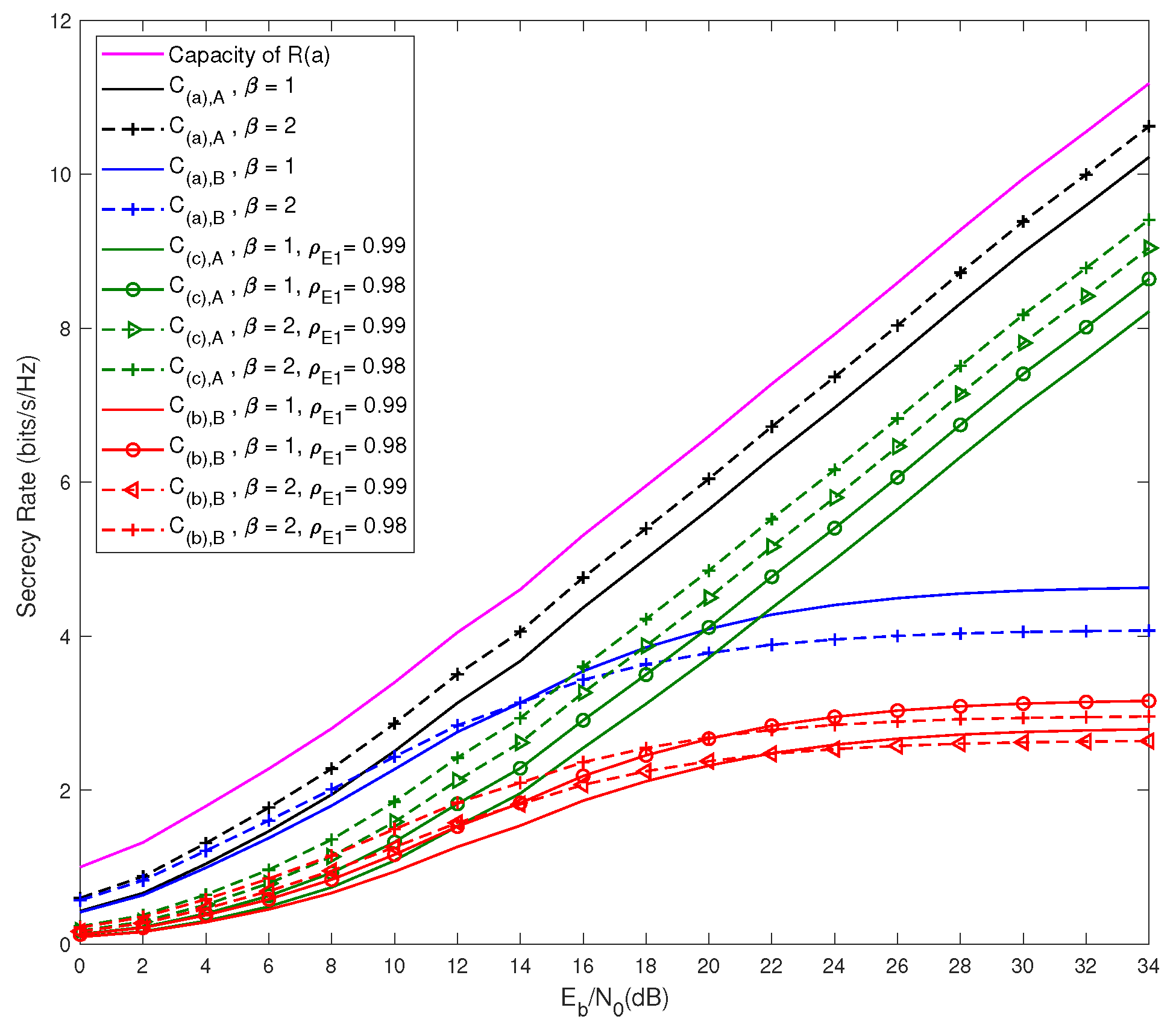
Figure 7 demonstrates the secrecy rate of $R\left(a\right)$ and $R\left(b\right)$ based on (17) and (18), respectively. Since $\xi \left(a\right)$ was always in the negative SINR region, ${\mathbb{C}}_{\left(a\right),A}$ had the best performance over ${\mathbb{C}}_{\left(c\right),A}$, ${\mathbb{C}}_{\left(a\right),B}$ and ${\mathbb{C}}_{\left(b\right),B}$. For any given $\beta$ value, ${\mathbb{C}}_{\left(c\right),A}$ always performed better than ${\mathbb{C}}_{\left(b\right),B}$ because in ${\mathbb{C}}_{\left(c\right),A}$, neither $\xi \left(c\right)$ nor $R\left(a\right)$ experienced channel estimation error. The performance of ${\mathbb{C}}_{\left(a\right),B}$ and ${\mathbb{C}}_{\left(b\right),B}$ did not improve when the SINR was greater than 20 dBm because $R\left(b\right)$ experienced precoding error due to the channel estimate error of the EH signals, which was ${ϵ}_{E1R}=0.02$, and it was independent of the SINR of the information signal as observed in (15) and (16). The results of ${\mathbb{C}}_{\left(c\right),A}$ and ${\mathbb{C}}_{\left(a\right),B}$ proved that, at high SINR (i.e., greater than 20 dBm), ${\mathbb{C}}_{\left(c\right),A}$ could perform better than ${\mathbb{C}}_{\left(a\right),B}$, irrespective of $\xi$’s condition. At low SINR (i.e., less than 20 dBm), the performance of ${\mathbb{C}}_{\left(a\right),B}$ as compared to ${\mathbb{C}}_{\left(c\right),A}$ was better because $R\left(b\right)$ took advantage of $\xi \left(a\right)$’s poor performance, and this characteristic validated (15) and (16). Similar to the BER results, the secrecy rate performance of ${\mathbb{C}}_{\left(c\right),A}$ and ${\mathbb{C}}_{\left(b\right),B}$ was better when ${\rho }_{E1}=0.98$ than their performance when ${\rho }_{E1}=0.99$. The secrecy rate of $R\left(a\right)$ improved with the increase in $\beta$, but in the case of $R\left(b\right)$, contrary to the BER results, the secrecy rate degraded with the increase in $\beta$ due to the channel estimate error. Unlike the secrecy rate results of $R\left(b\right)$, the impact of channel estimate error on the BER of $R\left(b\right)$ was reduced due to the implementation the IB-DFE receiver.

4. Conclusions

In this paper, we implemented the SWIPT based self jamming physical layer security model, which relied on the channel precoding method to transmit information securely to the legitimate user. We considered different case studies by assuming that the eavesdropper had high channel correlation with the legitimate user. We also considered the possibility of channel estimate error (the channel link between jamming antennas to the legitimate user), which negatively affected the channel precoding. All the study cases were analyzed with the theoretical expressions supported by the simulation results.

The BER performance of the legitimate user and eavesdropper was improved by using the IB-DFE receiver, and we concluded that the channel precoding error could be further reduced at the legitimate user by taking advantage of all the available knowledge (i.e., including the variance of channel precoding error) in the IB-DFE receiver. Thus, the legitimate user could perform better than the eavesdropper, and the performance of the legitimate user improved over the eavesdropper with the increase in the jamming signal power. The secrecy rate analysis of legitimate user demonstrated that the performance of the legitimate user with the channel precoding error did not improve beyond 20 dBm SINR and slightly degraded with the increase in jamming signal power. In the case of perfect channel precoding, the secrecy rate performance of the legitimate user improved proportionally with the increase in SINR and with the increase in the jamming signal power.