Intrinsically Distributed Probabilistic Algorithm for Human–Robot Distance Computation in Collision Avoidance Strategies
Abstract
1. Introduction
1.1. Prior Work
1.2. Aim and Organization of the Work
2. Materials and Methods
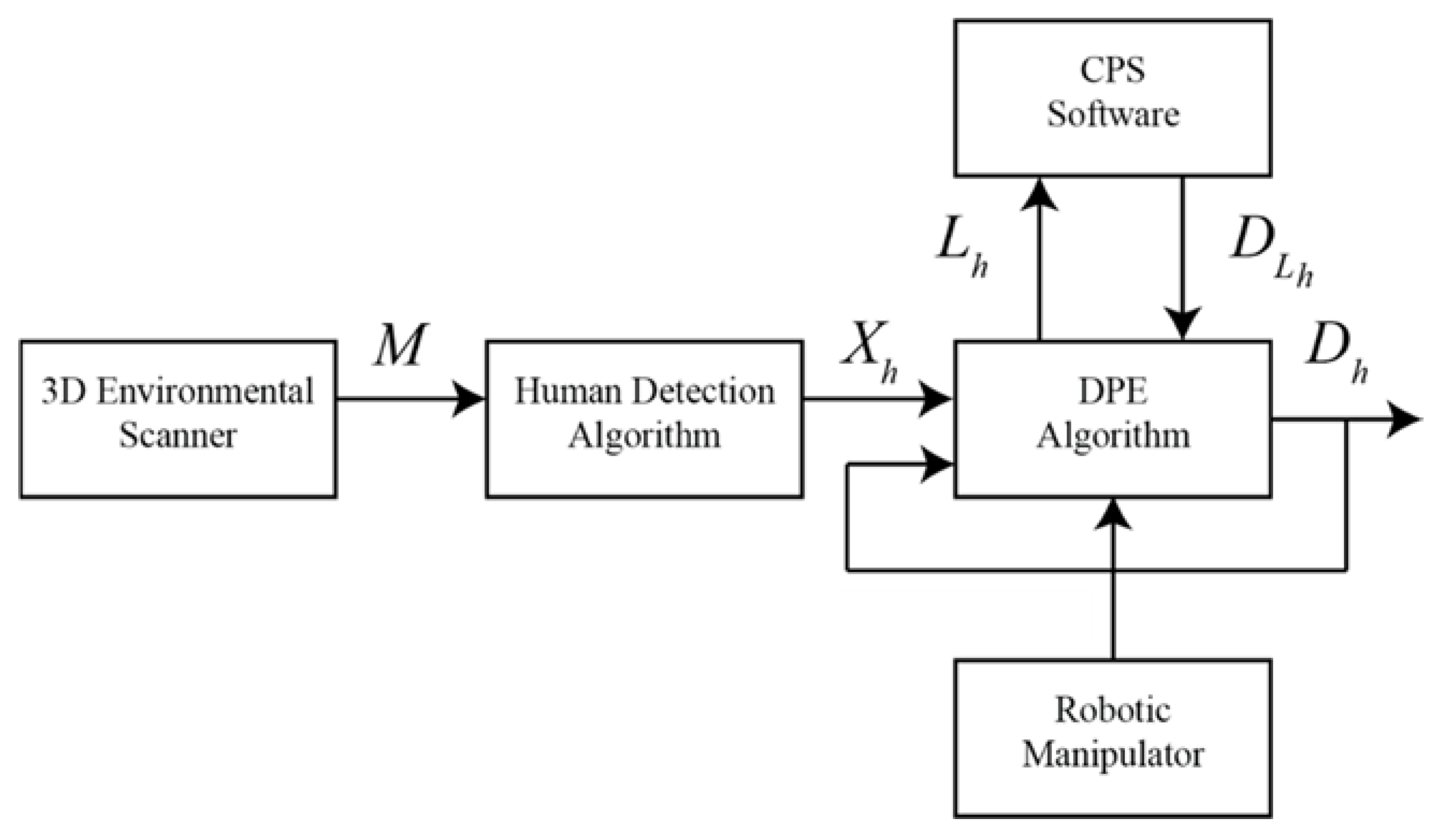
2.1. System Flowchart
2.2. Environmental Scanner and Detection of Humans
2.3. Collision and Proximity Simulator
2.4. Distance Probability Estimation Algorithm
2.5. Experimental Validation
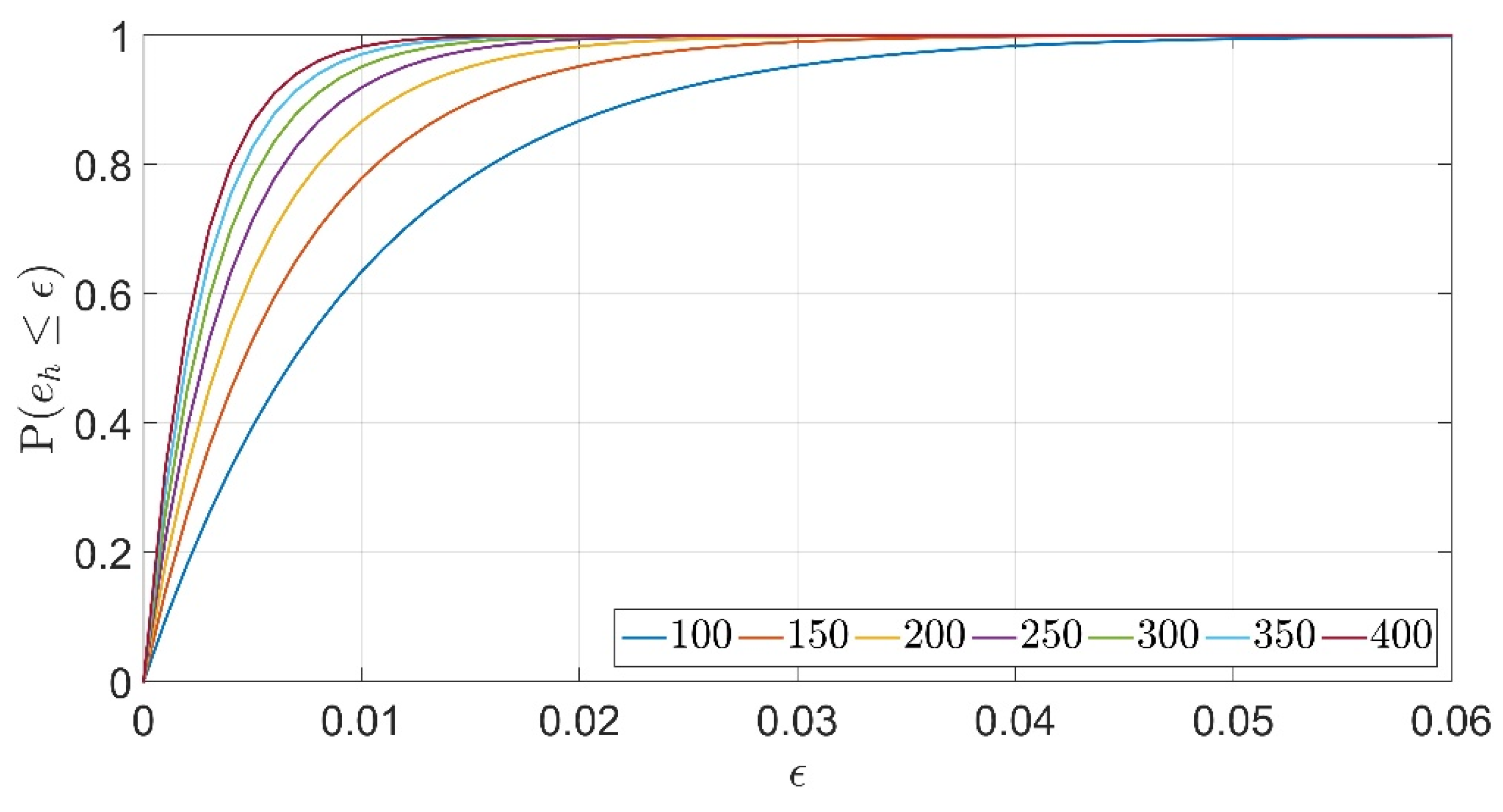
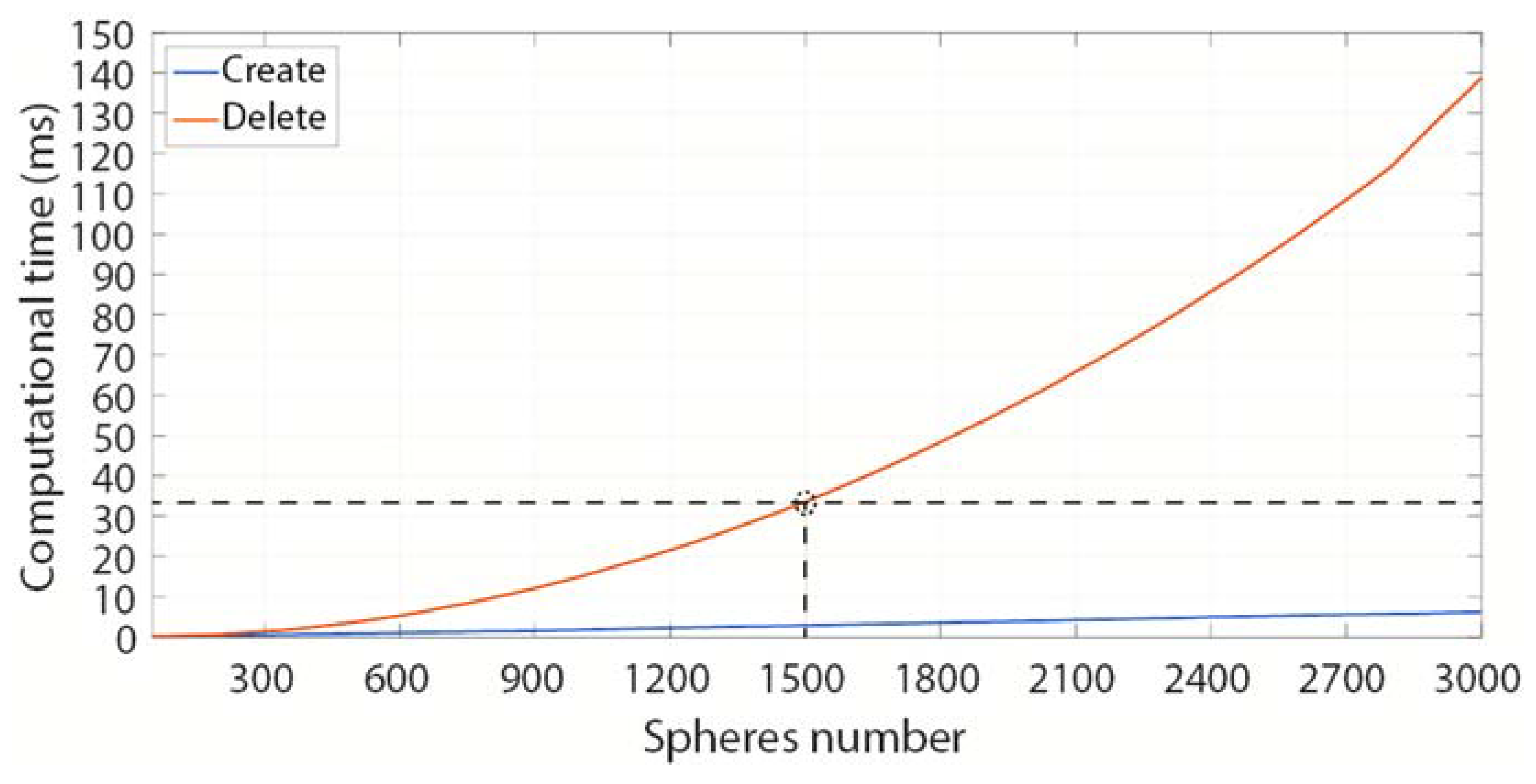
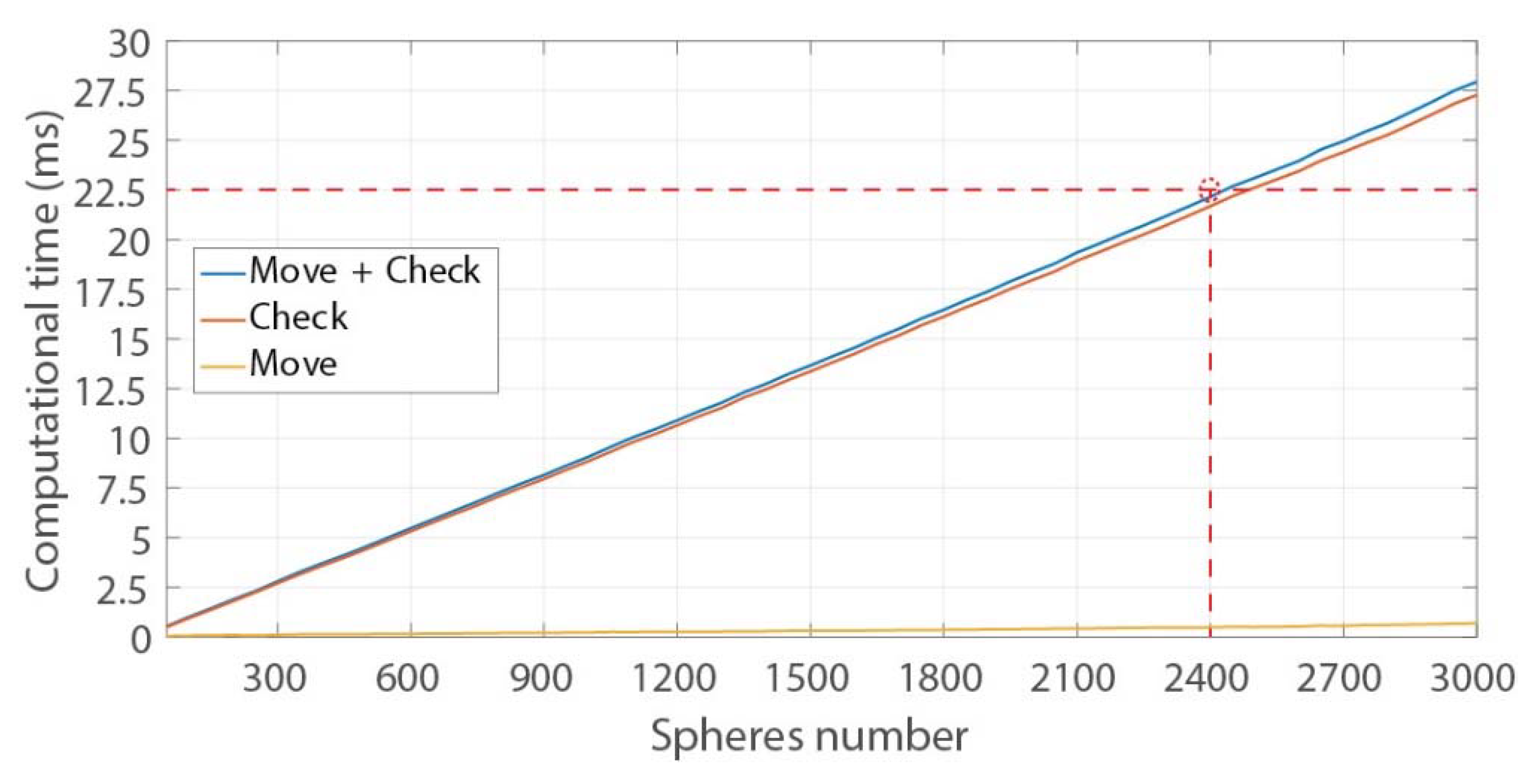
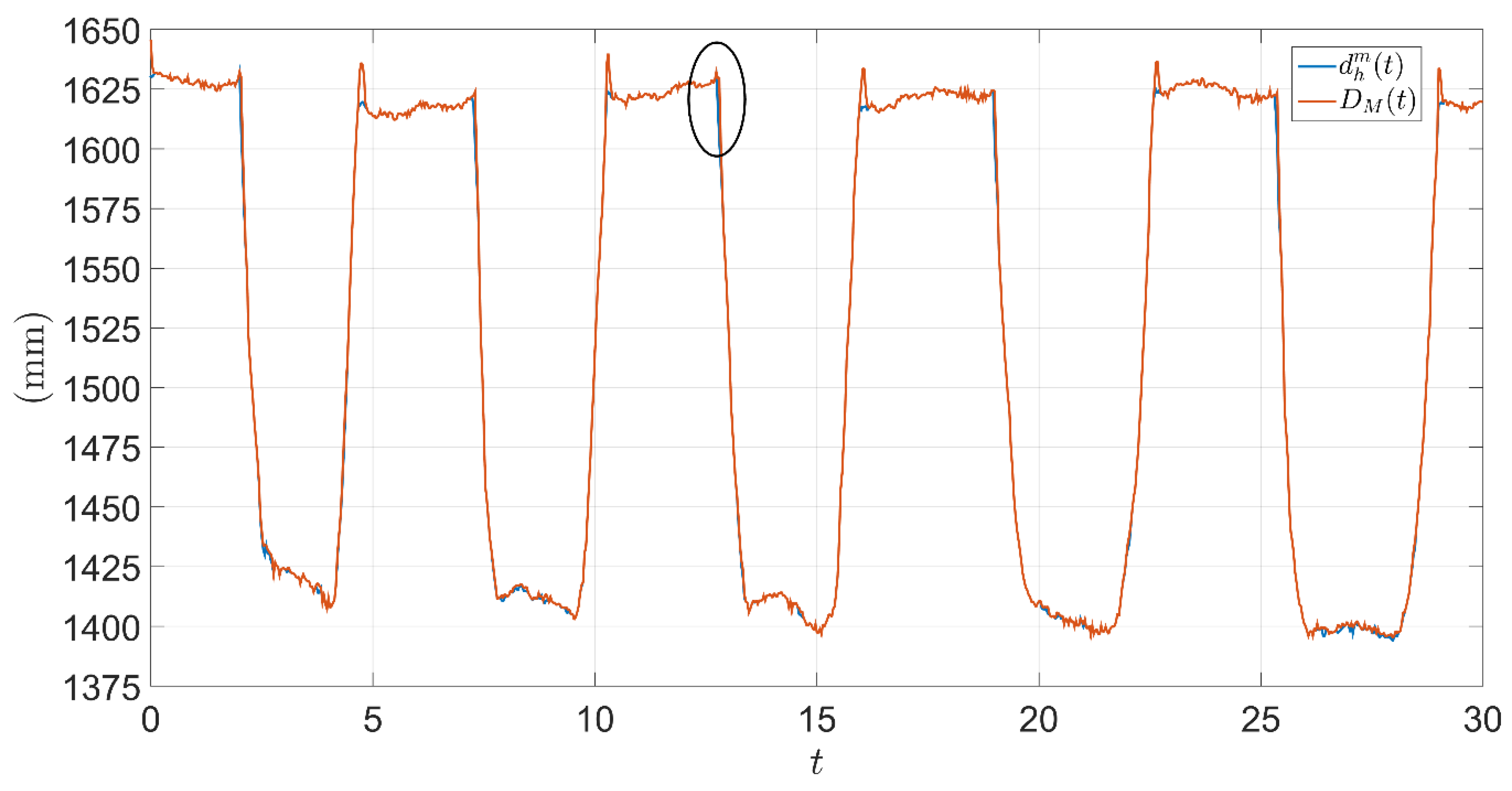
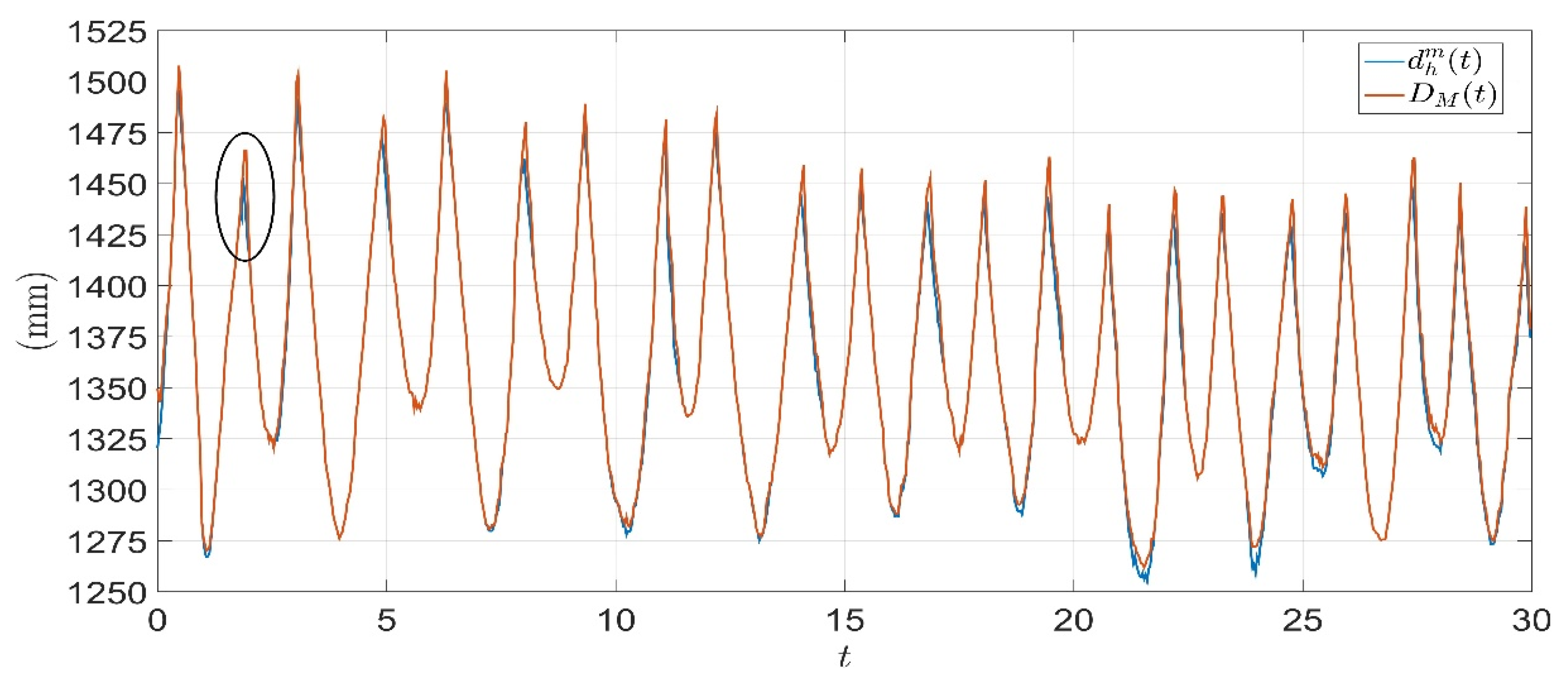
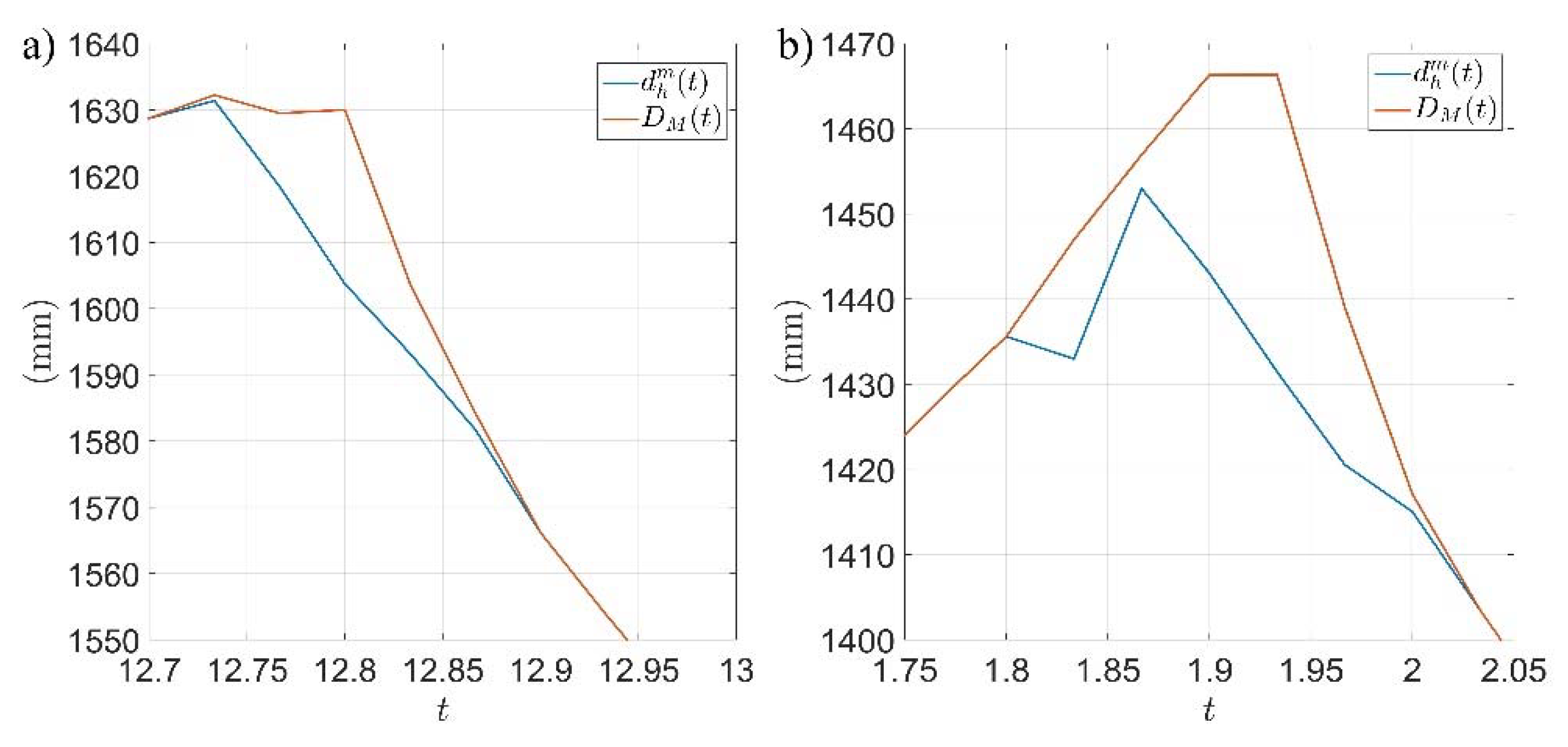
3. Results
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johannsmeier, L.; Haddadin, S. A Hierarchical Human-Robot Interaction-Planning Framework for Task Allocation in Collaborative Industrial Assembly Processes. IEEE Robot. Autom. Lett. 2016, 2, 41–48. [Google Scholar] [CrossRef]
- Diodato, A.; Cafarelli, A.; Schiappacasse, A.; Tognarelli, S.; Ciuti, G.; Menciassi, A. Motion compensation with skin contact control for high intensity focused ultrasound surgery in moving organs. Phys. Med. Boil. 2018, 63, 035017. [Google Scholar] [CrossRef] [PubMed]
- Haddadin, S.; Albu-Schaffer, A.; De Luca, A.; Hirzinger, G. Collision Detection and Reaction: A Contribution to Safe Physical Human-Robot Interaction. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3356–3363. [Google Scholar]
- Mazzocchi, T.; Diodato, A.; Ciuti, G.; De Micheli, D.M.; Menciassi, A. Smart sensorized polymeric skin for safe robot collision and environmental interaction. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 837–843. [Google Scholar]
- O’Neill, J.; Lu, J.; Dockter, R.; Kowalewski, T. Practical, stretchable smart skin sensors for contact-aware robots in safe and collaborative interactions. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Washington, DC, USA, 26–30 May 2015; pp. 624–629. [Google Scholar]
- Magrini, E.; De Luca, A. Hybrid force/velocity control for physical human-robot collaboration tasks. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 857–863. [Google Scholar]
- Kasaei, S.H.; Sock, J.; Lopes, L.S.; Tomé, A.M.; Kim, T.-K. Perceiving, Learning, and Recognizing 3D Objects: An Approach to Cognitive Service Robots. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Ragaglia, M.; Bascetta, L.; Rocco, P. Detecting, tracking and predicting human motion inside an industrial robotic cell using a map-based particle filtering strategy. In Proceedings of the 2015 International Conference on Advanced Robotics (ICAR), Washington, DC, USA, 26–30 May 2015; pp. 369–374. [Google Scholar]
- Morato, C.; Kaipa, K.N.; Zhao, B.; Gupta, S.K. Toward Safe Human Robot Collaboration by Using Multiple Kinects Based Real-Time Human Tracking. J. Comput. Inf. Sci. Eng. 2014, 14, 011006. [Google Scholar] [CrossRef]
- Kulic, D.; Croft, E. Safe planning for human-robot interaction. J. Robot. Syst. 2005, 22, 383–396. [Google Scholar] [CrossRef]
- Safeea, M.; Mendes, N.; Neto, P. Minimum Distance Calculation for Safe Human Robot Interaction. Procedia Manuf. 2017, 11, 99–106. [Google Scholar] [CrossRef]
- Phan, A.; Ferrie, F.P. Towards 3D human posture estimation using multiple kinects despite self-contacts. In Proceedings of the 2015 14th IAPR International Conference on Machine Vision Applications (MVA), Miraikan, Tokyo, Japan, 18–22 May 2015; pp. 567–571. [Google Scholar]
- Cefalo, M.; Magrini, E.; Oriolo, G. Parallel collision check for sensor based real-time motion planning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1936–1943. [Google Scholar]
- Dell’Acqua, F.; Fisher, R. Reconstruction of planar surfaces behind occlusions in range images. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 569–575. [Google Scholar] [CrossRef]
- Fabrizio, F.; De Luca, A. Real-Time Computation of Distance to Dynamic Obstacles with Multiple Depth Sensors. IEEE Robot. Autom. Lett. 2016, 2, 56–63. [Google Scholar] [CrossRef]
- Flacco, F.; Kröger, T.; De Luca, A.; Khatib, O. A depth space approach to human-robot collision avoidance. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 338–345. [Google Scholar]
- Yang, L.; Zhang, L.; Dong, H.; Alelaiwi, A.; El Saddik, A. Evaluating and Improving the Depth Accuracy of Kinect for Windows v2. IEEE Sens. J. 2015, 15, 1. [Google Scholar] [CrossRef]
- Cosgun, A.; Bunger, M.; Christensen, H.I. Accuracy analysis of skeleton trackers for safety in HRI. In Proceedings of the Workshop on Safety and Comfort of Humanoid Coworker and Assistant (HUMANOIDS), Atlanta, GA, USA, 15 October 2013; pp. 15–17. [Google Scholar]
- Boeing, A.; Braunl, T. Evaluation of real-time physics simulation systems. In Proceedings of the 5th International Conference on Technological Ecosystems for Enhancing Multiculturality–TEEM 2017, Cádiz, Spain, 18–20 October 2007; p. 281. [Google Scholar]
- Ong, C.J.; Gilbert, E. Fast versions of the Gilbert-Johnson-Keerthi distance algorithm: Additional results and comparisons. IEEE Trans. Robot. Autom. 2001, 17, 531–539. [Google Scholar]
- Corke, P. A Simple and Systematic Approach to Assigning Denavit–Hartenberg Parameters. IEEE Trans. Robot. 2007, 23, 590–594. [Google Scholar] [CrossRef]
- Xia, J.; Jiang, Z.; Liu, H.; Cai, H.; Wu, G. A Novel Hybrid Safety-Control Strategy for a Manipulator. Int. J. Adv. Robot. Syst. 2014, 11, 58. [Google Scholar] [CrossRef]



| References | Hardware | Shape for Human Reconstruction | Computational Time (ms) | Mean Distance Error (mm)* |
|---|---|---|---|---|
| Ragaglia et al. [8] | Multiple cameras | Rectangular | 880–2720 | N/A |
| Morato et al. [9] | Multiple cameras | Spherical | N/A | 10 |
| Kulic et al. [10] | None | Spherical | N/A | N/A |
| Safeea et al. [11] | Single camera | Cylindrical | N/A | N/A |
| Phan et al. [12] | Multiple cameras | Spherical (geodesic distance) | 600 | 149 |
| Cefalo et al. [13] | Single camera | None | 20 | 300 |
| Fisher et al. [14] | Multiple cameras | None | 80 (increasing with number of layers) | N/A |
| Flacco et al. [16] | Multiple cameras | Spherical | 3.3 | 40 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiurazzi, M.; Diodato, A.; Vetrò, I.; Ortega Alcaide, J.; Menciassi, A.; Ciuti, G. Intrinsically Distributed Probabilistic Algorithm for Human–Robot Distance Computation in Collision Avoidance Strategies. Electronics 2020, 9, 548. https://doi.org/10.3390/electronics9040548
Chiurazzi M, Diodato A, Vetrò I, Ortega Alcaide J, Menciassi A, Ciuti G. Intrinsically Distributed Probabilistic Algorithm for Human–Robot Distance Computation in Collision Avoidance Strategies. Electronics. 2020; 9(4):548. https://doi.org/10.3390/electronics9040548
Chicago/Turabian StyleChiurazzi, Marcello, Alessandro Diodato, Irene Vetrò, Joan Ortega Alcaide, Arianna Menciassi, and Gastone Ciuti. 2020. "Intrinsically Distributed Probabilistic Algorithm for Human–Robot Distance Computation in Collision Avoidance Strategies" Electronics 9, no. 4: 548. https://doi.org/10.3390/electronics9040548
APA StyleChiurazzi, M., Diodato, A., Vetrò, I., Ortega Alcaide, J., Menciassi, A., & Ciuti, G. (2020). Intrinsically Distributed Probabilistic Algorithm for Human–Robot Distance Computation in Collision Avoidance Strategies. Electronics, 9(4), 548. https://doi.org/10.3390/electronics9040548









