1. Introduction
Object detection is an important and challenging field in computer vision, one which has been the subject of extensive research [
1]. The goal of object detection is to detect all objects and class the objects. It has been widely used in autonomous driving [
2], pedestrian detection [
3], medical imaging [
4], industrial detection [
5], robot vision [
6], intelligent video surveillance [
7], remote sensing images [
8], etc.
In recent years, deep learning techniques have been applied in object detection [
9]. Deep learning uses low-level features to form more abstractive high-level features, and to hierarchically represent the data in order to improve object detection [
10]. Compared with traditional detection algorithms, the deep learning-based object detection method based has better performance in terms of robustness, accuracy and speed for multi-classification tasks.
Object detection methods based on deep learning mainly include region proposal-based methods, and those based on a unified pipeline framework. The former type of method firstly generates a series of region proposals from an input image, and then uses a convolution neural network to extract features from the generated regions and construct a classifier for object classes. The region-based convolution neural network (R-CNN) method [
11] is the earlier method used to introduce convolution neural networks into the field of object detection. It uses the selection search method to generate region proposals from the input images, and uses a convolution neural network to extract features from the generated region proposals. The extracted features are used to train the support vector machine. Based on the R-CNN method, Fast R-CNN [
12] and Faster R-CNN [
13] were also proposed to reduce training time and improve the mean average precision. Although region proposal-based methods have higher detection accuracy, the structure of the method is complex, and object detection is time-consuming. The latter type of method (based on a unified pipeline framework) directly predicts location information and class probabilities of objects with a single-feed forward convolution neural network from the whole image, and does not require the generation of region proposals and post-classification. Therefore, the structure of the unified pipeline framework approach is simple and can detect objects quickly; however, it is less accurate than the region proposal-based approach. The two kinds of methods have different advantages and are suitable for different applications. In this paper, we mainly discuss the unified pipeline framework-based approach.
Researchers have proposed a wide range of unified pipeline framework-based methods in recent years, one of which is the You Only Look Once v2 (YOLOv2) method [
14]. YOLOv2 uses batch normalization to improve convergence and prevent overfitting, and anchor boxes to predict bounding boxes, in order to increase the recall. Other innovations include a high-resolution classifier, direct location prediction, dimension cluster, and multi-scale training, all of which lend greater detection accuracy. Pedoeem and Huang recently proposed a shallow real-time detection method for Non-GPU computers based on the YOLOv2 method [
15]; their method reduces the size of input image by half in order to speed up the detection speed, and removes the batch normalization of shallow layers in order to reduce the amount of model parameters. Shafiee et al. have proposed the Fast YOLO method, whereby YOLOv2 can be applied to embedded devices [
16]: this employs an evolutionary deep intelligence framework to generate an optimized network architecture. The optimized network architecture can be used in the motion-adaption inference framework to speed up the detection process and thus reduce the energy consumption of the embedded device. Simon et al. have developed a complex-YOLO method [
17], which uses a specific complex regression strategy to estimate multi-class 3D boxes in Cartesian space for detecting RGB images; the authors report a significant improvement in the speed of 3D object detection. Liu et al. have developed the Single Shot MultiBox Detector (SSD) method [
18], which generates multi-scale feature maps in order to detect objects of different sizes. This method strikes a careful balance between speed and accuracy of detection, but the expression ability of the feature map is insufficient in the shallow layer. In order to enhance the expression ability of shallow feature maps, Fu et al. have proposed the Deconvolutional Single Shot Detector (DSSD) method [
19], which uses the ResNet extraction network (generating better features) [
20], a deconvolution layer and skip connection in order to improve the expression ability of shallow feature maps. In order to improve the detection accuracy of the SSD method for small objects, Qin et al. have proposed a new SSD method based on the feature pyramid [
21]. Their method applies a deconvolution network in the high-level of the feature pyramid in order to extract semantic information, and expands the convolution network so as to learn low-level position information. Their method constructs a multi-scale detection structure so as to improve the detection accuracy of small objects. Redmon and Farhadi have proposed applying the YOLOv3 method for using binary cross-entropy loss for class predictions [
22], which employs scale prediction to predict boxes at different scales, and thus improves the detection accuracy with regard to small objects.
In this
Section 1, we have reviewed recent developments related to object detection. In
Section 2, we outline the concepts and processes of the YOLOv3 object detection method, and in
Section 3 we describe our proposed method. In
Section 4, we illustrate and discuss our simulation results.
2. YOLOv3
The YOLOv3 method considers object detection as a regression problem. It directly predicts class probabilities and bounding box offsets from full images with a single feed forward convolution neural network. It completely eliminates region proposal generation and feature resampling, and encapsulates all stages in a single network in order to form a true end-to-end detection system.
The YOLOv3 method divides the input image into
small grid cells. If the center of an object falls into a grid cell, the grid cell is responsible for detecting the object. Each grid cell predicts the position information of
bounding boxes and computes the objectness scores corresponding to these bounding boxes. Each objectness score can be obtained as follows:
whereby
is the objectness score of the
th bounding box in the
th grid cell.
is merely a function of the object. The
represents the intersection over union (IOU) between the predicted box and ground truth box. The YOLOv3 method uses binary cross-entropy of predicted objectness scores and truth objectness scores as one part of loss function. It can be expressed as follows:
whereby
is the number of grid cells of the image, and
is the number of bounding boxes. The
and
are the predicted abjectness score and truth abjectness score, respectively.
The position of each bounding box is based on four predictions:
,
, on the assumption that
is the offset of the grid cell from the top left corner of the image. The center position of final predicted bounding boxes is offset from the top left corner of the image by
. Those are computed as follows:
whereby
is a sigmoid function. The width and height of the predicted bounding box are calculated thus:
whereby
,
are the width and height of the bounding box prior. They are obtained by dimensional clustering.
The ground truth box consists of four parameters (
,
,
and
), which correspond to the predicted parameters
,
,
and
, respectively. Based on (3) and (4), the truth values of
,
,
and
can be obtained as follows:
The YOLOv3 method uses the square error of coordinate prediction as one part of loss function. It can be expressed as follows:
3. Proposed Method
Before developing the YOLOv3 model, it is necessary to determine the width and height of bounding box priors (
and
in (4) and (5), respectively), as they directly affect the performance of the YOLOv3 method. In the YOLOv3 method, it uses k-means clustering algorithm to select the representative width and height of bounding box priors to avoid consuming much time in adjusting the width and height. The complexity of k-means clustering method is expressed as
for the data based on
dimension and
cluster centers, whereby
is the number of data. The larger the dataset, the more time-consuming the modelling process. In addition, the YOLOv3 method is sensitive to the initial cluster center. To overcome this problem, we apply the AFK-MC
2 method [
23] in order to estimate the width and height of bounding box priors.
For the purpose of convenience, we suppose that the width and height of ground truth boxes are
. Firstly, we randomly select a couple of width and height values
as one initial cluster center
from the set
. To obtain the other
initial cluster centers, we repeat the following procedure for
times in order to build
Markov chains with length
. The procedure begins by computing all proposal distributions, or
. Each
is calculated as follows:
whereby
,
,
is the first initial cluster center. The AFK-MC
2 method directly uses the Euclidean distance to compute the distance between two parameters. In this paper, we use the intersection over union method to compute distance. This is expressed as:
whereby
is the intersection over union betwee j-th bounding boxes
and the first initial cluster center
. It is used to measure the overlap between
and
. If the
is larger, it means that there are more overlaps between
and
.
is distance from
to the initial cluster center
.
Secondly, we randomly select a couple of width and height values
as an initial point of the Markov chain. For the other points in the same Markov chain, we select a candidate
from set
based on proposal distribution
from set
, and compute the sampling probability
as follows:
whereby
is the set of selected cluster centers,
is minimum value of
. We compute the distance from candidate
cluster center in set
using equation (8), and select the minimum value as
. Based on the sampling probability and proposal distribution of
, we can compute the acceptance probability that
can be accepted as the next point in the Markov chain. This can be expressed as follows:
whereby
is the current point in the Markov chain. If the acceptance probability
is greater than the threshold
, then
can be accepted as the next point in the Markov chain. Otherwise,
is also used as the next point in the Markov chain. Therefore, we can construct a Markov chain with length
. Based on the above procedure, we can construct
different Markov chains with length
and use the last point of every Markov chains as the initial cluster center. The obtained initial cluster centers of the Markov chains and the randomly set initial cluster center form
initial cluster centers
.
In constructing a Markov chain, each candidate point requires to calculate the distance between the candidate point and the selected cluster centers, if the selected candidate point is a point that has been selected as the cluster center, the distance between the candidate point and the selected cluster centers is 0, and the acceptance probability of the candidate point is 0. The candidate point will not be used as a point in the Markov chain. This avoids using the selected cluster center as one point of Markov chain in constructing different Markov chains. Therefore, the selected initial cluster centers are different.
Thirdly, we randomly select
points from set
to form set
, and compute the distances between the each point in the
and
cluster centers. If one point is closest to one cluster center, we assign the point to the cluster at which the cluster center is located. Therefore, we can construct
clusters using
points and
cluster centers. We use the all-points mean in every cluster as the new cluster center, i.e.,
whereby
is the new cluster center in the new cluster
,
, and is the number of points in the cluster
,
. Next, we reselect
points from set
and compute the distances between the points and
new cluster centers. We also construct the new cluster according the computed distance and use equations (11) and (12) to obtain a new cluster center. If the new cluster center is invariant, we can obtain the final cluster center. The flowchart of our proposed method is shown in
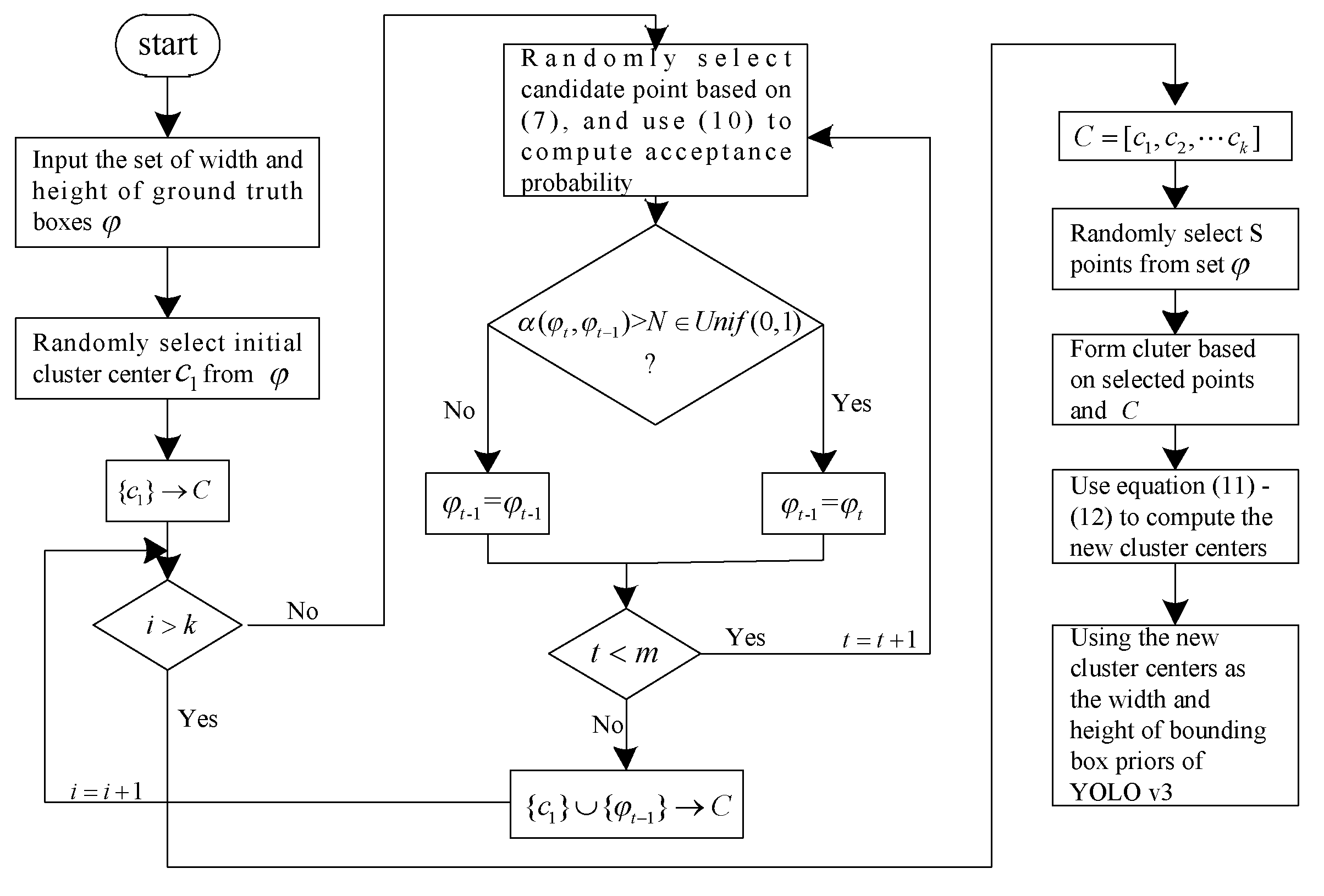
Figure 1.
The k-means method used in YOLOv3 randomly selects couples of width and height values as initial cluster centers, so the k-means method is sensitive to the initial cluster center. Secondly, it requires computing the distances between all points and cluster centers, and this will consume a large amount of time for large-scale detection dataset in adjusting cluster centers. Our proposed method only randomly selects a couple of width and height values as one initial cluster, and then selects cluster centers by constructing different Markov chains of length . Therefore, our proposed method reduces the sensitivity to the initial cluster centers. Besides, we only randomly select points instead of all points from set , and compute distance between the points and cluster centers. It requires a shorter running time compared to the k-means method, especially for large-scale detection datasets. Therefore, using the YOLOv3 method, we can use the cluster centers as the width and height of bounding box priors so as to realize object prediction.
4. Simulation and Discussion
In this paper, we used two datasets, PASCAL VOC (Pattern Analysis, Statical Modeling and Computational Learning Visual Object Classes) and MS COCO (Microsoft Common Objects in Context) [
24]. The PASCAL VOC is a standardized dataset for image classification and object detection. The images contained in the PASCAL VOC dataset are from real scenes. These objects can be divided into twenty classes. There are 9963 images in the datasets which contain 24,640 annotated objects. The MS COCO is an authoritative and important benchmark tool used in the field of object recognition and detection. It is also used in the YOLOv3 method. It contains 117,264 training images and more than 5000 testing images with 80 classes. The Ubuntu 18.04 system is used for the simulations, and the method employs an Intel Xeon E5-2678 v3 CPU. The GPU is NVIDIA GeForce GTX 1080Ti, and the deep learning framework is PyTorch. The size of each image is
. The learning rate, momentum and decay are 0.001, 0.9 and 0.0005, respectively. The number of training images is 64 per batch. Our YOLOv3 model uses three output feature maps with different scales to detect differently sized objects, and we have tested it on 3, 6, 9, 12, 15 and 18 candidate cluster centers.
We use Avg IOU (Average Intersection over Union) between the boxes that are generated by using cluster centers and all ground truth boxes in order to measure the performance of each cluster method. This can be expressed as follows:
whereby
is the number of ground truth boxes (that is,
),
is the number of cluster centers, and
is the box generated using the width and height in the cluster centers. The larger the Avg IOU value, the better the clustering effect. We also use recall, mean value of average precision (mAP), and F1-score to measure the performance of different methods. The recall is the ratio of the number of objects that are successfully detected and the number of samples that contain the detected objects. The mAP is the mean value of average precision for the detection of all classes. The F1-score is the harmonic mean of precision and recall, the maximum value is 1 and the minimum value is 0.
Below, we compare the performance of the proposed cluster method and AFK-MC
2 method in terms of estimating the initial width and height of predicting boxes. The length of the Markov chain used in simulations for two methods is 200. We have also tried to increase and decrease the length of the Markov chain. When the length is increased, the Avg IOU and running time are also increased. When the length is decreased, the Avg IOU and running time are also decreased. For simplicity, we used 200 as the length of the Markov chain that is also used in [
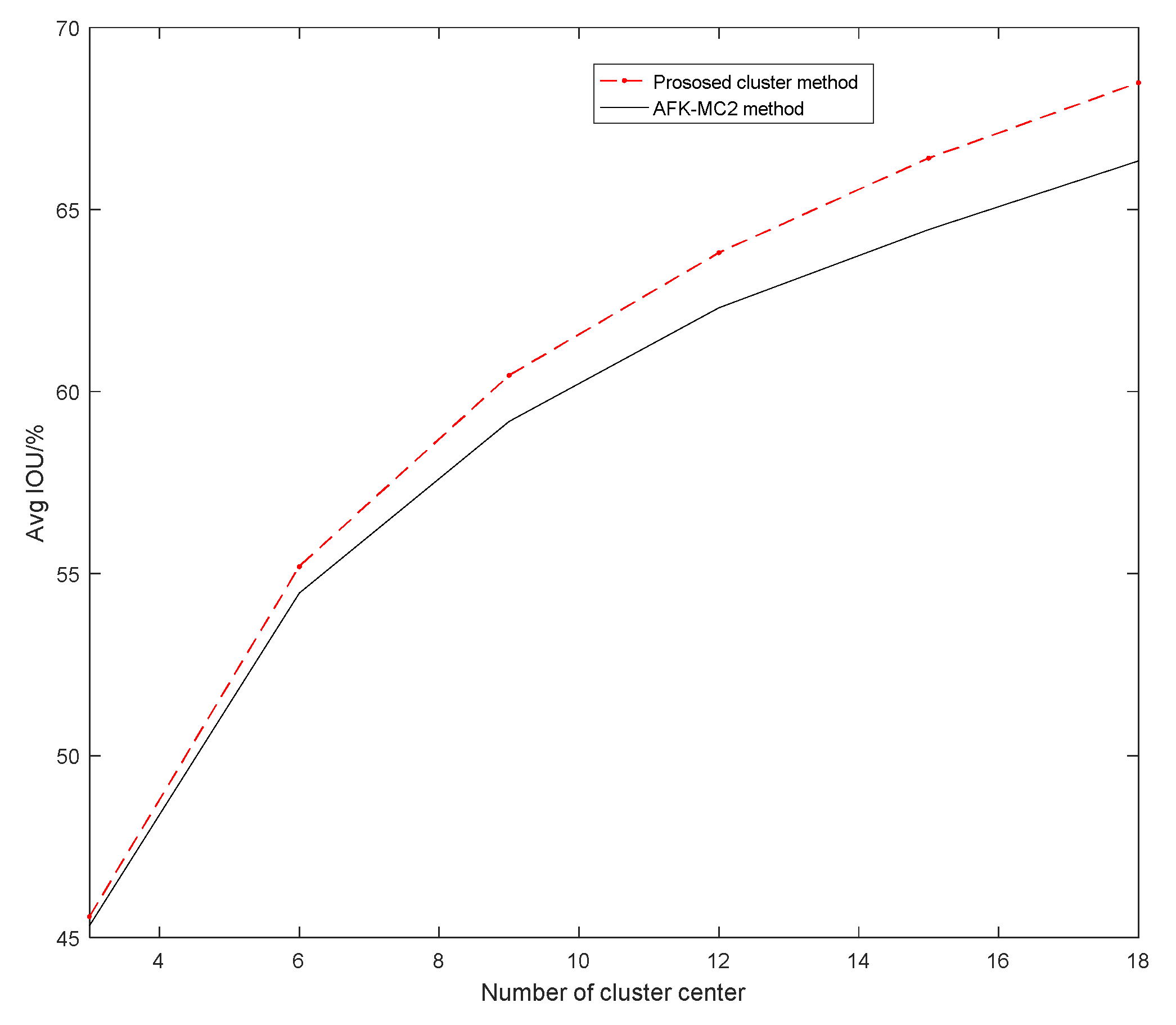
23]. On the MS COCO datasets, the Avg IOUs obtained by our proposed method and the AFK-MC
2 method are shown in
Figure 2: it can be seen that our proposed method has a larger Avg IOU than that of the AFK-MC
2 method for a different number of cluster centers. This means that the proposed method has better performance than the AFK-MC
2 method in terms of estimating the initial width and height of predicting boxes.
In order to compare the detection performance of the original YOLOv3 method and that based on our proposed cluster method, we use the same cluster center number that is used in the former method. The cluster center number is 9, and the results on the MS COCO and PASCAL VOC datasets are shown in
Table 1 and
Table 2, respectively. In
Table 1, the Avg IOU values for proposed cluster method and k-means method used in YOLOv3 are 60.44 and 59.88, respectively. The running time for proposed cluster method and k-means method used in YOLOv3 are 1183.083s and 3.972 s, respectively. The running time of k-means used in YOLOv3 is about 297 times that of our proposed cluster method. This shows that the proposed cluster has a larger Avg IOU and smaller running time than the k-means method used in YOLOv3. In
Table 2, the Avg IOU values for proposed cluster method and k-means method used in YOLOv3 are 67.34 and 67.45, respectively. The running time for the proposed cluster method and the k-means method used in YOLOv3 are 19.337 s and 0.239 s, respectively. The running time of k-means used in YOLOv3 is about 81 times that of our proposed cluster method. This also shows that the proposed cluster has a larger Avg IOU and smaller running time than the k-means method used in YOLOv3. The k-means method used in YOLOv3 requires computing the distance between all points and
cluster centers. This will consume a large amount of time for large-scale dataset detection. While we only randomly select
points instead of all points from set
, and compute distance between the
points and
cluster centers. Therefore, it requires a smaller running time compared with the k-means method, especially for large-scale detection dataset. The size of the MS COCO dataset is larger than PASCAL VOC dataset, so the difference of running time between our proposed method and the k-means method used in YOLOv3 is larger for the MS COCO dataset than for the PASCAL VOC dataset.
Table 3 shows the comparisons between the original YOLOv3 and improved YOLOV3 method (based on our proposed cluster method) on the MS COCO dataset: it can be seen that our YOLOv3 method produces larger recall, mAP and F1-score values, and therefore has better detection accuracy than the original YOLOv3 method.
We also randomly selected five images from the test sets of the MS COCO dataset in order to test the performance of small object detection; the object detection results are shown in
Figure 3. Subfigures (a), (c), (e), (g) and (i) show object detection results generated using the original YOLOv3 method, and subfigures (b), (d), (f), (h) and (j) show the object detection results generated using our proposed method. For the first image, the YOLOv3 method detected three objects, while our proposed method detected four objects (subfigures (a) and (b)). With the second image, the YOLOv3 method detected three objects, while our proposed method detected four objects (subfigures (c) and (d)). For the first and second image, our proposed method detected more objects, and it has higher scores in terms of detecting small objects. With the third image, the YOLOv3 method and our proposed method detected three objects (subfigures (e) and (f)), and our proposed method has higher scores in terms of detecting objects, especially small objects such as people in the distance and skateboards. With the fourth image, the YOLOv3 method and our proposed method detected two objects (subfigures (g) and (h)), and our proposed method has higher scores in terms of detecting objects, especially cups. With the fifth image, the YOLOv3 method and our proposed method detected three objects (subfigures (i) and (j)), and our proposed method has higher scores in terms of detecting objects, especially the giraffe in the distance. These ten sub-figures indicate that our proposed method has better performance in terms of detecting objects, especially for some small objects such as sports balls, tennis rackets, bottles, people in the distance, skateboards, cups, a giraffe in the distance, etc.