Profile-Splitting Linearized Bregman Iterations for Trend Break Detection Applications
Abstract
1. Introduction
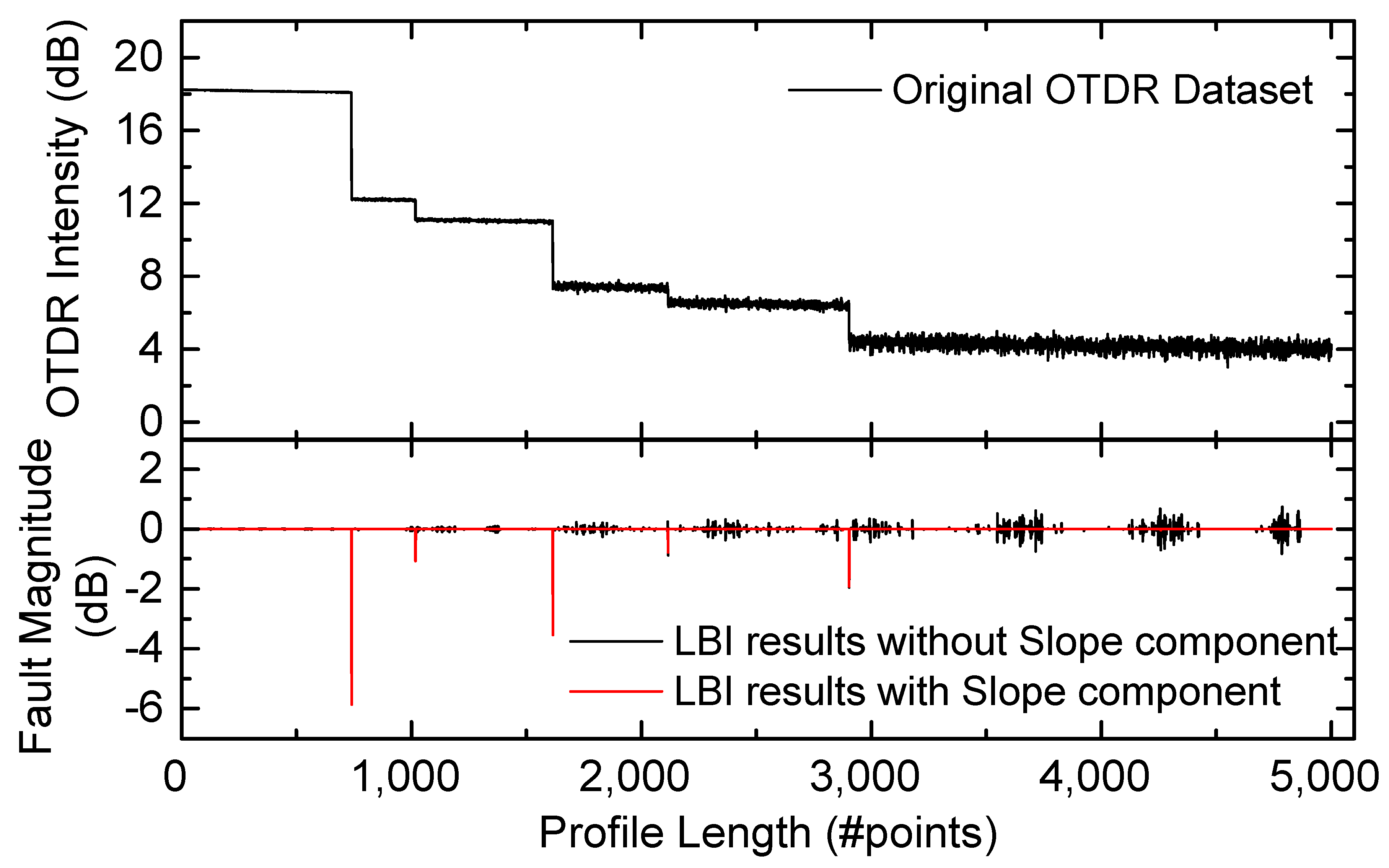
2. The LBI Algorithm Applied to the TBD Problem
| Algorithm 1 Linearized Bregman iteration for trend break detection |
| Require: Measurement vector , , , , L |
| Ensure: Estimated |
| 1: |
| 2: |
| 3: |
| 4: while do |
| 5: ▹ cyclic re-use of rows of |
| 6: |
| 7: ▹ instantaneous error with inner product |
| 8: |
| 9: for do |
| 10: |
| 11: shrink |
| 12: end for |
| 13: |
| 14: end while |
2.1. Application to Fiber Fault Detection
| Algorithm 2 Fiber dataset simulation. |
| Require: Fault vector , N, |
| Ensure: Output dataset |
| 1: |
| 2: |
| 3: |
| 4: |
2.2. Time Scaling with Data Length
3. Results: The Profile-Split Methodology
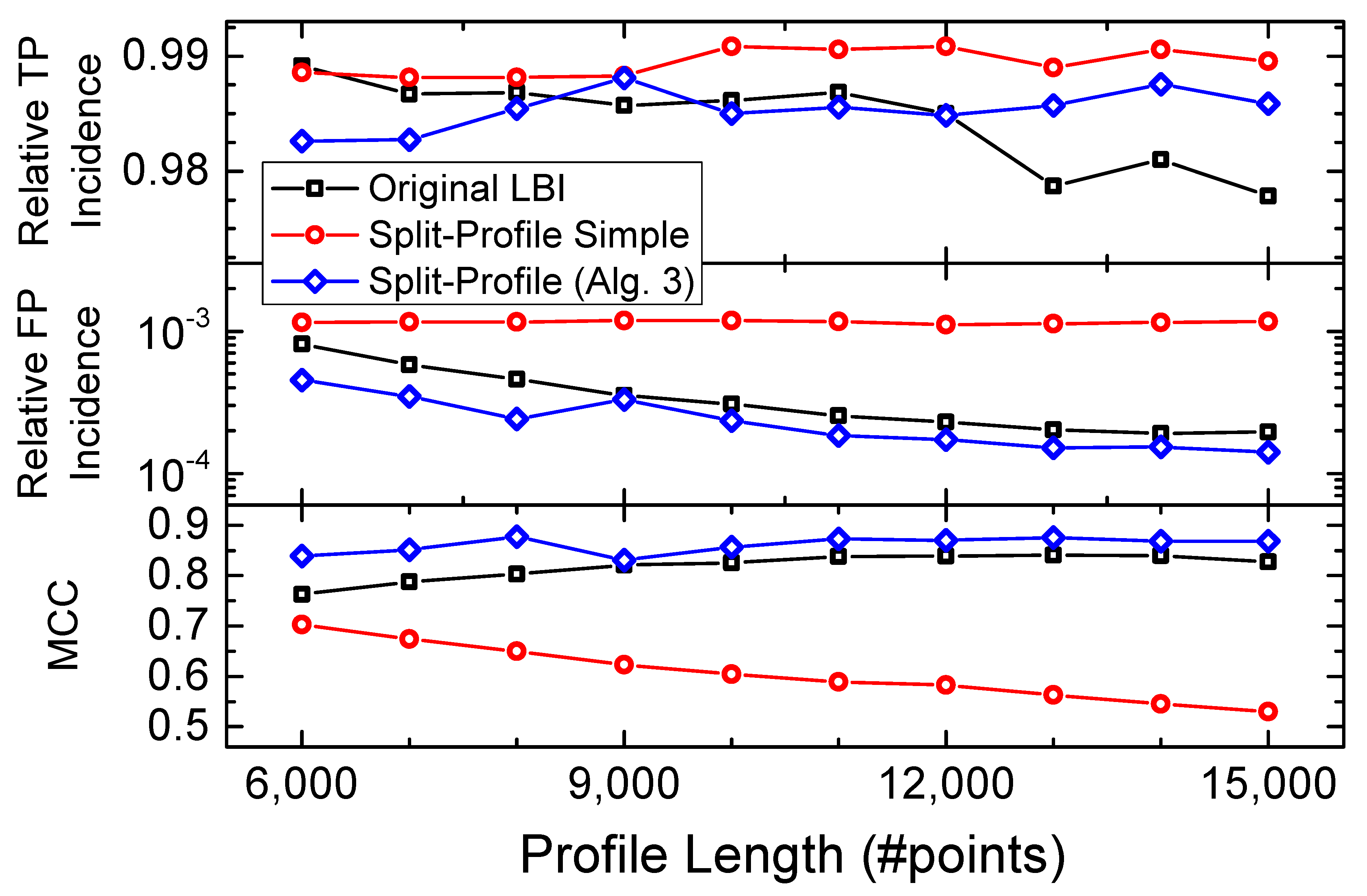
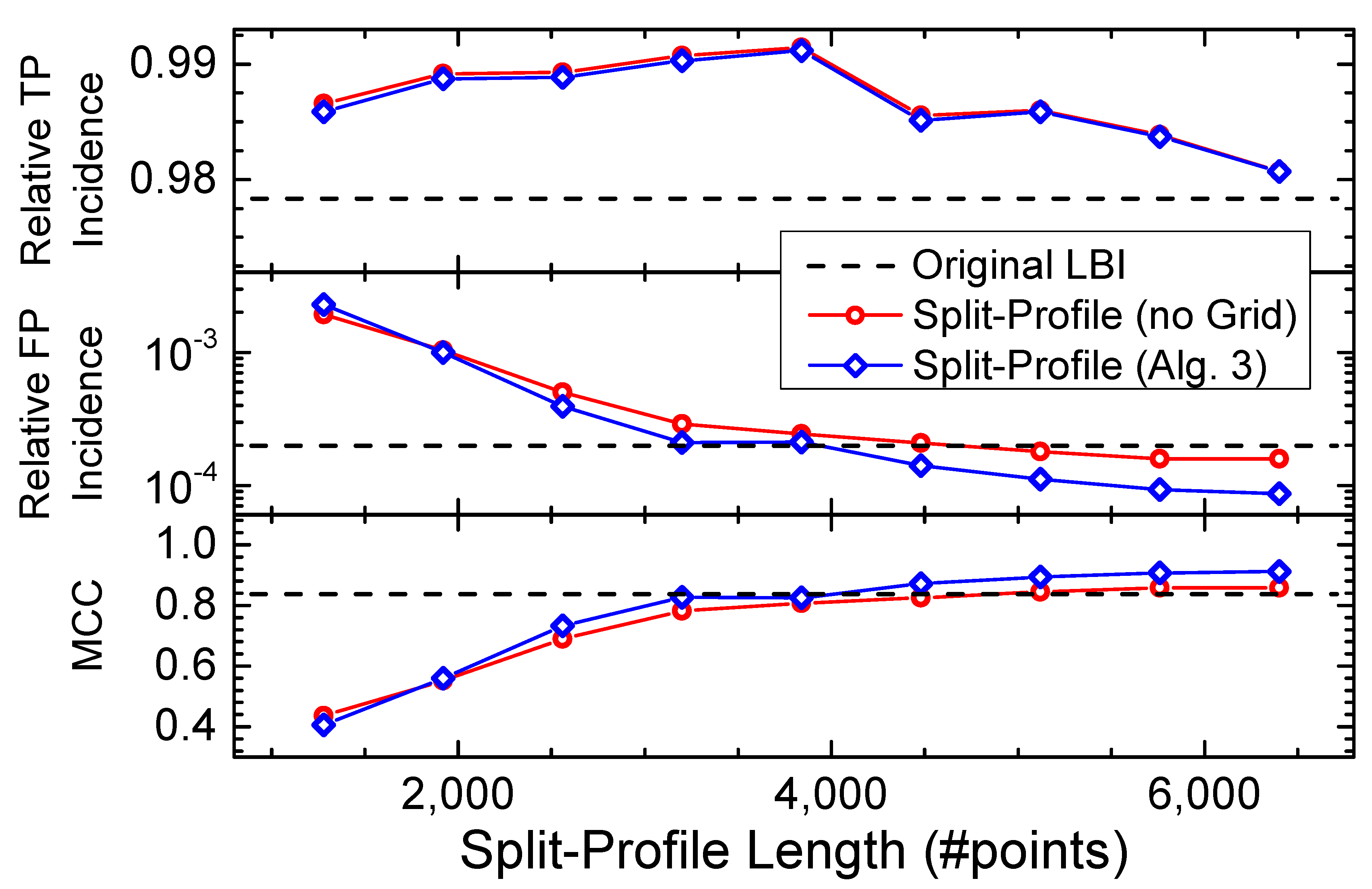
3.1. Selection
| Algorithm 3 Split-profile with selection. |
| Require: |
| Ensure: |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: fordo |
| 8: |
| 9: |
| 10: |
| 11: end for |
3.2. Split-Profile Length Analysis
3.3. Timing Results
4. Discussion: Parallelization of Profile-Split in Dedicated Hardware
- The analysis was restricted to the S V, since the C V did not offer enough resources for a fruitful analysis for a large range of profile lengths.
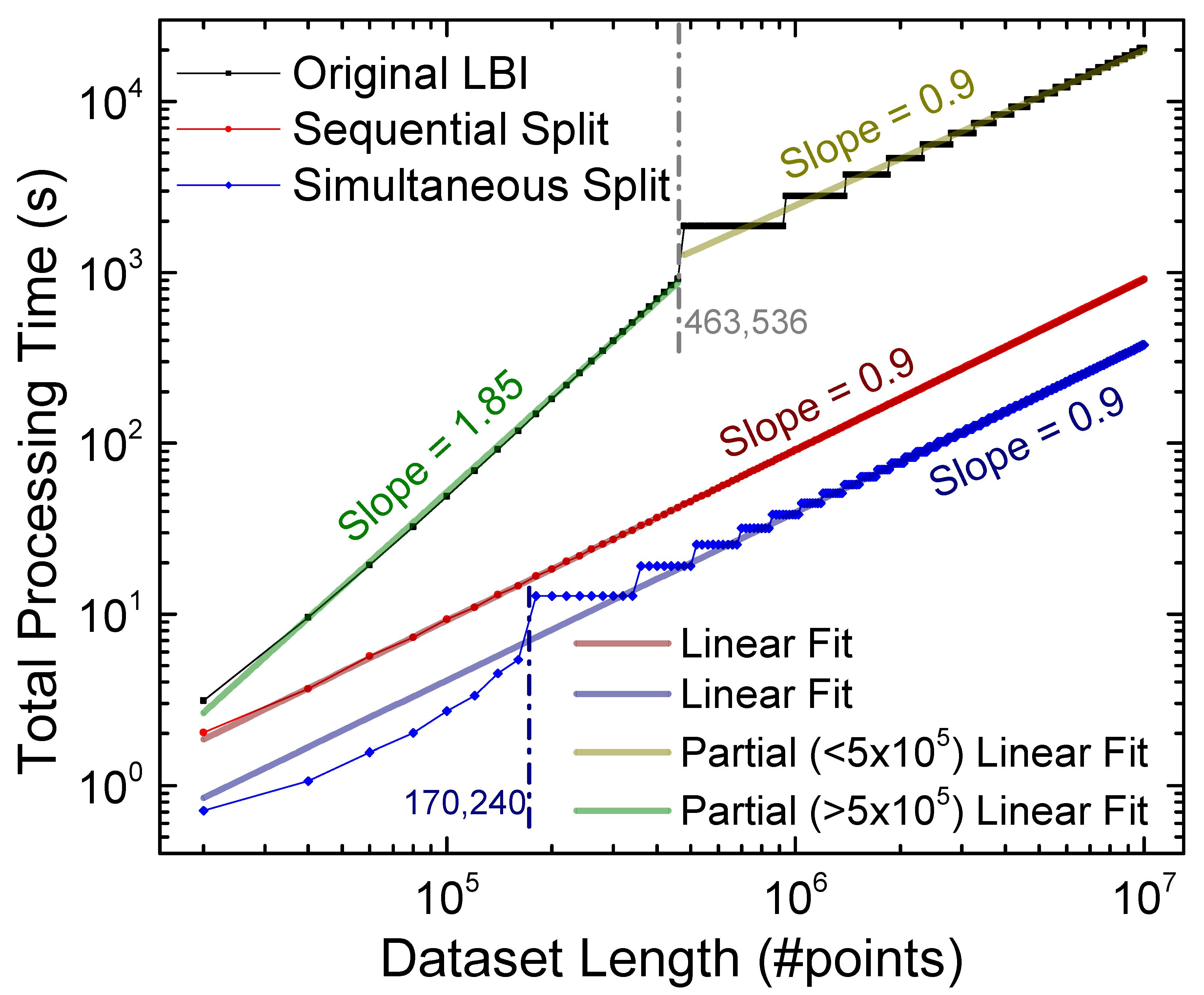
- Due to the fact that the difference in processing times between the split-profile and the original LBI was insignificant for datasets containing fewer than 20,000 points—according to the analysis of Figure 5—this was set as the starting point of the analysis.
- The goal was to observe the trend of the total processing time curve for the three hardware options (original LBI, sequential split, simultaneous split) as the dataset length increased. Therefore, up to points were considered for the analysis.
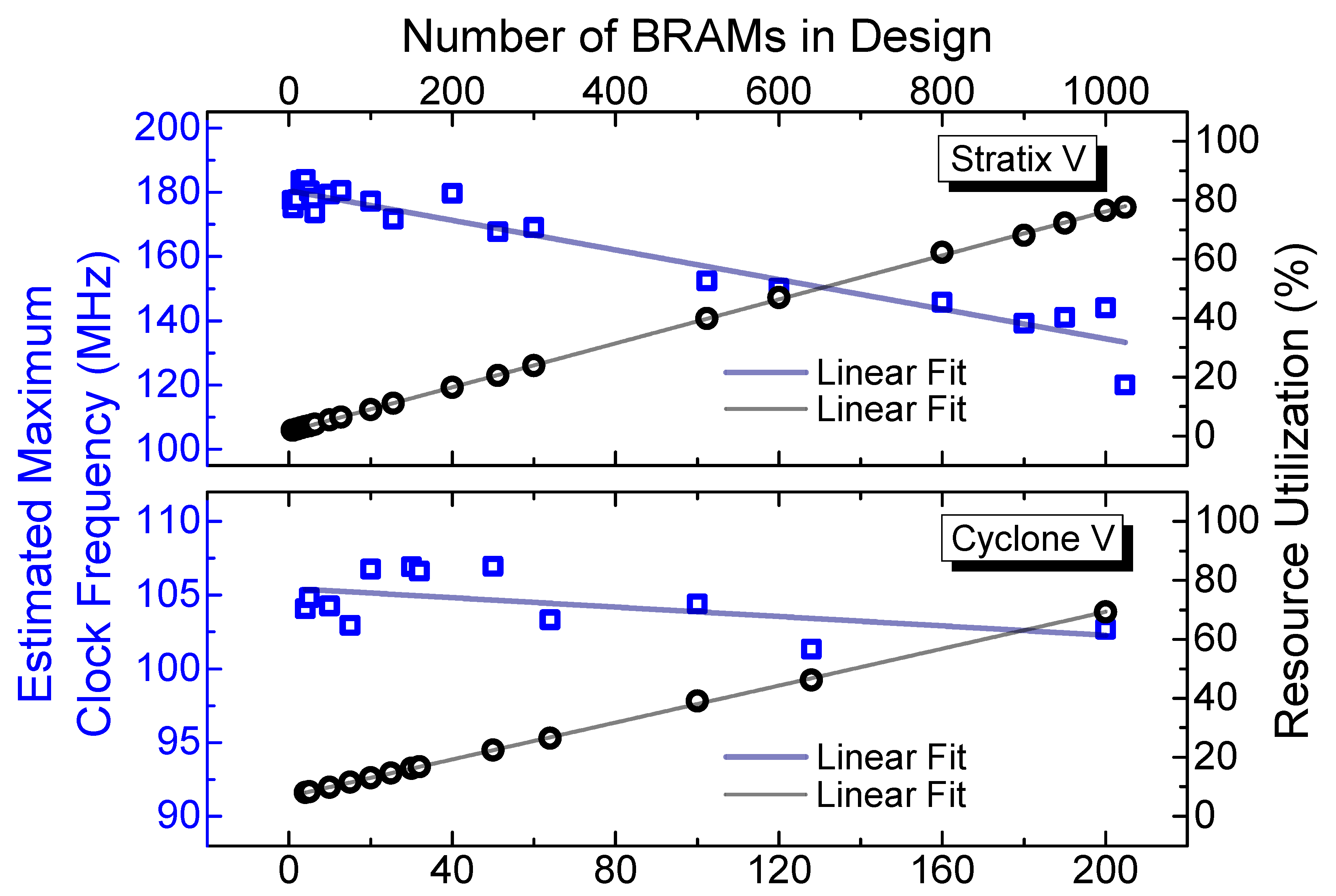
- Due to the data storage architecture and assuming a 20 bit long word BRAM with 1024 positions, each BRAM had a data capacity of 333 points [12].
- The BRAM storage capacity could be combined with the stipulated size of the profile-split () in order to determine the minimum number of BRAMs assigned to each unit (14).
- The curve that associated the resource usage in the FPGA to the number of instantiated BRAMs (Figure 6) could be used to determine the maximum number of individual split-profile units that could be simultaneously instantiated in the S V (38, with 98.08% resource usage) and, in turn, the maximum number of data points that could be stored ( 170,240, highlighted in Figure 7).
- The curve that associated the resource usage in the S V to the number of instantiated BRAMs (Figure 6) could be used to determine the maximum number of BRAMs that could be used for the original LBI implementation (1392, with 99.06% resource usage) and, in turn, the maximum number of data points that could be stored in the FPGA ( = 463,536, highlighted in Figure 7).
- If the dataset to be processed was longer than the maximum storage capacity of the hardware, full processing would not be possible in a single step, requiring the data points to be processed in batches.
- Processing data in batches required extra time necessary for loading/unloading of data to be taken into account. According to [12], this procedure took one clock cycle per data point and, although negligible, was included for completeness.
- Provided the sub-profile segmentation was respected through batch processing, no further care was needed in a profile-split scenario.
- In the original LBI implementation, batch processing required an additional selection step (as was necessary in the split-profile case), otherwise the performance would decrease drastically. The procedure described in Section 3 could be employed such that the original performance was maintained.
5. Materials and Methods
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FPGA | Field Programmable Gate Array |
| LBI | Linearized Bregman Iterations |
| TBD | Trend Break Detection |
| TP | True Positives |
| TF | False Positives |
| TN | True Negatives |
| FN | False Negatives |
| MCC | Matthews Correlation Coefficient |
| SNR | Signal-to-Noise Ratio |
| OTDR | Optical Time Domain Reflectometry |
| BIC | Bayesian Information Criterion |
References
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman iterative algorithms for ℓ_1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Cai, J.F.; Osher, S.; Shen, Z. Linearized Bregman iterations for compressed sensing. Math. Comput. 2009, 78, 1515–1536. [Google Scholar] [CrossRef]
- Cai, J.F.; Osher, S.; Shen, Z. Linearized Bregman iterations for frame-based image deblurring. SIAM J. Imaging Sci. 2009, 2, 226–252. [Google Scholar] [CrossRef]
- Osher, S.; Mao, Y.; Dong, B.; Yin, W. Fast linearized Bregman iteration for compressive sensing and sparse denoising. Commun. Math. Sci. 2010, 8, 93–111. [Google Scholar]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Choi, K.; Fahimian, B.P.; Li, T.; Suh, T.S.; Lei, X. Enhancement of four-dimensional cone-beam computed tomography by compressed sensing with Bregman iteration. J. X-ray Sci. Technol. 2013, 21, 177–192. [Google Scholar] [CrossRef]
- Lorenz, D.A.; Wenger, S.; Schöpfer, F.; Magnor, M. A sparse Kaczmarz solver and a linearized Bregman method for online compressed sensing. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 1347–1351. [Google Scholar]
- Lunglmayr, M.; Huemer, M. Efficient linearized Bregman iteration for sparse adaptive filters and Kaczmarz solvers. In Proceedings of the 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Rio de Janerio, Brazil, 10–13 July2016; pp. 1–5. [Google Scholar]
- Riley, W.J. Algorithms for frequency jump detection. Metrologia 2008, 45, S154–S161. [Google Scholar] [CrossRef]
- Babcock, H.P.; Moffitt, J.R.; Cao, Y.; Zhuang, X. Fast compressed sensing analysis for super-resolution imaging using L1-homotopy. Opt. Express 2013, 21, 28583–28596. [Google Scholar] [CrossRef]
- Lunglmayr, M.; Amaral, G.C. Linearized Bregman Iterations for Automatic Optical Fiber Fault Analysis. IEEE Trans. Instrum. Meas. 2018, 68, 3699–3711. [Google Scholar] [CrossRef]
- Calliari, F.; Amaral, G.C.; Lunglmayr, M. FPGA-Embedded Linearized Bregman Iterations Algorithm for Trend Break Detection. arXiv 2019, arXiv:1902.06003. [Google Scholar]
- Amaral, G.C.; Garcia, J.D.; Herrera, L.E.; Temporao, G.P.; Urban, P.J.; von der Weid, J.P. Automatic fault detection in wdm-pon with tunable photon counting otdr. J. Light. Technol. 2015, 33, 5025–5031. [Google Scholar] [CrossRef]
- Von der Weid, J.P.; Souto, M.H.; Garcia, J.D.; Amaral, G.C. Adaptive filter for automatic identification of multiple faults in a noisy otdr profile. J. Light. Technol. 2016, 34, 3418–3424. [Google Scholar] [CrossRef]
- Urban, P.J.; Vall-Llosera, G.; Medeiros, E.; Dahlfort, S. Fiber plant manager: An OTDR-and OTM-based PON monitoring system. IEEE Commun. Mag. 2013, 51, S9–S15. [Google Scholar] [CrossRef]
- Hornsteiner, A. Fiber Optic Technology Trends in Data Transmission: Digitalization of data advance the need for constant upgrading of data networks. Opt. Photonik 2017, 12, 20–24. [Google Scholar] [CrossRef]
- Candès, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Han, P.Z.; Li, P.H.; Yin, P.W. Compressive Sensing for Wireless Networks; Cambridge University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Calliari, F.; Herrera, L.E.; von der Weid, J.P.; Amaral, G.C. High-dynamic and high-resolution automatic photon counting OTDR for optical fiber network monitoring. In Proceedings of the 6th International Conference on Photonics, Optics and Laser Technology, Funchal, Portugal, 25–27 January 2018; Volume 1, pp. 82–90. [Google Scholar]
- Bühlmann, P.; Rütimann, P.; van de Geer, S.; Zhang, C.H. Correlated variables in regression: Clustering and sparse estimation. J. Stat. Plan. Inference 2013, 143, 1835–1858. [Google Scholar] [CrossRef]
- Bertsimas, D.; King, A.; Mazumder, R. Best subset selection via a modern optimization lens. Ann. Stat. 2016, 44, 813–852. [Google Scholar] [CrossRef]
- Saavedra, R.; Tovar, P.; Amaral, G.C.; Fanzeres, B. Full Optical Fiber Link Characterization With the BSS-Lasso. IEEE Trans. Instrum. Meas. 2018, 68, 4162–4174. [Google Scholar] [CrossRef]
- Barnoski, M.; Rourke, M.; Jensen, S.; Melville, R. Optical time domain reflectometer. Appl. Opt. 1977, 16, 2375–2379. [Google Scholar] [CrossRef]
- Amaral, G.C.; Herrera, L.E.; Vitoreti, D.; Temporão, G.P.; Urban, P.J.; der von Weid, J.P. WDM-PON monitoring with tunable photon counting OTDR. IEEE Photonics Technol. Lett. 2014, 26, 1279–1282. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro do Amaral, G.; Calliari, F.; Lunglmayr, M. Profile-Splitting Linearized Bregman Iterations for Trend Break Detection Applications. Electronics 2020, 9, 423. https://doi.org/10.3390/electronics9030423
Castro do Amaral G, Calliari F, Lunglmayr M. Profile-Splitting Linearized Bregman Iterations for Trend Break Detection Applications. Electronics. 2020; 9(3):423. https://doi.org/10.3390/electronics9030423
Chicago/Turabian StyleCastro do Amaral, Gustavo, Felipe Calliari, and Michael Lunglmayr. 2020. "Profile-Splitting Linearized Bregman Iterations for Trend Break Detection Applications" Electronics 9, no. 3: 423. https://doi.org/10.3390/electronics9030423
APA StyleCastro do Amaral, G., Calliari, F., & Lunglmayr, M. (2020). Profile-Splitting Linearized Bregman Iterations for Trend Break Detection Applications. Electronics, 9(3), 423. https://doi.org/10.3390/electronics9030423




