Robust Detection of Bearing Early Fault Based on Deep Transfer Learning
Abstract
1. Introduction
- (1)
- In order to improve detection accuracy for bearing early fault, we need to reduce the data distribution deviation, especially in a normal state. As a result, the detection model built on the bearings data under some working conditions (also called ) can be dynamically applied to the bearing data under another working condition (called ).
- (2)
- In order to build an effective online detection model in complex environment and noise interference, it is necessary to find a state assessment method with strong anti-interference ability. Meanwhile, this method should be able to achieve accurate recognition of early fault state on different bearing data. As a result, the robustness of detection model can be improved.
- (1)
- This paper proposes a robust method of state assessment for rolling bearings. Running with deep transfer learning, this method can accurately identify early fault state on the bearing data under different working conditions. In addition, this method has good anti-interference ability against irregular fluctuation in normal state data. According to our literature survey, the current research about state assessment is seldom concerned about the robustness of assessment results.
- (2)
- This paper proposes a new online detection method for bearing early fault. On the basis of the common feature representation obtained from source and target domains, this method can directly extract representative features for target bearing and identify the occurrence of early faults in real time with a much lower false alarm rate. To our best knowledge, very little research whose focus is robust early fault detection has been found, and there are no other research found about the application of transfer learning on early fault detection of bearings.
2. Preliminary Works
3. Robust Detection Method Based on Deep Transfer Learning
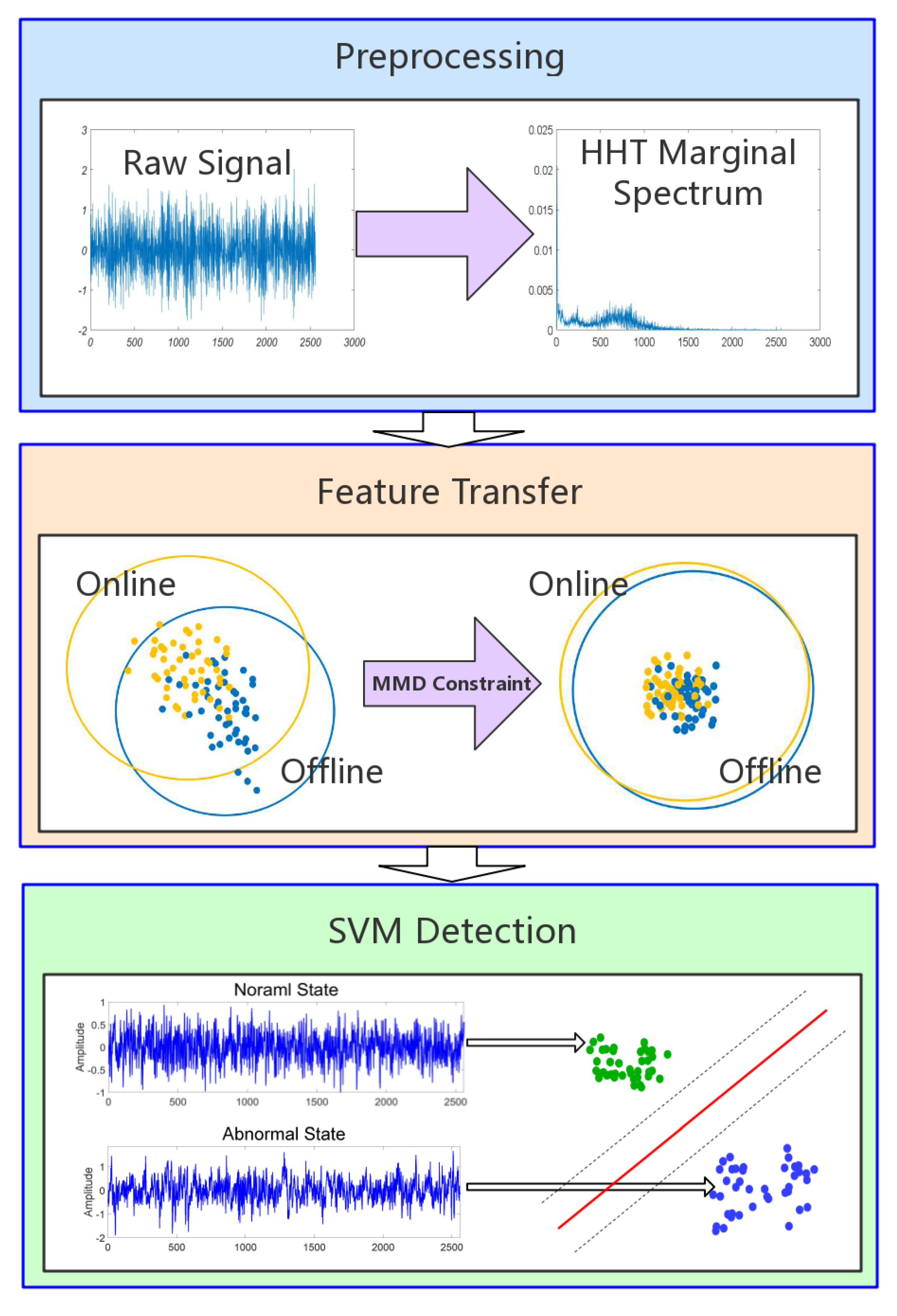
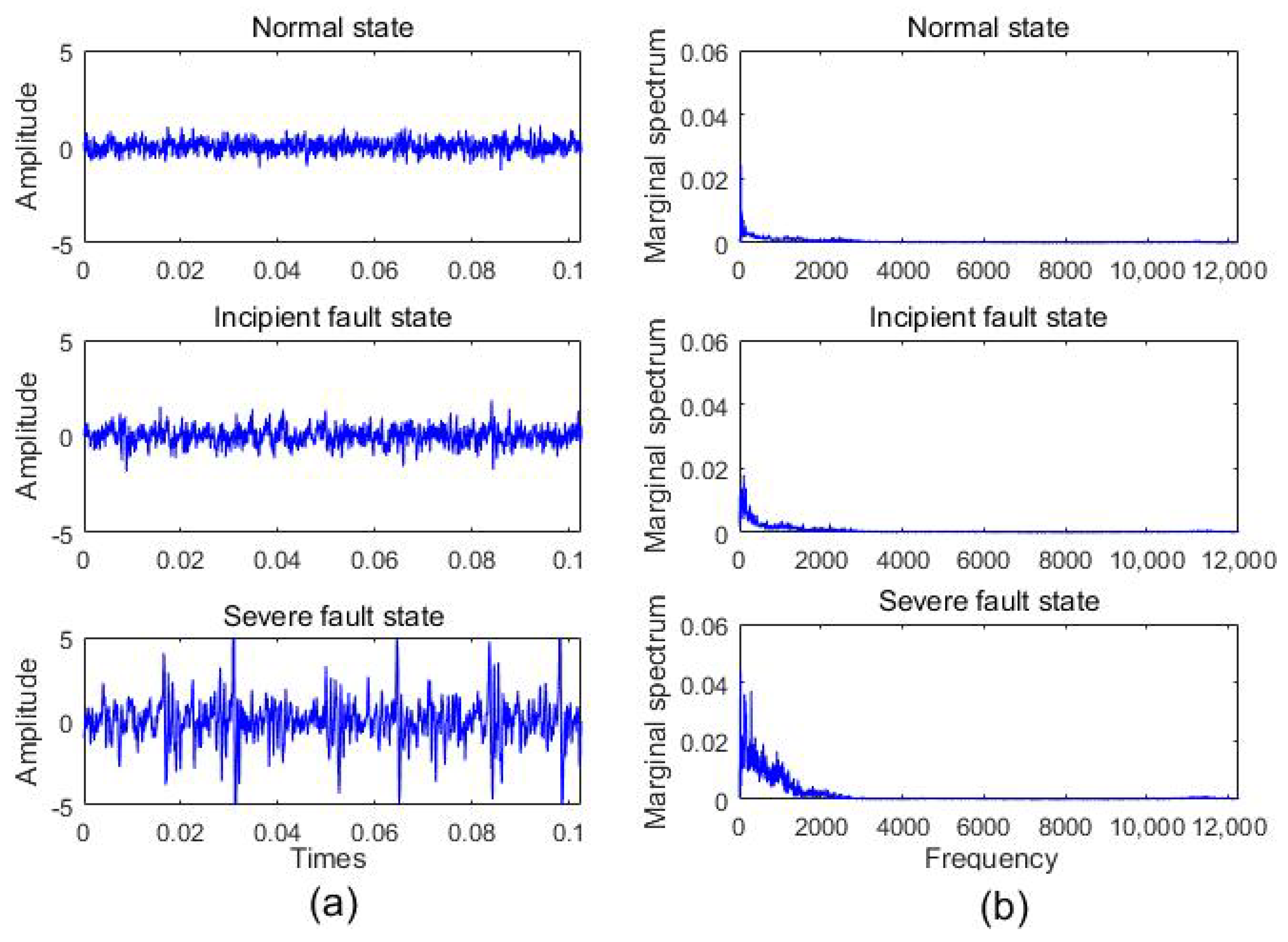
3.1. Preprocessing
- (1)
- Decompose the original vibration signal: , where denotes the original signal, denotes the i-th intrinsic mode function (IMF) component, and denotes the residual term.
- (2)
- Run Hilbert transform for each IMF component:.Construct the analytical signal: , where , , . The instantaneous frequency is: .
- (3)
- Construct Hilbert spectrum: . The final marginal spectrum can be obtained through an integral of Hilbert spectrum: .
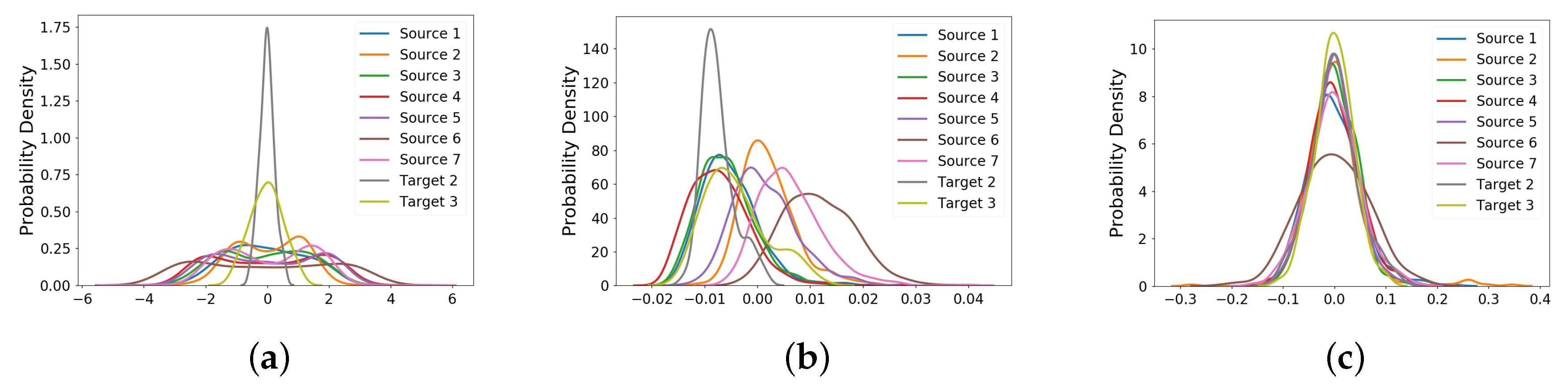
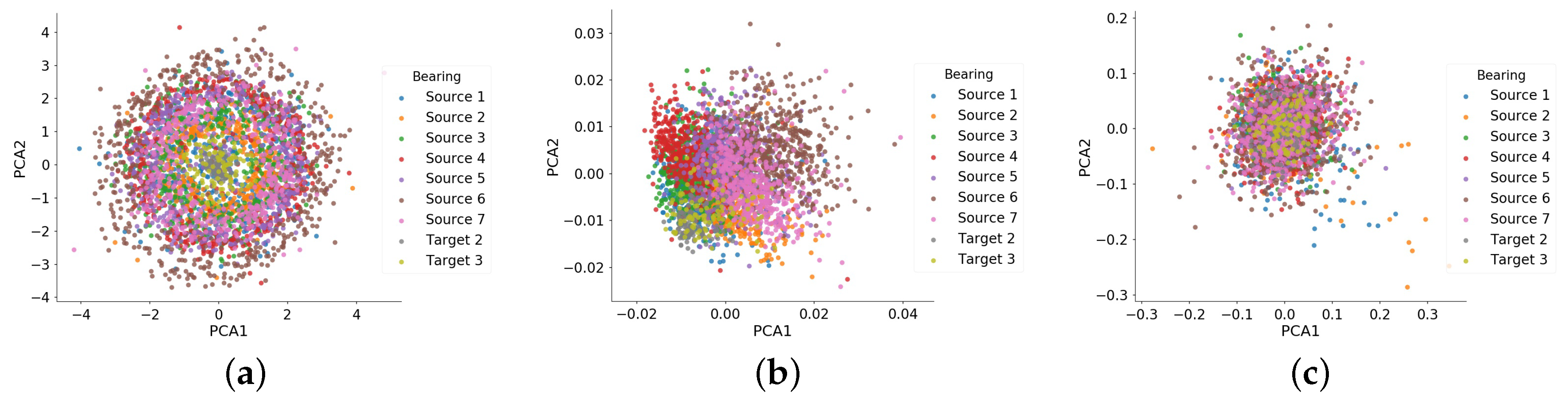
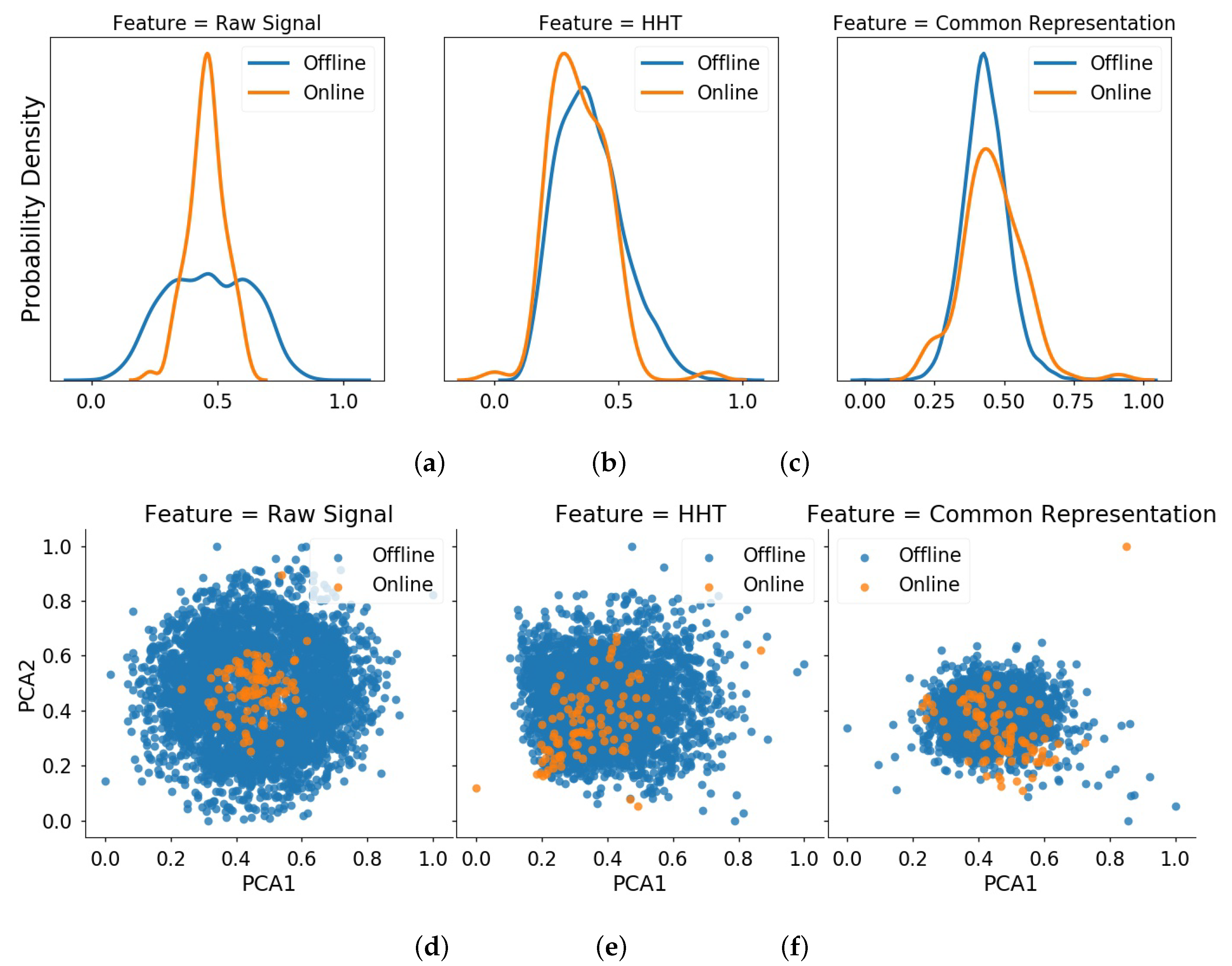
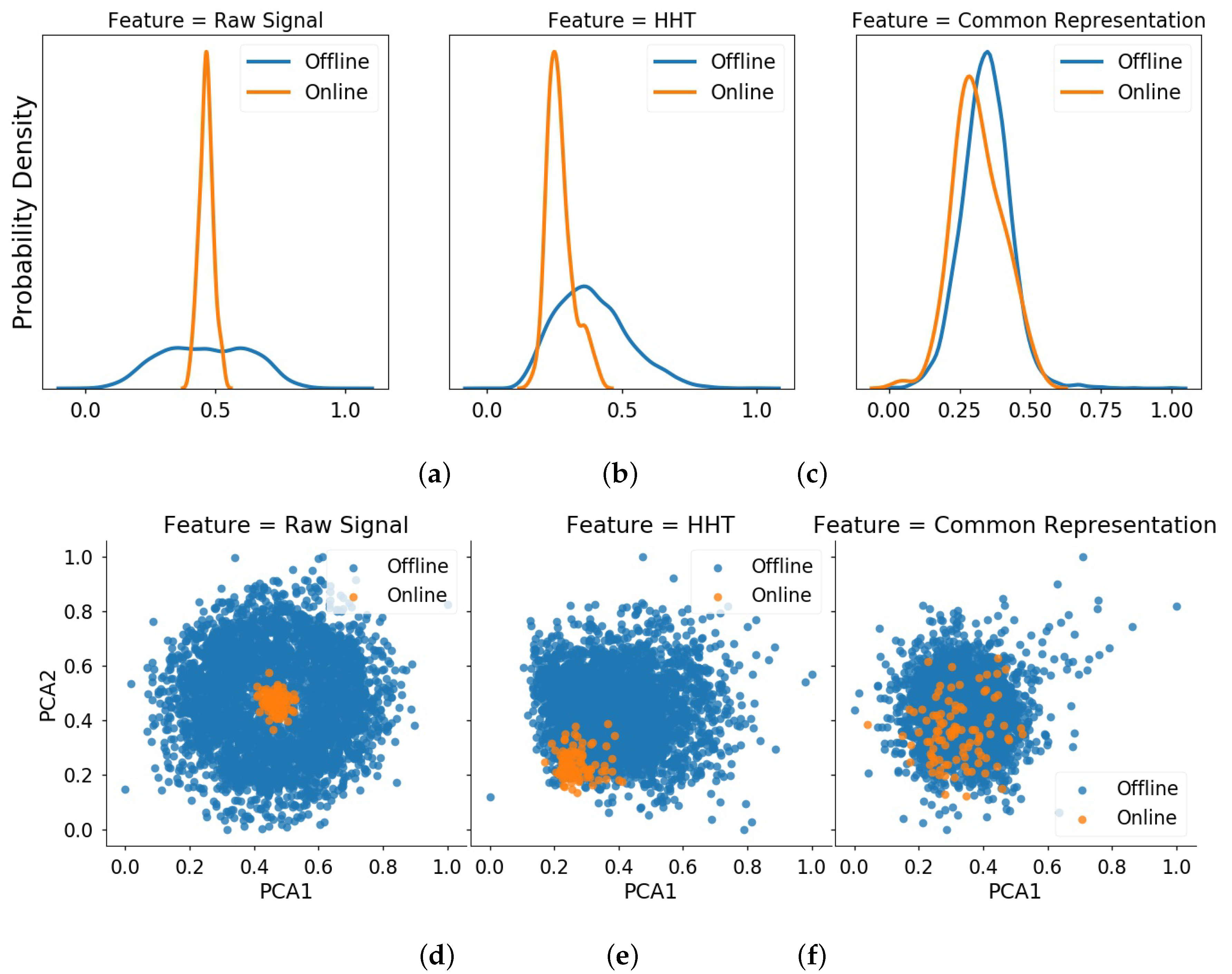
3.2. Common Feature Representation Based on Transfer Learning
- (1)
- The first one is the reconstruction term of traditional DAE:where X denotes the input sample matrix and R indicates the reconstruction feature of DAE, F indicates the Frobenius norm of matrix, and n is the number of samples.
- (2)
- The second one is an MMD regularizer which constrains the distribution discrepancy between normal data of different bearings. We define the symbol C as the combination of multiple auxiliary bearings. The MMD regularizer is defined as:where and represent the bearing samples in the source and target domains, respectively. In addition, and denote the number of samples in the source and target domains.
- (3)
- The third one is the weight regularization term that enhances the representative ability of features extracted from raw data, as follows:where is the width parameter, K is the total number of hidden layers, and is the weight matrix of the k-th layer.By integrating these three terms together, the final loss function of DAE with domain adaptation is:where > 0 and > 0 control the trade-off among three terms. Minimizing this loss function can be achieved using a gradient descent algorithm. It is worth noting that, different from [25] which adapts the data of different fault states under different working conditions, here we merely constrain the normal state data of training bearings to have a consistent data distribution for the building detection model. Please refer to the article [25] for the specific network structure.
3.3. Robust State Assessment Method
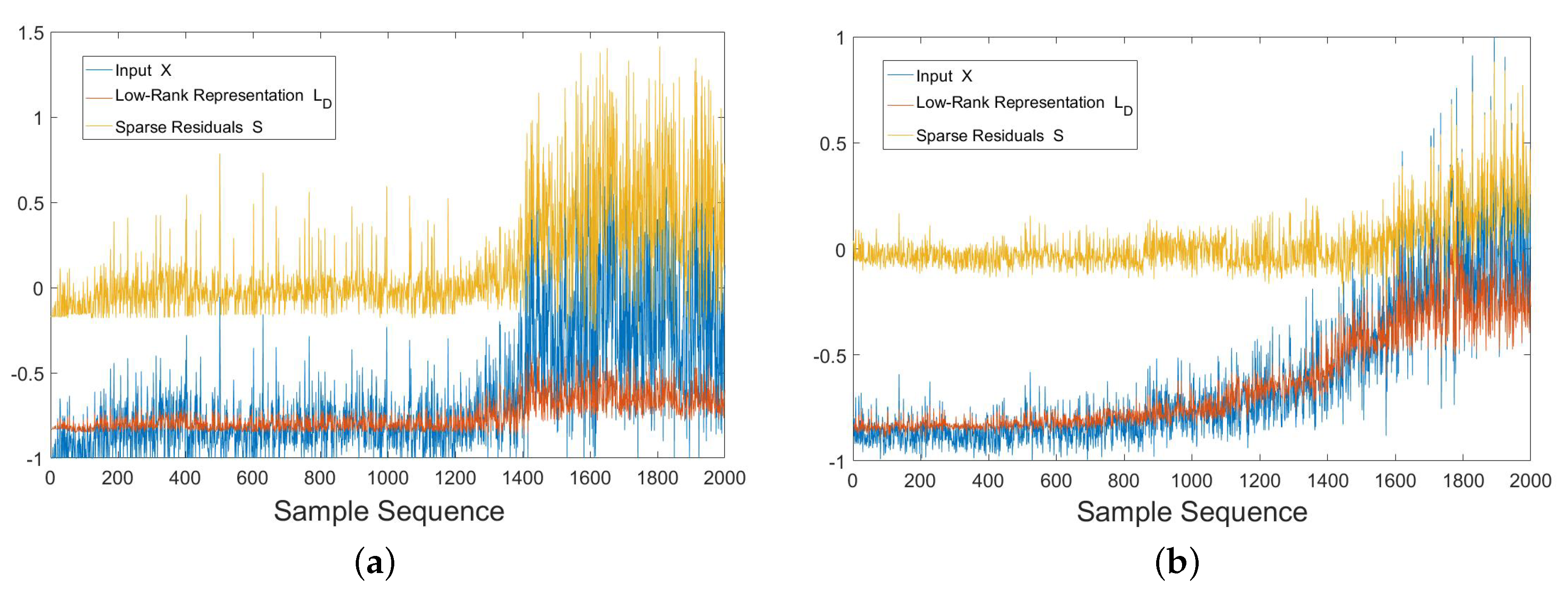
- (1)
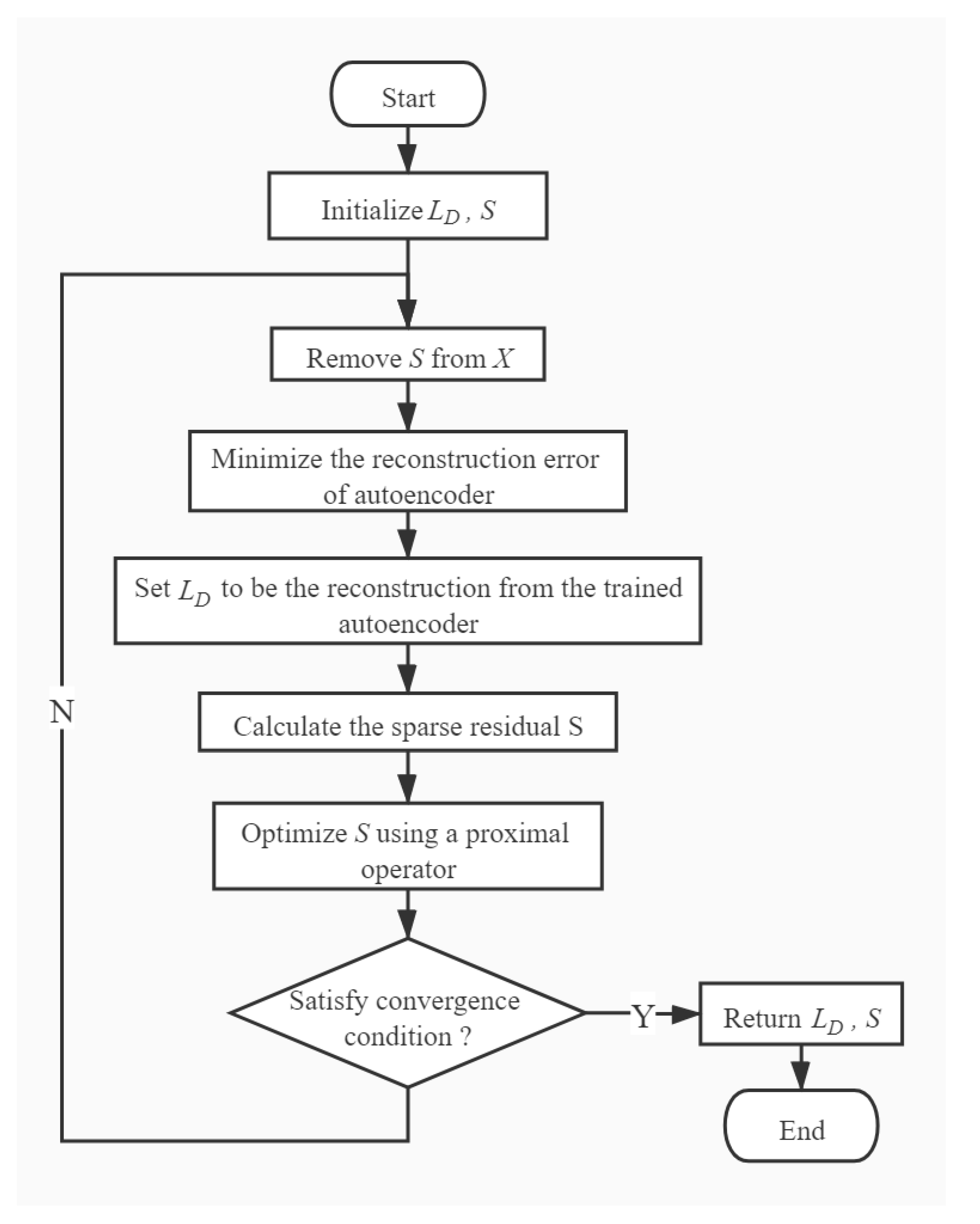
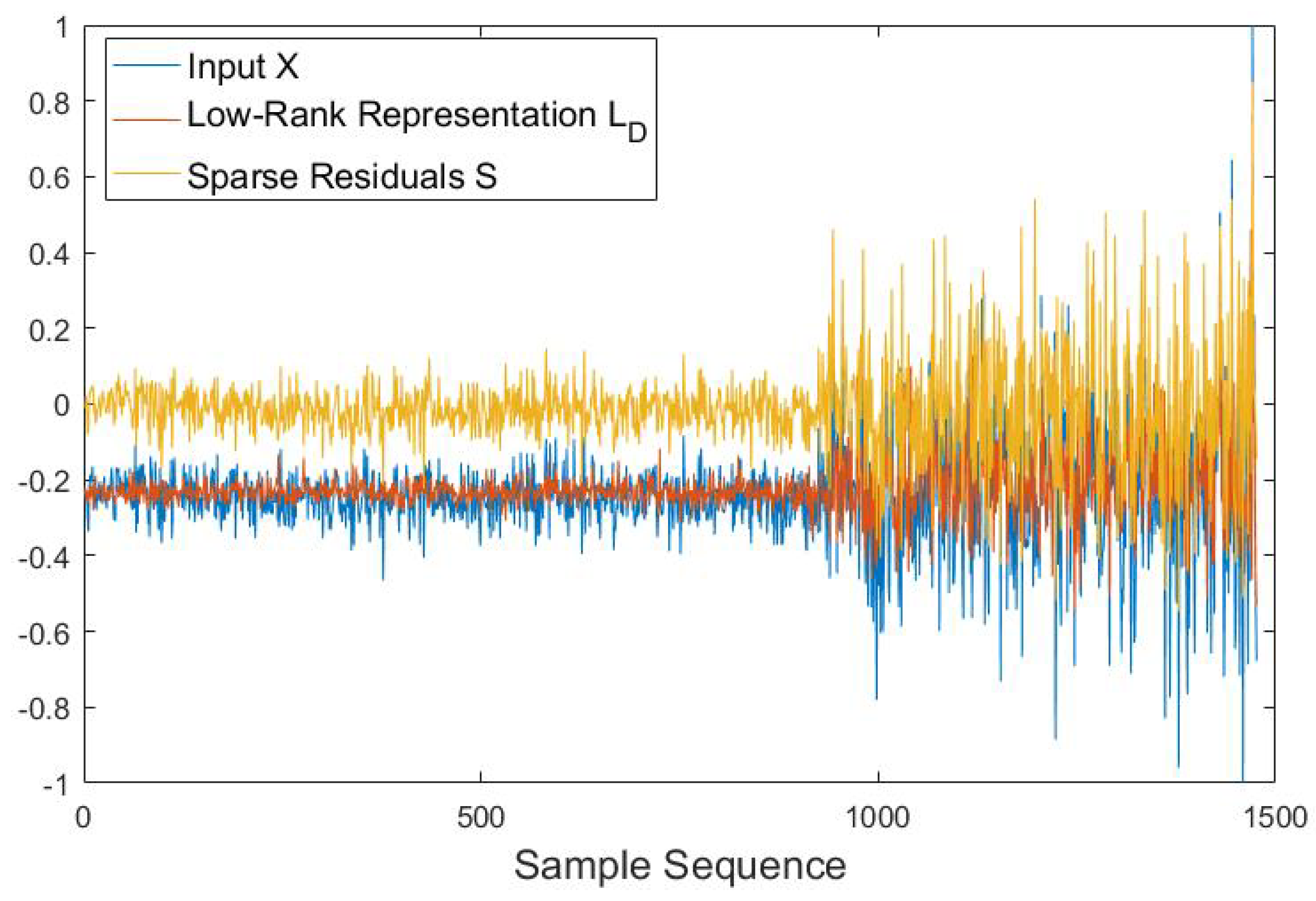
- For the common feature set X of auxiliary bearings extracted by DAE with domain adaptation, we feed them into RDA and calculate , which is the low-rank public representation of auxiliary bearing data. The specific steps to calculate are as follows [29]:
- A.
- Initialize , S to be zero matrices. Initialize an auto-encoder network with random parameters.
- B.
- Remove S from X and use the remainder to train the auto-encoder.
- C.
- Minimize the reconstruction error by using back-propagation algorithm.
- D.
- Set to be the reconstruction from the trained autoencoder: .
- E.
- Set S to be the difference between X and : .
- F.
- Optimize S using a proximal operator: .
- G.
- If the value of S changes less than a pre-defined threshold in two consecutive iterations, return and S, otherwise go to Step B.
- (2)
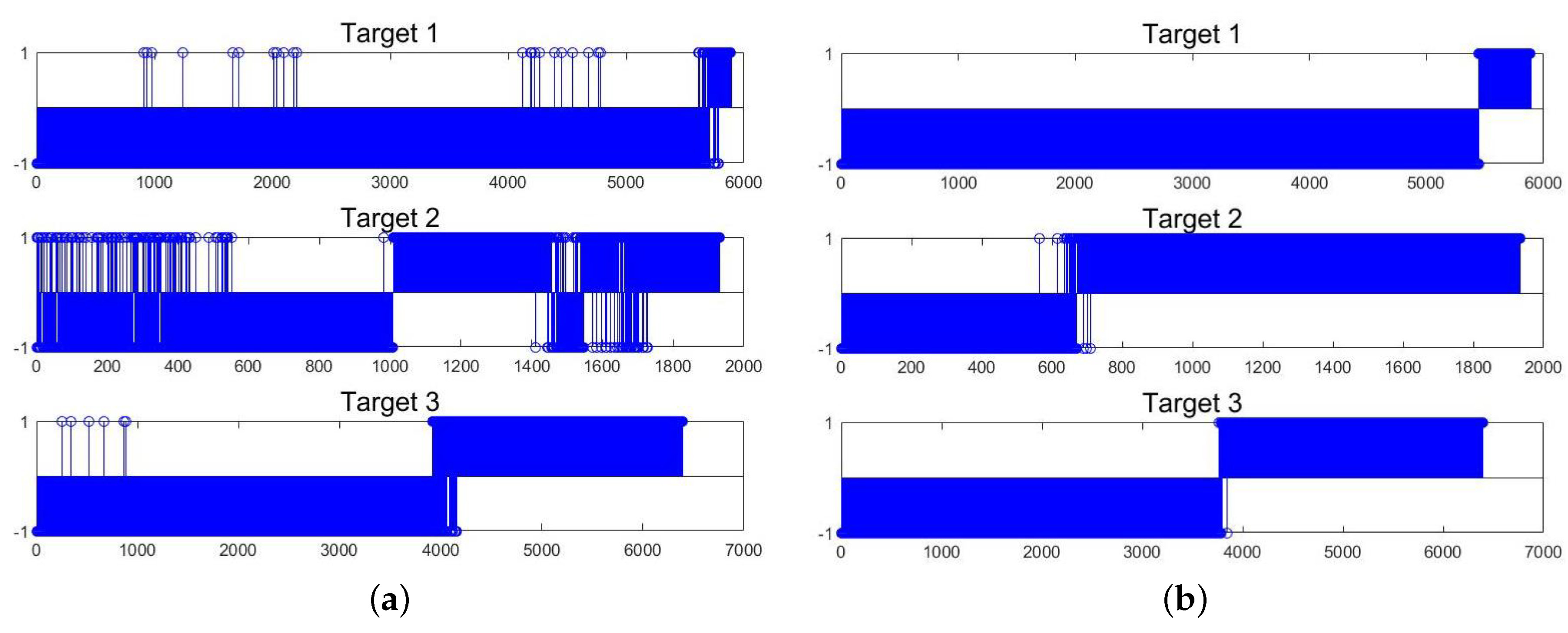
- For , we train a SVDD model by using the starting part of training data of each auxiliary bearing, and then use the obtained SVDD model to identify the state of each sample in . The SVDD model is a one-class classification algorithm which can detect abnormal samples only using positive samples [30]. SVDD constructs a hyper-sphere which covers as much as target data, and recognizes the sample outside the sphere’s boundary as anomaly. The optimization target of SVDD is:where a and R are the center and radius of hyper-sphere, respectively, indicates the distance from the sample to the center a, is slack variable, C is regularization parameter which makes a trade-off between the hyper-sphere volume and misclassification level. The SVDD model can be optimized by Lagrange multiplier method [30]. For auxiliary bearings, the starting part of offline data can be viewed as positive class data, and the position where anomalies occur can be judged by SVDD. Since a sample in corresponds to an original sample of auxiliary bearings, the state assessment for the auxiliary bearings is conducted.
3.4. Online Detection of Early Fault
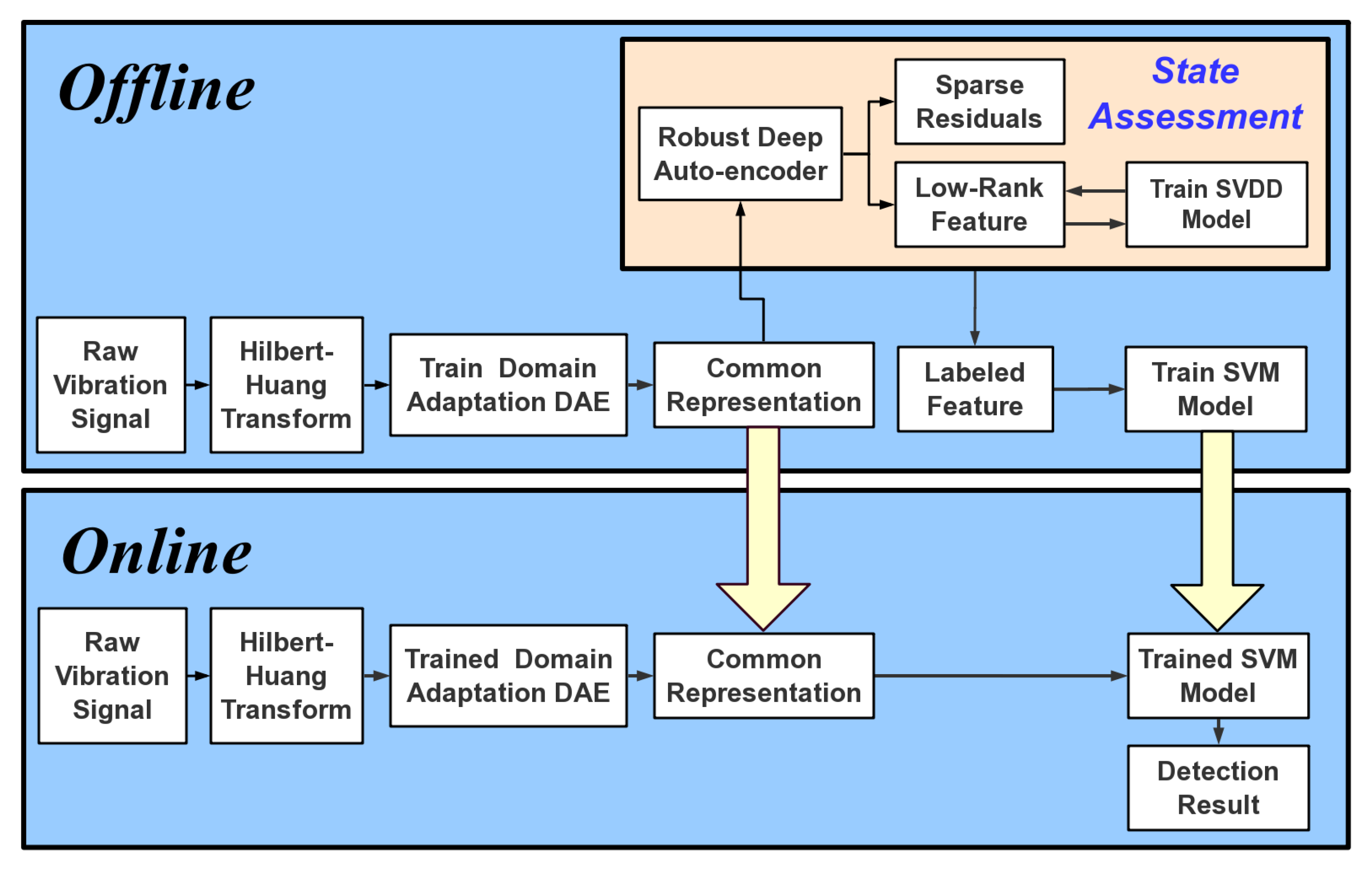
3.5. Process of the Proposed Method
3.5.1. Offline Stage
3.5.2. Online Stage
- (1)
- Extract marginal spectrum by HHT from online data batch of test bearing.
- (2)
- Feed the marginal spectrum data into the DAE with domain adaptation trained in offline stage to extract the common features.
- (3)
- Put the common features to the SVM classifier trained in the offline stage and then obtain detection results.
4. Experimental Results
4.1. Dataset Description
4.1.1. IEEE PHM Challenge 2012 Dataset
4.1.2. XJTU-SY Bearing Dataset
4.2. Experimental Setup
4.2.1. Experiment 1
4.2.2. Experiment 2
4.3. Experiment 1
4.3.1. Preprocessing
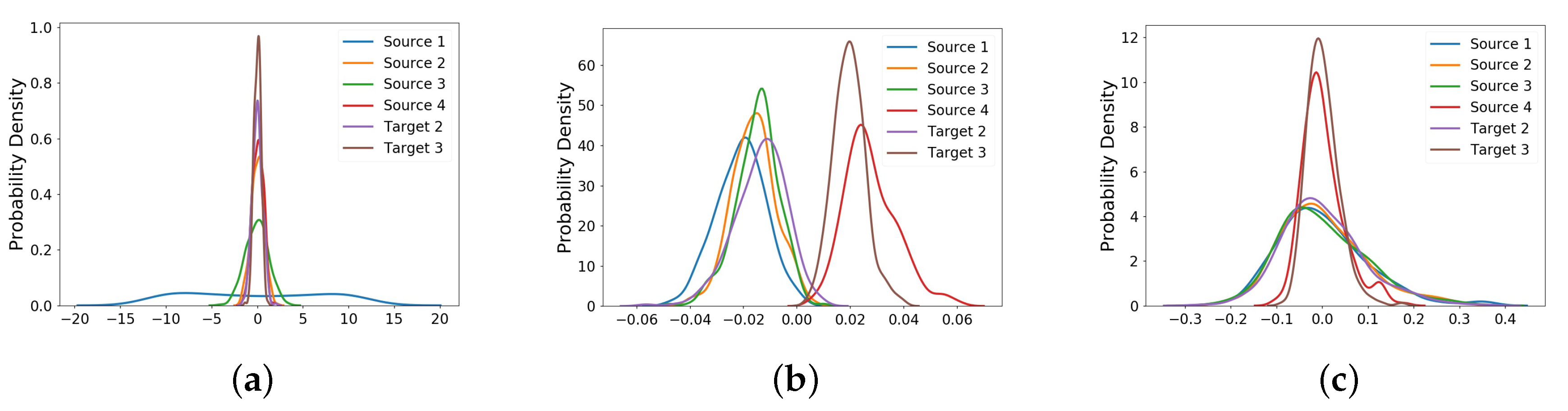
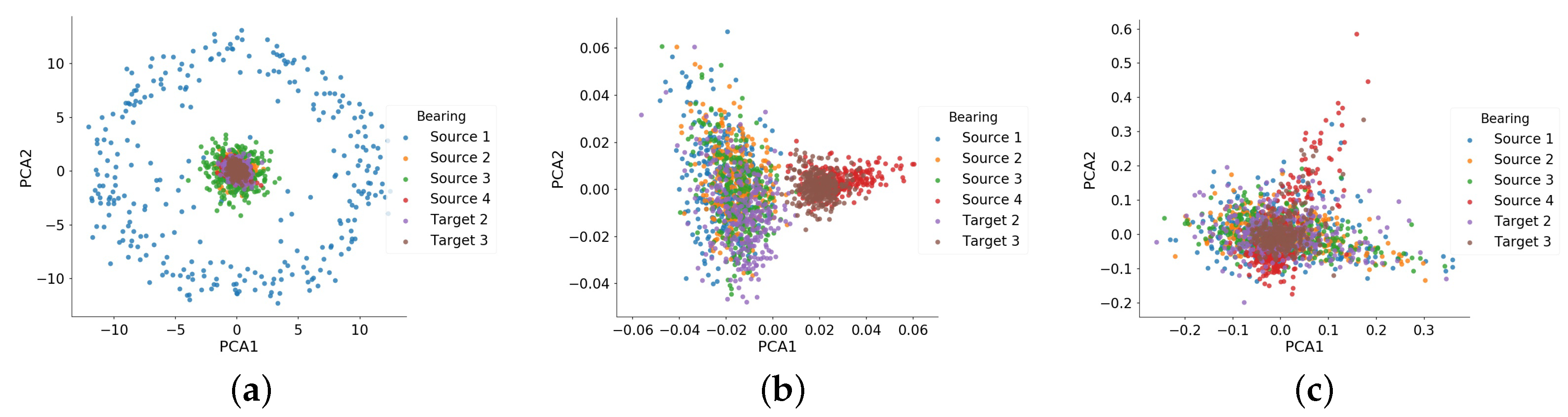
4.3.2. Extraction of Common Feature Representation by Transfer Learning
4.3.3. State Assessment Using RDA
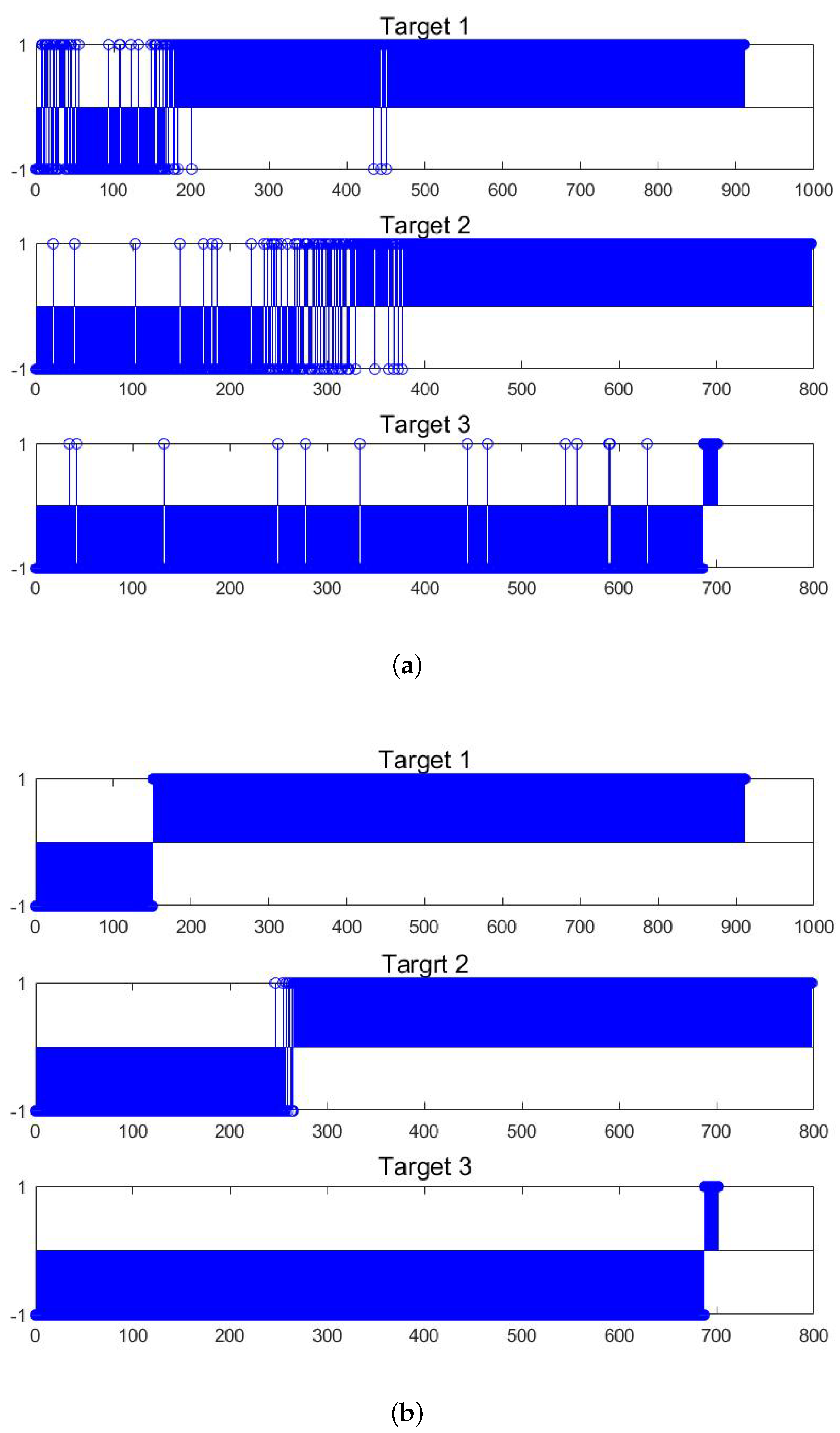
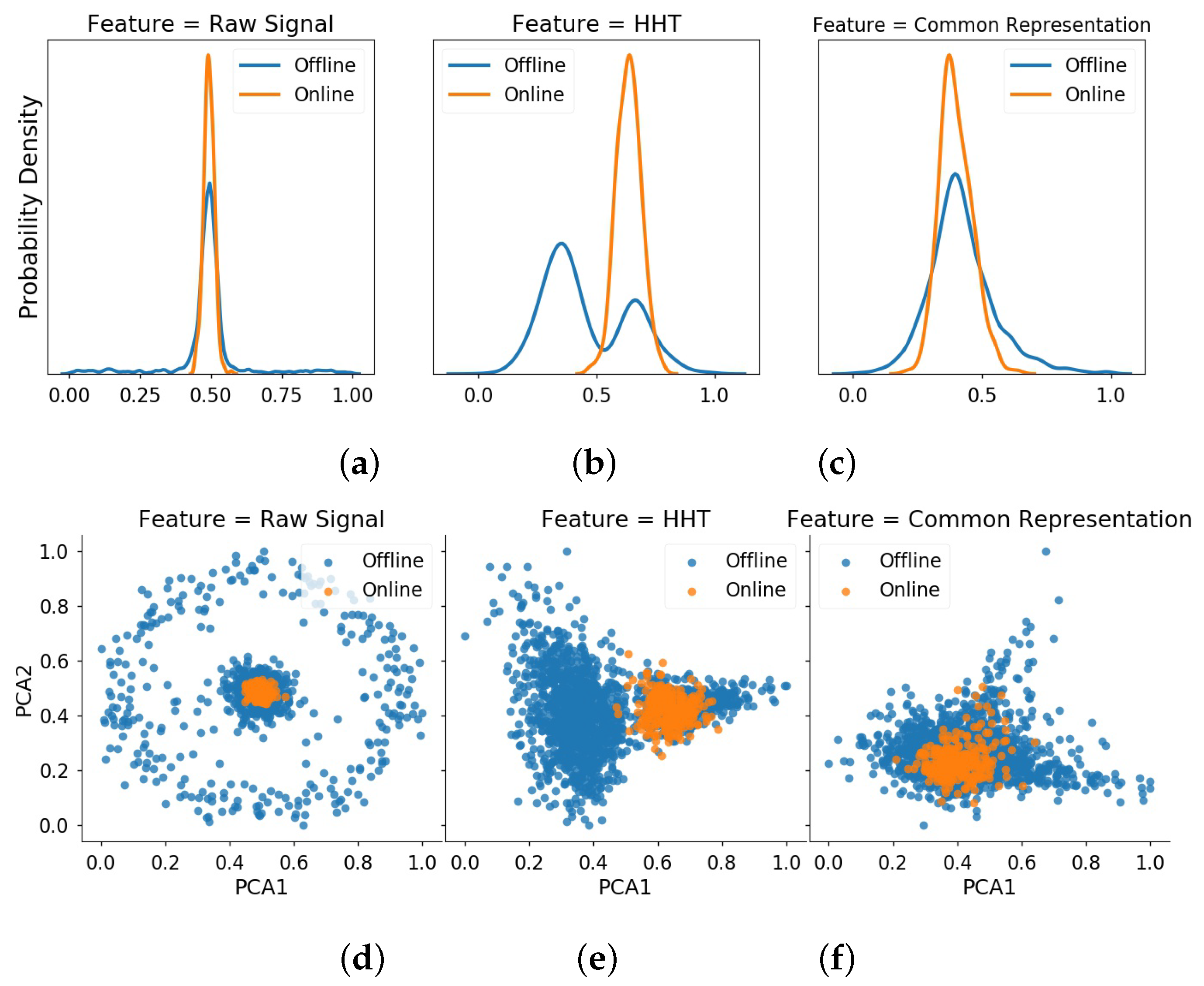
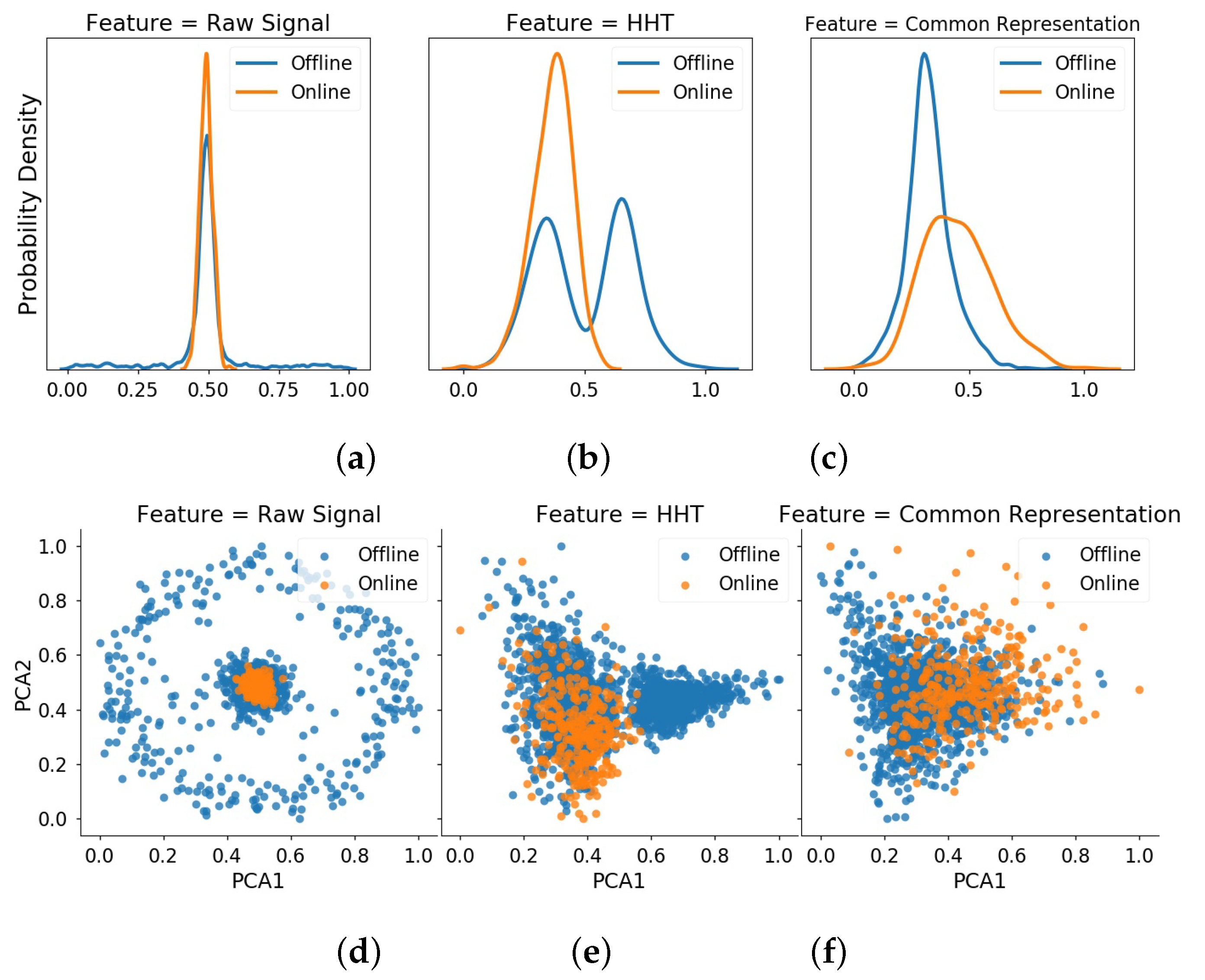
4.3.4. Comparative Results of Online Detection
4.4. Experiment 2
5. Comparative Experiment
6. Conclusions
- (1)
- Deep transfer learning works well to extract a common feature representation for different auxiliary bearings, which is vital in online detection.
- (2)
- State assessment can be achieved in a low-rank subspace by RDA, which will eliminate the negative effect of signal fluctuation and bring the robustness of detection model.
- (3)
- The proposed method is suitable for online detection with earlier detection location and less number of false alarms, as it can reduce the inconsistent data distribution between auxiliary bearings and target bearing.
Author Contributions
Funding
Conflicts of Interest
References
- Mao, W.; Feng, W.; Liang, X. A novel deep output kernel learning method for bearing fault structural diagnosis. Mech. Syst. Signal Process. 2019, 117, 293–318. [Google Scholar] [CrossRef]
- Mao, W.; He, L.; Yan, Y.; Wang, J. Online sequential prediction of bearings imbalanced fault diagnosis by extreme learning machine. Mech. Syst. Signal Process. 2017, 83, 450–473. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Tabrizi, A.; Garibaldi, L.; Fasana, A. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine. Meccanica 2015, 50, 865–874. [Google Scholar] [CrossRef]
- Li, F.; Wang, J.; Chyu, M. Weak fault diagnosis of rotating machinery based on feature reduction with Supervised Orthogonal Local Fisher Discriminant Analysis. Neurocomputing 2015, 168, 505–519. [Google Scholar] [CrossRef]
- Ocak, H.; Loparo, K. A new bearing fault detection and diagnosis scheme based on hidden Markov modeling of vibration signals. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; pp. 3141–3144. [Google Scholar]
- Tao, X.; Chen, W.; Du, B.; Xu, Y. A novel model of one-class bearing fault detection using SVDD and genetic algorithm. In Proceedings of the 2007 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; pp. 802–807. [Google Scholar]
- FernáNdez-Francos, D.; MartíNez-Rego, D.; Fontenla-Romero, O. Automatic bearing fault diagnosis based on one-class ν-SVM. Comput. Ind. Eng. 2013, 64, 357–365. [Google Scholar] [CrossRef]
- Ma, H.; Hu, Y.; Shi, H. Fault detection and identification based on the neighborhood standardized local outlier factor method. Ind. Eng. Chem. Res. 2013, 52, 2389–2402. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Xiong, J. Fault diagnosis of a rolling bearing using wavelet packet denoising and random forests. IEEE Sens. J. 2017, 17, 5581–5588. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Guo, L. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, X. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10, 1687814018817184. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Zhang, R.; Tao, H.; Wu, L. Transfer learning with neural networks for bearing fault diagnosis in changing working conditions. IEEE Access 2017, 5, 14347–14357. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 136–144. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. arXiv 2018, arXiv:1804.07265. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Zuo, M. Predicting remaining useful life of rolling bearings based on deep feature representation and transfer learning. IEEE Trans. Instrum. Meas. 2020. In press. [Google Scholar] [CrossRef]
- Lu, W.; Li, Y.; Cheng, Y. Early fault detection approach with deep architectures. IEEE Trans. Instrum. Meas. 2018, 67, 1679–1689. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2017, 65, 1539–1548. [Google Scholar] [CrossRef]
- Mao, W.; Chen, J.; Liang, X. A New Online Detection Approach for Rolling Bearing Incipient Fault via Self-Adaptive Deep Feature Matching. IEEE Trans. Instrum. Meas. 2020, 69, 443–456. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Borgwardt, K.; Gretton, A.; Rasch, M. Integrating structured biological data by kernel maximum mean discrepancy. Bioinformatics 2006, 22, 49–57. [Google Scholar] [CrossRef]
- Lu, W.; Liang, B.; Cheng, Y. Deep model based domain adaptation for fault diagnosis. IEEE Trans. Ind. Electron. 2016, 64, 2296–2305. [Google Scholar] [CrossRef]
- Mao, W.; Liu, Y.; Ding, L. Imbalanced Fault Diagnosis of Rolling Bearing Based on Generative Adversarial Network: A Comparative Study. IEEE Access 2019, 7, 9515–9530. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Li, Y. Bearing fault diagnosis with auto-encoder extreme learning machine: A comparative study. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1560–1578. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Adv. Neural Inf. Process. Syst. 2009, 2080−2088. [Google Scholar]
- Zhou, C.; Paffenroth, R. Anomaly detection with robust deep autoencoders. In Proceedings of the KDD 17: The 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 Augest 2017; pp. 665–674. [Google Scholar]
- Tax, D.; Duin, R. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Wang, B.; Lei, Y.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2019, 1–12. [Google Scholar] [CrossRef]
- Chang, C.; Lin, C. LIBSVM: A library for support vector machines. ACM trans. Intel. Syst. Technol. (TIST) 2011, 2, 27. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Liang, X. Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings. IEEE Trans. Ind. Electron. 2017, 64, 6506–6517. [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2010, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Gong, B.; Shi, Y.; Sha, F. Geodesic flow kernel for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2066–2073. [Google Scholar]
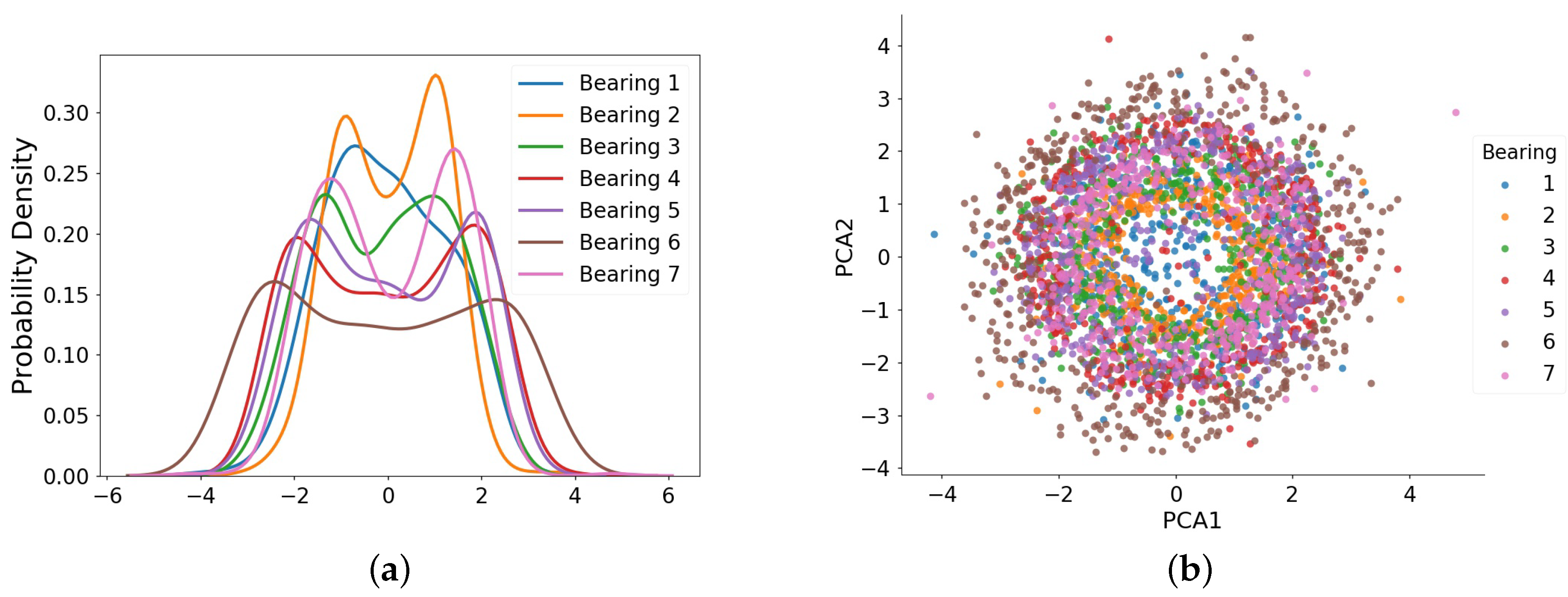
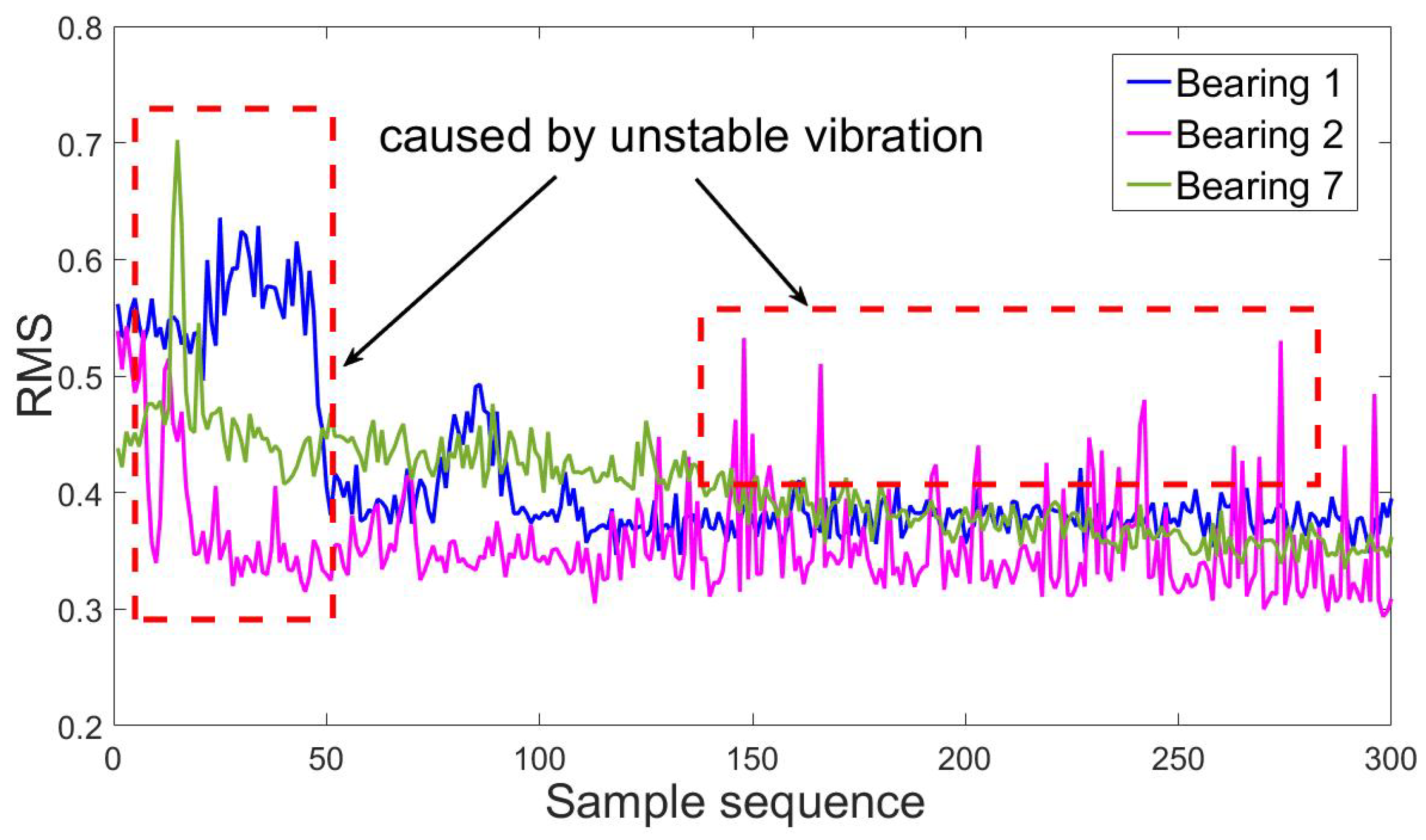



| Bearing in the Experiment 1 | Actual Bearing |
|---|---|
| Source 1 | Bearing1-1 |
| Source 2 | Bearing1-2 |
| Source 3 | Bearing1-3 |
| Source 4 | Bearing1-4 |
| Source 5 | Bearing1-5 |
| Source 6 | Bearing1-6 |
| Source 7 | Bearing1-7 |
| Target 1 | Bearing2-1 |
| Target 2 | Bearing2-2 |
| Target 3 | Bearing2-6 |
| Bearing in the Experiment 2 | Actual Bearing |
|---|---|
| Source 1 | Bearing 1-1 |
| Source 2 | Bearing 1-2 |
| Source 3 | Bearing 1-3 |
| Source 4 | Bearing 1-4 |
| Target 1 | Bearing 2-1 |
| Target 2 | Bearing 2-2 |
| Target 3 | Bearing 2-3 |
| Training Bearing | Normal State Period | Fault State Period |
|---|---|---|
| Source 1 | [1–1405] | [1405–2803] |
| Source 2 | [1–826] | [827–871] |
| Source 3 | [1–1174] | [1175–2375] |
| Source 4 | [1–1087] | [1088–1428] |
| Source 5 | [1–2443] | [2444–2463] |
| Source 6 | [1–1590] | [1591–2448] |
| Source 7 | [1–2212] | [2213–2559] |
| Target 2 | [1–255] | [255–797] |
| Target 3 | [1–688] | [688–701] |
| Method | PHM Bearing1-1 | XJTU-SY Bearing1-1 | ||
|---|---|---|---|---|
| Detection | False | Detection | False | |
| Result | Alarm | Result | Alarm | |
| 1. HHT + One-class SVM | 1410 | 138 | 967 | 52 |
| 2. RMS + One-class SVM | 1640 | 27 | 945 | 19 |
| 3. Kurtosis + One-class SVM | 2152 | 117 | 1023 | 117 |
| 4. HHT + SVDD | 1525 | 116 | 958 | 93 |
| 5. RMS + SVDD | 1735 | 20 | 959 | 20 |
| 6. Kurtosis + SVDD | 1642 | 58 | 1163 | 134 |
| 7. HHT + LOF | 2050 | 4 | 944 | 5 |
| 8. RMS + LOF | 2023 | 52 | 1275 | 8 |
| 9. Kurtosis + LOF | 2381 | 65 | 1372 | 33 |
| 10. HHT + iFOREST | 1556 | 82 | 1041 | 25 |
| 11. RMS + iFOREST | 2336 | 69 | 961 | 31 |
| 12. Kurtosis + iFOREST | 2057 | 159 | 1257 | 93 |
| 13. BEMD + AMMA | 1900 | – | 1130 | – |
| 14. SDFM | 1374 | 42 | 930 | 27 |
| 15. TCA + SVDD | 1427 | 33 | 986 | 28 |
| 16. GFK + SVDD | 1573 | 20 | 1146 | 17 |
| 17. Our method | 1401 | 14 | 937 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, W.; Zhang, D.; Tian, S.; Tang, J. Robust Detection of Bearing Early Fault Based on Deep Transfer Learning. Electronics 2020, 9, 323. https://doi.org/10.3390/electronics9020323
Mao W, Zhang D, Tian S, Tang J. Robust Detection of Bearing Early Fault Based on Deep Transfer Learning. Electronics. 2020; 9(2):323. https://doi.org/10.3390/electronics9020323
Chicago/Turabian StyleMao, Wentao, Di Zhang, Siyu Tian, and Jiamei Tang. 2020. "Robust Detection of Bearing Early Fault Based on Deep Transfer Learning" Electronics 9, no. 2: 323. https://doi.org/10.3390/electronics9020323
APA StyleMao, W., Zhang, D., Tian, S., & Tang, J. (2020). Robust Detection of Bearing Early Fault Based on Deep Transfer Learning. Electronics, 9(2), 323. https://doi.org/10.3390/electronics9020323






