Abstract
Path planning for mobile agents is one of the areas that has drawn the attention of researchers’, as evidenced in the large number of papers related to the collision-free path planning (CFPP) algorithm. The purpose of this paper is to review the findings of those CFPP papers and the methodologies used to generate possible solutions for CFPP for mobile agents. This survey shows that the previous CFPP papers can be divided based on four characteristics. The performance of each method primarily used to solve CFPP in previous research is evaluated and compared. Several methods are implemented and tested in same computing environment to compare the performance of generating solution in specified spatial environment with different obstacles or size. The strengths and weakness of each methodology for CFPP are shown through this survey. Ideally, this paper will provide reference for new future research.
1. Introduction
The usage of mobile agents (MAs) including unmanned aerial vehicles (UAVs), autonomous robots and automated guided vehicles (AGVs), in areas, such as container terminals, delivery to customers or manufacturing processes only continues to increase [1]. The design problem of Collision-free path planning (CFPP) is to determine a collision-free path of MAs within the target space of a specific environment [2]. Research also refers to this design problem as motion planning or piano mover’s problem [3]. The researchers have studied CFPP problem while using several kinematic constraints, including point robots or using robots with specific degree of freedom (DOF) [4,5,6]. Autonomous robots are also required to decide their motion using the logic. Researches have conducted extensive research in response to the increasing importance of MAs.
In this paper, we have arranged the survey papers of the CFPP based problem according to the paper’s original research purpose. Schwartz & Sharir [7] focused on classical geometry, topology, algebraic geometry, algebra, and combinatorics. Additionally, they briefly discuss the characteristic and complexity of geometric algorithms that are relevant to the CFPP problem. Hwang & Ahuja [8] researched the different methodologies, obstacles, and algorithms, and discussed the characteristics of the problem known as the gross motion plan. Sariff & Buniyamin [9] reviewed the algorithms for solving CFPP problem in different environments. The study further briefly presented the advantages and disadvantages of the algorithms. Masehian and Sedighizadeh [10] conducted a 35 years period chronological survey regarding the classic and meta-heuristic algorithms for the CFPP problem. Goerzen et al. [11] found that UAVs have significant differing issues than that of other robots, because it operates in a three-dimensional (3D) environment. Roberge et al. [12] reviewed the performance of algorithms, parallel genetic algorithm, and particle swarm optimization pertaining to the non-deterministic CFPP problem. In addition, the researchers examined the dynamic properties of a UAV’s path in a complex three-dimensional environment. A survey of heuristic based algorithm for solving CFPP was recently presented [13]. The research summarized chronological changes and sorted studies by algorithms, which were nature-inspired methods, fuzzy logic, neural networks, and the potential field method. The frequency of the problem attributes is also reviewed in the paper. Schwarting et al. [14] reviewed and provided emerging trends in autonomous problems. The paper summarized problems, such as integration of automation and safety guarantees when applied to robots.
Researchers in different fields have conducted similar studies; hence, there are problems with regards to the definitions and terms. For example, some of the papers use the name of problems as mover’s problem [15], motion planning problem [16] or path planning problem [2]. Numerous methodologies are provided in the research while using different key words [5,13,17,18]. However, a comparison of methodologies is rarely studied. Previous research has focused on the different characteristics of the CFPP problem, such as sampling-based algorithm [19], or has used a very small number of searching algorithms [12]. On the other hand, researches have not focused on the differences in terminology and meanings. In the writers’ opinion, this lack of uniformity and conformity in terminology makes it difficult to select and decide on an appropriate algorithm. Therefore, the objectives of this study are as follows. First, the purpose of this research is to unify the name and attributes. Secondly, to provide a method to classify algorithms for solving the problem. Third, the performance of the algorithms for solving CFPP is measured within a fundamental environment. These contributions will enable researchers, who study the CFPP problem to grasp the key point in a problem. Finally, researchers will be better able to choose searching algorithms, through the comparison of the different algorithms.
The rest of this paper is divided for four sections. The CFPP problem is defined in Section 2 and four different categories of CFPP problem are proposed. In Section 3, a plan of experiment for searching algorithms performance review is briefly introduced. Flowcharts of the algorithms are shown and environments for testing are suggested. Additionally, a method for tuning parameters, which are components of metaheuristic algorithms, is concisely shown. The results of the experiments are organized and analyzed in Section 4. In the final section, a conclusion and a summary are presented.
2. CFPP
The goal of collision-free path planning (CFPP) problem is helping MAs or robots to find a safe path from the starting point to ending (goal) point [2]. The path from a result of the CFPP problem is considered to be an effective bypass for MAs. The effectiveness is discussed from this perspective, which is the shortest distance for MAs. Additionally, this can be researched with multi-objective model, such as reducing resource consumption with shorter distances or finding a good solution in shorter time. Four different attributes are required to define the problem type; environment type (Env.T.; Section 2.1), environmental representation (Env.R.; Section 2.2), searching algorithm (S.Alg.; Section 2.3), and experimental type (Exp.T.; Section 2.4). Additionally, related works that emphasize and improve at least one point of any one of these characteristics are necessary to define the problem type. Details of the categories are shown in Figure 1.
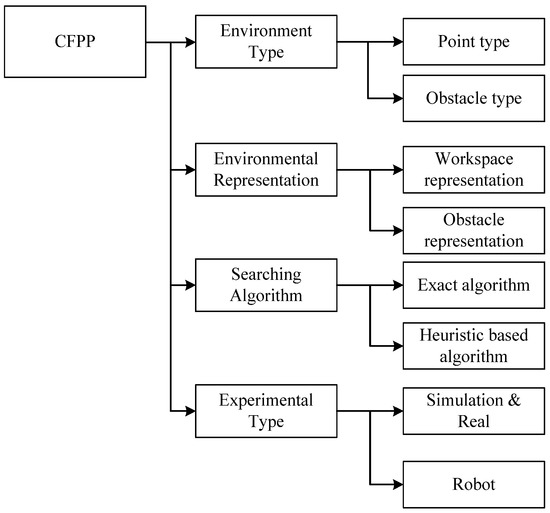
Figure 1.
Characteristics of the collision-free path planning (CFPP).
In order to deliver information efficiently, this paper uses shorthand notation. The notation is organized in Table 1.

Table 1.
Shorthand notation for the tables.
2.1. Environment Type
Environment types in CFPP problem are divided specifically, as follows: obstacle type (O.T.) and point type (P.T.). Each type has specific characteristics and detail descriptions of the characteristics are proposed as follows.
Firstly, the obstacle type is classified as static or dynamic [6,20]. Figure 2a describes static obstacle type and Figure 2b is an example of dynamic obstacle type. The static obstacle environment, which is also called the stationary obstacle environment, is a basic form of the CFPP problem. In this case, the obstacles do not change their shape or position. The CFPP problem in a static environment is the most basic model of the CFPP. This is one of the reasons why many papers use a static environment assumption [13]. The dynamic obstacle environment, which is also called the moving obstacle, can change the obstacle’s shape time dependently. This case considers the velocity and acceleration of MAs.
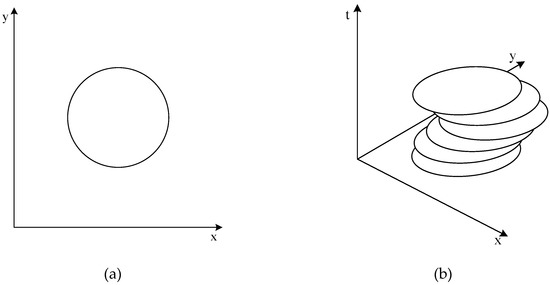
Figure 2.
Illustrations of the obstacle having different obstacle type: (a) Static obstacle; and, (b) Dynamic obstacle.
Second, point type is classified as certain or uncertain [21]. As there is inherent uncertainty in the MA’s sensing, point type should be assumed as certain or uncertain. Certain point type is assumed when the MAs position and goal point is an exact location. The assumption is often used in testing novel approaches while using simulation, because uncertain problem makes it difficult to solve the problem. Uncertain point type is set when the MA’s point and goal point is not known exactly. MAs use several sensors to recognize space. The sensors may include some errors, which MAs must recognize in an uncertain space. The type makes the problem more challenging than with a certain point type. This is one of the reasons why it is difficult to solve a CFPP problem with real MAs. The problem is solved while using the stochastic technique, such as the Monte-Carlo method [22,23,24].
2.2. Environmental Representation
Environmental representations in a CFPP problem have two different types: workspace representation (W.R.) and obstacle representation (Ob.R.). Diverse studies about these have been previously researched. The details of these studies are characterized below.
First, workspace representation has two representations: the coordinate system model and the network model. The coordinate system model uses Algebra for describing the environment and the MAs’ motion. This problem is called the Findspace problem, which is one aspect of spatial planning [25]. The Findspace problem has three different workspaces; the polygonal workspace; the polyhedral workspace; and, the semi-Algebraic workspace [21]. In addition, convexity and non-convexity are also important aspects of the Findspace problem. Simply, the greater the number of edges and vertices in a workspace representation, the greater the complexity of the problem. Therefore, a polyhedral workspace would be more difficult to solve for than a polygonal workspace [6]. Network model, which is also known as the Roadmap approach, uses links and nodes for describing the environment. In this model, researchers have modelled the routes of the MA’s as links and nodes using algorithms, such as the Voronoi diagram, the Visibility Graph, the Rapidly-exploring random tree, and the Probabilistic roadmap. Additionally, the algorithms are mainly differentiated from each other mainly by style generated. These include: the sampling-based algorithm and the geometric modeling algorithm [17]. LaValle et al. [26] conducted extensive researched of the sampling-based algorithm while using the Monte Carlo sampling method.
Their conclusions suggest that the basic grid network algorithm provides better performance in certain cases than does a sampling-based algorithm. Thrun et al. [23] proposed a model wherein the Monte Carlo localization is combined with the sampling-based algorithm. Janson et al. [24] posit that the Monte Carlo Motion Planning (MCMP) is effective in solving the CFPP problem. Englot and Hover [27] suggested the sampling-based algorithm under ACO framework to solve multi-goal CFPP problems. This technique allows for a solution that can take into account multi-objects, such as computational complexity and optimality. Ichter et al. [28] studied the sampling-based algorithm in a learning-based framework where non-uniform sampling strategies are used for the CFPP problem in “huge” spaces.
The sampling-based algorithm includes two common algorithms: the Probabilistic roadmap and the Rapidly-exploring random tree. Kavraki et al. [29] solve the CFPP problem for articulated robots while using two phases: the Probabilistic roadmap and the heuristic for searching within the roadmap. The proposed method can be applied to any holonomic robot. The theoretical performance of the Probabilistic roadmap was rarely studied before Kavraki et al. [19]. The paper studies the failure probability of connecting two points. Also, the relationship among the number of nodes, failure probability, and length of paths are studied. The Probabilistic roadmap and the Rapidly-exploring random tree are also studied in practical way with various robots [30,31]. Several simulated and real experiments using specific robots are performed. Complex and large environments, such as dynamic obstacles or urban areas, are considered in the experiments. Kim et al. [32] propose the Tangent Bundle Rapidly exploring random tree (TB-RRT) in order to improve the efficiency of the algorithm in a large space. Also, related works under complex environment are studied in succession [33,34]. A centralized case, such as spot-welding station with two to six robot manipulators in automobile manufacturing field, is researched and an application is made for the case [35,36]. These papers purport that centralized planning is more efficient than decentralized planning. Additionally, the sampling-based algorithms are applied to a geometrically complex problem and a multi-robot problem [37,38]. Wilmarth et al. [39] argue that the basic Probabilistic roadmap is an ineffective method for solving the CFPP problem in a narrow space. Thus, a novel algorithm, named MAPRM, is suggested for solving specific narrow space. Saha et al. [40] concluded the small-step retraction method can be applied to the CFPP problem. Meanwhile, the CFPP problem can be expanded to the tour problem, as can the traveling-salesman problem or task-planning problem [41,42]. The algorithms are mainly divided into two divisions: path finding and tour (sequence) finding in order to solve the problem,
Meanwhile, several papers have evaluated the performance of the sampling-based algorithm. The sampling configuration and probability measure are affected by the performance of the Probabilistic roadmap [43]. Further, Karaman and Frazzoli [44] studied the performance of the Probabilistic roadmaps and Rapidly-exploring random trees sampling-based algorithms. Recently, Marble and Bekris [45] discuss and introduce a method providing robust solution qualities. More details about related to sampling-based algorithm research are organized in Table 2.

Table 2.
Classification of the papers while using the sampling-based algorithm.
Whatever path that is generated in a network model, should be smoothed before applying to MAs [17]. Smoothing affects the performance of the algorithm [46], and it has been studied by some papers [47,48].
Secondly, Hwang and Ahuja [8] propose six basic obstacle representations that are chosen in consideration of workspace representation and an approximation of the obstacles. These six obstacle representations are: original objects, gird, cell tree, polygonal approximation, constructive solid geometry, and boundary representation. The representation styles are shown in Figure 3. These obstacle representations are chosen by workspace representation and approximation of the obstacles.
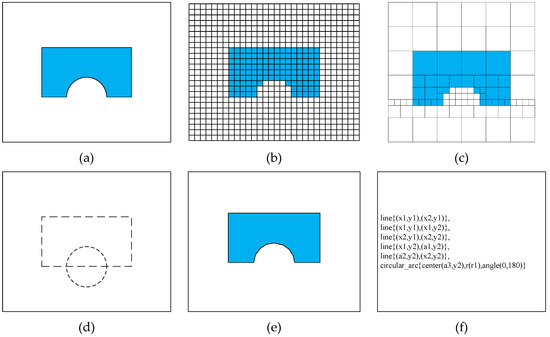
Figure 3.
Six different workspace representations [8]: (a) Original object; (b) Grid; (c) Cell tree; (d) Constructive solid geometry; (e) Polygonal approximation; and, (f) Boundary representation.
2.3. Searching Algorithms
Searching algorithms or query process in probabilistic roadmaps are chosen by workspace representation. Some searching algorithms are applied to specific representations. For example, A* and Dijkstra algorithms are only applicable under network conditions. For instance, to solve problem with network, A*, Dijkstra algorithm or heuristic-based algorithms are often used. On the other hand, optimal approaches are used for problem under a coordinate system. There is extensive research that provides searching algorithms for several conditions in reasonable time. The algorithms can be classified as classic algorithms or heuristic-based algorithms [10,13,18].
2.3.1. Classical Algorithm
Dijkstra Algorithm is a common used algorithm for solving the network problem [52]. This algorithm offers an optimal path in a network, when all of the network link distances are positive. The A* algorithm is also frequently used in order to solve the shortest path problem on network [53]. Some methodologies, which are a combination of a Voronoi diagram and the Dijkstra algorithm, are provided by several researches [54,55]. Additionally, the Dijkstra algorithm was studied as query process of probabilistic roadmaps [33,56]. An application was suggested for solving the CFPP problem while using the Dijkstra algorithm [57]. A* algorithm is broadly used to solve the CFPP problem under network conditions. Several research papers related to a visibility graph were applied to A* algorithm to solve CFPP problem [2,20,58]. On the other hand, some papers provide methods applied under a sampling-based environment [59,60]. Many papers suggested novel algorithms, which were developed using Dijkstra’s algorithm or A* algorithm [61,62,63]. Papers about A* and Dijkstra algorithms are shown in Table 3.

Table 3.
Classification of the papers using the exact algorithm.
2.3.2. Heuristic Based Algorithm
There are many heuristic-based methods for the CFPP problem. Wavefront algorithm is one of the heuristics that adopts the idea of a potential field and it was applied with various characteristics. For instance, the Wavefront algorithm is used for solving a problem with three-dimensional normal distributions transformations [65]. Several kinds of the metaheuristic are applied to the CFPP problem that have a network or coordinate system.
Evolutionary algorithms, such as the Genetic algorithm (GA), are usually studied under network environments [66,67,68,69] that are related to CFPP. Additionally, several algorithms are developed for under coordinate system conditions [70,71,72,73]. Some novel algorithms that are based on GA are provided from related works [74,75,76,77,78]. GA is one of the most applicable algorithms to solve the CFPP problem with multi-robot [79]. Table 4 briefly shows those papers which use Wavefront or GA.

Table 4.
Classification of the paper using the heuristic-based algorithm (Wavefront and Genetic algorithm (GA)).
Simulated Annealing (SA) is typically combined with the potential field method [80,81,82,83,84]. The other searching algorithms, such as general heuristic algorithm, population-based metaheuristic algorithm and fuzzy logic, and environmental representations, are also researched with SA [85,86,87,88,89,90]. SA based algorithms have also been applied in CFPP problems to solve vehicle congestion in smart cities. [91]. Papers that are based on SA, which are cited above, are organized in Table 5.

Table 5.
Classification of the paper using the heuristic-based algorithm (Simulated Annealing (SA)).
Particle swarm optimization (PSO) was originally defined in a continuous environment, so much CFPP research is studied under a coordinate system [46,92,93,94,95,96,97,98,99,100]. Chen and Li [99] use a distinguishable method for obstacle representation, which is circle approximation (Ci.A.). They assume the obstacles as being a circle. On the other hand, some research provide methods, which are PSO-based algorithms in a network condition [101,102,103,104]. Some research has focused on solving the multi-robots CFPP problem while using PSO [105,106]. In Table 6, additional information from previous research related to PSO is shown.

Table 6.
Classification of the paper using the heuristic-based algorithm (PSO).
Ant colony optimization (ACO) is usually studied under varying network environments, such as grid network and Voronoi diagram [107,108,109,110,111,112,113,114,115,116,117,118,119]. Few papers, likewise, researched GA with ACO and coordinate system [120]. A paper, which solves the CFPP problem with automated underwater vehicles (AUV), is studied [121]. This paper suggests an ACO based algorithm to solve large-scale CFPP problems. Table 7 organizes details regarding papers based on ACO.

Table 7.
Classification of the paper using the heuristic-based algorithm (ant colony optimization (ACO)).
2.4. Experimental Type
In experimental type, two characteristics, which are the robot type and experimental method, should be decided. Many previous works researched under different types of the robot, such as car-like robots, UAV, humanoid, and several degree of freedom (DOF) robots. Each robot has its own moving limitation. This constraint is a cause of different kinematic constraints [21]. Kinematic constraints should be considered under experimental method. When making experiments with real robot, computation, and resources for solving the problem is restricted. On the other hand, the simulation method might have some assumptions, which are different from real robot. The assumptions make a problem simplified to solve and this simple problem contributes to test novel methodologies.
3. Experiments Plan
In this paper, a simulation experiment for performances is considered under simple environments and a single point robot, which is able to move without kinematic constraints. The experiment is contributed to measure the performance of basic searching algorithms, as follows; Dijkstra algorithm, A* algorithm, Wavefront algorithm, Genetic algorithm, Simulated annealing, Ant colony optimization, and particle swarm optimization. Environment type is assumed as certain point type and static obstacle. The experiment uses grid network in order to make environment simple, and obstacles are represented as grid.
The object of the algorithm is to find a shortest path. Therefore, the objective function of the comparison experiment is formulated, as follows [74].
The function is representing a path length from to on network and the meaning of is network distance from node a to node b.
3.1. Algorithms
The Dijkstra algorithm, A* algorithm and Wavefront algorithm have been the most commonly applied algorithms applied to solve the CFPP problem. However, other metaheuristic algorithms have been applied, each a modified version based on flow and heuristics. The paper reviewed each simple form of each algorithm. The flows for each metaheuristic algorithm are shown in Figure 4, Figure 5, Figure 6 and Figure 7.
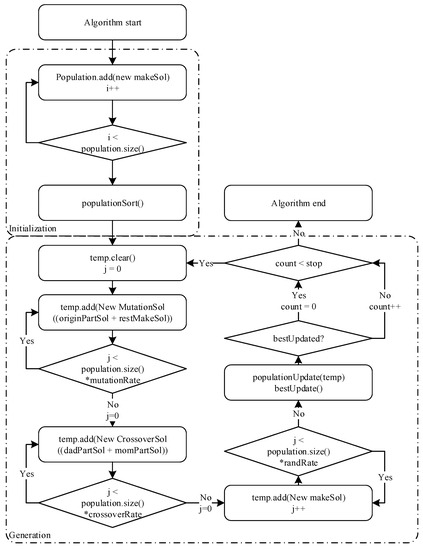
Figure 4.
The flowchart of GA.
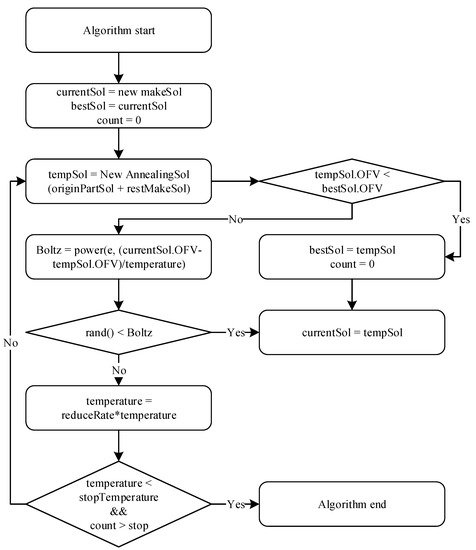
Figure 5.
The flowchart of SA.
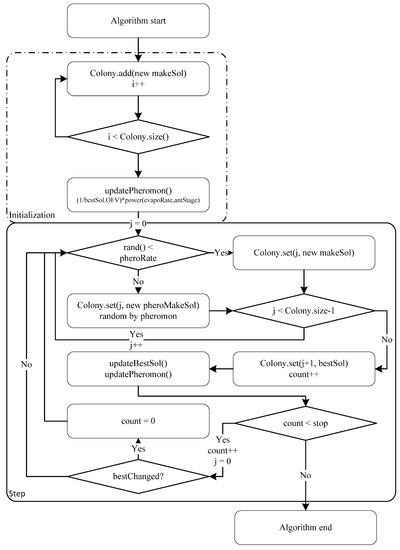
Figure 6.
The flowchart of ACO.
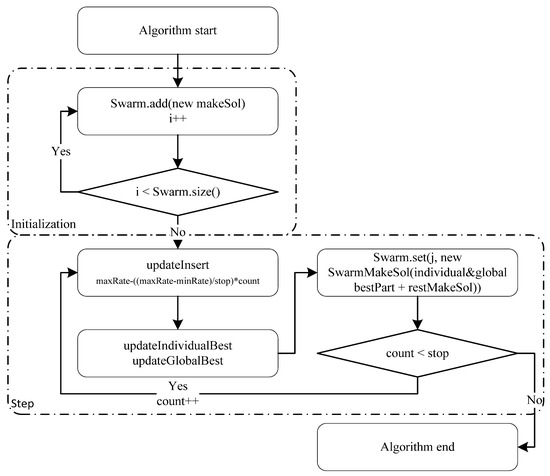
Figure 7.
The flowchart of PSO.
In Figure 4, flow of GA is divided into two parts: initialization and generation. The initialization part is initializing the GA’s population set, which is then improved in Generation part. The generation part has three methods: crossover, mutation, and random generation. Each new population set is generated through these methods and the next generations are updated based on the population set. The generation number is counted when the best solution is not updated and resets to zero when the best solution is updated. Executing a generation count completes the algorithm.
The flow of SA is shown in Figure 5. The algorithm has two different stop criteria; temperature and loop count. When a new solution in next loop fails the Boltzmann factor check, a pre-determined reduction rate reduces the temperature. When a new solution in next loop passes the Boltzmann factor check, the loop number is increased when the best solution is not updated. Again, as in Figure 4, the number is reset to zero when updating the optimal solution.
ACO flow has two steps, initialization and improvement step, as shown in Figure 6. Ant colony is initialized in the initialization using the same method used with other algorithms. In the improvement step, a solution will be generated in one of two ways. The first way is a pheromone concept and the other is a reusing method in Initialization step. Each link has its own probability and ants find a path following the probability in order to make pheromone concept. The link probability is added by the following equation.
the improvement step has a step count trigger for escaping the loop. The number is increased by one, when the flow pass a loop and it is set as zero, when the best solution is updated.
In Figure 7, flow of PSO is introduced as two parts: initialization and improvement step. The algorithm has a similar structure to that of ACO. However, instead of concept of pheromone, PSO uses a concept of inertia rate for mimicking the movement of swarm. Previous solutions are destroyed by the inertia rates and new solutions are rebuilt using the best solution and an overlapped method for making a new solution. A number for stopping criteria is counted by passing the loop and the number is set as zero, when the best global solution is updated.
A method for making a new initial solution influences the performance of the algorithms. Thus, in Figure 4, Figure 5, Figure 6 and Figure 7, the algorithms use the same method, called ‘makeSol’ in order to limit its effects on the algorithms. The flow of the method which includes a concept of potential field attempting to connect to the goal point is shown in Figure 8.
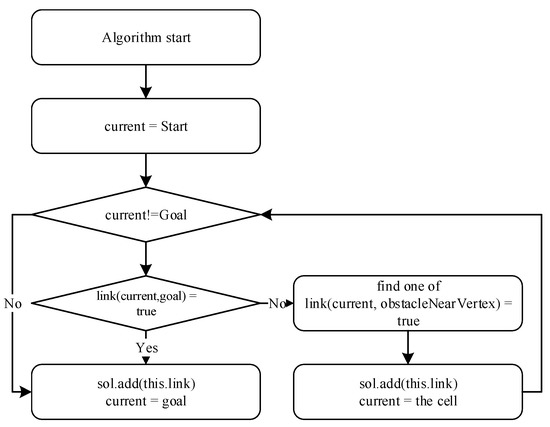
Figure 8.
The flowchart of ‘makeSol’ logic.
3.2. Envionments
In order to test the performance under several different environments, this research uses typical environments. In this paper, three different environment sizes are used for the experiments. Figure 9 shows six environments which have 10 × 10 cells. These environments are formed archetypal patterns, such as ‘n’ shape, rectangles and slots. Environments, which have ‘n’ shape obstacle, are presented in Figure 9a,b,d. Figure 9c is a simple environment with squared obstacle and Figure 9e has slot obstacles which are known as difficult problem. The obstacle in Figure 9f is a part of environment in the paper by Karaman [44].
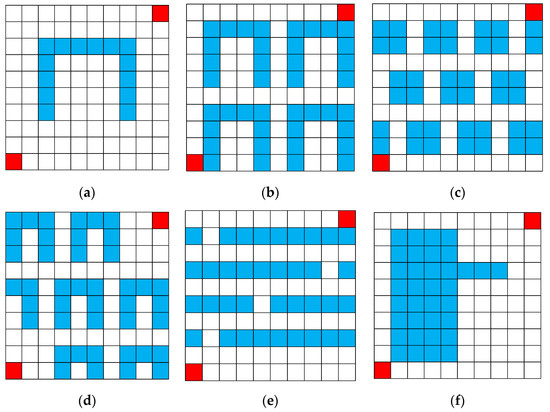
Figure 9.
The experimental configuration of the 10 × 10 cells: (a) 10_1n; (b) 10_4n; (c) 10_11s; (d) 10_7n; (e) 10_4ch; and, (f) 10_1o.
Two environments with 20 × 20 cells are presented on Figure 10. These environments also are reconfigured from the environment which is introduced in the paper by Karaman. An environment shown in Figure 10a is reproduced from the origin figure and Figure 10b is reconstituted based on the environment.
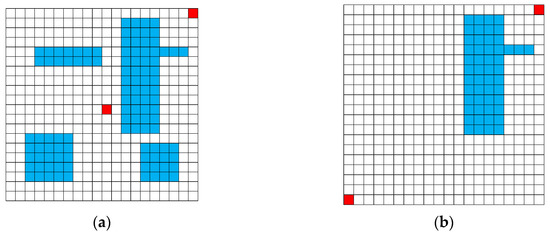
Figure 10.
The experimental configuration of the 20 × 20 cells: (a) 20_4o; (b) 20_1o.
Three environments with 40 × 40 girds are presented in in Figure 11. in order to measure the different performance by network size. The environments have same shape as the environments in Figure 9a,c,f, with the only difference being that the figures are divided into smaller grids.
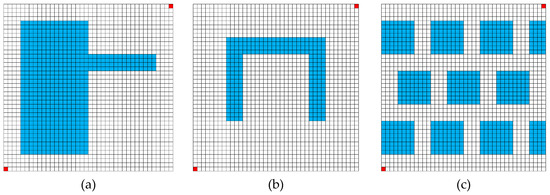
Figure 11.
The experimental configuration of the 40 × 40 cells: (a) 40_1o; (b) 40_1n; and, (c) 40_11s.
3.3. Metaheuristic Parameter
Metaheuristic algorithms are affected by their parameters. This is a reason why parameters must be carefully defined. The parameters used in this paper are determined by each searching algorithm and they are shown in Table 8. This research controlled two styles of parameters: population (ant and particle) number and stop criteria. The population number is set as 10 and stop criteria is set as 100.

Table 8.
Tuning range of the parameters.
Many experimental design techniques are used, including full factorial experimental design, in order to tune the algorithm parameters. In this paper, one of the packages in R, named ‘irace’, is used to set the algorithm parameters [122]. The software package makes automatic sampling configurations and measures the configurations while using Friedman’s test or t-test. Additionally, it is designed to redefine the distribution of the sampling and the package iterates this flow. The tuning procedure is performed for environment sets with a budget of 2000 experiments and the initial parameter ranges are defined, as follows: ; ; ; . Each configuration is measured total summation of all environments objective function value. Table 9 shows the result of the tuned parameter.

Table 9.
Tuned value of the parameters.
4. Computational Results
Using the tuned parameter by ‘irace’, this paper provides performance of the algorithms through repeatability. The experiment is run 1000 times under the same computational environment, with the following specifications: Intel Core i9-7900X central processing unit (CPU) (3.30GHz) processor; 32 GB of memory; and, Windows 10. The algorithm is developed using Java jdk11.0.1. The used environments for the experiment are three sizes are and they are shown in Figure 9, Figure 10 and Figure 11. The results of the experiment are organized in following tables. In the table, ‘processing time’ means that the shortest consumed time of best OFV. The result is rounded off to three decimal places. Additionally, the notated number ‘0.0’ on time means that measured time is less than 1 millisecond.
Table 10 and Table 11 show the results of experiment under 10 × 10 grid environments. The performances of metaheuristic algorithm are distinguished clearly, depending on obstacle type, the number of obstacles, and algorithms. SA takes a shorter time to solve the problem than population-based algorithms, which are GA, ACO, and PSO, but the solution quality of SA has larger fluctuations. In Table 10, some cases of reported time variances of GA and ACO are larger than others. This shows that the proposed GA and ACO have more unsettled performance than others in some cases. The algorithms have a weakness for a problem with a huge local optimum, termed the 10_4ch problem. Additionally, the larger number of obstacles, which are 10_7n and 10_11s problems, decreases the algorithm performance.

Table 10.
Experimental results of the metaheuristic algorithms within 10 × 10 case.

Table 11.
Experimental results of the other algorithms within 10 × 10 case.
The algorithms in Table 11 are heuristic algorithms, so each algorithm provides a unique solution. The algorithms are usually dominantly faster than metaheuristic algorithms when solving this size of problem. Wavefront algorithm is easily trapped in local optimum, such as 10_4ch, 10_4n, 10_7n, and 10_1n problem. However, the processing time of Wavefront algorithm is lower than other algorithms, except for the 10_4ch case. In this case, the algorithm cannot find a reasonable solution, because of local optimum. The algorithms find a unique and the best solution for each problem, as Dijkstra algorithm and A star algorithm function as exact algorithms with the condition of these experiments.
Figure 12 and Figure 13 show the best represented solutions while using the algorithm. Figure 12a shows the notation of the paths. Among the notations, ‘others’ means that all of the algorithms, except algorithms, which are shown individually in the figure. Some of them find the shortest path and the weakness of wavefront algorithm is easily found. In case of Figure 12d,f,h and Figure 13d, the solutions of wavefront algorithm are trapped by obstacles, which has ‘n’ shapes or small slots.
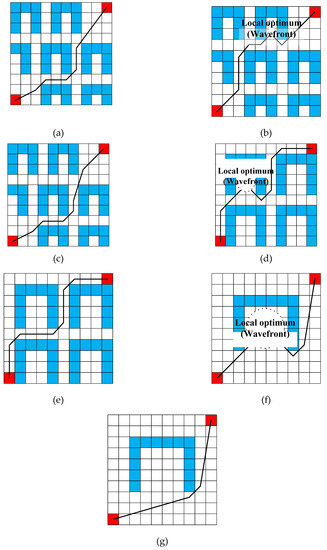
Figure 12.
The best path of each algorithms with ‘n’ shape obstacles (a) 10_7n (GA, SA, PSO); (b) 10_7n (Wavefront); (c) 10_7n (Others); (d) 10_4n (Wavefront); (e) 10_4n (Others); (f) 10_1n (Wavefront); and, (g) 10_1n (Others).
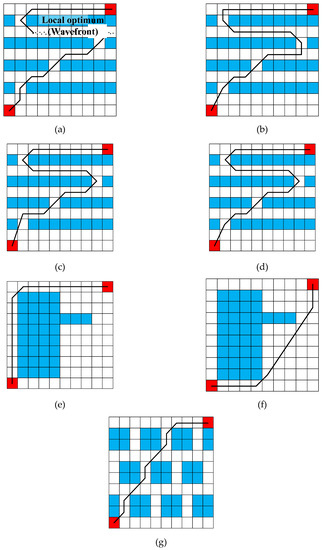
Figure 13.
The best path with the rest environment (a) 10_4ch (Wavefront); (b) 10_4ch (ACO); (c) 10_4ch (SA, PSO); (d) 10_4ch (Others); (e) 10_1o (Wavefront); (f) 10_1o (Others); and, (g) 10_11s (all algorithms).
The results with 20 × 20 cell environments are organized in Table 12 and Table 13. Average processing time of Dijkstra algorithm and A star algorithm is recognizably increased in comparison with the results of 10 × 10 grid environments. The value, which is OFV variance of 20_4o with SA, is noticeably larger than other OFV variance. On the other hand, the other, the processing time, is only marginally different. For example, wavefront algorithm has a similar level with the outcome from the smaller problem. Metaheuristic algorithms are still slower than other algorithms in this environment size and their average processing time have similar characteristics with the results of 10 × 10 grid environments.

Table 12.
Experimental results of the metaheuristic algorithms within 20 × 20 case.

Table 13.
Experimental results of the other algorithms within 20 × 20 case.
Table 14 and Table 15 show the experiment results under 40 × 40 cell. On this size of network, the searching speed of metaheuristic algorithms under some environments is faster than the speed of the Dijkstra algorithm and A star algorithm. For instance, PSO is a faster method for problems named 40_1o, 40_1n in comparison with the Dijkstra and A star algorithm. The best OFV of these experiments is the same as the outcome of the exact algorithm, which means that the OFV is the global optimum. The Wavefront algorithm is the fastest algorithm among these seven algorithms, but it is not able to escape from the local optimum, such as the 40_1n case. Meanwhile, in the case of 40_11s, the average processing time of GA and ACO significantly shows the weakness of the algorithms. The number of obstacles make their processing times increase when compared to 40_1o and 40_1n. Time variance is also unstable in the case with GA and ACO.

Table 14.
Experimental results of the metaheuristic algorithms within 40 × 40 case.

Table 15.
Experimental results of the other algorithms within 40 × 40 case.
Average processing time of these two algorithms is dramatically increased. In order to recognize the time changes clearly, Figure 14 is presented. The graph is the result of following equation.
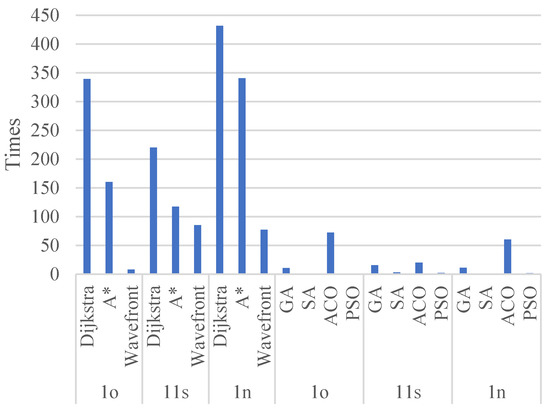
Figure 14.
The process time increasing rate between 40 probs and 10 probs.
As shown in the graph, Dijkstra and A star algorithms are remarkably more sensitive for network size than other algorithms, implying that network size is the weakness of the algorithms.
5. Conclusions
The problem of collision-free path planning has been studied in various areas resulting in many different criteria for studying the problem. These differences have given rise to several different terms with similar meanings, which, in turn, may actually hinder research for developing new methodologies for the problem of collision-free path planning. Meanwhile, many papers use varied searching algorithms, but their performances are not measured across the board under the exact same experimental conditions. The searching algorithm of research papers was selected from related works, because the algorithm is “typically used” and “good enough”. For this reason, some papers provide performance reviews under the same categories, such as sampling-based algorithms. However, the papers do not show the differences between the exact algorithms and heuristic based algorithms at the same time. The algorithms each have their own advantages and disadvantages. Integrated research is required in order to measure the pros and cons. Thus, this paper has two main contributions, which are categorization considering criteria and searching algorithms performance review under grid environments.
Firstly, this research has organized the problem while considering these criteria as four categories: environment type; environmental representation; searching algorithm; and experimental type. Each category has specific classes of characteristics and the difference in the characteristics make contribution of the other researches about CFPP problem. Through these categories, this research contributes to understand CFPP problem structure and recently studied topics.
Second, a performance review for seven different searching algorithms for a network environment are proposed in this study. Each algorithm has its own significant characteristics. The performance can be altered according to network size, feature of obstacles or number of obstacles. The experiments show that searching speed of Dijkstra and A star algorithm rapidly increases, depending on network size more so than metaheuristic algorithms. Performance of the metaheuristic algorithm fluctuates based on the number or shape of the obstacles. Therefore, this paper evaluated the performance of these searching algorithms.
Recently, CFPP problem is studied under dynamic, stochastic or multi tasks condition recently. However, the performance result of this paper focused on stationary obstacles, network model, and single task condition. Many other conditions, such as kinematic constraint, different environmental representation, or environment type, should be researched for measuring their effect. Also, metaheuristic algorithms are defined as simplified form, thus they may have a performance gap between the suggested algorithms and the studied algorithm recently.
We plan to redeem the limitation of this paper, as follows. Our further research will be studying performance of recent algorithms under various conditions using a car-like robot. Through this plan, various combined conditions of kinematic constraint, environmental representation, and environmental type can be expected to consider. Also, an actual robot has limited specifications, such as the limitation of sensing vague objects in real-time and computational limitations. With this further research, these limitations can be considered while using a car-like robot.
On the other hand, the extension of the algorithm can be adopted and applied to real-time environment specially in vision enabled mobile machines. The information captured by such vision would provide much more accurate information for a mobile agent to aid in avoiding collisions. Thus, future research could include the direction of path planning in a real time environment with a vision enabled system.
Author Contributions
Conceptualization, J.C., and H.S.; Data curation, H.S.; Formal analysis, H.S.; Funding acquisition, J.C.; Investigation, H.S.; Methodology, H.S.; Project administration, J.C.; Resources, H.S.; Software, H.S.; Supervision, J.C.; Validation, H.S.; Visualization, H.S.; Writing—original draft, H.S.; Writing—review & editing, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Korea Aerospace University faculty research grant.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grazia Speranza, M. Trends in transportation and logistics. Eur. J. Oper. Res. 2018, 264, 830–836. [Google Scholar] [CrossRef]
- Lozano-Pérez, T.; Wesley, M.A. An algorithm for planning collision-free paths among polyhedral obstacles. Commun. ACM 1979, 22, 560–570. [Google Scholar] [CrossRef]
- Schwartz, J.T.; Sharir, M. On the “piano movers” problem I. The case of a two-dimensional rigid polygonal body moving amidst polygonal barriers. Commun. Pure Appl. Math. 1983, 36, 345–398. [Google Scholar] [CrossRef]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Trajectory Planning in Robotics. Math. Comput. Sci. 2012, 6, 269–279. [Google Scholar] [CrossRef]
- Canny, J. The Complexity of Robot Motion Planning; The MIT Press: Cambridge, MA, USA, 1988; ISBN 9780262031363. [Google Scholar]
- Sharir, M. Algorithmic motion planning in robotics. Computer 1989, 22, 9–19. [Google Scholar] [CrossRef]
- Schwartz, J.T.; Sharir, M. A survey of motion planning and related geometric algorithms. Artif. Intell. 1988, 37, 157–169. [Google Scholar] [CrossRef]
- Hwang, Y.K.; Ahuja, N. Gross motion planning—A survey. ACM Comput. Surv. 1992, 24, 219–291. [Google Scholar] [CrossRef]
- Sariff, N.; Buniyamin, N. An overview of autonomous mobile robot path planning algorithms. In Proceedings of the 2006 4th Student Conference on Research and Development, Selangor, Malaysia, 27–28 June 2006; pp. 183–188. [Google Scholar]
- Masehian, E.; Sedighizadeh, D. Classic and Heuristic Approaches in Robot Motion Planning–A Chronological Review. World Acad. Sci. Eng. Technol. 2007, 29, 101–106. [Google Scholar]
- Goerzen, C.; Kong, Z.; Mettler, B. A Survey of Motion Planning Algorithms from the Perspective of Autonomous UAV Guidance. J. Intell. Robot. Syst. 2010, 57. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28. [Google Scholar] [CrossRef]
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and Decision-Making for Autonomous Vehicles. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Reif, J.H. Complexity of the mover’s problem and generalizations. In Proceedings of the 20th Annual Symposium on Foundations of Computer Science (sfcs 1979), San Juan, Puerto Rico, USA, 29–31 October 1979; pp. 421–427. [Google Scholar] [CrossRef]
- Ó’Dúnlaing, C.; Yap, C.K. A “retraction” method for planning the motion of a disc. J. Algorithms 1985, 6, 104–111. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780511546877. [Google Scholar]
- Mohanty, P.; Parhi, D. Controlling the Motion of an Autonomous Mobile Robot Using Various Techniques: A Review. J. Adv. Mech. Eng. 2013, 1, 24–39. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Kolountzakis, M.N.; Latombe, J.-C. Analysis of probabilistic roadmaps for path planning. IEEE Trans. Robot. Autom. 1998, 14, 166–171. [Google Scholar] [CrossRef]
- Alexopoulos, C.; Griffin, P.M. Path planning for a mobile robot. IEEE Trans. Syst. Man Cybern. 1992, 22, 318–322. [Google Scholar] [CrossRef]
- Latombe, J.-C. Robot Motion Planning; The Springer International Series in Engineering and Computer Science; Springer: New York, NY, USA, 2012; ISBN 9781461540229. [Google Scholar]
- Barraquand, J.; Latombe, J.-C. A Monte-Carlo algorithm for path planning with many degrees of freedom. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 1712–1717. [Google Scholar]
- Thrun, S.; Fox, D.; Burgard, W.; Dellaert, F. Robust Monte Carlo localization for mobile robots. Artif. Intell. 2001, 128, 99–141. [Google Scholar] [CrossRef]
- Janson, L.; Schmerling, E.; Pavone, M. Monte Carlo Motion Planning for Robot Trajectory Optimization Under Uncertainty. In Robotics Research; Springer: New York, NY, USA, 2018; pp. 343–361. [Google Scholar]
- Lozano-Pérez, T. Spatial Planning: A Configuration Space Approach. IEEE Trans. Comput. 1983, 32, 108–120. [Google Scholar] [CrossRef]
- LaValle, S.M.; Branicky, M.S.; Lindemann, S.R. On the Relationship between Classical Grid Search and Probabilistic Roadmaps. Int. J. Robot. Res. 2004, 23, 673–692. [Google Scholar] [CrossRef]
- Englot, B.; Hover, F. Multi-goal feasible path planning using ant colony optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2255–2260. [Google Scholar]
- Ichter, B.; Harrison, J.; Pavone, M. Learning Sampling Distributions for Robot Motion Planning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 7087–7094. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Hsu, D.; Kindel, R.; Latombe, J.-C.; Rock, S. Randomized Kinodynamic Motion Planning with Moving Obstacles. Int. J. Robot. Res. 2002, 21, 233–255. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA. Millennium Conference, IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 995–1001. [Google Scholar]
- Kim, B.; Um, T.T.; Suh, C.; Park, F.C. Tangent bundle RRT: A randomized algorithm for constrained motion planning. Robotica 2016, 34, 202–225. [Google Scholar] [CrossRef]
- Malone, N.; Lesser, K.; Oishi, M.; Tapia, L. Stochastic reachability based motion planning for multiple moving obstacle avoidance. In Proceedings of the 17th International Conference on Hybrid Systems: Computation and Control, Berlin, Germany, April 2014; pp. 51–60. [Google Scholar]
- Kuwata, Y.; Karaman, S.; Teo, J.; Frazzoli, E.; How, J.P.; Fiore, G. Real-Time Motion Planning With Applications to Autonomous Urban Driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Sánchez, G.; Latombe, J. On Delaying Collision Checking in PRM Planning: Application to Multi-Robot Coordination. Int. J. Robot. Res. 2002, 21, 5–26. [Google Scholar] [CrossRef]
- Sanchez, G.; Latombe, J.-C. Using a PRM planner to compare centralized and decoupled planning for multi-robot systems. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington DC, USA, 11–15 May 2002; pp. 2112–2119. [Google Scholar]
- Sánchez, G.; Latombe, J.-C. A Single-Query Bi-Directional Probabilistic Roadmap Planner with Lazy Collision Checking. In Proceedings of the International Symposium on Robotics Research, Lorne, VIC, Australia, 9–12 November 2001; pp. 403–417. [Google Scholar]
- Solovey, K.; Salzman, O.; Halperin, D. Finding a needle in an exponential haystack: Discrete RRT for exploration of implicit roadmaps in multi-robot motion planning. Int. J. Robot. Res. 2016, 35, 501–513. [Google Scholar] [CrossRef]
- Wilmarth, S.A.; Amato, N.M.; Stiller, P.F. MAPRM: A probabilistic roadmap planner with sampling on the medial axis of the free space. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; pp. 1024–1031. [Google Scholar]
- Saha, M.; Latombe, J.-C.; Chang, Y.-C.; Prinz, F. Finding Narrow Passages with Probabilistic Roadmaps: The Small-Step Retraction Method. Auton. Robot. 2005, 19, 301–319. [Google Scholar] [CrossRef]
- Saha, M.; Roughgarden, T.; Latombe, J.-C.; Sánchez-Ante, G. Planning Tours of Robotic Arms among Partitioned Goals. Int. J. Robot. Res. 2006, 25, 207–223. [Google Scholar] [CrossRef]
- Dantam, N.T.; Kingston, Z.K.; Chaudhuri, S.; Kavraki, L.E. Incremental Task and Motion Planning: A Constraint-Based Approach. In Proceedings of the Robotics: Science and Systems; Ann Arbor, Michigan, USA, 18–22 June 2016. [Google Scholar]
- Hsu, D.; Latombe, J.; Kurniawati, H. On the probabilistic foundations of probabilistic roadmap planning. Int. J. Robot. Res. 2006, 25, 627–643. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Marble, J.D.; Bekris, K.E. Asymptotically Near-Optimal Is Good Enough for Motion Planning. In Robotics Research; Springer: New York, NY, USA, 2017; pp. 419–436. [Google Scholar]
- Tharwat, A.; Elhoseny, M.; Hassanien, A.E.; Gabel, T.; Kumar, A. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm. Clust. Comput. 2019, 22, 4745–4766. [Google Scholar] [CrossRef]
- Bottasso, C.L.; Leonello, D.; Savini, B. Path Planning for Autonomous Vehicles by Trajectory Smoothing Using Motion Primitives. IEEE Trans. Control. Syst. Technol. 2008, 16, 1152–1168. [Google Scholar] [CrossRef]
- Yang, K.; Sukkarieh, S. An Analytical Continuous-Curvature Path-Smoothing Algorithm. IEEE Trans. Robot. 2010, 26, 561–568. [Google Scholar] [CrossRef]
- Hsu, D.; Latombe, J.-C.; Motwani, R. Path planning in expansive configuration spaces. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, April 1997; pp. 2719–2726. [Google Scholar]
- Alterovitz, R.; Simeon, T.; Goldberg, K. The Stochastic Motion Roadmap: A Sampling Framework for Planning with Markov Motion Uncertainty. In Proceedings of the Robotics: Science and Systems, Atlanta, GA, USA, 27–30 June 2007. [Google Scholar]
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Gavrilova, M.L. Voronoi diagram in optimal path planning. In Proceedings of the 4th International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2007), Glamorgan, UK, 9–11 July 2007; pp. 38–47. [Google Scholar]
- Ho, Y.-J.; Liu, J.-S. Collision-free curvature-bounded smooth path planning using composite Bezier curve based on Voronoi diagram. In Proceedings of the 2009 IEEE International Symposium on Computational Intelligence in Robotics and Automation-(CIRA), Daejeon, South Korea, 15–18 December 2009; pp. 463–468. [Google Scholar]
- Janson, L.; Ichter, B.; Pavone, M. Deterministic sampling-based motion planning: Optimality, complexity, and performance. Int. J. Robot. Res. 2018, 37, 46–61. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Yuan, Q. Application of Dijkstra algorithm in robot path-planning. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011; pp. 1067–1069. [Google Scholar]
- Herman, M. Fast, Three-Dimensional, Collision-Free Motion Planning. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; pp. 1056–1063. [Google Scholar]
- Bohlin, R.; Kavraki, L.E. Path planning using lazy PRM. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 521–528. [Google Scholar]
- van den Berg, J.; Ferguson, D.; Kuffner, J. Anytime path planning and replanning in dynamic environments. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 2366–2371. [Google Scholar]
- Noto, M.; Sato, H. A method for the shortest path search by extended Dijkstra algorithm. In Proceedings of the SMC 2000 Conference Proceedings, 2000 IEEE International Conference on Systems, Man and Cybernetics. “Cybernetics Evolving to Systems, Humans, Organizations, and their Complex Interactions” (Cat. No.00CH37166), Nashville, TN, USA, 8–11 October 2002; pp. 2316–2320. [Google Scholar]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Duchoň, F.; Babinec, A.; Kajan, M.; Beňo, P.; Florek, M.; Fico, T.; Jurišica, L. Path Planning with Modified a Star Algorithm for a Mobile Robot. Procedia Eng. 2014, 96, 59–69. [Google Scholar] [CrossRef]
- Fu, L.-C.; Liu, D.-Y. An efficient algorithm for finding a collision-free path among polyhedral obstacles. J. Robot. Syst. 1990, 7, 129–137. [Google Scholar] [CrossRef]
- Stoyanov, T.; Magnusson, M.; Andreasson, H.; Lilienthal, A.J. Path planning in 3D environments using the Normal Distributions Transform. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3263–3268. [Google Scholar]
- AL-Taharwa, I.; Sheta, A.; Al-Weshah, M. A Mobile Robot Path Planning Using Genetic Algorithm in Static Environment. J. Comput. Sci. 2008, 4, 341–344. [Google Scholar] [CrossRef]
- Cai, Z.; Peng, Z. Cooperative coevolutionary adaptive genetic algorithm in path planning of cooperative multi-mobile robot systems. J. Intell. Robot. Syst. Theory Appl. 2002, 33, 61–71. [Google Scholar] [CrossRef]
- Yang, Q.; Yoo, S.-J. Optimal UAV Path Planning: Sensing Data Acquisition Over IoT Sensor Networks Using Multi-Objective Bio-Inspired Algorithms. IEEE Access 2018, 6, 13671–13684. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, S.X. A knowledge based genetic algorithm for path planning of a mobile robot. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA ’04, New Orleans, LA, USA, 26 April–1 May 2004; pp. 4350–4355. [Google Scholar]
- Jiang, A.; Yao, X.; Zhou, J. Research on path planning of real-time obstacle avoidance of mechanical arm based on genetic algorithm. J. Eng. 2018, 1579–1586. [Google Scholar] [CrossRef]
- Elshamli, A.; Abdullah, H.A.; Areibi, S. Genetic algorithm for dynamic path planning. In Proceedings of the Canadian Conference on Electrical and Computer Engineering 2004 (IEEE Cat. No.04CH37513), Niagara Falls, ON, Canada, 2–5 May 2004; pp. 677–680. [Google Scholar]
- Zhao, M.; Ansari, N.; Hou, E.S.H. Mobile manipulator path planning by a genetic algorithm. J. Robot. Syst. 1994, 11, 143–153. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Yazdani, A.M.; Sammut, K.; Powers, D.M. Online path planning for AUV rendezvous in dynamic cluttered undersea environment using evolutionary algorithms. Appl. Soft Comput. 2018, 70, 929–945. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Shin, H.; Chae, J. Path Planning for Mobile Agents Using a Genetic Algorithm with a Direction Guided Factor. Electronics 2018, 7, 212. [Google Scholar] [CrossRef]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Tuncer, A.; Yildirim, M. Dynamic path planning of mobile robots with improved genetic algorithm. Comput. Electr. Eng. 2012, 38, 1564–1572. [Google Scholar] [CrossRef]
- Sedighi, K.H.; Ashenayi, K.; Manikas, T.W.; Wainwright, R.L.; Tai, H.-M. Autonomous local path planning for a mobile robot using a genetic algorithm. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portand, OR, USA, 19–23 June 2004; pp. 1338–1345. [Google Scholar]
- Tu, J.; Yang, S.X. Genetic algorithm based path planning for a mobile robot. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; pp. 1221–1226. [Google Scholar]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Janabi-Sharifi, F.; Vinke, D. Robot path planning by integrating the artificial potential field approach with simulated annealing. In Proceedings of the Proceedings of IEEE Systems Man and Cybernetics Conference-SMC, Le Touquet, France, 17–20 October 1993; pp. 282–287. [Google Scholar]
- Zhu, Q.; Yan, Y.; Xing, Z. Robot Path Planning Based on Artificial Potential Field Approach with Simulated Annealing. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jinan, China, 16–18 October 2006; pp. 622–627. [Google Scholar]
- Park, M.G.; Jeon, J.H.; Lee, M.C. Obstacle avoidance for mobile robots using artificial potential field approach with simulated annealing. In Proceedings of the 2001 IEEE International Symposium on Industrial Electronics Proceedings (Cat. No.01TH8570), Pusan, South Korea, 12–16 June 2001; pp. 1530–1535. [Google Scholar]
- Janabi-Sharifi, F.; Vinke, D. Integration of the artificial potential field approach with simulated annealing for robot path planning. In Proceedings of the 8th IEEE International Symposium on Intelligent Control, Chicago, IL, USA, 25–27 August 1993; pp. 536–541. [Google Scholar]
- Park, M.G.; Lee, M.C. Experimental evaluation of robot path planning by artificial potential field approach with simulated annealing. In Proceedings of the 41st SICE Annual Conference, Osaka, Japan, 5–7 August 2002; pp. 2190–2195. [Google Scholar]
- Miao, H.; Tian, Y.-C. Robot path planning in dynamic environments using a simulated annealing based approach. In Proceedings of the 2008 10th International Conference on Control, Automation, Robotics and Vision, Hanoi, Vietnam, 17–20 December 2008; pp. 1253–1258. [Google Scholar]
- Martínez-Alfaro, H.; Gómez-García, S. Mobile robot path planning and tracking using simulated annealing and fuzzy logic control. Expert Syst. Appl. 1998, 15, 421–429. [Google Scholar] [CrossRef]
- Tavares, R.S.; Martins, T.C.; Tsuzuki, M.S.G. Simulated annealing with adaptive neighborhood: A case study in off-line robot path planning. Expert Syst. Appl. 2011, 38, 2951–2965. [Google Scholar] [CrossRef]
- Miao, H.; Tian, Y.-C. Dynamic robot path planning using an enhanced simulated annealing approach. Appl. Math. Comput. 2013, 222, 420–437. [Google Scholar] [CrossRef]
- Kroumov, V.; Yu, J. 3D path planning for mobile robots using annealing neural network. In Proceedings of the 2009 International Conference on Networking, Sensing and Control, Okayama, Japan, 26–29 March 2009; pp. 130–135. [Google Scholar]
- Carriker, W.F.; Khosla, P.K.; Krogh, B.H. The Use of Simulated Annealing to Solve the Mobile Manipulator Path Planning Problem. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 204–209. [Google Scholar]
- Amer, H.M.; Al-Kashoash, H.; Hawes, M.; Chaqfeh, M.; Kemp, A.; Mihaylova, L. Centralized simulated annealing for alleviating vehicular congestion in smart cities. Technol. Forecast. Soc. Chang. 2019, 142, 235–248. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L.; Xu, L.; Alsaadi, F.E. A new approach to smooth global path planning of mobile robots with kinematic constraints. Int. J. Mach. Learn. Cybern. 2019, 10, 107–119. [Google Scholar] [CrossRef]
- Foo, J.L.; Knutzon, J.; Oliver, J.; Winer, E. Three-Dimensional Multi-Objective Path Planner for Unmanned Aerial Vehicles Using Particle Swarm Optimization. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1881. [Google Scholar]
- Zhang, Y.; Gong, D.; Zhang, J. Robot path planning in uncertain environment using multi-objective particle swarm optimization. Neurocomputing 2013, 103, 172–185. [Google Scholar] [CrossRef]
- Fu, Y.; Ding, M.; Zhou, C. Phase Angle-Encoded and Quantum-Behaved Particle Swarm Optimization Applied to Three-Dimensional Route Planning for UAV. IEEE Trans. Syst. Man Cybern. Part. A Syst. Hum. 2011, 42, 511–526. [Google Scholar] [CrossRef]
- Gong, D.; Zhang, J.; Zhang, Y. Multi-objective Particle Swarm Optimization for Robot Path Planning in Environment with Danger Sources. J. Comput. 2011, 6, 1554–1561. [Google Scholar] [CrossRef]
- Saska, M.; Macaš, M.; Přeučil, L.; Lhotská, L. Robot path planning using particle swarm optimization of ferguson splines. IEEE Int. Conf. Emerg. Technol. Fact. Autom. ETFA 2006, 19, 833–839. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Wang, S. UCAV Path Planning by Fitness-Scaling Adaptive Chaotic Particle Swarm Optimization. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y. Smooth Path Planning of a Mobile Robot Using Stochastic Particle Swarm Optimization. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, Henan, China, 25–28 June 2006; pp. 1722–1727. [Google Scholar]
- Masehian, E.; Sedighizadeh, D. A multi-objective PSO-based algorithm for robot path planning. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Vina del Mar, Chile, 14–17 March 2010; pp. 465–470. [Google Scholar]
- Wang, X.; Zhang, G.; Zhao, J.; Rong, H.; Ipate, F.; Lefticaru, R. A Modified Membrane-Inspired Algorithm Based on Particle Swarm Optimization for Mobile Robot Path Planning. Int. J. Comput. Commun. Control. 2015, 10, 732–745. [Google Scholar] [CrossRef]
- Phung, M.D.; Quach, C.H.; Dinh, T.H.; Ha, Q. Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection. Autom. Constr. 2017, 81, 25–33. [Google Scholar] [CrossRef]
- Shiltagh, N.A.; Jalal, L.D. Optimal Path Planning For Intelligent Mobile Robot Navigation Using Modified Particle Swarm Optimization. Int. J. Eng. Adv. Technol. 2013, 2, 260–267. [Google Scholar]
- Kang, H.I.; Lee, B.; Kim, K. Path Planning Algorithm Using the Particle Swarm Optimization and the Improved Dijkstra Algorithm. In Proceedings of the 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, China, 19–20 December 2008; pp. 1002–1004. [Google Scholar]
- Alejo, D.; Cobano, J.A.; Heredia, G.; Ollero, A. Particle Swarm Optimization for collision-free 4D trajectory planning in Unmanned Aerial Vehicles. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 298–307. [Google Scholar]
- Thabit, S.; Mohades, A. Multi-Robot Path Planning Based on Multi-Objective Particle Swarm Optimization. IEEE Access 2019, 7, 2138–2147. [Google Scholar] [CrossRef]
- Xing, L.N.; Rohlfshagen, P.; Chen, Y.W.; Yao, X. A Hybrid Ant Colony Optimization Algorithm for the Extended Capacitated Arc Routing Problem. IEEE Trans. Syst. Man Cybern. Part. B (Cybern.) 2011, 41, 1110–1123. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Z.; Ma, K.; Rong, Y.; Wang, P.; Zhang, H.; Wang, S. A path planning method using adaptive polymorphic ant colony algorithm for smart wheelchairs. J. Comput. Sci. 2018, 25, 50–57. [Google Scholar] [CrossRef]
- Garcia, M.A.P.; Montiel, O.; Castillo, O.; Sepúlveda, R.; Melin, P. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation. Appl. Soft Comput. 2009, 9, 1102–1110. [Google Scholar] [CrossRef]
- Yen, C.-T.; Cheng, M.-F. A study of fuzzy control with ant colony algorithm used in mobile robot for shortest path planning and obstacle avoidance. Microsyst. Technol. 2018, 24, 125–135. [Google Scholar] [CrossRef]
- Hsiao, Y.T.; Chuang, C.L.; Chien, C.C. Ant colony optimization for best path planning. In Proceedings of the IEEE International Symposium on Communications and Information Technology, Sapporo, Japan, 26–29 October 2004; pp. 109–113. [Google Scholar]
- Akka, K.; Khaber, F. Mobile robot path planning using an improved ant colony optimization. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.-N.; Gu, T.; Yuan, H.; Zhang, H.; Zhang, J. ACO-A*: Ant Colony Optimization Plus A* for 3-D Traveling in Environments With Dense Obstacles. IEEE Trans. Evol. Comput. 2019, 23, 617–631. [Google Scholar] [CrossRef]
- Chia, S.H.; Su, K.L.; Guo, J.H.; Chung, C.Y. Ant Colony System Based Mobile Robot Path Planning. In Proceedings of the 2010 Fourth International Conference on Genetic and Evolutionary Computing, Shenzhen, China, 13–15 December 2010; pp. 210–213. [Google Scholar]
- Brand, M.; Masuda, M.; Wehner, N.; Yu, X.-H. Ant Colony Optimization algorithm for robot path planning. In Proceedings of the 2010 International Conference On Computer Design and Applications, Qinhuangdao, Chian, 25–27 June 2010. [Google Scholar]
- Zhang, C.; Zhen, Z.; Wang, D.; Li, M. UAV path planning method based on ant colony optimization. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 3790–3792. [Google Scholar]
- Cong, Y.Z.; Ponnambalam, S.G. Mobile robot path planning using ant colony optimization. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 851–856. [Google Scholar]
- Xiong, C.; Chen, D.; Lu, D.; Zeng, Z.; Lian, L. Path planning of multiple autonomous marine vehicles for adaptive sampling using Voronoi-based ant colony optimization. Robot. Auton. Syst. 2019, 115, 90–103. [Google Scholar] [CrossRef]
- Wang, L.; Kan, J.; Guo, J.; Wang, C. 3D Path Planning for the Ground Robot with Improved Ant Colony Optimization. Sensors 2019, 19, 815. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.P.; Luo, X.; Yi, S.; Yang, S.Y.; Zhang, H. Optimal path planning for mobile robots based on intensified ant colony optimization algorithm. In Proceedings of the IEEE International Conference on Robotics, Intelligent Systems and Signal Processing, Changsha, Hunan, China, 8–13 October 2003; pp. 131–136. [Google Scholar]
- Ma, Y.-N.; Gong, Y.-J.; Xiao, C.-F.; Gao, Y.; Zhang, J. Path Planning for Autonomous Underwater Vehicles: An Ant Colony Algorithm Incorporating Alarm Pheromone. IEEE Trans. Veh. Technol. 2019, 68, 141–154. [Google Scholar] [CrossRef]
- López-Ibáñez, M.; Dubois-Lacoste, J.; Pérez Cáceres, L.; Birattari, M.; Stützle, T. The irace package: Iterated racing for automatic algorithm configuration. Oper. Res. Perspect. 2016, 3, 43–58. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).