Interference Analysis for Vehicle-to-Vehicle Communications at 28 GHz
Abstract
1. Introduction
1.1. Related Work
1.2. Motivation and Contributions
1.3. Organization
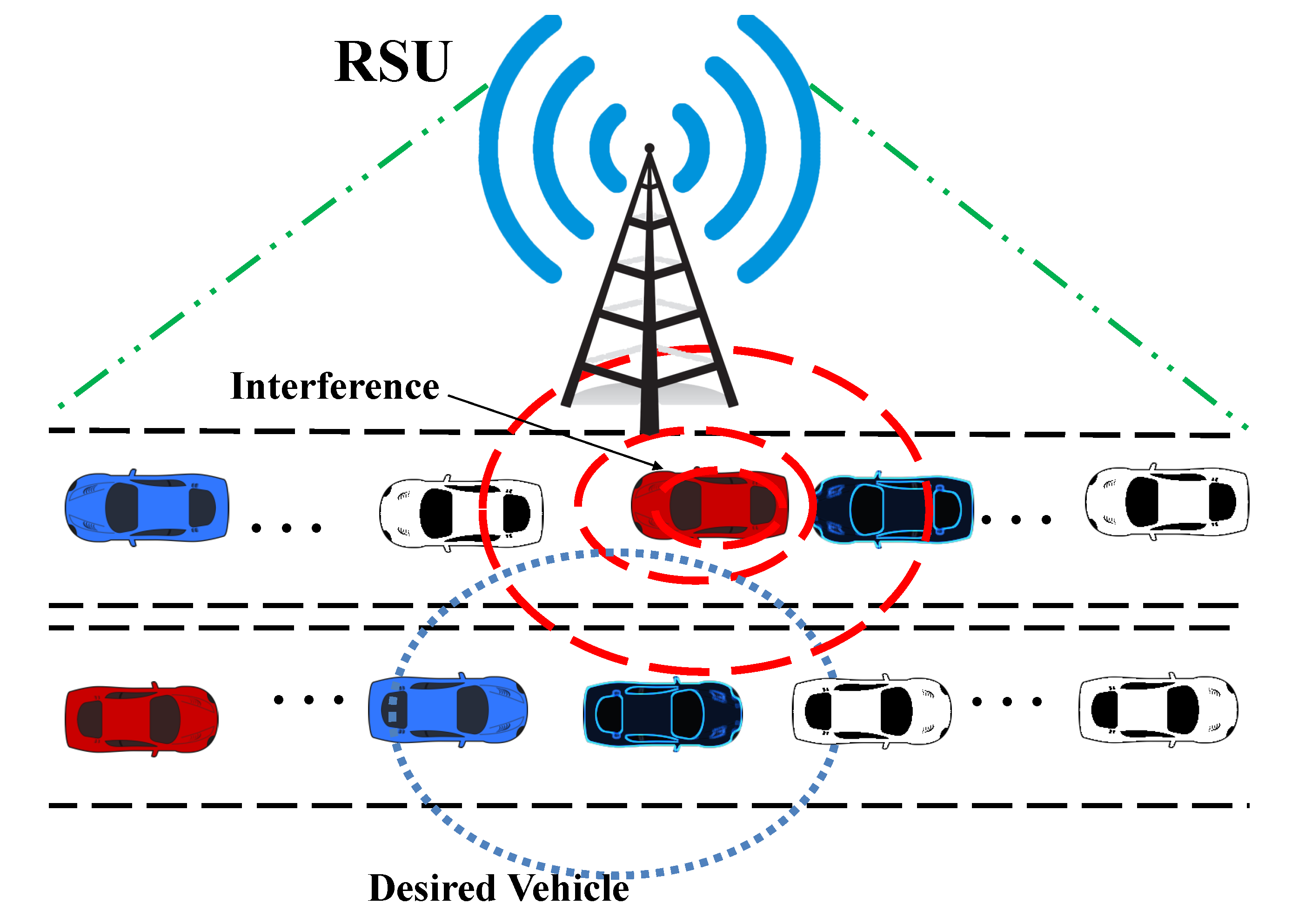
2. System Model
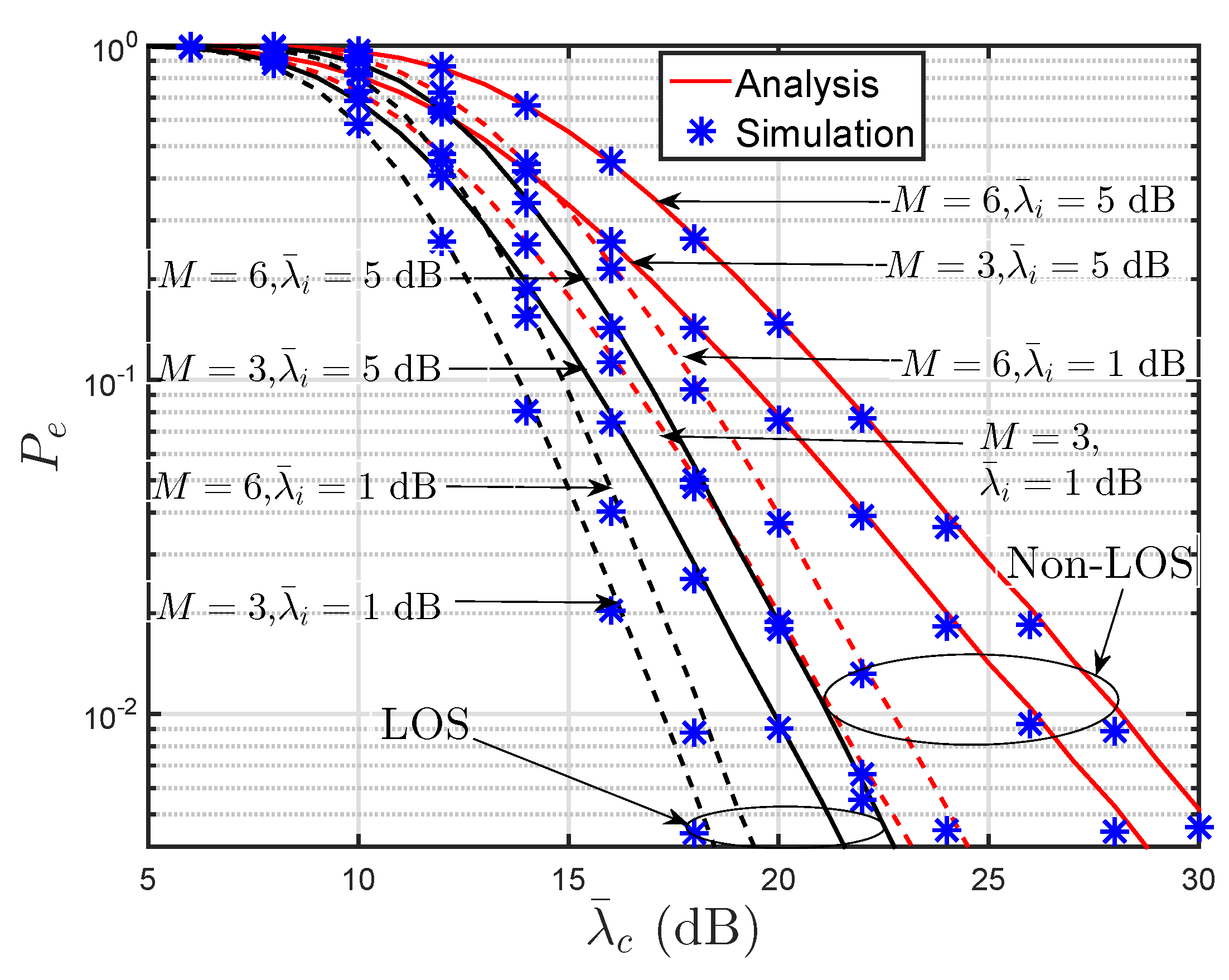
3. Analysis of PEP
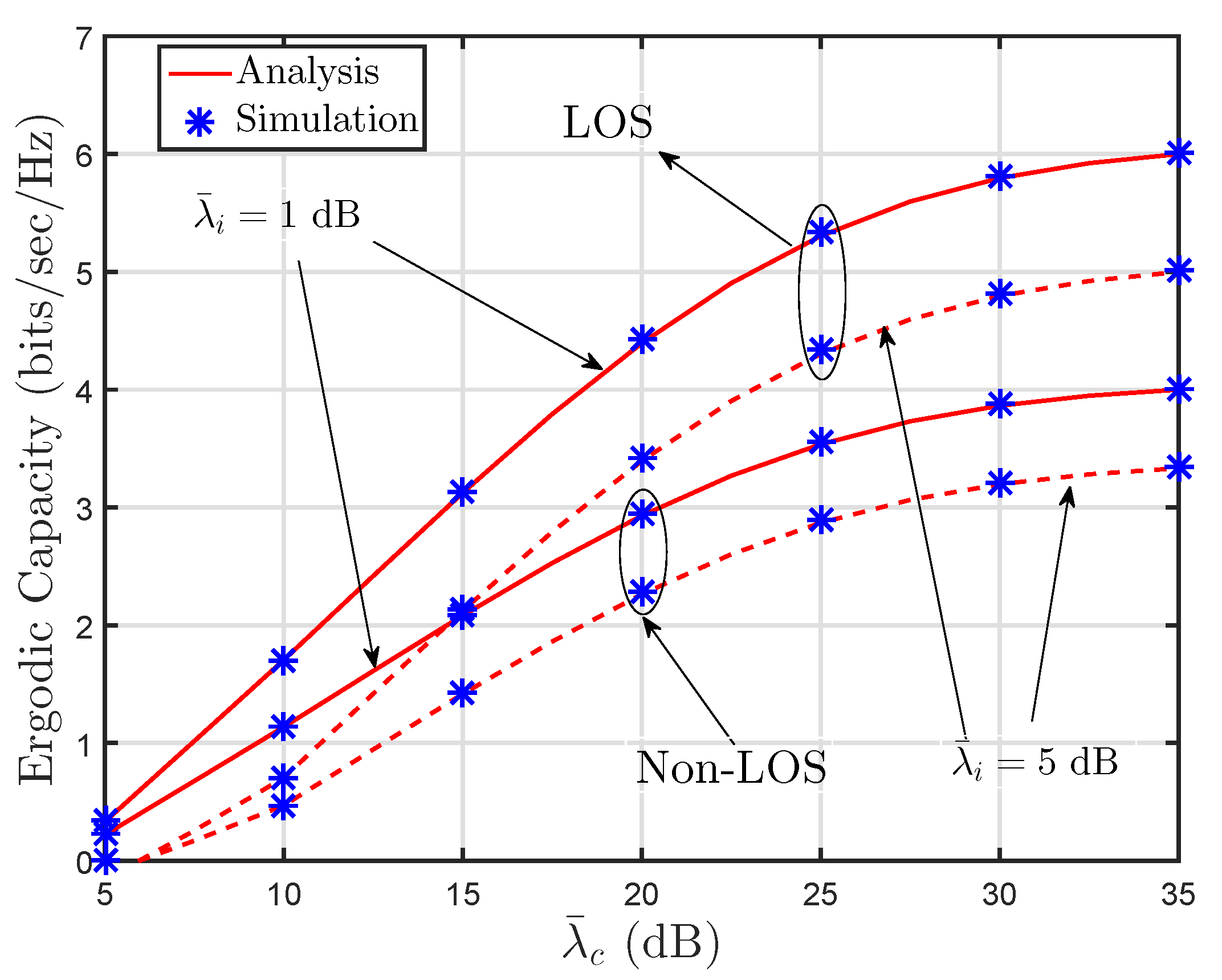
4. Ergodic Capacity
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PEP | Packet error probability |
| LOS | Line-of-sight |
| V2X | Vehicle-to-everything |
| BS | Base station |
| ICI | Inter-carrier-interference |
| SNR | Signal-to-noise ratio |
| FCC | Federal Communications Commission |
| RSU | Road side unit |
| AWGN | Additive white Gaussian noise |
| CH | Cluster head |
| CDF | Cumulative distribution function |
| Probability density function | |
| ETSI | European Telecommunications Standards Institute |
| V2I | Vehicle-to-infrastructure |
| MIMO | Multiple-input multiple-output |
| ITS | Intelligent transportation system |
| mmWave | Millimeter wave |
| V2V | Vehicle-to-vehicle |
References
- Jameel, F.; Chang, Z.; Huang, J.; Ristaniemi, T. Internet of Autonomous Vehicles: Architecture, Features, and Socio-Technological Challenges. IEEE Wirel. Commun. 2019, 26, 21–29. [Google Scholar] [CrossRef]
- Ligo, A.; Peha, J.M. Spectrum Policies for Intelligent Transportation Systems. TPRC 45: The 45th Research Conference on Communication, Information and Internet Policy. 2017. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2943688 (accessed on 6 January 2020).
- ETSI. Intelligent Transport Systems (ITS); Access Layer Specification for Intelligent Transport Systems Operating in the 5 GHz Frequency Band; Technical Report EN 302 663; Version 1.2.0; 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE. 2012. Available online: https://www.etsi.org/deliver/etsi_en/302600_302699/302663/01.02.01_30/en_302663v010201v.pdf (accessed on 6 January 2020).
- IEEE.802.11. IEEE Standard for Information Technology–Telecommunications and Information Exchange between Systems Local and Metropolitan Area Networks–Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; IEEE Std 802.11-2016 (Revision of IEEE Std 802.11-2012); IEEE Standards, USA. 2016, pp. 1–3534. Available online: https://ieeexplore.ieee.org/document/7786995 (accessed on 6 January 2020). [CrossRef]
- 3GPP: Initial Cellular V2X standard completed. 3GPP News Journal, USA. 2016. Available online: https://www.3gpp.org/news-events/3gpp-news/1798-v2x_r14 (accessed on 6 January 2020).
- Choi, J.; Va, V.; Gonzalez-Prelcic, N.; Daniels, R.; Bhat, C.R.; Heath, R.W. Millimeter-Wave Vehicular Communication to Support Massive Automotive Sensing. IEEE Commun. Mag. 2016, 54, 160–167. [Google Scholar] [CrossRef]
- Jameel, F.; Wyne, S.; Nawaz, S.J.; Chang, Z. Propagation channels for mmWave vehicular communications: State-of-the-art and future research directions. IEEE Wirel. Commun. 2018, 26, 144–150. [Google Scholar] [CrossRef]
- Shimizu, T.; Va, V.; Bansal, G.; Heath, R.W. Millimeter Wave V2X Communications: Use Cases and Design Considerations of Beam Management. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 183–185. [Google Scholar] [CrossRef]
- Schafer, W. Channel modelling of short-range radio links at 60 GHz for mobile intervehicle communication. In Proceedings of the 41st IEEE Vehicular Technology Conference, St. Louis, MO, USA, 19–22 May 1991; pp. 314–319. [Google Scholar] [CrossRef]
- Andrisano, O.; Chiani, M.; Tralli, V.; Frullone, M.; Moss, C.R. Millimetre Wave Short Range Communications for Advanced Transport Telematics. Eur. Trans. Telecommun. 1993, 4, 403–414. [Google Scholar] [CrossRef]
- ElHalawany, B.M.; Jameel, F.; Da Costa, D.B.; Dias, U.S.; Wu, K. Performance Analysis of Downlink NOMA Systems over κ-μ Shadowed Fading Channels. IEEE Trans. Veh. Technol. 2019, 69, 1046–1050. [Google Scholar] [CrossRef]
- Anwar, W.; Franchi, N.; Fettweis, G. Performance Evaluation of Next Generation V2X Communication Technologies: 5G NR-V2V vs. IEEE 802.11bd. In Proceedings of the IEEE 90th Vehicular Technology Conference (VTC-Fall 2019), At Honolulu, HI, USA, 22–25 September 2019. [Google Scholar]
- Magueta, R.; Teodoro, S.; Castanheira, D.; Silva, A.; Dinis, R.; Gameiro, A. Multiuser Equalizer for Hybrid Massive MIMO mmWave CE-OFDM Systems. Appl. Sci. 2019, 9, 3363. [Google Scholar] [CrossRef]
- Magueta, R.; Castanheira, D.; Silva, A.; Dinis, R.; Gameiro, A. Hybrid multi-user equalizer for massive MIMO millimeter-wave dynamic subconnected architecture. IEEE Access 2019, 7, 79017–79029. [Google Scholar] [CrossRef]
- Castanheira, D.; Lopes, P.; Silva, A.; Gameiro, A. Hybrid beamforming designs for massive MIMO millimeter-wave heterogeneous systems. IEEE Access 2017, 5, 21806–21817. [Google Scholar] [CrossRef]
- Magueta, R.; Castanheira, D.; Silva, A.; Dinis, R.; Gameiro, A. Hybrid iterative space-time equalization for multi-user mmW massive MIMO systems. IEEE Trans. Commun. 2016, 65, 608–620. [Google Scholar] [CrossRef]
- Jameel, F.; Haider, M.A.A.; Butt, A.A. Second order fading statistics of UAV networks. In Proceedings of the 2017 Fifth International Conference on Aerospace Science & Engineering (ICASE), Islamabad, Pakistan, 14–16 November 2017; pp. 1–6. [Google Scholar]
- Jameel, F.; Jabeen, F.; Hamid, Z. Analysis of co-channel interference in VANETs under nakagami-m fading. In Proceedings of the 2016 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 19–21 December 2016; pp. 153–158. [Google Scholar]
- Khan, F.; Pi, Z. mmWave mobile broadband (MMB): Unleashing the 3–300 GHz spectrum. In Proceedings of the 34th IEEE Sarnoff Symposium, Princeton, NJ, USA, 3–4 May 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Jameel, F.; Haider, M.A.A.; Butt, A.A. Robust localization in wireless sensor networks using RSSI. In Proceedings of the 2017 13th International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 27–28 December 2017; pp. 1–6. [Google Scholar]
- Giordani, M.; Mezzavilla, M.; Dhananjay, A.; Rangan, S.; Zorzi, M. Channel Dynamics and SNR Tracking in Millimeter Wave Cellular Systems. In Proceedings of the 22th European Wireless Conference, VDE Association, Oulu, Finland, 18–20 May 2016; pp. 306–313. Available online: https://arxiv.org/abs/1604.05623 (accessed on 6 January 2020).
- Verdone, R. Outage probability analysis for short-range communication systems at 60 GHz in ATT urban environments. IEEE Trans. Veh. Technol. 1997, 46, 1027–1039. [Google Scholar] [CrossRef]
- Wang, Y.; Venugopal, K.; Heath, R.W.; Molisch, A.F. MmWave vehicle-to-infrastructure communication: Analysis of urban microcellular networks. IEEE Trans. Veh. Technol. 2018. [Google Scholar] [CrossRef]
- Petrov, V.; Kokkoniemi, J.; Moltchanov, D.; Lehtomaki, J.; Juntti, M.; Koucheryavy, Y. The Impact of Interference From the Side Lanes on mmWave/THz Band V2V Communication Systems with Directional Antennas. IEEE Trans. Veh. Technol. 2018, 67, 5028–5041. [Google Scholar] [CrossRef]
- Giordani, M.; Rebato, M.; Zanella, A.; Zorzi, M. Coverage and connectivity analysis of millimeter wave vehicular networks. Ad Hoc Netw. 2018, 80, 158–171. [Google Scholar] [CrossRef]
- Bazzi, A.; Masini, B.; Zanella, A.; Thibault, I. On the performance of IEEE 802.11p and LTE-V2V for the Cooperative Awareness of Connected Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 10419–10432. [Google Scholar] [CrossRef]
- Bazzi, A.; Masini, B.M.; Zanella, A. How many vehicles in the LTE-V2V awareness range with half or full duplex radios? In Proceedings of the 2017 15th International Conference on ITS Telecommunications (ITST), Warsaw, Poland, 29–31 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Anwar, W.; Kulkarni, K.; Augustin, T.R.; Franchi, N.; Fettweis, G. PHY Abstraction Techniques for IEEE 802. 11p and LTE-V2V: Applications and Analysis. In Proceedings of the 2018 IEEE Global Communications Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Chen, J.; Mao, G.; Li, C.; Zafar, A.; Zomaya, A.Y. Throughput of Infrastructure-Based Cooperative Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2964–2979. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Bai, T.; Alkhateeb, A.; Heath, R.W. Coverage and capacity of millimeter-wave cellular networks. IEEE Commun. Mag. 2014, 52, 70–77. [Google Scholar] [CrossRef]
- Wang, H.; Liu, R.P.; Ni, W.; Chen, W.; Collings, I.B. VANET Modeling and Clustering Design Under Practical Traffic, Channel and Mobility Conditions. IEEE Trans. Commun. 2015, 63, 870–881. [Google Scholar] [CrossRef]
- Jameel, F.; Khan, F.; Haider, M.A.A.; Haq, A.U. On physical layer security of two way energy harvesting relays. In Proceedings of the 2017 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 18–20 December 2017; pp. 35–40. [Google Scholar]
- Dos Anjos, A.A.; Marins, T.R.R.; de Souza, R.A.A.; Yacoub, M.D. Higher Order Statistics for the α-η-κ-μ Fading Model. IEEE Trans. Antennas Propag. 2018, 66, 3002–3016. [Google Scholar] [CrossRef]
- Yacoub, M.D. The α-η-κ-μ Fading Model. IEEE Trans. Antennas Propag. 2016, 64, 3597–3610. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Brychkov, Y.A.; Marichev, O.; Prudnikov, A. Integrals and Series, Vol. 3: More Special Functions; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Ansari, I.S.; Abdallah, M.M.; Alouini, M.S.; Qaraqe, K.A. Outage performance analysis of underlay cognitive RF and FSO wireless channels. In Proceedings of the 2014 3rd International Workshop in Optical Wireless Communications (IWOW), Funchal, Portugal, 17 September 2014; pp. 6–10. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saraereh, O.A.; Ali, A.; Khan, I.; Rabie, K. Interference Analysis for Vehicle-to-Vehicle Communications at 28 GHz. Electronics 2020, 9, 262. https://doi.org/10.3390/electronics9020262
Saraereh OA, Ali A, Khan I, Rabie K. Interference Analysis for Vehicle-to-Vehicle Communications at 28 GHz. Electronics. 2020; 9(2):262. https://doi.org/10.3390/electronics9020262
Chicago/Turabian StyleSaraereh, Omar A., Ashraf Ali, Imran Khan, and Khaled Rabie. 2020. "Interference Analysis for Vehicle-to-Vehicle Communications at 28 GHz" Electronics 9, no. 2: 262. https://doi.org/10.3390/electronics9020262
APA StyleSaraereh, O. A., Ali, A., Khan, I., & Rabie, K. (2020). Interference Analysis for Vehicle-to-Vehicle Communications at 28 GHz. Electronics, 9(2), 262. https://doi.org/10.3390/electronics9020262







