Complex Bianisotropy Effect on the Propagation Constant of a Shielded Multilayered Coplanar Waveguide Using Improved Full Generalized Exponential Matrix Technique
Abstract
1. Introduction
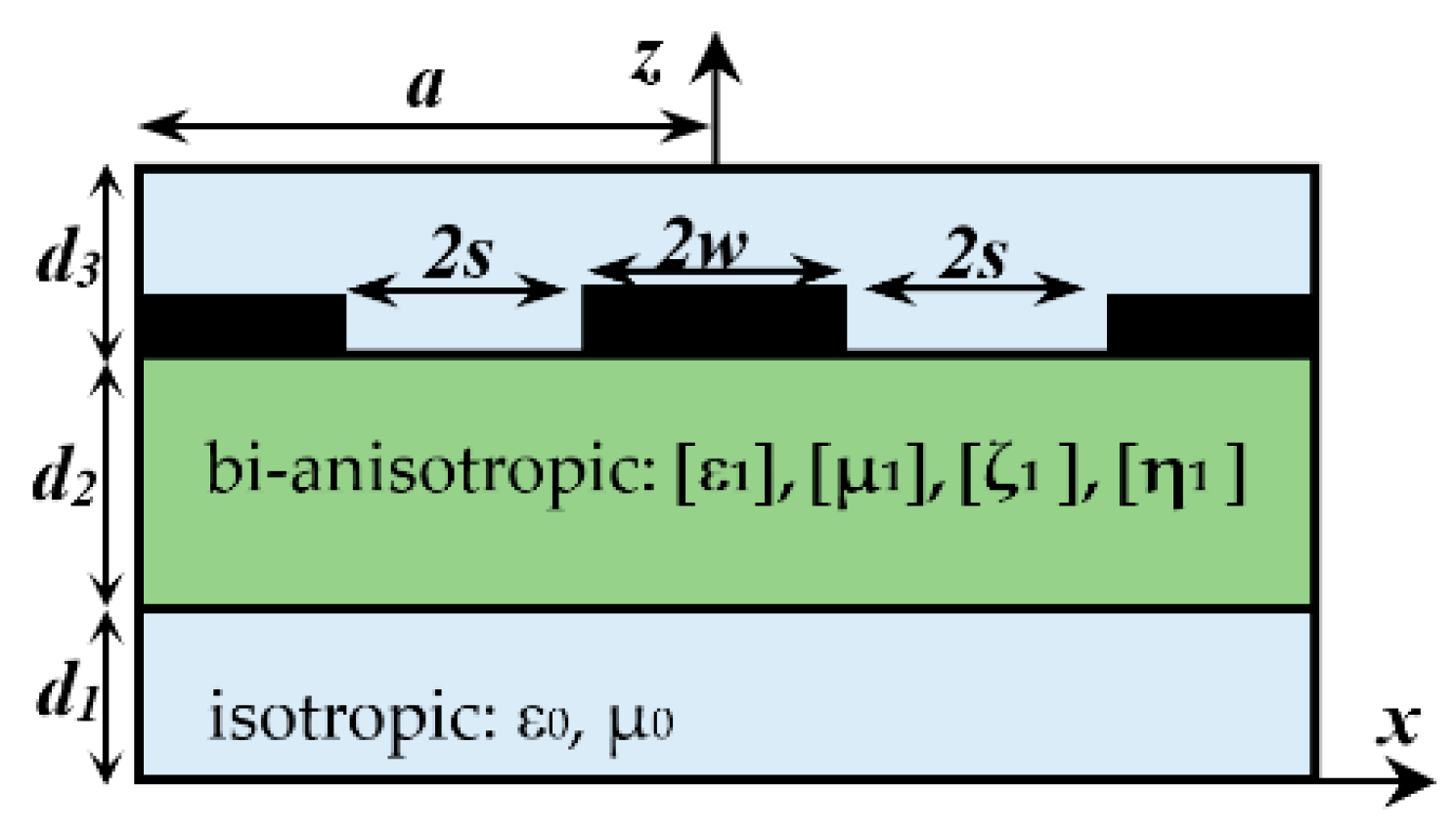
2. Exponential Matrix Technique Formulation
2.1. Implementation of the Acceleration Procedure
2.2. Derivation of the Initial Value Expression of the Effective Relative Permittivity
3. Method of Solution
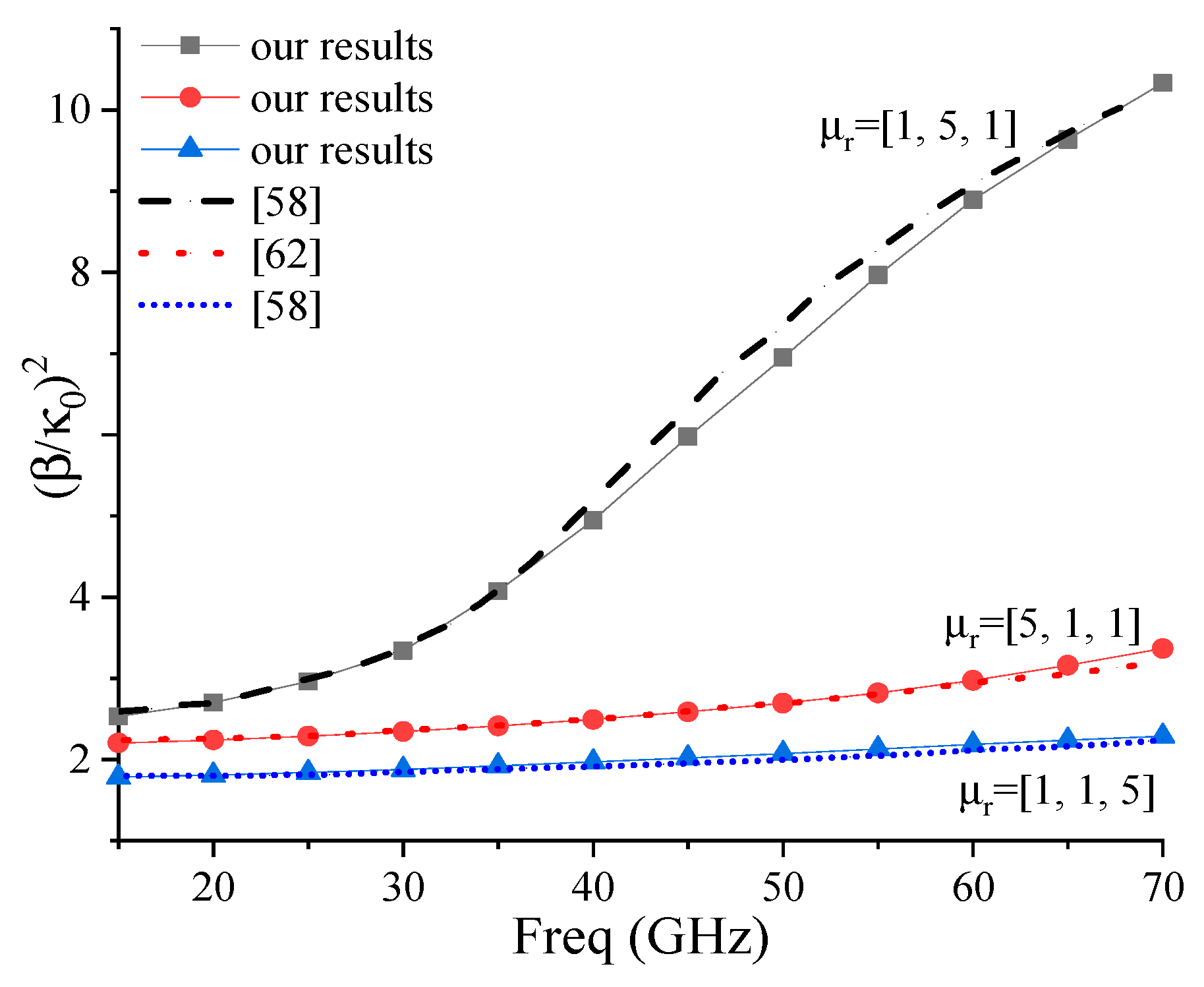
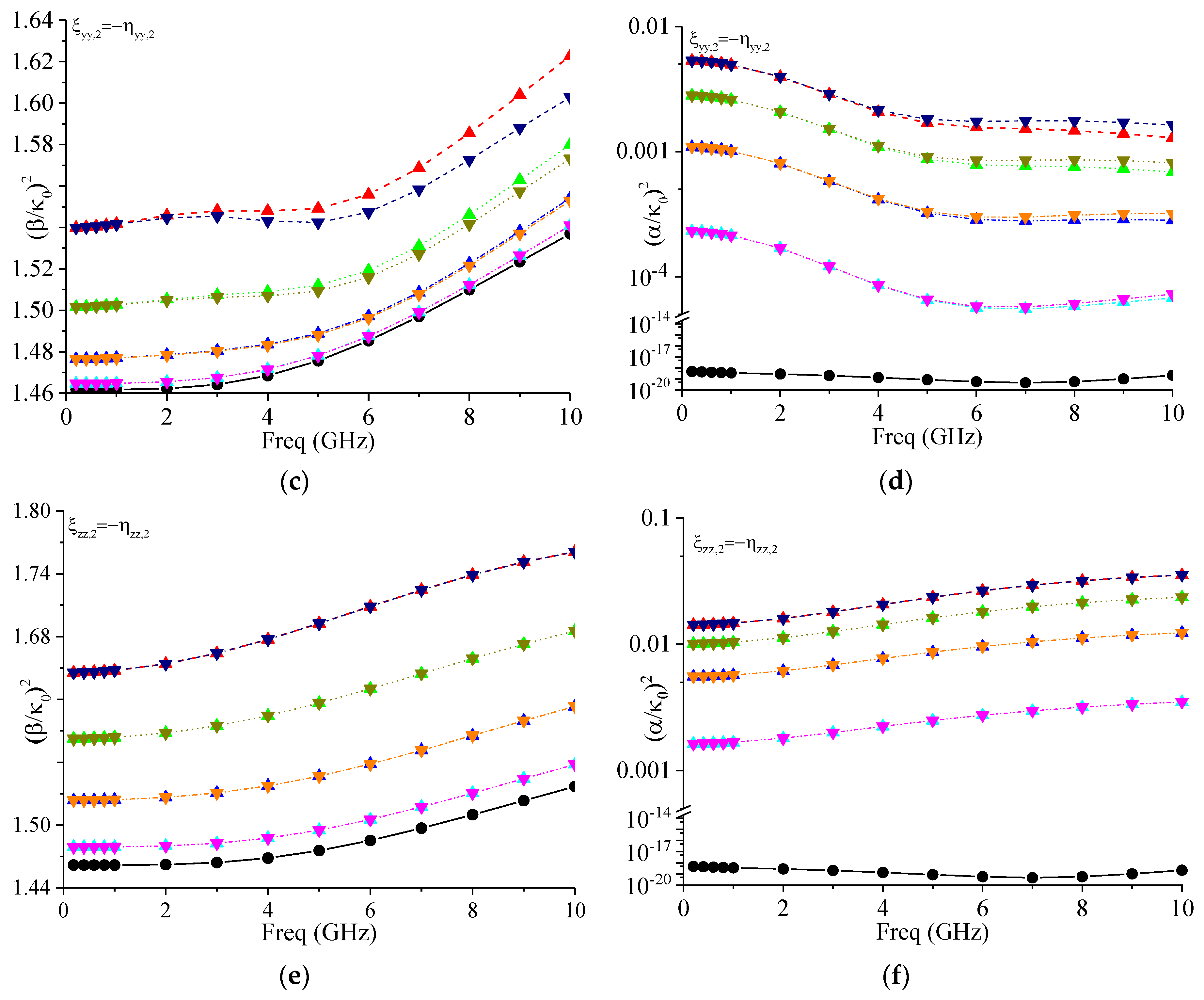
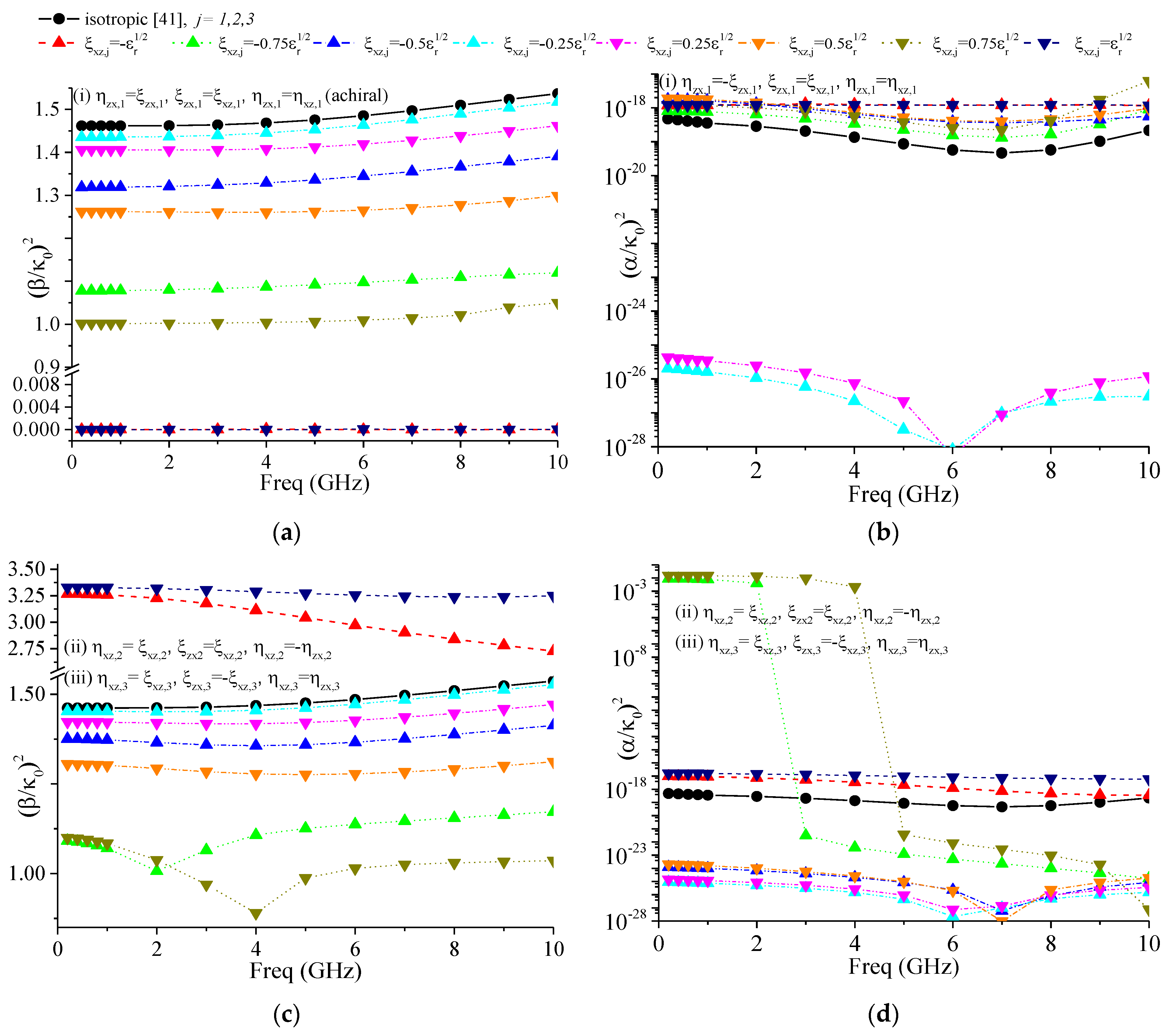
4. Results and Discussions
4.1. Effect of Diagonal Bianisotropy
- , ;
- , ;
- , .
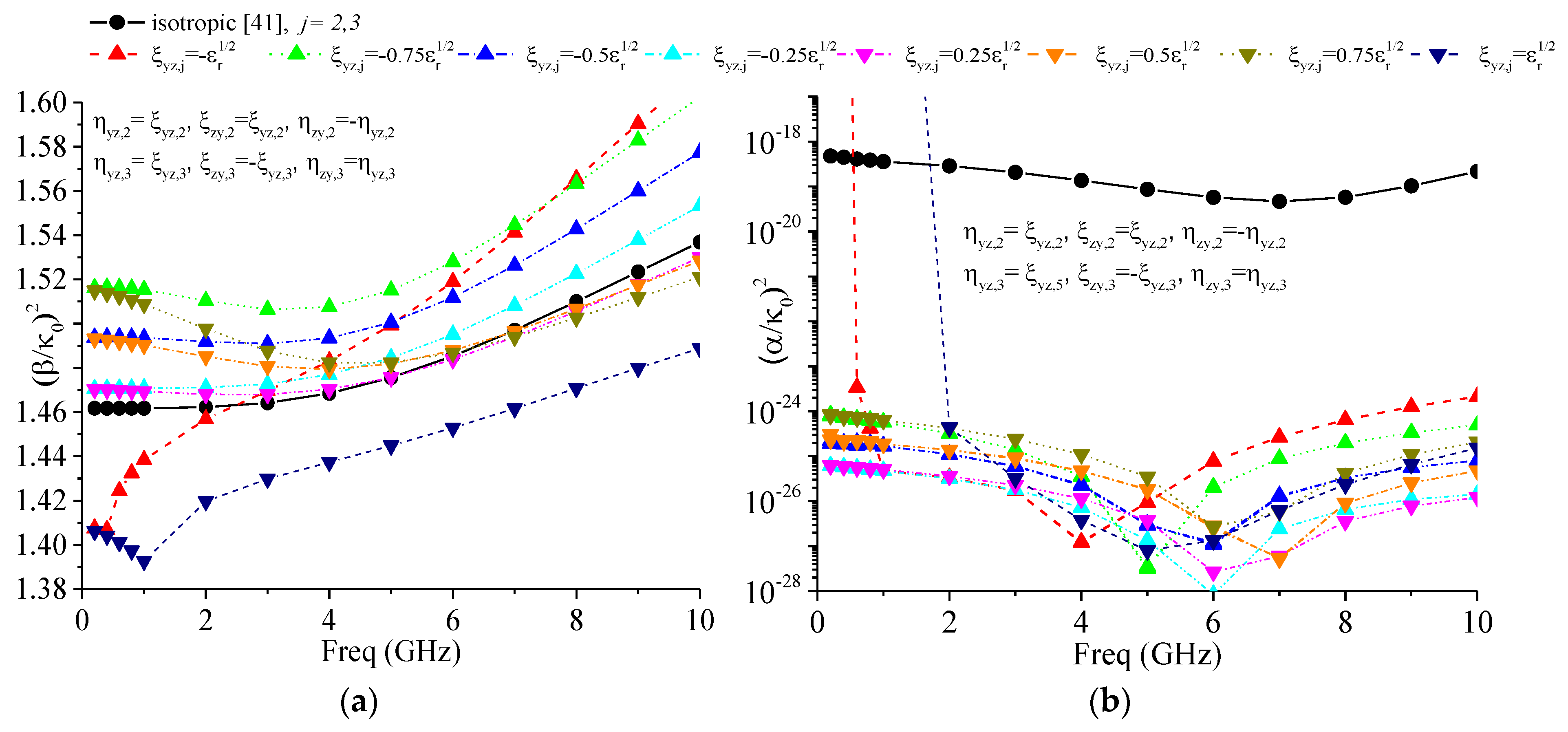
4.2. Effect of Gyrotropic Bianisotropy
- , , ;
- ;
- ;
- ;
- ;
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Capolino, F. Theory and Phenomena of Metamaterials; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Asadchy, V.S.; Díaz-Rubio, A.; Tretyakov, S.A. Bianisotropic metasurfaces: Physics and applications. Nanophotonics 2018, 7, 1069–1094. [Google Scholar] [CrossRef]
- Ra’di, Y.; Grbic, A. Magnet-free nonreciprocal bianisotropic metasurfaces. Phys. Rev. B 2016, 94, 195432. [Google Scholar] [CrossRef]
- Sihvola, A.; Semchenko, I.; Khakhomov, S. View on the history of electromagnetics of metamaterials: Evolution of the congress series of complex media. Photonics Nanostructures-Fundam. Appl. 2014, 12, 279–283. [Google Scholar] [CrossRef][Green Version]
- Novitsky, A.; Shalin, A.S.; Lavrinenko, A.V. Spherically symmetric inhomogeneous bianisotropic media: Wave propagation and light scattering. Phys. Rev. A 2017, 95, 053818. [Google Scholar] [CrossRef]
- Wang, N.; Wang, G.P. Effective medium theory with closed-form expressions for bi-anisotropic optical metamaterials. Opt. Express 2019, 27, 23739–23750. [Google Scholar] [CrossRef] [PubMed]
- Sihvola, A.; Lindell, I.V. Bianisotropic materials and PEMC. In Theory and Phenomena of Metamaterials; CRC Press: Boca Raton, FL, USA, 2017; pp. 26-1–26-7. [Google Scholar]
- Kesari, V.; Keshari, J.P. Hybrid-mode analysis of circular waveguide with chiral dielectric lining for dispersion characteristics for potential application in broadbanding a gyro-traveling-wave tube. J. Electromagn. Waves Appl. 2019, 33, 204–214. [Google Scholar] [CrossRef]
- Crowgey, B.R.; Tuncer, O.; Tang, J.; Rothwell, E.J.; Shanker, B.; Kempel, L.C.; Havrilla, M.J. Characterization of Biaxial Anisotropic Material Using a Reduced Aperture Waveguide. IEEE Trans. Instrum. Meas. 2013, 62, 2739–2750. [Google Scholar] [CrossRef]
- Wu, B.; Wang, W.; Pacheco, J.; Chen, X.; Lu, J.; Grzegorczyk, T.; Kong, J.A.; Kao, P.; Theophelakes, P.A.; Hogan, M.J. Anisotropic metamaterials as antenna substrate to enhance directivity. Microw. Opt. Technol. Lett. 2006, 48, 680–683. [Google Scholar] [CrossRef]
- Bodnar, D.G.; Bassett, H.L. Analysis of an anisotropic dielectric radome. IEEE Trans. Antennas Propag. 1975, 23, 841–846. [Google Scholar] [CrossRef]
- Zebiri, C.; Sayad, D.; Elfergani, I.; Iqbal, A.; Mshwat, W.F.; Kosha, J.; Rodriguez, J.; Abd-Alhameed, R. A compact semi-circular and arc-shaped slot antenna for heterogeneous RF front-ends. Electronics 2019, 8, 1123. [Google Scholar] [CrossRef]
- Meshram, M.R.; Agrawal, N.K.; Sinha, B.; Misra, P.S. Characterization of M-type barium hexagonal ferrite-based wide band microwave absorber. J. Magn. Magn. Mater. 2004, 271, 207–214. [Google Scholar] [CrossRef]
- Kamra, V.; Dreher, A. Efficient analysis of multiple microstrip transmission lines with anisotropic substrates. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 636–638. [Google Scholar] [CrossRef]
- Buzov, A.L.; Buzova, M.A.; Klyuev, D.S.; Mishin, D.V.; Neshcheret, A.M. Calculating the Input Impedance of a Microstrip Antenna with a Substrate of a Chiral Metamaterial. J. Commun. Technol. Electron. 2018, 63, 1259–1264. [Google Scholar] [CrossRef]
- Klyuev, D.S.; Minkin, M.A.; Mishin, D.V.; Neshcheret, A.M.; Tabakov, D.P. Characteristics of Radiation from a Microstrip Antenna on a Substrate Made of a Chiral Metamaterial. Radiophys. Quantum Electron. 2018, 61, 445–455. [Google Scholar] [CrossRef]
- Zhou, Z.; Keller, S.M. The Application of Least-Squares Finite-Element Method to Simulate Wave Propagation in Bianisotropic Media. IEEE Trans. Antennas Propag. 2019, 67, 2574–2582. [Google Scholar] [CrossRef]
- Zebiri, C.; Lashab, M.; Benabdelaziz, F. Effect of anisotropic magneto-chirality on the characteristics of a microstrip resonator. IET Microw. Antennas Propag. 2010, 4, 446–452. [Google Scholar] [CrossRef]
- Balbastre, J.V.; Nuño, L. Modelling the propagation of electromagnetic waves across complex metamaterials in closed structures. J. Comput. Appl. Math. 2019, 352, 40–49. [Google Scholar] [CrossRef]
- Xiong, Y.; Russer, J.A.; Che, W.; Shen, G.; Han, Y.; Russer, P. Dispersion analysis of a fishnet metamaterial based on the rotated transmission-line matrix method. IET Microw. Antennas Propag. 2015, 9, 1345–1353. [Google Scholar] [CrossRef]
- Aib, S.; Benabdelaziz, F.; Zebiri, C.; Sayad, D. Propagation in diagonal anisotropic chirowaveguides. Adv. Optoelectron. 2017, 2017, 9524046. [Google Scholar] [CrossRef]
- Zebiri, C.; Daoudi, S.; Benabdelaziz, F.; Lashab, M.; Sayad, D.; Ali, N.T.; Abd-Alhameed, R.A. Gyro-chirality effect of bianisotropic substrate on the operational of rectangular microstrip patch antenna. Int. J. Appl. Electromagn. Mech. 2016, 51, 249–260. [Google Scholar] [CrossRef]
- Alù, A.; Krishnaswamy, H. Artificial nonreciprocal photonic materials at GHz-to-THz frequencies. MRS Bull. 2018, 43, 436–442. [Google Scholar] [CrossRef]
- Kamra, V.; Dreher, A. Discrete mode matching method for the analysis of microstrip lines on uniaxial anisotropic substrates. In Proceedings of the International Applied Computational Electromagnetics Society Symposium ACES, Firenze, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]
- Oueslati, N.; Aguili, T. An Improved MoM-GEC Method for Fast and Accurate Computation of Transmission Planar Structures in Waveguides: Application to Planar Microstrip Lines. Prog. Electromagn. Res. 2016, 48, 9–24. [Google Scholar] [CrossRef][Green Version]
- Ardakani, H.H.; Mehrdadian, A.; Forooraghi, K. Analysis of graphene-based microstrip structures. IEEE Access 2017, 5, 20887–20897. [Google Scholar] [CrossRef]
- Han, D.; Lee, C.; Kahng, S. Formulation of the Green’s Functions for Coplanar Waveguide Microwave Devices as Genetic Algorithm-Based Complex Images. J. Electr. Eng. Technol. 2017, 12, 1600–1604. [Google Scholar]
- Hu, Y.; Fang, Y.; Wang, D.; Zhan, Q.; Zhang, R.; Liu, Q.H. The scattering of electromagnetic fields from anisotropic objects embedded in anisotropic multilayers. IEEE Trans. Antennas Propag. 2019, 67, 7561–7568. [Google Scholar] [CrossRef]
- Daoudi, S.; Benabdelaziz, F.; Zebiri, C.; Sayad, D.; Abdussalam, F.M.; Abd-Alhameed, R. Dispersion characteristics of a gyro-chiro-ferrite shielded multilayered microstrip line using the generalized exponential matrix technique. In Proceedings of the ITA Internet Technologies and Applications, Wrexham, UK, 12–15 September 2017; pp. 293–298. [Google Scholar]
- Zebiri, C.; Lashab, M.; Benabdelaziz, F. Rectangular microstrip antenna with uniaxial bianisotropic chiral substrate-superstrate. IET Microw. Antennas Propag. 2011, 5, 17–29. [Google Scholar] [CrossRef]
- Kamra, V.; Dreher, A. Analysis of Anisotropic Inhomogeneous Dielectric Waveguides With Discrete Mode Matching Method. In Proceedings of the IMS International Microwave Symposium, Boston, MA, USA, 2–8 June 2019; pp. 24–27. [Google Scholar]
- Kamra, V.; Dreher, A. Multilayered Transmission Lines on Quasi-planar Substrates With Anisotropic Medium. Adv. Radio Sci. 2019, 17, 77–82. [Google Scholar] [CrossRef]
- Horikis, T.P. Dielectric waveguides of arbitrary cross sectional shape. Appl. Math. Model. 2013, 37, 5080–5091. [Google Scholar] [CrossRef]
- She, S.X. Iterated-moment method for the analysis of optical waveguides of arbitrary cross section. JOSA A 1989, 6, 1031–1037. [Google Scholar] [CrossRef]
- Yang, W.D.; Pregla, R. The method of lines for analysis of integrated optical waveguide structures with arbitrary curved interfaces. J. Lightwave Technol. 1996, 14, 879–884. [Google Scholar] [CrossRef]
- Hasar, U.C.; Barroso, J.J.; Sabah, C.; Kaya, Y.; Ertugrul, M. Stepwise technique for accurate and unique retrieval of electromagnetic properties of bianisotropic metamaterials. J. Opt. Soc. Am. B 2013, 30, 1058–1068. [Google Scholar] [CrossRef]
- Hasar, U.C.; Barroso, J.J.; Bute, M.; Muratoglu, A.; Ertugrul, M. Boundary effects on the determination of electromagnetic properties of bianisotropic metamaterials from scattering parameters. IEEE Trans. Antennas Propag. 2016, 64, 3459–3469. [Google Scholar] [CrossRef]
- Hasar, U.C.; Muratoglu, A.; Bute, M.; Barroso, J.J.; Ertugrul, M. Effective Constitutive Parameters Retrieval Method for Bianisotropic Metamaterials Using Waveguide Measurements. IEEE Trans. Microw. Theory Tech. 2017, 65, 1488–1497. [Google Scholar] [CrossRef]
- Hasar, U.C.; Buldu, G.; Kaya, Y.; Ozturk, G. Determination of Effective Constitutive Parameters of Inhomogeneous Metamaterials With Bi-anisotropy. IEEE Trans. Microw. Theory Tech. 2018, 66, 3734–3744. [Google Scholar] [CrossRef]
- Tsalamengas, J.L. Interaction of electromagnetic waves with general bianisotropic slabs. IEEE Trans. Microw. Theory Tech. 1992, 40, 1870–1878. [Google Scholar] [CrossRef]
- Daoudi, S.; Benabdelaziz, F.; Zebiri, C.; Sayad, D. Generalized Exponential Matrix Technique Application for the Evaluation of the Dispersion Characteristics of a Chiro-Ferrite shielded Multilayered Microstrip Line. Prog. Electromagn. Res. M 2017, 61, 1–14. [Google Scholar] [CrossRef][Green Version]
- Sayad, D.; Zebiri, C.; Daoudi, S.; Benabdelaziz, F. Analysis of the Effect of a Gyrotropic Anisotropy on the Phase Constant and Characteristic Impedance of a Shielded Microstrip Line. Adv. Electromagn. 2019, 8, 15–22. [Google Scholar]
- Bianconi, G.; Mittra, R. Efficient Numerical Techniques for Analyzing Microstrip Circuits and Antennas Etched on Layered Media via the Characteristic Basis Function Method. In Computational Electromagnetics; Springer: New York, NY, USA, 2014; pp. 111–148. [Google Scholar]
- Park, S.-O.; Balanis, C.A. Analytical technique to evaluate the asymptotic part of the impedance matrix of Sommerfeld-type integrals. IEEE Trans. Antennas Propag. 1997, 45, 798–805. [Google Scholar] [CrossRef]
- Sayad, D.; Benabdelaziz, F.; Zebiri, C.; Daoudi, S.; Abd-Alhameed, R.A. Spectral domain analysis of gyrotropic anisotropy chiral effect on the input impedance of a printed dipole antenna. Prog. Electromagn. Res. M 2016, 51, 1–8. [Google Scholar] [CrossRef][Green Version]
- Jain, S.; Song, J. Accelerated spectral domain approach for shielded microstrip lines by approximating summation with super convergent series. In Proceedings of the Digests of the 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010; p. 1. [Google Scholar]
- Lucido, M. A new high-efficient spectral-domain analysis of single and multiple coupled microstrip lines in planarly layered media. IEEE Trans. Microw. Theory Tech. 2012, 60, 2025–2034. [Google Scholar] [CrossRef]
- Jain, S.; Song, J.; Kamgaing, T.; Mekonnen, Y.S. Acceleration of spectral domain approach for generalized multilayered shielded microstrip interconnects using two fast convergent series. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 401–410. [Google Scholar] [CrossRef]
- Xu, H.; Jain, S.; Song, J.; Kamgaing, T.; Mekonnen, Y.S. Acceleration of spectral domain immitance approach for generalized multilayered shielded microstrips using the Levin’s transformation. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 92–95. [Google Scholar] [CrossRef]
- Medina, F.; Horno, M. Quasianalytical static solution of the boxed microstrip line embedded in a layered medium. IEEE Trans. Microw. Theory Tech. 1992, 40, 1748–1756. [Google Scholar] [CrossRef]
- Tsalamengas, J.L.; Fikioris, G. Rapidly converging spectral-domain analysis of rectangularly shielded layered microstrip lines. IEEE Trans. Microw. Theory Tech. 2003, 51, 1729–1734. [Google Scholar] [CrossRef]
- Railton, C.J.; McGeehan, J.P. A rigorous and computationally efficient analysis of microstrip for use as an electro-optic modulator. IEEE Trans. Microw. Theory Tech. 1989, 37, 1099–1104. [Google Scholar] [CrossRef]
- Tao, J.-W.; Angenieux, G.; Flechet, B. Full-wave description of propagation and losses in quasi-planar transmission lines by quasi-analytical solution. IEEE Trans. Microw. Theory Tech. 1994, 42, 1246–1253. [Google Scholar] [CrossRef]
- Cano, G.; Medina, F.; Horno, M. Efficient spectral domain analysis of generalized microstrip lines in stratified media including thin, anisotropic and lossy substrates. IEEE Trans. Microw. Theory Tech. 1992, 40, 217–227. [Google Scholar] [CrossRef]
- MATLAB 9.4 (R2018a), The MathWorks, Inc.: Natick, MA, USA, 2018.
- Yang, H.Y. A numerical method of evaluating electromagnetic fields in a generalized anisotropic medium. IEEE Trans. Microw. Theory Tech. 1995, 43, 1626–1628. [Google Scholar] [CrossRef]
- Mariotte, F.; Pelet, P.; Engheta, N. A review of recent study of guided waves in chiral media. Prog. Electromagn. Res. 1994, 9, 311–350. [Google Scholar]
- Krowne, C.M. Electromagnetic propagation and field behavior in highly anisotropic media. Adv. Imaging Electron Phys. 1995, 92, 79–214. [Google Scholar]
- Nguyen, C. Analysis Methods for RF, Microwave, and Millimeter-Wave Planar Transmission Line Structures; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Mirshekar-Syhakal, D. Spectral Domain Method for Microwave Integrated Circuits; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Maze-Merceur, G.; Tedjini, S.; Bonnefoy, J.L. Analysis of a CPW on electric and magnetic biaxial substrate. IEEE Trans. Microw. Theory Tech. 1993, 41, 457–461. [Google Scholar] [CrossRef]
- Khodja, A.; Yagoub, M.C.E.; Touhami, R.; Baudrand, H. Practical Recurrence Formulation for Composite Substrates: Application to Coplanar Structures with Bi-Anisotropic Dielectrics. In Proceedings of the 18th Mediterranean Microwave Symposium (MMS), Istanbul, Turkey, 31 October–2 November 2018; pp. 341–344. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sayad, D.; Zebiri, C.; Elfergani, I.; Rodriguez, J.; Abobaker, H.; Ullah, A.; Abd-Alhameed, R.; Otung, I.; Benabdelaziz, F. Complex Bianisotropy Effect on the Propagation Constant of a Shielded Multilayered Coplanar Waveguide Using Improved Full Generalized Exponential Matrix Technique. Electronics 2020, 9, 243. https://doi.org/10.3390/electronics9020243
Sayad D, Zebiri C, Elfergani I, Rodriguez J, Abobaker H, Ullah A, Abd-Alhameed R, Otung I, Benabdelaziz F. Complex Bianisotropy Effect on the Propagation Constant of a Shielded Multilayered Coplanar Waveguide Using Improved Full Generalized Exponential Matrix Technique. Electronics. 2020; 9(2):243. https://doi.org/10.3390/electronics9020243
Chicago/Turabian StyleSayad, Djamel, Chemseddine Zebiri, Issa Elfergani, Jonathan Rodriguez, Hasan Abobaker, Atta Ullah, Raed Abd-Alhameed, Ifiok Otung, and Fatiha Benabdelaziz. 2020. "Complex Bianisotropy Effect on the Propagation Constant of a Shielded Multilayered Coplanar Waveguide Using Improved Full Generalized Exponential Matrix Technique" Electronics 9, no. 2: 243. https://doi.org/10.3390/electronics9020243
APA StyleSayad, D., Zebiri, C., Elfergani, I., Rodriguez, J., Abobaker, H., Ullah, A., Abd-Alhameed, R., Otung, I., & Benabdelaziz, F. (2020). Complex Bianisotropy Effect on the Propagation Constant of a Shielded Multilayered Coplanar Waveguide Using Improved Full Generalized Exponential Matrix Technique. Electronics, 9(2), 243. https://doi.org/10.3390/electronics9020243









