Abstract
The Marching On-In-Time (MOT) unstructured Partial Element Equivalent Circuit (PEEC) method for time domain electromagnetic problems is presented. The method allows the transient analysis of electrically large electromagnetic devices consisting of conductive, dielectric, and magnetic media coupled with external lumped circuits. By re-formulating PEEC following the Coulombian interpretation of magnetization phenomena and by using electric and magnetic vector potentials, the proposed approach allows for a completely equivalent treatment of electric and magnetic media and inhomogeneous and anisotropic materials are accounted for as well. With respect to the recently proposed Marching On-In-Time PEEC approach, based on the standard (structured) discretization of PEEC, the method presented in this paper uses a different space and time MOT discretization, which allows for a reduction in the number of the unknowns. Analytical and industrial test cases consisting in electrically large devices are considered (e.g., the model of a Neutral Beam Injector adopted in thermonuclear fusion applications). Results obtained from the simulations show that the proposed method is accurate and yields good performances. Moreover, when rich harmonic content transient phenomena are considered, the unstructured MOT–PEEC method allows for a significant reduction of the memory and computation time when compared to techniques based on Inverse Discrete Fourier Transform applied to the frequency domain unstructured PEEC approach.
1. Introduction
Integral equation (IE) methods are particularly suited for the study of electromagnetic (EM) devices in unbounded domains since they do not require the introduction of artificial absorbing boundary conditions for truncating the computational domain and they avoid the discretization of regions with the characteristic of vacuum [1,2,3]. In particular, the Partial Element Equivalent Circuit (PEEC) method, introduced by Ruehli in 1972 [4], has been shown to be well suited for the analysis of several classes of EM devices, such as interconnecting [5,6] antennas [7,8,9], and other complex electric and electronic devices [10,11,12,13]. IE methods such as the PEEC approach are widely used for time-harmonic EM problems and they are also particularly suited for transient analysis, usually performed by means of traditional time-stepping algorithms, e.g., forward and backward Euler, Crank–Nicolson, and Runge–Kutta methods.
However, in the context of transient analyses with electrically large devices, where time delay effects on the propagation of the EM fields need to be considered, traditional time-stepping algorithms cannot be easily used. Among all the different possibilities to develop Time Domain Integral Equation (TDIE) methods, the Marching On-In-Time (MOT) scheme [14] allows for naturally considering the effects of the time delay on the EM fields propagation and such scheme has been been widely adopted over the years [15].
The possibility of combining the MOT procedure with the structured version of PEEC has been shortly discussed in [16,17], whereas, in the literature, time domain PEEC methods under the assumption of electrically small structures have been mostly proposed (i.e., without time delay effects). Recently, a MOT–PEEC method based on the structured PEEC approach has been presented in [18] for the study of conductive and dielectric media only (i.e., non–magnetic media). Another PEEC based ad hoc approach for the study of a wire structure excited by a distant lightning channel has been proposed in [19].
The aim of this work is to provide a general and efficient numerical tool by combining the MOT scheme with the unstructured version of the PEEC approach [20]. Indeed, differently from existing MOT–PEEC approaches, the formulation proposed herein is based on the unstructured version of PEEC [10], and the MOT procedure is differently applied to the PEEC formulation with respect to [16]. As a further innovative feature, unlike [18], magnetic media are also treated by the proposed MOT–PEEC method by following the recently proposed harmonic PEEC formulation based on the Coulombian interpretation of magnetization phenomena [21]. This also allows for a reduction in the number of unknowns. Furthermore, the proposed formulation provides the same well-known circuit interpretation of the harmonic PEEC method, allowing for a very easy coupling of discretized devices and lumped circuits’ components. Moreover, inhomogeneous and anisotropic media can be considered as well. Therefore, the typical target problems for the MOT–PEEC approach are electrically large devices consisting of a wide class of materials. For instance, the method is well suited for the study of scattering problems. Moreover, thanks to the features of integral equation methods which avoid the air meshing, the time domain response of large and complex devices to rich harmonic content excitations in unbounded domains can been efficiently evaluated. Indeed, as shown in the numerical results section, with respect to approaches based on standard Inverse Discrete Fourier Transform applied to frequency domain methods, the proposed MOT–PEEC technique allows for a significant reduction in the computation time and memory requirements.
The rest of the paper is organized as follows. First, in Section 2, the delayed time domain PEEC formulation based on the frequency domain PEEC formulation proposed in [21] is presented. Then, in Section 3, the spatial and temporal MOT discretization is applied to the unstructured–PEEC formulation. In the last part of Section 3, some numerical aspects concerning the proposed unstructured MOT–PEEC scheme are discussed and possible extensions and modifications of the numerical approach based on the vast literature concerning MOT and TDIE are discussed. In Section 4, to show the usefulness of the MOT–PEEC method for the study of different problems which include electrically large structures, several numerical test cases simulated with the proposed unstructured MOT–PEEC approach are presented and the numerical results show good performances in terms of both computation time and memory. First, the MOT–PEEC is validated by studying the analytical case of a dielectric shell excited by an EM plane wave. Then, the case of a Neutral Beam Injector used for Thermonuclear Fusion applications is considered [22,23]. Finally, the numerical results obtained from a MOT–PEEC method for equivalent surface models are presented and the same stability analysis proposed in [24] is applied to one of these cases.
2. MOT–PEEC Formulation
In this section, the formulation of the Unstructured MOT–PEEC method is presented. In this work, magnetic media are considered by following the approach proposed in [21], based on magnetic currents and charges (i.e., the Coulombian interpretation of the magnetization phenomena [21,25,26]).
Let , , and be the conductive (), the dielectric (), and the magnetic () domains, respectively, where is the electric conductivity, is the relative electric permittivity, and is the relative magnetic permeability. The electric domain is also defined as and the following boundaries are defined: , , , and . The computational domain is . As in [21], where a time harmonic PEEC method is proposed, the electric, , and magnetic, , fields can be written in terms of electric and magnetic potentials, i.e.,
where and are electric and magnetic vector potentials, and are electric and magnetic scalar potentials, and and are external electric and magnetic fields produced by the source domain . Electromagnetic quantities in (1) and (2) are evaluated in the field point and at the present time instant t.
Moreover, as in [21], the conduction, , the polarization, , and the magnetic, , currents are introduced together with the following time domain constitutive relations:
where is the electric resistivity,
is the equivalent electric resistivity of dielectric media and
is the equivalent magnetic resistivity of magnetic media. and are the vacuum permittivity and permeability, respectively.
In (1) and (2), and its time derivative are given by
where is the electric current density, is the integration point, and is the retarded time; is the speed of light in vacuum.
Similarly, and are given by:
The scalar electric potential is given by:
where and are the volume and surface electric charges [21], respectively. and are related to by means of charge conservation relations:
where is the outward unit normal vector of .
3. Spatial and Time Discretization
The computational domain is now discretized into a tetrahedral (or 8-node hexahedral elements with planar quadrilateral faces) unstructured grid , as proposed in [21]. Moreover, a temporal discretization of the time interval of interest is also introduced consisting of time steps, equally spaced by .
Then, is expanded in terms of degrees of freedoms (DoFs) by using face functions for the spatial discretization and temporal basis functions for the time discretization [3]:
where , with , is the flux of through the kth face of the mesh (i.e., the kth branch of the equivalent circuit) at the sth time step, and are the number of spatial (i.e., faces of the mesh) and temporal basis functions, respectively.
At each sth time instant (i.e., ), with , the DoFs are stored in the array . and are expanded likewise, leading to the arrays and of dimension and , respectively, where is the number of faces of the mesh of and is the number of faces of the mesh of .
For simplicity reasons, from now on, T is considered as the well-known hat shape function with support , where is the chosen time step. This leads to a causal MOT scheme. However, as discussed in the following, different choices of the basis function can be made, leading to non–causal MOT systems [3].
Following [14], a Galerkin approach for the spatial discretization and a collocation method for the temporal discretization are applied to the equations obtained by combining (1) and (2) combined with (3)–(17). At each sth time step, this operation leads to the following matrix equations:
for the conductive media,
for the dielectric media, and
for the magnetic media.
In (19)–(21), and are the array of DoFs related to in and , respectively, and is the array of DoFs related to in , i.e.:
The coefficients of the resistance () and inductance () matrices in (19)–(21) are given by
where and when temporal hat shape functions are used. T is the temporal (hat) basis function centered in the origin (i.e., ). Matrices and have dimension , where, for the sake of conciseness, and depending on the domain.
The coefficients of the mutual interaction matrices between electric and magnetic domains () are instead given by:
Matrices , , and in (19)–(21) are the incidence (gradient) matrices. Matrix has dimension , where and are the number of volume and boundary faces of the mesh of , respectively. Matrix has dimension , where and are the number of volume and boundary faces of the mesh of , whereas has dimension , where and are the number of volume and boundary faces of the mesh of .
Matrices and in (19)–(21), with , represent the electromagnetic interactions between the unknowns at the time instant s and unknowns at the previous time instant . When , these matrices represent instantaneous interactions between unknowns at the same time instant. Instead, when , these matrices represent retarded interactions between unknowns that are separated in time by a quantity equal to . indicates how many previous time steps actually interact with the present solution, where is the maximum distance between two mesh elements of and is the ceiling operator.
These instantaneous and retarded interactions are exemplified in Figure 1: unknowns which are close to each other interact instantaneously (orange cross vs. red unknowns). Instead, unknowns which are far from each other interact with a retardation which increases with the spatial distance (orange cross vs. green, blue, and black unknowns).
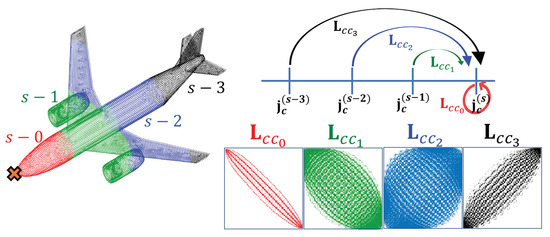
Figure 1.
Marching matrices interactions exemplification.
Following a leap-frog scheme [17] and according to the classical Tonti diagram, and are expanded onto the dual spatial and temporal grids and obtained by the barycentric subdivision of and , respectively. Figure 2 shows the primal and dual temporal grids: and , respectively. As in [21], and are the arrays of scalar electric potentials related to the conductive and dielectric domains. Instead, is the array of scalar magnetic potentials.
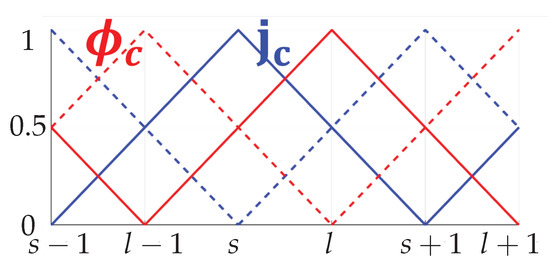
Figure 2.
Primal () and dual () temporal discretization.
In the same fashion of the frequency–domain PEEC method [21], the time derivative of , , and is related to the divergence of the electric and magnetic current array of DoFs (i.e., the electric and magnetic charge array of DoFs) by means of integral potential matrices, i.e.:
where, as in [21], the potential matrices () are subdivided into volume, surface, and volume–surface matrices, i.e.,
and the same holds for the other potential matrices in (34)–(36). Matrices have dimension , where, for the sake of conciseness, and depending on the domain. The coefficients of the potential matrices are given by
where, for the sake of conciseness, and , and indicates the measure (i.e., volume or area) of either volume or surface elements.
The arrays , , and are related to and , with , (i.e., the nodes of the equivalent circuit) at the instant . Thus, , , and are also given by
where subscript l in (46)–(48) refers to the time instant , whereas , , and are given by
Equations (19)–(21) and (52)–(54) (scaled by to improve the conditioning) are finally combined, leading to the final system of linear equations to be solved at each sth and lth time step where (for each sth and lth time step) the unknowns are , , , , , and , i.e.,
where
The left-hand side of (55) consists of resistance, incidence, and instantaneous matrices only (i.e., those ones with ) and is the same for each time step. The right–hand side is instead updated at each time step by multiplying the marching matrices (i.e., ones with ) with the previous solutions, as shown in (56)–(61). It is worth noting that instantaneous and marching matrices are in general sparse with a sparsity ratio which depends on the choice of (i.e., the smaller , the lower the sparsity ratio and the greater ). As a distinctive feature of PEEC, connections with lumped circuit elements are easily considered by adding the circuit currents and node potentials of the lumped components to the unknowns and solving Kirchhoff’s Voltage and Currents Laws together with (55).
With the aim of increasing the stability and the accuracy of the MOT scheme applied to integral equation methods, several authors have proposed different temporal shape functions (e.g., higher order with a more extended [27] and/or not–causal support [3]) and different choices of the unknowns (e.g., electric and magnetic polarizations and or densities fields and ). Indeed, these different choices (which also allow for reducing the number of unknowns by neglecting the scalar potentials from the independent unknowns [3]) seem to generally improve the accuracy and the stability of the MOT method. Indeed, the use of a smoothly varying temporal shape functions alleviates the instability issues caused by the numerical integration of integral matrix coefficients subject to the encroachment of the propagating electromagnetic wave [28,29] (see Figure 3).
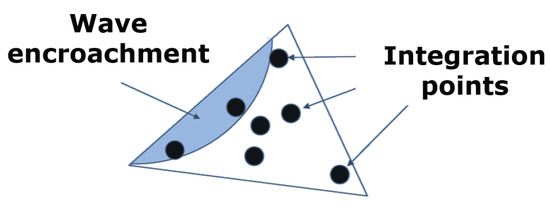
Figure 3.
Exemplification of integration inaccuracy due to the wave encroachment.
However, the use of temporal shape functions with large support deteriorates the sparsity ratio of the matrices. Moreover, when temporal basis functions with non-causal support are chosen, several future solutions must be predicted as proposed in [30].
In the context of the proposed MOT–PEEC method, in accordance with the analysis presented in [18], hat shape functions have been chosen since they provide a good trade-off between stability, accuracy, and numerical performances. However, the discretization process proposed herein can be easily modified by considering different temporal shape functions and/or predictor–corrector schemes [30]. Indeed, the proposed MOT–PEEC method (which is intended as a basic and general formulation) can be however modified by following more sophisticated approaches [31,32,33,34] and parallelization techniques, as proposed in [15].
Lastly, the choice of considering the scalar potentials as independent unknowns makes it possible to separate the inductive () and capacitive () effects, avoiding instabilities which can be attributed to round–off errors equivalent to those due to the breakdown in frequency issue in harmonic problems.
4. Numerical Results
The MOT–PEEC code has been developed with MATLAB® and parallel MEX–FORTRAN functions based on OpenMP libraries. Thin wire, triangular, and hexahedral mesh elements are considered. Simulations were run on a Linux machine equipped with dual 6-core/12-thread processors (Xeon E5-2643 v4 @3.40 GHz) and 512 GB RAM.
4.1. Dielectric Shell
The first test case consists of a dielectric shell ( m outer radius, m inner radius) excited by a Gaussian Modulated Pulse (GMP) [15]:
with MHz, MHz, and , . Three cases are considered:
- homogeneous medium with ,
- anisotropic medium with
- non–homogeneous medium with .
The results obtained from the MOT–PEEC code are compared with those obtained from a frequency–domain PEEC (FD–PEEC) code [21]. For case 1 only, the results are also compared with the MIE solution. Discrete Fourier Transform (DFT) and Inverse–DFT (IDFT) are adopted to extract frequency domain results from time simulations and vice versa. Figure 4 shows the scattered magnetic field magnitude (in time domain) evaluated in the target point for case . For cases 1, 2, and 3, Figure 5 shows the frequency spectra of the three components of the scattered magnetic field. The same hexahedral mesh with 3072 elements is adopted for both MOT–PEEC and FD–PEEC.
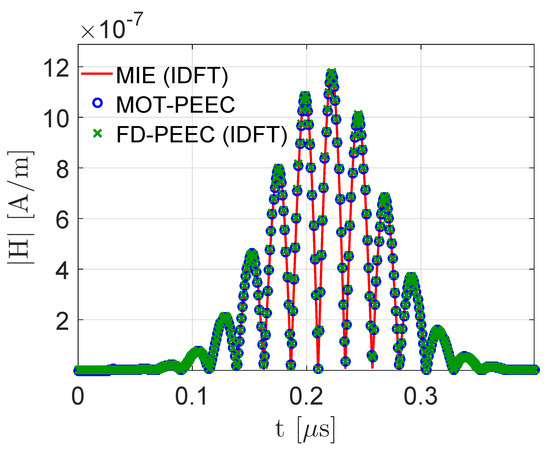
Figure 4.
Scattered magnetic field norm for case 1.
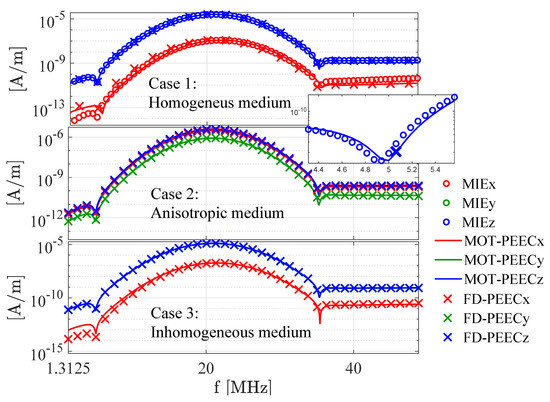
Figure 5.
Frequency spectra of , , and evaluated in the target point —Cases 1, 2, and 3.
Results show good agreement and some small discrepancy can be observed only for the smallest components of .
4.2. Neutral Beam Injector
Neutral Beam Injectors (NBIs) are electrically large devices adopted in Thermonuclear Fusion for plasma heating. In these devices, the protection against the grid breakdown and other possible failures is a very sensitive issue [22,23]. NBIs are complex devices fed by very long transmission lines (e.g., m for ITER), which, with good approximation, can be modeled as coaxial cables. With the aim of protecting NBIs against possible breakdowns (i.e., damping dangerous voltage oscillations), magnetic core snubbers (combined also with other technologies) are usually adopted. Here, the simplified case of NBI shown in Figure 6 is considered.
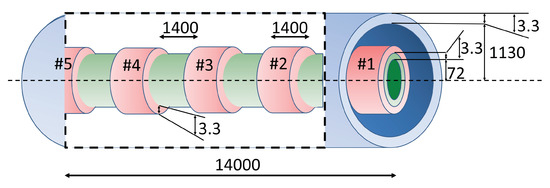
Figure 6.
NBI PEEC model (not in scale). Blue: external shell; green: internal shell; red: magnetic core snubbers. Values in mm.
The NBI model consists of two 14 m long concentric cylindrical shells. The inner and the outer shells have an inner radius of 72 mm and 1130 mm, respectively. Both shells have mm thickness of and 100 kS/m conductivity. The device is fed by a voltage source by means of short circuits which connect the end points of the voltage source with the boundary faces which discretize the initial cross sections of the external and internal shells of the NBI model. Five equally spaced cylindrical magnetic shells (, m long, thickness 3.3 mm, inner radius mm) are placed around the internal conductive shell of the NBI (magnetic core snubbers). The voltage source generates a unit step voltage with rising time 150 ns.
The simulations were run using ns, , 6840 conducting and 1140 magnetic hexahedral elements. The results in terms of the time evolution of the current flowing through the voltage source are compared with those obtained by applying the IDFT to the FD–PEEC code with a frequency sweep of 150 equally spaced values in the range from 0 Hz to 20 MHz. Figure 7 shows the results obtained by truncating the sweep after 10, 20, 30, 70, and 150 frequency simulations. Since retardation effects must be considered, the dense integral matrices of the FD–PEEC must be updated at each frequency simulation. Thus, to avoid prohibitive computation time of FD–PEEC, the exponential term of the (harmonic) dynamic Green’s function is considered to be constant within every single cell (with a good approximation) in order to avoid the re-evaluation of the integrals at each frequency step. Thus, the inductance and potential PEEC matrices are updated at each frequency value by multiplying each matrix entry with the related (retardation) coefficient.
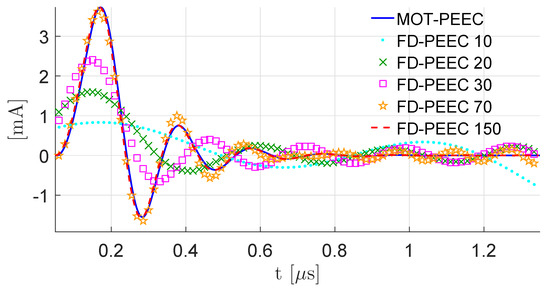
Figure 7.
Current flowing in the VS connected to the NBI.
The Peak Memory Usage (PMU) of the MOT–PEEC method is GB, the time for the generation of the matrices is s, and the time for a single time solution is s. For the sake of comparison, the computational details of the IDFT FD–PEEC are 15 GB of PMU (due to the need of storing the non–retarded matrices, the retardation coefficients, and the system to be solved), s, and s (i.e., time for the updating of the matrices and the assembling and solution of the system). Thus, the total simulation time of MOT–PEEC is s, whereas the one of FD–PEEC is s. Indeed, due to the rich harmonic content of the problem, the MOT–PEEC code allows for significantly reducing the computational effort with respect to the FD–PEEC.
4.3. Equivalent Surface Models
The MOT–PEEC formulation can be easily modified for the study of equivalent surface models. In this paragraph, some of the numerical results obtained from a MOT–PEEC formulation for equivalent surface models (i.e., thin structures) are briefly presented.
Figure 8 shows a snapshot of the electric potential wave propagating on an airplane excited by a GMP (62) ( MHz, , ). The model consists of 33,290 triangular elements, resulting in 83,240 unknowns (i.e., the edges of the mesh). The resistivity of the plane is m, with a thickness of 1 mm. A time step of ns has been used and the simulation consisted of time steps. The computation time required by the simulation was s, for the generation of the MOT matrices, and s for each time step solution. The PMU reached by the simulation was 78 GB.
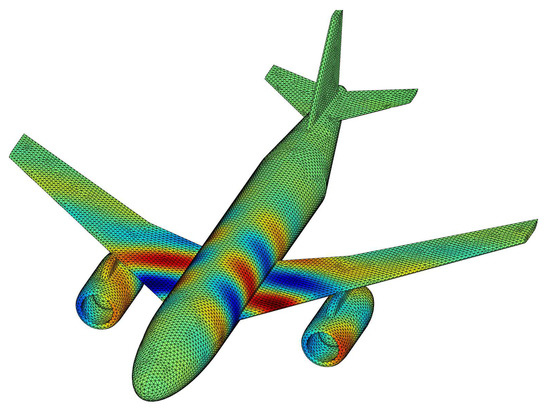
Figure 8.
Airplane excited by a GMP. Snapshot of the electric potential wave propagation obtained from the unstructured MOT–PEEC code for equivalent surface models.
Figure 9 instead shows the transient evolution of an electromagnetic wave in a transmission line fed by a sinusoidal lumped voltage source ( MHz, ns). The conductivity of the transmission line is S/m with a thickness of 1 mm. The other geometrical details of the case are shown in Figure 9.
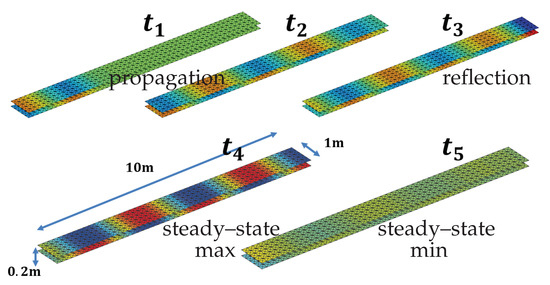
Figure 9.
Snapshots of the electromagnetic wave propagating along a transmission line fed by a sinusoidal voltage source. Results obtained from the unstructured MOT–PEEC code for equivalent surface models.
Finally, the MOT–PEEC formulation for the case of equivalent surface conductive models is validated on the case of a m square plate with normal excited by the GMP (62) with Hz, , , and Hz.
The thickness of the plate is 1 mm and the resistivity is m. The chosen time step is s. Figure 10 shows the temporal evolution of the current density (x–component) in one of the triangular mesh elements obtained from the MOT–PEEC code for equivalent surface models. The results are compared with the ones obtained from the IDFT applied to a FD–PEEC code [20] and the well-known commercial software FEKO® based on IE methods.
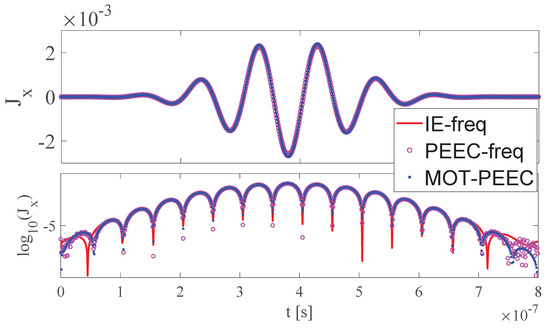
Figure 10.
Current evolution on the square plate excited by a GMP.
4.4. Stability Analysis
Finally, when the dimension of the problem is relatively small, the stability analysis proposed in [24] and based on the eigenvalues distribution of the MOT transmission matrix can be applied (i.e., the method is unconditionally stable if the magnitude of all eigenvalues is smaller than 1). Figure 11 shows the eigenvalue distribution of the MOT–PEEC transmission matrix for the case of the square plate considered above.
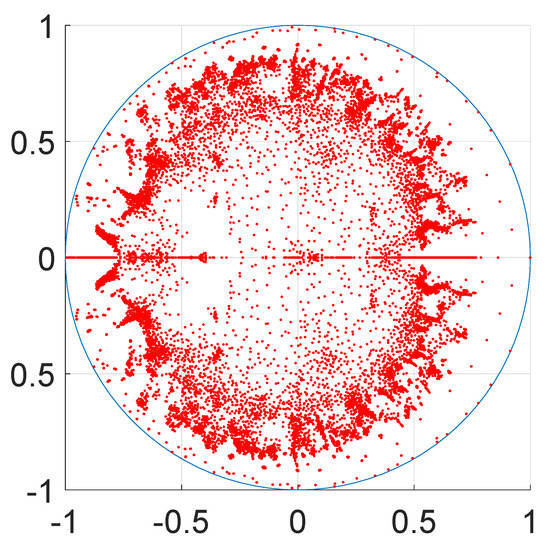
Figure 11.
Eigenvalues distribution of the transmission MOT matrix in the complex plane for the case of the conductive plate.
5. Conclusions
The unstructured Marching On-In-Time Partial Element Equivalent Circuit method for the study of conductive, dielectric, and magnetic media has been presented with several application examples including inhomogeneous and anisotropic media. When fast transients need to be analyzed, the proposed method shows itself to be competitive with frequency domain methods combined with Inverse Discrete Fourier Transform. The proposed MOT–PEEC method is also suitable for the application of more sophisticated temporal discretization approaches [3] and parallelization techniques, as proposed in [15].
Author Contributions
Conceptualization, R.T.; methodology, R.T.; software, R.T.; validation, R.T., D.V. and P.B.; formal analysis, R.T.; investigation, R.T.; resources, P.A. and R.T.; data curation, R.T.; writing—original draft preparation, R.T.; writing—review and editing, R.T., P.A., F.M.; visualization, R.T.; supervision, P.A., P.B., and F.M.; project administration, F.M. and P.A.; funding acquisition, P.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Università degli Studi di Padova, Italy, BIRD 2019 program (No. BIRD 195949/19).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rubinacci, G.; Ventre, S.; Villone, F.; Liu, Y. A fast technique applied to the analysis of resistive wall modes with 3D conducting structures. J. Comput. Phys. 2009, 228, 1562–1572. [Google Scholar] [CrossRef]
- Forestiere, C.; Miano, G.; Rubinacci, G.; Tamburrino, A.; Udpa, L.; Ventre, S. A Frequency Stable Volume Integral Equation Method for Anisotropic Scatterers. IEEE Trans. Antennas Propag. 2017, 65, 1224–1235. [Google Scholar] [CrossRef]
- Sayed, S.B.; Ülkü, H.A.; Bağcı, H. A Stable Marching On-In-Time Scheme for Solving the Time-Domain Electric Field Volume Integral Equation on High-Contrast Scatterers. IEEE Trans. Antennas Propag. 2015, 63, 3098–3110. [Google Scholar] [CrossRef]
- Ruehli, A.E. Inductance Calculations in a Complex Integrated Circuit Environment. IBM J. Res. Dev. 1972, 16, 470–481. [Google Scholar] [CrossRef]
- Romano, D.; Antonini, G. Partial Element Equivalent Circuit-Based Transient Analysis of Graphene-Based Interconnects. IEEE Trans. Electromagn. Compat. 2016, 58, 801–810. [Google Scholar] [CrossRef]
- Romano, D.; Kovačević-Badstübner, I.; Parise, M.; Grossner, U.; Ekman, J.; Antonini, G. Partial Element Equivalent Circuit-Based Transient Analysis of Graphene-Based Interconnects. IEEE Trans. Electromagn. Compat. 2016, 63, 1499–1510. [Google Scholar] [CrossRef]
- Cao, Y.S.; Jiang, L.J.; Ruehli, A.E. An Equivalent Circuit Model for Graphene-Based Terahertz Antenna Using the PEEC Method. IEEE Trans. Antennas Propag. 2016, 64, 1385–1393. [Google Scholar] [CrossRef]
- Baumgartner, P.; Renhart, W.; Birò, O.; Hackl, A.; Magele, C.; Bauernfeind, T.; Torchio, R. Multi-Objective Optimization of Yagi–Uda Antenna Applying Enhanced Firefly Algorithm with Adaptive Cost Function. IEEE Trans. Magn. 2018, 54, 8000504. [Google Scholar] [CrossRef]
- Voltolina, D.; Bettini, P.; Alotto, P.; Moro, F.; Torchio, R. High-Performance PEEC Analysis of Electromagnetic Scatterers. IEEE Trans. Magn. 2019, 55, 7201204. [Google Scholar] [CrossRef]
- Torchio, R.; Moro, F.; Meunier, G.; Guichon, J.-M.; Chadebec, O. An Extension of Unstructured-PEEC Method to Magnetic Media. IEEE Trans. Magn. 2019, 55, 7200404. [Google Scholar] [CrossRef]
- Cirimele, V.; Torchio, R.; Virgillito, A.; Freschi, F.; Alotto, P. Challenges in the Electromagnetic Modeling of Road Embedded Wireless Power Transfer. Energies 2019, 12, 2677. [Google Scholar] [CrossRef]
- Ardon, V.; Aime, J.; Chadebec, O.; Clavel, E.; Guichon, J.; Vialardi, E. EMC Modeling of an Industrial Variable Speed Drive with an Adapted PEEC Method. IEEE Trans. Magn. 2010, 46, 2892–2898. [Google Scholar] [CrossRef]
- Bandinelli, M.; Mori, A.; Galgani, G.; Romano, D.; Antonini, G.; Dieudonné, A.G.; Dunand, M. A Surface PEEC Formulation for High-Fidelity Analysis of the Current Return Networks in Composite Aircrafts. IEEE Trans. Electromagn. Compat. 2015, 57, 1027–1036. [Google Scholar] [CrossRef]
- Manara, G.; Monorchio, A.; Reggiannini, R. A space-time discretization criterion for a stable time-marching solution of the electric field integral equation. IEEE Trans. Antennas Propag. 1997, 45, 527–532. [Google Scholar] [CrossRef]
- Liu, Y.; Yücel, A.C.; Bağcı, H.; Michielssen, E. A Scalable Parallel PWTD-Accelerated SIE Solver for Analyzing Transient Scattering From Electrically Large Objects. IEEE Trans. Antennas Propag. 2016, 64, 663–674. [Google Scholar] [CrossRef]
- Antonini, G. Fast Multipole Method for Time Domain PEEC Analysis. IEEE Trans. Mobile Comput. 2003, 2, 275–287. [Google Scholar] [CrossRef]
- Sekine, T.; Asai, H. Full-wave PEEC time domain solver based on leapfrog scheme. In Proceedings of the 2011 IEEE 20th Conference on EPEPS, San Jose, CA, USA, 23–26 October 2011; pp. 181–184. [Google Scholar]
- Gianfagna, C.; Lombardi, L.; Antonini, G. Marching-on-in-time solution of delayed PEEC models of conductive and dielectric objects. IET Microw. Antennas Propag. 2018, 13, 42–47. [Google Scholar] [CrossRef]
- Qi, R.; Du, Y.P.; Chen, M. Time-Domain PEEC Transient Analysis for a Wire Structure above the Perfectly Conducting Ground with the Incident Field from a Distant Lightning Channel. IEEE Trans. Electromagn. Compat. 2019. [Google Scholar] [CrossRef]
- Freschi, F.; Repetto, M. A general framework for mixed structured/unstructured PEEC modelling. Appl. Comput. Electromagn. Soc. J. 2008, 23, 200–206. [Google Scholar]
- Torchio, R. A Volume PEEC Formulation Based on the Cell Method for Electromagnetic Problems from Low to High Frequency. IEEE Trans. Antennas Propag. 2019, 67, 7452–7465. [Google Scholar] [CrossRef]
- Pesce, A.; de Lorenzi, A.; Grando, L. A new approach to passive protection against high energy and high current breakdowns in the ITER NBI accelerator. Fusion Eng. Design 2009, 84, 1499–1504. [Google Scholar] [CrossRef]
- Bigi, M.; de Lorenzi, A.; Grando, L.; Watanabe, K.; Yamamoto, M. A model for electrical fast transient analyses of the ITER NBI power supplies and the MAMuG accelerator. Fusion Eng. Design 2009, 84, 446–450. [Google Scholar] [CrossRef]
- Walker, S.P.; Bluck, M.J.; Chatzis, I. The stability of integral equation time-domain scattering computations for three-dimensional scattering; similarities and differences between electrodynamic and elastodynamic computations. Int. J. Numerical Model. 2002, 15, 459–474. [Google Scholar] [CrossRef]
- Fano, R.M.; Chu, L.J.; Adler, R.B. Electromagnetic Fields, Energy, and Forces; M.I.T. Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Bobbio, S. Electrodynamics of Materials: Forces, Stresses, and Energies in Solids and Fluids, 1st ed.; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Van’t Wout, E.; van der Heul, D.R.; van der Ven, H.; Vuik, C. Design of Temporal Basis Functions for Time Domain Integral Equation Methods with Predefined Accuracy and Smoothness. IEEE Trans. Antennas Propag. 2013, 61, 271–280. [Google Scholar] [CrossRef]
- Shanker, B.; Lu, M.; Yuan, J.; Michielssen, E. Time Domain Integral Equation Analysis of Scattering from Composite Bodies via Exact Evaluation of Radiation Fields. IEEE Trans. Antennas Propag. 2009, 57, 1506–1520. [Google Scholar] [CrossRef]
- Shi, Y.; Xia, M.; Chen, R.; Michielssen, E.; Lu, M. Stable Electric Field TDIE Solvers via Quasi-Exact Evaluation of MOT Matrix Elements. IEEE Trans. Antennas Propag. 2011, 59, 574–585. [Google Scholar] [CrossRef]
- Ülkü, H.A.; Bağcı, H.; Michielssen, E. Marching On-In-Time Solution of the Time Domain Magnetic Field Integral Equation Using a Predictor-Corrector Scheme. IEEE Trans. Antennas Propag. 2013, 61, 4120–4131. [Google Scholar] [CrossRef]
- Sadigh, A.; Arvas, E. Treating the instabilities in marching-on-in-time method from a different perspective (electromagnetic scattering). IEEE Trans. Antennas Propag. 1993, 41, 1695–1702. [Google Scholar] [CrossRef]
- Jiao, D.; Ergin, A.A.; Shanker, B.; Michielssen, E.; Jin, J.-M. A fast higher-order time-domain finite element-boundary integral method for 3D electromagnetic scattering analysis. IEEE Trans. Antennas Propag. 2002, 50, 1192–1202. [Google Scholar] [CrossRef]
- Li, J.; Shanker, B. Time-Dependent Debye–Mie Series Solutions for Electromagnetic Scattering. IEEE Trans. Antennas Propag. 2015, 63, 3644–3653. [Google Scholar] [CrossRef]
- Weile, D.S.; Pisharody, G.; Chen, N.W.; Shanker, B.; Michielssen, E. A novel scheme for the solution of the time-domain integral equations of electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 283–295. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).