Price Based Demand Response for Optimal Frequency Stabilization in ORC Solar Thermal Based Isolated Hybrid Microgrid under Salp Swarm Technique
Abstract
:1. Introduction
- The application of electricity pricing-based demand response (PBDR) for TCLs for the optimal management of energy utilization by the users;
- Comparison of the dynamic responses of various PI and PID controllers in the hybrid isolated microgrid system with and without PBDR;
- The optimization of (PI and PID) controller gains by applying the genetic algorithm (GA) and SSA in the developed model.
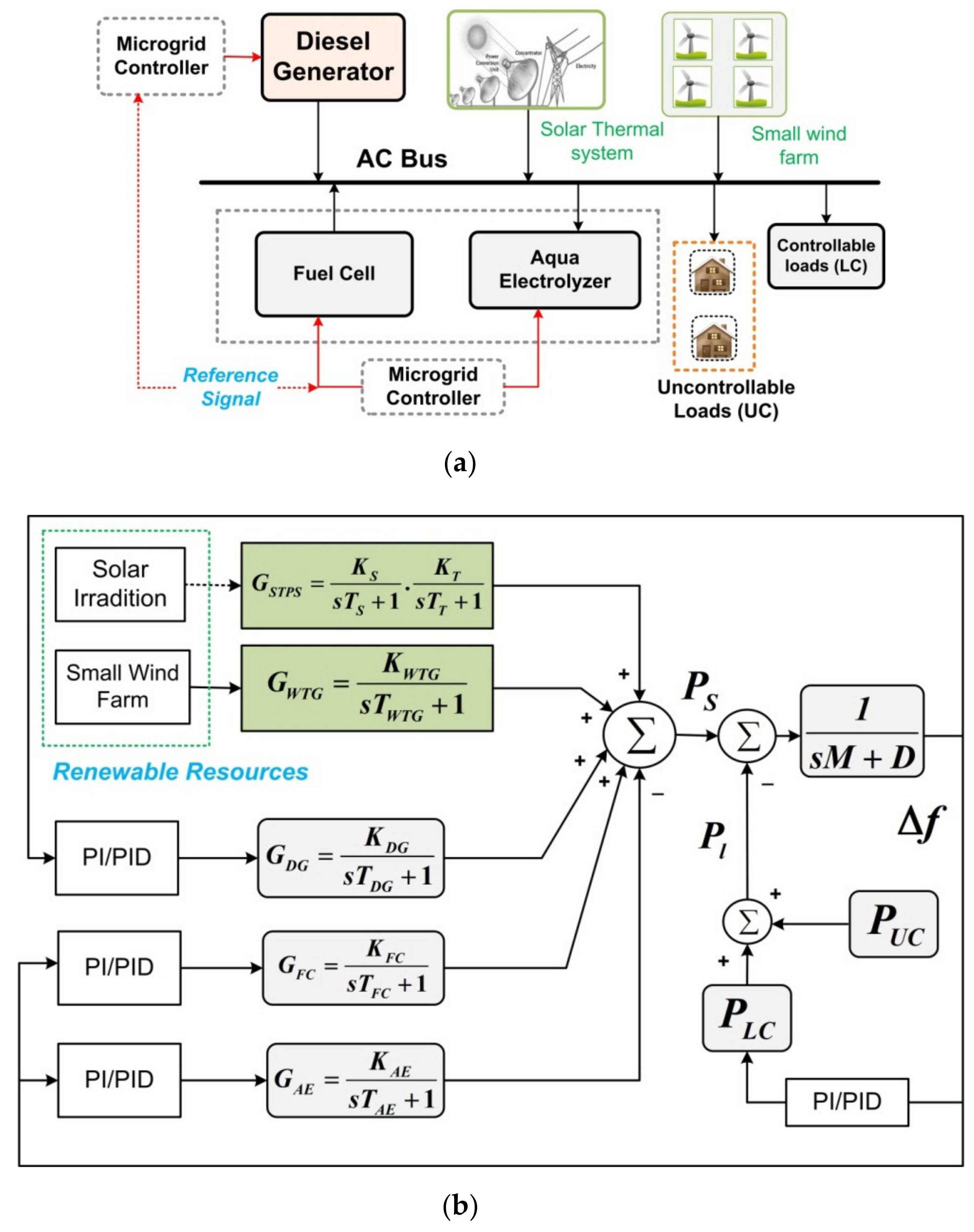
2. Dynamic Modeling of Hybrid Energy System
2.1. Wind Turbine Generator (WTG)
2.2. ORC Solar Thermal Power System (STPS)
2.3. Diesel Engine Generator (DEG)
2.4. Fuel Cell (FC)
2.5. Aqua Electrolyzer (AE)
3. Real-Time Pricing for Smart TCLs
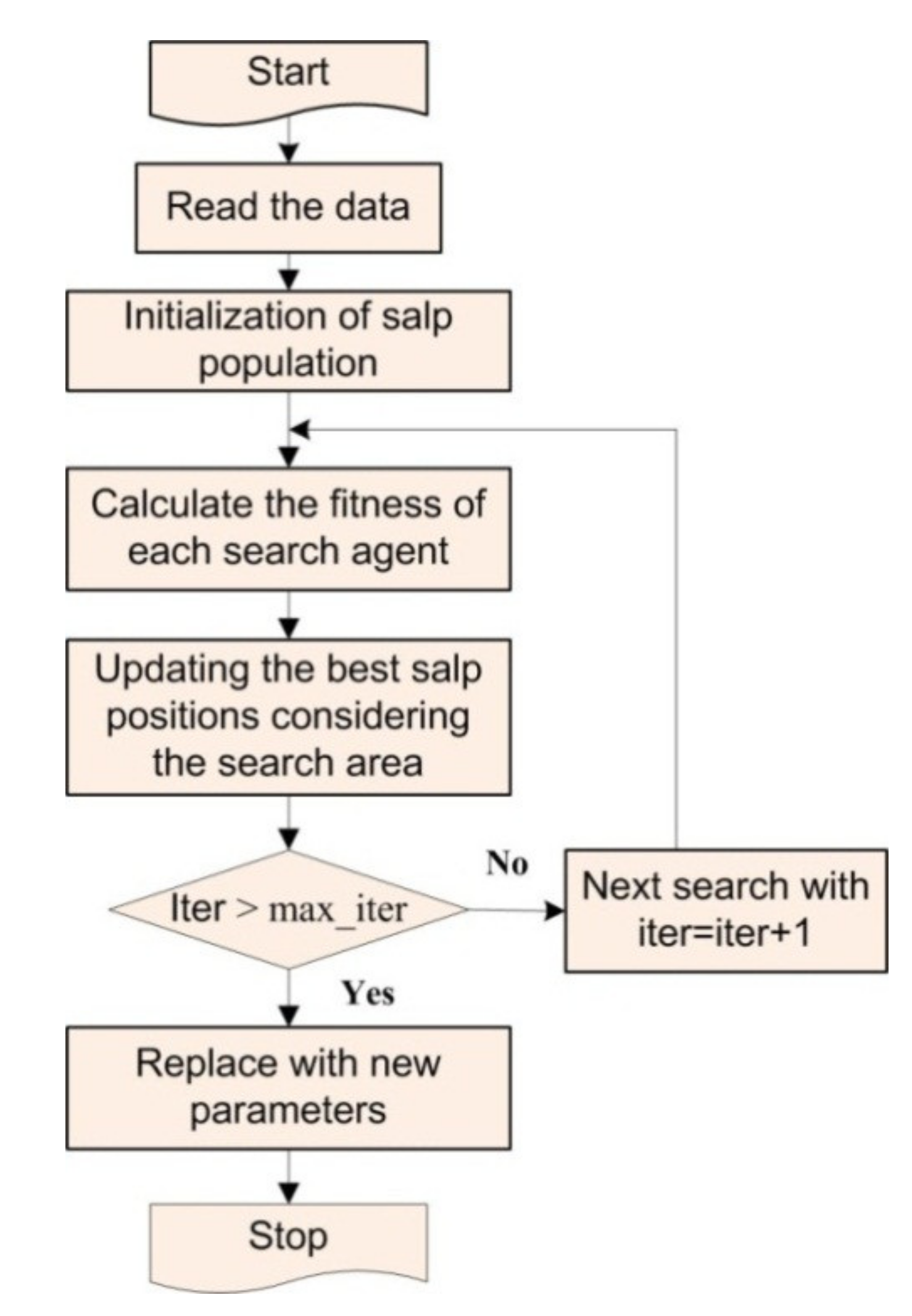
4. Salp Swarm Technique (SSA)
- Initiation of the salp population with random positions for the solution of the parameters (Kp, Ki, Kd);
- Calculating the fitness value of each salp, and assigning the salp with the best ability to lead to the food source. Here, the objective function in Equation (15) is considered as a fitness function;
- Updating the salp positions. For every dimension, the position of the leading and following salps are updated, keeping all the salps in the frontiers of the search space. This updating salp position gives a solution to the problem;
- Repeating all the above steps except Step 1 until the termination criterion or the best solution is reached.
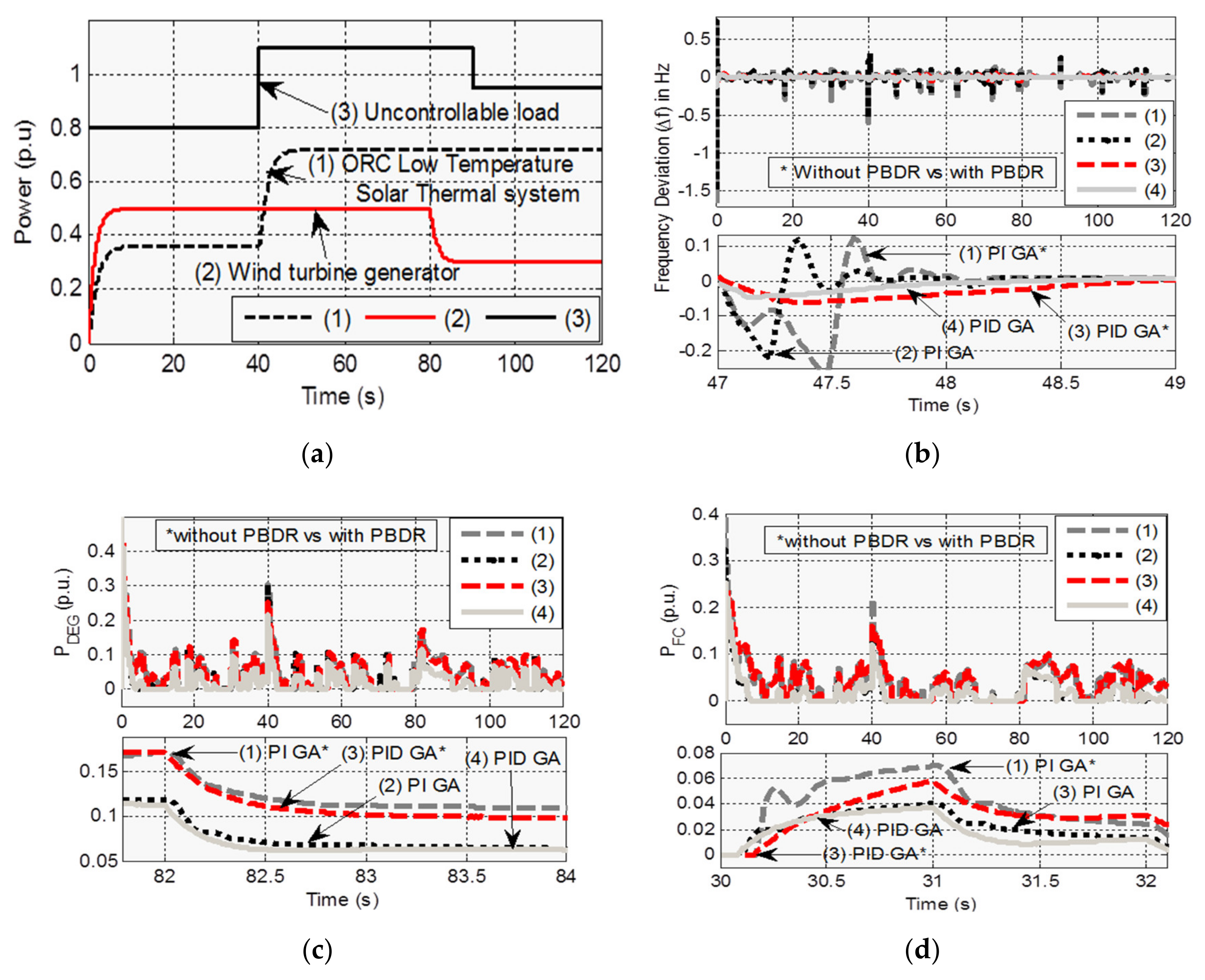
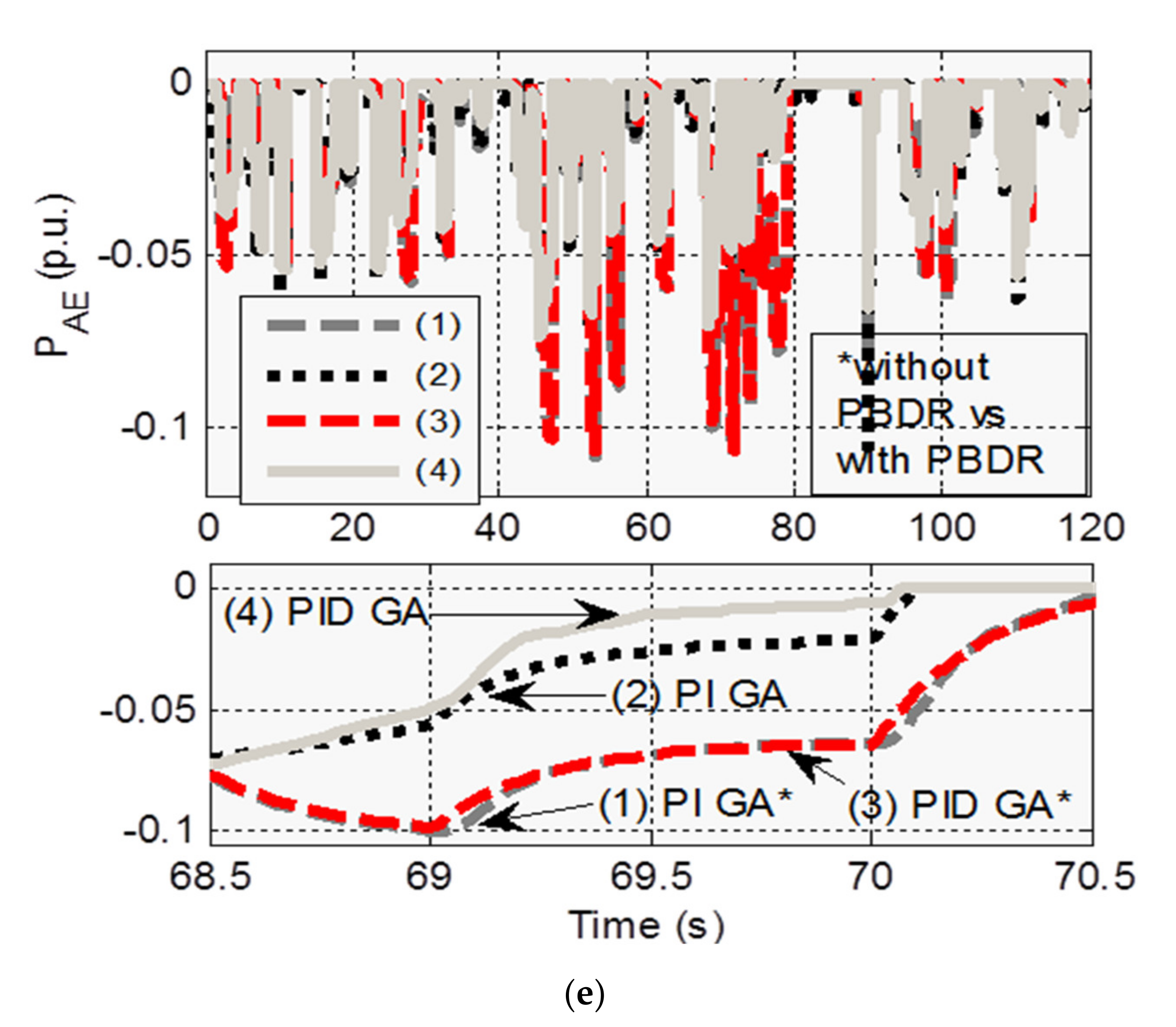
5. Frequency Response Simulation Results
5.1. Case 1: Under Step Vitiation
5.2. Case 2: Under Random Disturbances
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ∆f | System frequency fluctuation |
| Ksys | Overall constant frequency characteristic |
| Gsys(s) | Overall transfer function of proposed system |
| PDEG | Extractable power of diesel generator |
| GDEG(s) | Transfer function of DEG |
| KDEG | DEG’s gain |
| TDEG | Constant time of DEG |
| PFC | Extractable power of FC |
| KFC | FC’s gain |
| TFC | FC’s constant time value |
| GFC(s) | Transfer function of FC |
| PSTPS | Dispatchable power of organic Rankine cycle-based STPS |
| GSTPS(s) | Overall transfer function of organic Rankine cycle STPS |
| Ts | Solar receiver’s constant time value |
| TT | Constant charge time of the turbine |
| KS | Solar receiver’s gain |
| KT | Turbine’s gain |
| GAE(s) | Overall transfer function of AE |
| PAE | Extractable power hydrogen aqua electrolyzer |
| KAE | Hydrogen aqua electrolyzer’s gain |
| TAE | Hydrogen aqua electrolyzer’s fixed time |
| PS | Total generated output power |
| Pl | Demanded load power |
| ∆Pe | Mismatch between generated power and demand |
| M | Overall proposed system inertia |
| D | Overall proposed system damping coefficient |
| PWTG | Dispatchable power WTG |
| GWTG(s) | Overall transfer function of WTG |
| KWTG | WTG’s gain |
| TWTG | WTG’s time constant |
| ∆Q | Change in work done by thermostatic loads |
| ∆ρ | Change in electricity pricing |
| ∆TST | Change in thermostat set point |
| K | Gain factor of smart thermostat |
| PLC | Power consumption by controllable loads |
| PUC | Power consumption by uncontrollable loads |
References
- Lu, N.; Katipamula, S. Control strategies of thermostatically controlled appliances in a competitive electricity market. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 202–207. [Google Scholar]
- Das, D.C.; Sinha, N.; Roy, A.K. Automatic Generation Control of an Organic Rankine Cycle Solar-Thermal/Wind-Diesel Hybrid Energy System. Energy Technol. 2014, 2, 721–731. [Google Scholar]
- Jiang, L.; Low, S. Real-time demand response with uncertain renewable energy in smart grid. In Proceedings of the 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 1334–1341. [Google Scholar]
- Nguyen, H.K.; Bin, S.J.; Han, Z. Distributed Demand Side Management with Energy Storage in Smart Grid. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 3346–3357. [Google Scholar]
- Ranjan, S.; Das, D.C.; Latif, A.; Sinha, N. LFC for Autonomous Hybrid Micro Grid System of 3 Unequal Renewable Areas using Mine Blast Algorithm. Int. J. Renew. Energy Res. (IJRER) 2018, 8, 1297–1308. [Google Scholar]
- Gao, J.; Xiao, Y.; Liu, J.; Liang, W.; Chen, C.L.P. A survey of communication/networking in Smart Grids. Futur. Gener. Comput. Syst. 2012, 28, 391–404. [Google Scholar]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A survey on demand response programs in smart grids: Pricing methods and optimization algorithms. IEEE Commun. Surv. Tutor. 2015, 17, 152–178. [Google Scholar]
- Saele, H.; Grande, O.S. Demand response from household customers: Experiences from a pilot study in Norway. IEEE Trans. Smart Grid 2011, 2, 102–109. [Google Scholar]
- Imamura, A.; Yamamoto, S.; Tazoe, T.; Onda, H.; Takeshita, H.; Okamoto, S.; Yamanaka, N. Distributed demand scheduling method to reduce energy cost in smart grid. In Proceedings of the 2013 IEEE Region 10 Humanitarian Technology Conference, Sendai, Japan, 26–29 August 2013; pp. 148–153. [Google Scholar]
- Li, D.; Jayaweera, S.K. Uncertainty Modeling and Price-Based Demand Response Scheme Design in Smart Grid. IEEE Syst. J. 2017, 11, 1743–1754. [Google Scholar]
- Kenna, K.M.; Keane, A. Residential Load Modelling of Price-Based Demand Response for Network Impact Studies. IEEE Trans. Smart Grid 2016, 7, 2285–2294. [Google Scholar]
- Rahimi, F.; Ipakchi, A. Demand Response as a Market Resource under the Smart Grid Paradigm. IEEE Trans. Smart Grid 2010, 1, 82–88. [Google Scholar]
- Chanana, S.; Kumar, A. Demand response by dynamic demand control using frequency linked real time prices. Int. J. Energy Sect. Manag. 2010, 4, 1. [Google Scholar]
- Du, P.; Lu, N. Appliance commitment for household load scheduling. IEEE Trans. Smart Grid 2011, 2, 411–419. [Google Scholar]
- Datchanamoorthy, S.; Senthilkumar, D.; Ozturk, Y.; Lee, G.K. Optimal time-of-use pricing for residential load control. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 375–380. [Google Scholar]
- Latif, A.; Das, D.C.; Biswas, K.; Kumar, K.; Kumar, R.; Hussain, S.I. Non-critical demands managed load frequency stabilization of dish-stirling-biodiesel based islanded microgrid system using FF optimized controller. Intell. Tech. Appl. Sci. Technol. 2020, 12, 188–196. [Google Scholar]
- Kishore, S.; Snyder, L.V. Control mechanisms for residential electricity demand in Smart Grids. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 443–448. [Google Scholar]
- Al-Badi, A.H.; El-Saadany, E. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar]
- Ravindran, P.; Das, K.R.; Mohan, A.S. Flexible demand response in smart grid based Automatic Generation Control. In Proceedings of the 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE), Coimbatore, India, 6–8 March 2014; pp. 1–6. [Google Scholar]
- Chanana, S.; Arora, M. Demand response for residential air conditioning load using a programmable communication thermostat. Int. J. Electr. Electron. Sci. Eng. 2013, 7, 12. [Google Scholar]
- Babahajiani, P.; Shafiee, Q.; Bevrani, H. Intelligent Demand Response Contribution in Frequency Control of Multi-Area Power Systems. IEEE Trans. Smart Grid 2018, 9, 1282–1291. [Google Scholar]
- Latif, A.; Das, D.C.; Barik, A.K.; Ranjan, S. Illustration of demand response supported co-ordinated system performance evaluation of YSGA optimized dual stage PIFOD-(1+ PI) controller employed with wind-tidal-biodiesel based independent two-area interconnected microgrid system. IET Renew. Power Gener. 2020, 14, 1074–1086. [Google Scholar]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Optimum Synthesis of a BOA optimized novel dual-stage PI-(1+ID) controller for frequency response of a microgrid. Energies 2020, 13, 3446. [Google Scholar]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. State-of-the-art of Controllers and Soft Computing Techniques for Regulated Load Frequency Management of Single/Multi-Area Traditional and Renewable Energy based Power Systems. Appl. Energy 2020, 266, 114858. [Google Scholar]
- Shivakumar, R.; Lakshmipathi, R. Implementation of an innovative bio inspired GA and PSO algorithm for controller design considering steam GT dynamics”. IJCSI Int. J. Comput. Sci. Issues 2010, 7, 18–28. [Google Scholar]
- Mirjalili, S. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. in Eng. Softw. 2017, 114, 163–191. [Google Scholar]
- Abd-Elazim, S.M.; Ali, E. Load frequency controller design of a two-area system composing of PV grid and thermal generator via firefly algorithm. Neural Comput. Appl. 2016, 30, 607–616. [Google Scholar] [CrossRef]
- Das, D.C.; Roy, A.; Sinha, N. GA based frequency controller for solar thermal–diesel–wind hybrid energy generation/energy storage system. Int. J. Electr. Power Energy Syst. 2012, 43, 262–279. [Google Scholar] [CrossRef]
- Latif, A.; Pramanik, A.; Das, D.C.; Hussain, I.; Ranjan, S. Plug in hybrid vehicle-wind-diesel autonomous hybrid power system: Frequency control using FA and CSA optimized controller. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 1147–1158. [Google Scholar] [CrossRef]
- Charan, P.N.; Kumar, S.B.; Prasad, B.D.; Pranati, D.; Kumar, D.M. A novel application of ALO -based fractional order fuzzy PID controller for AGC of power system with diverse sources of generation. Int. J. Electr. Eng. 2019, 56, 1–23. [Google Scholar]
- Abdulbaset, E.H.; Dong, S.Z.; Meysam, K. A comparative study on recently-introduced nature-based global optimization methods in complex mechanical system design. Algorithms 2017, 10, 120. [Google Scholar]
- Mohsenian-Rad, A.-H.; Leon-Garcia, A. Optimal Residential Load Control with Price Prediction in Real-Time Electricity Pricing Environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]
- Jay, D.; Swarup, K.S. Price based demand response of aggregated thermostatically controlled loads for load frequency control. In Proceedings of the National Power Systems Conference (NPSC), Varanasi, Uttar Pradesh, India, 12–14 December 2012. [Google Scholar]
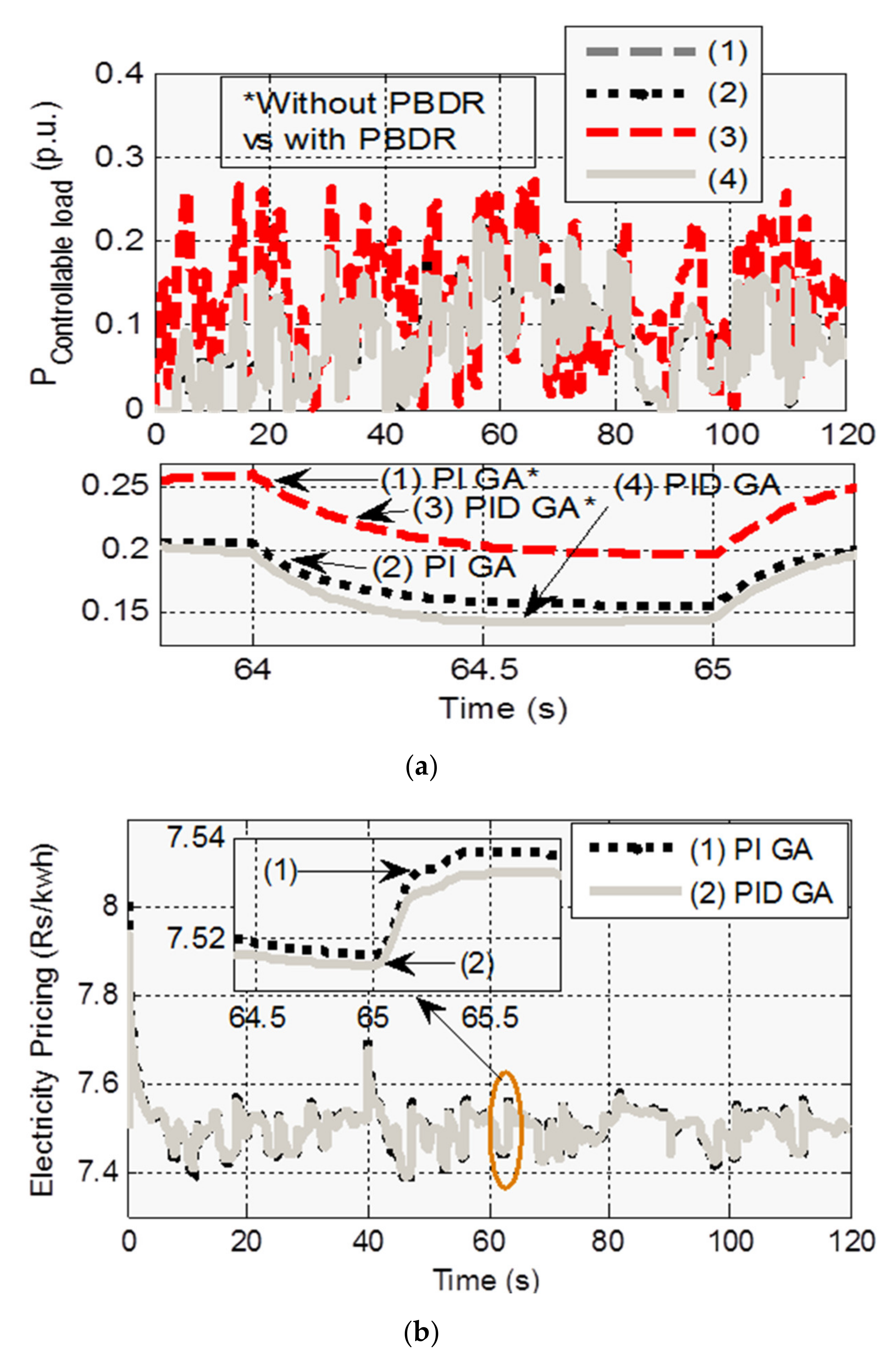
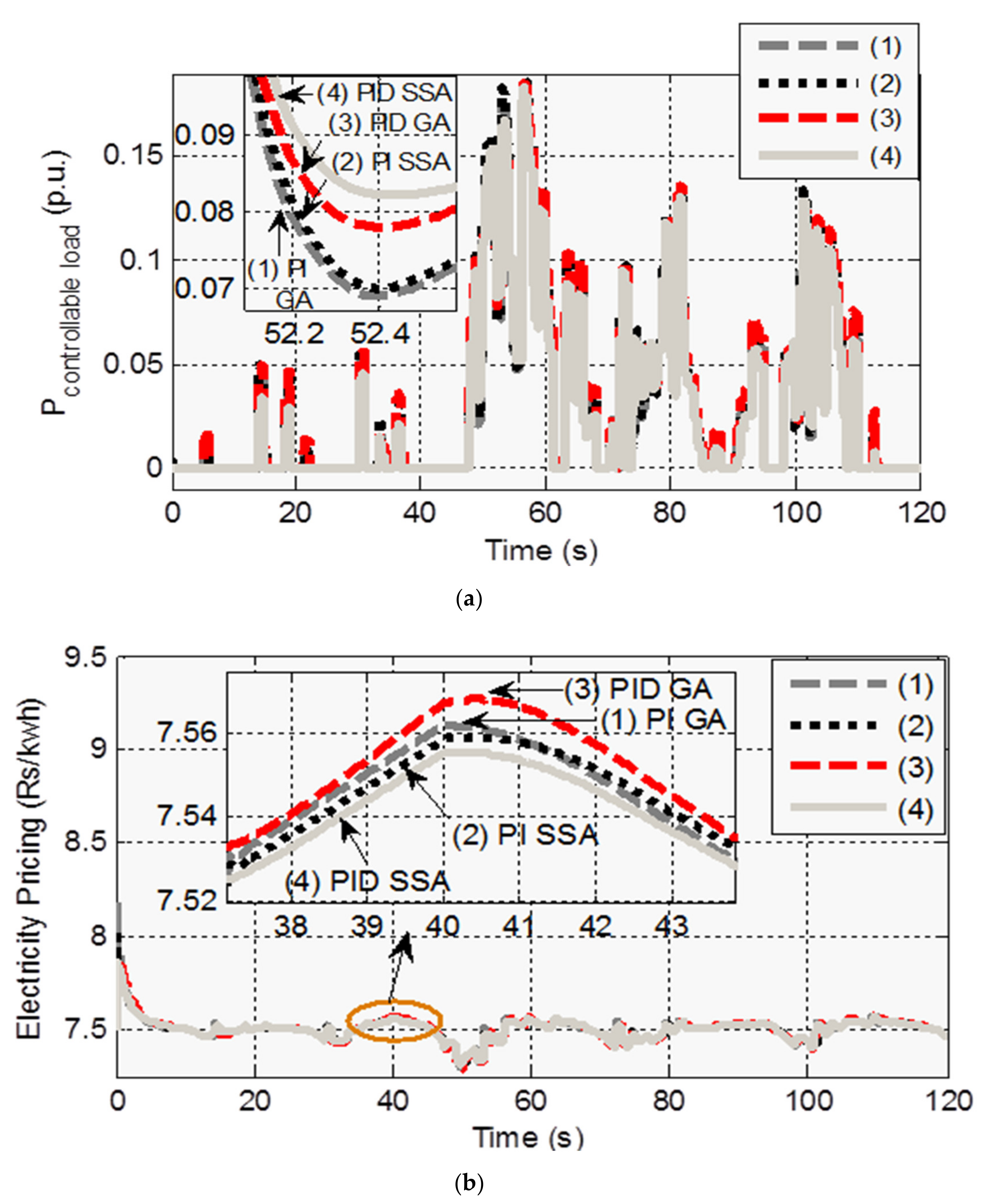
| Generating Units | Gains | Constant Values (s) |
|---|---|---|
| ORC-STPS | Ks = 1.8 KT = 1 | TS = 1.8 TT = 0.3 |
| DEG | KDG = 1/300 | TDG = 2 |
| FC | KFC = 1/100 | TFC = 4 |
| AE | KAE = −1/500 | TAE = 0.5 |
| WTG | KWTG = 1 | TWTG = 1.5 |
| Description | Value |
|---|---|
| Number of Salp population | 20 |
| Maximum number of iterations | 100 |
| Number of search agents | 20 |
| Probability of crossover | 0.8 |
| Probability of mutation | 0.01 |
| Maximum number of iterations | 100 |
| Case | Subcomponents | Response Time (s) | Operating Conditions |
|---|---|---|---|
| 1. | WTG, ORC low-temperature STPS, DEG, FC, AE and Load | 120 s | PWTG = 0.5 p.u at 0 < t < 80 s = 0.3 p.u at t > 80 s |
| PSTPS = 0.2 p.u at 0 < t < 40 s = 0.4 p.u at t > 40 s | |||
| Pl = 0.8 p.u at 0 < t < 40 s | |||
| = 1.1 p.u at 40 s < t < 90 s = 0.95 p.u at t > 90 s | |||
| 2. | WTG, ORC low-temperature STPS, DEG, FC, AE and Load | 12 s | Concurrent random changes in WTG, ORC-STPS and Load |
| Controller Gain Case 1 | GA Values | |
|---|---|---|
| Without PBDR | With PBDR | |
| PI Controllers | ||
| KpDEG | 1.450 | 1.690 |
| KiDEG | 1.0333 | 1.31401 |
| KpFC | −1.280 | −1.1634 |
| KiFC | −1.380 | −1.650 |
| KpAE | −1.0084 | −1.482 |
| KiAE | −1.2177 | −1.5316 |
| KpLOAD | 0 | 1.980 |
| KiLOAD | 0 | 1.490 |
| PID Controllers | ||
| KpDEG | 1.450 | 1.690 |
| KiDEG | 1.230 | 1.850 |
| KdDEG | 0.490 | 0.490 |
| KpFC | −0.970 | −1.150 |
| KiFC | −1.380 | −1.650 |
| KdFC | −0.72196 | −0.7271 |
| KpAE | −0.99567 | −1.250 |
| KiAE | −1.06374 | −1.375 |
| KdAE | −0.750 | −0.750 |
| KpLOAD | 0 | 1.980 |
| KiLOAD | 0 | 1.2665 |
| KdLOAD | 0 | 0.650 |
| Controller Gain Case 2 | With PBDR | |
|---|---|---|
| GA-Optimized | SSA-Optimized | |
| PI Controllers | ||
| KpDEG | 1.980 | 1.9558 |
| KiDEG | 1.7690 | 1.5255 |
| KpFC | −1.270 | −1.4183 |
| KiFC | −1.950 | −1.9325 |
| KpAE | −1.3801 | −1.6188 |
| KiAE | −1.325 | −1.4049 |
| KpLOAD | 2.100 | 1.7953 |
| KiLOAD | 1.56948 | 1.6175 |
| PID Controllers | ||
| KpDEG | 1.980 | 1.7348 |
| KiDEG | 1.850 | 1.6828 |
| KdDEG | 0.490 | 0.5263 |
| KpFC | −1.270 | −1.4189 |
| KiFC | −1.950 | −1.906 |
| KdFC | −0.725 | −0.6976 |
| KpAE | −1.350 | −1.6316 |
| KiAE | −1.478 | −1.5043 |
| KdAE | −0.750 | −0.6865 |
| KpLOAD | 2.031 | 1.9147 |
| KiLOAD | 1.860 | 1.5507 |
| KdLOAD | 0.8473 | 0.8175 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latif, A.; Paul, M.; Das, D.C.; Hussain, S.M.S.; Ustun, T.S. Price Based Demand Response for Optimal Frequency Stabilization in ORC Solar Thermal Based Isolated Hybrid Microgrid under Salp Swarm Technique. Electronics 2020, 9, 2209. https://doi.org/10.3390/electronics9122209
Latif A, Paul M, Das DC, Hussain SMS, Ustun TS. Price Based Demand Response for Optimal Frequency Stabilization in ORC Solar Thermal Based Isolated Hybrid Microgrid under Salp Swarm Technique. Electronics. 2020; 9(12):2209. https://doi.org/10.3390/electronics9122209
Chicago/Turabian StyleLatif, Abdul, Manidipa Paul, Dulal Chandra Das, S. M. Suhail Hussain, and Taha Selim Ustun. 2020. "Price Based Demand Response for Optimal Frequency Stabilization in ORC Solar Thermal Based Isolated Hybrid Microgrid under Salp Swarm Technique" Electronics 9, no. 12: 2209. https://doi.org/10.3390/electronics9122209
APA StyleLatif, A., Paul, M., Das, D. C., Hussain, S. M. S., & Ustun, T. S. (2020). Price Based Demand Response for Optimal Frequency Stabilization in ORC Solar Thermal Based Isolated Hybrid Microgrid under Salp Swarm Technique. Electronics, 9(12), 2209. https://doi.org/10.3390/electronics9122209







