Abstract
Dynamical systems described by fractional-order difference equations have only been recently introduced inthe literature. Referring to chaotic phenomena, the type of the so-called “self-excited attractors” has been so far highlighted among different types of attractors by several recently presented fractional-order discrete systems. Quite the opposite, the type of the so-called “hidden attractors”, which can be characteristically revealed through exploring the same aforementioned systems, is almost unexplored in the literature. In view of those considerations, the present work proposes a novel 3D chaotic discrete system able to generate hidden attractors for some fractional-order values formulated for difference equations. The map, which is characterized by the absence of fixed points, contains only one nonlinear term in its dynamic equations. An appearance of hidden attractors in their chaotic modes is confirmed through performing some computations related to the 0–1 test, largest Lyapunov exponent, approximate entropy, and the bifurcation diagrams. Finally, a new robust control law of one-dimension is conceived for stabilizing the newly established 3D fractional-order discrete system.
1. Introduction
The study of discrete-time chaotic systems has featured prominently in the past few years [1]. The dynamics of a lot of chaotic systems/maps have been deeply analysed, especially with regard to the logistic map, the Arnold’s cat map, the Hénon map, the Lozi map, and the tent map [1,2]. All the chaotic attractors in those discrete systems belong to the most common type of attractors with the property that their corresponding initial states are placed close to the unstable periodic orbits or fixed points [3]. Since these attractors can be readily found, they are called “self-excited attractors” [3,4]. On the other hand, chaotic phenomena, which have been also discovered in discrete-time systems, are distinguished with the nonexistence of fixed points or the existence of the stable fixed points [5]. Since the initial conditions in these systems can be only found via massive numerical search, these chaotic attractors are hard to be found [6,7]. Consequently, this type of attractor has been called “hidden attractor” in literature [6,7]. Referring to this topic, some papers have been recently published [8,9,10]. For example, the chaotic dynamics of a 1D discontinuous discrete system without fixed points have been studied in [8]. Moreover, “hidden attractors” have been found in 2D and 3D chaotic discrete systems with stable fixed points only in [10]. Additionally, some 2D quadratic discrete systems with “hidden attractors” have been illustrated in [9]. These systems, which are characterized by the absence of fixed points, have no discontinuity in their right-hand equations [9].
All the considerations illustrated above are related to integer-order discrete-time systems. However, some research workers have recently concentrated their considerations on studying the chaotic behaviours associated with the dynamics of the Fractional-order Discrete Systems (FoDSs), i.e., maps outlined by Fractional-order Difference Equations (FoDEs) [11,12]. To this purpose, the chaotic dynamics of some FoDSs have been recently explored and analyzed in [13,14,15,16,17,18,19]. In particular, a generalized version of a 3D fractional-order Hénon system has been investigated in [14], while the fractional-order Wang, Rossler, and Stefanski discrete systems have been demonstrated in [13]. Additionally, the fractional discrete double scroll has been introduced in [16], whereas the chaotic dynamics of the fractional Grassi-Miller map have been studied in [15]. Referring to very recent results in literature for fractional discrete systems, a fractional logistic map characterized by two-parameters has been illustrated in [20]. A novel short-memory fractional modeling approach has been applied to memristors in [21]. A new variable-order fractional chaotic system (defined via a piecewise constant function) has been conceived in [22]. Note that all these FoDSs exhibit the “self-excited attractors”, since all initial conditions for generating chaos are placed close to the unstable fixed points [13,14,15,16]. Quite the opposite, the study of chaotic behavior of the FoDSs distinguished by “hidden attractors” (i.e., without fixed points) is almost unexplored in literature [17,18,19,23].
In view of the aforesaid motivations, the present work proposes a novel chaotic 3D-FoDS without any fixed point, which contains only one nonlinear term. The performed analysis underlines that the hidden attractors can be yielded for certain fractional-order values within difference equations. Through performing some calculations related to the Largest Lyapunov Exponent (LLE) and implementing bifurcation diagrams, the existence of chaos is verified for the FoDSs. Additionally, the 0–1 test and the computation of the Approximate Entropy (ApEn) are carried out, with the aim to further confirm that the discovered “hidden attractors” are truly chaotic. However, the remaining of this article is arranged in the following manner. Section 2 introduces the main definition of the fractional Caputo difference operator, along with some fundamental preliminaries associated with the discrete fractional calculus. In Section 3, a novel 3D-FoDS with only one nonlinear term and without fixed points is presented as well as the phase diagrams, the bifurcation diagrams and the LLEs that are discussed and analysed by taking different fractional-order values in a single difference equation. In Section 4, the 0–1 test and the ApEn are discussed. Finally, in Section 5, a novel control law of one-dimension is designed for stabilizing the chaotic dynamics of the newly established 3D-FoDS.
2. Necessary Discrete Fractional Operators
This part briefly presents some preliminaries and fundamental notions associated with discrete fractional calculus. Throughout this work, the time scale will be considered as the main domain in which , where . Let X be denote any function defined on , then the fractional sum of order can be outlined as [24]:
Observe that the term indicates to the so-called falling function which can be defined as follows:
In view of the above definition, it is possible to define the so-called fractional Caputo-like difference operator of order as reported in the following definition.
Definition 1.
For , the fractional Caputo-like difference operator of order γ is outlined as [25]:
where X here denotes any function defined on .
In order to derive the main coming discrete formula for the new FoDS, we briefly summarize the following theorem.
Theorem 1
([26]). Consider the following two FoDEs:
3. A New FoDS with Only One Nonlinear Term
The authors Haibo Jiang et.al. in [10] preformed a systematic search to construct three dimensional discrete-time systems with no fixed points or with stable fixed point. The objective was to find the algebraically simplest cases which cannot be further reduced by the removal of terms without destroying the chaos. For each case that was found, a computer search was preformed to find chaotic solutions that are deemed “elegant” in the sense of Sprott [27], by which it means that as many coefficients as possible are set to zero where the others are set to ±1 or otherwise to a small integer or decimal fraction with the fewest possible digits. Motivated by this strategy, in this part, we remove and added some terms to obtain the following three dimensional FoDS:
where A, B are some parameters of bifurcation, whereas x, y, z are the states of system (7). It can be seen that the fractional-order map (7) has only one quadratic nonlinear term. The novel system can be transformed into a system without fixed point by introducing a condition of hidden attractor into the fixed points. We denote the fixed point of the FODT system (7) with . Equation (7) can be transformed into Equation (8) for calculating the fixed points
Suppose that and by taking in mind that , the fixed points of system (7) can be typically gained by solving the algebraic equations reported below
from which we can obtain:
When the system’s parameters A and B satisfy Equation (10) has no real solution; implying that system (7) has no fixed points. Hence, this system could display hidden attractors in view of appropriate selections of the initial conditions and the fractional-order values as well. In order to investigate this remarkable property, some numerical formula is designed as:
where , , and are the initial conditions. Under the following values: , , , , , , system (7) generates bounded strange attractor as shown in Figure 1. This attractor is, actually, hidden due to .
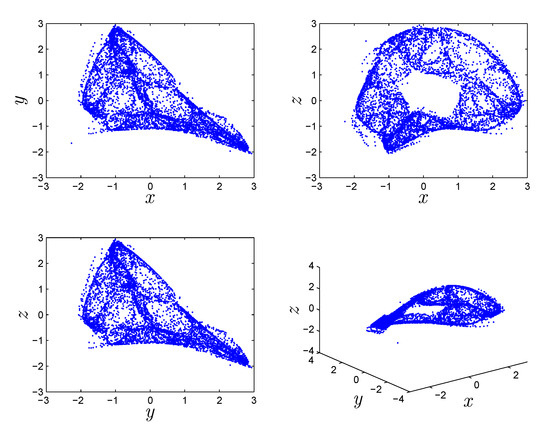
Figure 1.
Different phase space projection of the hidden chaotic attractor of the FoDS given in (7), when .
In the present section, the dynamical behaviours of the newly established system given in (7) are studied by detailed simulation analysis using two indicators: The bifurcation diagrams and the largest Lyapunov exponent (LLE). Actually, such bifurcation diagrams together with the LLEs represent powerful analysis tools that can be employed to visualize different scenarios to chaos in nonlinear systems. In particular, a deterministic nonlinear system is considered chaotic whenever its LLE is positive [28]. We firstly investigates the dynamics of system (7) in the case that the parameter B is relatively changed, while the other parameter A is fixed at 0.7. The bifurcation diagram and its related LLE for the fractional-order value are exhibited in Figure 2a,b, respectively. Obviously, one can observe that when the system’s parameter B increases from −0.6267, system (7) will be changed from limit cycles to eight periodic orbits (see Figure 2). Besides, system (7) becomes periodic when and is chaotic when . Actually, the chaotic behavior is affirmed by the LLE as displayed in Figure 2b. Secondly, we investigate the effect of the fractional-order values on the system’s bifurcation behaviors. Figure 3 and Figure 4 depict, respectively, the bifurcation diagrams versus B for and . With decreasing the order , we observe that the chaotic rang of system (7) will be decreased and shifted to the left. Therefore, we can note that the diagram of bifurcation is consistent well with its corresponding LLEs diagram.
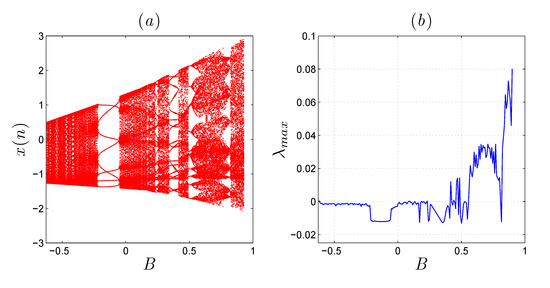
Figure 2.
(a) The bifurcation diagram versus B, when , and let . (b) The LLE in accordance with diagram (a).
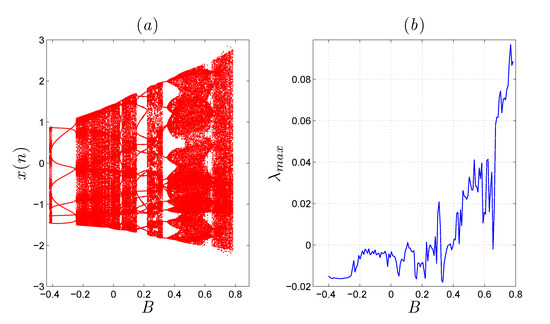
Figure 3.
(a) The bifurcation diagram versus B, when , and let . (b) The LLE in accordance with diagram (a).
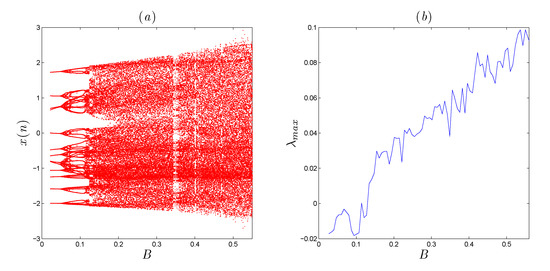
Figure 4.
(a) The bifurcation diagram versus B, when and . (b) The LLE in accordance with diagram (a).
To clearly observe the origination of chaotic hidden attractors of system (7), the bifurcation diagrams, in terms of the parameter A, are examined for two different values of fractional-order. Here, we fix to gain the bifurcation diagrams of x with and , which are provided in Figure 5a,b, respectively. From Figure 5a, one can observe that the FoDS given in (7) displays a periodic behaviour along the range , and it also displays a chaotic behaviour along the range . Besides, as the order decreases to the value 0.98, we notice that the bifurcation diagram shrinks along the A-axis with the augmentation of the periodic windows. Moreover, based on the above simulation results given in Figure 5, it can be concluded that the proposed map generates hidden attractors when the fractional-order is varied and when the parameter .
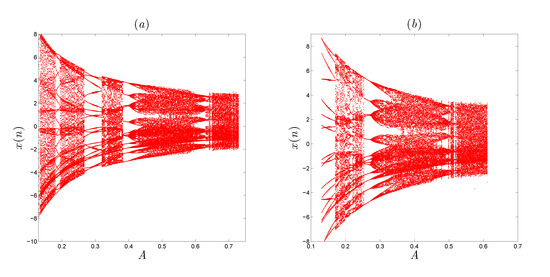
Figure 5.
(a) The bifurcation diagram versus A, when and . (b) The diagram of bifurcation versus A, when and .
4. Test of Chaos
For the purpose of reflecting the sensitivity of the FoDS, the 0–1 test is considered in this section. This test was proposed in [29] to characterize between chaotic and regular dynamics of FoDSs. As opposed to the LEs method, the 0–1 test is applied to known or unknown systems regarding the phase plane [30]. Thus, it is able to identify the chaos in a series of data where the phase space reconstruction is not necessary. The FoDS is judged to be chaotic if the plot of the translation components p and q in the plane presents a Brownian–like trajectories and also if K approaches 1, while it becomes regular as K approaches 0 as well as p and q display bounded–like trajectories. Figure 6, however, depicts these results for , and . Obviously, the trajectories of p and q demonstrate Brownian behavior in the plane (see Figure 6b). At the same time, the rate of asymptotic growth, which corresponds to Figure 6, approaches 1 as , as illustrated in Figure 6a. In view of all those findings, we confirm that the hidden attractor exhibited in Figure 1 is chaotic.
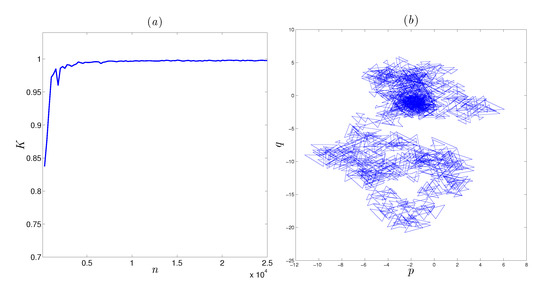
Figure 6.
The 0–1 test of the FoDS given in (7), when , and ; (a) The dependence of the rate of asymptotic growth K on the iteration number n, (b) The Brownian motion in the plane.
Entropy
A complexity measure plays important role in analyzing dynamic properties of chaotic systems. The complexity of the FoDS (7) with B varying is analyzed here by means of the approximate entropy (ApEn). The idea is that instead of looking at the phase plots of bifurcation diagrams, an exact measure of the information generated in a sequence is more indicative of the level of chaos. An approximate entropy (ApEn) measure was proposed in [31], where it has been used extensively in the literature to investigate chaos in discrete dynamical systems [23]. Basically, the ApEn is one of the most famous method which had been used since 1991 to measure the complexity of a dynamical system from data. The complexity of the FODT system (7) is tested by the ApEn in terms of parameter B, and with the same parameters setting in Figure 1, results are reported in Table 1. In view of the fact that the larger value of ApEn yields more complexity of the chaotic system, we can deduce that system (7) has a high-level of complexity when .

Table 1.
Approximate entropy of the FoDS (7) for various values of B.
5. Chaos Control
This part designs a control law of one-dimension for the purpose of stabilizing the chaotic trajectories of the proposed FoDS. At the outset, let us recall a significant theorem declared in [32], which identifies the conditions of asymptotic stability of the trivial solution to the FoDSs.
Theorem 2.
The zero equilibrium point of the following linear FoDS:
is asymptotically stable if
for all eigenvalues λ’s of and for all , where , and .
Note that Theorem 2 has been illustrated and proved in reference [32].
Here, we want to design a suitable controller, say , to ensure that all discrete-states of system (7) will asymptotically converge to zero. In order to achieve this goal, the subsequent theorem is proposed.
Theorem 3.
The 3D-FoDS given in (7) can be stabilized under the following one–dimensional control law:
where β, η and δ are some suitable parameters.
Proof.
The controlled 3D-FoDS can be acquired by just appending to system (7), i.e.;
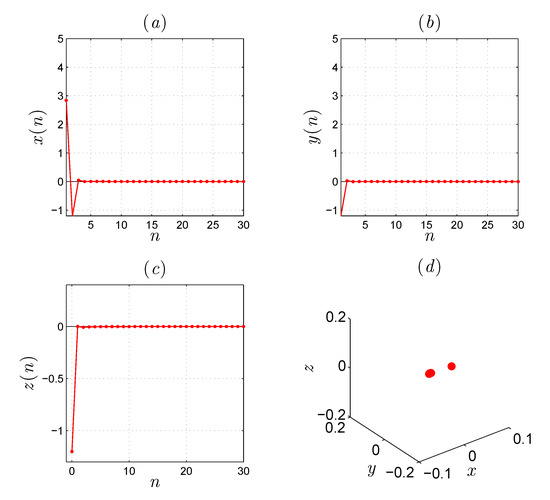
In order to corroborate the aforementioned theoretical findings, we intend to provide the phase space plots and also the states’ evolution of the controlled system. In Figure 7, the parameter values are selected to be as , , , and . Obviously, the one–dimensional controller forces all states of the system to be tended to zero.
6. Conclusions
All chaotic Fractional-order Discrete Systems (FoDSs) presented so far in the literature have displayed attractors that belong to “self-excited attractors”. Since the issue of FoDSs showing “hidden attractors” is almost unexplored, the present work has added a contribution to the topic of fractional-order systems through introducing a new initial example of a 3D-FoDS with only one nonlinear term and without fixed points. Such example has displayed hidden attractors clearly for proper values of the FoDS through its corresponding difference equations. An existence of chaos has been confirmed by means of some computations performed for the Largest Lyapunov Exponent (LLE), the 0–1 test, Approximate Entropy (ApEn), and also the bifurcation diagrams. Finally, a one-dimensional control law has been established for the purpose of stabilizing all dynamics of the proposed 3D-FoDS at zero.
Author Contributions
Conceptualization, A.-A.K.; Data curation, A.O.; Formal analysis, A.-A.K. and G.G.; Investigation, Z.D.; Methodology, I.M.B.; Resources, G.G.; Software, A.O.; Supervision, S.M.; Visualization, S.M.; Writing—original draft, I.M.B.; Writing—review & editing, Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to express their deepest gratitude and acknowledgments to the College of Humanities and Sciences of Ajman University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, G.; Huang, Y. Chaotic Maps: Dynamics, Fractals, and Rapid Fluctuations; Morgan & Claypool Publishers: San Rafael, CA, USA, 2011. [Google Scholar]
- Kocarev, L.; Szczepanski, J.; Amigo, J.M.; Tomovski, I. Discrete Chaos—I: Theory. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 1300–1309. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V. Hidden attractor in smooth Chua systems. Phys. D Nonlinear Phenom. 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Kiseleva, M.; Solovyeva, E.; Zaretskiy, A. Hidden oscillations in mathematical model of drilling system actuated by induction motor with a wound rotor. Nonlinear Dyn. 2014, 77, 277–288. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Sharma, P.R.; Shrimali, M.D.; Prasad, A.; Kuznetsov, N.V.; Leonov, G.A. Controlling dynamics of hidden attractors. Int. J. Bifurc. Chaos 2015, 25, 1550061. [Google Scholar] [CrossRef]
- Jafari, S.; Pham, V.T.; Golpayegani, S.M.R.H.; Moghtadaei, M.; Kingni, S.T. The relationship between chaotic maps and some chaotic systems with hidden attractors. Int. J. Bifurc. Chaos 2016, 26, 1650211. [Google Scholar] [CrossRef]
- Panahi, S.; Sprott, J.C.; Jafari, S. Two simplest quadratic chaotic maps without equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850144. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, Y.; Wei, Z.; Zhang, L. A new class of three-dimensional maps with hidden chaotic dynamics. Int. J. Bifurc. Chaos 2016, 26, 1650206. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Xie, H.P.; Chen, F.L. Chaos synchronization of fractional chaotic maps based on the stability condition. Phys. A Stat. Mech. Appl. 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Wang, X.; Pham, V.T.; Alsaadi, F.E. Chaos, control, and synchronization in some fractional-order difference equations. Adv. Differ. Equ. 2019, 2019, 412. [Google Scholar] [CrossRef]
- Jouini, L.; Ouannas, A.; Khennaoui, A.A.; Wang, X.; Grassi, G.; Pham, V.T. The fractional form of a new three-dimensional generalized Hénon map. Adv. Differ. Equ. 2019, 2019, 122. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Grassi, G.; Bendoukha, S. On chaos in the fractional-order Grassi–Miller map and its control. J. Comput. Appl. Math. 2019, 358, 293–305. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Bendoukha, S.; Grassi, G. On the Dynamics and Control of a Fractional form of the Discrete Double Scroll. Int. J. Bifurc. Chaos 2019, 29, 1950078. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pham, V.T.; El-Khazali, R. Hidden attractors in a new fractional—Order discrete system: Chaos, complexity, entropy, and control. Chin. Phys. B 2020, 29, 050504. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Grassi, G.; Pham, V.T. Chaos and control of a three-dimensional fractional order discrete-time system with no equilibrium and its synchronization. AIP Adv. 2020, 10, 045310. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Grassi, G.; Pham, V.T.; El-Khazali, R.; Vo Hoang, D. A Quadratic Fractional Map without Equilibria: Bifurcation, 0–1 Test, Complexity, Entropy, and Control. Electronics 2020, 9, 748. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Banerjee, S.; Wu, G.C. Discrete tempered fractional calculus for new chaotic systems with short memory and image encryption. Optik 2020, 218, 163698. [Google Scholar] [CrossRef]
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short Memory Fractional Differential Equations for New Memristor and Neural Network Design. Available online: https://link.springer.com/article/10.1007/s11071-020-05572-z (accessed on 17 December 2020).
- Wu, G.C.; Deng, Z.G.; Baleanu, D.; Zeng, D.Q. New variable-order fractional chaotic systems for fast image encryption. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083103. [Google Scholar] [CrossRef]
- Ouannas, A.; Wang, X.; Khennaoui, A.A.; Bendoukha, S.; Pham, V.T.; Alsaadi, F.E. Fractional form of a chaotic map without fixed points: Chaos, entropy and control. Entropy 2018, 20, 720. [Google Scholar] [CrossRef] [PubMed]
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 2009. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Sprott, J.C. Elegant Chaos: Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Wu, G.C.; Baleanu, D. Jacobian matrix algorithm for Lyapunov exponents of the discrete fractional maps. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 95–100. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. On the implementation of the 0–1 test for chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Lampart, M.; Zapomel, J. Dynamical properties of a non-autonomous bouncing ball model forced by non-harmonic excitation. Math. Methods Appl. Sci. 2016, 39, 4923–4929. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Cermak, J.; Gyori, I.; Nechvatal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).