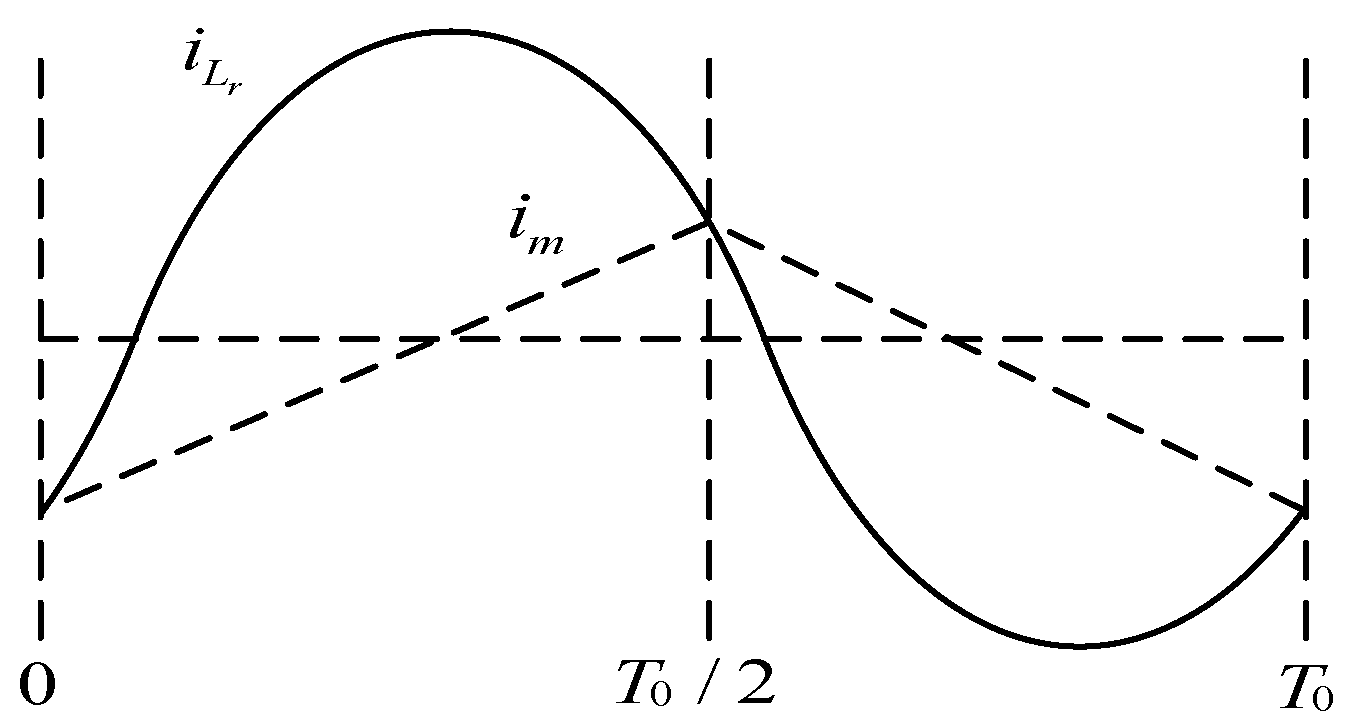Optimal Design of LLC Resonant DC Transformer under Adaptive Frequency Tracking Strategy

Abstract

In recent years, the LLC (inductor–inductor–capacitor) DC transformer has been widely used in communication and computer power supply because of its advantages of zero voltage conduction of primary switch and zero current turn off concerning the output rectifier diode. To obtain higher transmission efficiency and make the LLC DC transformer always run at the optimal operating point, the switching frequency of the LLC DC transformer should work at the resonance frequency of the circuit. In actual conditions, the optimal operating frequency of the LLC DC transformer will be changed due to the influences of the working condition on the circuit parameters and the load change. Therefore, the LLC DC transformer controlled by the fixed frequency mode will not be in the best working condition. In this paper, an adaptive frequency tracking method is used to control the circuit; when the circuit parameters change, the LLC DC transformer can always be in the best working state. Then, the influence of circuit parameters such as output power and excitation inductor on the optimal working point of the LLC DC transformer is analyzed in detail. Finally, a 1 kW LLC resonant converter prototype is designed under laboratory conditions to verify the feasibility of the control strategy.

1. Introduction

The DC (direct current) transformer is a necessary link for interconnecting DC networks of different voltage levels. It has been widely used in the field of new energy, fuel cells, supercapacitors, and where there are a DC bus and unidirectional transmission of energy in servers and communications [1,2]. To achieve high efficiency and high-power density DC transformers, many scholars have done a lot of research. Though the topology of the LCL (inductor–capacitor–inductor) resonant DC transformer is simple, it requires a large inductor on the DC side, which increases the cost, size, and weight of the converter. This type of DC transformer has no electrical isolation, which makes it easy to cause power reflow, and the probability of causing an electric shock accident is greatly increased. Therefore, more attention has been paid to DC transformers with electrical isolation. The dual active bridge (DAB) converter has a simple structure, can achieve soft switching (ZVS) characteristics, and energy flows in both directions [3,4]. However, its ZVS range is limited, and the switch also has a high turn-off current, resulting in a reduction in power conversion efficiency [5]. Even if the performance of the circuit can be improved by other modulation strategies, the complexity of the system control will increase accordingly [6]. The LLC resonant converter can achieve soft switching characteristics in the full load range and does not require complex control strategies [7,8]. Therefore, the research on the LLC converter has received extensive attention.

The LLC (inductor–inductor–capacitor) resonant converter can work in two modes: DC–DC converter with output voltage regulation under frequency modulation operation and DC transformer with fixed frequency operation whose output voltage changes with input. Literature [9,10] proposed the concept of parallel regulation. In those papers, the LLC resonant DCX (direct current transformer) and the PWM (pulse width modulation) DC–DC converter are cascaded to make the input side in series and the output side in parallel. Then, by processing the output power of the auxiliary parallel PWM DC–DC converter, the output voltage can be strictly regulated and the overall converter efficiency can be reduced. Similar to the above idea, literature [11,12] added an auxiliary transformer in the resonant cavity. The primary winding of the auxiliary transformer is connected in series with the main transformer, and the secondary winding is connected in parallel with the main transformer. Combined with the corresponding control, the LLC resonant converter works in DCX mode. However, the above methods all need to add additional circuits, which increases the volume of DCX.

To ensure that the LLC resonant converter always works at the optimal frequency, it must be ensured that the LLC resonant converter operates at the same frequency as the resonant frequency [13]. However, for LLC resonant converters operating under fixed frequency conditions, it is difficult to ensure that they work at the optimal frequency at all times. In actual industrial products, due to manufacturing processes and other reasons, the actual parameters of the LLC resonant converter resonant tank have a certain deviation from the set parameters. Due to the impact of changes in the actual operating environment of the LLC resonant converter, there are also differences between actual operating parameters and theoretical calculation parameters [14]. Based on the above factors, it can be seen that the resonant frequency of the resonant converter changes dynamically under actual operation. To synchronize the operating frequency with the resonant frequency, it is necessary to add a frequency tracking control link to maximize the transmission efficiency of the circuit [15,16] and then perform voltage regulation through the cascaded PWM DC–DC converter. The frequency tracking of the circuit in [15,16] is based on the detection of the cavity current signal. However, the load in the actual circuit changes, which has a great influence on the resonant cavity current of the LLC resonant converter. When the load is light, the resonant cavity current does not change much, and the detection is difficult, which greatly affects the detection accuracy and brings certain uncertainty. The method of voltage detection is less affected by the load [17,18,19]. The advantages and disadvantages of the detection methods mentioned above are summarized in

Table 1. Comparison of advantages and disadvantages.

	Detection Method	Advantages	Disadvantages
Current detection method	Detect the resonant current cycle flow	Direct detection frequency	Low detection accuracy at light load
	Total Harmonic Distortion (THD)	Direct detection frequency	Low detection accuracy at light load, complicated calculation and long response time
	Detecting rectifier conduction time	Direct detection frequency	The control circuit is complicated and the accuracy is low
Voltage detection method	Detect rectifier voltage and output voltage	High detection accuracy under light load. The control is simple. The response speed is fast.	Indirect detection frequency

. However, the existing literature only proposes a frequency tracking method and does not analyze in detail the mechanism of the LLC DC transformer to achieve the optimal operating point for voltage sampling, and the impact of different operating conditions on the optimal operating point.

This paper analyses and summarizes the frequency tracking method of the LLC resonant converter in the existing paper, and proposes a new method of frequency tracking based on voltage detection, which solves the shortcoming of current detection in the current method that it is difficult to distinguish the working range of the circuit at light load. The influence of load and magnetizing inductor change on the optimal operating point of LLC resonant converter is analyzed, and a theoretical analysis is given. In Section 2, modal analysis of the LLC resonant circuit is made for the three cases of f_s > f_r, f_s < f_r, f_s = f_r. The characteristics of the voltage and current waveforms in the three cases are found. In Section 3, this paper analyses the driving waveform of the primary side switch when operating below the optimal resonance point, the current waveform of the resonant circuit, the voltage waveform of the secondary side rectifier diode, and the output voltage waveform of the LLC resonant DC transformer, and the implementation method of adaptive frequency tracking strategy is given. In Section 4, the influence of the manufacturing process in practice is considered, the influence of the change of output power and the change of the excitation inductor of the resonance tank on the optimal operating point of the circuit are analyzed. 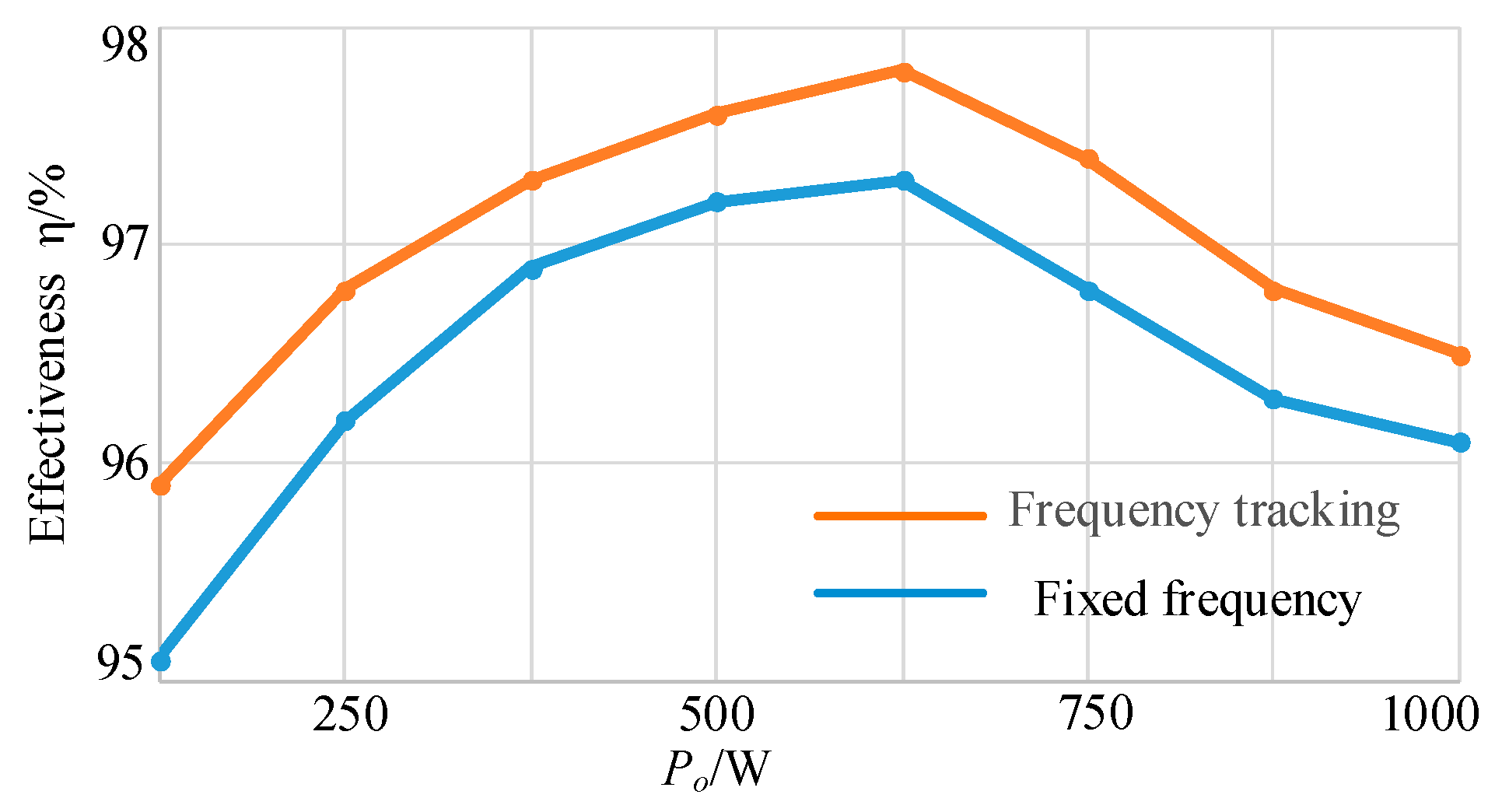As outlined in Section 5, the above analysis was simulated and verified, and then a 1 kW LLC resonant converter prototype was designed and built under laboratory conditions. The experiment proved the influence of load change on the optimal operating point of DCX and verified the adoption of the correctness of the control strategy.

2. Operational Analysis

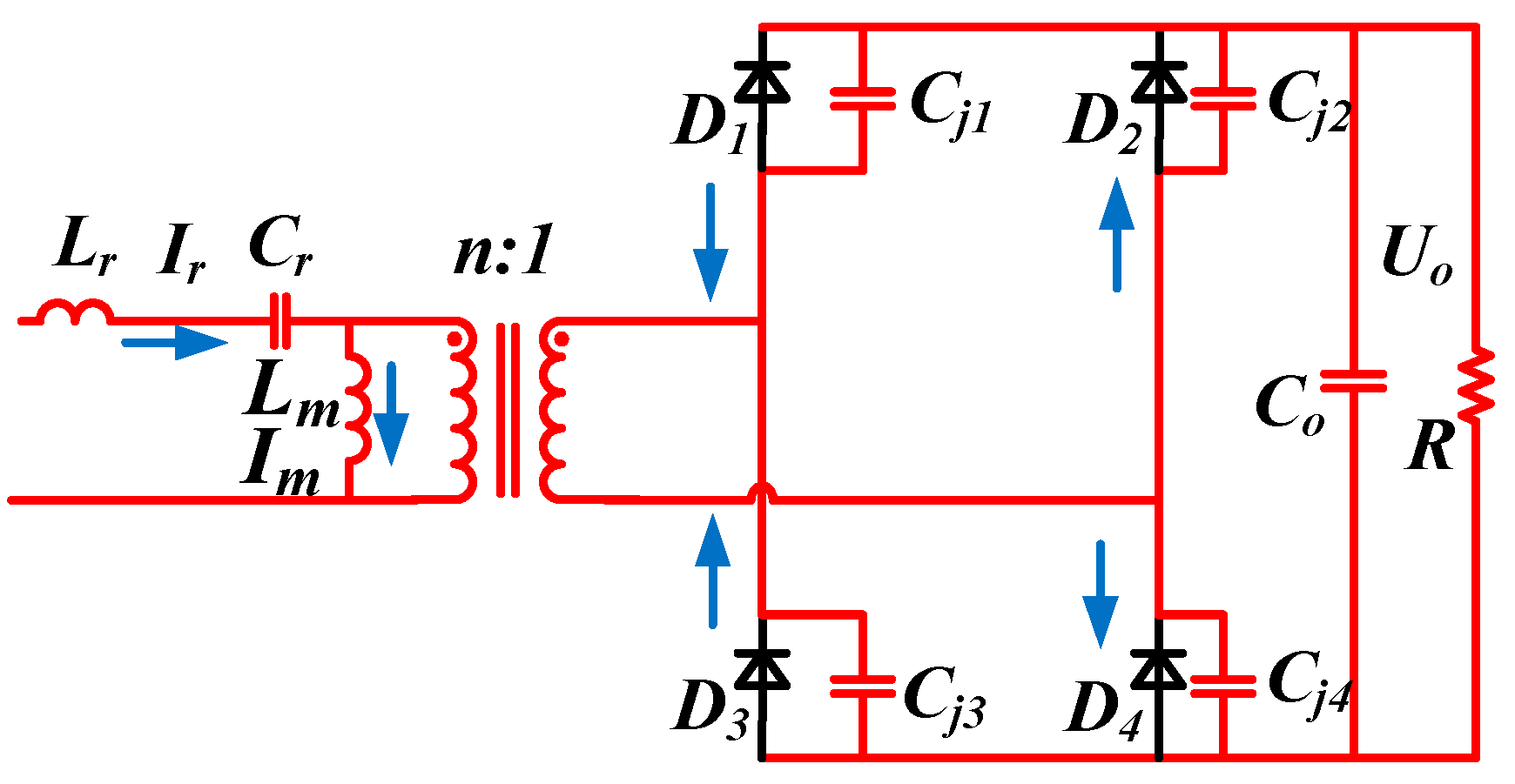
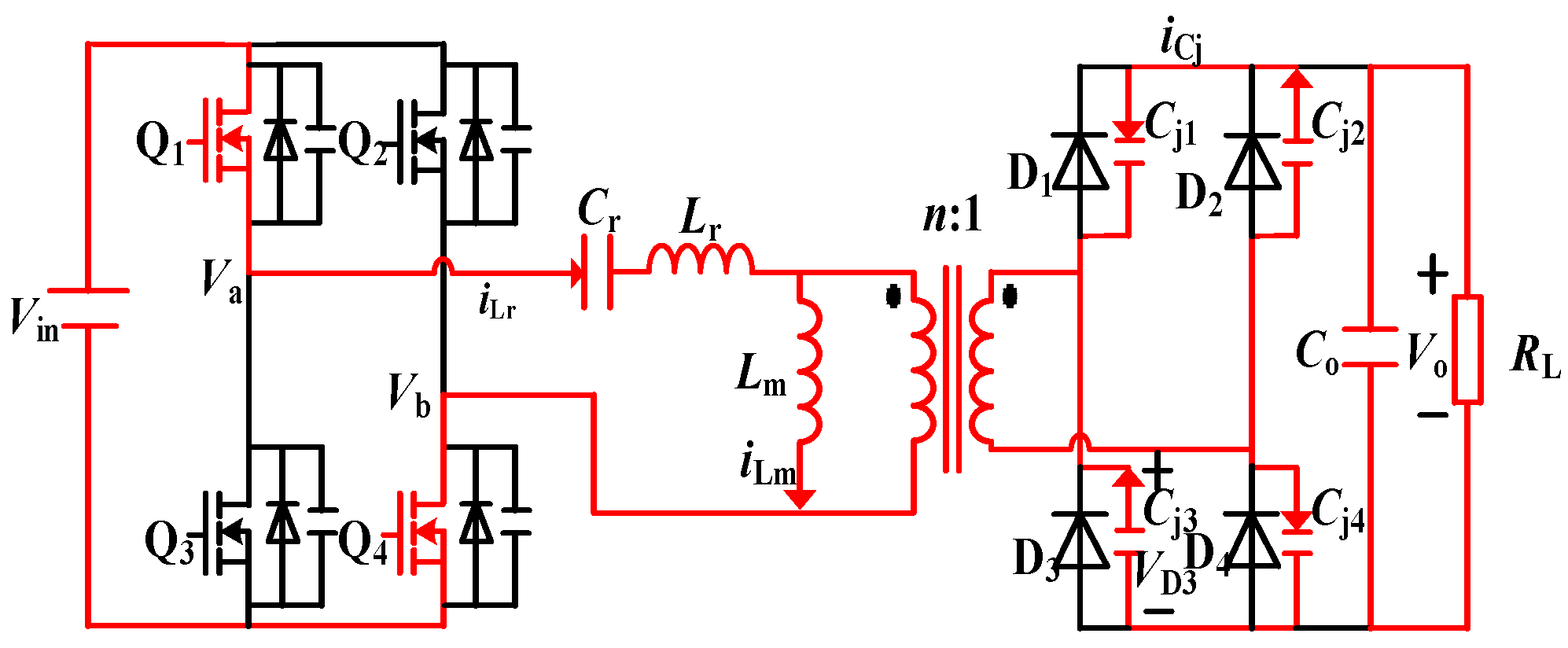
Figure 1 shows a full-bridge rectified LLC resonant converter. Q₁~Q₄ are primary switching transistors, L_r is a resonant inductor, C_r is a resonant capacitor, L_m is a magnetizing inductor, and D₁~D₄ are output rectifier diodes. Unlike traditional PWM converters, LLC resonant converters adjust the output voltage by adjusting the switching frequency. When the converter operates in different frequency ranges, the secondary diode voltage and current waveforms will be different.

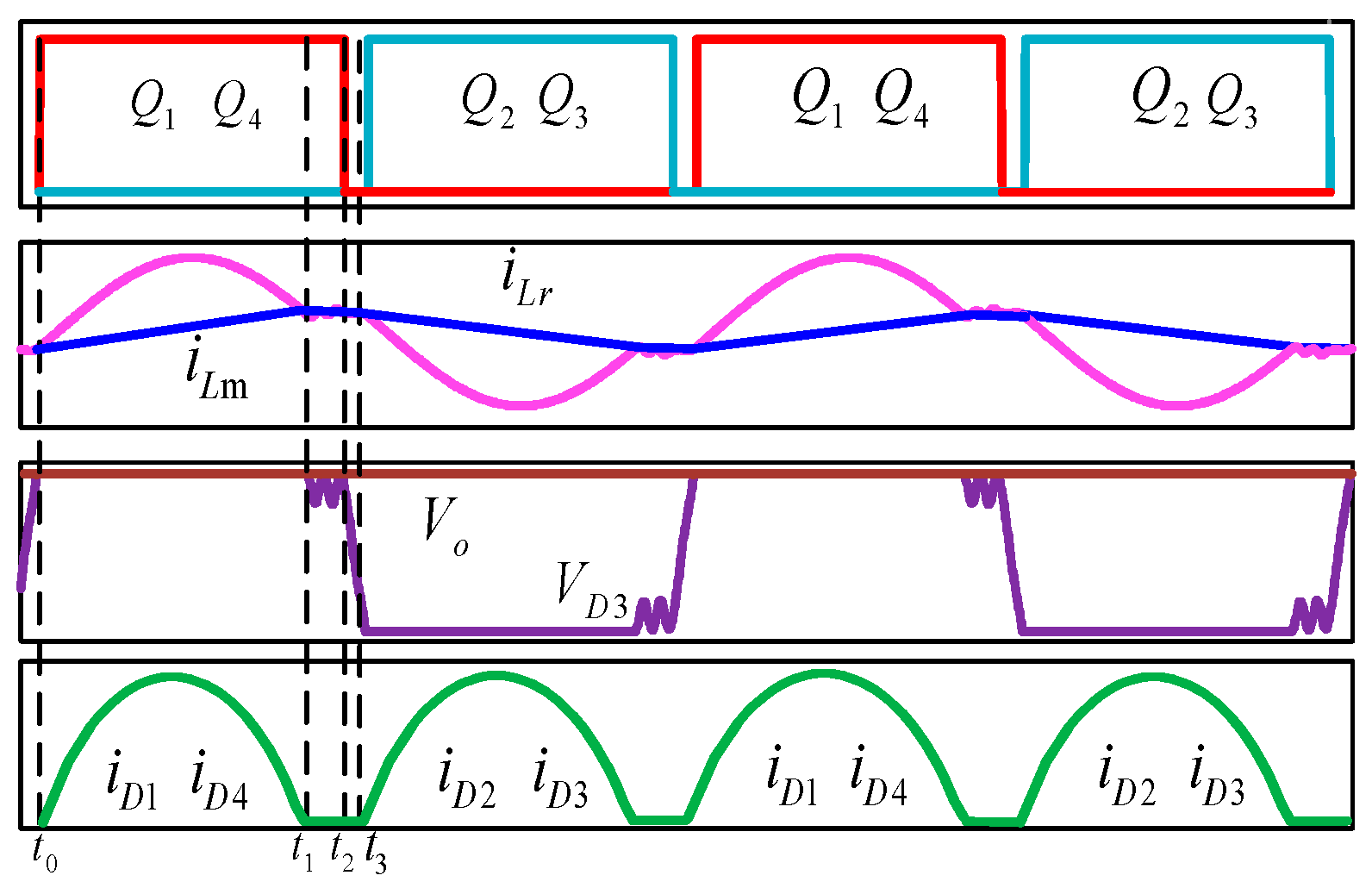
The main voltage and current waveforms of the LLC resonant converter for f_s < f_r (f_s is the working frequency of switch, f_r is the resonant frequency of LLC converter) are shown in Figure 2. At t₁, the resonance current I_r and the excitation current I_m start to be equal, the secondary diodes D₁ and D₄ have a current of 0, and zero current shutdown can be achieved. At t₂, the primary switches Q₁ and Q₄ of the converter are turned off. During [t₁–t₂], the voltage across the excitation inductor is not clamped by the output voltage and the converter enters a three-element resonance state. As the current through the diode drops to zero, the D₁ and D₄ junction capacitors are charged, the D₂ and D₃ junction capacitors are discharged, and the capacitor of the output rectifier diode resonates with the resonant inductor L_r; the resonant current of the resonant circuit and the voltage across capacitor D₃ oscillate. Detailed analysis of the oscillation process is given in Section 3 of this article. 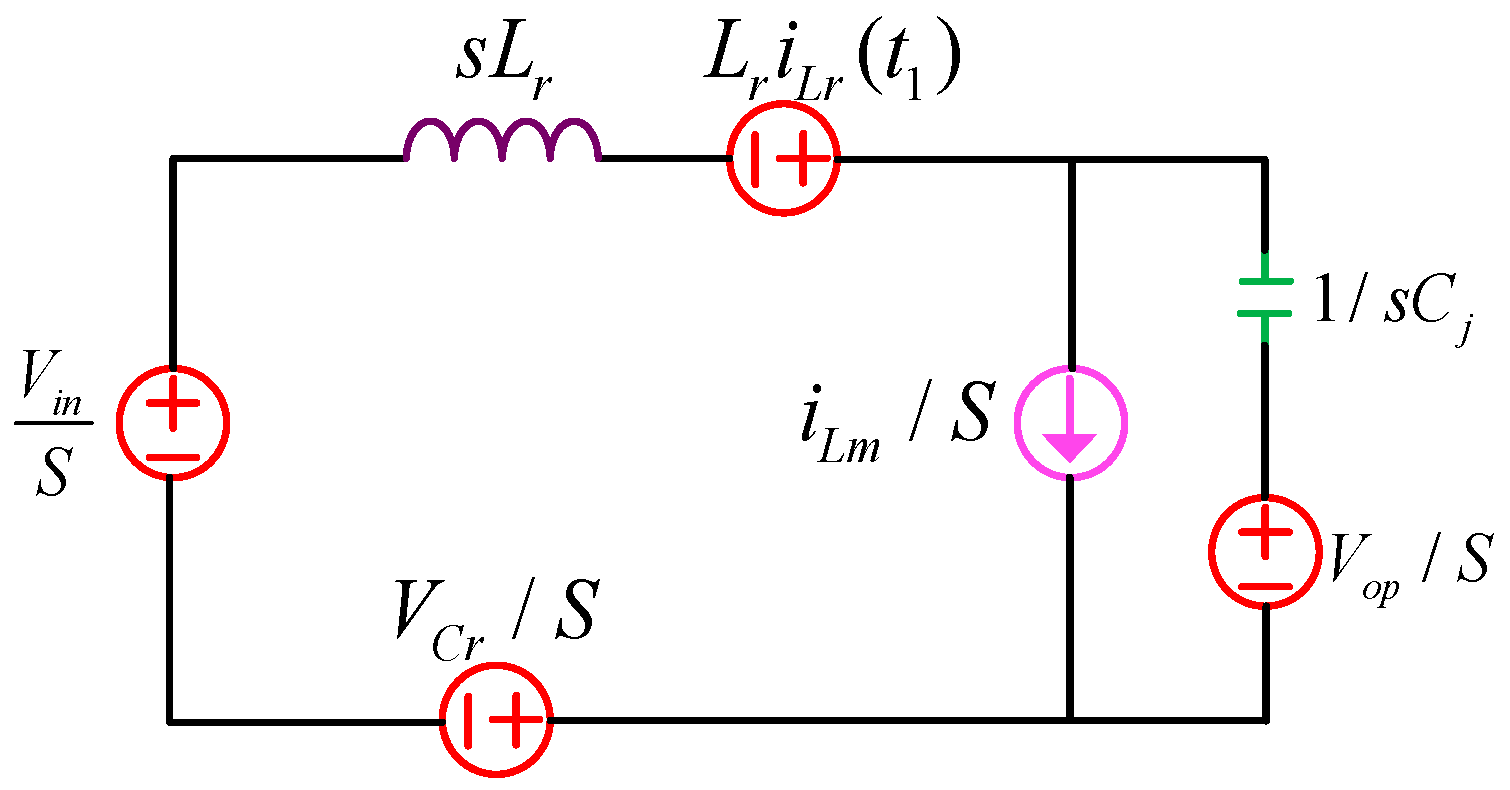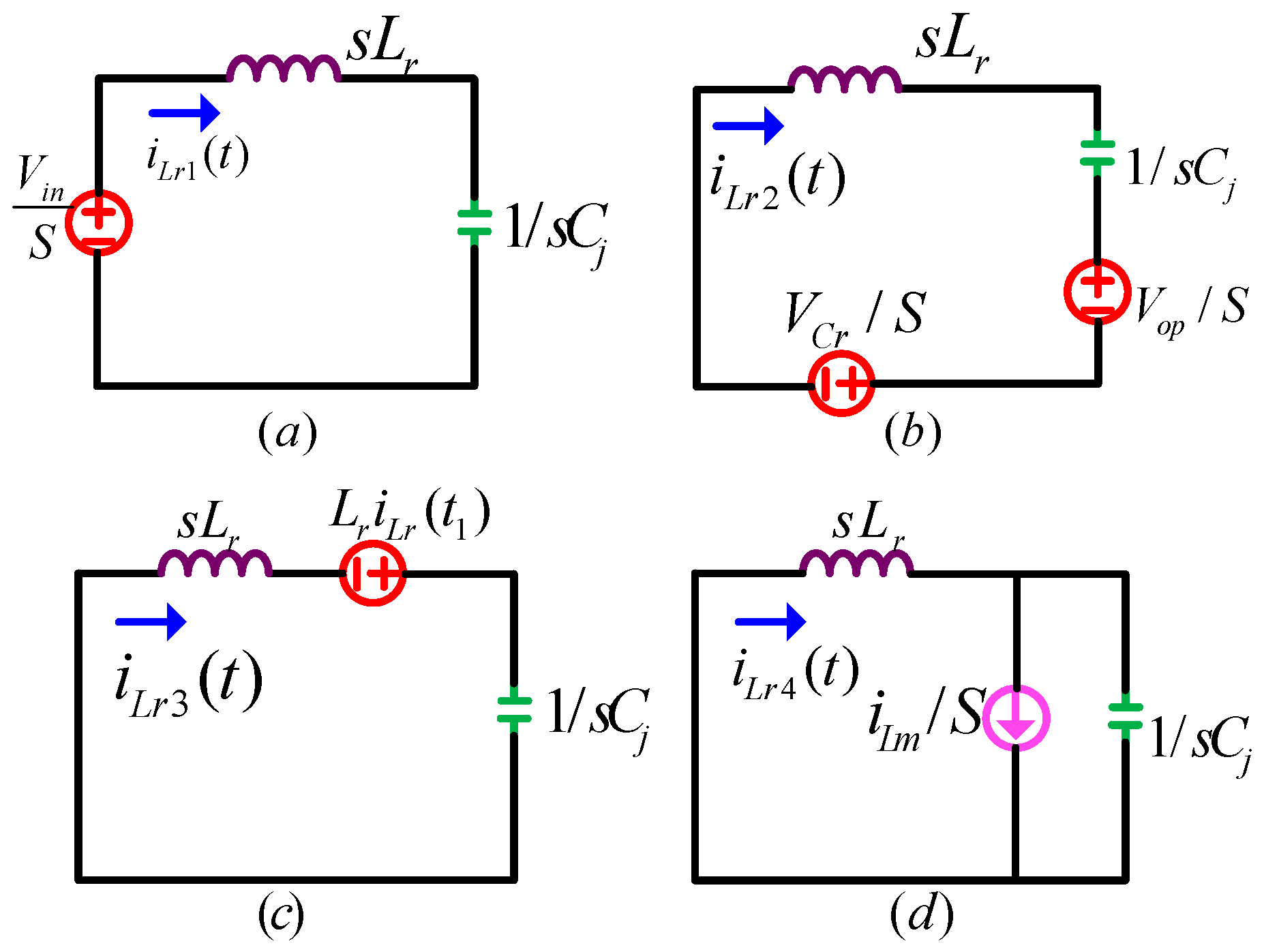At the moment when the switches Q₁ and Q₄ are turned off, the diode voltage V_D3 across the rectifier D₃ is less than V_o; the equivalent circuit diagram of this period is shown in Figure 3. During [t₂–t₃], the voltage V_D3 across the capacitor D₃ drops rapidly. At t₃, V_D3 drops to 0, the resonance inductor and the excitation inductor start to be unequal, the secondary rectifiers D₂ and D₃ start to conduct, and the next cycle is started. It can be known from the above analysis that when f_s < f_r, the LLC resonant converter has two working modes during [t₁–t₃].

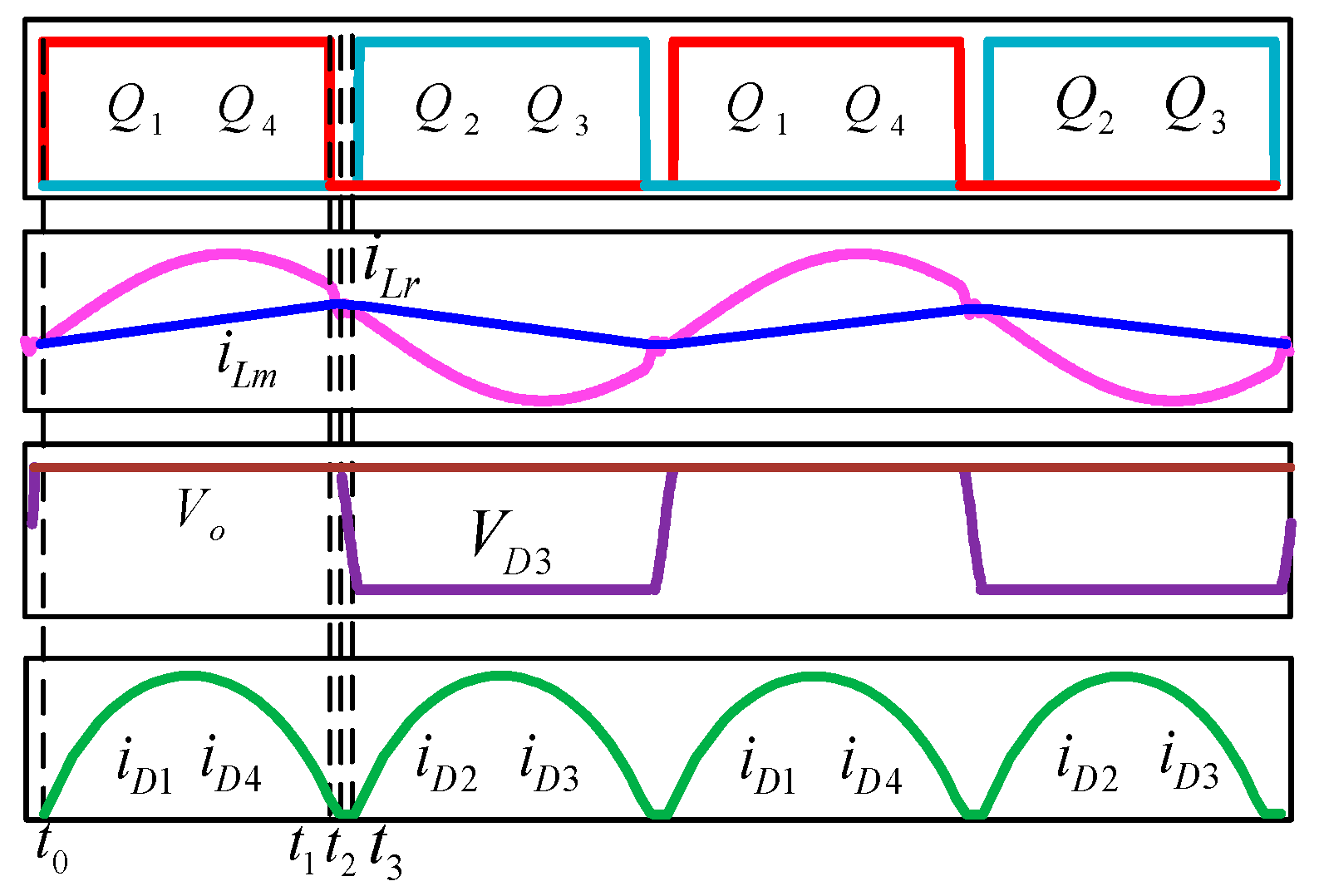
The main voltage and current waveforms of the LLC resonant converter for f_s > f_r are shown in Figure 4. Because the resonance period is smaller than the switching period, the resonance tank current i_Lr curve cannot intersect with the excitation inductor current i_Lm curve when the primary side switches Q₁ and Q₄ are closed at t₁, resulting in the current flowing through the rectifier diodes D₁ and D₄ not being zero, and the voltage V_D3 of the rectifier D₃ remaining at the output voltage V_o. The excitation inductor voltage is affected by the output voltage clamping, and the excitation inductor current continues to increase for a short time. Because the switches Q₁ and Q₄ are closed, the bridge arm voltage V_ab becomes zero, and the resonance tank current drops rapidly. The equivalent circuit diagram for [t₁–t₂] is shown in Figure 5. At t₂, the resonance current i_Lr and the excitation inductor current i_Lm are equal, after which the voltage V_D3 of the rectifier D₃ drops rapidly, preparing for the output rectifier diode rectification. During [t₂–t₃], the voltage V_D3 of the rectifier diode D₃ drops to 0 at t₃, the resonance inductance and the excitation inductance begin to be unequal, the rectifier diodes D₂ and D₃ start to conduct, and the next cycle begins. It works in the same way as f_s < f_r in the period [t₂–t₃].

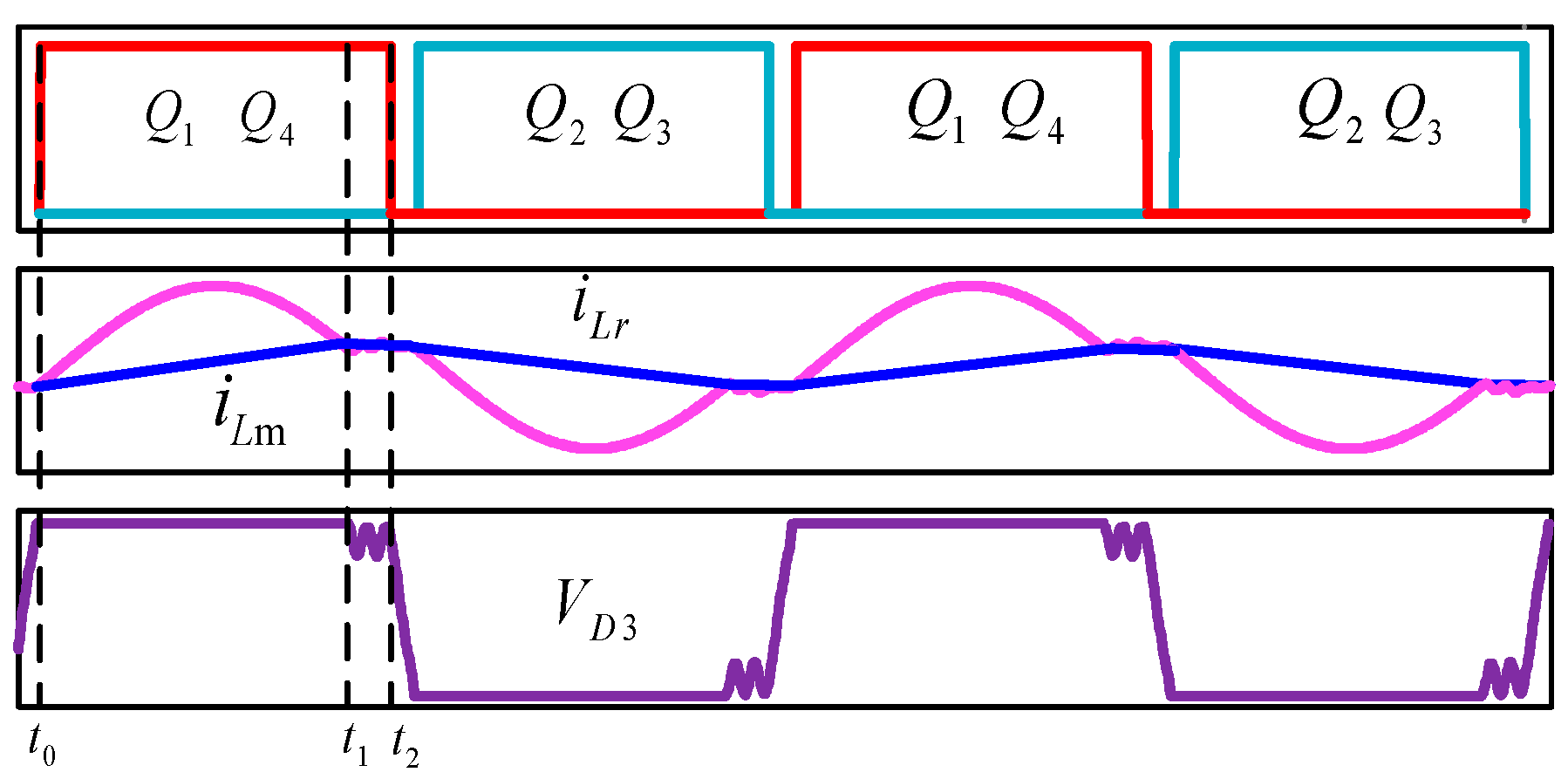
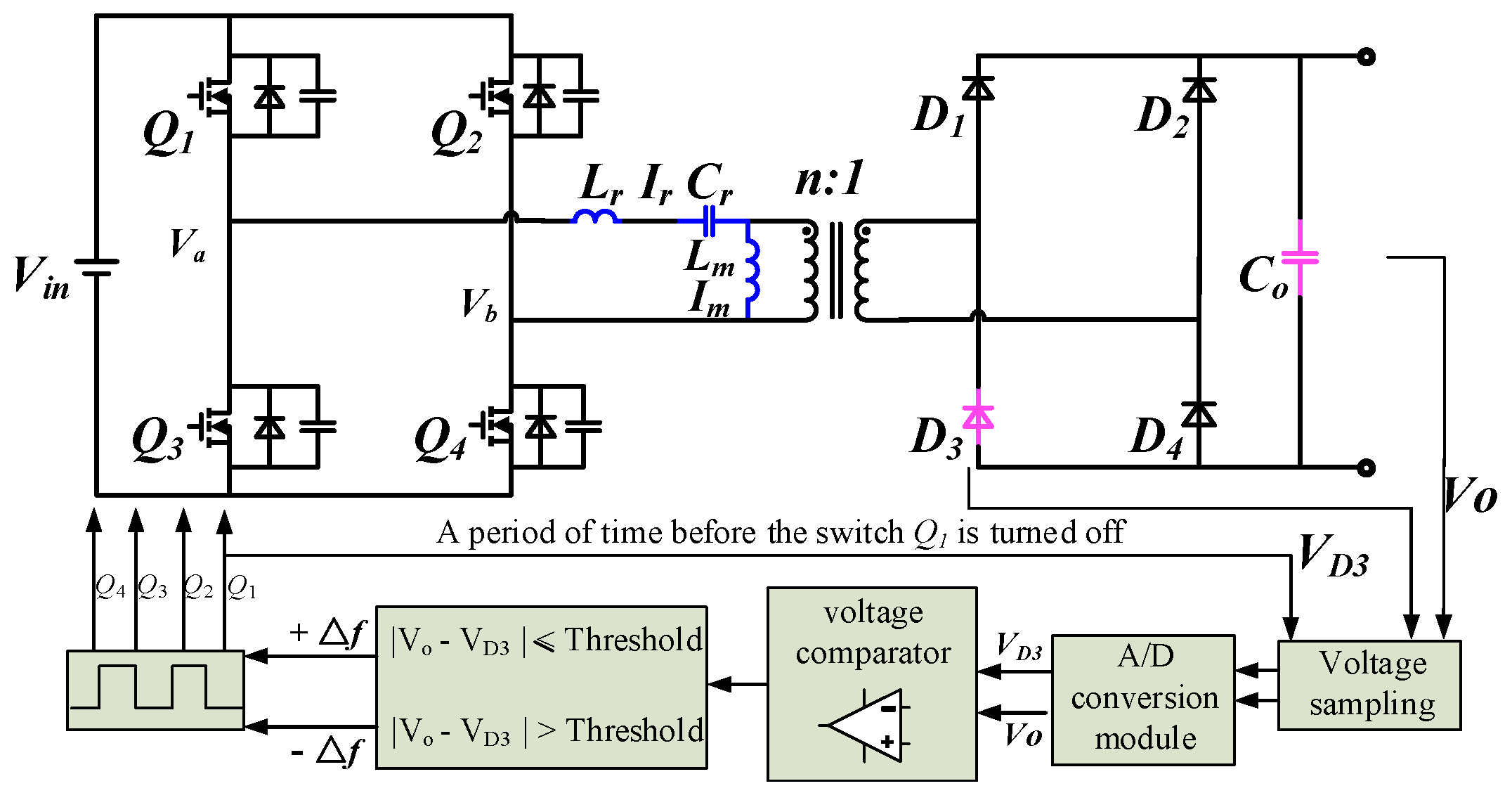
The main voltage and current waveforms of the LLC resonant converter for f_s = f_r are shown in Figure 6. At t₁, the primary side switches Q₁ and Q₄ are disconnected, and the resonance tank current i_Lr and the excitation inductor current i_Lm intersect. During [t₁–t₂], the working mode is the same as the previous two cases during [t₂–t₃]. Therefore, when f_s = f_r, there is one less working mode than the first two cases. Through the above analysis, it can be seen that, when the LLC resonant converter works in different frequency ranges, the working model is slightly different. When the primary switch is turned off, the voltage on the output rectifier diode is different. Therefore, the frequency tracking control can be realized by judging the voltage of the rectifier diode when the switch is turned off.

According to the above analysis, when working below the resonant frequency (f_s < f_r), there is more circulating energy in the resonant tank, which causes the switch to conduct more RMS current and generate more conduction losses. When working below the resonant frequency (f_s > f_r), the primary side switch has a higher current when it is closed, which causes more switching losses. Therefore, when the LLC resonant converter operates at f_s = f_r, the working efficiency of the converter is the highest. When the LLC resonant converter is in a different frequency range, the voltage of the secondary side rectifier diode is different at the moment when the primary side switches Q₁ and Q₄ are cut off. When f_s < f_r, V_D3 is less than V_o, and when f_s > f_r, V_D3 is equal to V_o. Therefore, by judging the voltage on the rectifier diode D₃ when the primary switches Q₁ and Q₄ are turned off, the best operating frequency can be tracked.

3. Adaptive Frequency Tracking Analysis

3.1. Analysis of Diode Voltage Oscillation Mechanism

When the switching frequency of the LLC resonant converter is less than the resonant frequency, during the period from t₁ to t₂, the resonant tank current and the voltage of the secondary rectifier diode oscillate. The specific waveform is shown in Figure 7.

During [t₁–t₂], the primary switching transistors Q₁ and Q₄ are on state, and after the resonant tank current intersects with the magnetizing inductor current the carrying capacitor of the secondary rectifier diodes begins to charge and discharge and resonates with the primary resonant inductor. The specific operating mode is shown in Figure 8.

Since the resonant capacitor and the magnetizing inductor in the LLC resonant converter are relatively large, the [t₁–t₂] period is relatively short, so it can be considered that the resonant capacitor voltage and the magnetizing inductor current remain unchanged during [t₁–t₂]. Therefore, the resonant capacitor is equivalent to the voltage source V_cr, and the magnetizing inductor is equivalent to the current source i_Lm so that the equivalent circuit of the S domain during [t₁–t₂] can be obtained. The specific circuit is shown in Figure 9, where C_j1 = C_j2 = C_j3 = C_j4, C_j = C_j1/n², V_op = nV_o, where n is the turns ratio of the transformer.

To find the resonant current i_Lr, the superposition theorem is used to solve the resonant currents of the five independent voltages or the current source alone, and the two polarities of V_cr/s and V_op/s are placed in the same group. Figure 10 is an equivalent circuit diagram of the independent sources of Figure 9 when operating alone or in combination.

The resonant current i_Lr can be obtained from Figure 10a.

$$i_{Lr1}(s)=\frac{V_{in}/L}{s^2+1/(C_j{L}_r)}$$

(1)

w₁ is defined as the resonant angular frequency:

$${\omega }_1=\frac{1}{\sqrt{C_j{L}_r}}$$

(2)

The inverse Laplace transform of Equation (1) can be obtained:

$$i_{Lr1}(t)=\frac{V_{in}}{{\omega }_1{L}_r}\sin ({\omega }_{1}t)$$

(3)

Similarly:

$$i_{Lr2}(t)=-\frac{V_{op}+V_{cr}}{{\omega }_1{L}_r}\sin ({\omega }_{1}t)$$

(4)

$$i_{Lr3}(t)=i_{Lr}(t_1)\cos ({\omega }_{1}t)$$

(5)

$$i_{Lr4}(t)=i_{Lm}(1-\cos ({\omega }_{1}t))$$

(6)

In summary, the resonant current i_Lr(t) during [t₁–t₂] can be obtained as:

$$i_{Lr}(t)=\frac{i_{Lm}{\omega }_1{L}_r+(i_{Lr}(t_1)-i_{Lm}){\omega }_1{L}_r\cos {\omega }_{1}t}{w_1{L}_r}+\frac{(V_{in}-V_{Cr}-V_{op})\sin {\omega }_{1}t}{{\omega }_1{L}_r}$$

(7)

The secondary side rectifier diode is charged to the capacitor charging current:

$$\begin{array}{l}{i}_{Lr}(t)=\frac{i_{Lm}{\omega }_1{L}_r+(i_{Lr}(t_1)-i_{Lm}){\omega }_1{L}_r\cos {\omega }_{1}t}{{\omega }_1{L}_r}+\frac{(V_{in}-V_{Cr}-V_{op})\sin {\omega }_{1}t-{\omega }_1{L}_r{i}_{Lm}}{{\omega }_1{L}_r}\\ \end{array}$$

(8)

The diode voltage V_D3 is:

$$V_{D3}(t)=V_o-0.5(L_r{\omega }_1{i}_{Lr}(t_1)\sin ({\omega }_{1}t)-\sqrt{\frac{L_r}{C_j}}{i}_{Lm}\sin ({\omega }_{1}t))-(V_{op}-V_{in}+V_{Cr})(1-\cos ({\omega }_{1}t))$$

(9)

3.2. Control Strategy

From the above analysis, when the primary switching transistors Q₁ and Q₄ are turned off, the magnitude of the output rectifier diode voltage V_D3 reflects the working area of the LLC resonant converter. Therefore, the frequency tracking control can be performed by sampling the rectifier diode voltage. The control flow chart of frequency tracking is shown in Figure 11. In the actual implementation, the accuracy of the judgment is ensured by sampling the V_D3 in a certain time interval before the switching off of the switch multiple times, thereby avoiding the condition that a single sampling point may be close to V_o to judge the problem of inaccuracy.

The control block diagram after adding frequency tracking control is shown in Figure 12. In the actual frequency tracking control process, the converter is first transitioned from the initial state to the stable state smoothly by the soft start and the timer delay, preventing the excessive starting current from damaging the transformer and the corresponding switching device. After the circuit reaches a steady state, due to the delay of the hardware circuit, the voltage V_D3 and output voltage V_o on the rectifier diode D₃ at the sampling output end are required to make some fine adjustments on the sampling time during a period of time before the driving signals of the primary switches Q₁ and Q₄ change from high to low. Then compare the voltage V_D3 with the output voltage Vo. The switching frequency is less than the resonant frequency and needs to be increased by a certain step if the difference between the two frequencies is greater than the set threshold. Conversely, if the difference between the two frequencies is less than the set threshold, the switching frequency is greater than the resonant frequency. The switching frequency needs to be reduced by a certain step. The step of the frequency change is determined by the clock cycle and frequency tracking accuracy of the digital controller. By repeating the above steps, the final switching frequency will swing on both sides of the resonant frequency, thereby achieving frequency tracking control.

4. Analysis of the Influence of Frequency

Accurate analysis of LLC resonant converter will produce a very complex model; the process is more cumbersome. Therefore, to analyze the LLC resonant converter simply and effectively, the method currently used is the fundamental approximation method (first harmonic approximation; FHA). This method assumes that the energy transfer from the input to the output is mainly caused by the fundamental component of the voltage and current while ignoring other higher harmonic components that have little effect on the entire system.

First, the Fourier series expansion of the output voltage V_ab of the inverter bridge is [20]:

$$V_{ab}\left(t\right)=\frac{4V_{in}}{\pi }{\displaystyle \sum _{i=1,3,5,...}^{\infty }\frac{1}{n}}\sin \left(2n\pi f_{s}t+\theta \right)$$

(10)

In the Equation (10), f_s = 1/T_s, T_s is the switching period.

The fundamental component of V_ab is:

$$V_{ab1}\left(t\right)=\frac{4V_{in}}{\pi }\sin \left({\omega }_{0}t+\theta \right)$$

(11)

Then the valid value of V_ab1 is:

$$V_{rms-p}=\frac{2\sqrt{2}{V}_{in}}{\pi }$$

(12)

Since the converter works at the resonance point, the resonance current can be expressed as:

$$i_{Lr}(t)=\sqrt{2}{I}_{rms\_p}\sin ({\omega }_{0}t+\theta +\phi )$$

(13)

where $\theta$ is the phase difference between the resonance current and the excitation current and $\phi$ is the phase difference between the input voltage and the resonance current.

The working waveform of the full-bridge LLC resonant converter for when the converter works at the resonance frequency point is shown in Figure 13.

It can be seen from Figure 13 that the fundamental component waveform of the input voltage and the waveform of the resonance current are almost the same at the resonance point. Since the dead time of the control circuit is fixed, and the dead time is much shorter than the switching period, it can be considered that the phase difference between the input voltage and the resonant current is approximately $\phi =0$.

It can be obtained from the above analysis that the input power of the entire circuit is:

$$P_{in}=V_{rms-p}*I_{rms-p}\cos \phi \approx V_{rms-p}*I_{rms-p}$$

(14)

The output power of the entire circuit is:

$$P_{out}=\frac{V_0^2}{R_L}$$

(15)

where R_L is the load resistor.

Ignoring the loss of the LLC resonant converter, according to the principle of energy conservation, the output power is equal to the input power.

$$P_{in}=V_{rms-p}*I_{rms-p}=P_{out}=\frac{{V_0}^2}{R_L}$$

(16)

It can be known from Equation (12) that the effective value of the input voltage is only related to the input voltage V_in and keeps the output voltage unchanged, according to Equation (16). Due to power conservation, when the load is doubled, the input voltage remains constant, and the effective value of the resonant current doubles.

It can also be seen from Figure 14 that the excitation current and the resonance current are equal during the half-resonance period. The peak value of the excitation current at this time is:

$$i_{Lm-pk}=\frac{n{V}_0}{L_m}\frac{T_0}{4}$$

(17)

At the same time, within half a resonance period, the difference between the average value of the resonance current and the excitation current is the average value of the output current converted to the primary side, establishing the following two equations:

$$i_{Lr}\left(\frac{T_0}{2}\right)=i_{Lm-pk}$$

(18)

$$\frac{{\displaystyle {\int }_0^{\frac{T_0}{2}}\left[i_{Lr}\left(t\right)-i_{Lm}\left(t\right)\right]}dt}{\frac{T_s}{2}}=\frac{n{V}_0}{R_L}$$

(19)

In Equation (19), T_o is the resonance period, and the relationship between T_s and the dead time T_d is:

$$T_S=T_0+2T_d$$

(20)

According to Equations (18) and (19), the expression of primary-side current effective value is:

$$I_{rms-p}=\frac{V_0}{2}\sqrt{\frac{n^2\cdot T_S^2\cdot {\pi }^2}{2R_L^2\cdot T^2}+\frac{T^2}{8L_m^2}}$$

(21)

The simultaneous Equations (16) and (21) can be expressed:

$$P_{out}=\frac{T_0{}^2\cdot V_0^2\cdot V_{in}}{2\pi L_m\sqrt{\left|T_0{}^2\cdot V_0^2-n^2\cdot {(T_0+2T_d)}^2\cdot V_{in}^2\right|}}$$

(22)

It can be known from Equation (22) that, when the parameters of the resonant converter are determined, the resonant period T_o increases as the load increases. The trend is shown in Figure 15. The relationship curve between power and resonance frequency is drawn in MATLAB as shown in Figure 16. From that figure, it can be concluded that the resonance frequency decreases as the load increases.

When the parameters of the resonant converter are determined, Equation (22) becomes the relationship between the output power P_out and the resonant period T₀. Through mathematical derivation, it can be concluded that the resonant period T₀ will increase with the decrease of the output power P_out. Figure 15 shows the relationship between the inductive current i_Lr and the exciting inductive current i_m under different working conditions, as well as the corresponding output current waveform. Taking the zero-crossing point of excitation inductor current i_m as the coordinate base point, the relationship curve between inductor current i_Lr and excitation inductor current i_m under three different working conditions of full load, heavy load, and light load is obtained. It can be seen from the figure that when the output power P_out decreases the intersection point of excitation inductor current i_m and inductor current i_Lr, i.e., resonance period T₀, also decreases. By adopting an adaptive frequency tracking control strategy, the output current i_o can be in the critical continuous state under different working conditions. Figure 16 shows the curves of resonant frequency f_s and output power P_out of excitation inductor i_m at different times. When the output power P_out does not change, the resonance frequency F_S decreases with the increase of excitation inductor i_m; when the resonance frequency F_S does not change, the output power P_out decreases with the increase of excitation inductor L_m.

5. Simulation and Experimental Verifications

5.1. Simulation Verification

To verify the precision of the above control strategy, the control block diagram shown in Figure 12 is first constructed in the simulation software PSIM, and the specific parameters of the LLC resonant converter are shown in

Table 2. Specific parameters of the 1 kW LLC resonant converter.

Technical Parameters	Parameters
Input voltage Vin	400 V
Output voltage Vo	400 V
Output power Pout	1 kW
Resonant inductor Lr	20 μH
Resonant capacitor Cr	110 nF
Magnetizing inductance Lm	800 μH

. The parameters used in the experiment are the same as those used in the simulation and both use the parameters provided in the table.

The frequency tracking control process is to eliminate the voltage oscillation of the output rectifier diode so that when the primary-side switching transistor Q₁ is turned off the voltage across D₃ is just the output voltage V_o. The simulation is used to verify the precision of this control strategy under different output loads and sudden changes in input and output. The simulation waveforms are shown in Figure 17.

It can be seen from Figure 17 that when the output load is full load, the final tracking frequency of the converter is 101.6 kHz; when the output load is 1/8, the final tracking frequency of the converter is 106.6 kHz. As the output load decreases, the intersecting time point of the resonant inductor current and the excitation inductor current advances. As the intersection time point advances, the switching frequency increases. Therefore, the relationship between the load and the resonance frequency can be obtained: As the load decreases, the resonance frequency increases. This proves the correctness of the theoretical analysis in Section 4.

It can be seen from Figure 18 that when the three current control methods reach a steady state under light load conditions, there is an oscillation phenomenon in the rectifier voltage waveform, and the frequency of the optimal operating point is not tracked. Since the current detection is to track the optimal frequency operating point by detecting the resonant current and the flow time of the secondary rectifier, the current is small due to the small power under light load; the detection accuracy of the above detection method reduces. The voltage detected by the voltage detection method will not change much in various working modes. Compared with the above-mentioned control method, the adaptive frequency tracking control method proposed in this paper solves the shortcoming of low detection accuracy of the current detection method under light load conditions.

5.2. Experimental Verification

A 1 kw LLC resonant converter hardware platform was built in the laboratory to verify the precision of the proposed control strategy by changing the input voltage and output load. The specific experimental waveform is shown in the figure below. The platform established in the lab is shown in Figure 19.

LLC resonant converter uses the energy stored in the excitation inductor to drain the energy from the host capacitor of the primary switching transistor so that the LLC resonant converter can realize ZVS in the full load range. It can be seen from Figure 20 that before the driving signal changes from a low level to a high level, the voltage V_DS of MOSFET reduces to zero, thus realizing ZVS switching on.

At full load, the oscilloscope captures the converter frequency tracking process as shown in Figure 21. As the switching frequency increases, the voltage oscillation across the diode gradually decreases. When the switching frequency is 100.8 kHz, the oscillation disappears and the resonant tank current approaches the sine wave, indicating that frequency tracking has been achieved at this time.

Figure 22 shows an experimental waveform with a tracking frequency of 102.2 kHz at 1/2 load. Figure 23 is an experiment waveform of a 1/8 load with a tracking frequency of 107.8 kHz. It can be seen from the above experimental waveform that the resonance point can be tracked under various loads, which proves the correctness of the control method. The tracking frequency increases as the output power decreases, which conforms to the converter’s input–output power conservation principle. Through the above analysis, the experimental results are consistent with the theoretical results. When tracking the resonance point, when the main switch is turned off, the current flowing through the resonant tank is exactly zero, and the voltage across the secondary diode drops rapidly during the subsequent dead time. The resonant frequencies under different loads obtained from the theoretical analysis in Section 3 and the above experiments are shown in the following table. It can be seen from the table that the theoretical analysis and experiment have the same changing trend, and the resonance frequency decreases as the load increases.

$$\eta \%=\frac{P_{out}}{P_{in}}=\frac{V_0{I}_0}{P_{in}}$$

(23)

The actual work effectiveness calculation formula is shown above, where I_o is the output current and V_o is the output voltage. The actual work effectiveness in this paper is obtained by measurement of the experimental platform using the power analyzer MAGTROL MODEL 6530 in the laboratory. It can be seen from Figure 24 that with the frequency tracking control strategy proposed in this paper, the LLC resonant converter can achieve higher energy transmission efficiency. Compared with the fixed switching frequency control strategy, the adaptive frequency tracking strategy can reduce the effective value of the resonant tank current, making the switching conduction loss smaller and the converter transmission efficiency higher. The frequency tracking points under different loads are shown in

Table 3. The resonant frequencies under different loads.

	Full Load	1/2 Load	1/8 Load
Theoretical calculation	100.6 k	103.7 k	105.4 k
Simulation results	101.6 k	104.3 k	106.6 k
Experimental results	100.8 k	102.2 k	107.8 k

below.

6. Conclusions

Compared with the frequency tracking method of current control, the frequency tracking method of voltage control has higher detection accuracy at light load. According to simulations and experiments under different loads, it is proved that the influences of different loads on the optimal operating point are as follows:

• As the load increases, the frequency of the optimal operating point of the LLC DC transformer will decrease;
• With the increase of the magnetizing inductor, the frequency of the optimal operating point will be reduced.

Based on voltage-type control, this paper proposes an adaptive frequency tracking method. The biggest advantage of this working method is that it can track the optimal working point of the LLC DC transformer under light load so that the LLC DC transformer can work with better performance. According to simulations and experiments, and compared with the traditional fixed switching frequency control strategy, it can be seen that the adaptive frequency tracking strategy can not only achieve zero-voltage turn-on, but also approximately achieve zero-current turn-off, which reduces switch conduction losses and achieves higher energy transmission efficiency.