Dimensionality Reduction for Smart IoT Sensors
Abstract
1. Introduction
2. Materials and Methods
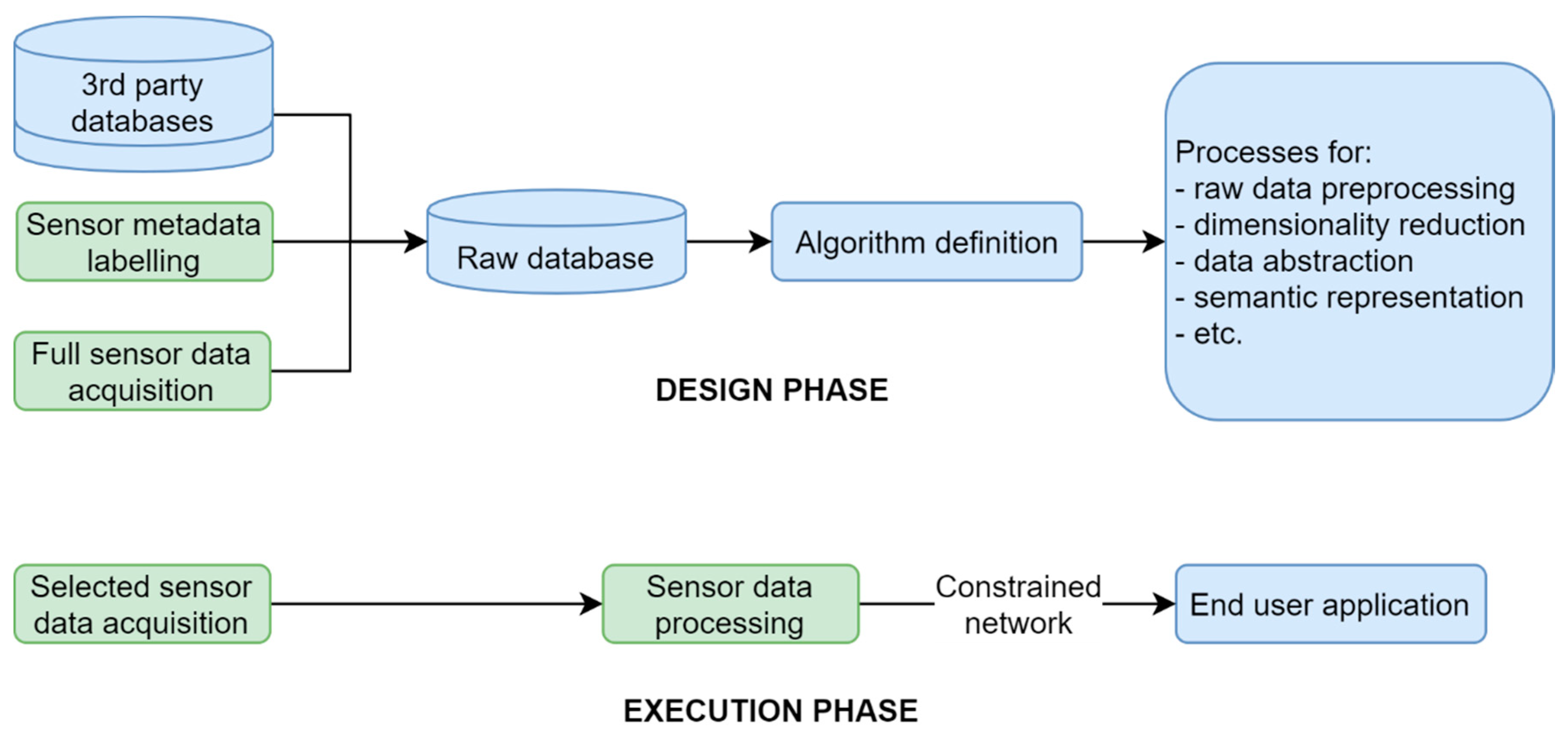
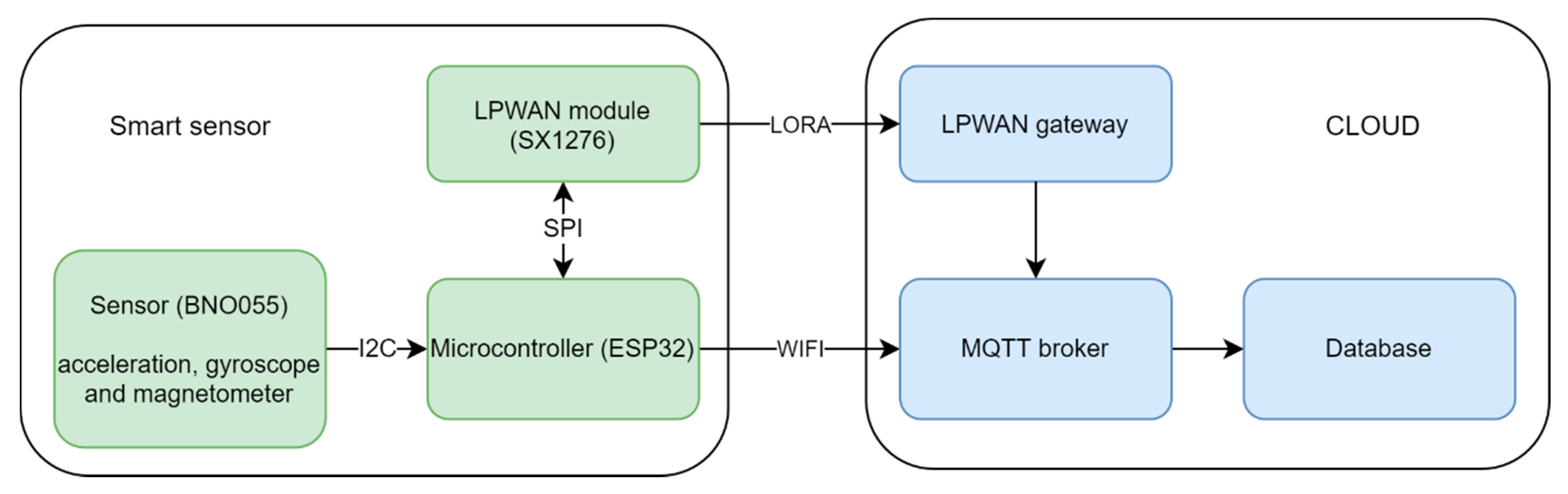
2.1. Data Processing Proposal
2.1.1. Data Pre-Processing
- Raw data subsampling. In order to obtain more input data for training purposes, a subsampling option is included in the sensor sample rate (Tsoriginal) for the database. In this proposal, we considered three sampling frequencies: the original frequency, plus half-frequency subsampling, and quarter-frequency subsampling (Ts), producing two and four new signals, respectively, thus allowing us to increase the data collected.
- Window maker. There are two parameters that are used to define the window size (TW): the sensor sampling frequency (Ts) and the full sample time (Tf). To evaluate their impacts, different combinations have been tested, with the only restriction being that the window size must always be a natural number.
- Statistical data normalisation. Once the TW for the data window (xi) is defined, it is standardized by subtracting its mean and dividing this quantity by its standard deviation, resulting in the standardized data window (xi′) (see Equation (1)). The later data submission will include the mean value, the standard deviation, and the associated VQ index for (xi′). Two additional VQs can be implemented to code the mean and standard deviation values, resulting in a data submission consisting of three fully encrypted indexes. However, for simplicity, in this work, only the standardized data vector is compressed.
2.1.2. Dimensionality Reduction
| Algorithm 1. Adaptative VQ training |
| --- Perform initialization α0 = initial learning factor, αF = final learning factor, T = max training epoch, target_error = max error W = random(N, TW)--- Initial random codebook matrix W with N centroids of size TW Vmag = ones(N)--- Initial local magnitude vector Vmag for N centroids repeat--- training loop Wupdate = zeros(N, TW) --- Init weight-updating matrix Wupdate t = current training epoch repeat --- codebook update loop --- Compute quantification error Qerror for sample x: Qerror[k] = (x − W[k, :])2 for k = 0, …, N – 1 --- Select Best Matching Unit: BMU = argmin(Qerror) --- Exclude BMU from Qerror list and select Next Matching Unit in the new list Qerror’: Qerror’[k] = Qerror[k] for k = 0, …, N − 1 k ≠ BMU NMU = argmin(Qerror’) --- Select Local Best Matching Unit to the product of Qerror and Vmag among BMU and NMU: LBMU = argmin(Vmag[BMU]*Qerror[BMU], Vmag[NMU]*Qerror[NMU]) --- Update weight-updating matrix for LBMU: Wupdate[LBMU, :] += x − W[LBMU, :] until end_of_data --- end of codebook update loop --- Update learning factor α and codebook W: α = α0 + (αF − α0) * sqrt(t/T) W = W + α * Wupdate --- Perform local magnitude update (only if local magnitude is ESCL or FSCL) if magnitude is ESCL or magnitude is FSCL then Vmag = zeros(N) --- Init centroids local magnitude vector repeat --- local magnitude update loop --- Compute sample error: Qerror[k] = (x − W[k, :])2 k = 0, …, N − 1 --- Select Best Matching Unit: BMU = argmin(Qerror) --- Update local magnitude BMU: if magnitude is ESCL then Vmag[BMU] += Qerror[BMU] --- cumulate quantification error else --- magnitude is FSCL Vmag[BMU] += 1 --- cumulate centroid activation frequency end if until end_of_data --- end of local magnitude update loop end if until error < target_error or t > T --- end of training loop |
2.2. Analysis of Method Performances
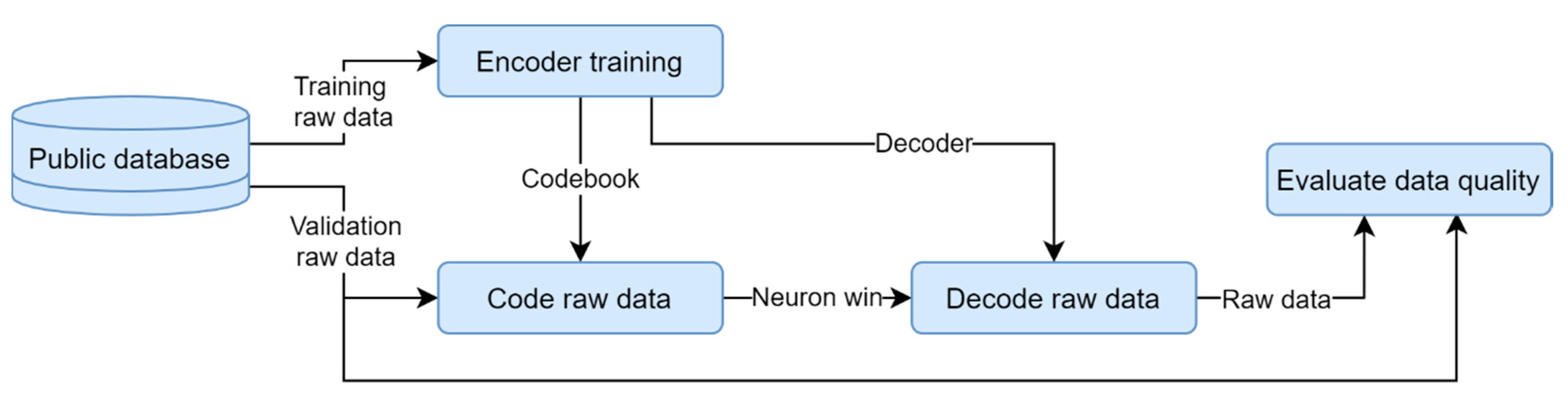
2.2.1. Offline Training and Run Validation
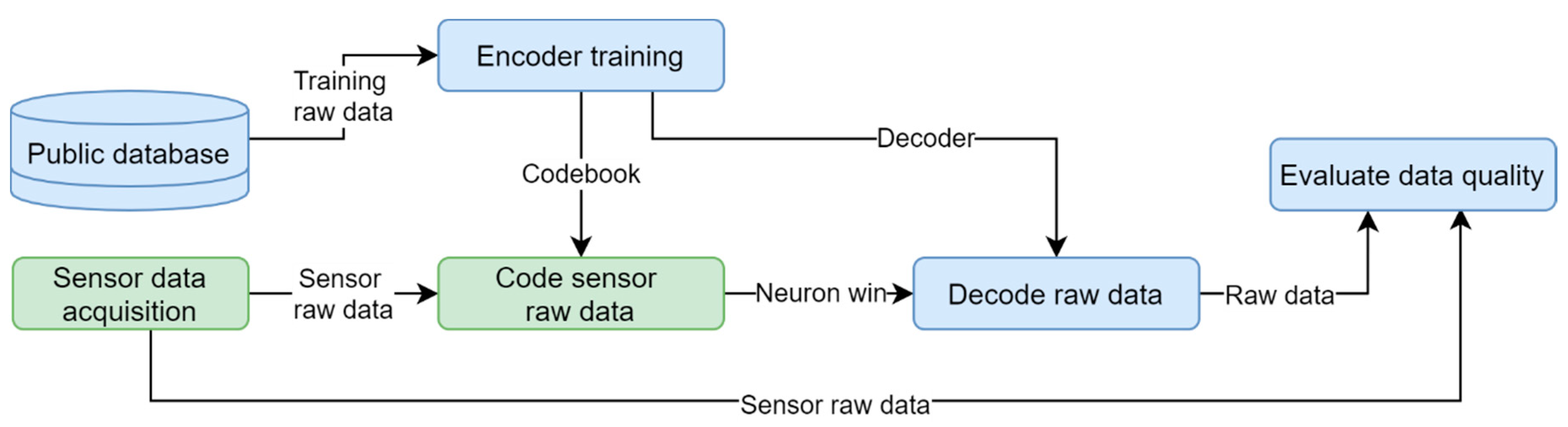
2.2.2. Offline Training and Online Run Validation
3. Results
3.1. Offline Training and Run Validation
3.2. Offline Training and Online Run Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stisen, A.; Blunck, H.; Bhattacharya, S.; Prentow, T.S.; Kjaergaard, M.B.; Dey, A.; Sonne, T.; Jensen, M.M. Smart devices are different: Assessing and mitigatingmobile sensing heterogeneities for activity recognition. In Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems, Seoul, Korea, 1–4 November 2015; ACM: New York, NY, USA, 2015; pp. 127–140. [Google Scholar]
- Banos, O.; Moral-Munoz, J.; Diaz-Reyes, I.; Arroyo-Morales, M.; Damas, M.; Herrera-Viedma, E.; Hong, C.S.; Lee, S.; Pomares, H.; Rojas, I.; et al. mDurance: A Novel Mobile Health System to Support Trunk Endurance Assessment. Sensors 2015, 15, 13159–13183. [Google Scholar] [PubMed]
- Banos, O.; Villalonga, C.; Garcia, R.; Saez, A.; Damas, M.; Holgado, J.A.; Lee, S.; Pomares, H.; Rojas, I. Design, implementation and validation of a novel open framework for agile development of mobile health applications. Biomed. Eng. Online 2015, 14, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Ganz, F.; Puschmann, D.; Barnaghi, P.; Carrez, F. A Practical Evaluation of Information Processing and Abstraction Techniques for the Internet of Things. IEEE Internet Things J. 2015, 2, 340–354. [Google Scholar] [CrossRef]
- Prasertsung, P.; Horanont, T. A classification of accelerometer data to differentiate pedestrian state. In Proceedings of the 2016 International Computer Science and Engineering Conference (ICSEC), Chiang Mai, Thailand, 14–17 December 2016; pp. 1–5. [Google Scholar]
- Noor, M.; Salcic, Z.; Wang, K. Adaptive sliding window segmentation for physical activity recognition using a single tri-axial accelerometer. Pervasive Mob. Comput. 2017, 38, 41–59. [Google Scholar] [CrossRef]
- Banos, O.; Galvez, J.; Damas, M.; Pomares, H.; Rojas, I. Window Size Impact in Human Activity Recognition. Sensors 2014, 14, 6474–6499. [Google Scholar] [CrossRef]
- Krishnan, N.C.; Panchanathan, S. Analysis of low resolution accelerometer data for continuous human activity recognition. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3337–3340. [Google Scholar]
- Marqués, G.; Basterretxea, K. Efficient algorithms for accelerometer-based wearable hand gesture recognition systems. In Proceedings of the 2015 IEEE 13th International Conference on Embedded and Ubiquitous Computing, Porto, Portugal, 21–23 October 2015; pp. 132–139. [Google Scholar]
- Sukor, A.S.A.; Zakaria, A.; Rahim, N.A. Activity recognition using accelerometer sensor and machine learning classifiers. In Proceedings of the 2018 IEEE 14th International Colloquium on Signal Processing & Its Applications (CSPA), Batu Feringghi, Malaysia, 9–10 March 2018; pp. 233–238. [Google Scholar]
- Jahanjoo, A.; Tahan, M.N.; Rashti, M.J. Accurate fall detection using 3-axis accelerometer sensor and MLF algorithm. In Proceedings of the 2017 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA), Shahrekord, Iran, 19–20 April 2017; pp. 90–95. [Google Scholar]
- Sancheti, P.; Shedge, R.; Pulgam, N. Word-IPCA: An improvement in dimension reduction techniques. In Proceedings of the 2018 International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 575–578. [Google Scholar]
- Padmaja, D.L.; Vishnuvardhan, B. Comparative study of feature subset selection methods for dimensionality reduction on scientific data. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 31–34. [Google Scholar]
- Dua, Y.; Kumar, V.; Singh, R. Comprehensive review of hyperspectral image compression algorithms. Opt. Eng. 2020, 59. [Google Scholar] [CrossRef]
- Sustika, R.; Sugiarto, B. Compressive Sensing Algorithm for Data Compression on Weather Monitoring System. TELKOMNIKA Telecommun. Comput. Electron. Control 2016, 14, 974. [Google Scholar] [CrossRef]
- Moon, A.; Kim, J.; Zhang, J.; Son, S.W. Lossy compression on IoT big data by exploiting spatiotemporal correlation. In Proceedings of the 2017 IEEE High. Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 12–14 September 2017; pp. 1–7. [Google Scholar]
- Fragkiadakis, A.; Charalampidis, P.; Tragos, E. Adaptive compressive sensing for energy efficient smart objects in IoT applications. In Proceedings of the 2014 4th International Conference on Wireless Communications, Vehicular Technology, Information Theory and Aerospace & Electronic Systems (VITAE), Aalborg, Denmark, 11–14 May 2014; pp. 1–5. [Google Scholar]
- Deepu, C.; Heng, C.; Lian, Y. A Hybrid Data Compression Scheme for Power Reduction in Wireless Sensors for IoT. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 245–254. [Google Scholar] [CrossRef] [PubMed]
- Azar, J.; Makhoul, A.; Barhamgi, M.; Couturier, R. An energy efficient IoT data compression approach for edge machine learning. Future Gener. Comput. Syst. 2019, 96, 168–175. [Google Scholar] [CrossRef]
- Razzaque, M.; Bleakley, C.; Dobson, S. Compression in wireless sensor networks. ACM Trans. Sens. Netw. 2013, 10, 1–44. [Google Scholar] [CrossRef]
- Stojkoska, B.R.; Nikolovski, Z. Data compression for energy efficient IoT solutions. In Proceedings of the 2017 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; pp. 1–4. [Google Scholar]
- M, L.; Sarvagya, M. MICCS: A Novel Framework for Medical Image Compression Using Compressive Sensing. Int. J. Electr. Comput. Eng. 2018, 8, 2818. [Google Scholar] [CrossRef]
- Ayoobkhan, M.; Chikkannan, E.; Ramakrishnan, K. Lossy image compression based on prediction error and vector quantisation. EURASIP J. Image Video Process. 2017, 2017, 35. [Google Scholar] [CrossRef]
- Choudhury, S.; Bandyopadhyay, S.; Mukhopadhyay, S.; Mukherjee, S. Vector quantization and multi class support vector machines based fingerprint classification. In Proceedings of the 2016 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; Volume 2, pp. 1–4. [Google Scholar]
- Banerjee, A.; Ghosh, J. Frequency-sensitive competitive learning for scalable balanced clustering on high-dimensional hyperspheres. IEEE Trans. Neural Netw. 2004, 15, 702–719. [Google Scholar] [CrossRef] [PubMed]
- Pelayo, E.; Buldain, D.; Orrite, C. Magnitude Sensitive Competitive Learning. Neurocomputing 2013, 112, 4–18. [Google Scholar] [CrossRef]
- Lee, S.M.; Yoon, S.M.; Cho, H. Human activity recognition from accelerometer data using convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Korea, 13–16 February 2017; pp. 131–134. [Google Scholar]
- Altun, K.; Barshan, B. Human activity recognition using inertial/magnetic sensor units. In Human Behavior Understanding; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Casale, P.; Pujol, O.; Radeva, P. Personalization and user verification in wearable systems using biometric walking patterns. Per. Ubiquitous Comput. 2012, 16, 560–580. [Google Scholar] [CrossRef]
- Healy, M.; Newe, T.; Lewis, E. Security for wireless sensor networks: A review. In Proceedings of the 2009 IEEE Sensors Applications Symposium, New Orleans, LA, USA, 17–19 February 2009; pp. 80–85. [Google Scholar]




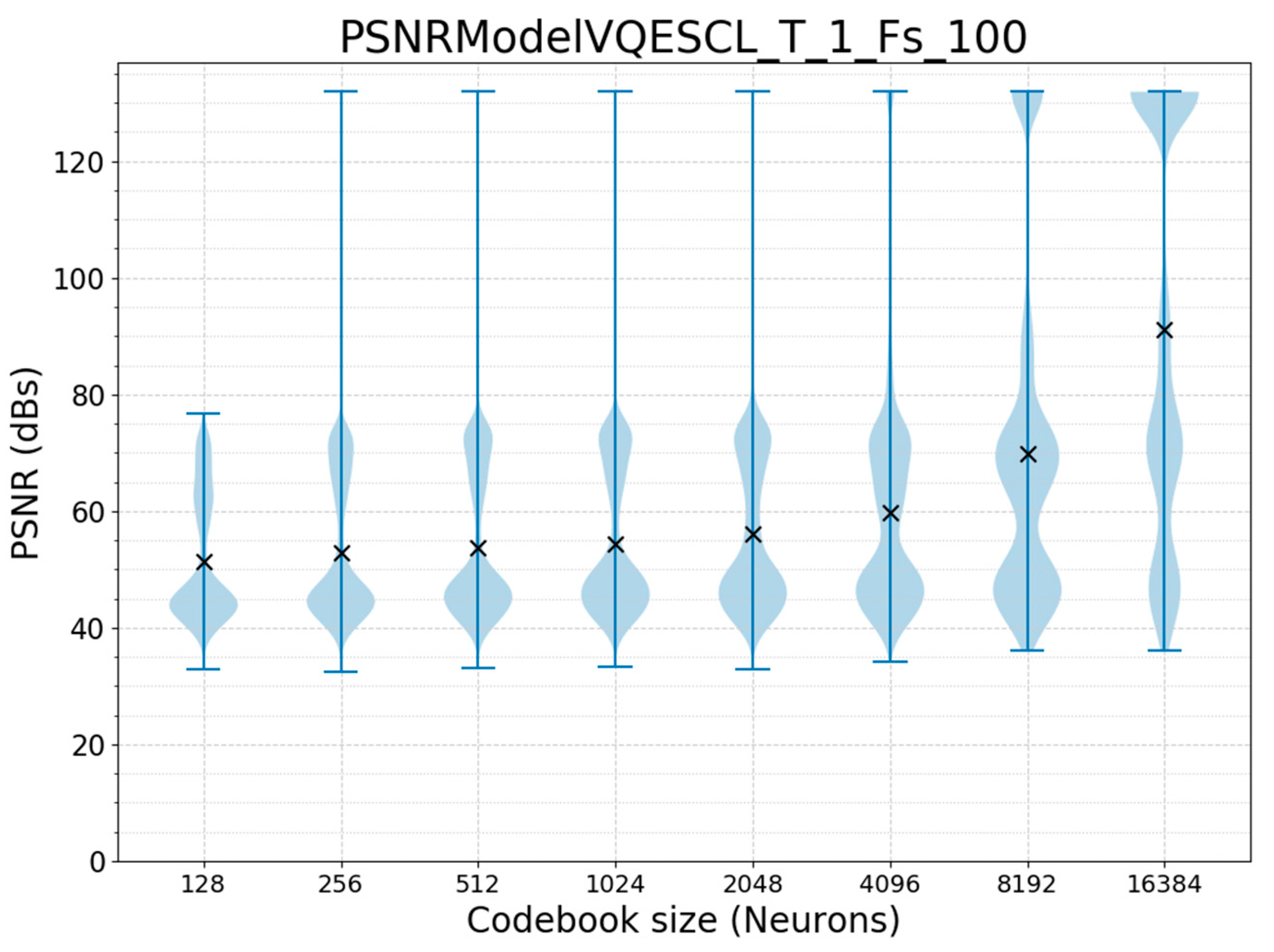


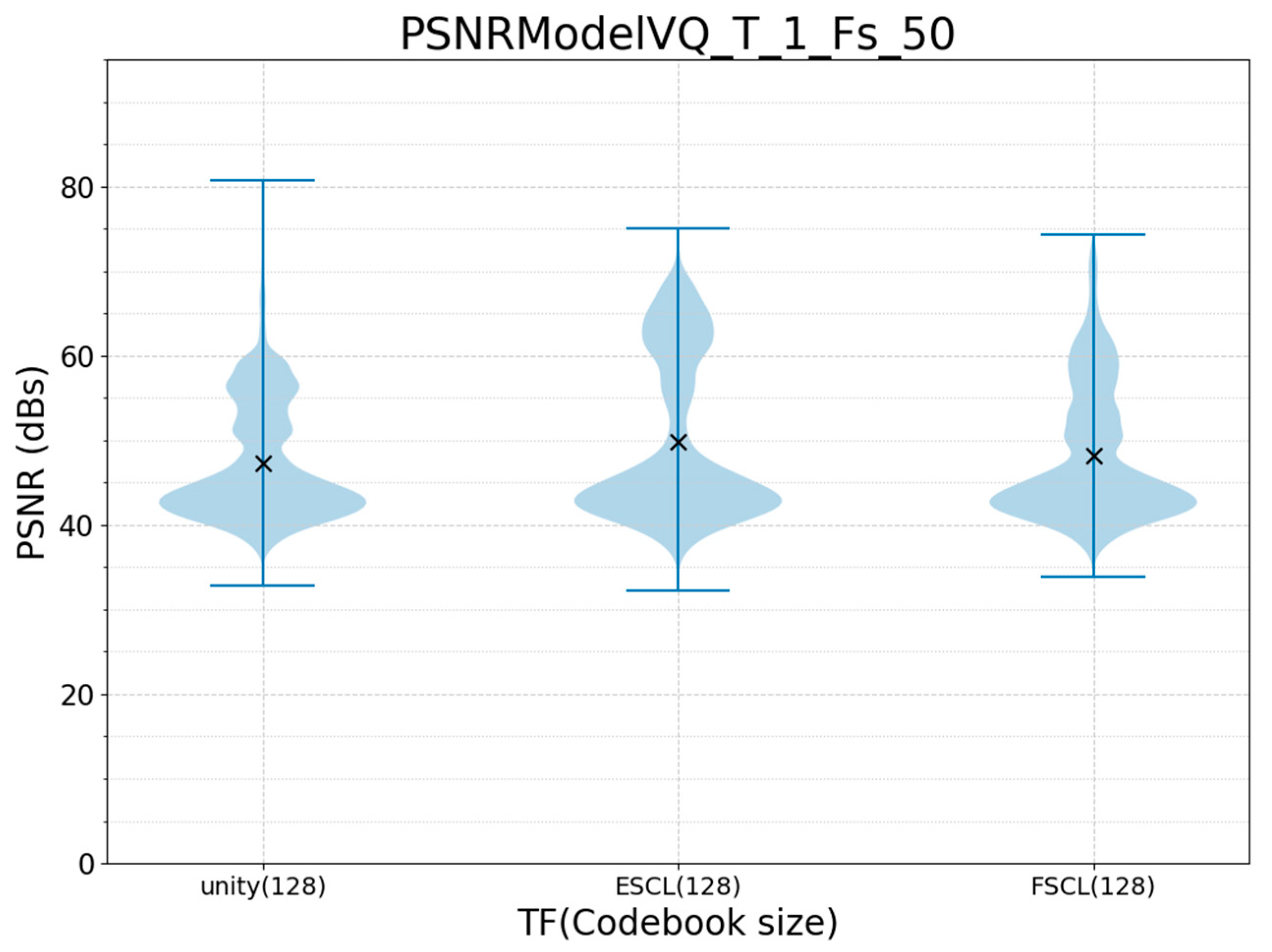
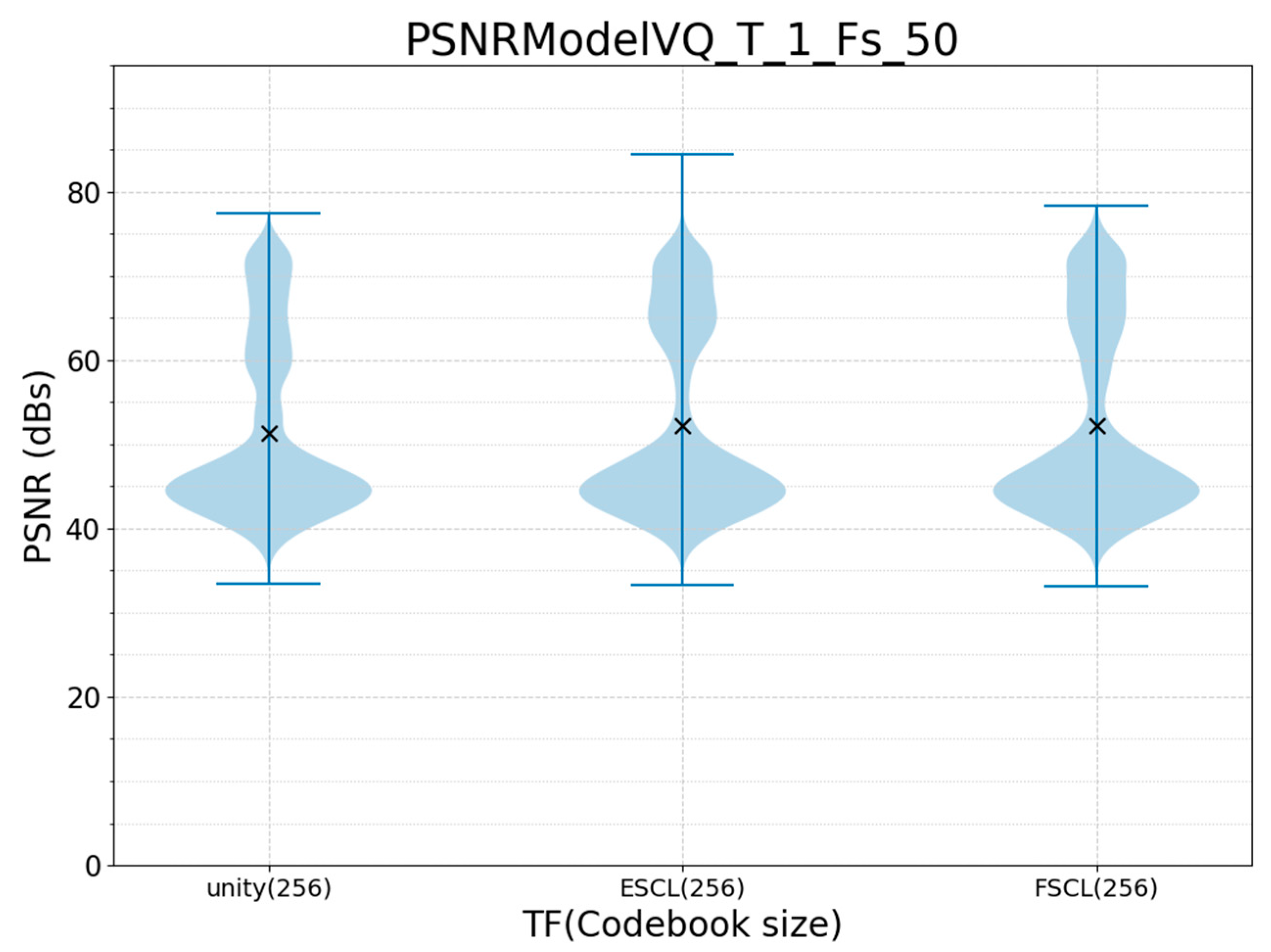

| Configuration | MSE_Train | Compression Rate | LUT-Size (kB) | |||
|---|---|---|---|---|---|---|
| F = 25 Hz | T = 0.6 s | N = 512 | TF = FSCL | 0.0320434 | 45 | 46.08 |
| F = 50 Hz | T = 0.6 s | N = 512 | TF = FSCL | 0.0335083 | 90 | 92.16 |
| F = 100 Hz | T = 0.6 s | N = 512 | TF = FSCL | 0.0351562 | 180 | 184.32 |
| F = 25 Hz | T = 1 s | N = 512 | TF = FSCL | 0.0381469 | 75 | 76.8 |
| F = 50 Hz | T = 1 s | N = 512 | TF = FSCL | 0.0406799 | 150 | 153.6 |
| F = 100 Hz | T = 1 s | N = 512 | TF = FSCL | 0.0426330 | 300 | 307.2 |
| F = 25 Hz | T = 1.6 s | N = 512 | TF = FSCL | 0.0445556 | 120 | 122.88 |
| F = 50 Hz | T = 1.6 s | N = 512 | TF = FSCL | 0.0483703 | 140 | 245.76 |
| F = 100 Hz | T = 1.6 s | N = 512 | TF = FSCL | 0.0509948 | 480 | 491.52 |
| Configuration | MSE_Train | Compression Rate | LUT-Size (kB) | |||
|---|---|---|---|---|---|---|
| F = 100 Hz | T = 1 s | N = 128 | TF = ESCL | 0.049156436 | 600 | 76.8 |
| F = 100 Hz | T = 1 s | N = 256 | TF = ESCL | 0.043934487 | 600 | 153.6 |
| F = 100 Hz | T = 1 s | N = 512 | TF = ESCL | 0.039818928 | 300 | 307.2 |
| F = 100 Hz | T = 1 s | N = 1024 | TF = ESCL | 0.036260296 | 300 | 614.4 |
| F = 100 Hz | T = 1 s | N = 2048 | TF = ESCL | 0.03284163 | 300 | 1228.8 |
| F = 100 Hz | T = 1 s | N = 4096 | TF = ESCL | 0.027240828 | 300 | 2457.6 |
| F = 100 Hz | T = 1 s | N = 8192 | TF = ESCL | 0.019781198 | 300 | 4915.2 |
| Configuration | PSNR_Mean | Compression Rate | LUT-Size (kB) | |||
|---|---|---|---|---|---|---|
| F = 50 Hz | T = 1 s | N = 128 | TF = ESCL | 49.83103058 | 300 | 38.4 |
| F = 50 Hz | T = 1 s | N = 256 | TF = ESCL | 52.18381027 | 300 | 76.8 |
| F = 100 Hz | T = 1 s | N = 128 | TF = ESCL | 51.46948697 | 600 | 76.8 |
| F = 100 Hz | T = 1 s | N = 256 | TF = ESCL | 52.83481729 | 600 | 153.6 |
| Configuration | PSNR_Mean | Compression Rate | LUT-Size (kB) | |||
|---|---|---|---|---|---|---|
| F = 50 Hz | T = 1 s | N = 128 | TF = ESCL | 41.10897725 | 300 | 38.4 |
| F = 100 Hz | T = 1 s | N = 256 | TF = ESCL | 41.7319738 | 300 | 76.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vizárraga, J.; Casas, R.; Marco, Á.; Buldain, J.D. Dimensionality Reduction for Smart IoT Sensors. Electronics 2020, 9, 2035. https://doi.org/10.3390/electronics9122035
Vizárraga J, Casas R, Marco Á, Buldain JD. Dimensionality Reduction for Smart IoT Sensors. Electronics. 2020; 9(12):2035. https://doi.org/10.3390/electronics9122035
Chicago/Turabian StyleVizárraga, Jorge, Roberto Casas, Álvaro Marco, and J. David Buldain. 2020. "Dimensionality Reduction for Smart IoT Sensors" Electronics 9, no. 12: 2035. https://doi.org/10.3390/electronics9122035
APA StyleVizárraga, J., Casas, R., Marco, Á., & Buldain, J. D. (2020). Dimensionality Reduction for Smart IoT Sensors. Electronics, 9(12), 2035. https://doi.org/10.3390/electronics9122035





