Abstract
Security of currently deployed public-key cryptography algorithms is foreseen to be vulnerable against quantum computer attacks. Hence, a community effort exists to develop post-quantum cryptography (PQC) algorithms, most notably the NIST PQC standardization competition. In this work, we have investigated how lattice-based candidate algorithms fare when implemented in hardware. To achieve this, we have assessed 12 lattice-based algorithms in order to identify their basic building blocks. We assume the algorithms will be implemented in an application-specific integrated circuit (ASIC) platform and the targeted technology is 65 nm. To estimate the characteristics of each algorithm, we have assessed the following characteristics: memory requirements, use of multipliers, and use of hashing functions. Furthermore, for these building blocks, we have collected area and power figures for all studied algorithms by making use of commercial memory compilers and standard cells. Our results reveal interesting insights about the relative importance of each building block for the overall cryptosystem, which can be used for guiding ASIC designers when selecting an algorithm or when deciding where to focus optimization efforts such that the final design respects requirements and design constraints.
1. Introduction
Electronic devices are vulnerable to an array of security threats, a problem that is more widespread than ever in the internet-of-things era. The backbone technology ensuring that sensitive data can be transmitted over an unsecured public channel is cryptography. Generally, it has two distinct flavors, i.e., private-key and public-key cryptography. Over the last few decades, public-key cryptography (PKC) has become a fundamental security protocol for all forms of digital communication, both wired and wireless.
For PKC, the security strength of currently deployed algorithms (e.g., RSA and Elliptic Curve Cryptography) is based on the difficulty of solving integer factorization and discrete logarithm problems. However, it has been shown that quantum computers can factorize integers in a polynomial-time—the consequence being that traditional PKC algorithms may become vulnerable [1]. Thus, to keep current communication practices secure, crypto researchers are investigating different cryptographic “hard problems” (e.g., isogeny, lattices, multivariates, etc.) to develop new algorithms that are robust against quantum computers.
Towards assessing different cryptographic methods against quantum attacks, the ongoing NIST post-quantum cryptography (PQC) standardization process serves as a beacon for the security community. Considering several parameters (i.e., security, cost, performance, implementation characteristics, etc.), 43 and 11 algorithms were excluded after first and second rounds, respectively, while the remaining 15 algorithms were kept for the third round [2]. The algorithms that remained in the second round can be categorized into five different cryptographic hard problems: (a) isogeny-based (1 algorithm), (b) lattice-based (12 algorithms), (c) code-based (7 algorithms), (d) multivariate polynomial cryptography (4 algorithms), and (e) hash-based digital signatures (2 algorithms) [2,3]. The security hardness of lattice-based cryptographic algorithms depends on solving the shortest vector problem (SVP), [4]. For complete mathematical formulations and constructions, interested readers can consult [4,5,6]. Several mathematical problems can be used to construct lattice-based schemes. However, the most commonly used mathematical problems are learning with errors (LWE) and learning with rounding (LWR). The LWE scheme is based on finding a vector when given a matrix and a vector , where is a small error vector [5]. On the other hand, the LWR problem is a variant of LWE where one replaces random errors with deterministic rounding [6]. The following algorithms rely on the LWE problem: FrodoKEM [7], NewHope [8], Crystals-KYBER [9], ThreeBears [10], LAC [11], NTRU [12], qTesla [13], and Falcon [14]. The LWR problem, on the other hand, is considered in TRU-Prime [15], Round5 [16], and Saber [17] algorithms. Finally, another popular mathematical problem to construct a lattice-based scheme includes short vectors in lattices, as used in the Crystals-Dilithium [18] algorithm. The aforementioned 12 algorithms were part of the NIST PQC standardization process and are the objects of this study.
Security is the primary evaluation criterion driving the NIST PQC competition and, understandably, the software implementations of the candidates focus on it. However, even before the competition process is finalized, the selected candidate(s) are being considered for hardware acceleration [19,20,21,22,23,24]. The most suitable platforms for acceleration are: (1) field-programmable gate array (FPGAs), (2) ASICs, and hardware/software (HW/SW) co-design. As compared to ASICs, FPGAs and HW/SW co-designs provide flexible solutions due to reconfigurability characteristic and are relatively less expensive. However, they cannot meet the same performance-at-power efficiency of an ASIC. Consequently, ASIC designers will be tasked to improve performance, reduce area footprint, and reduce power consumption of PQC accelerators. Being so, it is imperative that we understand the constraints and characteristics of the algorithms in terms of their building blocks when implemented as ASICs such that we can then judge their feasibility of implementation for resource-constrained application domains.
1.1. Existing Implementations of NIST PQC Algorithms
The algorithms considered in NIST’s standardization process have received a fair share of attention [19,20,21,22,23,24,25,26] and have been implemented in different platforms, including FPGA, ASIC, and HW/SW co-design.
FPGA-based implementations [19,20,21,22]. The authors in [19,20] have leveraged a high-level synthesis (HLS) approach through which they evaluate different design characteristics (i.e., area, clock frequency, and the number of cycles required for the overall computation). The Xilinx Artix-7 FPGA has often been used as a benchmarking platform for FPGA-based implementations. Therefore, in [19], qTesla and Crystals-Dilithium are evaluated on an Artix-7 device for key-pair generation, signature generation, and signature verification. Using distinct optimization techniques, i.e., loop-unrolling and pipelining, area and latency results for different security levels are reported. According to [19], Crystals-Dilithium requires lower hardware resources as compared to qTesla for all key-pair generation, signature generation, and signature verification operations. An implementation and comparison study of a few of the lattice-based algorithms is provided in [20], where a Zynq UltraScale system-on-chip (SoC) platform has been utilized. For each key-encapsulation and -decapsulation operation, the hardware implementation results reveal that the selected NIST PQC algorithms are 396 and 712 times faster than their software-based implementations. Additionally, the implementations reported in [20] differ from [19] as it describes complete cryptosystem designs for various NIST PQC algorithms (instead of only encapsulation). A parameterized implementation of qTesla hash algorithm on Artix-7 FPGA is discussed in [21] where each key-pair generation, signing, and verification of the execution (for the parameter set of security level-1) takes 7.7 ms, 34.4 ms, and 7.8 ms, respectively. In [22], an efficient architecture for NewHope is presented using a low-complexity Number Theoretic Transformation (NTT)/inverse NTT-based modular multiplications. A low-complexity solution is achieved by merging the pre-processing of NTT and the post-processing of INTT into the Fast Fourier Transform (FFT) algorithm, which results in a decrease in N and 2N modular multiplications for N-point NTT and INTT operations, respectively.
ASIC-based implementations [23,24,25,26]. Similar to FPGA-based implementations, RTL is generated through HLS by the authors of [23,24] where they also evaluate different design characteristics. Instead of describing dedicated cryptocores, solutions that make use of an RISC-V microprocessor are described in [25,26]. Still referring to [23], ASIC-specific discussion and results over 65 nm standard cell library are reported for seven lattice-based algorithms (Saber, Crystals-KYBER, NewHope, FrodoKEM, NTRU, Crystals-Dilithium, and qTesla) where loop-unrolling and pipelining techniques have been utilized to optimize design parameters such as area, latency, clock frequency, and power. The key-encapsulation algorithms (Saber, Crystals-KYBER, NewHope, NTRU, and Crystals-Dilithium) targeted in [23] require an area of 4.7, 3.3, 3.2, 1.2, and 4.7 mm. Moreover, the corresponding power values are 54.49 mW, 39.21 mW, 38.02 mW, 14.30 mW, and 51.24 mW. A design-space exploration of key generation, signature generation, and signature verification components of two digital signature algorithms (qTesla and Crystals-Dilithium) is presented in [24] where the authors also make use of a 65 nm standard cell library in their results. The Crystals-Dilithium in [24] operates at a faster clock frequency as compared to qTesla. The power values for Crystals-Dilithium do not increase with the increase in security level, while area does. On the other hand, power values of qTesla implementation increase with the security level, while area does not.
A configurable crypto-processor for post-quantum lattice-based protocols referred to as Sapphire has been presented in [25], where the authors developed a dedicated instruction set, an arithmetic logical unit (ALU), and a control unit that interfaces with data and instruction memories. All the components/units used inside Sapphire are secure against timing and simple power analysis side-channel attacks. Moreover, the Sapphire processor was integrated with an RISC-V microprocessor to demonstrate FrodoKEM, NewHope, qTesla, Crystals-Kyber, and Crystals-Dilithium algorithms. Similarly, an integrated domain-specific vector co-processor for post-quantum cryptography algorithms with RISC-V microprocessor has been presented in [26].
1.2. Limitations in the Existing Implementations of NIST PQC Algorithms
Although there are several implementations where area and power constraints have been evaluated over distinct implementation platforms [19,20,21,22,23,24,25,26], there are various shortcomings in these implementations, listed as follows:
- Unfortunately, several reference works [19,20,21,22,23,24,25,26] attempting to compare PQC algorithms only do it for a small number of algorithms at a time. Our approach stands out because we assess all 12 lattice-based algorithms involved in the NIST PQC standardization.
- In [19,20,23,24], an HLS approach has been used to evaluate area and power constraints while abstracting their essential building blocks and functions (e.g., memory instances, arithmetic operators, logical operators, hash functions, etc.). While HLS allows for a fast architectural evaluation, we opt not to make use of HLS in our study since HLS still is more convenient for FPGA-based implementations where BRAMs can be easily inferred. In ASICs, this method still presents some enormous challenges as the tools have no direct interface to proprietary memory compilers.
- The performance of a crypto-system often depends on the performance of the utilized multiplier. The functional C/C++ routines of multipliers written in reference implementations of the selected NIST PQC algorithms, when submitted to an HLS tool, yield an architecture where the input and output parameters are uint16_t/uint32_t/uint64_t [7,8,9,10,11,12,13,14,15,16,17,18]. Such a solution might not be optimal in terms of latency, even if it brings a decrease in area and power [19,20,23,24]. To fully understand the design space, actual input and output operand sizes of arithmetic operators have to be identified.
1.3. Our Contributions
The key contribution of this work is to provide an experimental study that investigates the building blocks of selected NIST PQC algorithms. The term “building block” refers to the fundamental components that are used inside each lattice-based NIST PQC algorithm and that together make up the composition of the cryptosystem. The additional contributions of this work are given as follows:
- To identify the essential building blocks, we have defined a set of rules (see Section 2) which allows us to fairly assess each reference implementation to (1) estimate the required memory sizes, (2) identify large arithmetic operators (i.e., multipliers), and (3) to identify the utilized hashing functions.
- Area and power values for read-only memory (ROM) and random-access memory (RAM) instances are calculated using specific memory compilers provided by a partner foundry. Naturally, ROMs allow only read operations while RAMs allow both read and write operations. The target technology is 65 nm bulk CMOS with a “low-power” flavor (details are provided in Section 3.1 and Section 4.1).
- Amongst the identified arithmetic operators, we focus on the multipliers as they are often large and a bottleneck for the performance. Therefore, to calculate the actual hardware costs, we have developed Verilog RTL models for the multipliers (Schoolbook, 2-Way Karatsuba, 3-Way Toom-Cook, and 4-Way Toom-Cook) and synthesized several variants of them using a commercial standard cell library (details are provided in Section 3.2 and Section 4.2). Furthermore, we have shown performance trends for the aforementioned multiplier architectures over different input operand lengths ( to ) in terms of power, area, and clock frequency (see Appendix A).
- We have developed code in Verilog RTL for the identified hash functions (total = 10) according to their required input and output lengths (details are given in Section 3.3 and Section 4.3).
- Finally, we put all the building blocks together and compile results for the combined memory/logic footprints of each studied algorithm. The motivation for this effort is not to serve as a benchmarking measure. Instead, we provide this comparison to demonstrate that the block-by-block deconstruction has merit.
Our paper is organized as follows: a research protocol is defined in Section 2 to assess the reference implementations of selected algorithms. The characteristics of each assessed algorithm are described in Section 3, where we identify memory instances, arithmetic operators (and the size of their operands), and hashing functions. Using memory compilers and standard cell libraries, required hardware resources are provided in Section 4. The final evaluation of each studied algorithm, in terms of area and power, is presented in Section 5. Finally, our conclusions are given in Section 6.
2. Principles Definition
We have defined a set of rules to select and evaluate the performance of PQC algorithms. These rules include the inclusion-exclusion principles (Section 2.1), selection of the algorithms for evaluations in this work (Section 2.2), the criterion to estimate memory instances, and finally, the rules for estimating the memory, inputs, and outputs of utilized arithmetic operators (Section 2.3).
2.1. Inclusion-Exclusion Principles
We have defined the following principles for inclusion-exclusion of a particular PQC algorithm:
- Participation in the NIST competition. Include only algorithms that were considered on the NIST competition for standardization.
- Underlying cryptographic primitive. Include only algorithms that are built on the security problems of lattice-based cryptography.
- Security levels. For each studied algorithm, we consider only the parameters that determine the highest security level.
- Purpose of the algorithm. For each particular algorithm, there might be a number of implementations, either for encryption/decryption or key encapsulations/establishments. We opt not to include all these as they serve inherently different purposes. Instead, we consider only the encryption/decryption implementations.
2.2. Selection of Algorithms
Based on the inclusion-exclusion principles defined above, we have selected 12 algorithms for this study, as shown in Figure 1. Note that the selected algorithms have many different security parameters (described in the corresponding reference documents [7,8,9,10,11,12,13,14,15,16,17,18] and in red colored text in Figure 1) for different security levels (SLi). NIST has defined five different security levels (SL1−SL5) for the standardization process: security levels SL1, SL3, and SL5 are equivalent to security levels of AES-128, AES-192, and AES-256 bit key search. The remaining SL2 and SL4 are equivalent to SHA-256/SHA3-256 and SHA-384/SHA3-384 bit collision search.
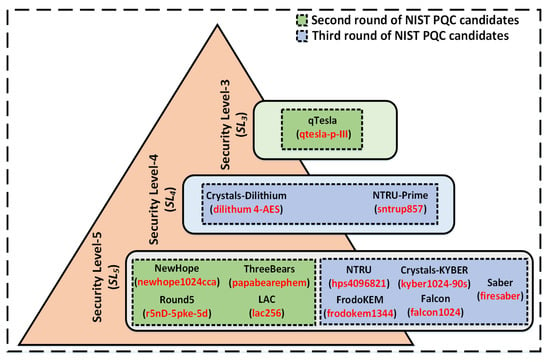
Figure 1.
Selected algorithms and the corresponding implementations utilized in this study.
2.3. Calculation of Memory and Operand Sizes
Memories can easily take most of the area of a chip, so correctly estimating their number, type, and sizes is critical for assessing the size of an ASIC design. Memories bear a large influence on the floorplan of a chip, and therefore it is important to correctly estimate the required memory instances using actual memory compilers. In the studied algorithms, variables to which only read operations are allowed are considered as a candidate for an ROM. Variables that present both read and write operations are considered as RAM candidates. However, not all variables are of interest in this exercise. For instance, variables that serve as flags or for temporary storage would not require an RAM as these would most likely reside in flip-flops or register banks. The same is true for small constants that do not require an ROM.
To estimate the size of each ROM and RAM instance, we assess the total number of memory addresses (p), as well as the number of bits stored at each address (q). Regarding operand sizes for logic/arithmetic, the total number of inputs and outputs are identified based on the parameters passed to a given function of interest, while the size of each operand is identified based on its datatype. In a few cases, we had to resort to contacting the authors for clarification on the operand sizes. Moreover, for the many hashing operations used in the selected PQC algorithms [7,8,9,10,11,12,13,14,15,16,17,18], sizes are already standardized by NIST itself and the effort lies in identifying the correct hashing function employed. Now that we have defined rules to assess the building blocks of PQC algorithms (memory estimations, identification of arithmetic operators and their operand sizes, hashing functions, etc.), we are ready to assess their implementations in ASIC.
3. Assessment of Building Blocks of the Selected NIST PQC Candidates
3.1. Memory Estimations according to the Defined Criteria
Based on the principles defined in Section 2.3, we provide sizes for the ROM and RAM instances in Table 1. The first column lists the name of the studied algorithm and the selected reference model. The other columns determine: (2) required memory instances (n), (3) number of memory addresses per instance (p), (4) number of bits stored at each address (q), (5) size of each memory instance (r = p × q in Kbytes), (6) size of n memory instances (s = n × r in Kbytes), and finally, (7) the total size (Totalsize) is the sum of size for n memory instances, i.e., (Totalsize = ∑ (s) in Kbytes).

Table 1.
Estimated sizes of required random-access memory (RAM) and read-only memory (ROM) memory instances.
Concerning Table 1, we describe where the memory requirements are coming from for each algorithm in the next paragraphs. NTRU-Prime requires RAM to store intermediate and final results of arithmetic (modular addition and subtraction) and logical operations that take place during the algorithm. FrodoKEM requires RAM instances to perform modular addition and subtraction operations over matrices of size M × N. Saber requires different RAM instances to pack and unpack 3 and 4 bits, to implement the transformation function BS2POL() of byte string into polynomial and to implement the transformation functions, i.e., POLVECN2BS() and BS2POLVECN(). All the RAM instances with sizes of 1.642 Kbytes each are required to keep intermediate and final results of the NTRU algorithm. ThreeBears uses RAM instances to hold private and public-keys, to hold capsule and message seed bytes and to keep encapsulation seed bytes and shared secret bytes. Round5 requires RAM instances to store inputs/outputs to/from an AES core [27] and to keep the key for the execution of AES algorithm. The implementation of Crystals-Dilithium requires only 3 RAM instances to keep intermediate results for polynomial addition and subtraction operations. Crystals-KYBER requires RAM instances to keep original and the inverse of original Zeta values for the NTT computations. Furthermore, it utilizes RAM to decompress the polynomials, to perform polynomial arithmetic operations—modular addition and subtraction, to convert polynomial coefficients for modular multiplications from Montgomery to the normal domain and to convert bytes to polynomials.
NewHope requires RAM instances to keep pre-computed constant values for its execution, to re-order the polynomials, and to compute the inverses of powers of nth root of unity and −1 in Montgomery domain in bit reversed order. Further, it utilizes RAM to hold inverses of powers of the nth root of −1 divided by n in Montgomery domain with R = and to compute arithmetic operations (instead of modular multiplications) over polynomial representations. LAC requires RAM instances for numerous operations: secret-key, the public-key, and the cipher texts. qTesla: to keep initial power and log values for the polynomial computations, to hold modulus values required for the reduction of polynomials after multiplication operation, to keep bytes of the generated secret-key, the public-key and the cipher texts. qTesla requires ROM instances to hold initial values for the Gaussian sampler with 32-bit words and 64-bit words, constants for the Zeta computations, and constants for the inverse Zeta computations. It also requires RAM instances to pack the secret-key, encode and decode the public-key and sampled message, and to perform polynomial addition and subtraction operations. Falcon utilizes ROM instances to keep initial values for discrete Gaussian distributions and bit reversal index table, to hold precomputed continuous cumulative distribution function (CoDF) values and precomputed cumulative distribution function (CDF) values for small/large primes. It requires ROM to keep initial values for the computation of NTT and inverse NTT operations for binary, cubic, and ternary polynomials. It also requires RAM instances to generate small prime numbers and initial parameters using the Gaussian distribution function.
As summarized, the requirements for ROM and RAM sizes are relatively small by modern software standards. However, when considering ASIC implementations, these memory sizes are not modest and may render some algorithms severely less attractive than others. To give a better understanding of the magnitude of the memory sizes, we later provide area values in Section 4.1.
3.2. Common Arithmetic Operators and Operand Sizes
According to the rules defined in Section 2.3, the identified common arithmetic operators and the length of input and output operands are shown in Table 2. In the first column, the name of the particular algorithm and its reference model are presented. The second column is further divided into three subcolumns: (1) identified common arithmetic operators, (2) used function name in the provided reference implementations and the name of algorithm/method used for implementations (in parentheses), and finally, (3) the length of required input (OP1, OP2, OP3), and output (OP4) operands, in bits.

Table 2.
Required common arithmetic operators and the length of input and output operands.
The arithmetic additions and subtraction operations, shown in column three of Table 2, are commonly implemented by using the schoolbook method. It is worth mentioning that several algorithms make use of rather large operands (see the fourth column of Table 2). Several different methods are considered, including schoolbook [28], 2-Way Karatsuba [29], 4-Way Toom-Cook [30], NTT [31], and Montgomery [32] methods. Consequently, in the text that follows, we discuss the identified multiplication methods utilized by the candidates of the NIST PQC competition.
Schoolbook method (SBM). The schoolbook method by generating partial products and matrix multiplications is often applied to lattice-based cryptography [28]. In the studied algorithms, it was applied in [7,11,12,15,16]. Multiplications by generating partial products is implemented in NTRU-Prime, LAC, and NTRU algorithms. In both NTRU-Prime and LAC algorithms, a modular reduction mod_q is applied to reduce the resultant polynomial. Matrix multiplication using schoolbook method is considered in FrodoKEM and Round5 algorithms. In the Round5 algorithm, row-wise matrix multiplication method is implemented in ringmul_p() and ringmul_q() functions. FrodoKEM uses 16 bit data types in reference implementations, so a modulo is used for modular reduction (see Section 1.2.3 in reference [7]) while in Round5, modq reduction is implemented (see Section 2.2 in reference [16]).
Karatsuba (KM) [29,33] and Toom-Cook (TCM) [30] multipliers. Both KM and TCM are based on the idea of splitting input operands into n parts, where n determines the length of each split operand. Then, the multiplication of each split part (n) is recursively computed using addition and shift operations. For mathematical formulations, interested readers can turn to [29,30,33]. In [17], the authors exploit 2-Way and 4-Way methods for multiplication with an operand length of 4096 bits. ThreeBears is based on polynomial multiplication and addition, it computes multiplication using a 2-Way KM with an input operand sizes of 3120 bits and generates 3120 bits as an output after modulo-n reduction.
NTT method [34]. NTT is the generalized form of Discrete Fourier Transform (DFT) which exploits the convolution feature to multiply large operands [31]. The NTT method for polynomial multiplications with Montgomery reduction is utilized in NewHope, Crystals-KYBER, qTesla, and Crystals-Dilithium algorithms. The Crystals-KYBER algorithm has 256 coefficients and each coefficient is in the set {0, 1, …, 3328} so, Crystals-KYBER takes 256 × 12 = 3072 bits in length for each operand. The NewHope and qTesla algorithms contain 1024 coefficients and each coefficient is 16 bits in length, so 16,384 (1024 × 16) bits for each operand is required. Similarly, the required operand length of multiplier functions in the Crystals-Dilithium algorithm is 8192 bits.
Montgomery multiplier [32]. The input operands are first converted into the Montgomery domain and then multiplication is performed on Montgomery representation. For complete mathematical formulations regarding the Montgomery algorithm, we redirect the reader to [32]. Falcon algorithm computes polynomial multiplications using the Montgomery multiplication with the operand size of 32 bits and 24,576 bits.
The required computational cost (in terms of clock cycles) of SBM, 2-Way KM, 4-Way TCM, NTT, and Montgomery multiplication methods, when ignoring coordinate/domain conversions, are m-1, (m/2)-1, (m/4)-1, 2m+2log2, and 2m-1, where m is the operand length.
3.3. Hashing Algorithms
Apart from the memories and arithmetic operators, NIST PQC algorithms also make use of known cryptographic primitives. In practice, a hash function may be considered to perform three functions, i.e., (1) convert variable-length keys into a fixed length, (2) scramble the bits of a key so that the resulting values are uniformly distributed over the keyspace, and (3) map key values into ones less than or equal to the size of the message. However, in NIST PQC algorithms, hash functions are frequently utilized for scrambling purposes. As shown in Table 3, the lattice-based PQC algorithms involved in the competition use a combination of both SHA2 and SHA3 functions and two extendable-output hash functions (XOF), named SHAKE-128 and SHAKE-256. The SHAKE-128 and SHAKE-256 functions can be used as customizable SHAKE (cSHAKE-128 and cSHAKE-256) with two additional inputs, i.e., function name bit string (N) and a customization bit string (S).

Table 3.
Hash algorithms utilized in the reference implementations of lattice-based post-quantum cryptography (PQC) algorithms.
NTRU-Prime uses SHA2-512 for hashing a session key but only the first 256 bits of output generated by SHA-512 are used to generate the public-key. For mathematical descriptions, readers are redirected to Sections 3.1 and 4.7 of [15]. FrodoKEM comes in two flavors, either using AES or SHAKE. Naturally, the AES variants (FrodoKEM-640-AES, FrodoKEM-976-AES, and FrodoKEM-1344-AES) are more convenient for devices containing AES hardware acceleration such as AES-NI on Intel platforms, but SHAKE variants (FrodoKEM-640-SHAKE, FrodoKEM-976-SHAKE, and FrodoKEM-1344-SHAKE) provide better performance [7]. Therefore, we have used an instance of AES-128 for matrix generation and an instance of SHAKE-256 for key generation and encryption processes.
SHAKE-128, SHA3-256, and SHA3-512 are utilized for generation of pseudorandom matrix A from a seedA and for public and secret-key pair generations in Saber (see algorithms 15–17 on pages 22 and 23 of [17]). In NTRU, SHA3-256 function with an output length of 256 bits is required for key encapsulation and decapsulation processes (see Section 1.12 on page 19 of [12]). ThreeBears uses cSHAKE-256 for multiple purposes such as to generate uniform and noise samplers, keypair generation, encapsulation and decapsulation (see algorithms 1,5–7 on pages 18–26 of [10]). We have used an instance of the aforementioned cSHAKE function with an output length of 256 bits to evaluate the hardware resources.
Round5 also uses cSHAKE-256 and an instance of AES-256 for hashing purposes. cSHAKE-256 is used in the construction of the permutations while AES-256 is utilized as an alternative to generating random data. Two XOF functions, i.e., SHAKE-128 and SHAKE-256, are required for matrix generation, signature signing, and verification procedures in Crystals-Dilithium. An instance of SHAKE-256 with an output length of 384 bits is used and an instance of SHAKE-128 with an output length of 256 bits is used to generate a public matrix that is needed for both signature signing and its verification (see lines 1 and 2 in Figure 4 of [18]). In the selected variant of Crystals-KYBER (kyber1024-90s), there are four hash functions utilized: an XOF using AES-256 in CTR mode, an H function using SHA2-256, a G function using SHA2-512, a PRF(s, b) function using AES-256 where s is used as the key and b is zero-padded to a 12-byte nonce, and finally a KDF function that utilizes SHAKE-256 (see Section 1.4 on page 11 of [9]). We have used an instance of SHAKE-256 for our evaluations with an output length of 256 bits.
NewHope uses SHAKE-128 and SHAKE-256 functions, SHAKE-128 generates the public parameters and SHAKE-256 (512, 768, and 1024 bits) has been used to hash and extend the output of the random number generator in key generation, encapsulation, and decapsulation functions (see algorithms 1, 4, 17–21 in reference [8]). Therefore, we have used an instance each of SHAKE-128 and SHAKE-256 for output lengths 1600 (200 bytes × 8) and 1024 bits, respectively. In the selected qtesla-p-III variant, SHAKE-256, cSHAKE-128, and cSHAKE-256, all with identical output lengths of 256 bits have been used. SHAKE-256 is used for seed generation and for hash functions G, H. A cSHAKE-256 function is used to sample polynomial y using GaussSampler and ySampler functions. cSHAKE-128 is used for generation of public polynomials using function GenA and for encoding purposes using function Enc (see algorithm 9–14 in reference [13]). SHAKE-256 is utilized in Falcon, where it takes an arbitrary length string as an input and produces 16 bits of hashed chunks as an output (see algorithm 3 at top of page 32 in reference [14]). However, for efficient utilization of SHAKE-256, instead of 16, 64 bits can be extracted as an output [14].
4. Implementing Building Blocks in ASIC
In this section, we provide actual implementation characteristics of the identified building blocks. We make use of commercial memory compilers and a standard cell library, both designed for the same 65 nm “low-power” technology. For the sake of comparison, while not revealing foundry privileged information, we clarify that the nominal supply voltage is 1.2 V for both memories and logic. Without loss of generality, our analysis is performed only for the typical-typical corner (TT), i.e., P = 1, V = 1.2 V, and T = 25 C.
In Section 4.1, we present our ROM and RAM data. In Section 4.2, we provide the implementation results for selected SBM multiplier. Hashing functions and their implementation are given in Section 4.3. Some caveats of our approach are carefully discussed later in Section 5.
4.1. Memory Characteristics
Area, max frequency, and power characteristics of each memory instance required by the many different algorithms are obtained from commercial memory compilers. The compilers output several files, including datasheets, LEF abstracts, LIB timing information, and GDSII layouts. The information presented in this section was extracted from over 50+ datasheets.
Knowing the number of addresses and the size of each address is, unfortunately, not enough to estimate the characteristics of each memory instance. The most significant limitation comes from the choice of a column-mux ratio, which not only determines the aspect ratio of the actual memory, but also determines the bounds for address and data ranges. Thus, the valid range for p (number of addresses) and q (bits stored at each address) depends on the column-mux ratio. Without loss of generality, we have selected 8 as a column-mux ratio for calculations of both ROM and RAM memory instances. The ROM and RAM memory compilers used in this work are very similar, except that we have to define the data content for the ROMs. To this end, we have prepared a MATLAB script to make sure that the ROMs are initialized with a representative ratio of zeros and ones, otherwise the power estimation would be skewed.
The values collected from the generated compiled memories are shown in Table 4. The first column in Table 4 lists the related algorithm while the second column presents numerical values for p (memory addresses) and q (number of bits at each address) that were provided as inputs to the memory compiler. Due to certain limitations in the tool, as discussed earlier, the present form of values of p and q (shown in the second column of Table 4) could not be used directly as an input to the commercial memory compiler. Therefore, we have rounded off the values of p and q to make it possible to use it as input to the memory compiler. The sizes of the ROM and RAM instances, given by W (width of the memory cell) and H (height of the memory cell), are shown in column three of Table 4. For n number of required memory instances, the total area is calculated using the product of width of the memory cell, the height of the memory cell and the number of required memory instances (n), as shown in column four of Table 4. Power consumption values, both static (in μW) and dynamic (μW × F), are provided in column five of Table 4. In the same way, columns from eight to fifteen provide the same data for ROM calculations. All generated memories are single port and perform one operation per clock cycle.

Table 4.
Characteristics of RAMs and ROMs generated using commercial memory compiler.
4.2. Implementation of Identified Multipliers
It is important to emphasize that there are many options available to implement the multiplication operations required by the studied algorithms. For this reason, we have shown implementation results for operand size of up to 4096 bits for 2-Way KM, 3-Way TCM, and 4-Way TCM multipliers, which are comparable with state-of-the-art implementations [34,35,36]. These results are shown in Appendix A, the outcome of this discussion is that the SBM is advantageous as it leads to a low area, reasonable frequency of operation, and, most importantly, the lowest power consumption of the compared architectures. This characteristic, even if it comes at a cost in latency, led us to select the SBM as the multiplier of choice for implementing all multipliers.
In order to provide a fair comparison in terms of clock frequency, we make use of 500 MHz as our frequency of choice in the experiments that follow (Synthesis is performed with high area and high power effort on 65 nm technology). The SBM multiplier takes two inputs OP1 and OP2 and results in a product with size bits. Therefore, it is essential to perform a reduction to achieve a product length that matches the input length. One approach to perform reduction is to perform bitwise XOR operation over first m bits of s with cyclic shifts to left on the remaining n bits of s and repeated until all n bits of s are processed. Thus, a unified architecture for reduction and multiplication takes 2(m-1) cycles to compute. Our results for the implemented multipliers are shown in Table 5, where the first column shows the name of the particular algorithm and the length of input operands in parentheses (i.e., OP1× OP2). The number of combinational cells, sequential cells, reported area (in mm), dynamic power (in W), and leakage power values are provided in the next 5 columns, respectively. As shown in column three of Table 5, the number of flip flops for the SBM multiplier is roughly 2 times the length of input operands. A handful of additional flops are required for controlling the shift and add operation and for setting its termination condition.

Table 5.
Implementation results for SBM multiplier using a 65 nm standard cell library. Target frequency is 500 MHz.
4.3. Implementation of Identified Hash Algorithms
The lattice-based NIST PQC candidates use different hash functions with different input and output lengths. This section deals with the implementation of identified hash functions. Therefore, we have developed our own RTL cores in Verilog for the identified hash and XOF functions, which include SHA2-256, SHA2-512, SHA3-256, SHA3-512, SHAKE-128, SHAKE-256, cSHAKE-128, and cSHAKE-256. In one clock cycle, each developed core takes 64 bits of a message as an input and results in the desired hash value as an output (as described in Section 3.3).
However, the sum of clock cycles for Mlength/64 and the number of rounds determine the total clock cycles required to generate a hash value over a message of arbitrary length. For each hash and XOF function, the behavioral simulations of each developed core are verified by providing an empty “ ” message string as an input and the resultant hash value achieved in 256 and 512 bits in length is compared with the corresponding hash values (test vectors for verification’s—provided by the NIST—available at [37]). We have selected an open-source AES core (for 128 and 256 bits) from references [27,38], respectively. The implementation results over 500 MHz are provided in Table 6. The name of the NIST PQC candidate, combinational cells and sequential cells are provided in the first, second, and third columns of Table 6, respectively. Required area (in ) is shown in column three, while columns four and five provide values for dynamic (in ) and leakage power (in ), respectively.

Table 6.
Implementation of identified hash algorithms using 65 nm standard cell library. Target frequency is 500 MHz.
5. Evaluation of NIST PQC Algorithms as Hardware Accelerators
In this section, we treat the algorithms as “accelerators” completely described as specialized hardware—there are no processor/software components. Therefore, for each accelerator, we provide the aggregated results that take into account all the identified building blocks. We emphasize that complete implementations of NIST lattice-based PQC algorithms are not described in this work for the reason that we have not accounted for the “glue logic” that gives meaning to each algorithm—instead, we focus on the individual building blocks. Our aim when showing the combined contribution of the individual blocks was to allow a degree of comparison with other works. Unfortunately, it is not trivial to perform a block by block comparison, so we must compare accelerators to accelerators, even if technically we do not build full-fledged accelerators ourselves.
Area and power figures for each accelerator are calculated by using Equations (1) and (2), respectively, in which we sum the contributions of each building block (NTRU-Prime and Falcon employ more than one multiplier. We sum the contributions of both multipliers for each algorithm. For NTRU-Prime in particular, this might not be the optimal design choice since both multipliers take at least one input of 6088 bits, meaning that resources can be easily shared.).
The aggregate results for area and power are presented in Figure 2 and Figure 3, respectively. Results are presented in ascending order. As we described earlier in this work, having large multipliers is a common requirement for several of the NIST PQC candidates. There are many multiplier architectures that can be used, including solutions that rely on digitized computation [36,39]. These multipliers should be adapted to the characteristics of each algorithm and to the application requirements. The information provided in Figure 2 and Figure 3 is very useful in that regard, while also identifying which building block is the best candidate for being replaced, optimized, or even offloaded elsewhere. Regarding area, our analysis reveals that FrodoKEM is too far above a reasonable size and would be a perfect candidate for a digitized multiplier architecture. We opt not to show FrodoKEM in these charts.
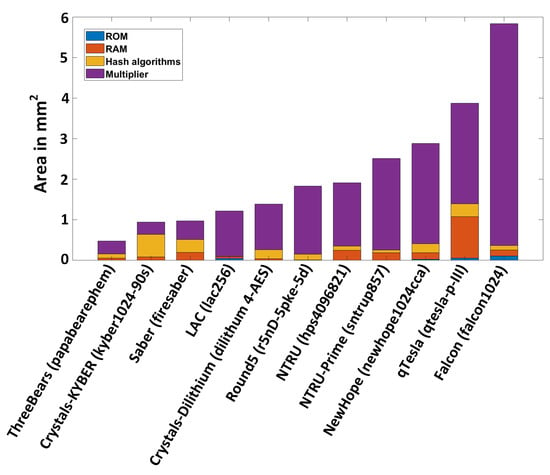
Figure 2.
Total area of the studied NIST lattice-based PQC algorithms, ordered.
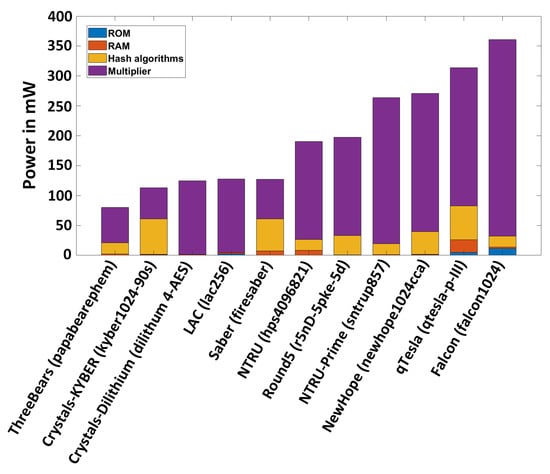
Figure 3.
Total power consumption of the studied NIST lattice-based PQC algorithms, ordered.
As shown in Figure 3, the highest power consumption comes from the Falcon algorithm while qTesla is the second-highest power hungry algorithm. Often, multipliers contribute significantly to the total power consumption of an algorithm, but the power profile of Crystals-KYBER is completely different as it consumes 112.77 mW of power. Here, the hash core is responsible for approximately 53% of the power consumption (59.01 mW out of 112.77 mW). The contribution of memories to the accelerator area is more pronounced, even if the total area is still strongly dominated by the multiplier area. Regarding the frequency of operation, the bottleneck in all of our experiments is always the multiplier.
5.1. Comparison to State-of-the-Art Implementations
After providing descriptions and evaluations of critical building blocks of NIST lattice-based PQC candidates in Section 3 and Section 4, now we have to frame these results with respect to state-of-the-art implementations of lattice-based algorithms in hardware.
As described in Section 1.2, the available literature on NIST lattice-based PQC candidates considers FPGA and ASIC implementation platforms [19,20,21,22,23,24,25,26,40,41], where different technologies (i.e., 65 nm, 40 nm, and 28 nm) have been used to evaluate area and power profiles. Moreover, the results reported in [23,24] use the same 65 nm node as we do in our experiments. The authors have provided results for Crystals-Kyber, NewHope, FrodoKEM, NTRU, Saber, Crystals-Dilithium, and qTesla. Except for FrodoKEM, we provide comparisons to these accelerators in Table 7.

Table 7.
Implementation details of NIST lattice-based PQC candidates on 65 nm application-specific integrated circuit (ASIC) technology.
It is noteworthy that the implementation of NTRU in [23] requires 32% more area than our estimation, while for remaining candidates our estimated area values are much lower than the implementations described in [23,24]. This can be attributed mostly to the fact that we focus on building blocks and disregard the ‘glue logic’ between them.
As shown in the last column of Table 7, the power values achieved in this work are much higher than the counterparts reported in [23,24]. There are various reasons for such, including our use of multiple hashing cores per algorithm. It is also worth mentioning that HLS was utilized for generating RTL code in [23,24], which implies the C/C++ routines written for multipliers are operated in a loop fashion where the input and output parameters are uint16_t/uint32_t/uint64_t. Such a solution is no different than a digitized/segmented multiplier, which should decrease area and power at the cost of execution time/latency. Thus, we have also provided area and power values for a segmented SBM multiplier with a segment size of only 8 digits for qTesla (16,384 × 16,384). The reduced area and power values relative to the segmented version of the SBM multiplier are shown at the bottom of Table 7. The power requirements can further be reduced by increasing the number of digits/segments in the multiplier. Finally, the power requirements for the other remaining algorithms can also be reduced by utilizing segmented multipliers in their datapaths as we did for qTesla in this work. A thorough exploration of the segmentation/digitizing design space is beyond the scope of our work and is left for the ASIC designer to perform.
The use of higher security levels in our work is also a (small) factor that results in higher hardware resources and power consumption, as shown in column three of Table 7. Therefore, we achieved lesser hardware resources at the expense of higher power consumption as compared to state-of-the-art implementations. Regarding power, we show comparison values at the bottom of Table 7 for which we have matched the frequency of operation. Otherwise, our accelerators tend to consume much more power than their counterparts, which is explained by our much higher frequency of operation and the additional buffering required to attain this frequency. There is always a trade-off between clock frequency (performance) and area/power. In this paper, we opted to target a really challenging clock frequency with the assumption that performance is paramount.
5.2. Limitations of this Work
Despite the fact that this paper has assessed the building blocks of NIST PQC candidates based on the strict rules defined in Section 2.1, there are still certain limitations and caveats:
- Table 2 lists many of the identified arithmetic operators, but our analysis focuses on multiplication as we consider it to be more challenging than other operations. This is not enough to generate a functional crypto accelerator, but it ought to be enough to capture the characteristics of it. There are various other operators, including transformations from one domain to another, that are required for a complete implementation of a lattice-based crypto accelerator.
- For each particular algorithm, there is a number of reference models that target different security levels. For each studied algorithm, we consider only the reference model with the highest security level. This approach might be overkill for several applications that would otherwise be satisfied with an AES-128 equivalent level of security.
- Results for area and power are collected after logic synthesis. However, an accelerator still has to go through physical synthesis, where many additional cells are added and routing resources have to be accounted for.
- We make assumptions based on reference implementations that were submitted to NIST for standardization. As the name implies, these are reference implementations and may not be optimized for the sake of readability.
6. Conclusions
In this paper, we have evaluated how lattice-based algorithms participating in the NIST PQC standardization process would perform as ASIC hardware accelerators. To achieve this, we have studied the C/C++ codes of reference implementations to extract the relevant information on this study which we refer to as building blocks. Based on the extracted memory characteristics, we have compiled ROMs and RAMs for 12 lattice-based PQC algorithms. Thereafter, we have developed various RTL cores in Verilog for different multipliers (e.g., Schoolbook, 2-Way KM, 3-Way Toom-Cook, and 4-Way Toom-Cook) architectures. The area and power profiles are compiled for different input operands lengths, i.e., (2–2). We selected the SBM multiplier architecture to obtain area and power values for the multiplier required by the various NIST PQC algorithms. We ran dozens of synthesis for selected SBM multiplier over required operand sizes, reported the corresponding area and power values for the targeted frequency of 500 MHz. We have equally developed several RTL cores in Verilog for the required hash algorithms to report area and power figures.
From the onset, our goal was to provide ASIC designers with information that can guide their future implementations of lattice-based crypto cores. For this matter, the results provided in Section 4 give designers an insight into the wide design space and should allow designers to quickly identify where to focus their optimization efforts when conceiving a PQC cryptosystem.
Author Contributions
Conceptualization, M.I. and Z.U.A.; data extraction, M.I. and Z.U.A.; results compilation, M.I. and Z.U.A.; validation, M.I., Z.U.A.; writing—original draft preparation, M.I.; critical review, S.P.; draft optimization, M.I. and Z.U.A.; supervision, S.P.; funding acquisition, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the EC through the European Social Fund in the context of the project “ICT programme”.
Acknowledgments
We would like to acknowledge the technical support of few authors of NIST PQC candidates to clarify different parts of their algorithms.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the data collection, analyses, extraction of data, in writing the manuscript, and in the decision to publish the results.
Appendix A. Area, Power, and Frequency Trends for Different Multipliers
To provide representative trends, we have developed codes in Verilog for several of the multipliers employed by the reference implementations (see Section 3.2). Next, we performed a logic synthesis of the multipliers using a range of operand sizes. The tool utilized for this experiment is Cadence Genus. The standard cell library is a commercial one and the process node is 65 nm.
Appendix A.1. SBM, 2-Way KM, 3-Way, and 4-Way TCM Multipliers
We have developed our own codes in RTL form for SBM, 2-Way KM, 3-Way TCM, and 4-Way TCM multipliers, which all take two input operands and produce one single output. The inputs are identical in size and are given in the form , where n is an integer value in the range 1 to 12. In these multipliers, the output is considered without any reduction operation (i.e., the output is 2 bits in length). To evaluate the performance of SBM, 2-Way KM, 3-Way TCM and 4-Way TCM multipliers, we show trends with respect to input operand sizes in Figure A1, Figure A2 and Figure A3.
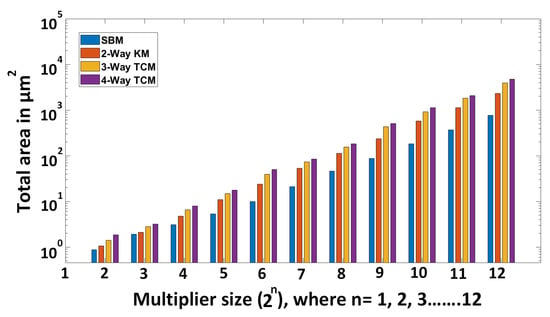
Figure A1.
Required area (in m) for different multipliers and sizes.
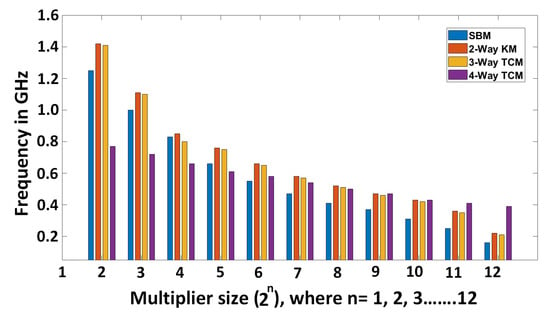
Figure A2.
Achieved clock frequency (in GHz) for different multipliers and sizes.
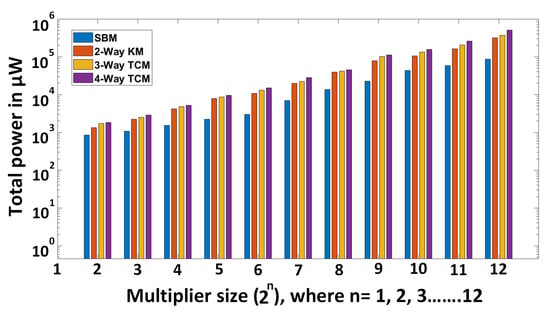
Figure A3.
Total power consumption (in W) for different multipliers and sizes.
As shown in Figure A1, the SBM multiplier utilizes lower hardware resources in terms of area as compared to its counterparts. The 2-Way KM multiplier requires a lower hardware resources than 3-Way and 4-Way TCM multipliers, as expected. When comparing 3-Way TCM to 4-Way TCM multipliers, the former utilizes a lower hardware area than the latter. Still, regarding area increase trends, it can be seen that the SBM, 2-Way KM, 3-Way TCM, and 4-Way TCM multipliers show an exponential increase in size with the operand size. This is a strong argument in favor of digitized computation.
For different multipliers with diverse operand lengths, the maximum achieved clock frequency is shown in Figure A2. These values were obtained by performing synthesis runs repeatedly until the performance could no longer be improved (i.e., the constraints were pushed iteratively until they were no longer met). Based on the implementation results, it becomes clear that the 2-Way KM multiplier could be used as an efficient replacement for the 3-Way TCM multiplier as it achieves comparable clock frequency while utilizing less area. For large input sizes, all multipliers outperform SBM since they benefit from breaking down the problem in chunks. Conversely, the 4-Way TCM presents the highest frequency in the comparison shown in Figure A2.
Regarding power consumption, as shown in Figure A3, the SBM multiplier outperforms all other multipliers—this is an important characteristic that influenced our choice of SBM as the multiplier for the PQC algorithms studied in this paper. When considering the power consumption of 2-Way KM, 3-Way TCM, and 4-Way TCM multipliers, 4-Way TCM consumes more power than 2-Way KM and 3-Way TCM multipliers. There is an increase in power consumption as the length of inputs to the multipliers are increased, as well as an increase with the number of ’ways’ each multiplier uses.
Appendix A.2. NTT Multiplier
For the analysis of NTT multipliers, we have adapted the pipeline architecture described in [35]. Contrary to the previously discussed multipliers, here it makes little sense to decouple the pipelining from the core idea of the algorithm. In fact, it would be fair to refer to [35] as a multiplier architecture instead of a simple multiplier implementation. For this reason, our NTT multiplier analysis is presented separately. We emphasize that it is a complex architecture, for which the authors carefully selected many parameters (e.g., polynomial-size, residual size, number of parallel units, reduction tables, etc.) when targeting an FPGA platform.
After our analysis, and in line with the results of [35], we have found the critical path of the NTT multiplier to be dependent on a 30-bit integer multiplier and the reduction operation that follows it (i.e., the operation that brings the 60-bit result back to 30 bits). We have considered multiple pipeline depths (1, 2, 3, and 4) and multiple operand sizes for its integer multiplier (20, 25, 35, and 40) in our analysis [34]. In Figure A4, we show how the critical path changes depending on the pipeline depth of the integer multiplier as well as the width of operands. From our results, it appears that the clock frequency saturates when 3 stages are used for pipelining, whereas in [35] the implementation makes use of 4 stages. We believe this difference comes from the FPGA DSP unit that implements the integer multiplier in [35]. In our analysis, this unit has been replaced by a ChipWare component. For the sake of providing a basis for comparison to other multipliers, we have evaluated the area required for the 30-bit/4-stage version of the NTT code, which comes to be 209,740 m (approximately 52 k cells). However, this result includes many black boxes for the memory hierarchy that is required to implement this NTT architecture. These values should not be directly compared to other multipliers since they are known to be underestimated.
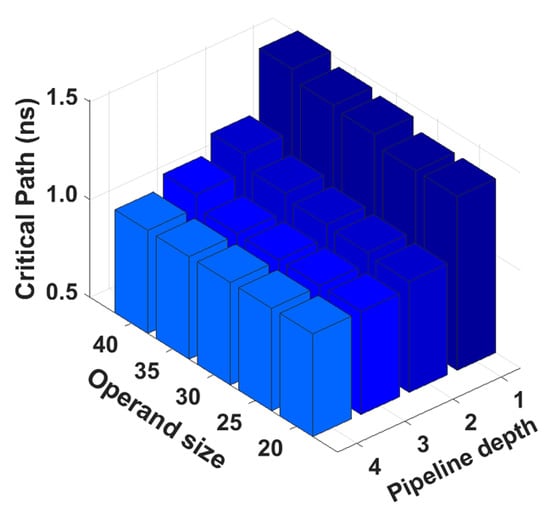
Figure A4.
Analysis of NTT multiplier (obtained from [35] and slightly modified for ASIC).
Appendix A.3. Summary of the Multipliers Trend
Due to bit serial structure, the implemented SBM multiplier requires m-1 clock cycles for m bit operands length. The implemented 2-Way KM, 3-Way TCM, and 4-Way TCM multiplier require m/2-1, m/3-1, and m/4-1 clock cycles. This reduction comes with a cost in resources, naturally. Implementation of NTT multiplier requires 2m+2log2 clock cycles, where n determines the number of NTT points.
The performance of the evaluated multipliers could be improved significantly by using different optimization techniques, most notably pipelining and digitizing. However, in these plots (Figure A1, Figure A2 and Figure A3) we have not provided optimized results either for pipelining or digitizing, as we are interested in showing trends that capture the core idea of each algorithm.
Consequently, there is always a trade-off when selecting an appropriate multiplier and evaluating its area, frequency, and power characteristics. In this work, the SBM multiplier was deemed more appropriate due, its flexibility, its lower area footprint, and its lower power consumption (with respect to the other multipliers we considered).
Finally, regarding NTT-based multipliers, while it appears tremendously advantageous, generating a single NTT multiplier architecture that would be a good fit for all NIST candidates is not feasible. The parameter space requires careful algorithm-specific exploration.
References
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 1999, 26, 1484–1509. [Google Scholar] [CrossRef]
- Moody, D.; Alagic, G.; Apon, D.C.; Cooper, D.A.; Dang, Q.H.; Kelsey, J.M.; Liu, Y.K.; Miller, C.A.; Peralta, R.C.; Perlner, R.A.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process; NIST Interagency/Internal Report (NISTIR)—8309; NIST Interagency: Gaithersburg, MD, USA, 2020.
- NIST. Post-Quantum Cryptography, Round 2 Submissions. 2020. Available online: https://csrc.nist.gov/projects/post-quantum-cryptography/round-2-submissions (accessed on 20 April 2020).
- Chuang, Y.; Fan, C.; Tseng, Y. An Efficient Algorithm for the Shortest Vector Problem. IEEE Access 2018, 6, 61478–61487. [Google Scholar] [CrossRef]
- Khalid, A.; Oder, T.; Valencia, F.; O’ Neill, M.; Güneysu, T.; Regazzoni, F. Physical Protection of Lattice-Based Cryptography: Challenges and Solutions. In Proceedings of the 2018 on Great Lakes Symposium on VLSI; GLSVLSI ’18; Association for Computing Machinery: New York, NY, USA, 2018; pp. 365–370. [Google Scholar] [CrossRef]
- Alwen, J.; Krenn, S.; Pietrzak, K.; Wichs, D. Learning with Rounding, Revisited. In Advances in Cryptology—CRYPTO 2013; Canetti, R., Garay, J.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 57–74. [Google Scholar]
- Alkim, E.; Bos, J.W.; Ducas, L.; Longa, P.; Mironov, I.; Naehrig, M.; Nikolaenko, V.; Peikert, C.; Raghunathan, A.; Stebila, D.; et al. FrodoKEM Learning with Errors Key Encapsulation Algorithm. 2020. Available online: https://frodokem.org/files/FrodoKEM-specification-20200930.pdf (accessed on 18 April 2020).
- Alkim, E.; Avanzi, R.; Bos, J.; Ducas, L.; de la Piedra, A.; Pöppelmann, T.; Schwabe, P.; Stebila, D.; Albrecht, M.R.; Orsini, E.; et al. NewHope. 2020. Available online: https://newhopecrypto.org (accessed on 12 May 2020).
- Avanzi, R.; Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehle, D. CRYSTALS-KYBER. 2020. Available online: https://pq-crystals.org (accessed on 11 April 2020).
- Hamburg, M. Post-Quantum Cryptography Proposal: ThreeBears. 2020. Available online: https://sourceforge.net/projects/threebears/ (accessed on 13 March 2020).
- Lu, X.; Liu, Y.; Jia, D.; Xue, H.; He, J.; Zhang, Z.; Liu, Z.; Yang, H.; Li, B.; Wang, K. LAC: Practical Ring-LWE Based Public-KeyEncryption with Byte-Level Modulus. Available online: https://eprint.iacr.org/2018/1009.pdf (accessed on 9 March 2020).
- Chen, C.; Danba, O.; Hoffstein, J.; Hülsing, A.; Rijneveld, J.; Saito, T.; Schanck, J.M.; Schwabe, P.; Whyte, W.; Xagawa, K.; et al. NTRU. 2020. Available online: https://ntru.org (accessed on 14 May 2020).
- Akleylek, S.; Alkim, E.; Bindel, N.; Buchmann, J.; Eaton, E.; Gutoski, G.; Krämer, J.; Longa, P.; Polat, H.; Ricardini, J.E.; et al. Submission to NIST’s Post-Quantum project (2nd Round): Lattice-Based Digital Signature Scheme qTESLA. 2020. Available online: https://qtesla.org/wp-content/uploads/2020/04/qTESLA_round2_14.04.2020.pdf (accessed on 29 March 2020).
- Fouque, P.A.; Hoffstein, J.; Kirchner, P.; Lyubashevsky, V.; Pornin, T.; Prest, T.; Ricosset, T.; Seiler, G.; Whyte, W.; Zhang, Z. Falcon: Fast-Fourier Lattice-Based Compact Signatures over NTRU Specifications v1.1. 2020. Available online: https://falcon-sign.info (accessed on 14 April 2020).
- Bernstein, D.J.; Chuengsatiansup, C.; Lange, T.; van Vredendaal, C. NTRU Prime: Round 2–20190330. 2020. Available online: https://ntruprime.cr.yp.to (accessed on 4 May 2020).
- Baan, H.; Bhattacharya, S.; Fluhrer, S.; Garcia-Morchon, O.; Laarhoven, T.; Player, R.; Rietman, R.; Saarinen, M.J.O.; Tolhuizen, L.; Torre-Arce, J.L.; et al. Round5: KEM and PKE Based on (Ring) Learning with Rounding. 2020. Available online: https://round5.org (accessed on 8 April 2020).
- D’Anvers, J.P.; Karmakar, A.; Roy, S.S.; Vercauteren, F. SABER: Mod-LWR Based KEM (Round 2 Submission). 2020. Available online: https://www.esat.kuleuven.be/cosic/pqcrypto/saber/ (accessed on 7 March 2020).
- Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. CRSTALS-Dilithium. 2019. Available online: https://tches.iacr.org/index.php/TCHES/article/view/839 (accessed on 10 February 2020).
- Soni, D.; Basu, K.; Nabeel, M.; Karri, R. A hardware evaluation study of NIST Post-quantum cryptographic signature schemes. In Proceedings of the Second PQC Standardization Conference, Santa Barbara, CA, USA, 22–24 August 2019; pp. 1–4. [Google Scholar]
- Farahmand, F.; Dang, V.B.; Andrzejczak, M.; Gaj, K. Implementing and benchmarking seven round 2 lattice-based key encapsulation mechanisms using a software/hardware codesign approach. In Proceedings of the Second PQC Standardization Conference, Santa Barbara, CA, USA, 22–24 August 2019; pp. 1–36. [Google Scholar]
- Wang, W.; Tian, S.; Jungk, B.; Bindel, N.; Longa, P.; Szefer, J. Parameterized Hardware Accelerators for Lattice-Based Cryptography and Their Application to the HW/SW Co-Design of qTESLA. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 3, 123–151. [Google Scholar]
- Zhang, N.; Yang, B.; Chen, C.; Yin, S.; Wei, S.; Liu, L. Highly Efficient Architecture of NewHope-NIST on FPGA using Low-Complexity NTT/INTT. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2, 49–72. [Google Scholar] [CrossRef]
- Basu, K.; Soni, D.; Nabeel, M.; Karri, R. NIST Post-Quantum Cryptography- A Hardware Evaluation Study. Cryptology ePrint Archive, Report 2019/047. 2019. Available online: https://eprint.iacr.org/2019/047 (accessed on 27 January 2020).
- Soni, D.; Nabeel, M.; Basu, K.; Karri, R. Power, Area, Speed, and Security (PASS) Trade-Offs of NIST PQC Signature Candidates Using a C to ASIC Design Flow. In Proceedings of the 2019 IEEE 37th International Conference on Computer Design (ICCD), Abu Dhabi, UAE, 17–20 November 2019; pp. 337–340. [Google Scholar]
- Banerjee, U.; Ukyab, T.S.; Chandrakasan, A.P. Sapphire: A Configurable Crypto-Processor for Post-Quantum Lattice-based Protocols. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 4, 17–61. [Google Scholar] [CrossRef]
- Xin, G.; Han, J.; Yin, T.; Zhou, Y.; Yang, J.; Cheng, X.; Zeng, X. VPQC: A Domain-Specific Vector Processor for Post-Quantum Cryptography Based on RISC-V Architecture. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2672–2684. [Google Scholar] [CrossRef]
- Strömbergson, J. A Verilog Implementation of the Symmetric Block Cipher AES (NIST FIPS 197). Available online: https://github.com/secworks/aes (accessed on 5 March 2020).
- Liu, W.; Fan, S.; Khalid, A.; Rafferty, C.; O’Neill, M. Optimized Schoolbook Polynomial Multiplication for Compact Lattice-Based Cryptography on FPGA. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 2459–2463. [Google Scholar] [CrossRef]
- Kashif, M.; Cicek, I.; Imran, M. A Hardware Efficient Elliptic Curve Accelerator for FPGA Based Cryptographic Applications. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; pp. 362–366. [Google Scholar]
- Bodrato, M. Towards Optimal Toom-Cook Multiplication for Univariate and Multivariate Polynomials in Characteristic 2 and 0. In Arithmetic of Finite Fields; Carlet, C., Sunar, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 116–133. [Google Scholar]
- Longa, P.; Naehrig, M. Speeding up the Number Theoretic Transform for Faster Ideal Lattice-Based Cryptography. In Cryptology and Network Security; Foresti, S., Persiano, G., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 124–139. [Google Scholar]
- Walter, C.D. Montgomery’s Multiplication Technique: How to Make It Smaller and Faster. In Cryptographic Hardware and Embedded Systems; Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 80–93. [Google Scholar]
- Weimerskirch, A.; Paar, C. Generalizations of the Karatsuba Algorithm for Efficient Implementations. IACR Cryptol. EPrint Arch. 2006, 2006, 224. [Google Scholar]
- Harvey, D. Faster arithmetic for number-theoretic transforms. J. Symb. Comput. 2014, 60, 113–119. [Google Scholar] [CrossRef]
- Sinha Roy, S.; Turan, F.; Jarvinen, K.; Vercauteren, F.; Verbauwhede, I. FPGA-Based High-Performance Parallel Architecture for Homomorphic Computing on Encrypted Data. In Proceedings of the 2019 IEEE International Symposium on High Performance Computer Architecture (HPCA), Washington, DC, USA, 16–20 February 2019; pp. 387–398. [Google Scholar]
- Rafferty, C.; O’Neill, M.; Hanley, N. Evaluation of Large Integer Multiplication Methods on Hardware. IEEE Trans. Comput. 2017, 66, 1369–1382. [Google Scholar] [CrossRef]
- NIST. Computer Security Division—Computer Security Resource Center. 2016. Available online: https://csrc.nist.gov (accessed on 3 August 2020).
- Rijndael. AES (Rijndael) IP Core, 2002. A Ultra-Compact Advanced Encryption Standard (AES, FIPS-197) Core. Available online: http://www.ipcores.com/aes_ip_core.htm (accessed on 15 March 2020).
- Imran, M.; Rashid, M. Architectural review of polynomial bases finite field multipliers over GF(2m). In Proceedings of the2017 International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 331–336. [Google Scholar]
- Roma, C.; Tai, C.E.A.; Hasan, M.A. Energy Consumption of Round 2 Submissions for NIST PQC Standards. Available online: http://cacr.uwaterloo.ca/techreports/2019/cacr2019-03.pdf (accessed on 18 June 2020).
- Huang, W.L.; Chen, J.P.; Yang, B.Y. Power Analysis on NTRU Prime. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 1, 123–151. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).