1. Introduction
To efficiently solve decomposable binary optimization problems that consist of completely separated sub-problems by an evolutionary algorithm (EA), the EA first needs to detect linkages that represent sets of variables forming the sub-problems and then utilize the detected linkages to produce solution candidates. If EA disrupts linkages during the search frequently, it cannot achieve an efficient search. For instance, if a fixed-operator-based EA does not have a recombination operator, matching linkages of a problem, it has exponential scalability in terms of population size required for a successful search [
1].
One such EA to achieve an efficient search is a model-based EA. A model-based EA builds a model representing linkages using some machine learning techniques and produces solution candidates using the built model. The model-based EA, using a probabilistic model, is called the probabilistic model-building GA (PMBGA) [
2] or the estimation distribution algorithm (EDA) [
3].
Recently, several efficient model-based EAs have been developed to solve hard decomposable binary optimization problems. For instance, the hierarchical Bayesian optimization algorithm (hBOA) [
4], the linkage identification with epistasis measure (LIEM) [
5], the dependency structure matrix genetic algorithm (DSMGA) [
6], the linkage tree genetic algorithm (LTGA) [
7], and the dependency structure matrix genetic algorithm II (DSMGA-II) [
8] have been shown to have high scalability for hard decomposable problems. However, it is generally time-consuming to detect linkages in a large size of problem. So, EAs are required to be able to solve problems with less computational time.
Model-based EAs have also been applied to problems with overlaps among linkages and problems that do not have relevant structures or whose structures are hard to identify. However, it has been shown that EAs cannot solve those problems as efficiently in terms of the number of function evaluations as the decomposable problems. So, EAs are required to be able to efficiently solve not only decomposable problems but other ones.
Meanwhile, to overcome the the problem of fixed-operator-based EAs, we previously proposed a mutation-based EA [
9]. The mutation-based EA evolves timings at which probabilities for generating phenotypic variables values change, and brings different evolution speed to each phenotypic variable, so that it can solve a given problem partly and sequentially. In the study, it was shown that the mutation-based EA sequentially solves sub-problems comprising a hard uniformly-scaled problem in which there is no prioritized variable. Concretely, the four-bit trap deceptive function [
10] was used as a hard uniformly-scaled problem, and the scale-up of the mutation-based EA in terms of the number of function evaluations was shown to be sub-exponential experimentally.
In addition, in our most recent paper [
11], in order to improve the mutation-based EA, we proposed a new EA by adding a crossover operator to the mutation-based EA. We referred to this EA as the evolutionary algorithm evolving developmental timings (EDT). Then, we devised a new test problem that conventional EAs, such as the population-based incremental learning (PBIL) [
12] and the compact genetic algorithm (cGA) [
13], are likely to fail in solving and for which features of the proposed EA are well utilized. The test problem consists of multiple two-bit functions with a factor of deception, among which there is hierarchical dependency, and has a feature that the hierarchical dependency is represented by a graph structure. We applied the EDT and the conventional EAs for comparison, the PBIL and the cGA, to the new test problem and showed the usefulness of the evolution of developmental timing.
Both the mutation-based EA and the above-mentioned EDT take the same strategy. That is to say, they fuse evolutionary operators as conventional EAs conduct and a method for learning the distribution of population that PMBGA and EDA conduct. Their evolutionary operators and methods for learning the distribution of population are relatively simple. Especially, the method for learning the distribution of population basically just observes the appearance frequency of possible values at each position of a phenotypic variables vector and then changes the appearance probability of each possible value at each position based on the observed frequency. Then, the mechanism that identifies linkages, which are close relations among multiple positions on a phenotypic variables vector in terms of contribution to a fitness value, relies on differences in timings of changing probabilities for determining phenotypic variables values and evolution of the timings. Thus, the salient feature of the mutation based EA and the EDT is that they evolve timings of events that a phenotypic variable’s value can be determined by. Such evolution has not been considered in conventional EAs. In biology, a process to form a phenotype is called development, and change in timings of events during development is called heterochrony [
14].
By the evolution of timings of changing probabilities for determining phenotypic variable values, both of the mutation based EA and the EDT can bring different evolution speeds to each phenotypic variable. In other words, they can fix some variable values prior to others and find appropriate values of the others under the fixation of the variable values. We can logically think that a problem for the mutation based EA and the EDT to most efficiently solve is not a decomposable problem that a model-based EA relying on linkage detection, such as the LTGA, can efficiently solve, but a problem in which a phenotypic variable is involved in multiple overlapped linkages and the optimum value of the variable varies with linkage. In such a problem, it is hard to identify all linkages that are heavily overlapped and also hard to decide optimum values for the variables even if the linkages are successfully detected. In this case, we expect that only way to have a progress of searching is to force some variables to fix their values and find appropriate values for the other variables as the mutation based EA and the EDT do.
Under this expectation of the performance, in the paper, we investigate the search performance of the EDT for decomposable problems, problems with some overlaps among linkages, and problems that do not have relevant structures or whose structures are hard to identify, compared to existing methods. We use the Hierarchical If-And-Only-If (HIFF) function and the Hierarchical Trap (HTRAP) function as decomposable problems [
4] and the Hierarchically Dependent function (HDEP) [
11], which we previously proposed, and N-K Landscape function (K = 4) (NKL-K4) [
15] as problems with some overlaps among linkages, and the Multidimensional Knapsack Problem (MKP) [
16] as a problem whose structure is hard to identify. As existing methods for comparison, we use the LTGA, which is expected to yield good search performance for decomposable problems, the extended compact genetic algorithm (ecGA) [
13], which is one of the traditional PMBGAs using a marginal product model as a probabilistic model, and Chu and Beasley Genetic Algorithm (CBGA) [
16], which was shown to have better performance for MKP than the LTGA [
17], and the simple genetic algorithm (SGA) [
18], which is one of the simplest operator-based GAs.
Simulation results in the paper reveal that the EDT has much worse performances than the LTGA for decomposable problems and also that the difference in the performance between them becomes smaller for problems with some overlaps among linkages and also that the EDT has better performance than the LTGA for problems whose structures are hard to identify. In fact, both EDT and the LTGA have problems that they cannot solve efficiently. In addition, the results basically support our expectation on search performance mentioned above. In addition, for all problems used in the paper, the EDT basically has similar search performance to the CBGA. The CBGA does not detect linkages, but is meant to maintain the diversity of the population well.
The idea of the LTGA mentioned above has been applied to real-valued GAs [
19]. Additionally, the DSMGA-II mentioned above has been kept improving since it was developed [
20]. However, these model-based GAs tackle mainly with decomposable problems. So, it is worthwhile investigating the EDT because so far there has been no EA that can solve both decomposable problems and problems whose structures are hard to identify efficiently, and also it has not yet been revealed if all-round algorithms that can solve all such problems exist. One example is shown in [
17]. We have to pursuit such all-round algorithms and the contribution of the paper is to empirically answer if the EDT is the desired algorithm. Although it is not a binary optimization problem but a problem to appropriately decompose a neural network into modules for higher performance, it has been shown that when the optimal decomposition is quite obvious, an objective to guide a population to the optimal structure works well and also that when the optimal decomposition is less obvious, an objective to bring structural diversity to a population works well [
21]. This finding suggests that a suitable strategy depends on the decomposability of a given problem, and this is similar to the suggestion from our paper.
2. Related Work
The origin of studies on evolutionary algorithms for binary optimization problems is the study of the simple genetic algorithm (SGA) [
18] that uses binary coding. The schema theory for the SGA indicates that the number of individuals (binary strings as solution candidates) matching the schema that has the average fitness value over the population, a low order, and a small definition length, increases exponentially in the population. Originating from the schema theory, the mainstream of the binary-coded GA study has been to efficiently solve problems that can be decomposed into independent sub-problems, and have deceptive structures, which means the optimum solution does not match the most promising schema that the schema theory says, and have loci (positions) forming a sub-problem distant from each other, which means the definition length of the schema representing the sub-problem is quite large. A set of loci forming a sub-problem is called “linkage”.
Standard operator-based GAs using binary coding cannot achieve efficient searches when their crossover operators frequently break linkages [
1]. Since linkage structures cannot be known in advance, problems that such operator-based GAs can efficiently solve are limited. Then, genetic codes that can vary the original linkage structures were proposed for operator-based GAs. Such a genetic code theoretically enables loosely linked linkages on a phenotype to be tightly linked on a genotype. As GAs use such a genetic code, the linkage learning GA (LLGA) [
22] and the genetic algorithm using grammatical evolution (GAuGC) [
23] were proposed. However, it was experimentally shown that LLGA is unable to make tightly linked linkages on a genotype for uniformly-scaled problems [
22], in which all sub-problems contribute equally to a fitness value. Additionally, it was experimentally shown that the population size of the GAuGE required for obtaining a global optimum of uniformly-scaled deceptive problem increases exponentially as the size of the problem increases [
24].
Thus, operator-based GAs using only fitness values of solution candidates were unable to efficiently solve uniformly-scaled problems with deceptive structures and loosely linked linkages. The approach that has been attracting attention following this until the present is model-based GAs. This approach first detects linkages by applying a machine learning technique to a uniformly-scaled problem and then utilizes a model based on the detected linkages for producing new solution candidates. If a model to produce new solution candidates with detected linkages is a probabilistic model, GA using such a model is called PMBGA or EDA as mentioned above. The probabilistic model provides generation probabilities of values for linkages.
Model-based GAs examine dependencies between variables to detect linkages. Model-based GAs are classified into two types with respect to a way to examine the dependencies. One type examines dependencies among multiple variables at one time. The other type always examines pairwise dependency between two variables or a variable and a cluster or two clusters at one time. The ecGA and Baysian Optimization Algorithm (BOA) are the former type. The DSMGA, the DSMGA-II, and the LTGA are the latter type. The DSMGA and the DSMGA-II make groups of variables using a threshold value after detecting pairwise dependencies. The LTGA represents pairwise dependencies among variables as a tree structure. Since the tree structure expresses groups of variables, they do not use a threshold value for grouping variables as the DSMGA and the DSMGA-II do. All those algorithms conduct a recombination of units of linkage based on the detected linkages. Additionally, the metrics of dependency among variables for all those algorithms are different in detail but are all entropy-based.
Furthermore, the parameter-less population pyramid (P3) [
25] has similarities with the LTGA, but unlike the LTGA, P3 does not need the tuning of the population size. In the P3, each depth of the tree structure in the LTGA corresponds to a hierarchy of the pyramid structure. Executable recombination of unit of linkage differs at each hierarchy, and only when a solution candidate produced by the recombination has a better fitness value than the best fitness value at the hierarchy of focus, the produced solution candidate moves up to a higher hierarchy by one. Then, a hill-climbing method is applied to the solution candidate to obtain better solution candidates around it, which are added to the same high hierarchy.
The performance of the LTGA for the Multi-dimensional Knapsack Problem (MKP), which is used as an algorithm for comparison in the paper, was investigated in detail in [
17]. The work [
17] used all instances of MKP that can be downloaded from [
26]. Chu and Beasley Genetic Algorithm (CBGA) [
16] was used as an algorithm for comparison. In addition, not only the original LTGA but its many variants that maintain the diversity of the population. The work showed that the mechanisms for the diversity maintenance always enhance the performance of the original LTGA. However, the performances of the variant LTGAs are worse than CBGA for all instances. Moreover, the performance of the original LTGA for MKP is almost equal to that of the LTGA with a randomly produced linkage tree. Namely, the linkage detection by the LTGA is not effective for MKP. Thus, it has been already shown that the LTGA cannot solve MKP efficiently, but as a comparison algorithm for the EDT, the LTGA is applied to some instances of MKP that can be downloaded from [
26] in this paper.
The investigation in this paper is not about detailed performance comparison among multiple algorithms for decomposable problems but about which approach is suitable for each of the various problems such as decomposable problems, problems with overlapped linkages, and non-decomposable problems. Therefore, as a model-based GA which examines dependencies among multiple variables at one time, the ecGA is used for comparison. As a model-based GA, which examines pairwise dependencies among variables at one time, the LTGA is used for comparison. Additionally, as an operator-based GA, the CBGA and the SGA are used for comparison.
The EDT that is a target of investigation in the paper includes a vector of probabilities to independently decide a value of each variable as a part of individual. However, only use of the vector of probabilities does not enable recombination of unit of variables forming a sub-problem. In fact, the EDT does not make groups of variables explicitly, but includes developmental timings that decide the change speed in a value of variable as a part of individual. Variables to which the same or similar developmental timing is assigned from a group of variables that have similar evolution speed. A group of variables that have slow evolution speed can decide their values based on the stabilized values of variables that have fast evolution speed. In this way, it is expected that sub-problems forming a decomposable problem are sequentially solved.
3. The Evolutionary Algorithm Evolving Developmental Timings
We investigate the evolutionary algorithm evolving developmental timings (EDT) [
11] previously proposed by us. In this section, we explain the EDT.
3.1. Individual
An individual in conventional EAs is usually equivalent to a genotype. An individual, which means a genotype, is mapped into a phenotype in a fixed manner. Then, in generational EAs, each individual is evaluated only once during a generation and proceeds to a selection phase.
Meanwhile, an individual in the EDT consists of two types of vectors. One type is a vector whose element represents a cycle time of changing a probability to determine a phenotypic value. This vector is a primary object to which evolutionary operators are applied, and its elements can be considered to be developmental timings. We refer to this vector and its element as a genotype and a gene, respectively. The other type is a vector whose element is a probability for determining a phenotypic value. For example, a probability to generate one at a certain phenotypic position is an element of the vector. The vector of probabilities varies during a generation, as mentioned later. Meanwhile, the vector of the cycle times does not vary during a generation.
The lengths of a genotype and a vector of probabilities are the same as the length of a phenotype. Each position in these two vectors corresponds to the same position in a phenotype.
3.2. Individual Development
As mentioned in the previous section, an individual within a generation has a lifespan and consists of a genotype and a vector of probabilities. A time in a lifetime of an individual is denoted by
, where
N is the algorithm parameter representing the end of the life of the individual. In addition, let
and
be the genotype and the vector of probabilities, respectively, where
is an integer number within
and
is a real number within
.
is the algorithm parameter representing the possible maximum cycle time. The genotype does not vary during the lifetime of the individual, but the vector of probabilities varies during its lifetime. In this section, we explain how the vector of probabilities varies due to the developmental timings composing the genotype and how
N phenotypes are time-sequentially produced from the genotype and the vector of probabilities. An overview of the individual development is shown in
Figure 1.
The initialization of the individuals is performed as follows. The genotypes are randomly generated. All elements of the vector of probabilities are set , which represents the probability with which zero is generated. A phenotype is generated using the vector of probabilities at each time during the lifetime of the individual. After every generation of a phenotype, by comparing the current time, n, and each element of the genotype, , it is determined whether it is time to change the probability to generate each phenotypic value. If n is a multiple of , then is modified.
The modification of the elements of the vector of probabilities is performed as follows. Suppose that the
i-th gene is
. The modification of the
i-th element of the vector of probabilities,
, is carried out every
time step during the development of the individual. When the time is
, where
a is an integer number, the modification is performed using the phenotypes generated within
to
and their fitness values. For example, when
is 2, if the phenotypic values at the
i-th position in the phenotypes generated between time of one and time of two are 1 and 0, and if the phenotypic value at the
i-th position in the phenotype with the best fitness value among these two values,
, is 0, then the probability with which 0 is generated on the
i-th position in the phenotype,
, increases in proportion to the number of 0s in the two phenotypic values generated,
. If
is 1, then
decreases in proportion to the number of 1,
. The new probability,
, is determined by Equation (
1).
where
C is the algorithm parameter. This can be considered as a type of learning process, not for the distribution of all phenotypes in the phenotypic space, but rather for the distribution of pieces of the phenotypes.
Figure 2 also illustrates an example of the modification of the vector of probabilities during the lifetime of the individual.
The best fitness value among all of the phenotypes generated during the lifespan of the individual is set as the fitness value of the individual, and the individual proceeds to the selection, crossover, and mutation phases.
3.3. Crossover Operator
The EDT cannot rearrange phenotypic variables on a phenotype. Therefore, if the EDT uses a fixed crossover (recombination) operator, for example, one-point crossover, it depends on optimization problems to be solved whether it can efficiently solve the problems. So, the crossover operator designed for the EDT does not break good linkages between phenotypic variables that the EDT has identified so far but brings them to the next generation.
The crossover operator estimates the dependency between phenotypic variables from element values of the vector of probabilities of the individual. When the i-th element value of the vector of probabilities of some parent individual, , is close to 0 (or 1), the i-th phenotypic value becomes 1 (or 0) mostly. That is to say, it can be said that the i-th phenotypic variable’s value has almost converged. We consider that multiple phenotypic variables whose values have almost converged at some moment depend on each other. Then, the crossover operator copies the i-th gene of that parent individual, , onto the genotype of another parent individual. The reason for not copying element values of the vector of probabilities but genes of the genotype to decide the developmental timings is that phenotypic values might have converged incorrectly.
Before applying the crossover operator, the EDT does not conduct selection for reproduction but just randomly divides all individuals of the present population into pairs thoroughly. When the population size is
P, the number of the parent pairs is
, where
P is an even number. Each pair of parent individuals produces two new individuals, so that the total number of individuals produced is
P. The condition in which the
i-th gene of a parent individual of focus,
, is copied onto the genotype of another parent individual is that the
i-th element value of the vector of probabilities of the parent individual of focus,
, satisfies
or
, where
and
are the algorithm parameters. An application example of the crossover is shown in
Figure 3.
3.4. Mutation and Selection Operators
A mutation operator is applied to each element of the genotype and the vector of probabilities. The mutation rates for the
i-th element of the genotype and the vector of probabilities,
, are the same, and the rate is determined using the
i-th element of the genotype,
. The mutation rate,
, is determined by Equation (
2).
This equation indicates that the smaller the cycle time, the larger the mutation rate. In addition, the mutation rate is always greater than zero.
The mutation to the genotype randomly changes its element value. The mutation to the vector of probabilities sets its element value as . Using this mutation operator, a parent-individual generates R child-individuals. When the population size is P, child-individuals are generated in one generation. P and R are the algorithm parameters.
A selection operator for survival selects P individuals with better fitness values from among child-individuals plus P parent-individuals as the population of the next generation.
4. Simulations for Performance Evaluation
In this section, we investigate the search performance of the EDT for decomposable binary optimization problems, problems with overlaps among linkages, and problems that do not have relevant structures or whose structures are hard to identify.
4.1. Test Problems
All test problems used in the simulations are shuffled versions. In the shuffled version all variables of the problem are randomly positioned on the string of a solution candidates. The shuffled versions of the problems are generally hard for conventional operator-based evolutionary algorithms to optimize, because the algorithms do not have a mechanism for arranging variables for their operators to work effectively.
4.1.1. Hierarchical If-And-Only-If Function (HIFF)
The structure of the Hierarchical If-And-Only-If function is represented as a balanced binary tree. Each leaf node of the tree takes a value of 0 or 1 and a set of leaf nodes is equal to a solution candidate. The fitness value of each leaf node is 1, no matter what its value is. The value of a parent node in the tree is 0 when all its children nodes have a value of 0 and the value of a parent node is 1 when all its children nodes have a value of 1. In all other cases, a parent node is not assigned any value. The internal and parent nodes have the fitness , where X is a node and is a distance from its leaf nodes, if and only if all their children nodes have either 0 or 1. Otherwise, they have the fitness value of 0. The entire fitness value of a solution candidate is the sum of the fitness values of all nodes in the tree and each level of the tree contributes to the entire fitness value at the same magnitude.
We call this problem HIFF hereinafter. HIFF is a hierarchically decomposable problem. As the problem size of ℓ, we use 32, 64, and 128 here.
4.1.2. Hierarchical Trap Function (HTRAP)
The structure of the Hierarchical Trap function is represented as a balanced
k-
tree with
. Each leaf node of the tree takes a value of 0 or 1 and a set of leaf nodes is equal to a solution candidate. The bit length of a solution candidate is
k to the
a-th power, where
a is a positive integer number. The value of a parent node in the tree is 0 when all its children nodes have a value of 0 and the value of a parent node is 1 when all its children nodes have a value of 1. In all other cases, a parent node is not assigned any value. In the tree,
k nodes in every level of the tree is regarded as
k-bit deceptive problem and the fitness value of a parent node of the
k nodes is given by
, where
X is a parent node of focus and
is the fitness value of the
k-bit deceptive problem represented by Equation (
3).
At the root node = 1 and = 0.9, while for all other internal nodes = = 1. The global optimal solution is thus the string of all ones. However, HTRAP biases the search to the solution of all zeroes on each but the top level. In addition, the top level is fully deceptive with the all-zeroes solution as a deceptive attractor. We call this problem HTRAP hereafter. HTRAP is a hierarchically decomposable problem. As the problem size of ℓ, we use 9, 27, and 81 here.
4.1.3. Hierarchically Dependent Function (HDEP)
We devised this test problem previously. The problem includes hierarchical dependency among variables in terms of fitness values, and it is hard to determine values of variables at higher hierarchies correctly, and this leads to the incorrect determination of values of variables at lower hierarchies if the determination at higher hierarchies is incorrect.
The general procedure to produce an instance of the problem is as follows.
- 1.
Generate a connected graph with some topology. The number of nodes in the graph is equal to the number of variables, that is, the length of a binary string as a solution candidate, ℓ.
- 2.
Assign position numbers of a binary string as a solution candidate, , to each of the ℓ nodes on the generated graph.
- 3.
Define Lm-bit problems with a factor of deception on the generated graph. In the graph, nodes of higher degree form higher hierarchies. Degree means the number of edges. If multiple nodes of the same degree are included in an m-bit problem, the nodes with smaller position numbers become those of higher degree.
The general procedure to calculate a fitness value of a solution candidate is as follows. It is a maximization problem.
Assign bits of a solution candidate to corresponding nodes in the graph of the problem instance.
Calculate the sum of fitness values of Lm-bit problems defined on the graph and then divide the sum by L. A solution candidate of an m-bit problem consists of m bits that the m nodes sequentially connected by edges have. More concretely, the solution candidate is formed by arranging m bits that the m nodes have from higher to lower in terms of hierarchy.
Set the value obtained by the division to be a fitness value of a solution candidate of the entire problem instance.
In the simulations, we concretely determine the general procedures above as follows.
We generate the topology of the connected graph with the algorithm described in [
27]. The topology follows a power law [
28] with respect to the distribution of degree. We use two-bit problems with the factor of deception. One two-bit problem consists of two nodes connected by an edge. The dependency between two two-bit problems is introduced by setting a node of the lower hierarchy in one two-bit problem to be a node of the higher hierarchy in another two-bit problem. The total number of the two-bit problems defined on the generated graph is equal to the number of the edges of the graph.
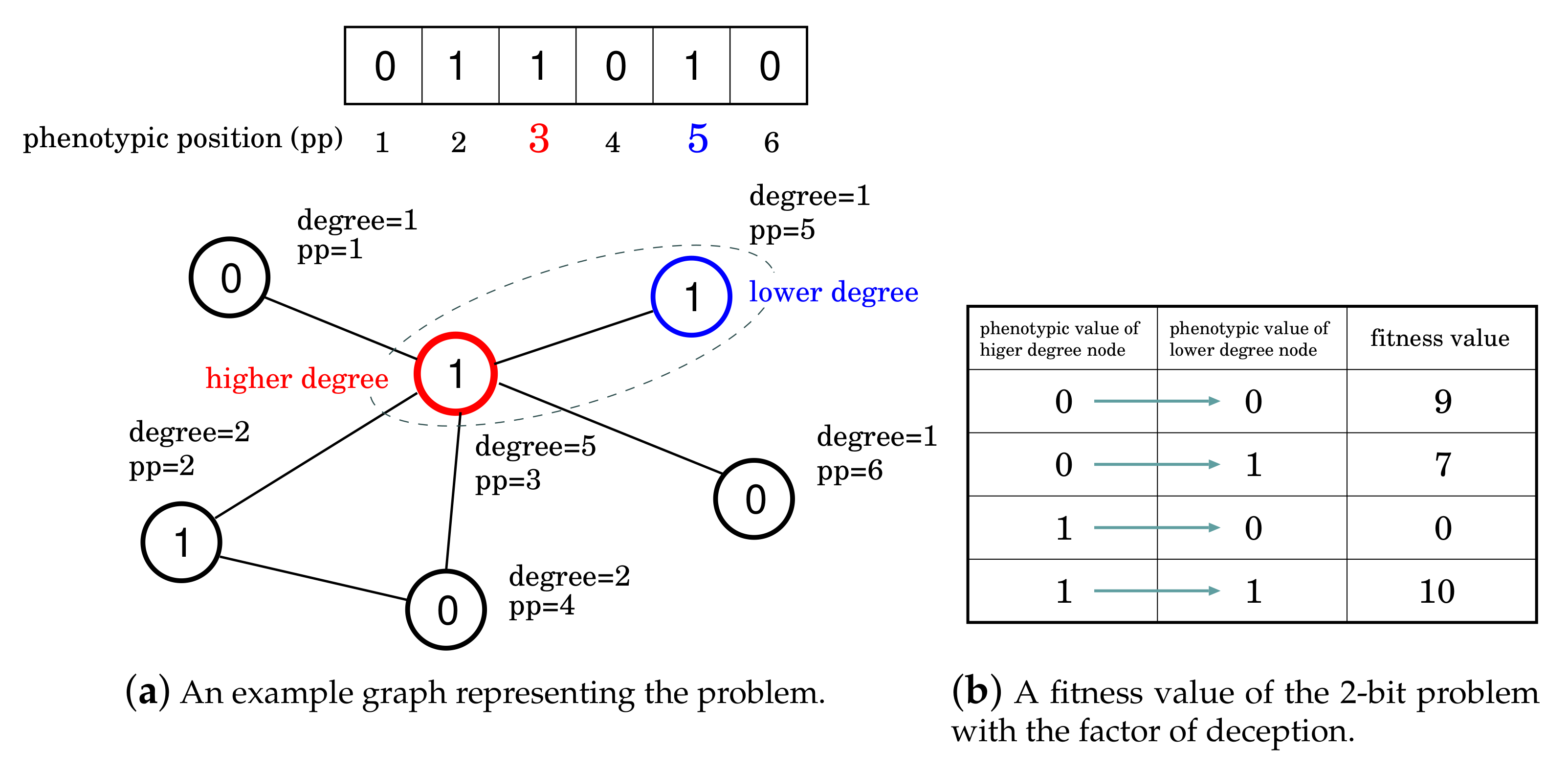
Figure 4a shows an example graph representing a problem instance and
Figure 4b shows a way to determine a fitness value of the two-bit problem with the factor of deception. As shown in
Figure 4b, the optimum solution for the two-bit problem is “11”, and the global optimum of the entire problem is obtained when all bits that all nodes have are 1. The second best solution for the two-bit problem is “00”. Then, comparing the average fitness value of solution candidates matching the schema of 0* and that matching the schema of 1*, the schema of 0* is better than that of 1*. So, we can say that HDEP includes the factor of deception. Due to the factor of deception of the problem, it is likely that the local optimum in which all bits are 0 is obtained. We call this problem HDEP hereinafter. HDEP is a problem with overlaps among linkages in which two sub-problems share just one variable. As the problem size of
ℓ, we use 20, 30, and 40 here.
Figure 5 shows the degree distributions of the graphs representing the problem instances used here.
4.1.4. N-K Landscape Function (K = 4) (NKL-K4)
This problem is a problem with overlaps among linkages.
N represents the size of the problem and is equivalent to
ℓ that is used as the notation of the problem size in this paper. Each variable of the problem takes 0 or 1 and the fitness value of each variable depends on its
K neighboring variables. In this paper we use K = 4. We call this problem NKL-K4 hereafter. NKL-K4 is a problem with overlaps among linkages in which two sub-problems shares four variables. As the problem size of
ℓ, we use 20, 30, and 40 here. In NKL-K4, as presented in
Figure 6, the fitness value of
g in the sequential five bits, (
,
,
,
,
), is determined by referring to
Table 1, in which all possible combinations of values of (
,
,
,
,
) and their corresponding fitness values are presented. In addition, the most-right bit (the most-left bit) is connected to the most-left bit (the most-right bit). The fitness of a solution candidate is obtained by dividing the sum of fitness values of all variables by
.
4.1.5. Multidimensional Knapsack Problem (MKP)
The multidimensional knapsack problem is a problem that does not have relevant structures or whose structures are hard to identify. The problem is represented by Equation (
4).
where
ℓ is the number of items, and
m is the number of knapsacks (constraints), and
is a value of the
j-the variable of a solution candidate, and
represents a value (price) of the
j-th item and
represents a cost of the
j-th item for the
i-th knapsack and
is the capacity of the
i-th knapsack and
is a tightness ratio. We call this problem MKP hereinafter. The problem instances can be downloaded from [
26] and we use the 10th, 20th, and 30th problem instances that have
of 0.25, 0.50, and 0.75, respectively, described in “mknapcb1.txt”. The smaller the value of
, the harder the problem. In those problem instances used here, the number of items (the problem size),
ℓ, is 100, and the number of knapsacks,
m, is 5.
When solving MKP, infeasible solution candidates can be generated. Infeasible solution candidates are repaired to feasible ones by a method a little different from that introduced in [
17]. The method for repair firstly represents the utility of the
j-th item as
, and secondly, arranges all items in ascending order with respect to the utility, and thirdly, removes an item one by one in the order until the solution candidate becomes feasible, where
represents a value of the
j-th item and
represents a cost of the
j-th item for the
i-th knapsack and
is the capacity of the
i-th knapsack. Larger values of
are better. In Reference [
17], after removing an item one by one in ascending order of utility from the present infeasible solution candidate until it becomes feasible, an item not contained in the feasible solution candidate is added in it one by one in descending order of utility unless it becomes infeasible. However, in this paper, we execute not the latter addition but the former, removing only.
4.2. Algorithm for Comparison
We used the simple genetic algorithm (SGA) [
18], Chu and Beasley Genetic Algorithm (CBGA) [
16], the extended compact genetic algorithm (ecGA) [
13], and the linkage tree genetic algorithm (LTGA) [
29] as algorithms for comparison. We made the program of the SGA, the CBGA, and the ecGA by ourselves, but downloaded the program of the LTGA from the web page of the first author of [
29].
The SGA is one of the most basic and traditional operator-based genetic algorithms. It uses a roulette selection operator, a one-point crossover operator, and a bit-flip mutation operator.
The CBGA is one of the most effective GA for MKP. The CBGA was used as a method for comparison with the LTGA in [
17] and was shown to be far superior to the LTGA for MKP. The CBGA uses binary representation, binary tournament selection, uniform crossover, and mutation of two bits. It avoids inserting duplicated solution candidates in the population to maintain the diversity of the population.
The ecGA is PMBGA. The ecGA uses a marginal product model (MPM) as a probabilistic model for generating solution candidates. The ecGA builds MPM for generating a next generation of solution candidates based on the minimum description length (MDL) metric. MPM consists of independent and non-overlapping sub-groups of the variables, and the ecGA decides the MPM as its MDL becomes the minimum. To find the MDM with the minimum MDL, the ecGA uses a greedy algorithm. The algorithm first makes each of the ℓ variables form a sub-group, and then merges two sub-groups to maximize the improvement of the MDL of the model at every iteration of the model building. If the improvement does not occur at some iteration, the model building is finished and the current model is used for generating a next generation of solution candidates. The sub-groups of the variables in the eventually obtained MPM are considered to be a single variable and the probability distribution with respect to the single variable is calculated and solution candidates are generated according to the probability distribution.
The LTGA is a model building genetic algorithm, but not PMBGA. The LTGA, as the ecGA does, deals with each variable as a sub-group. Then, it repeats making a pair of sub-groups with the highest similarity among any pairs a new sub-group, and that results in independent and non-overlapped sub-groups of variables. The grouping, that is, the clustering, is done by the algorithm called UPGMA. The similarity between two sub-groups of variables is measured based on the normalized variation of information. The process of the grouping can be represented by a tree structure, having all variables as leaf nodes, and the tree is referred to as the linkage tree. The LTGA produces new solution candidates with the crossover operator utilizing the linkage tree. The crossover operator is applied between each solution candidate in the population and one randomly selected from among the population. It copies values of a sub-group in the linkage tree from the randomly selected solution candidate to the solution candidate of focus, and only if the solution candidate produced by receiving the values is better than the solution candidate of focus in terms of a fitness value, the solution candidate of focus is replaced by the newly produced one. The crossover operator is applied to the solution candidate of focus for every sub-group in the linkage tree in the same manner.
4.3. Configurations
The stop condition of all algorithms used here is function evaluations.
The population sizes of the EDT are 4, 6, 8, 10, 20, 40, 60, 80, or 100 for all test problems. The lifetime of the individual, , is , , or , where ℓ is the problem size as mentioned before. The parameter of C, which is used for updating probability for determining phenotypic values, is set to be 0.05. The number of child-individuals generated from a parent-individual, M, is set to be 5. The values of the parameters of the crossover operator of the EDT, and , are 0.08 and 0.92, respectively.
The population size P of the CBGA and the SBGA is 2000. The population size P of the ecGA is 5000 for all test problems and that of the LTGA is 200, 300, or 400 for all problems except HIFF and HTRAP. The population size of the LTGA is 40, 50, or 60 for HIFF with , , or , respectively, and is 100 or 110 for HTRAP with or , respectively.
The SGA uses the crossover rate of 0.9 and the mutation rate of 0.01. The CBGA does not have any parameter to be set a value except the population size. The ecGA uses the tournament selection with the tournament size of 2 and the crossover rate is 100% and the mutation rate is 0%. The ecGA builds the probabilistic model by the greedy algorithm, as mentioned above, and stops running when the probabilistic model converges. The convergence of the probabilistic model means that the probability of generating 0 at every position of a solution candidate becomes less than 0.000001 or more than 0.999999. The LTGA stops running when the deviation of the fitness values of all solution candidates in the population becomes zero.
4.4. Results
The simulation results for HIFF, HTRAP, HDEP, NKL-K4, and MKP are shown in
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6, respectively. Then, we did not obtain a result of the ecGA for a problem with the problem size of
ℓ larger than or equal to 100 because it takes an enormous amount of time to obtain a result. In addition, the results of the LTGA for HIFF and HTRAP are extracted from [
7]. In all tables,
P represents a population size of each algorithm and
represents a period of lifetime of an individual of the EDT.
represents the number of success runs out of 30 runs.
represents the average number of evaluations for
success runs.
represents the standard deviation of the number of evaluations used for calculating
.
stands for the average of the best fitness values ever-obtained at the end.
stands for the standard deviation of the fitness values used for calculating
. In order to decide the best result for each algorithm, we prioritize
,
, and
as this order, which means
has the highest priority. The best result of each algorithm for each problem of each size is shown by coloring the value of
in red in all tables. In each table, only results for P = 4, 60, 80, 100 are shown for the EDT and only the best result is shown for the LTGA.
Furthermore, we relatively compare the values of
,
, and
among the EDT, the SGA, the CBGA, and the LTGA. Then, we give the rankings to each algorithm for each problem of each size—for example, as (1,2,3)—which means that the algorithm has the first ranking regarding the value of
, the second ranking regarding the value of
, and the third ranking regarding the value of
. We describe the rankings in
Table 7. To simplify the rankings, we also describe the average ranking of each algorithm for each problem of each size in
Table 7.
First, we focus on the EDT and the SGA. For all problems except the fitness values for HTRAP, the EDT is better than the SGA. The EDT does not seem to be able to overcome the deception.
Next, we focus on the EDT and the CBGA. Their performances are basically similar. For the two decomposable problems, HIFF and HTRAP, the EDT is slightly worse than the CBGA. For the two problems with overlaps among the linkages, HDEP and NKL-K4, the EDT is slightly better than the CBGA for HDEP, but their performances are almost equal for NKL-K4. For the problem whose structure is hard to identify, MKP, the EDT is slightly better than the CBGA.
Next, we focus on the EDT and the ecGA. For the two decomposable problems, HIFF and HTRAP, the EDT is worse or equal to the ecGA. Especially for HTRAP, the EDT has much worse performance than the ecGA. However, the performance of the ecGA becomes worse as the problem size increases. So, probably, for HIFF that does not include the factor of the deception, the EDT yields better performance for a HIFF of larger size. For the two problems with overlaps among the linkages, HDEP and NKL-K4, the EDT is better than the ecGA. For the problem whose structure is hard to identify, MKP, we do not execute the ecGA due to its high computational cost. So, we do not compare their results.
Next, we focus on the EDT and the LTGA. For the two decomposable problems, HIFF and HTRAP, the EDT is worse than the LTGA. Especially for HTRAP, the EDT has much worse performance than the EDT. For one of the two problems with overlaps among the linkages, HDEP, the EDT is worse than the LTGA. However, the difference in the performance among them is not as large as that for HIFF or HTRAP. For another problem with overlaps among the linkages, NKL-K4, the EDT is almost equal to the LTGA. For the problem whose structure is hard to identify, MKP, the EDT is better than the LTGA.
Finally, we focus on the SGA, the CBGA, the ecGA, and the LTGA. The ecGA and the LTGA takes the same basic strategy to solve problems, that is, the strategy that decomposes the entire problem into independent sub-problems using a machine learning technique. However, for all problems, the LTGA is better than the ecGA. So, hereafter, we focus only on the LTGA among the ecGA and the LTGA and discuss the observations mentioned above in the next section. In addition, interestingly, the CBGA is better than the LTGA for NKL-K4 and MKP, as the EDT and the SGA are better than the LTGA with respect only to the fitness values for MKP.
4.5. Discussion
4.5.1. Why the EDT Solves MKP Better Than the LTGA
Each knapsack in MKP can be considered to be a sub-problem, that is, a linkage. So, a linkage in MKP is equal to a set of all variables. The size of the linkage in MKP is quite long compared to other problems used in the paper. In MKP, the value of each item is the same for all multiple knapsacks, but the cost to put the item in each knapsack is different. Therefore, an optimal set of items that meets the constraint and yields the maximum sum of values is different in each knapsack. More concretely, the optimal value of a variable, which represents whether the corresponding item is included in all knapsacks and takes a value of either 0 or 1, is not the same for all knapsacks. In such a situation, it would be generally hard to identify variables that highly contribute to better fitness values and decide values of the identified variables. In this situation, it would be better to decide whether to put some items in all knapsacks in advance of other items sometimes by force and then under the fixation of the items, consider some of remaining items, and repeat this until all items are given decisions. Otherwise, even local optimum is unlikely to be obtained.
As we revealed in our previous studies [
9,
11], the EDT partially sequentially decides values of variables even for uniform-scaled problem. That is to say, the EDT brings different evolution speeds to variables of a problem. So, we first confirm if the EDT exposes the characteristics to the problems used in the paper.
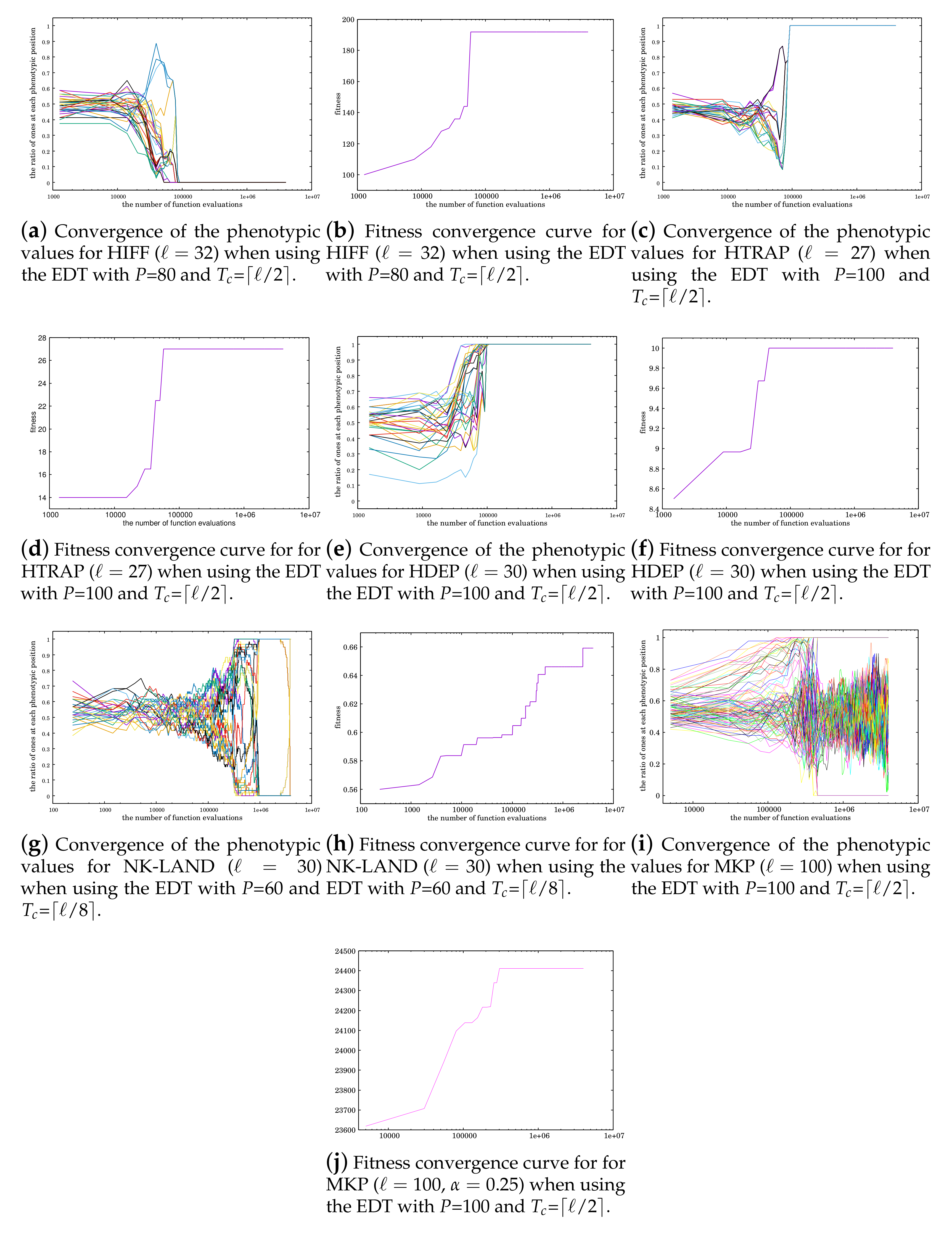
Figure 7 shows the time-variation of the ratio of 1 for each variable and the convergence curves of fitness values. Note that the horizontal axis representing the number of fitness evaluations is log-scaled.
We can observe from
Figure 7 that the EDT partially sequentially converges values of variables over the entire search period of time for HDEP, NKL-K4, and MKP. For HIFF and HTRAP, the EDT did so until the middle phase of the search, but converged them all together in the last phase. This fact is related to the reason why the EDT cannot solve HIFF and HTRAP better than the LTGA, and discuss that in the next section.
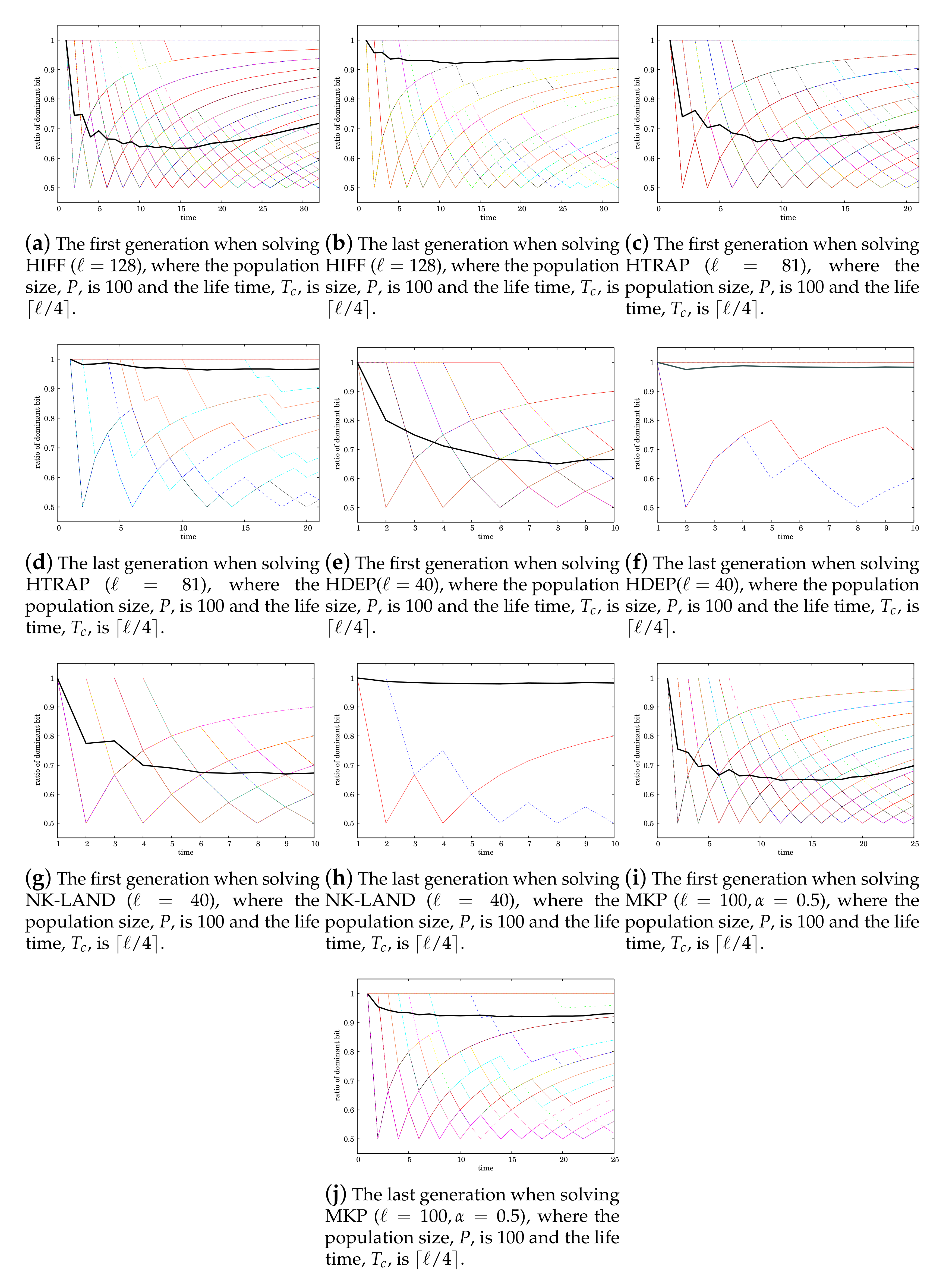
To reveal what induces the characteristics of the EDT shown in
Figure 7, we focus on the development of an individual.
Figure 8 shows the time variation of a ratio of a dominant value of each variable, 0 or 1, in the development of an individual at the first and the last generations for each problem. At the time of 1 in the development of an individual, only one phenotype is generated, so that the ratio of the dominant value is 1.0. After that, the ratio varies at each time.
We can observe from
Figure 8 that, for all test problems used in the development of the individual at the first generation, values of the variables partially sequentially converge. Meanwhile, we can also observe that in the development of the individual at the last generation, values of almost all variables converge at the beginning. Thus, we can say that the characteristics of the EDT that it determines values of variables partially sequentially is induced by the partial sequential convergence of values of variables in the development of individuals.
The characteristics of the EDT confirmed above must be suitable for solving MKP. To understand how the EDT actually solves MKP, we look at the results of MKP shown in
Figure 7i,j. Then, we can observe that values of the variables converge partially sequentially until the time at which the global optimum is found. However, after finding the global optimum, some variables’ values do not converge but keep fluctuating. One of the reasons for that would be that infeasible solution candidates are repaired to feasible ones this time. That is to say, multiple infeasible solution candidates with different values for a few variables can be repaired to the same solution candidate, so that the target variables for repair would never converge.
Meanwhile, since MKP would have multiple linkages (sub-problems), which is a set of all variables, and the best variables’ values depend on the linkages, the LTGA is likely to identify the linkage incorrectly. In addition, the crossover based on the incorrect linkage information is not expected to yield better solutions. In fact, the fitness values of the LTGA for MKP are worse than those of the SGA. Since MKP is the shuffled version as mentioned above, the one-point crossover of the SGA is not expected to work well to the problem. However, the one-point crossover might not be so disruptive. In addition, the population size of the SGA is larger than the LTGA and it helps the SGA maintain the diversity of the population.
Similar to MKP, NKL-K4 also have multiple linkages overlapped and the optimal values for the linkages can be different. However, in NKL-K4, a linkage consists of five variables and the maximum number of variables overlapped in two linkages is four. The size of the linkage is quite significantly smaller than MKP’s. Therefore, NKL-K4 seems to be easier for the EDT than MKP. To understand how the EDT actually solves NKL-K4, we look at the results of NKL-K4, shown in
Figure 7g,h. Then, we can observe that the EDT converges values of the variables partially sequentially by the middle phase of the search and then takes a long time to find optimal values for very few variables. The average number of evaluations required for a successful search, shown in
Table 5, also supports this observation. That is to say, we can see that the global optimum is found at the number of evaluations close to the maximum number allowed.
Meanwhile, the NKL-K4 would basically be easier than MKP for the LTGA because the size of the linkage is smaller. However, as the problem size of the NKL-K4 becomes larger, the total number of variables overlapped among linkages simply increases and the total number of overlapped variables that take different optimal values in the linkages also simply increases, and therefore, the LTGA would degrade its performance with the increasing size of problem. In fact, the LTGA is inferior to the EDT with respect to the number of times it finds the global optimum when the problem size becomes larger.
HDEP also has multiple linkages and shares variables among the linkages. However, the linkage consists of two variables, and the number of overlapped variables between any two linkages is just one, and the optimal value for the overlapped variable is the same among the linkages. In addition, the sub-problems that are hierarchically overlapped have the factor of deception. HDEP seems easy for the LTGA because the number of overlapped variables among the linkages is small and the optimal value for the overlapped variable among them is the same. In addition, there is a factor of deception that is hard for the EDT to overcome. Therefore, the LTGA has better search performance than the EDT.
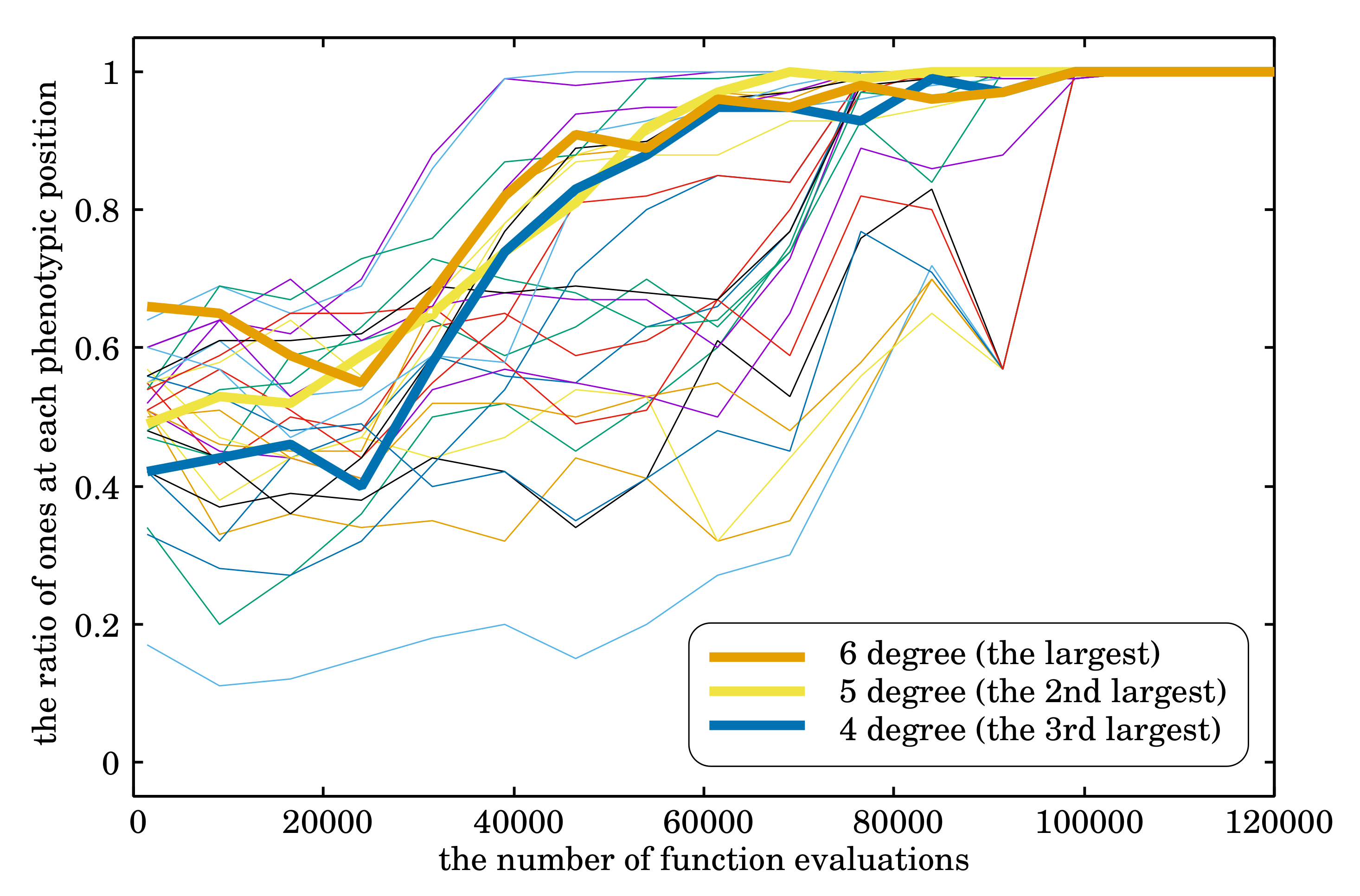
When solving HDEP by the EDT, if a few number of variables cannot obtain appropriate values prior to others, the EDT cannot yield good fitness values. Those variables correspond to vertexes of high degree in the graph where vertexes are equivalent to variables. To confirm that the EDT indeed determines appropriate values for those variables prior to others, convergence of the values of the variables corresponding to the vertexes of high degree is shown in
Figure 9. This result suggests that for non-uniformly scaled problems in which variables have different contributions to a fitness value, the EDT can converge values of variables in the order of priorities of the variables.
4.5.2. Why the EDT Solves HIFF and HTRAP Worse Than the LTGA
HIFF and HTRAP are decomposable problems. If all sub-problems at a lower hierarchy in HIFF and HTRAP are not solved correctly, another sub-problem at a higher hierarchy that consist of the sub-problems at the lower hierarchy do not give any fitness value. The LTGA first decomposes the whole problem into sub-problems, that is linkages—correctly—and then efficiently create better solution candidates by the crossover using the linkage information. Although the LTGA would take more evaluations to solve HTRAP than HIFF due to the deception of HTRAP, the LTGA solves both problems very efficiently.
Meanwhile, the EDT cannot identify linkages in decomposable problems well. In addition, the EDT increases the appearance frequency of values of variables that yielded better fitness values during the lifetime of an individual in newly produced solution candidates. This way would not suitable for solving a deceptive function because its global optimum does not match a schema with higher average fitness values than other schemas. In fact, we can see from
Table 4 that the EDT is much worse than the LTGA for HTRAP. Furthermore, to find the global optimum of HTRAP, all variables values have to be set correctly and simultaneously due to the deception existing at the top hierarchy. Therefore, as shown in
Figure 7, even the EDT cannot realize partial and sequential convergence of variables values right before the global optimum is found, and all variables values converge simultaneously. Meanwhile, HDEP has not only overlaps among linkages, which the EDT overcomes well, but also the factor of deception, which the EDT does not overcome well, so that the EDT would not be able to yield better performance than the LTGA.
4.5.3. Why the Performances of the EDT and the CBGA Are Similar
The EDT has the main search strategy in that it forces us to temporarily fix some variables’ values first and then determines the remaining variables’ values under the fixation of those variables’ values. In addition, the EDT has the mutation that guarantees not to fix any variable values. That is to say, the EDT has a method to maintain the diversity of produced solution candidates. Meanwhile, the CBGA uses a uniform crossover operator, which mixes variables values randomly and maximally among two solution candidates, a tournament selection operator with tournament size of two, which gives very weak selection pressure to existing solution candidates, a bit-flip mutation operator, which certainly changes values of two randomly selected variables of a produced solution candidate, and a particular steady-state generation gap model, which replaces the worst solution candidate in a population by a newly produced solution candidate and does not allow a population to hold duplicated solution candidates. Thus, the main strategy of CBGA is just the maintenance of diversity of solution candidates in a population. So, the common element of the EDT and the CBGA is that they are good at maintaining the diversity of produced solution candidates. That is the basic reason for the similar search performances among the two.
However, there are small differences in the search performances among them.
For HIFF and HTRAP, the CBGA is superior to the EDT. HIFF and HTRAP require optimization algorithms to simultaneously correctly solve all sub-problems to obtain their global optima. However, as mentioned before, the EDT fixes some variable values prior to others for any problem, although it is not completely impossible for all variable values to converge at almost same timing, and therefore, it is hard to achieve the efficient improvement of the solution candidates for those problems. The CBGA does not have any special procedure suitable for those problems but all variables have the same evolution speed theoretically, so that it would be easier for the CBGA to improve solution candidates for those problems compared to the EDT.
For HDEP, the EDT is superior to the CBGA. HDEP requires optimization algorithms to correctly determine some variables values prior to others to efficiently solve, the main search strategy of the EDT matches the characteristics of HDEP, and therefore, the EDT would be more effective.
For NKL-K4, the search performances of the EDT and the CBGA are almost the same, but there are small differences. The EDT obtains the global optimum faster and the CBGA obtains it more frequently. The CBGA takes a larger number of fitness evaluations to obtain the global optimum not only for NKL-K4 but also for all other problems used here. That would be because the main search strategy of the CBGA is just maintenance of the diversity of a population. In addition, it is suggested that NKL-K4 requires quite high randomness to obtain the global optimum.
Finally, for MKP, the EDT is superior to the CBGA. In MKP, the importance of an item is decided depending on what items are included together in all multiple knapsacks. That is, the contribution of each variable to a fitness value depends on other variables. Furthermore, just a few variables’ values can affect the optimal values of many other variables. The EDT, which has not only the main strategy mentioned above but the ability in maintaining diversity of produced solution candidate, would handle this problem effectively.
4.5.4. What Configurations Are Better for the EDT
The parameters of the EDT are the population size, P, the length of the lifetime of an individual, , the degree of change in the vector of probabilities, C, the number of offspring individuals by the mutation of one parent individual, R, and the threshold values for execution of the crossover, and . In the simulations of this section, only P and are changed. Although there are a few exceptions, the best settings of the parameters of P and are values close to 100 and , respectively, which are the largest population size and the longest life time. A larger population size yields more diverse solution candidates, that is, contribution to exploration, and a longer lifetime facilitates local search, that is, contribution to exploitation. We need further investigation on how to balance the exploration and the exploitation within the limited number of evaluations, but we can say from the simulation results here that the maximum number of times of fitness evaluations is large enough, so that maximally conducting both exploration and exploitation yields better results.
However, one feature of the EDT is that it does not cause very bad search performance even with very small population size like four. Relying on this feature, the EDT might be able to adaptively adjust the population size with an initial small population size. The adaptive adjustment of a population size is one direction for future work of the EDT.
As for the population size of the LTGA, P, the larger the population size is, the search performance becomes worse for HDEP, NKL-K4, and MKP. The reason for that is unclear at the present. We need further investigation on this.