Prediction-Based Error Correction for GPU Reliability with Low Overhead
Abstract
:1. Introduction
2. Motivation
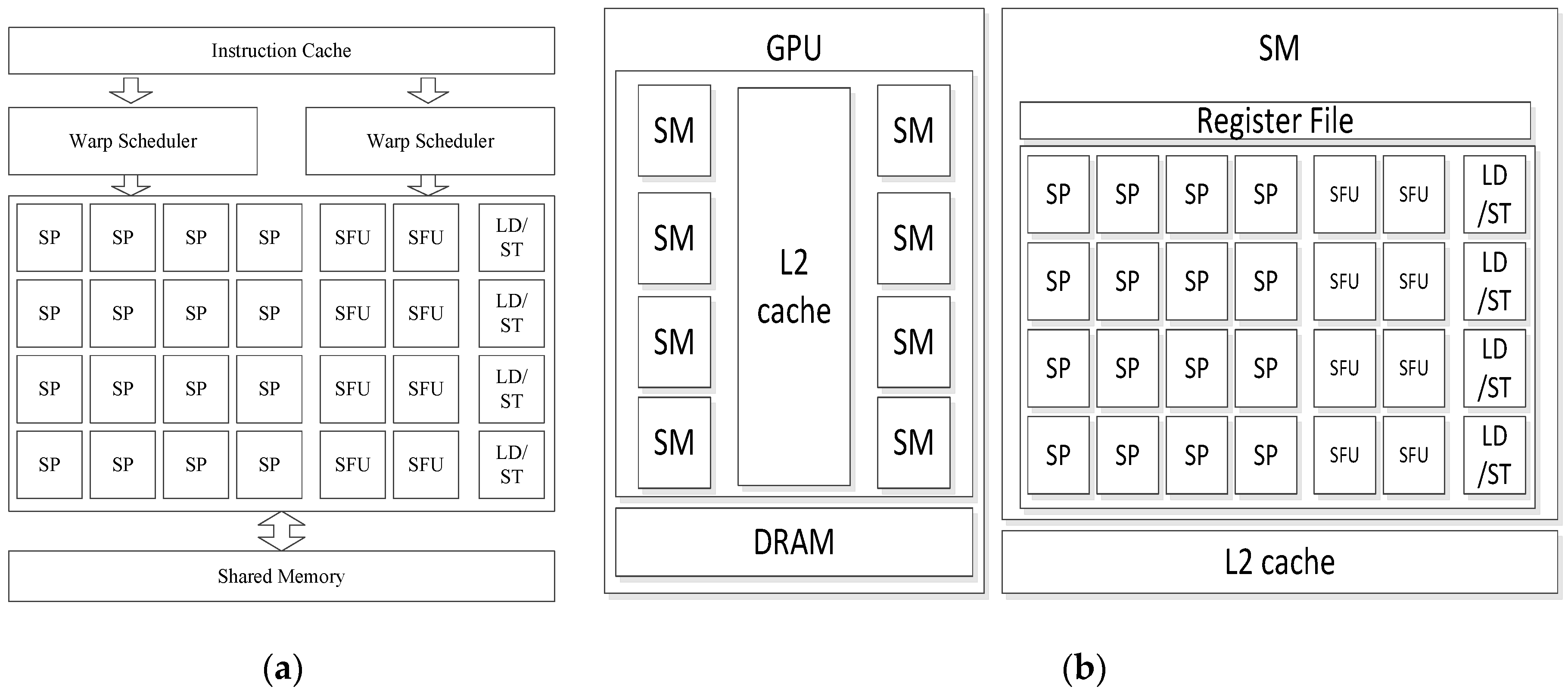
2.1. GPU Architecture
2.2. Resilience Support in GPU Architecture
2.3. Related Works
3. Proposed Methodology
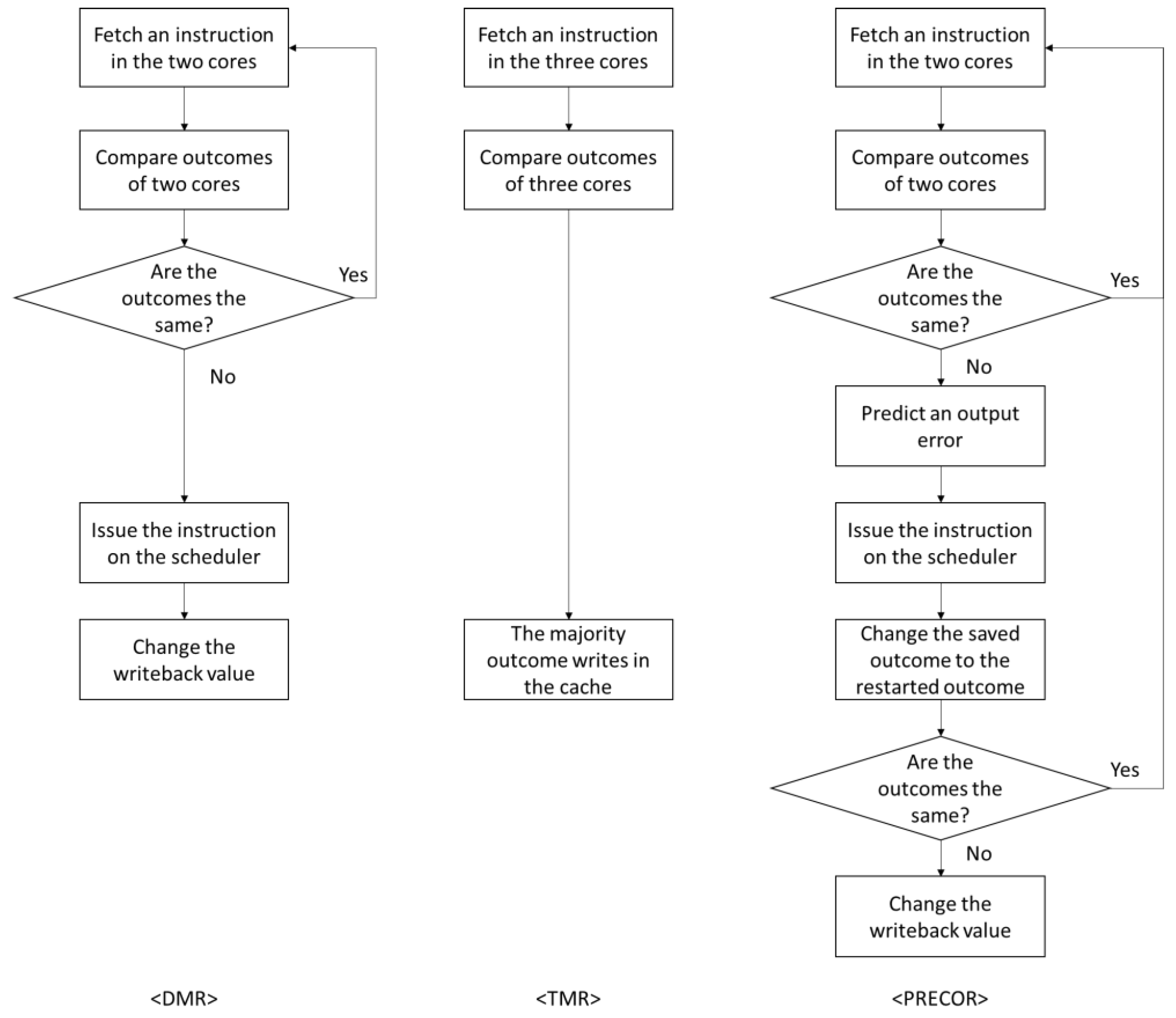
3.1. The PRECOR Approach
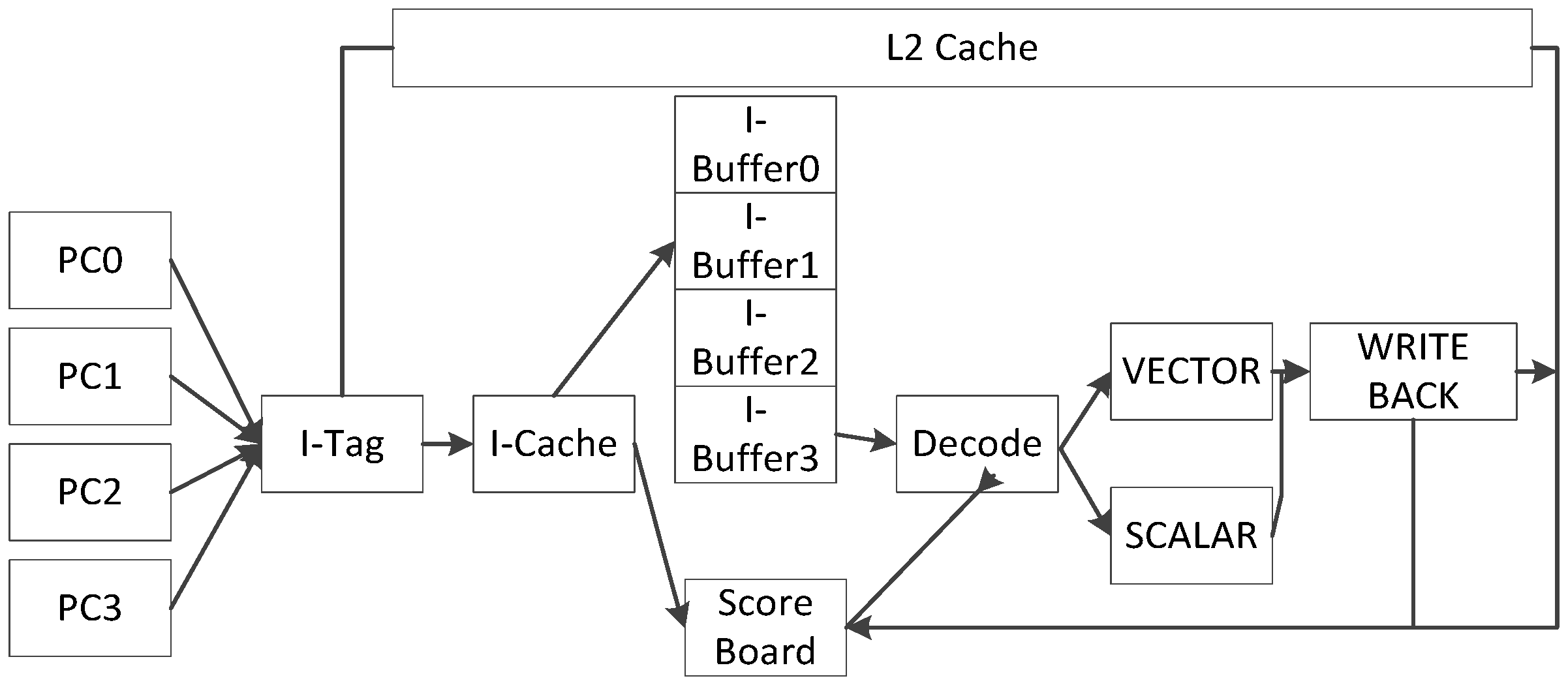
3.2. Microarchitectural Support
4. Experimental Results and Analysis
4.1. Experimental Setup
4.2. Fault Coverage
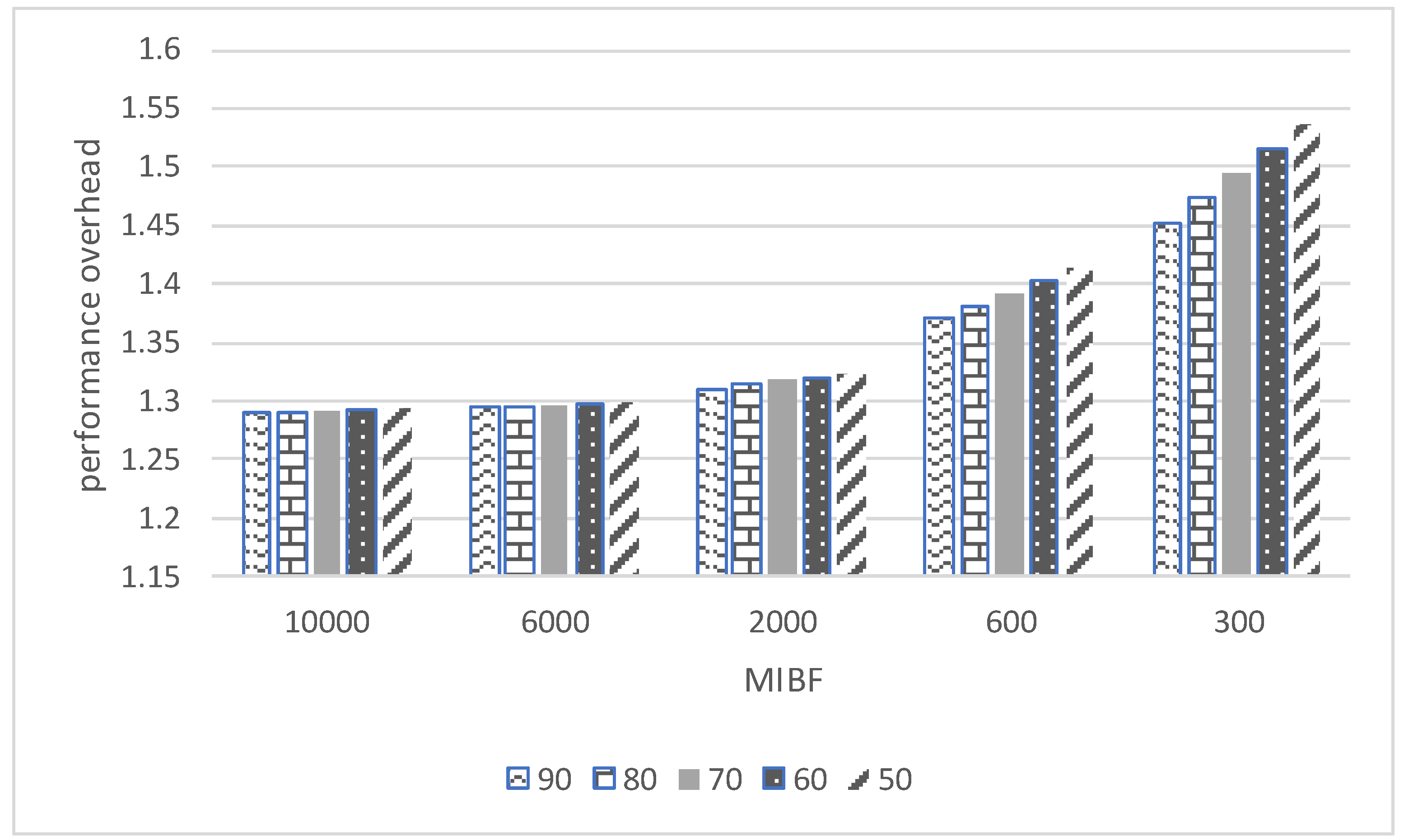
4.3. Comparison of Performance Overheads
4.4. Comparison of Area Overheads
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, L.; Zhu, W.; Yin, S.; Wei, S. A Binary-Feature-Based Object Recognition Accelerator With 22 M-Vector/s Throughput and 0.68 G-Vector/J Energy-Efficiency for Full-HD Resolution. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 38, 1265–1277. [Google Scholar] [CrossRef]
- Cousins, D.B.; Rohloff, K.; Sumorok, D. Designing an FPGA-accelerated homomorphic encryption co-processor. IEEE Trans. Emerg. Top. Comput. 2016, 5, 193–206. [Google Scholar] [CrossRef]
- Wang, C.; Gong, L.; Yu, Q.; Li, X.; Xie, Y.; Zhou, X. DLAU: A scalable deep learning accelerator unit on FPGA. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2016, 36, 513–517. [Google Scholar] [CrossRef]
- De Donno, D.; Esposito, A.; Monti, G.; Tarricone, L. GPU-based acceleration of MPIE/MoM matrix calculation for the analysis of microstrip circuits. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011; pp. 3921–3924. [Google Scholar]
- Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU computing. Proc. IEEE 2008, 96, 879–899. [Google Scholar] [CrossRef]
- De Oliveira, D.A.G.G.; Pilla, L.L.; Santini, T.; Rech, P. Evaluation and mitigation of radiation-induced soft errors in graphics processing units. IEEE Trans. Comput. 2015, 65, 791–804. [Google Scholar] [CrossRef]
- Saggese, G.P.; Wang, N.J.; Kalbarczyk, Z.T.; Patel, S.J.; Iyer, R.K. An experimental study of soft errors in microprocessors. IEEE Micro 2005, 25, 30–39. [Google Scholar] [CrossRef]
- Constantinescu, C. Trends and challenges in VLSI circuit reliability. IEEE Micro 2003, 23, 14–19. [Google Scholar] [CrossRef]
- Nvidia, C. Nvidia’s next generation cuda compute architecture: Fermi. Comput. Syst 2009, 26, 63–72. [Google Scholar]
- Shi, G.; Enos, J.; Showerman, M.; Kindratenko, V. On testing GPU memory for hard and soft errors. In Proceedings of the Symposium on Application Accelerators in High-Performance Computing, Urbana, IL, USA, 28–30 July 2009. [Google Scholar]
- Haque, I.S.; Pande, V.S. Hard data on soft errors: A large-scale assessment of real-world error rates in gpgpu. In Proceedings of the 2010 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing, Melbourne, Australia, 17–20 May 2010; pp. 691–696. [Google Scholar]
- Borkar, S. Designing reliable systems from unreliable components: The challenges of transistor variability and degradation. IEEE Micro 2005, 25, 10–16. [Google Scholar] [CrossRef]
- Tiwari, D.; Gupta, S.; Gallarno, G.; Rogers, J.; Maxwell, D. Reliability lessons learned from gpu experience with the titan supercomputer at oak ridge leadership computing facility. In Proceedings of the SC’15: International Conference for High Performance Computing, Networking, Storage and Analysis, Austin, TX, USA, 15–20 November 2015; pp. 1–12. [Google Scholar]
- Santos, F.F.d.; Rech, P. Analyzing the criticality of transient faults-induced SDCS on GPU applications. In Proceedings of the 8th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems, Denver, CO, USA, 12–17 November 2017; pp. 1–7. [Google Scholar]
- Li, G.; Pattabiraman, K.; Cher, C.-Y.; Bose, P. Understanding error propagation in GPGPU applications. In Proceedings of the SC’16: International Conference for High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 13–18 November 2016; pp. 240–251. [Google Scholar]
- Soundararajan, N.K.; Parashar, A.; Sivasubramaniam, A. Mechanisms for bounding vulnerabilities of processor structures. In Proceedings of the 34th International Symposium on Computer Architecture (ISCA 2007), San Diego, CA, USA, 9–13 June 2007; pp. 506–515. [Google Scholar]
- Biswas, A.; Racunas, P.; Cheveresan, R.; Emer, J.; Mukherjee, S.S.; Rangan, R. Computing architectural vulnerability factors for address-based structures. In Proceedings of the 32nd International Symposium on Computer Architecture (ISCA’05), Madison, WI, USA, 4–8 June 2005; pp. 532–543. [Google Scholar]
- Sheaffer, J.W.; Luebke, D.P.; Skadron, K. A hardware redundancy and recovery mechanism for reliable scientific computation on graphics processors. In Proceedings of the Graphics Hardware, San Diego, CA, USA, 4–5 August 2007; pp. 55–64. [Google Scholar]
- Mitra, S.; McCluskey, E.J. Word-voter: A new voter design for triple modular redundant systems. In Proceedings of the 18th IEEE VLSI Test Symposium, Montreal, QC, Canada, 30 April–4 May 2000; pp. 465–470. [Google Scholar]
- Jeon, H.; Annavaram, M. Warped-dmr: Light-weight error detection for gpgpu. In Proceedings of the 2012 45th Annual IEEE/ACM International Symposium on Microarchitecture, Vancouver, BC, Canada, 1–5 December 2012; pp. 37–47. [Google Scholar]
- Abdel-Majeed, M.; Dweik, W.; Jeon, H.; Annavaram, M. Warped-re: Low-cost error detection and correction in gpus. In Proceedings of the 2015 45th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, Rio de Janeiro, Brazil, 22–25 June 2015; pp. 331–342. [Google Scholar]
- Liu, Q.; Jung, C.; Lee, D.; Tiwari, D. Clover: Compiler directed lightweight soft error resilience. ACM Sigplan Not. 2015, 50, 1–10. [Google Scholar]
- Nathan, R.; Sorin, D.J. Argus-G: Comprehensive, Low-Cost Error Detection for GPGPU Cores. IEEE Comput. Archit. Lett. 2014, 14, 13–16. [Google Scholar] [CrossRef]
- Meixner, A.; Bauer, M.E.; Sorin, D. Argus: Low-cost, comprehensive error detection in simple cores. In Proceedings of the 40th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO 2007), Chicago, IL, USA, 1–5 December 2007; pp. 210–222. [Google Scholar]
- Aamodt, T.M.; Fung, W.W.; Singh, I.; El-Shafiey, A.; Kwa, J.; Hetherington, T.; Gubran, A.; Boktor, A.; Rogers, T.; Bakhoda, A. GPGPU-Sim 3. X Manual. 2012. Available online: http://gpgpu-sim.org/manual/index.php/Main_Page (accessed on 4 November 2020).
- Che, S.; Boyer, M.; Meng, J.; Tarjan, D.; Sheaffer, J.W.; Lee, S.-H.; Skadron, K. Rodinia: A benchmark suite for heterogeneous computing. In Proceedings of the 2009 IEEE International Symposium on Workload Characterization (IISWC), Austin, TX, USA, 4–6 October 2009; pp. 44–54. [Google Scholar]
- Bush, J.; Dexter, P.; Miller, T.N.; Carpenter, A. Nyami: A synthesizable GPU architectural model for general-purpose and graphics-specific workloads. In Proceedings of the 2015 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Philadelphia, PA, USA, 29–31 March 2015; pp. 173–182. [Google Scholar]
- Nikhil, R. Bluespec System Verilog: Efficient, correct RTL from high-level specifications. In Proceedings of the Second ACM and IEEE International Conference on Formal Methods and Models for Co-Design, 2004, MEMOCODE’04, San Diego, CA, USA, 23–25 June 2004; pp. 69–70. [Google Scholar]







| Erroneous Output | TMR | Anticipated Correct Output (ACO) | Anticipated Incorrect Output (AIO) | |||||
|---|---|---|---|---|---|---|---|---|
| Output | Result | Output | Prediction | Result | Output | Prediction | Result | |
| O1 | O2 | Correct | O3 | Failure | Correct | O3 | Failure | Correct |
| O2 | O1 | Correct | O1 | Success | Correct | O1 | Success | Correct |
| O3 | O1 | Correct | O1 | Success | Correct | O1 | Success | Correct |
| O1, O2 | X | Incorrect | O3 | Failure | Correct | O1 | Success | Incorrect |
| O1, O2 | X | Incorrect | O3 | Failure | Incorrect | O1 | Success | Incorrect |
| O2, O3 | X | Incorrect | O3 | Failure | Incorrect | O1 | Success | Correct |
| O1, O2, O3 | X | Incorrect | O3 | Failure | Incorrect | O1 | Success | Incorrect |
| Additional Area Overhead | Total Area | Overhead (%) | |
|---|---|---|---|
| Normal | 0 | 768,824 | 0.00% |
| DMR [18] | 56,388 | 825,213 | 6.83% |
| TMR | 42,588 | 811,412 | 5.24% |
| PRECOR | 52,974 | 821,798 | 6.44% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, H.; Kim, T.H.; Kang, S. Prediction-Based Error Correction for GPU Reliability with Low Overhead. Electronics 2020, 9, 1849. https://doi.org/10.3390/electronics9111849
Lim H, Kim TH, Kang S. Prediction-Based Error Correction for GPU Reliability with Low Overhead. Electronics. 2020; 9(11):1849. https://doi.org/10.3390/electronics9111849
Chicago/Turabian StyleLim, Hyunyul, Tae Hyun Kim, and Sungho Kang. 2020. "Prediction-Based Error Correction for GPU Reliability with Low Overhead" Electronics 9, no. 11: 1849. https://doi.org/10.3390/electronics9111849
APA StyleLim, H., Kim, T. H., & Kang, S. (2020). Prediction-Based Error Correction for GPU Reliability with Low Overhead. Electronics, 9(11), 1849. https://doi.org/10.3390/electronics9111849






