A Simulator to Support Machine Learning-Based Wearable Fall Detection Systems

Abstract

People’s life expectancy is increasing, resulting in a growing elderly population. That population is subject to dependency issues, falls being a problematic one due to the associated health complications. Some projects are trying to enhance the independence of elderly people by monitoring their status, typically by means of wearable devices. These devices often feature Machine Learning (ML) algorithms for fall detection using accelerometers. However, the software deployed often lacks reliable data for the models’ training. To overcome such an issue, we have developed a publicly available fall simulator capable of recreating accelerometer fall samples of two of the most common types of falls: syncope and forward. Those simulated samples are like real falls recorded using real accelerometers in order to use them later as input for ML applications. To validate our approach, we have used different classifiers over both simulated falls and data from two public datasets based on real data. Our tests show that the fall simulator achieves a high accuracy for generating accelerometer data from a fall, allowing to create larger datasets for training fall detection software in wearable devices.

1. Introduction

According to the World Health Organization (WHO), the number of people over 60 years of age is set to double by 2050. This ageing of the world population will require major societal changes to improve life quality in the elderly [1]. Care of such population from the social perspective will require a significant effort, not only from the point of view of the administration, but also from the family, as ageing is usually related to dependency. In this sense, one concern is how to take care of seniors living alone. Such cases represent a challenge that comprises independence and supervision. Particularly, it is important to supervise the health condition of independent people, by monitoring their environment for being able to respond to unexpected conditions.

One condition that often affects independent elderly people are falls. It is known that falls in the elderly are a public health problem [2], as reported by the WHO in a global report [3]. They are not only a significant source of problems associated with the elderly for their direct consequences (such as trauma), but also because falls are a symptom of infirmity (such as heart attack) [4]. Therefore, the research and development of fall detection systems are becoming relevant, as a quick response in such events can save lives. This fact is confirmed by the increasing amount of literature on fall detection.

In the literature, we can see that this problem is being approached from different perspectives [5]. For instance, we can highlight the usage of Machine Learning (ML) applied both to image and video recognition [6], as well as audio processing [7] for fall detection. In particular, we want to underline our LARES project [8], whose main objective is the passive monitorization of dependent people in opposition to common (and less effective) active systems based on teleasistance, in which the dependent has to activate a necklace to ask for assistance. This objective is achieved through the deployment of a Wireless Sensor Network along with a low-cost robot, supervised by a dependent’s family member or a caregiving service via a Web-based system. In order to achieve a better monitorization, this project aims to include a fall detection system based in ML techniques, gathering the required data using a tri-axial accelerometer embedded in a smartwatch or bracelet worn by the dependent person. Using the information provided by the different components of LARES, we can quickly provide assistance to the person in case of a fall, or other unexpected events.

The main disadvantage of the classical telecare systems is the psychological rejection of the dependant to any device that reveals his/her dependency. A workaround that is commonly used is to provide a smartwatch to the dependant, that looks like a regular watch and does not have negative connotations. Those devices are becoming more sophisticated, including multiple health monitoring capabilities. Among them, the most common are accelerometers, typically used to monitor daily activities such as walk or sleep, that can be used to detect falls. Moreover, the smartwatch is always located in the wrist, easing the development of fall detection algorithms, as they will use the same relative position with respect to the body.

In spite of the extensive research about ML techniques for fall detection systems, a key problem that every research faces is the scarce amount of realistic fall datasets available; proper training of ML models requires large amounts of data. In order to contribute to the research efforts of building reliable datasets suitable for ML purposes, we propose the Intelligent Systems Group (ISG) Fall Simulator, a fall simulator for the generation of falls in a realistic way. The simulator allows the customization of the physiology of the humanoid as well as the falls conditions.

The simulator is built upon a physics engine used in the video game industry. Using a video game engine for physics simulation as a solution to real testing (more expensive and, sometimes, impracticable) has already been explored in the literature. For instance, we can mention the CARLA simulator [9], made with the Unreal Engine, a powerful yet free to (non-commercial) use game engine. This simulator is built to validate autonomous driving systems, reducing the cost and complexity associated to perform real test benches. The high degree of realism of this kind of physics engine, along with its customization capabilities, allows us to simulate a broad variety of simulated, yet realistic, falling sequences that can be used to generate large synthetic fall datasets.

In this paper, we present an extension and validation of our previous work [10] in which we have developed a fall simulator using the Unity game engine. More in detail, we have extended the simulator capabilities, allowing the parameterization of the falls. The simulator is able to automatically generate and gather data from several falls, by recreating the data that a tri-axial accelerometer registers during the simulated fall. In our current implementation, the accelerometer is placed on the humanoid’s wrist but can be easily switched to different positions. Moreover, we can simulate the two most common types of fall that can occur at home: syncope and forward falls. They are typically the consequence of a loss of consciousness or a stumbling block, respectively, and they are the two most frequent falls types in the elderly people according to experts consulted. We should mention that many conditions such as a heart attack or a hip fracture end in a syncope fall since the first reaction to any serious health condition uses to be falling down. For validating the updated fall simulator, we have performed a comparison of the simulated accelerometer measurements against two publicly accessible fall datasets that have already been used in the field: the University of Malaga dataset, UMAfall [11], and Panamerican University, UP-fall [12] dataset. In this regard, we have trained different classification algorithms using the aforementioned datasets and, then, validated the classifiers using the measurements generated by our simulator.

The rest of the paper is structured as follows. The following section gives an overview of the current state of the art related to our work. Section 3 presents both the underlying physics of the simulator as well as the specific implementation inside the game engine. Next, the experimental results showcases a comparison between the simulated data and the previously mentioned public datasets. Finally, some conclusions are outlined.

2. Related Work

The main requirement for an ML algorithm is the availability of the data to train the models. Some ML techniques such as deep neural networks are especially dependent on the availability of large amounts of data [13]. Focusing on fall detection, the problem is not only related to the data gathering, but also with the technology and methodology used to retrieve the fall information. In our previous works related to the monitoring of elderly people falling, we faced the problem of collecting related data [7,8] in order to satisfy our needs at the moment. After consulting with experts in geriatrics, the use of a dummy was suggested. Our experience in both these instances led us to the realization of the inherent shortcomings of this method.

It is clear that, for feeding an ML algorithm, we need to collect a large amount of data, which is in most cases impracticable. Despite the difficulty to retrieve data for ML fall detection models, several works have been carried out in order to supply quality samples that may be used for such a task, producing public datasets.

Notwithstanding, as stated in E. Casilari et al. [14] survey on fall datasets, one of the main problems of publicly available datasets is their lack of homogeneity. Their length and number of samples, typology of the emulated falls and Activities of Daily Life (ADL), traits of the test subjects, features and positions, hardware specifications of the accelerometers, as well as the development of each kind of fall, greatly varies between different sources. Furthermore, individual differences in the gait and movements of each subject greatly impacts accuracy in the developed ML algorithms. This issue is compounded by the need to use cushioning in order to prevent damage to the subjects, potentially polluting data collected in this way. Additionally, subjects are often young adults in order to prevent damage to the elderly, which leads to further divergences from actual behaviours that need to be monitored [15,16]. Namely, the shift of the center of gravity, while ageing, tends to be displaced forward and downward due to an increased separation between the legs and curvature of the trunk. Additionally, the rotational capabilities of the elders’ limbs are significantly reduced, and their reaction time, increased. All of these problems can be circumvented by the usage of a simulator, due to the ability to configure and customize the scenario that needs to be simulated at any given time.

Aside from the already established advantages of a simulator, it is also possible to configure the number, location and initial orientation of accelerometers. It is, then, possible to gather larger amounts of data for each location, without incurring any additional effort or cost.

Other approaches focus on biomechanics simulations that allow researchers to understand and recreate the conditions that accompanied an injury [17]. For example, we can analyze the causes that provoke a car accident [18], a person’s fall [19] or generate valuable data without putting any person or property at risk [20]. Within this approach, some authors follow a physical analysis of a person’s fall. We can mention the study of Lau et al. [21] that uses a mathematical model to estimate the height of a fall based on the damages experienced by different subjects. Barbuceanu et al. [22], on the contrary, focus on falls related to sport activities. They use a mathematical model of the bones and the joints of the muscular groups of the legs of a falling sportswoman.

Other authors approximate this problem by using computer-based simulations. O’Riordain et al. [23] recreate real head injuries as consequence of a fall. The work employs a multibody modelling software with random initial requirements in order to find the best fit with the real conditions. Alternately, Wach and Unarski [24] developed a virtual 3D model of a person’s fall from height in a stairwell to help forensic investigators to reconstruct the situation that caused the fall.

For the time being, mathematical models and closed source software are the main systems used to cover human movement and the development of falls. To our knowledge, there are no open source solutions that could be used to simulate different kind of falls. Additionally, current simulators do not offer enough data during the fall, making then not suitable for ML purposes, saving the work of O’Riordain et al. [23] which is focused around accelerations in the head.

However, there are some exceptions that have used physics simulations to recreate fall events, such as the work by Mastorakis et al. [25], started in 2007 using OpenSim to simulate a myoskeletal model, further developed in a later work [26] which added the usage of ML to simulate the fall with a higher degree of precision. Nevertheless, since our objective is to train ML algorithms to detect falls that do not necessarily start from a static position, those simulators do not fit our purposes; we need a highly customizable fall simulator from which we can record the measurements that wearable devices, such as bracelets or smartwatches, would have.

Neural Networks have been greatly improved in recent times [27,28,29]. This technique has consistently displayed a greater learning potential than traditional ML techniques. However, their very nature leads to data starvation issues, requiring large volumes of varied samples in order to satisfy the requirements to satisfactorily train any moderately complex classifier or regressor. Datasets based on gathering input from human beings fail to satisfy this need, due, in no small part, to the difficulty of gathering useful samples.

Then, in this work we present a customizable fall simulator to generate enough data from different types of falls to feed ML algorithms. In this regard, to validate our simulator, we will employ two of the publicly accessible falls datasets mentioned in the previous survey: UMAfall [11] and UP-fall [12]. They are selected because they are generated using real data (collected by physical triaxial accelerometers), so they are relevant in the literature and, also, they are public. Moreover, they exhibit the traits already mentioned, and they have been used for studies related to ML [27,30,31].

3. The Fall Simulator

One of the bigger challenges when dealing with ML applications is gathering enough high quality data to train and test the system. For the problem at hand, this issue is also compounded with the risks involved in having an actor perform a realistic fall in order to gather data. In the past, we explored the idea of using a dummy instead in order to generate samples. However, this approach presents significant problems, namely;

• Cost of the dummy: a dummy that has human-like physiology is very expensive.
• Damages over successive tests: for retrieving enough data, we need to recreate several falls, so the damage taken each fall is accumulated, wearing down the dummy articulations, compromising the recorded data.
• Dummy physiology is fixed: the physical characteristics of the dummy cannot be modified, so there is no possibility to modify the weight and height, so the data is restricted to those physical characteristics.
• Falls limitation: the dummy does not have locomotion capabilities, so only falls where the consciousness is lost can be recorded.
• Personnel and time constraints: Those tests have to be performed by a professional that can validate the development of the fall, therefore, the accelerometer data has to be recorded manually.
• Required hardware: an accelerometer is needed to collect the fall data. In the same way as the dummy, the accelerometer is subject to suffer damages due to the testing process.

Thus, the quality of the data obtained from such a method was found lacking for the purpose of ML.

We have simulated two types of falls, which we have named syncope and forward falls. The dynamics involved in each kind of fall are, as a result of their nature, different. As a result, their implementation needs had to be addressed independently of each other, paying special attention to the starting points and human reaction during the fall.

• Syncope falls are those falls resulting from a loss of consciousness, or heart conditions that prevent using the muscles to control the fall. Due to the loss of control over one’s body, these falls present a vertical motion, and can be divided in two distinct stages. Firstly, the subject’s knees hit on the ground, and then the trunk collapses forward until it impacts with the floor. For this kind of fall, we perform tests using a dummy [32] under the supervision of infirmary experts, who helped us understand how this kind of fall would actually happen on a real person. We realized there was a need to exert a small forward force onto the dummy so that it would fall properly, in case the person happened to be standing up. This appreciation was directly translated to our simulator, by applying a similar force and introducing a small amount of noise in both the direction and intensity of the force in order to generate varied results. Afterwards, all seemingly unnatural instances were discarded in order to curate the resulting dataset. This kind of fall is presented in Figure 1. In this scenario, in our opinion, it is better to obtain the data by means of a non-human source, be it a dummy or our simulator, since human reflexes could pollute the readings by trying to protect themselves from the damage of the fall. The use of our approach makes the application of the necessary force more consistent and greatly reduces the required human effort to record the data compared to the use of a dummy.
• Forward falls are originated by the collision of a foot with an object while the person is walking, losing balance and falling over. The trunk in this type of fall collapses forward, while the arms and hands, after some reaction time, try to cushion the fall in order the prevent further damage.

Following subsections describe the physics and the implementation of these falls in our simulator.

3.1. Physics

The simulation of the process of tripping and falling was based on a rigid-body physics engine, which implements the physical modelization. However, in order to implement the simulator, it is needed to gather acceleration measures on some parts of the simulated body. It can be envisioned as a virtual accelerometer able to obtain acceleration measures from the physics subsystem. This issue requires some considerations given that the physics model only provides data about the position and momentum.

It should be noted that the simulation operates in discrete time, although momentum and position are calculated using their physical definitions. Thus, whilst data points were computed from an already discrete sequence, the process involved in generating them heavily relied on continuous time functions. This function was fed with a time parameter, usually referred to as $\Delta t$, in order to smooth out the resulting output. The result of this simulation process was a set of 3D coordinates at different points in time. It was, then, necessary to establish the physical interpretation of these data in order to obtain acceleration values.

For that reason, we studied in the first place the analytical implications of such data synthesis. The simulated accelerometer provides discretized positions and it could be interpreted as a particle moving in a 3D space. Given that this motion is defined in continous time and space, we use the generalized tensor function in Equation (1) to describe it. Therefore, we compute the position $\overrightarrow{P}\left(t\right)$ of the particle or accelerometer at any given point in time with its position in the time step immediately preceding. Thus, the variation of the position can be expressed as a 3-dimensional tensor according to Equation (1).

$$\overrightarrow{P}\left(t\right)=\overrightarrow{P}(t-1)+\frac{\partial \overrightarrow{P}}{\partial t}\left(t\right).$$

(1)

In order to further simplify the problem, we apply the physical definition of velocity as the derivative of the position $\overrightarrow{P}\left(t\right)$ over time, that is, $\frac{\partial \overrightarrow{P}}{\partial t}\left(t\right)$. Provided that velocity is not static, we can approximate its value by adding its variation at any given time, resulting in the relation described in Equation (2).

$$\overrightarrow{V}\left(t\right)=\frac{\partial \overrightarrow{P}}{\partial t}\left(t\right)=\overrightarrow{V}(t-1)+\frac{\partial \overrightarrow{V}}{\partial t}\left(t\right).$$

(2)

Finally, classical mechanics defines acceleration as the variation of velocity over time. Therefore we can apply the same reasoning to obtain a discretization of the acceleration, by assuming its value to be the variation in velocity. Following this reasoning, we can express acceleration as a function of its value in the previous time step, as described in Equation (3).

$$\overrightarrow{A}\left(t\right)=\frac{\partial \overrightarrow{V}}{\partial t}\left(t\right)=\overrightarrow{A}(t-1)+\frac{\partial \overrightarrow{A}}{\partial t}\left(t\right).$$

(3)

With all the previous considerations, we are in position to describe the state of the system using a discrete time model. We should stress that the physical model provides us with the location of the accelerometer at a given time, and not the measures that it provided. In order to compute accelerations from the location data, we apply Equations (1)–(3) as follows.

$$\begin{array}{c}\hfill \overrightarrow{P}\left(t\right)=\overrightarrow{P}(t-1)+\frac{\partial \overrightarrow{P}}{\partial t}\left(t\right)=\\ \hfill \overrightarrow{P}(t-1)+\overrightarrow{V}\left(t\right)=\overrightarrow{P}(t-1)+\overrightarrow{V}(t-1)+\frac{\partial \overrightarrow{V}}{\partial t}\left(t\right)=\\ \hfill \overrightarrow{P}(t-1)+\overrightarrow{V}(t-1)+\overrightarrow{A}\left(t\right)\end{array}$$

resulting that acceleration is expressed by Equation (4).

$$\begin{array}{c}\hfill \Rightarrow \overrightarrow{A}\left(t\right)=\overrightarrow{P}\left(t\right)-\overrightarrow{P}(t-1)-\overrightarrow{V}(t-1)=\overrightarrow{V}\left(t\right)-\overrightarrow{V}(t-1).\end{array}$$

(4)

Equation (4) provides a proper and computationally efficient approximation to the acceleration, which lets us implement a sort of virtual accelerometer to measure the accelerations along the simulated falls.

3.2. Implementation

From the variety of game engines that include realistic physics simulations, we decided to use Unity (https://unity.com) game engine due to its free non-commercial nature, and the accuracy of the underlying physics engine, powered by NVidia’s Physx System Software (https://developer.nvidia.com/gameworks-physx-overview), considered as a standard in the industry. Additionally, this physics engine is not deterministic, meaning that the same initial situation may lead to different outcomes, which further increases the variety of the generated fall samples.

We used a humanoid 3D model as the starting point, adding the necessary colliders and joints to the model’s limbs. Then, we adjusted the weight of each limb as well as the rotational capabilities of each joint to human-like values, making it possible to simulate valid falls. After a base humanoid was properly configured, we made several modifications to make it more similar to an elderly person’s body: the weight was redistributed, increasing the total weight of the trunk and reducing it on the extremities, the rotational capabilities of each joint were limited, and the center of mass was slightly lowered to better match the elderly person’s movement pattern. This modelizaton was made under the supervision of experts in Geriatrics.

To simulate the selected kind of fall events, in both cases, we used an animation, which is not affected by the physics simulation, as the starting point. At a certain point, the animation is interrupted and the physics engine takes over, simulating the fall of the model.

Regarding the forward falls, the humanoid starts moving playing a walking animation, which is randomly selected from a variety of possibilities, all significantly different from each other to provide different starting points to the fall. While walking, the model will eventually collide with an obstacle, whose position, height, and orientation are randomized between certain values to provide a wide variety of heterogeneous falls. Once the model collides with the obstacle, we simulate a tripping reaction, letting the physics engine take over and applying forward forces to the trunk. Then, after a few milliseconds, emulating the reaction time of the person, upward forces are applied to the arms, to simulate the natural reaction of trying to cushion the fall, considering the reduced mobility of an elder. Additionally, since the final animation pose before the model trips and the physics simulation starts depends on the randomized position of the obstacle, each fall will be significantly different from the rest. The development of a forward fall in the simulator is depicted in Figure 2.

In the case of the syncope falls, the starting point will be either a walking animation or a daily life activity, for example, talking, moving objects, using the phone among others, or even the model standing idle. Then, to emulate the loss of consciousness, we suddenly stop the animation and let the physics engine simulate the consequent fall. In this particular instance, after some testing, we found the need to apply a small forward force so that the model falls similarly to a person. The development of a syncope fall in the simulator is shown in Figure 3.

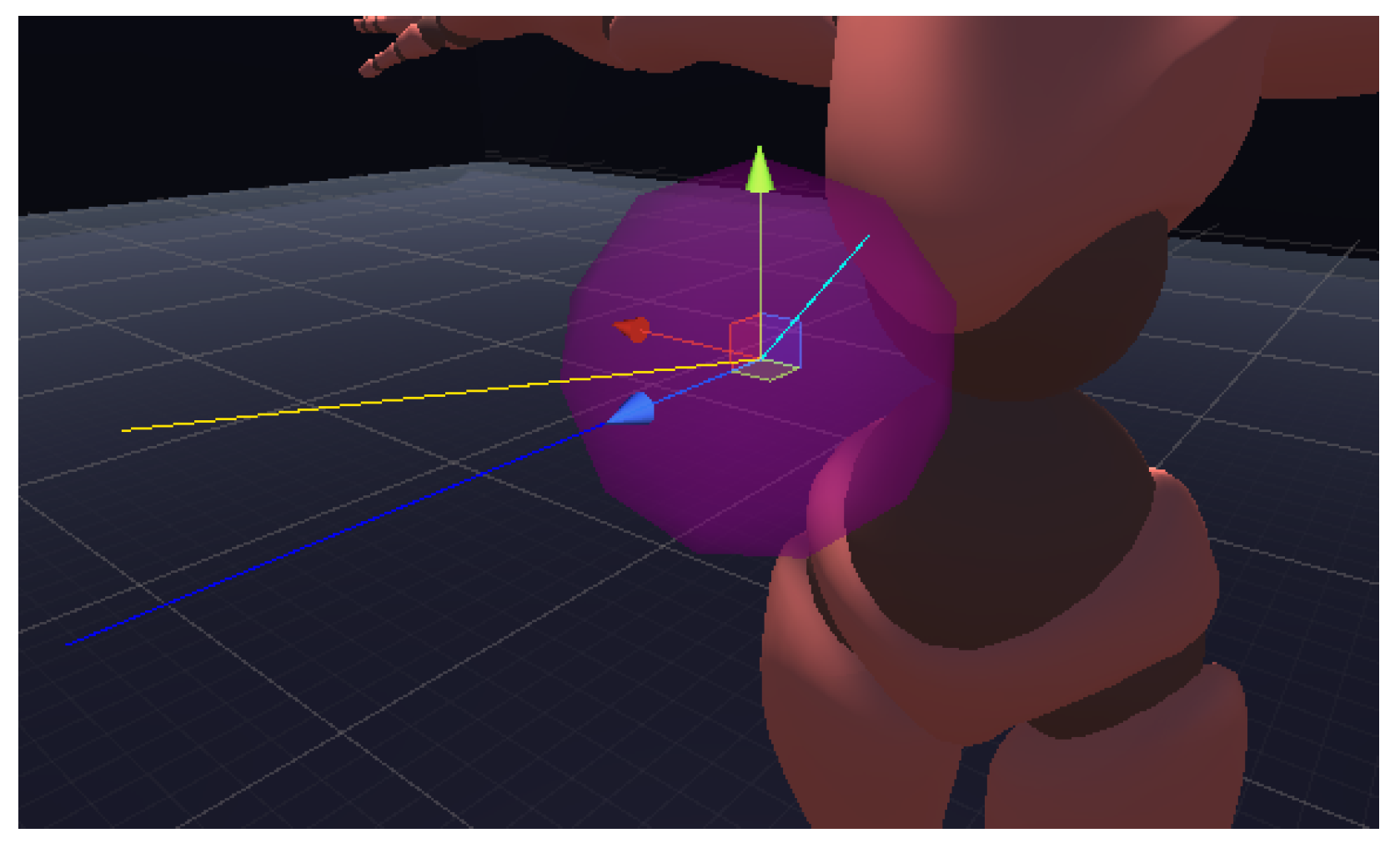
To further increase the diversity of the simulated falls we decided to slightly modify every force applied to the humanoid by the addition of some noise. This modification is not significant enough to make the falls unnatural, but it alters the falls enough so even if the previous conditions are similar, the fall will be developed in a somewhat different way. If we consider each force as a vector, its module will be multiplied by a value between two limits selected using a Gaussian distribution to alter the strength of the force. Additionally, the direction of the force will be further modified by adding a random point inside a small sphere and normalizing the direction of the resulting vector afterwards, as shown in Figure 4. In the figure, the blue line represents the unmodified force, the cyan line represents the modification that will be applied and the yellow line the final force that will be applied. This randomness in conjunction with the non-deterministic nature of Unity’s physics engine ends up in a wide variety of simulated falls.

To simulate the measurements that the accelerometer would have, we recorded the position that a smartwatch would have if it was attached to the left wrist of the model, using fixed time steps between each record of 20 ms. This is the usual maximum operational frequency of commercial grade accelerometers. We decided to use the maximum frequency since no information would be lost if the frequency had to be downsampled to match another accelerometer, but significant information would be lost if an upsampling process were applied. Additionally, to properly simulate the force of gravity, we calculated the direction of a vector pointing downwards in the local space of the wrist in each time step. The recorded directions and positions were then computed as presented in the previous section, obtaining the measures that a real accelerometer would have measured if it had been exposed to the same motions.

In order to perform said values transformation, it is necessary to adapt the logic applied in Equation (1) through Equation (4) to a discrete, sampled system. Provided that the simulation would be outputting specific positions, as measured by the simulated accelerometer, as well as the time between different measures being taken, it is possible to calculate the displacement vector between individual timesteps and obtain the velocity the simulated accelerometer was subjected to during it.

Let $\overrightarrow{v}$ represent the resulting velocity vector; $\Delta \overrightarrow{p}$ represents the displacement vector of the accelerometer between timesteps, and $dt$ represents the time difference between timesteps, then Equation (5) can be used to calculate the resulting velocity vector from the simulator’s raw data.

$$\overrightarrow{v}=\frac{\Delta \overrightarrow{p}}{dt}.$$

(5)

Likewise, provided that we can obtain the velocity vector between timesteps, let $\overrightarrow{a}$ represents the acceleration vector for the accelerometer in a given timestep, $\Delta \overrightarrow{v}$ the velocity difference between timesteps, represented as a vector, and $dt$ the time difference between timesteps; we can calculate the acceleration vector, and therefore the simulated accelerometer output, for any given timestep using Equation (6).

$$\overrightarrow{a}=\frac{\Delta \overrightarrow{v}}{dt}.$$

(6)

It should be noted that the resulting dataset will present clean data. Therefore, actual sensor readings must be filtered in order to be properly compared to. Likewise, in order to simulate actual, noisy sensor data, a noise function, such as a Gaussian noise function, must be applied over the result.

4. Experimental Results

In order to properly evaluate the simulator’s performance, we have compared the obtained accelerometer records in our simulated falls to the ones created using real-life subjects from previously validated works, namely, the UMA-Fall dataset [30], which contains accelerometer records generated by a group of 19 experimental subjects that emulated a set of predetermined ADLs and several types of falls; and the UP-Fall dataset [12], which contains records of 11 different activities performed by 17 different subjects, five of those were different kinds of falls.

Both datasets contain accelerometer recordings of several different activities, including falls, performed by a variety of subjects in a controlled environment, with the final objective of training ML classifiers, able to distinguish fall events from the other activities. The UMA-Fall dataset records the data using 4 accelerometers placed in different parts of the body (right ankle, left wrist, lower and upper trunk) and a smartphone in a trouser pocket, whereas the UP-Fall uses 6 accelerometers (ankle, right pocket, waist, neck, forehead and wrist) and infrared sensors. In both cases, the measurements that we will use are the ones recorded using an accelerometer located in the wrist, similar to our simulated one.

The way the falls develop is similar to that of the simulator, the subjects walk towards a thick pad until they collide with it, falling over, in the case of falls similar to the forward type. In the case of the syncope type, they just fall over the pad.

To develop a more precise evaluation, we also recorded accelerometer measures of different activities that did not include fall events using our simulator, similar to the ones included in the compared datasets. For doing that, we have used a variety of animations from the same source as the walking ones.

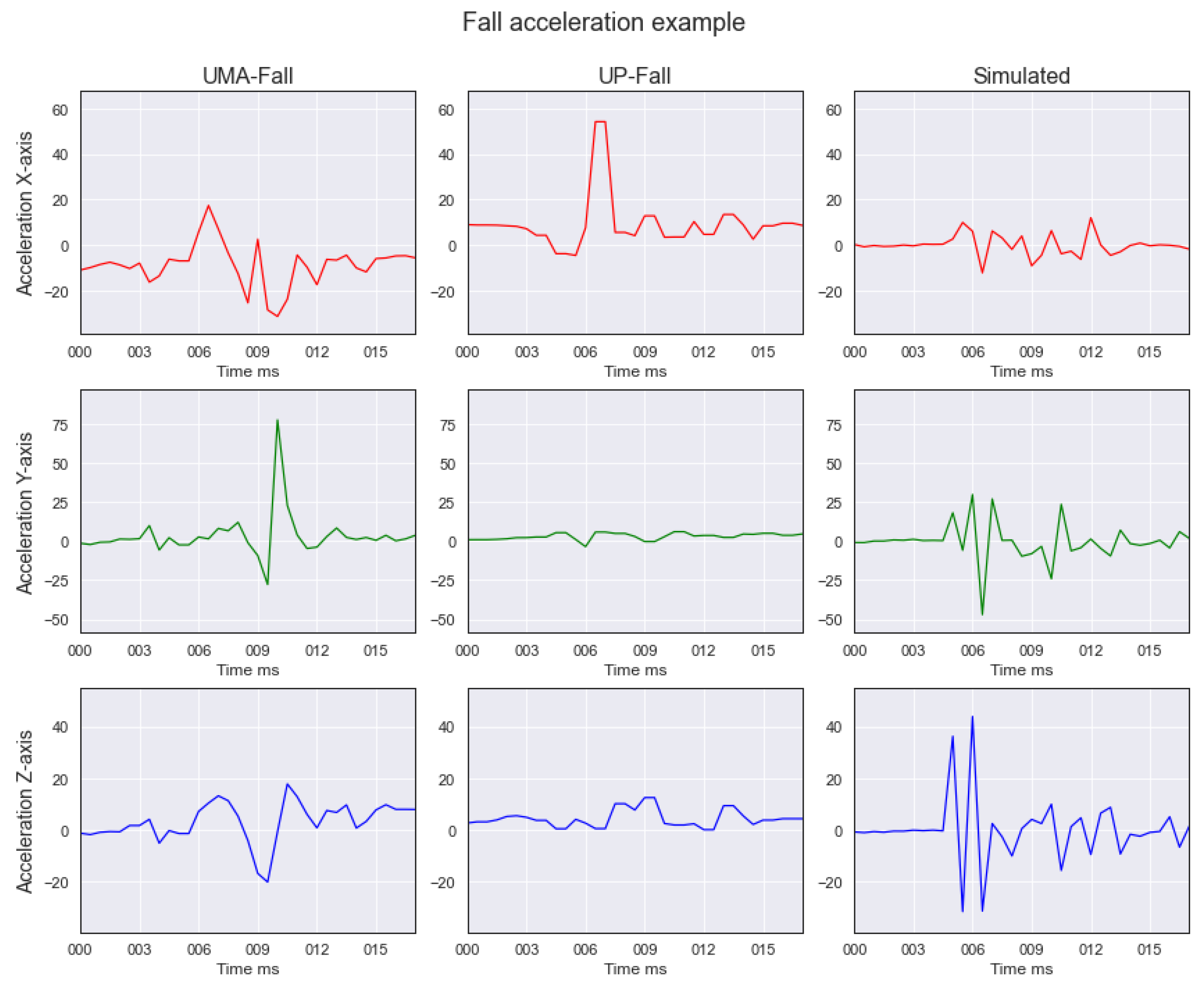
Figure 5 depicts a comparison of the accelerations recorded during a forward fall event, from the three datasets used in this work, the UMA-Fall (left), UP-Fall (center) and our simulated one (right). As we can see in the figure, an axis always presents much more variation than the other two; in the UMA-Fall record, the Y-axis presents the highest variation, whereas in the UP-Fall one it is the X-axis and finally, in the simulated fall the highest variation is found on the Z-axis. This is inherently caused by the way an accelerometer works, since the starting rotation of the accelerometer in the fall, makes it possible for two overall similar falls, to have similar variations on a different axis. Moreover, the maximum and minimum values that each accelerometer is able to record are strictly tied to the hardware capabilities, making the use of a scaler even more appealing.

Additionally, there are some important considerations regarding the specific problem of working with fall events and using accelerometers as the only source of information:

• The duration of the fall events is not fixed. Some falls, depending on how they develop, can have a much shorter or longer duration. For example, if a person first falls on his knees and then the rest of the trunk, the fall will be overall much longer than if he falls with his whole body directly; or if during the fall the body collides with another object before impacting the ground, the resulting accelerations will be greatly different.
• Since we are gathering the acceleration measures using an accelerometer located on the wrist, the initial position of the arm plays a major role in the fall events. In the case of forward falls, if the fall is initiated when the arm with the accelerometer is in front, the gathered measurements will be very different from how they would be if it was behind.
• The coordinates system is position dependent. Due to the coordinate system being centred around the accelerometer itself, and considering that each specific hardware may assign a different direction to each axis, evaluating each axis separately has no generalization value.

The previously mentioned inherent characteristics of this problem, make the metrics that are commonly used to evaluate the similarity of time series, such as Dynamic Time Warping or the Pearson Correlation Coefficient, of low analytic value. Instead, in our opinion, using ML classifiers is a more suitable approach to analyze the level of faithfulness achieved by the simulator.

Since our objective is to train algorithms for detecting a fall, regardless of which kind of fall happens, the problem can be approached as a binary classification: one ‘Fall’ class that encompasses all the different fall events (syncope and forward fall in our simulator). Whereas the other one, a null class, simply named ‘NotFall’, is composed of all the other different activities that do not feature falls. This approach makes available a wide variety of algorithms to perform the classification.

To properly classify the accelerometer measures, the process used in our previous work [7] was followed. We grouped the samples in time windows of fixed length, which contains samples that serve as input to the classifier. Those windows that contained samples featuring a fall were labeled ‘fall’; while the other windows that formed of the different activities without fall events were labeled as ‘not-fall’. This approach also indirectly considers history, since each time window contains historical values of accelerations. Additionally, the mean and standard deviation of each axis was calculated and included in each window as post-processing attributes.

In the context of the LARES project, our goal is to implement the classifier in a wearable device. Thus, classic binary lightweight classifiers that fit those needs and were already used in similar previous works, such as the simulator based on OpenSim from Mastorakis et al. [25], were considered as an indirect, yet appropriate, method of verifying the simulated data.

Because the accelerometer values can reach quite high values on the fall events (up to ±80 m/s${}^2$), and some algorithms are susceptible to the scaling of the data, we standardized the features by removing the mean and scaling to unit variance; by doing this, our data is both centred around 0 and scaled so the standard deviation is 1. Additionally, we minimize the difference than could appear due to different hardware capabilities regarding the recording process.

Due to the scarce number of fall instances present in the previous datasets in comparison to the instances of activities not featuring falls, we performed a random sampling from all those possible time windows in order to balance the number of instances of each class, obtaining 5243 time windows for each class from the UMA-Fall dataset and 5948 from the UP-Fall one. Then, we created time windows applying the same procedure to 40 simulated falls, obtaining 1548 time windows containing falls. As for the ‘not-fall’ class, we used the previously simulated activities, applying the same process as before, performing a random sampling until the instances of both classes were balanced.

To measure the performance of the algorithms we calculated the traditional $F_1$ score, which considers both the precision and recall computing their harmonic mean as shown in Equation (7), using the simulated data as the test dataset, additionally, to have an accurate benchmark for each dataset, we also performed the cross-validation with 10 Folds on each dataset. The results obtained for both classes on the various combinations of training and test datasets for each algorithm are shown in

Table 1. $F_1$ score evaluation for the binary falls classification. The training was executed using datasets from other works while the testing was against our simulated dataset or if against themselves, using cross-validation with ten folds.

Train	Test	Class	C4.5	PART	MLP	AdaBoost + Decision Stump	SVM	Random Forest
UMA	UMA	Fall	0.905	0.890	0.851	0.849	0.926	0.942
		NotFall	0.903	0.888	0.854	0.849	0.927	0.939
UMA	Simulated	Fall	0.821	0.822	0.966	0.933	0.954	0.948
		NotFall	0.828	0.860	0.964	0.926	0.950	0.948
UP	UP	Fall	0.936	0.921	0.871	0.849	0.926	0.966
		NotFall	0.933	0.921	0.871	0.842	0.927	0.964
UP	Simulated	Fall	0.782	0.863	0.963	0.887	0.916	0.936
		NotFall	0.718	0.853	0.963	0.873	0.918	0.938

.

$$F_1=2·\frac{\mathrm{precision}·\mathrm{recall}}{\mathrm{precision}+\mathrm{recall}}=\frac{\mathrm{tp}}{\mathrm{tp}+\frac{1}{2}(\mathrm{fp}+\mathrm{fn})}.$$

(7)

Additionally, each classifier had its hyper-parameters optimized using Grid Search in order to maximize its performance on the simulated dataset, even if that resulted in a worse performance on the cross-validation case.

As we can see, Random Forest and SVM algorithms are the two best performers; however, Random Forest slightly outperforms the SVM in three out of the four instances, achieving an F-Measure over 93% in every instance. In the case of the UMA-Fall dataset, our simulated dataset performs even better than the cross-validation on itself on the AdaBoost applied to the Decision Stump, the SVM, and the Random Forest algorithms.

All the algorithms have a very high degree of performance when tested using the cross-validation method. However, not all of them translate that performance when tested using our simulated dataset. Namely, C4.5 and PART have the worst performance on the simulated dataset; this is mainly caused by overfitting the training dataset, even after tuning the hyper-parameters to maximize that performance. As C4.5 is based on only one decision tree, it mainly focuses on the axis that best splits the training set according to its entropy, while partially ignoring the other two; and, since the direction that each axis represents is tied to the hardware itself, the axis on which falls are most evident, which is not the same on the simulated set, that leads to a drop in the performance. Then, since the PART algorithm is based on the building of partial C4.5 decision trees, the problem persists. The same could be said for the MLP, as every neural network, given sufficient training time, it will overfit the training set.

Moving on, the hyper-parameter optimization in conjunction with the better generalization capabilities of the remaining classifiers made them able to properly generalize the training using each dataset to obtain a very high degree of accuracy classifying the simulated dataset, sometimes at the cost of a loss of accuracy on the evaluation. In the case of Random Forest, this improvement is mainly motivated by the larger number of trees compared to C4.5, allowing the exploration of all the axis instead of focusing on the most predominant one. The same thing happens for AdaBoost combined with the Decision Stump, as shown in its better performance on the simulated dataset than on the cross-validation method, on both datasets. If we evaluate the attributes used to classify the time windows, these four better performing classifiers are all influenced by all the axes, although with some variation, especially focusing in the mean and standard deviation of each window to make the classification, whereas the first two used one axis in a more in-depth manner.

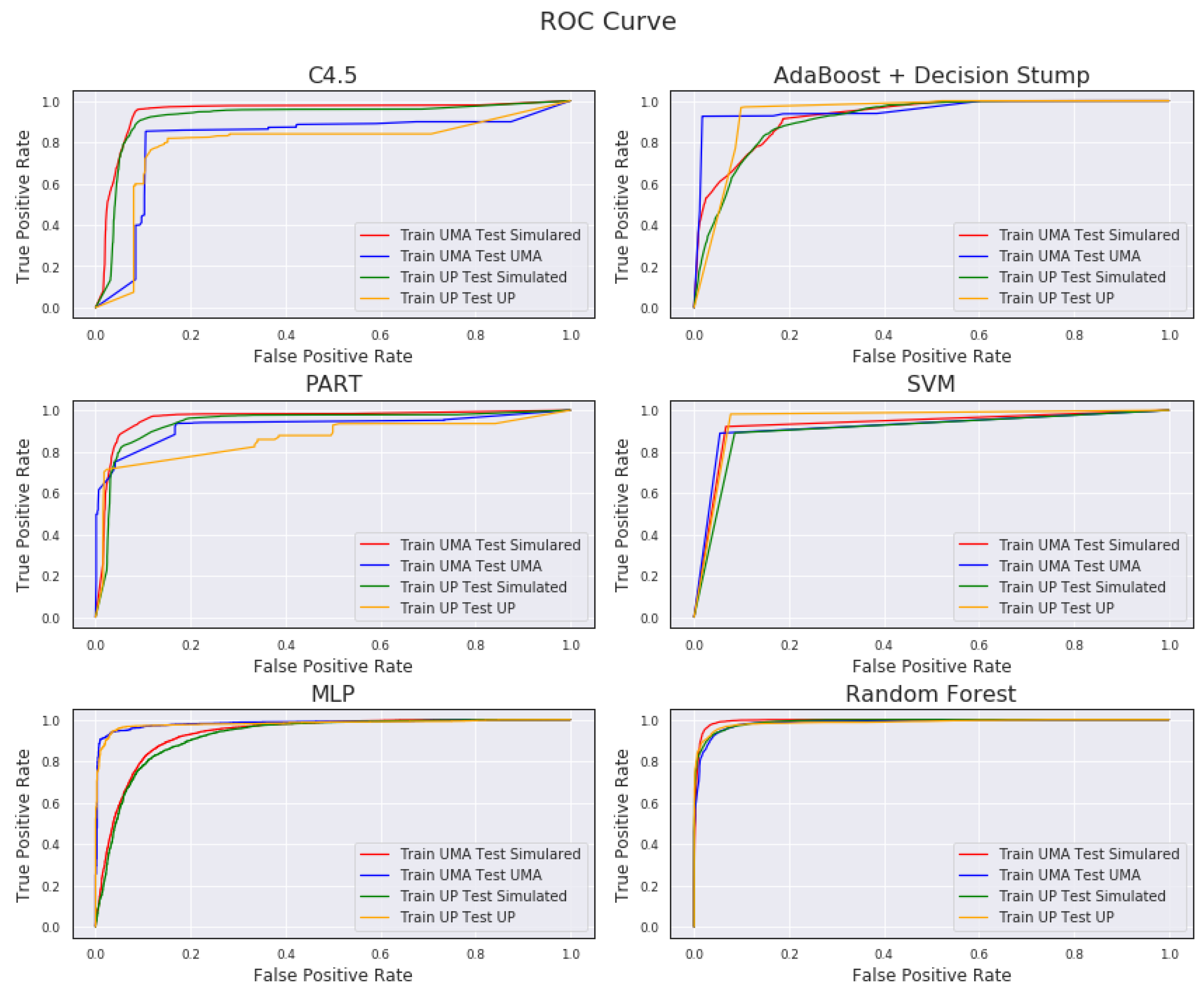
In Figure 6 the ROC curve for each classifiers is depicted for the ‘fall’ class for each of the combinations shown in Table 1. As we can see, the difference on C4.5, PART, AdaBoost and MLP classifiers when comparing the cross-validation against the simulated is much more considerable than on Random Forest and SVM, in which all the curves have a similar behaviour. In the other cases the cross-validation and the simulated curves evolve in pairs; in the case of MLP and AdaBoost classifiers, cross-validation achieves faster a high degree of sensitivity, while the simulation curve struggles to catch up the cross-validation. However, the ROC curves for the C4.5 and PART classifiers behave in the opposite way, the simulated ‘fall’ curve grows significantly faster that the cross-validation.

Finally, in

Table 2. Area Under ROC (AUC) evaluation for the binary falls classification. The training was executed using datasets from other works while the testing was against our simulated dataset or if against themselves, using cross-validation with 10 folds.

Train	Test	C4.5	PART	MLP	AdaBoost + Decision Stump	SVM	Random Forest
UMA	UMA	0.920	0.941	0.921	0.912	0.904	0.989
UMA	Simulated	0.788	0.862	0.987	0.938	0.904	0.989
UP	UP	0.936	0.965	0.930	0.924	0.927	0.994
UP	Simulated	0.811	0.924	0.987	0.958	0.917	0.986

we can see the weighted Area Under ROC (AUC) for each of the training-test pairs tested earlier. As we can see, with the exception of C4.5 in both the UMA-Fall and UP-Fall datasets and PART in the UMA-Fall case, every algorithm yields very promising values, bringing out the high degree of similarity of the simulated data with the real one.

5. Materials and Methods

Unity is a multi-purpose cross-platform 2D/3D video game engine for designing game or application scenes using a C# scripting API with a component based architectural design. It uses Nvidia PhysX for the 3D physics calculations and Box2D for the 2D ones. The workflow consists on creating Scenes, which can be understood as a unique level. Then GameObjects are placed into the scene and their functionality is added using Components, which can be of different types, such as colliders, renderers or scripts. In our simulator, we have a single scene where we place the dummy, and, in case of forward fall, an obstacle to trigger the fall. The dummy itself is a GameObject composed by several components, for instance, the joints, the animation controller, colliders and scripts implementing the tri-axial accelerometer. As well, those scripts write the recreated accelerometer measures to a CSV file.

The simulator developed and presented in this article can be freely downloaded and used (https://github.com/ISG-UAH/ISG_FallSimulator). This repository contains both a compiled version of the simulation environment, as well as the source code, which requires the Unity development environment version 2019.2.20f1. In the same repository, the simulated data generated for the validation presented in this paper can be found in the data folder along with the required scripts to properly process it. Both datasets used to verify the simulator’s quality are also available in their respective repositories: the UMA-Fall dataset [11] (http://webpersonal.uma.es/de/ECASILARI/Fall_ADL_Traces/UMA_FALL_ADL_dataset.html), and the UP-Fall dataset [12] (https://sites.google.com/up.edu.mx/har-up/).

6. Conclusions

The ageing of the population and the health complications associated to falls in the elderly lead to the usage of fall detection systems using wearable devices. These devices often feature ML algorithms for the fall detection, but lacks on reliable data for the models’ training. To overcome such an issue, we have developed a fall simulator, using a game engine with complex physics, for generating accelerometer fall samples. Particularly, the simulator is capable of recreating falls for two of the most common types of falls in the elderly: syncope and forward falls. The simulated falls create accelerometer samples that are pretty similar to real falls recorded, allowing us to use them as input for ML applications. Moreover, the current simulation can be customized by means of the parametrization of different components, such as the forces applied, the physical characteristics of the dummy or the activities that were being carried prior to the fall. To validate our approach, we have used different classifiers over both simulated falls and data from two public datasets based on real data. Our validation shows that the fall simulator achieves a high accuracy, compared to the aforementioned datasets, for generating accelerometer data from a fall, allowing to create larger datasets for training fall detection wearable devices using ML techniques.