Self-Attentive Multi-Layer Aggregation with Feature Recalibration and Deep Length Normalization for Text-Independent Speaker Verification System

Abstract

One of the most important parts of a text-independent speaker verification system is speaker embedding generation. Previous studies demonstrated that shortcut connections-based multi-layer aggregation improves the representational power of a speaker embedding system. However, model parameters are relatively large in number, and unspecified variations increase in the multi-layer aggregation. Therefore, in this study, we propose a self-attentive multi-layer aggregation with feature recalibration and deep length normalization for a text-independent speaker verification system. To reduce the number of model parameters, we set the ResNet with the scaled channel width and layer depth as a baseline. To control the variability in the training, we apply a self-attention mechanism to perform multi-layer aggregation with dropout regularizations and batch normalizations. Subsequently, we apply a feature recalibration layer to the aggregated feature using fully-connected layers and nonlinear activation functions. Further, deep length normalization is used on a recalibrated feature in the training process. Experimental results using the VoxCeleb1 evaluation dataset showed that the performance of the proposed methods was comparable to that of state-of-the-art models (equal error rate of 4.95% and 2.86%, using the VoxCeleb1 and VoxCeleb2 training datasets, respectively).

1. Introduction

Speaker recognition aims to analyze the speaker representation from input audio. A subfield of speaker recognition is speaker verification, which determines whether the utterance of the claimed speaker should be accepted or rejected by comparing it to the utterance of the registered speaker. Speaker verification is divided into text dependent and text independent. Text-dependent speaker verification aims to recognize only the specified utterances when verifying the speaker. Examples include Google’s “OK Google” and Samsung’s “Hi Bixby.” Meanwhile, text-independent speaker verification is not limited to the type of utterances to be recognized. Therefore, the problems to be solved using text-independent speaker verification are more difficult. If the performance is guaranteed, text-independent speaker verification can be utilized in various biometric systems and e-learning platforms, such as biometric authentication for chatbots, voice ID, and virtual assistants.

Owing to advances in computational power and deep learning techniques, the performance of text-independent speaker verification has been improved. Text-independent speaker verification using deep neural networks (DNN) is divided into two streams. The first one is an end-to-end system [1]. The input of the DNN is a speech signal, and the output is the verification result. This is a single-pass operation in which all processes can be operated at once. However, the input speech of a variable length is difficult to handle. To address this problem, several studies have applied a pooling layer or temporal average layer to an end-to-end system [2,3]. The second is a speaker embedding-based system [4,5,6,7,8,9,10,11,12,13,14], which generates an input of variable length into a vector of fixed length using a DNN. The generated vector is used as an embedding to represent the speaker. The speaker embedding-based system can handle input speech of variable length and can generate speaker representations from various environments.

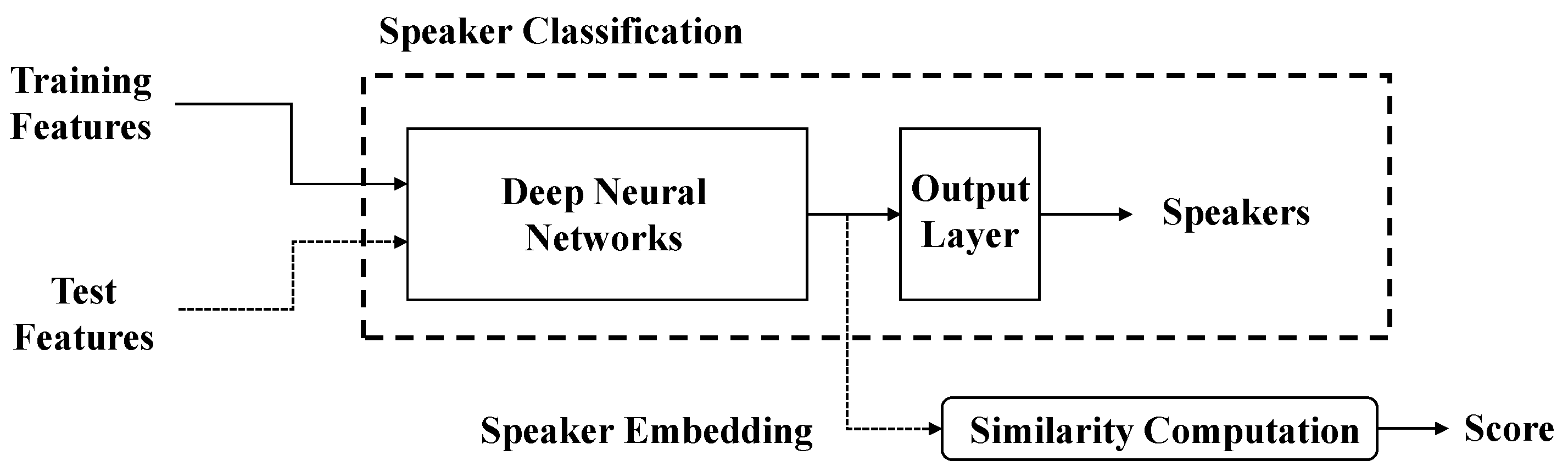
As shown in Figure 1, a DNN has been used as a speaker embedding extractor in a speaker embedding-based system. In general, a speaker embedding-based system executes the following processes [4,5,6,7]:

• The speaker classification model is trained.
• The speaker embedding is extracted by using the output value of the inner layer of the speaker classification model.
• The similarity between the embedding of the registered speaker and the claimed speaker is computed.
• The acceptance or rejection is determined by a previously decided threshold value.

In addition, back-end methods, for example, probabilistic linear discriminant analysis, can be used [8,9,10].

The most important part in the above system is the speaker embedding generation [13]. Speaker embedding is a high-dimensional feature vector that contains speaker information. An ideal speaker-embedding maximizes inter-class variations and minimizes intra-class variations [10,14,15]. The component that directly affects the speaker embedding generation is the encoding layer. The encoding layer takes a frame-level feature and converts it into a compact utterance-level feature. It also converts variable-length features to fixed-length features.

Most encoding layers are based on various pooling methods, for example, temporal average pooling (TAP) [10,14,16], global average pooling (GAP) [13,15], and statistical pooling (SP) [6,14,17,18]. In particular, self-attentive pooling (SAP) has improved performance by focusing on the frames for a more discriminative utterance-level feature [10,19,20], and pooling layers provide compressed speaker information by rescaling the input size. These are mainly used with convolutional neural networks (CNN) [10,13,14,15,16,17,20]. The speaker embedding is extracted using the output value of the last pooling layer in a CNN-based speaker model.

To improve the representational power of the speaker embedding, residual learning derived from ResNet [21] and squeeze-and-excitation (SE) blocks [22] were adapted for the speaker models [10,13,14,15,16,20,23]. Residual learning maintains input information through mappings between layers called “shortcut connections.” A large-scale CNN using shortcut connections can avoid gradient degradation. The SE block consists of a squeeze operation (which condenses all of the information on the features) and an excitation operation (which scales the importance of each feature). Therefore, a channel-wise feature response can be adjusted without significantly increasing the model complexity in the training.

The main limitation of the previous encoding layers is that the model uses only the output feature of the last pooling layer as input. In other words, the model uses only one frame-level feature when performing speaker embedding. Therefore, similar to [14,24], a previous study presented a shortcut connection-based multi-layer aggregation to improve the speaker representations when calculating the weight at the encoding layer [13]. Specifically, the frame-level features are extracted from between each residual layer in ResNet. Then, these frame-level features are fed into the input of the encoding layer using shortcut connections. Consequently, a high-dimensional speaker embedding is generated.

However, the previous study [13] has limitations. First, the model parameter size is relatively large, and the model generates high-dimensional speaker embeddings (1024 dimensions, about 15 million model parameters). This leads to inefficient training and thus requires a sufficiently large amount of data for training. Second, the multi-layer aggregation approach increases not only the speaker’s information but also the intrinsic and extrinsic variation factors, for example, emotion, noise, and reverberation. Some of these unspecified factors increase variability while generating speaker embedding.

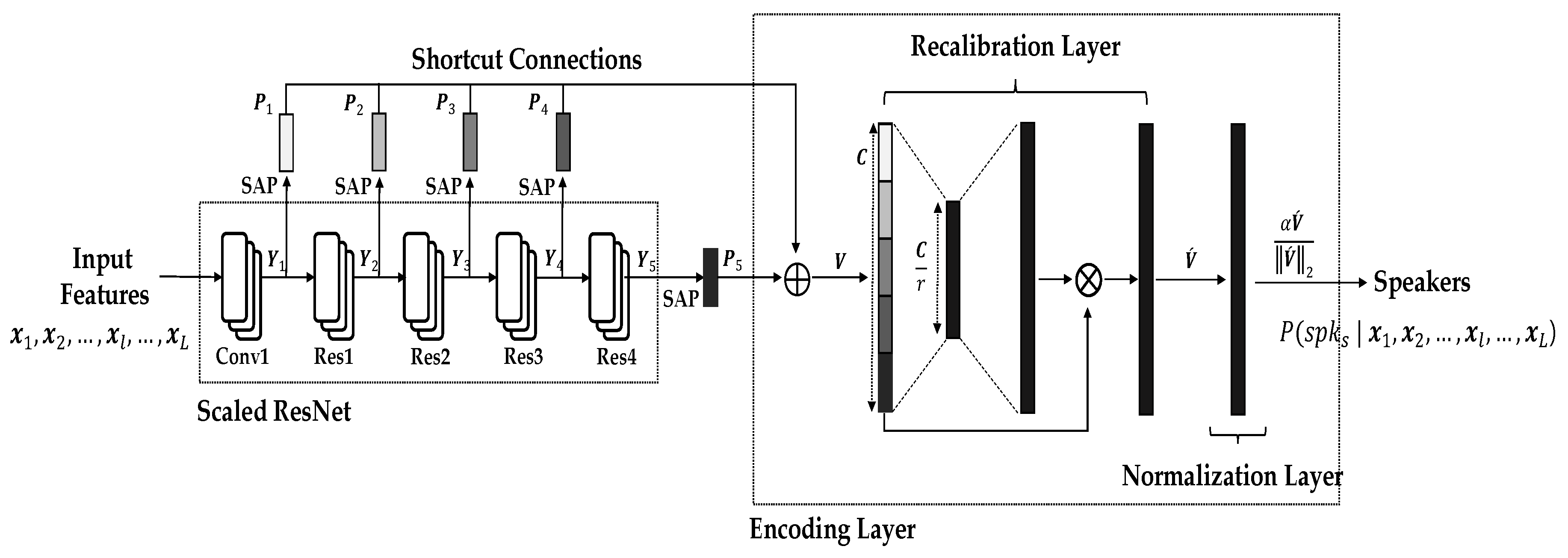
Hence, we propose a self-attentive multi-layer aggregation with feature recalibration and deep length normalization for a text-independent speaker verification system, as shown in Figure 2. We present an improved version of the previous study, as described in the following steps:

• A ResNet with a scaled channel width and layer depth is used as a baseline. The scaled ResNet has fewer parameters than the standard ResNet [21].
• A self-attention mechanism is applied to perform multi-layer aggregation with dropout regularizations and batch normalizations [25]. It helps construct a more discriminative utterance-level feature while considering frame-level features of each layer.
• A feature recalibration layer is applied to the aggregated feature. Channel-wise dependencies are trained using fully-connected layers and nonlinear activation functions.
• Deep length normalization [11] is also used for a recalibrated feature in the training process.

The remainder of this paper is organized as follows. Section 2 describes a baseline system using shortcut connections-based multi-layer aggregation. Section 3 introduces the proposed self-attentive multi-layer aggregation method with feature recalibration and normalization. Section 4 discusses our experiments, and conclusions are drawn in Section 5.

2. Baseline System: Shortcut Connections-Based Multi-Layer Aggregation

2.1. Prior System

In a previous study [13], a shortcut connections-based multi-layer aggregation with ResNet-18 was proposed. Its main difference from the standard ResNet-18 [21] is the manner that speaker embedding is aggregated. Multi-layer aggregation uses not only the output feature of the last residual layer but also the output features of all previous residual layers. These features are concatenated into one feature through shortcut connections. The concatenated feature is fed into several fully-connected layers to construct high-dimensional speaker embedding. The prior system improved the performance by a simple method.

However, it has large parameters because the system uses multi-layer aggregation, as presented in

Table 1. Comparison of model parameters and computational time in training between standard ResNet models and the prior system (MLA = multi-layer aggregation; Dim = speaker embedding dimension; Params = model parameters; FBTT = forward–backward training time (ms/batch)).

Model	Use of MLA	Dim	Params	FBTT
Standard ResNet-18	w/o	512	≈11.8 M	≈6.025
Standard ResNet-34	w/o	512	≈21.9 M	≈10.326
(ResNet-18-based) prior system	w/	1024	≈15.6 M	≈6.576
(ResNet-34-based) prior system	w/	1024	≈25.7 M	≈10.820

. The model parameters of standard ResNet-18 and standard ResNet-34 number are approximately 11.8 million and 21.9 million, respectively. Conversely, the model parameters of the prior system based on ResNet-18 and ResNet-34 are approximately 15.6 million and 25.7 million, respectively. In addition, the forward–backward training times of standard ResNet-18 and standard ResNet-34 are approximately 6.025 ms and 10.326 ms, respectively. However, the forward–backward training times of the prior system based on ResNet-18 and ResNet-34 are approximately 6.576 ms and 10.820 ms, respectively (when measuring the forward–backward training time, three units of GTX1080Ti and 96 mini-batch size were used).

2.2. Modifications

As discussed in Section 2.1, the prior system improved the performance; however, the model parameters were too large. The prior system is modified considering scaling factors, such as layer depth, channel width, and input resolution, for efficient learning in the CNN [26]. First, we used high-dimensional log-Mel filter banks with data augmentation for the input resolution. We extracted an input feature map of size D × L, where D is the number of single-frame spectral features and L is the number of frames. Here, Mel-filter banks determine dimension D from zero to 8,000 Hz. Subsequently, the channel width is reduced, and the layer depth is expanded because ResNet can improve the performance without significantly increasing the parameters when the layer depth is increased.

Consequently, the scaled ResNet-34 was constructed, as shown in

Table 2. Architecture of scaled ResNet-34 using multi-layer aggregation as a baseline (D = input dimension; L = input length; N = number of speakers; GAP = global average pooling; SE = speaker embedding).

Layer	Output Size	Channels	Blocks	Encoding
conv1	D × L	32	-	-
poo1	1 × 32	-	-	GAP
res1	D × L	32	3	-
pool2	1 × 32	-	-	GAP
res2	D/2 × L/2	64	4	-
pool3	1 × 64	-	-	GAP
res3	D/4 × L/4	128	6	-
pool4	1 × 128	-	-	GAP
res4	D/8 × L/8	256	3	-
pool5	1 × 256	-	-	GAP
concat	1 × 512	-	-	SE
output	512 × N	-	-	-

. The scaled ResNet-34 is composed of three, four, six, and three residual blocks. It has reduced the number of channels by half compared to the standard ResNet-34 [21]. In addition, shortcut connections-based multi-layer aggregation is added to the model using the GAP encoding method. The output features of each GAP are concatenated and fed into the output layer. Then, high-dimensional speaker embedding is generated from a penultimate layer in a network. Thus, the scaled ResNet-34 has only approximately 5.9 million model parameters compared to the prior system, as presented in

Table 3. Comparison of model parameters and computational time in training between the prior system and the scaled ResNet model (MLA = multi-layer aggregation; Dim = speaker embedding dimension; Params = model parameters; FBTT = forward–backward training time (ms/batch)).

Model	Use of MLA	Dim	Params	FBTT
(ResNet-34-based) prior system	w/	1024	≈25.7 M	≈11.186
Scaled ResNet-34	w/	512	≈5.9 M	≈5.658

. In addition, the forward–backward training time in milliseconds of the scaled ResNet-34 is faster than the prior system based on ResNet-34 (the forward–backward training time in milliseconds of the scaled ResNet-34 is approximately 5.658 ms).

3. Self-Attentive Multi-Layer Aggregation with Feature Recalibration and Normalization

As discussed in Section 1, the previous study has two problems. The model parameter problem is addressed by building a scaled ResNet-34. However, the problem of multi-layer aggregation remains. Multi-layer aggregation uses output features of multiple layers to develop the speaker embedding system. It is assumed that not only speaker information but also other unspecified factors exist in the output feature of the layer. The unspecified factor lowers the speaker verification performance. Therefore, we proposed three methods: self-attentive multi-layer aggregation, feature recalibration, and deep length normalization.

3.1. Model Architecture

As presented in Figure 2 and

Table 4. Architecture of proposed scaled ResNet-34 model using self-attentive multi-layer aggregation with feature recalibration and deep length normalization layers (D = input dimension; L = input length; N = number of speakers; $\mathit{P}$ = output features of pooling layers; $\mathit{V}$ = output features of concatenation layer; $\acute{\mathit{V}}$ = output features of feature recalibration layer; FR = feature recalibration; DLN = deep length normalization; SAP = self-attentive pooling; SE = speaker embedding).

Layer	Output Size	Channels	Blocks	Encoding
conv1	D × L	32	-	-
poo1	1 × 32	-	-	SAP (${\mathit{P}}_1)$
res1	D × L	32	3	-
pool2	1 × 32	-	-	SAP (${\mathit{P}}_2)$
res2	D/2 × L/2	64	4	-
pool3	1 × 64	-	-	SAP (${\mathit{P}}_3)$
res3	D/4 × L/4	128	6	-
pool4	1 × 128	-	-	SAP (${\mathit{P}}_4)$
res4	D/8 × L/8	256	3	-
pool5	1 × 256	-	-	SAP (${\mathit{P}}_5)$
concat	1 × 512	-	-	$\mathit{V}$
FR	1 × 512	-	-	$\acute{\mathit{V}}$
DLN	1 × 512	-	-	SE
output	512 × N	-	-	-

, the proposed network mainly consists of a scaled ResNet and an encoding layer. Frame-level features are trained in the scaled ResNet, and utterance-level features are trained in the encoding layer.

In the scaled ResNet, given an input feature $\mathit{X}=\left[{\mathit{x}}_1,{\mathit{x}}_2, \dots , {\mathit{x}}_l,\dots ,{\mathit{x}}_L\right]$ of length $L$ (${\mathit{x}}_l\in {ℝ}^d$), output features ${\mathit{P}}_i=\left[{\mathit{p}}_1,{\mathit{p}}_2, \dots , {\mathit{p}}_c,\dots ,{\mathit{p}}_C\right]$ (${\mathit{p}}_c\in ℝ$) from each residual layer of the scaled ResNet are generated using SAP. Here, the length $C_i$ is determined by the number of channels in the $i^{th}$ residual layer. Then, the generated output features are concatenated into one feature $\mathit{V}$ as in Equation (1) (where $[+]$ indicates concatenation).

$$\mathit{V}={\mathit{P}}_1 [+] {\mathit{P}}_2 [+] {\mathit{P}}_3 [+] {\mathit{P}}_4 [+] {\mathit{P}}_5$$

(1)

The concatenated feature $\mathit{V}=\left[{\mathit{v}}_1,{\mathit{v}}_2, \dots , {\mathit{v}}_c,\dots ,{\mathit{v}}_C\right]$ (length $C=C_1+C_2+C_3+C_4+C_5$, ${\mathit{v}}_c\in ℝ$) is a set of frame-level features and is used as the input of the encoding layer.

The encoding layer comprises a feature recalibration layer and a deep length normalization layer. In the feature recalibration layer, the concatenated feature $\mathit{V}$ is recalibrated by fully-connected layers and nonlinear activations. Consequently, a recalibrated feature $\acute{\mathit{V}}=\left[{\acute{\mathit{v}}}_1,{\acute{\mathit{v}}}_2, \dots , {\acute{\mathit{v}}}_c,\dots ,{\acute{\mathit{v}}}_C\right]$ (${\acute{\mathit{v}}}_c\in ℝ$) is generated. Then, the recalibrated feature is normalized according to the length of input $\acute{\mathit{V}}$ in the deep-length normalization layer. The normalized feature is used as a speaker embedding and is fed into the output layer. Further, a log probability for speaker classes $s$, $\mathit{P}(sp{k}_s | {\mathit{x}}_1,{\mathit{x}}_2, \dots , {\mathit{x}}_l,\dots ,{\mathit{x}}_L$), is generated in the output layer.

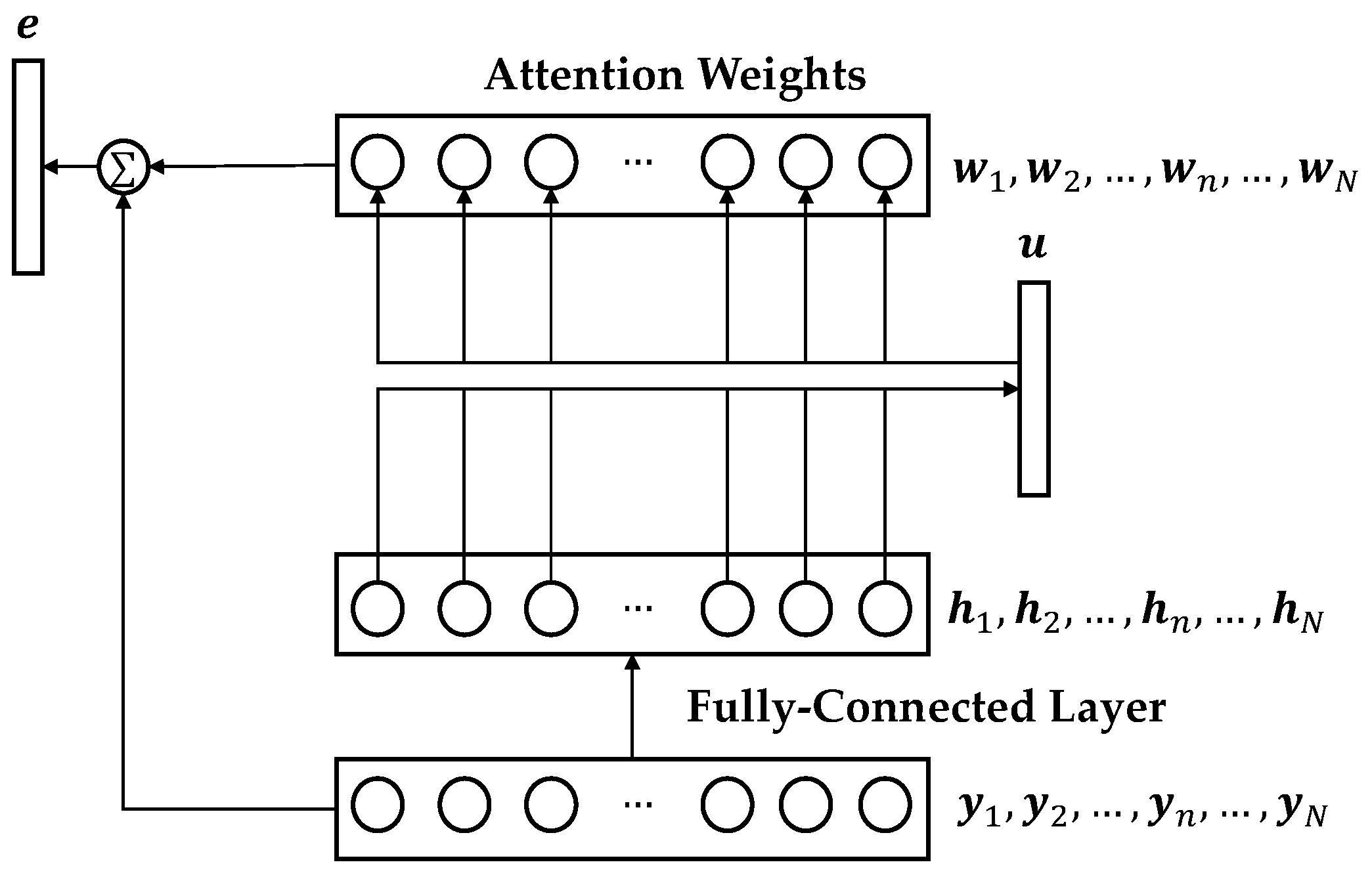
3.2. Self-Attentive Multi-Layer Aggregation

As shown in Figure 2 and Figure 3, SAP is applied to each residual layer using shortcut connections. For every input feature, given an output feature of the first convolution layer or the $i^{th}$ residual layers after conducting an average pooling, ${\mathit{Y}}_i=\left[{\mathit{y}}_1,{\mathit{y}}_2, \dots , {\mathit{y}}_n,\dots ,{\mathit{y}}_N\right]$ of length $N$ (${\mathit{y}}_n\in {ℝ}^c$) is obtained. The number of dimensions $c$ is determined by the number of channels.

Then, the average feature is fed into a fully-connected hidden layer to obtain ${\mathit{H}}_i=\left[{\mathit{h}}_1,{\mathit{h}}_2,\dots ,{\mathit{h}}_n,\dots ,{\mathit{h}}_N\right]$ using a hyperbolic tangent activation function. Given ${\mathit{h}}_n\in {ℝ}^c$ and a learnable context vector $\mathit{u}\in {ℝ}^c$, the attention weight ${\mathit{w}}_n$ is measured by training the similarity between ${\mathit{h}}_n$ and $\mathit{u}$ with a softmax normalization as in Equation (2).

$${\mathit{w}}_n=\frac{exp\left({\mathit{h}}_n{}^T\mathit{u}\right)}{{{\displaystyle \sum }}_{n=1}^{N}exp\left({\mathit{h}}_n{}^T\mathit{u}\right)}$$

(2)

Then, the embedding $\mathit{e}\in {ℝ}^c$ is generated using the weighted sum of the normalized attention weights ${\mathit{w}}_n$ and ${\mathit{y}}_n$ as in Equation (3).

$$\mathit{e}={{\displaystyle \sum }}_{n=1}^N{\mathit{y}}_n{\mathit{w}}_n$$

(3)

The embedding vector $\mathit{e}$ can be rewritten as ${\mathit{P}}_i=\left[{\mathit{p}}_1,{\mathit{p}}_2, \dots , {\mathit{p}}_c,\dots ,{\mathit{p}}_C\right]$ (${\mathit{p}}_c\in ℝ$) in the order of the dimensions. Consequently, the SAP output feature ${\mathit{P}}_i$ is generated. This process helps generate a more discriminative feature while focusing on the frame-level features of each layer. Moreover, dropout regularization and batch normalization are used in ${\mathit{P}}_i$. Then, the generated features are concatenated into one feature, $\mathit{V}$, as in Equation (1).

3.3. Feature Recalibration

After the self-attentive multi-layer aggregation, the concatenated feature $\mathit{V}$ is fed into the feature recalibration layer. The feature recalibration layer aims to train the correlations between each channel of the concatenated feature; this is inspired by [22].

Given an input feature $\mathit{V}=\left[{\mathit{v}}_1,{\mathit{v}}_2, \dots , {\mathit{v}}_c,\dots ,{\mathit{v}}_C\right]$ (${\mathit{v}}_c\in ℝ$, where $C$ is the sum of all channels), the feature channels are recalibrated using two fully-connected layers and nonlinear activations, as in Equation (4).

$$\acute{\mathit{V}}=f_{FR}\left(\mathit{V},\mathit{W}\right)=\sigma \left({\mathit{W}}_2\delta \left({\mathit{W}}_1\mathit{V}\right)\right)$$

(4)

Here, $\delta$ refers to the leaky rectified linear unit activation; $\sigma$ refers to the sigmoid activation; ${\mathit{W}}_1$ is the front fully-connected layer, ${\mathit{W}}_1\in {ℝ}^{c\times \frac{c}{r}}$, and ${\mathit{W}}_2$ is the back fully-connected layer, ${\mathit{W}}_2\in {ℝ}^{\frac{c}{r}\times c}$. According to the reduction ratio $r$, a dimensional transformation is performed between the two fully-connected layers, such as a bottleneck structure, while channel-wise multiplication is performed. The rescaled channels are then multiplied by the input feature $\mathit{V}$. Consequently, an output feature $\acute{\mathit{V}}=\left[{\acute{\mathit{v}}}_1,{\acute{\mathit{v}}}_2, \dots , {\acute{\mathit{v}}}_c,\dots ,{\acute{\mathit{v}}}_C\right]$ (${\acute{\mathit{v}}}_c\in ℝ$) is generated. This generated feature $\acute{\mathit{V}}$ is the result of recalibration according to the importance of the channels.

3.4. Deep Length Normalization

As in [11], deep length normalization was applied to the proposed model. The L2 constraint is applied to the length axis of the recalibrated feature $\acute{\mathit{V}}$ with a scale constant, $\alpha$, as in Equation (5).

$$f_{DLN}\left(\acute{\mathit{V}}\right)=\frac{\alpha \acute{\mathit{V}}}{{\Vert \acute{\mathit{V}}\Vert }_2}$$

(5)

Then, the normalized $\acute{\mathit{V}}$ is fed into the output layer for speaker classification. This feature is used as a speaker embedding, as shown in Figure 4.

4. Experiments and Discussions

4.1. Datasets

In our experiments, we used the VoxCeleb1 [27] and VoxCeleb2 [16] datasets presented in

Table 5. Dataset statistics for both VoxCeleb1 and VoxCeleb2. There are no duplicate utterances between VoxCeleb1 and VoxCeleb2 (POI = person of interest).

Dataset	VoxCeleb1	VoxCeleb2
# of POIs (Total)	1251	6112
# of POIs (Training)	1211	5994
# of POIs (Evaluation)	40	118
# of utterances (Total)	153,516	1,128,246
# of utterances (Training)	148,642	1,092,009
# of utterances (Evaluation)	4874	36,237
# of hours	352	2442
Average # of utterances per POI	116	185
Average length of utterances (s)	8.2	7.8

. These datasets comprise various utterances of celebrities collected in real environments from YouTube, including noise, laughter, cross talk, channel effects, music, and other sounds [27]. All utterances were encoded at a 16-kHz sampling rate with 2 bytes per sample. These are large-scale text-independent speaker verification datasets, comprising more than 100 thousand and 1 million utterances with 1251 and 6112 speakers, respectively.

We used the VoxCeleb1 evaluation dataset, which includes 40 speakers and 37,220 pairs of official test protocols [27], as shown in Figure 5. The test protocols comprises eight pairs per utterance of the VoxCeleb1 evaluation set (four pairs of the same speaker and four pairs of different speakers). Among all possible 38,992 (4874 × 8) utterances, 37,720 pairs were determined. The pair decision is made in consideration of balance such as gender, utterance length, and the number of pairs per speaker. In addition, it is an open-set test that evaluates all speaker pairs that are unavailable for the training dataset.

4.2. Experimental Setup

During data preprocessing, we used 64-dimensional log Mel-filter-bank energies with a 25 ms frame length and 10 ms frame shift, which are the mean variance normalized over a sliding window of 3 s. For each training step, a 12 s interval was extracted from each utterance through cropping or padding. In addition, a preprocessing method was used to conduct time and frequency masking on the input features [28].

The model training specifications are as follows: we used a standard cross-entropy loss function, with a standard stochastic gradient descent optimizer, with a momentum of 0.9, a weight decay of 0.0001, and an initial learning rate of 0.1, reduced by a 0.1 scale factor on the plateau [29]. All experiments were trained for 200 epochs with a 96 mini-batch size. The scaling constant $\alpha$ was set to 10, and the reduction ratio $r$ was set to 8 [11,22]. As shown in Figure 6, we confirmed that the training loss converges for the baseline model, as described in Section 2.2, and the proposed model, as described in Section 3.1, was trained.

From the trained model, we generated a 512-dimensional speaker embedding for each utterance, as shown in Figure 7. The standard cosine similarity is computed for the speaker pair, and the equal error rate (EER, %) is calculated. The EER value is the crossing point of the two curves, the false rejection rate and the false acceptance rate, according to the decision threshold. This can also be expressed on the receiver operating characteristic (ROC) curve using the true-positive rate and false -positive rate. All of our proposed methods were implemented using the PyTorch toolkit [30].

4.3. Experimental Results

To evaluate the proposed methods, we first tested the baseline using different encoding methods and other networks and then we compared our proposed method with state-of-the-art encoding methods.

Table 6. Experimental results for modifying the baseline construction, using the VoxCeleb1 training and evaluation dataset (Dim = speaker embedding dimension; Params = model parameters; EER = equal error rate; GAP = global average pooling; SAP = self-attentive pooling; MLA = multi-layer aggregation; FR = feature recalibration; DLN = deep length normalization).

Model	Encoding Method	Dim	Params	EER
Scaled ResNet-34	GAP	256	≈5.6 M	6.85
	SAP	256	≈5.7 M	6.68
	GAP-MLA	512	≈5.9 M	5.83
	SAP-MLA	512	≈6.0 M	5.42
	SAP-MLA-FR	512	≈6.1 M	5.07
	SAP-MLA-FR-DLN	512	≈6.1 M	4.95

presents the results of baseline modifications, as described in Section 2.2. It demonstrates the effectiveness of modifications to the encoding methods. We experimented with basic encoding layers, such as GAP and SAP. We then combined the proposed methods individually to the baseline, for example, self-attentive multi-layer aggregation, feature recalibration, and deep length normalization. Specifically, the scaled ResNet-34 with GAP and SAP achieved EER values of 6.85 % and 6.68%, respectively. Because multi-layer aggregation was not applied with these encoding methods, the number of dimensions of the speaker embedding was 256. In addition, the gap in performance between GAP and SAP was not large. We then applied the multi-layer aggregation for scaled ResNet-34 with GAP and SAP. In particular, the scaled ResNet-34 using multi-layer aggregation and GAP is our baseline system described in Section 2.2. Although speaker embedding dimensions and model parameters were larger in number than those of GAP and SAP, the EER value was reduced from 6.85% to 5.83% and from 6.68% to 5.42%, respectively. Additional applications to self-attentive multi-layer aggregation using feature recalibration and deep length normalization also achieved EER values of 5.07% and 4.95%, respectively. In addition, the ROC curve of the proposed model showed the EER point, as shown in Figure 8. Consequently, the experimental results showed that when all of the proposed methods were applied, the model parameters increased by approximately 0.5 M compared to the scaled ResNet-34 with GAP, whereas the EER value improved by 1.9%.

Table 7. Experimental results comparing our proposed methods with other networks using the VoxCeleb1 training and evaluation dataset (Dim = speaker embedding dimension; EER = equal error rate; SP = statistical pooling; GAP = global average pooling; SAP = self-attentive pooling; MLA = multi-layer aggregation; FR = feature recalibration; DLN = deep length normalization).

Model	Encoding Method	Dim	EER
i-vector + PLDA	-	200	8.82
x-vector	SP	1500	8.19
Scaled ResNet-34	SAP-MLA-FR-DLN	512	4.95

shows a comparison of our proposed methods with other networks. All experiments used the VoxCeleb1 training and evaluation datasets. First, the i-vector extractor was trained according to the implementation in [27]. After generating 400-dimensional i-vectors, PLDA was applied to reduce the number of dimensions of i-vectors to 200. The i-vector with the PLDA system achieved an EER value of 8.82%. In addition, an x-vector system was trained according to the implementation in [18]. The x-vector system is based on the use of time-delay neural networks (TDNN) using an SP method, which is commonly applied for text-independent speaker verification along with a ResNet-based system. The 1500-dimensional x-vector was extracted from the TDNN, which achieved an EER value of 8.19%. Our proposed methods based on the scaled ResNet-34 showed an improved performance, compared to the previous systems (i.e., EER value of 4.95%).

Table 8. Experimental results comparing our proposed methods with state-of-the-art encoding methods using the VoxCeleb1 training and evaluation dataset (Dim = speaker embedding dimension; EER = equal error rate; TAP = temporal average pooling; LDE = learnable dictionary encoding; SAP = self-attentive pooling; GAP = global average pooling; MLA = multi-layer aggregation; FR = feature recalibration; DLN = deep length normalization).

Model	Encoding Method	Dim	EER
ResNet-34 [10]	TAP	128	5.48
ResNet-34 [10]	LDE	128	5.21
ResNet-34 [10]	SAP	128	5.51
ResNet-34 [15]	GAP	256	5.39
Scaled ResNet-34 (proposed)	SAP-MLA-FR-DLN	512	4.95

and

Table 9. Experimental results comparing our proposed methods with state-of-the-art encoding methods using the VoxCeleb2 training datasets and the VoxCeleb1 evaluation datasets (Dim = speaker embedding dimension; EER = equal error rate; TAP = temporal average pooling; SAP = self-attentive pooling; MLA = multi-layer aggregation; FR = feature recalibration; DLN = deep length normalization).

Model	Encoding Method	Dim	EER
ResNet-34 [16]	TAP	512	5.04
ResNet-50 [16]	TAP	512	4.19
Thin-ResNet-34 [7]	NetVLAD	512	3.57
Thin-ResNet-34 [7]	GhostVLAD	512	3.22
Scaled ResNet-34 (proposed)	SAP-MLA-FR-DLN	512	2.86

show a comparison of our proposed methods with state-of-the-art encoding approaches. Here, we compared encoding methods using a ResNet-based model and the cross-entropy loss function. Various encoding methods were compared, including TAP [10,16], learnable dictionary encoding (LDE) [10], SAP [10], GAP [15], NetVLAD [7], and GhostVLAD [7].

In Table 8, all experiments used the VoxCeleb1 training and evaluation datasets. ResNet-34 with TAP, LDE, SAP, or GAP achieved EER values of 5.48%, 5.21%, 5.51%, and 5.39%, respectively [10,15]. The speaker embedding dimensions of these systems were 128 or 256, which were smaller than those of the proposed methods. However, our proposed encoding methods based on the scaled ResNet-34 achieved an EER value of 4.95%. The performance was an improvement to that of other systems.

In Table 9, all experiments used the VoxCeleb2 training datasets and VoxCeleb1 evaluation datasets. As presented in Table 5, the VoxCeleb2 training datasets are seven times more than the VoxCeleb1 training datasets. Table 9 shows that increasing the amount of training dataset was effective for performance improvement. ResNet-34 and ResNet-50 with TAP achieved EER values of 5.04% and 4.95%, respectively [16]. In addition, a thin-ResNet-34 with NetVLAD and GhostVLAD achieved EER values of 3.57% and 3.22%, respectively [7]. The number of speaker embedding dimensions of these systems was 512, which is the same as that of our proposed methods. Our proposed encoding methods based on the scaled ResNet-34 achieved an EER value of 2.86%. Consequently, the experimental results showed that our proposed methods were superior to other state-of-the-art methods.

Furthermore, in the case of on-device speaker verification, the lower the speaker embedding dimension, the faster the system. Our proposed methods have limitations as a high-dimensional speaker embedding method, compared to other state-of-the-art encoding methods. Therefore, future research is required to address this dimension problem. In a future study, on-device speaker verification using low-dimensional speaker embedding will be conducted.

5. Conclusions

In previous multi-layer aggregation methods for text-independent speaker verification, the number of model parameters was relatively large, and unspecified variations increased during training. Therefore, we proposed a self-attentive multi-layer aggregation with feature recalibration and deep length normalization for a text-independent speaker verification system. First, we set the ResNet with the scaled channel width and layer depth as a baseline. Second, self-attentive multi-layer aggregation was applied when training the frame-level features of each residual layer in the scaled ResNet. Finally, the feature recalibration layer and deep length normalization were applied to train the utterance-level feature in the encoding layer. The experimental results using the VoxCeleb1 evaluation dataset showed that the proposed method achieved an EER value performance comparable to that of state-of-the-art models.