1. Introduction
The Information-Centric Network (ICN) has gained widespread attention in recent years. Different from host-to-host communication, ICN focuses on the content object itself, instead of the location. In ICN, content becomes the first-class citizen in the whole network and it is decoupled from physical addressing. By naming content at the network layer, ICN supports in-network caching, multicast and mobility mechanisms, thus making delivery of content to the users more efficiently and timelier [
1]. Besides, ICN can be realized as a network slice in 5G architecture, to support multiple scenarios with low latency and high reliability [
2].
In-network caching is the key factor of ICN. To realize in-network caching, routers (called as nodes in this paper) are equipped with cache and these routers construct caching networks. Content providers manage these routers and hire cache space to keep content replicas, to reduce the traffic load on the origin server that provides content [
3]. Users can get data from caching nodes rather than the remote source server. In this way, the network latency will be decreased significantly.
For a content provider, despite the potential benefits of in-network caching, it also needs to consider the cost of hiring the cache resource. Because of the financial constraints and competition from other content providers, it is not practical to hire cache without limit. The financial constraint can also be converted to a total capacity constraint for simplicity. To promote network performance, cache distribution also needs to be considered and the sum of cache capacity for all nodes is usually limited. If a cache node is close to users and with a high user access rate, then this node tends to be allocated more cache space. So to maximize the network performance with a given capacity constraint, how to allocate cache capacity to each node needs to be considered and we call this problem
the cache allocation problem. In References [
4,
5], cache capacity was recommended allocated to nodes close to users rather than core nodes. Manifold learning was used in Reference [
6] to calculate the importance of the node, while graph-related centralities of nodes were used for cache allocation in Reference [
7]. These methods improve network performance to some extent, while [
7] concluded that gain brought by heterogeneous cache capacity is very limited. The cache allocation problem is a complex optimization problem and factors such as network topology, user distribution, caching strategies or content popularity will have a potential impact on network performance. From a content-based perspective, the cache allocation problem can be formulated as a
content placement problem: under the same cache space budget, placing content into the network to obtain the largest benefit. References [
8,
9] considered the Zipf distribution of web content [
10] and network performance is further improved.
On one side, ubiquitous caching in ICN brings tangible benefits to both users and remote servers. On the other side, redundant replica and low content diversity limit the benefits of in-network caching. To improve this deficiency, we introduce the concept of the Expected Number of Copies (ENC)—each content cached on an ICN node has an ENC, to control the content number of copies cached on this node and downstream nodes. For popular content, a larger ENC allows more copies cached in the topology. For non-popular content, a smaller ENC allows fewer copies or no copy to be cached. How to calculate and apply the ENC is a question worth studying. Besides, ICN nodes need to make independent caching decisions or they can perform limited collaborative operations. So an appropriate caching mechanism is required to ensure network performance during data transfer.
In this paper, we focus on the cache allocation problem and the content placement problem under a given cache space budget, with the optimization goal: to minimize the average network hop count from data transfer. Particularly, this paper concerns about how each ICN node makes cache decisions during data transfer. Firstly, we propose a two-step lightweight method called LAM (Lightweight Allocation Method) to solve the cache allocation problem, as well as get the ENC of different content. LAM is suitable for the cache allocation scenario of all kinds of caching networks, such as ICN, CDN (Content Distribution Network) and cloud networks. Then, an on-path caching scheme based on ENC is proposed to handle the content placement problem in ICN. To the best of our knowledge, we are the first to calculate the optimal number of content copies in ICN and apply it for caching decisions. The main contributions of this paper are as follows:
We build an ICN hierarchical network model using the reduction of network hop count as the optimization target. We formulate the cache allocation problem as the network benefit maximization problem in the model we establish.
We propose a lightweight allocation method in ICN, which takes network information and content information into account. The method distributes the total cache budget across all nodes and places content to nodes, meanwhile maximizing network benefit. This method calculates the ENC of different content, to guide content placement. This method considers the newly placed copy will affect the benefit from existing copies, which is more realistic.
We propose an on-path caching scheme based on ENC. ENC is used to control the number of content copies, within the scope of a node and its downstream nodes. Each node manages the ENC of cached content and allocates an appropriate number of copies to downstream nodes. ENC reduces content redundancy and guarantees content diversity.
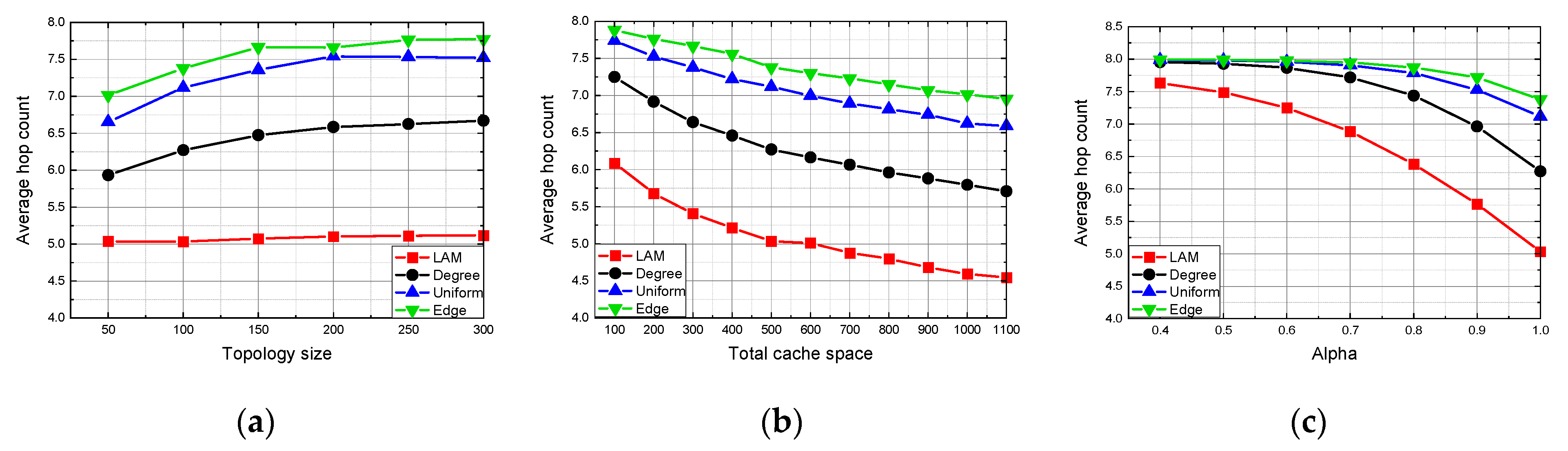
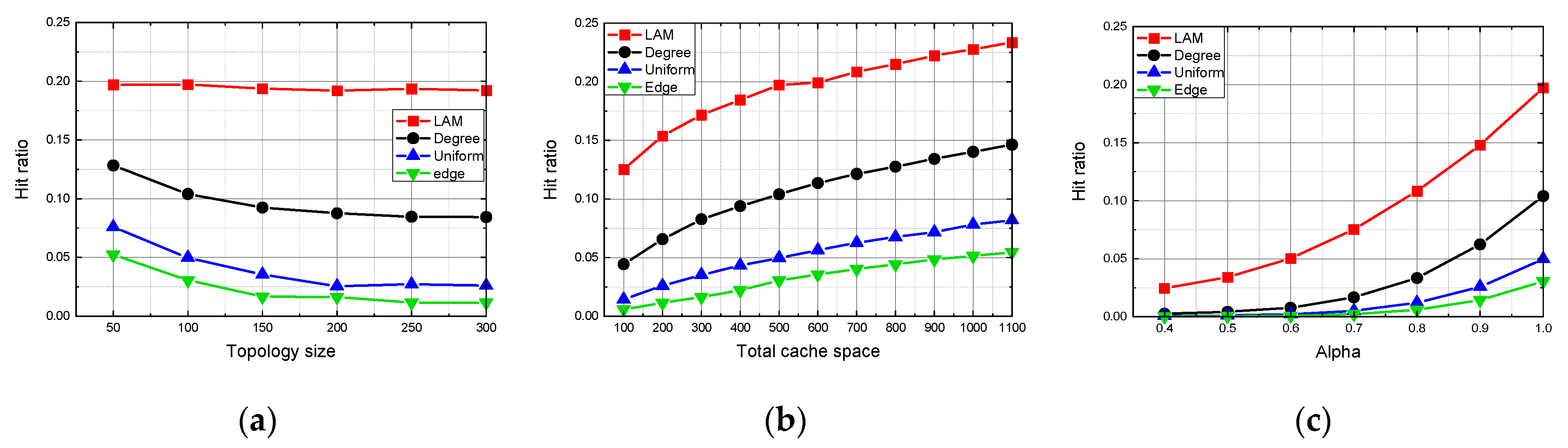
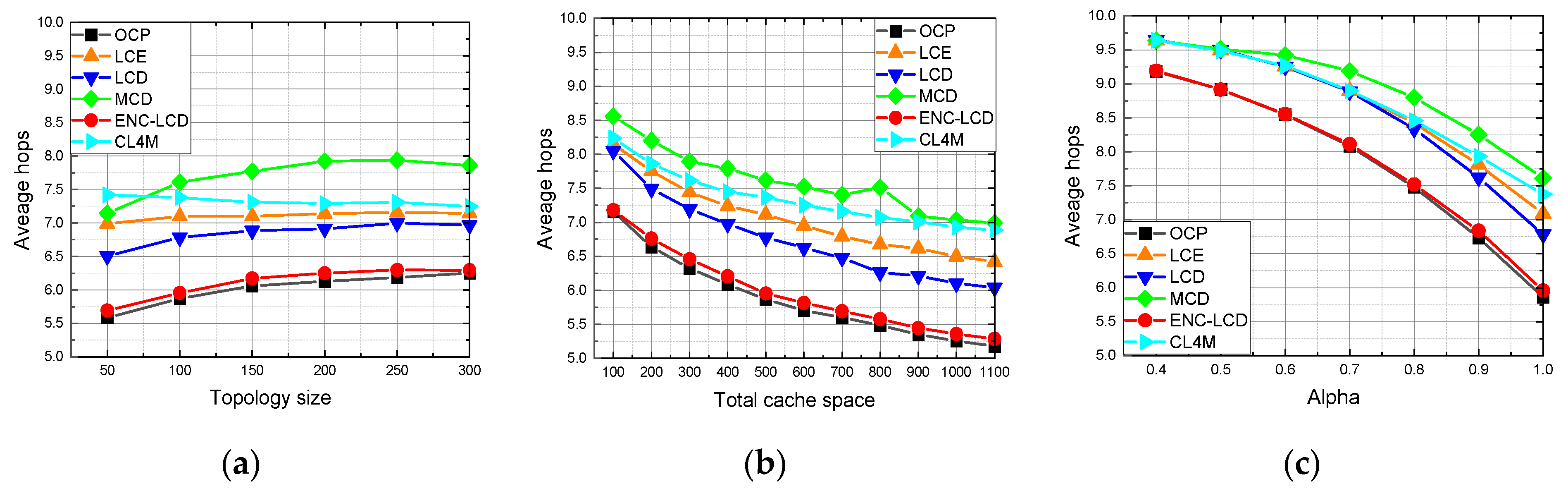
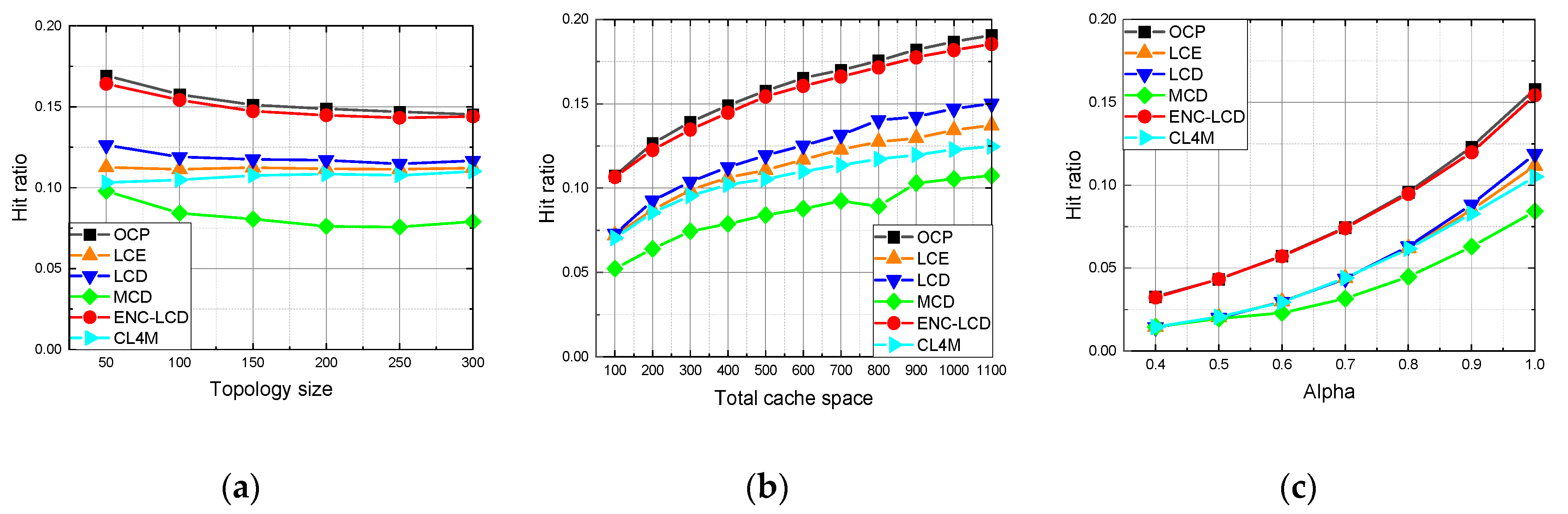
In the cache allocation scenario, the lightweight allocation method shows obvious advantages and performs better than all other baseline methods. In the content placement scenario, Leave Copy Down (LCD) based on ENC performs the second-best and is very close to Optimal Content Placement (OCP [
8]).
The rest of this paper is organized as follows: the related work is presented in
Section 2.
Section 3 displays a hierarchical ICN topology as well as the problem formulation.
Section 4 describes the lightweight allocation method for generating ENC.
Section 5 describes the on-path caching scheme based on ENC.
Section 6 presents the experiment design and results.
Section 7 gives a consideration of the improvement direction of our scheme.
Section 8 concludes the paper and analyzes some possible future studies.
3. Problem Statement
In this section we establish a hierarchical network model, as well as setting up the problem formulation, using network hop count as the optimization target.
Table 1 represents the main notations used in this paper.
3.1. Model Description
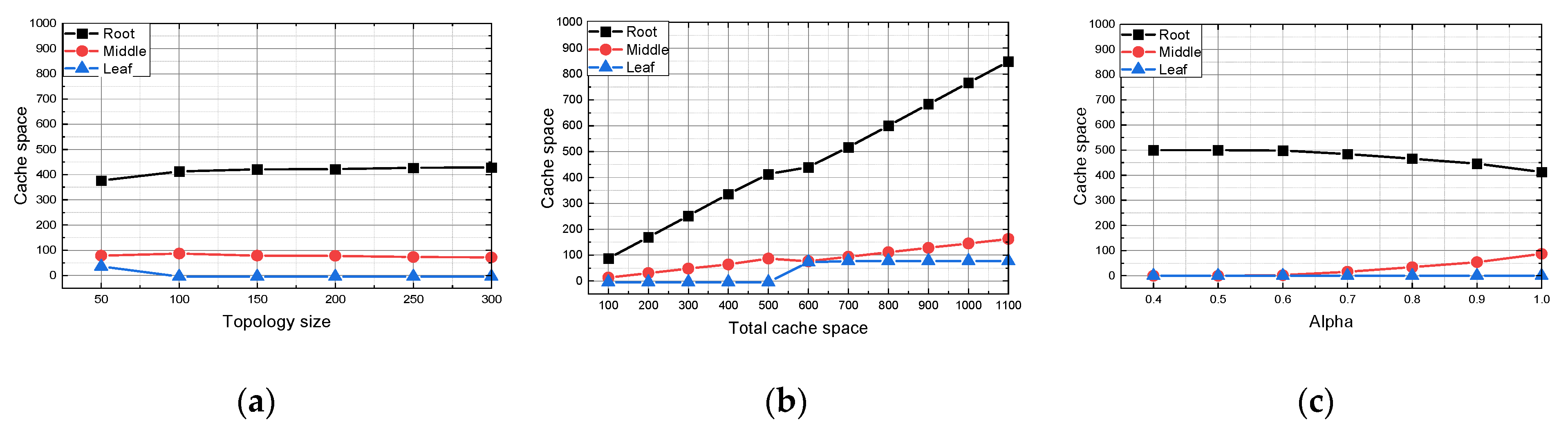
We choose the three-layer architecture to set up our model, to comprehensively analyze how topology size affects network benefit [
27]. It should be noted that the ICN hierarchical topology of any number of layers still applies to the model.
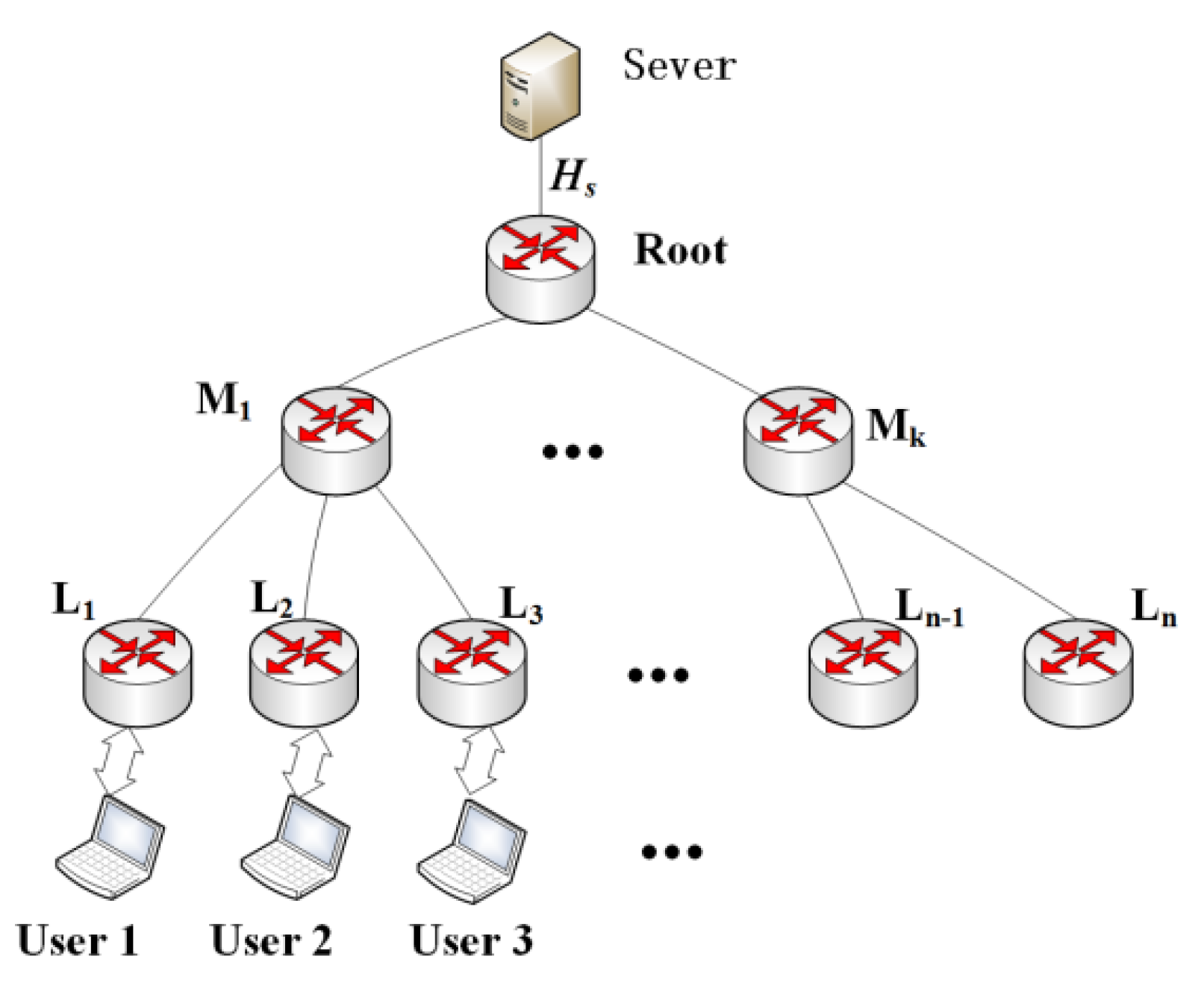
Figure 1 shows a three-layer hierarchical network containing one root node in the first layer connecting to one server,
middle nodes (also denoted as aggregation nodes) in the second layer and
leaf nodes in the third layer. The server keeps all the content permanently and is far away from users. For simplicity, all middle nodes are connected to the root node and connected to at least one leaf node. On the other hand, each leaf node only connects to one middle node. All nodes can be equipped with cache space to cache content. If a request arrives at a node that contains the requested content, the requested data will be sent from the hit node rather than from the origin server. This three-layer network can be easily extended to a larger multilayer tree topology, such as doing k-core decomposition for networks in Reference [
20]. We assume that all users are connected to the leaf nodes and their requests for content will arrive at leaf nodes first.
In this paper, to simplify the model, we make the following assumption:
All the leaf nodes are connected to the same number of users and the request frequency of the users is the same. Namely, all leaf nodes have the same request arrival rate.
Request routing is along the path to the origin server and the on-path cached content is capable to serve the request. Some measures such as applying the nearest replica routing strategy [
23] or applying some specific request routing algorithms like [
28] could also make use of content cache out of the path, while these methods will bring more traffic overhead. These measures are beyond the scope thus not discussed.
Nodes in the topology are represented by serial numbers, so as content. Furthermore, Content is named according to its popularity ranking.
3.2. Problem Formulation
The cache allocation problem and content placement problem share the same goal. Under the same cache space budget, they can be both solved by finding the optimal content copy distribution with maximal network benefit. We analyze these two problems in the scenario with one content provider, who owns a server storing all the content and plan to rent cache space under a given budget. First of all, a mechanism is required to compute the network benefit. In ICN, the cache benefit is usually measured by the reduction of the hop count to get the requested content [
8,
9]. Assuming a request for content
is sent to node
, which is the first encountered node with a cached copy of the content
. Compared with responding to the request at the server, the reduction of hop count equals the hop from node
to server, presented as
. Using
to present the content probability of content
, then the benefit, which is denoted as
, equals
. For a node, responding to more requests will bring more benefits. Here we use
to denote the number of requests asking for content
for node
will receive. Finally, we can calculate the benefit
using Equation (1).
It is worth noting that the benefit of a node will be affected by its downstream nodes. Suppose that there are only two copies of content
located at node
and
respectively in the topology of
Figure 1 and all users request content at the same frequency. On this occasion, requests for content
from user 1 will be served in node
and requests from user 2 and user 3 will be served in node
. So
is the hop count from node
to server, while
is the hop count from node
to
, i.e., one hop, for the reason that node
will serve the request if the node
does not cache content
. Besides, if a new copy of content
is placed to node
, the benefit from content
in node
will decrease, according to the reduction of
.
In more general cases, the network benefit can be expressed using the following equation:
Subject to:
where
is the set of nodes,
is the set of content,
is the set of content cached in node
,
is the cache space equipped in node
and
represents the reduced hop count for content
at node
. Equation (4) indicates that the cache space allocated from node
cannot exceed its original cache size. In Equation (5), the sum of the cache capacity of all nodes cannot exceed the given total cache capacity
.
3.3. Multiple Copy Placement of a Single Content
The benefit maximization problem is a special type of knapsack problems. Thus it cannot be solved in polynomial time. The benefit of content
at node
may change, as
is affected by the upstream nodes, while
is affected by the downstream nodes. Current optimal allocation methods proposed in References [
8,
9] work in the case that the benefit from one content copy is unchanged, so cannot be directly used in our model.
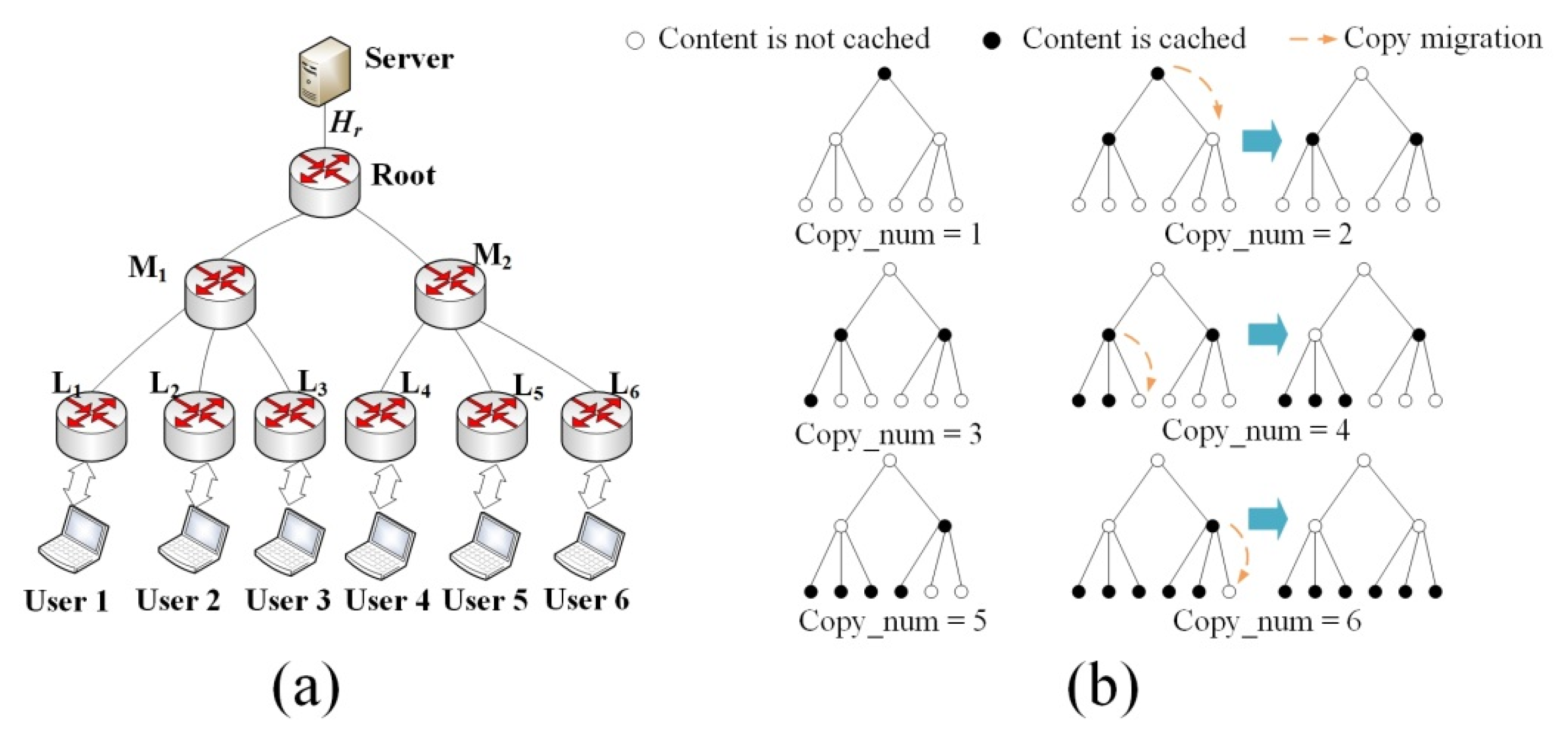
Based on the analysis of network benefits, a new copy will only affect the network benefits of existing copies of the same content. So we can calculate total network benefits by calculating the network benefits of different content and sum them up. We firstly analyze a special case of a single content in the network and then conclude the general features from this example. The example is shown in
Figure 2a, which consists of a server, a root node, two middle nodes and six leaf nodes. Content copies are placed step by step, aiming for the highest current network benefit. We use
to denote hop count from the root node to the server,
r to denote request arrive rate at each leaf node and content popularity is set to 1.
To place the first content copy, the benefits of the root node, each middle node and each leaf node are
,
and
. As long as
is larger than one hop, placing content at the root node will bring maximal benefit. To place the second content copy, we calculate the nodes bringing the highest benefit are node
and
. We choose
to place the second copy but it is not the optimal placement solution when the number of content copies is 2. It is easy to find that if we move the copy from root node to
, the network benefit will increase
(3 access leaf nodes with the request arrival rate
and each request hit at
will reduce one hop, from
to root node). The similar situation happens when the number of copies equals 4 or 6. Continue placing copies, we can get the content placement process as shown in
Figure 2b.
Two general features can be concluded from the example of
Figure 2. Firstly, Content copy migration to child nodes may happen, to gain higher network benefit. Such migration only happens when a node caches the content copy but only one child node does not cache the copy. In this situation, migrating the copy to this child node will save one hop for some requests. Secondly, when the number of copies equals
, the network benefit becomes the maximum. At this point, the optimal decision is placing one copy on every leaf node, for the reason that leaf nodes are closest to clients. The hop count for every request reduces to the minimum and a larger placed number of copies will not bring more benefit but cost more space.
We have already explored the relationship between the number of copies and network benefits, meanwhile recording content distribution in the network. The benefit information will be used to maximize the current network benefit and content distribution information will be used to locate the content position. Based on them, we can place the proper content greedily to seek the maximal network benefit.
4. Lightweight Allocation Method
In this section, the brief design of the Lightweight Allocation Method (LAM) is proposed. LAM solves the cache allocation problem under the given cache capacity budget, as well as gives the Expected Number of Copies (ENC) of popular content. We first illuminate the motivation to propose a lightweight allocation method. Then we show the specific steps of the algorithm in detail, as well as analyze the computational complexity of our method.
4.1. Motivation
As we have discussed before, heterogeneous cache allocation schemes have been proved efficient with large topology size. And the cache allocation problem requires a combination of many factors. Current lightweight allocation methods, such as graph-centralities-based methods, do not take advantage of the content information, resulting in poor performance. While most allocation methods using content information have high computational complexity. Besides, recent optimal allocation methods assume the network benefit of the content copy is fixed and our model is closer to the actual situation.
Based on the above discussion, we want to propose a lightweight allocation method, which considers both topology information and content information. As the problem raised in
Section 3.2 is NP-hard, the greedy method can be applied to get the approximate optimal solution. Different from the optimal allocation methods [
8,
9], we only focus on popular content. As the request workload for different content obeys heavy-tailed distribution, only the content that brings the maximal benefit will be taken into account. by getting the ENC of popular content, we can get the near-optimal cache allocation solution and use ENC to guide content placement.
4.2. Method Description
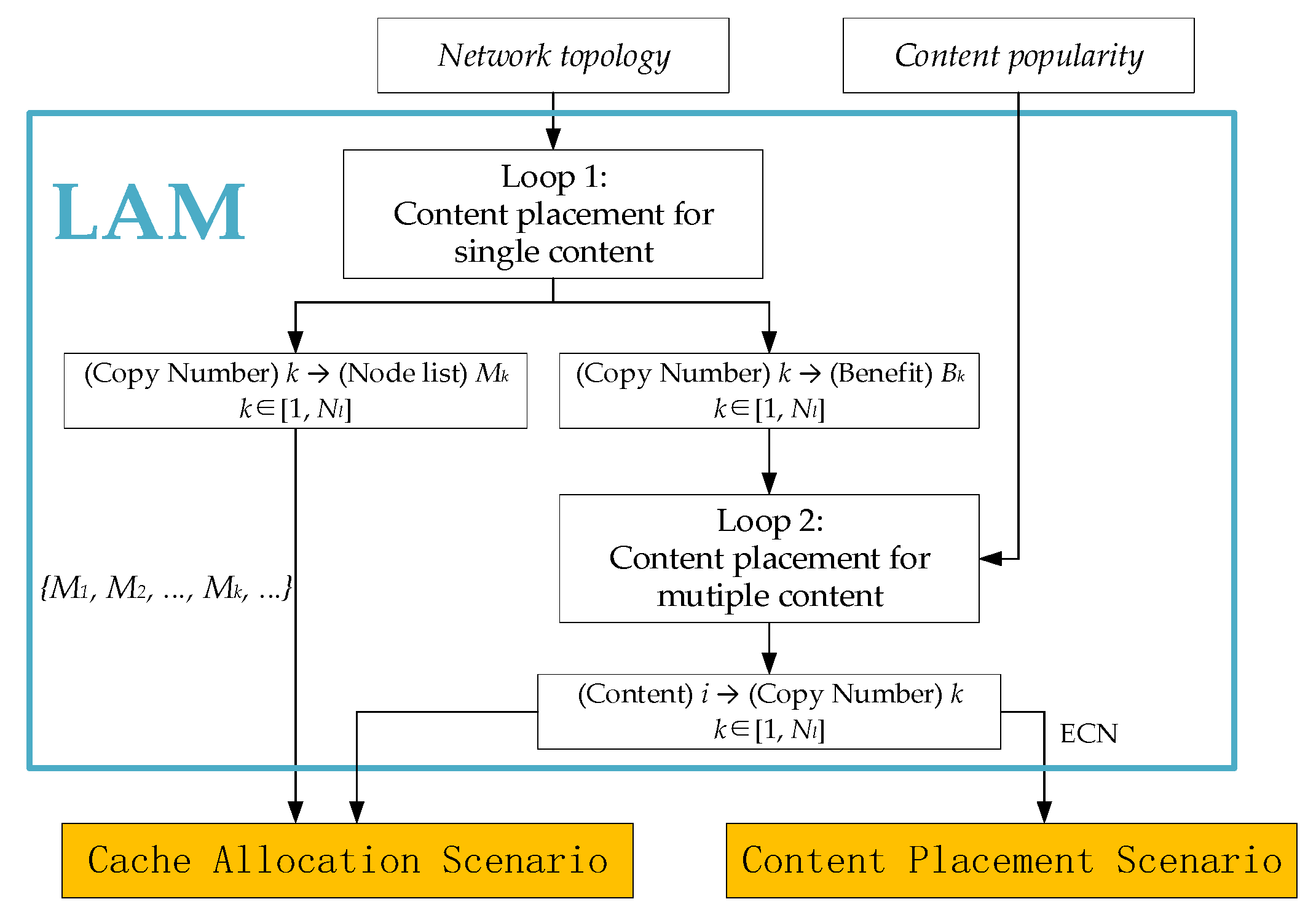
LAM is based on the above analysis. The overview of LAM is shown in
Figure 3 and the detailed step is presented in Algorithm 1. The input
Network_topology contains the necessary topology information,
is the total cache capacity to be allocated,
is the set of nodes and
is the set of content. The output {
,
, …,
} contains
sets, each of which records the content copy position and the subscript is the number of copies in the network. This output can locate the nodes to place the content copy. The output
records the relationship between content and its ENC in the topology. With these two output results, we can get the content placement solution, as well as the exact space to be allocated of each node.
The proposed LAM consists of two main loops. The first loop, from line 2 to 16 in Algorithm 1, computes the network benefit
Bi, where
i is the number of copies, as discussed in
Section 3.3. The list {
M1,
, …,
MNl} is also generated from this loop and
records nodes that have the copy when the number of copies is
k. The upper bound of the number of copies is
, i.e., the size of leaf nodes. For the
k-th copy (
k > 1),
is the set of nodes to choose for placement. We place a new copy based on the previous placing result and greedily choose the node that brings the maximal benefit to place the copy. After updating
, in line 12 to 16, we need to check whether to move the copy from the upstream nodes to downstream, as discussed in
Section 3.3. Then, we record the benefit as
, which will be used in the second main loop.
The second loop, from line 17 to 33 in Algorithm 1, is the placement process of multiple content. Firstly, we define as the most popular content which has not been placed in the topology yet. Each time to place a content copy, we compute the benefit of and benefits of content from , which records current content that is already placed in the topology. For content , its ENC in the topology is . When is less than , the benefit of placing a new copy of content can be computed as . In line 22, we compare the benefit per unit size of different content, to avoid the situation where some content is profitable but takes up too much space. After finding the maximal benefit per unit size of a content copy, we update the ENC of the chosen content. This placing process ends when the deployed cache space reaches .
The computational complexity of the first main loop is
and the second main loop is
. So the overall complexity of our allocation method is
. The computational complexity of optimal allocation method in Reference [
20] is
. Compared with the optimal allocation methods, the computational complexity of our method is relatively low.
and
are two main factors affecting the computational complexity. When
is relatively small,
becomes the major impact factor and the computational complexity ratio of our method to the optimal allocation method is
. When
is relatively large, the computational complexity ratio is
. Content space size
is much larger than the budget
, so our method also gets a low complexity in this case.
| Algorithm 1: LAM |
| Input:Network_topology, , , , |
| Output: {, , …, }, |
| 1: initialization: , , , |
| 2: for k from 1 to do |
| 3: , , |
| 4: for node in do |
| 5: compute for placing copy at node |
| 6: if |
| 7: |
| 8: |
| 9: end if |
| 10: end for |
| 11: |
| 12: if accords with moving criteria |
| 13: update and |
| 14: end if |
| 15: |
| 16: end for |
| 17: while do |
| 18: set as the most popular content from |
| 19: compute for placing |
| 20: find for the content with maximal benefit in |
| 21: set as the content with maximal benefit in |
| 22: if then |
| 23: |
| 24: |
| 25: end if |
| 26: |
| 27: if in |
| 28: |
| 29: |
| 30: else |
| 31: end if |
| 32: |
| 33: end for |
| 34: return {, , …, }, |
5. ENC-Based On-Path Caching Scheme
Although LAM gives a near-optimal solution of content placement, for each content, the set recording the node position is required during the data transmission process. This information will consume additional bandwidth [
8]. Besides, only using the optimal solution of content placement makes nodes lack autonomous decision-making abilities and the robustness and extensibility of the network will be limited.
To better fit ICN, we design an on-path caching scheme using ENC for content placement. Different on-path caching policies can be set, with the control of ENC of different content. Due to the trace-driven feature in ICN, user requests also potentially contain the location information, which helps to place content copies properly. Since the transmission path of data packets is from the core node to edge nodes, through the extended field of the data packet header, upstream nodes can indirectly manage the number of content copies from downstream nodes.
5.1. Scheme Description
The proposed on-path caching scheme uses ENC to control the number of content copies in the network. The origin server calculates the ENC of each content. When the content is transferred to the network, the first ICN node will cache the content and record its ENC. ENC represents the upper limit of the number of copies in a range, which includes the node that records this ENC and all its downstream nodes. With ENC, upstream nodes can pre-determine the number of content copies to be cached downstream. When an ICN request hits at an ICN node, this node will recalculate the ENC for downstream nodes. This ENC-based caching scheme applies to all on-path caching strategies.
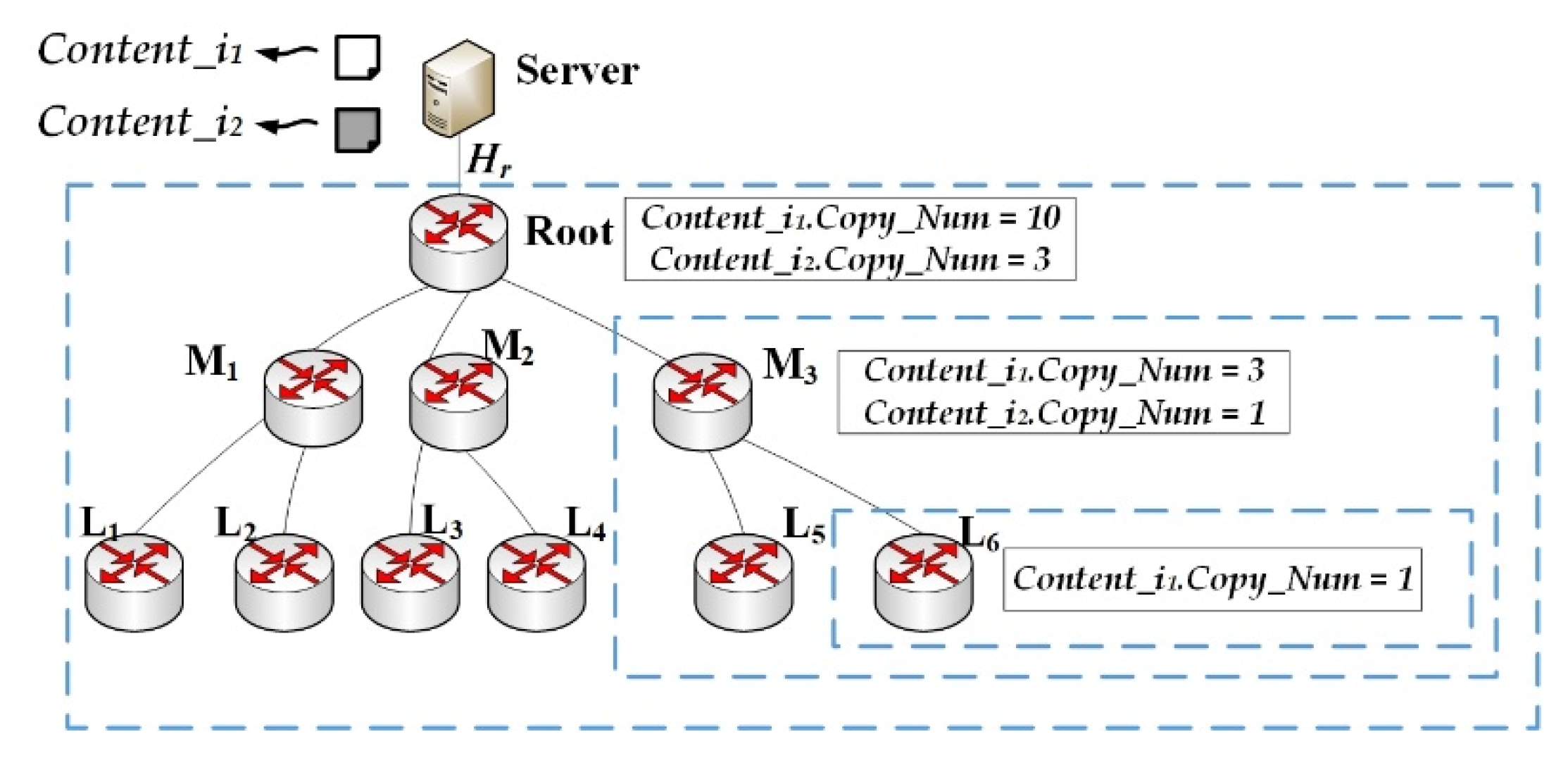
An example of the caching scheme is shown in
Figure 4. Suppose that the ENC of content
i1 and
i2 is 10 and 3 in turn, The server maintains the ENC of all content and informs the on-path nodes during the transmission of data packets. So when the root node caches content
i1 and
i2, it will record their ENC. Besides, the root node will recalculate the ENC of its child nodes. When M3 node caches content
i1 and
i2, the ENC of content
i1 and
i2 is allocated as 3 and 1. Similarly, L6 will only cache content
i1, as its upstream node M3 allocates ENC of content
i1 is 1 for L6 and ENC of content
i2 is 0.
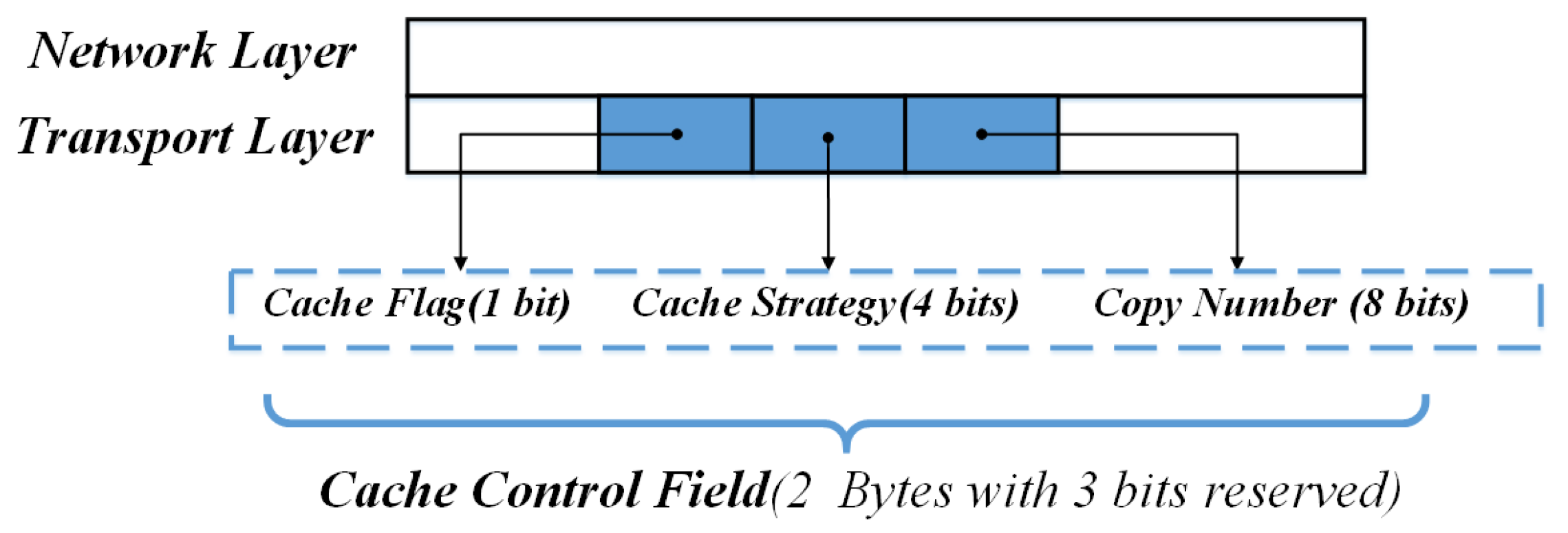
The ENC can be carried in the header of ICN data packets. We extend the cache control field in the transport layer header of ICN data packets, shown in
Figure 5. The cache control field includes three parts, the cache flag field, the cache strategy field and the copy number field. The cache flag field is used to quickly filter data that needs to be cached. If the cache flag is set to 0, all ICN nodes will forward the packet directly without caching it. This situation happens when the data packet is unpopular so on-path nodes will not cache it or the upstream node has cached it and modified the cache flag according to the cache strategy like LCD. If the cache flag is 1, the ICN nodes will cache the packet and further check the cache strategy field. The cache strategy field is used to instruct ICN nodes to execute different caching policies. The copy number field is used to control the number of content copies. When the ICN node decides to cache content, this node will record the value of the copy number field and recalculate the number of copies to be cached downstream. Lastly, the node will update the copy number field and forward the packet downstream.
5.2. ICN Packet Forwarding Process
The ENC-based caching scheme is implemented by constructing and processing ICN data packets. The key step is to modify the copy number field in the data packet. This allows downstream nodes to know how many copies should be placed. To modify the copy number field, the simplest way is allocating ENC equally according to the router port number or the degree of nodes. The second way is allocating ENC according to the traffic weight of router ports. The third way is allocating ENC according to the cache space of downstream nodes and this way requires nodes to know the cache space information of downstream nodes.
We choose the traffic weight for the allocation of ENC. The traffic information is influenced by the user’s activity degree, so it is more helpful compared with port number and cache space. When a node caches a content copy, the ENC of the content is also recorded. When a node plans to send content to the user, it will first find the out port to forward the content. Then, the node will get the traffic information of this out port and calculate the proportion of this out port traffic in the total traffic. Then, this node allocates the ENC according to the traffic proportion weight, to guide downstream nodes making caching decisions.
The request packet forwarding process is shown in Algorithm 2. When the request hits the cache at node
j, it will set the cache control field.
is used to record the expected number of copies for content
i.
denotes the physical port of node
j to forward the content
i and
denotes the traffic of
from node
j.
denotes the total traffic from node
j. When
is larger than 1, meaning that downstream nodes should cache more copies to get close to the expected number of copies. Each downstream node directly connected to node
j will record the expected number of copies for content
i as
when caching content
i.
| Algorithm 2: Request Packet Forwarding Process |
| 1: ICN node j gets a request packet for content i |
| 2: if node j has content i |
| 3: read the for content i, and from metadata |
| 4: if |
| 4: set to 1 |
| 5: set according to the caching strategy configuration |
| 6: set as |
| 7: else |
| 8: set to 0 |
| 9: set to 0 |
| 10: end if |
| 11: construct and forward the data packet |
| 12: else |
| 13: forward the request packet |
| 14: end if |
The data packet forwarding process is shown in Algorithm 3. When the cache flag is 0, on-path nodes will forward the packet to the destination without caching it or modifying the cache control field. When the cache flag is 1, the processing node will firstly check whether to modify the cache flag according to the caching strategy configuration. If the packet has been cached by the processing node, this node will directly forward it with the updated cache control field. Otherwise, the node will cache the packet before forwarding it.
| Algorithm 3: Data Packet Forwarding Process |
| 1: ICN node j gets a data packet belonging to content i |
| 2: if |
| 3: forward the data packet |
| 4: else |
| 5: set according to the caching strategy configuration |
| 6: if node j has content i |
| 7: update in node j with |
| 8: update as |
| 9: forward the data packet |
| 10: else |
| 11: cache the data packet at node j |
| 12: record in node j with |
| 13: update as |
| 14: forward the data packet |
| 15: end if |
| 16: end if |