Lateral-Acceleration-Based Vehicle-Models-Blending for Automated Driving Controllers
Abstract
1. Introduction
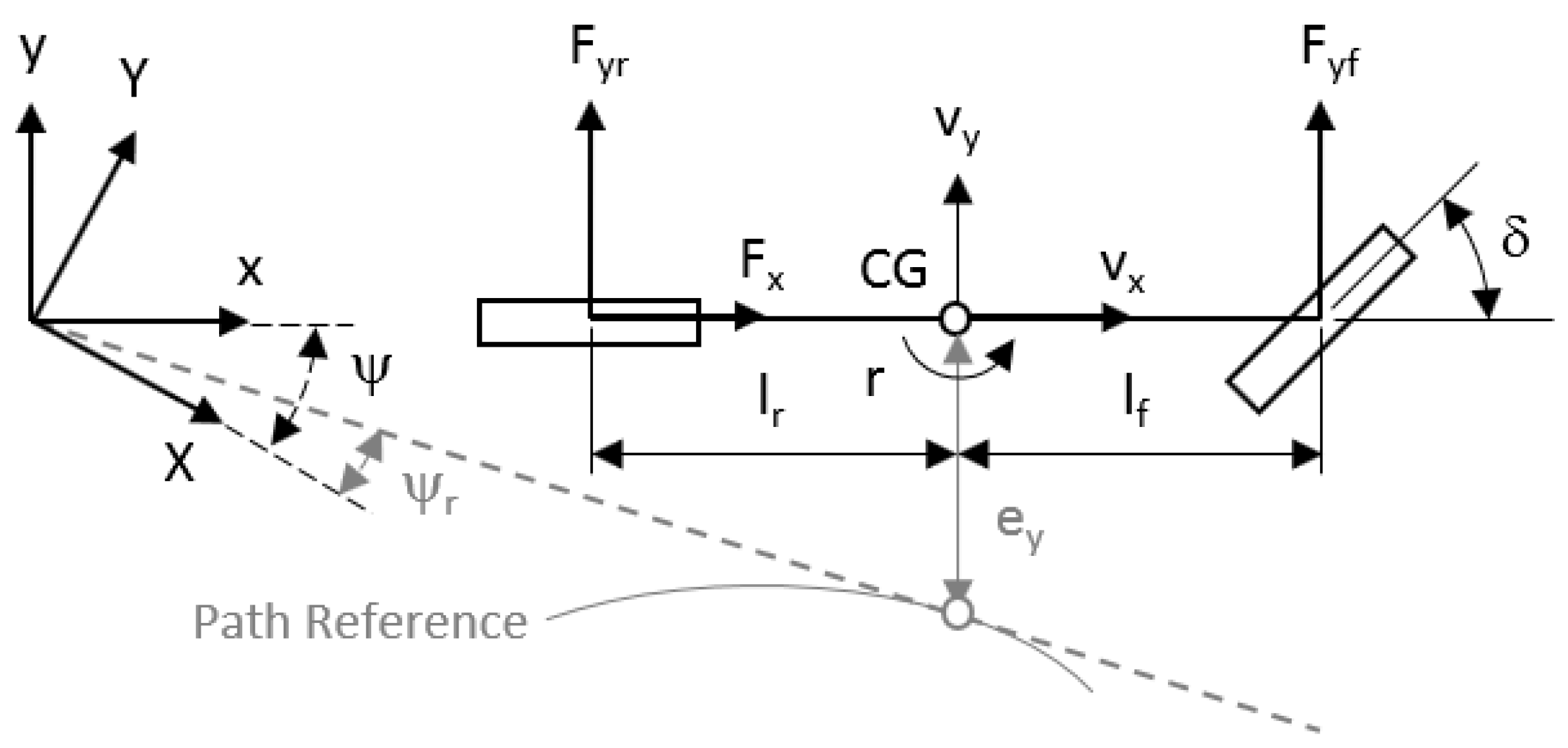
2. Vehicle Modeling
2.1. Kinematic Vehicle Model
2.2. Dynamic Vehicle Model
2.3. Blended Model for MPC Control
3. Tuning Procedure for Model Blending
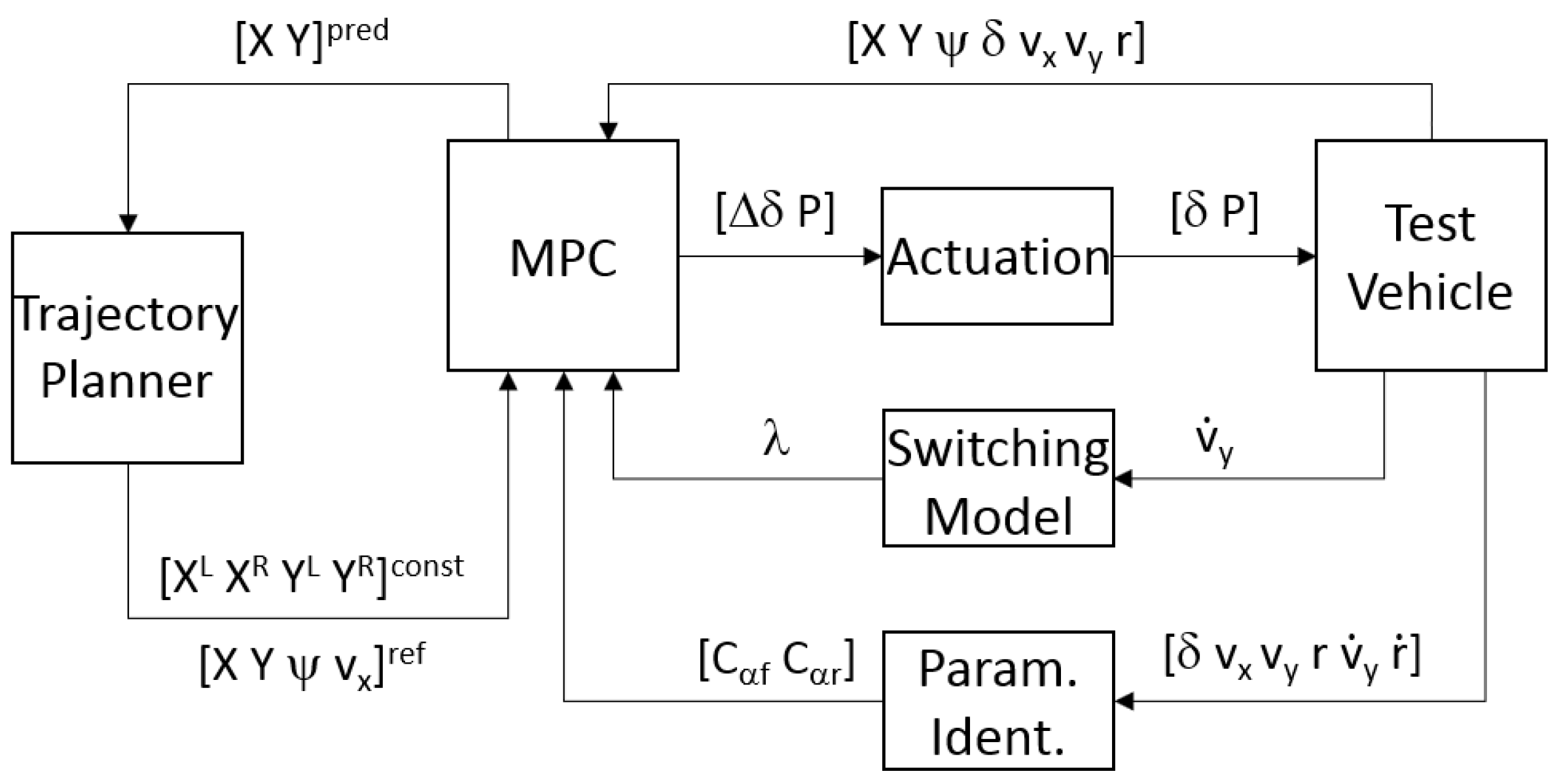
4. Case Study: An Urban Passenger Bus
4.1. Test Vehicle
4.2. Cornering Stiffness Identification
4.3. Switching Model
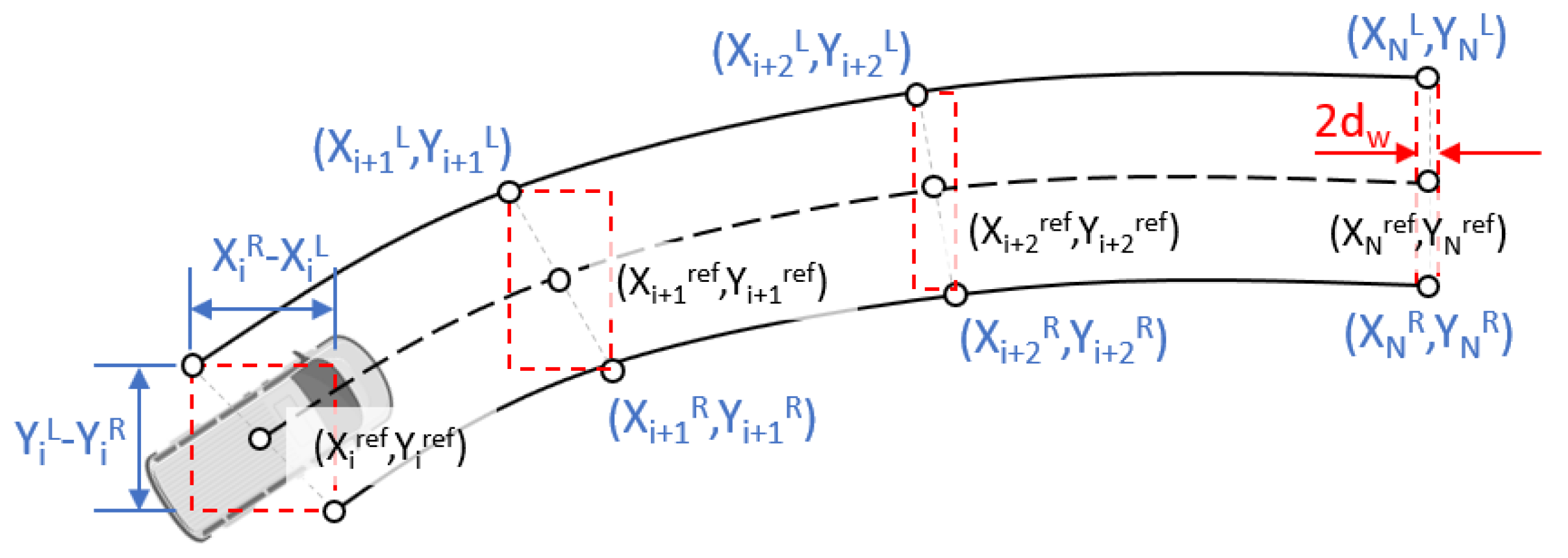
4.4. Trajectory Planner
4.5. Model Predictive Control
4.6. Actuation Stage
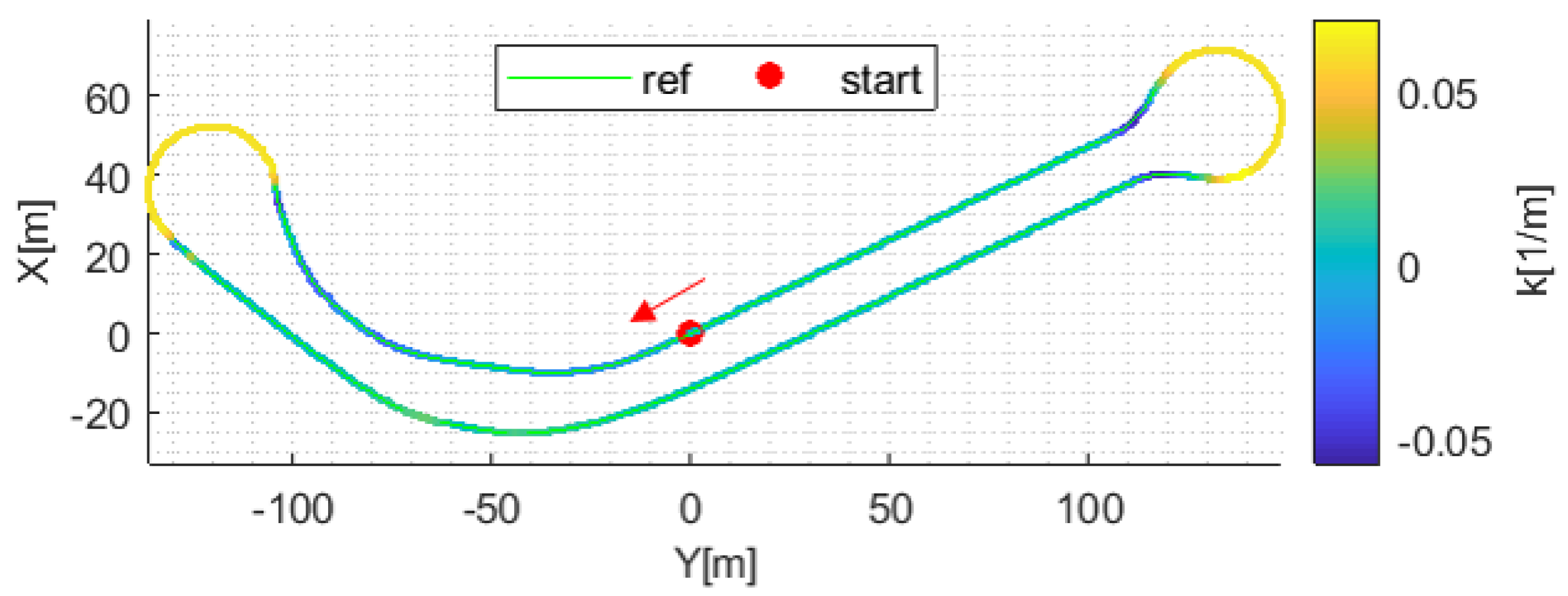
5. Results and Discussion
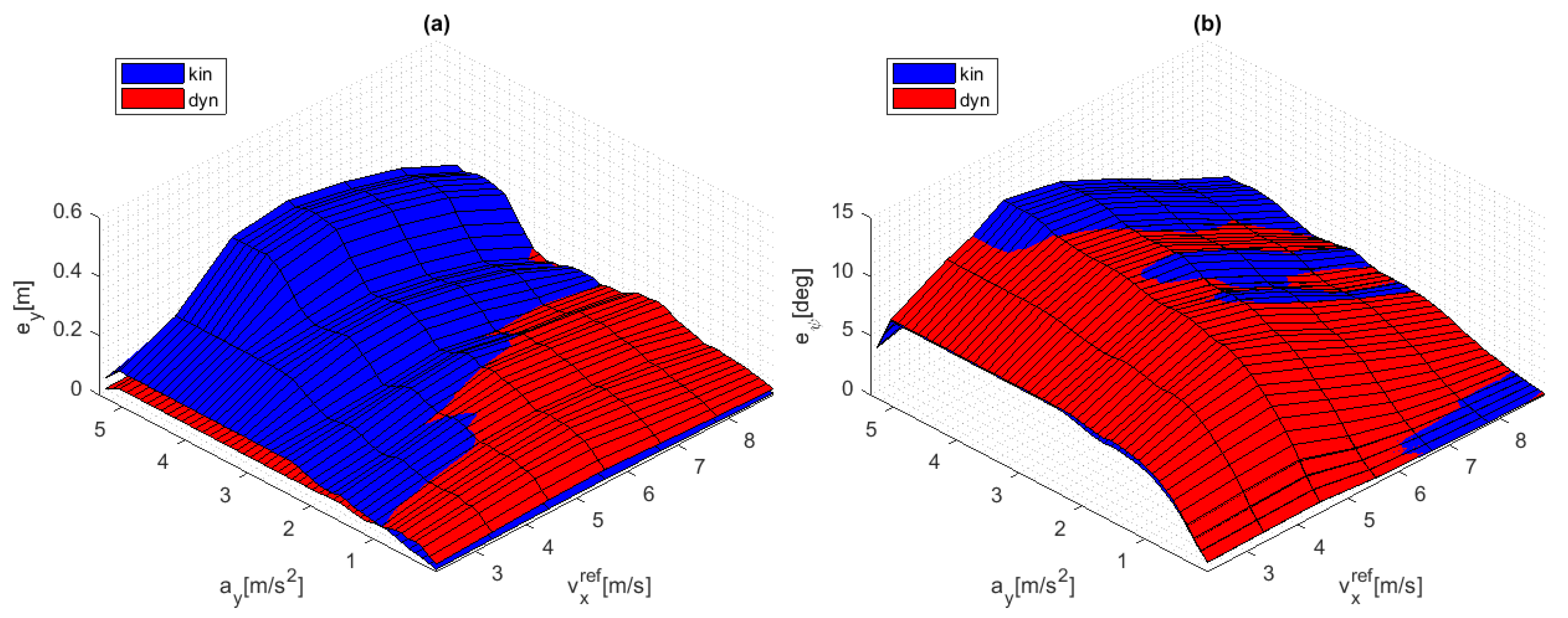
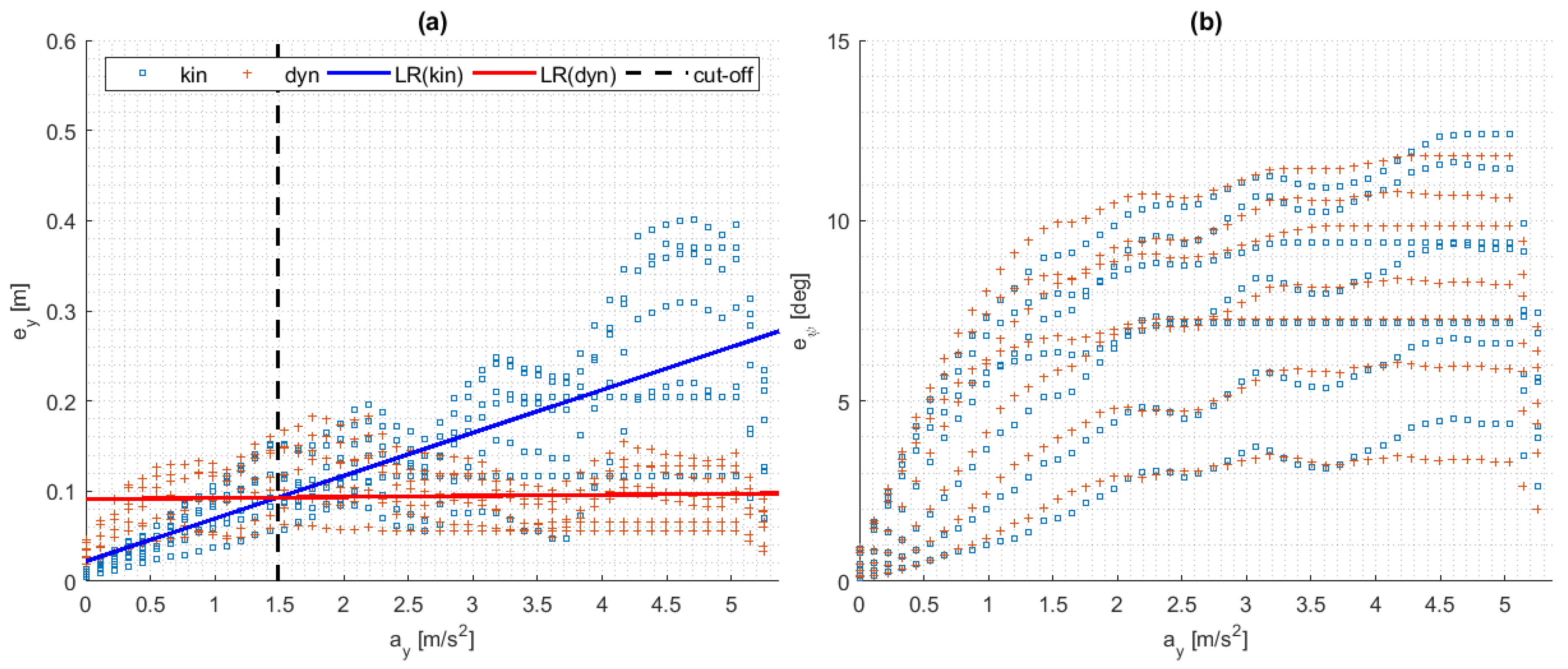
5.1. Tuning Procedure for Model Blending
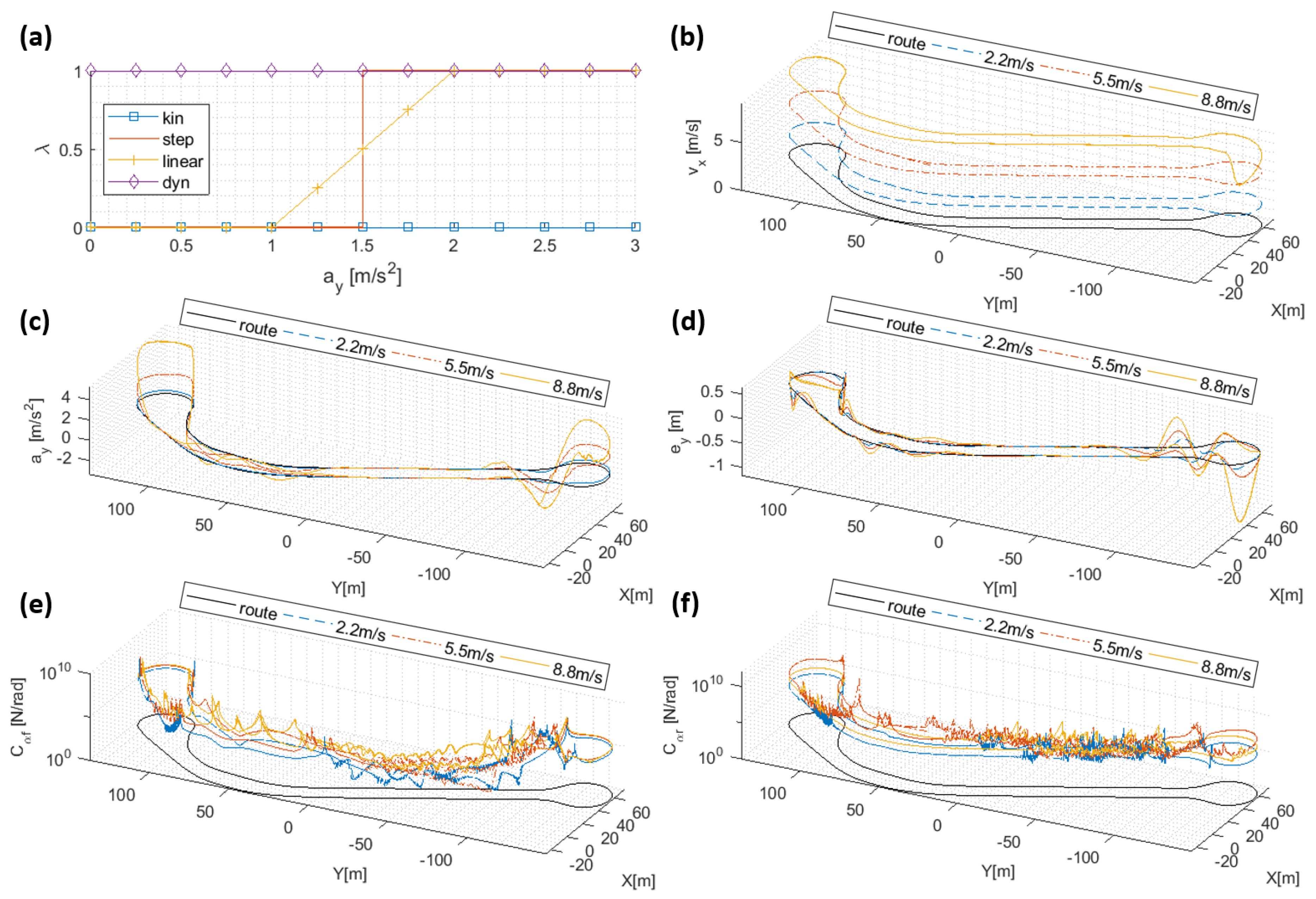
5.2. Trajectory-Tracking Response Analysis
5.3. Cornering Stiffness Estimation Analysis
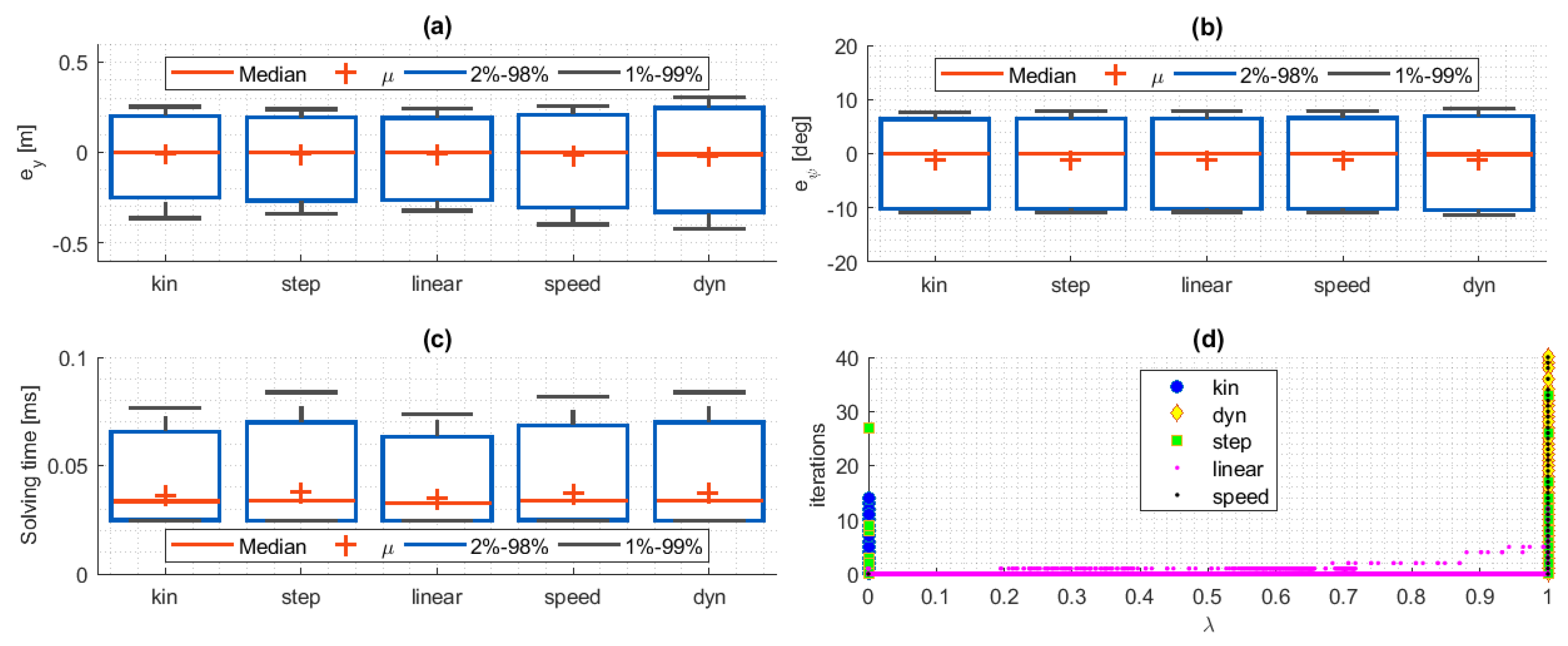
5.4. Lateral and Angular Error Analysis
5.5. Computational Cost Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dixit, S.; Fallah, S.; Montanaro, U.; Dianati, M.; Stevens, A.; Mccullough, F.; Mouzakitis, A. Trajectory planning and tracking for autonomous overtaking: State-of-the-art and future prospects. Annu. Rev. Control 2018, 45, 76–86. [Google Scholar] [CrossRef]
- Eskandarian, A.; Wu, C.; Sun, C. Research Advances and Challenges of Autonomous and Connected Ground Vehicles. IEEE Trans. ITS 2019, 1–29. [Google Scholar] [CrossRef]
- Sorniotti, A.; Barber, P.; De Pinto, S. Path tracking for automated driving: A tutorial on control system formulations and ongoing research. In Automated Driving; Springer: Cham, Switerland, 2017; pp. 71–140. [Google Scholar]
- Althoff, M. CommonRoad: Vehicle Models; Technische niversität München: Garching, Germany, 2017; pp. 1–25. [Google Scholar]
- Tomas-Gabarron, J.B.; Egea-Lopez, E.; Garcia-Haro, J. Vehicular trajectory optimization for cooperative collision avoidance at high speeds. IEEE Trans. ITS 2013, 14, 1930–1941. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking; Tech. Rep. CMU-RITR-09-08; Robotics Institute: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Amer, N.H.; Zamzuri, H.; Hudha, K.; Kadir, Z.A. Modelling and control strategies in path tracking control for autonomous ground vehicles: A review of state of the art and challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Jazar, R.N. Vehicle Dynamics: Theory and Application; Springer: Cham, Switerland, 2017. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer S&B Media: Boston, MA, USA, 2011. [Google Scholar]
- Matute, J.A.; Marcano, M.; Diaz, S.; Perez, J. Experimental Validation of a Kinematic Bicycle Model Predictive Control with Lateral Acceleration Consideration. IFAC-PapersOnLine 2019, 52, 289–294. [Google Scholar] [CrossRef]
- Matute-Peaspan, J.A.; Zubizarreta-Pico, A.; Diaz-Briceno, S.E. A Vehicle Simulation Model and Automated Driving Features Validation for Low-Speed High Automation Applications. IEEE trans. Intell. Transp. Syst. 2020, 1–10. [Google Scholar] [CrossRef]
- Gao, Y.; Gray, A.; Tseng, H.E.; Borrelli, F. A tube-based robust nonlinear predictive control approach to semiautonomous ground vehicles. Veh. Syst. Dyn. 2014, 52, 802–823. [Google Scholar] [CrossRef]
- Schildbach, G.; Borrelli, F. Scenario model predictive control for lane change assistance on highways. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 611–616. [Google Scholar]
- Liniger, A.; Domahidi, A.; Morari, M. Optimization-based autonomous racing of 1:43 scale RC cars. Optim. Control Appl. Methods 2015, 36, 628–647. [Google Scholar]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 163–168. [Google Scholar]
- Beal, C.E.; Gerdes, J.C. Model predictive control for vehicle stabilization at the limits of handling. IEEE Trans. CST 2012, 21, 1258–1269. [Google Scholar] [CrossRef]
- Tagne, G.; Talj, R.; Charara, A. Design and comparison of robust nonlinear controllers for the lateral dynamics of intelligent vehicles. IEEE Trans. ITS 2015, 17, 796–809. [Google Scholar] [CrossRef]
- Kritayakirana, K.; Gerdes, J.C. Autonomous vehicle control at the limits of handling. Int. J. Veh. Auton. Syst. 2012, 10, 271–296. [Google Scholar] [CrossRef]
- Besselmann, T.; Morari, M. Autonomous vehicle steering using explicit LPV-MPC. In Proceedings of the 2009 European Control Conference (2009 ECC), Budapest, Hungary, 23–26 August 2009; pp. 2628–2633. [Google Scholar]
- Bertolazzi, E.; Biral, F.; Da Lio, M. Real-time motion planning for multibody systems. MSD 2007, 17, 119–139. [Google Scholar] [CrossRef]
- Lattarulo, R.; He, D.; Pérez, J. A Linear Model Predictive Planning Approach for Overtaking Manoeuvres Under Possible Collision Circumstances. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1340–1345. [Google Scholar]
- Rupp, A.; Stolz, M. Survey on control schemes for automated driving on highways. In Automated Driving; Springer: Cham, Switerland, 2017; pp. 43–69. [Google Scholar]
- Kim, C.i.; Kim, M.s.; Lee, K.s.; Jang, H.S.; Park, T.S. Development of a full speed range path-following system for the autonomous vehicle. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015; pp. 710–715. [Google Scholar]
- Jo, K.; Chu, K.; Lee, K.; Sunwoo, M. Integration of multiple vehicle models with an IMM filter for vehicle localization. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 746–751. [Google Scholar]
- Kang, C.M.; Lee, S.H.; Chung, C.C. Vehicle lateral motion estimation with its dynamic and kinematic models based interacting multiple model filter. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 2449–2454. [Google Scholar]
- Ritschel, R.; Schrödel, F.; Hädrich, J.; Jäkel, J. Nonlinear model predictive path-following control for highly automated driving. IFAC-PapersOnLine 2019, 52, 350–355. [Google Scholar] [CrossRef]
- Kabzan, J.; Valls, M.d.l.I.; Reijgwart, V.; Hendrikx, H.F.C.; Ehmke, C.; Prajapat, M.; Bühler, A.; Gosala, N.; Gupta, M.; Sivanesan, R.; et al. Amz driverless: The full autonomous racing system. arXiv 2019, arXiv:1905.05150. [Google Scholar]
- Carvalho, A.; Lefévre, S.; Schildbach, G.; Kong, J.; Borrelli, F. Automated driving: The role of forecasts and uncertainty—A control perspective. Eur. J. Control 2015, 24, 14–32. [Google Scholar] [CrossRef]
- Polack, P.; Altché, F.; d’Andréa Novel, B.; de La Fortelle, A. The kinematic bicycle model: A consistent model for planning feasible trajectories for autonomous vehicles? In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 812–818. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pena, A.; Iglesias, I.; Valera, J.; Martin, A. Development and validation of Dynacar RT software, a new integrated solution for design of electric and hybrid vehicles. EVS26 Los Angeles 2012, 26, 1–7. [Google Scholar]
- Pacejka, H. Tire and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Sierra, C.; Tseng, E.; Jain, A.; Peng, H. Cornering stiffness estimation based on vehicle lateral dynamics. Veh. Syst. Dyn. 2006, 44, 24–38. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter (TR95-041); Department of Computer Science, University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 2006; 27599-3175. [Google Scholar]
- Lattarulo, R.; González, L.; Martí, E.; Matute, J.; Marcano, M.; Pérez, J. Urban motion planning framework based on n-bézier curves considering comfort and safety. J. Adv. Transp. 2018. [Google Scholar] [CrossRef]
- Houska, B.; Ferreau, H.J.; Diehl, M. ACADO toolkit—An open-source framework for automatic control and dynamic optimization. Optim. Control Appl. Methods 2011, 32, 298–312. [Google Scholar] [CrossRef]
- Marcano, M.; Matute, J.A.; Lattarulo, R.; Martí, E.; Pérez, J. Low speed longitudinal control algorithms for automated vehicles in simulation and real platforms. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Marques, O. Practical Image and Video Processing Using MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]

| Model | Strength(s) | Weakness(es) | Applications |
|---|---|---|---|
| Point-Mass | - Simplest model | - Ignores minimum turning | - Motion planning |
| - Easiest implementation | |||
| Geometric | - Considers minimum turn | - Ignores internal forces | - Motion planning/tracking |
| - Robust in most maneuvers | - Ignores vehicle acceleration | - Low speeds | |
| - Not suitable for high speeds | - Constant speed/curvature | ||
| Kinematic | - Simple motion description | - No wheel’s slip/skid | - Motion planning/tracking |
| - Considers chassis slip | - Speed range is limited | - Low speeds (<5 m/s) | |
| - Varying speed/curvature | |||
| Dynamic | - Accurate motion estimate | - Tire forces calculus | - Motion planning/tracking |
| - Handling dynamics | - Less numerical efficiency | - High speeds (>5 m/s) | |
| - Stability at handling limit | - ∞ linear tire model (V 0) | - Varying speed/curvature | |
| - Chassis slip angles < 5 deg | |||
| Multi-body | - Best accuracy | - Low numerical efficiency | - Motion planning |
| - All suspension forces | - Complex implementation | - Virtual test platform |
| Steps | Procedure |
|---|---|
| 1. | Plan a route for trajectory-tracking at constants |
| 2. | Execute motion control using kinematic vehicle model |
| 3. | Execute motion control using dynamic vehicle model |
| 4. | Average values in a grid of vs |
| 5. | Create surface plots from 4 |
| 6. | For step switching method: |
| 6.a. | Make Linear Regressions (LR) of vs |
| 6.b. | Intersect LRs to find a |
| 6.c. | The step switch is defined by 6b |
| 7. | For linear switching method: |
| 7.a. | Identify lowest in surfaces intersection from 5 |
| 7.b. | Estimate difference between 6b and 7a |
| 7.c. | Use 6b as point symmetry distance to 7a |
| 7.d. | The linear switch is defined by 7c |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 3.55 | m | m | 16,600 | kg | |
| 2.22 | m | 115,063 | kg-m | ||
| 7.34 | m | 0.65 | - | ||
| 1.21 | kg/m | g | 9.81 | m/s | |
| 3600 | N-m | 1:5.93 | - | ||
| 12,000 | N-m | 31:1 | - | ||
| 35 | N-m | 17 | kg-m | ||
| 0.45 | m | 100 | kg-m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matute-Peaspan, J.A.; Marcano, M.; Diaz, S.; Zubizarreta, A.; Perez, J. Lateral-Acceleration-Based Vehicle-Models-Blending for Automated Driving Controllers. Electronics 2020, 9, 1674. https://doi.org/10.3390/electronics9101674
Matute-Peaspan JA, Marcano M, Diaz S, Zubizarreta A, Perez J. Lateral-Acceleration-Based Vehicle-Models-Blending for Automated Driving Controllers. Electronics. 2020; 9(10):1674. https://doi.org/10.3390/electronics9101674
Chicago/Turabian StyleMatute-Peaspan, Jose A., Mauricio Marcano, Sergio Diaz, Asier Zubizarreta, and Joshue Perez. 2020. "Lateral-Acceleration-Based Vehicle-Models-Blending for Automated Driving Controllers" Electronics 9, no. 10: 1674. https://doi.org/10.3390/electronics9101674
APA StyleMatute-Peaspan, J. A., Marcano, M., Diaz, S., Zubizarreta, A., & Perez, J. (2020). Lateral-Acceleration-Based Vehicle-Models-Blending for Automated Driving Controllers. Electronics, 9(10), 1674. https://doi.org/10.3390/electronics9101674







