Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter
Abstract
1. Introduction
2. Mathematical Model of IM
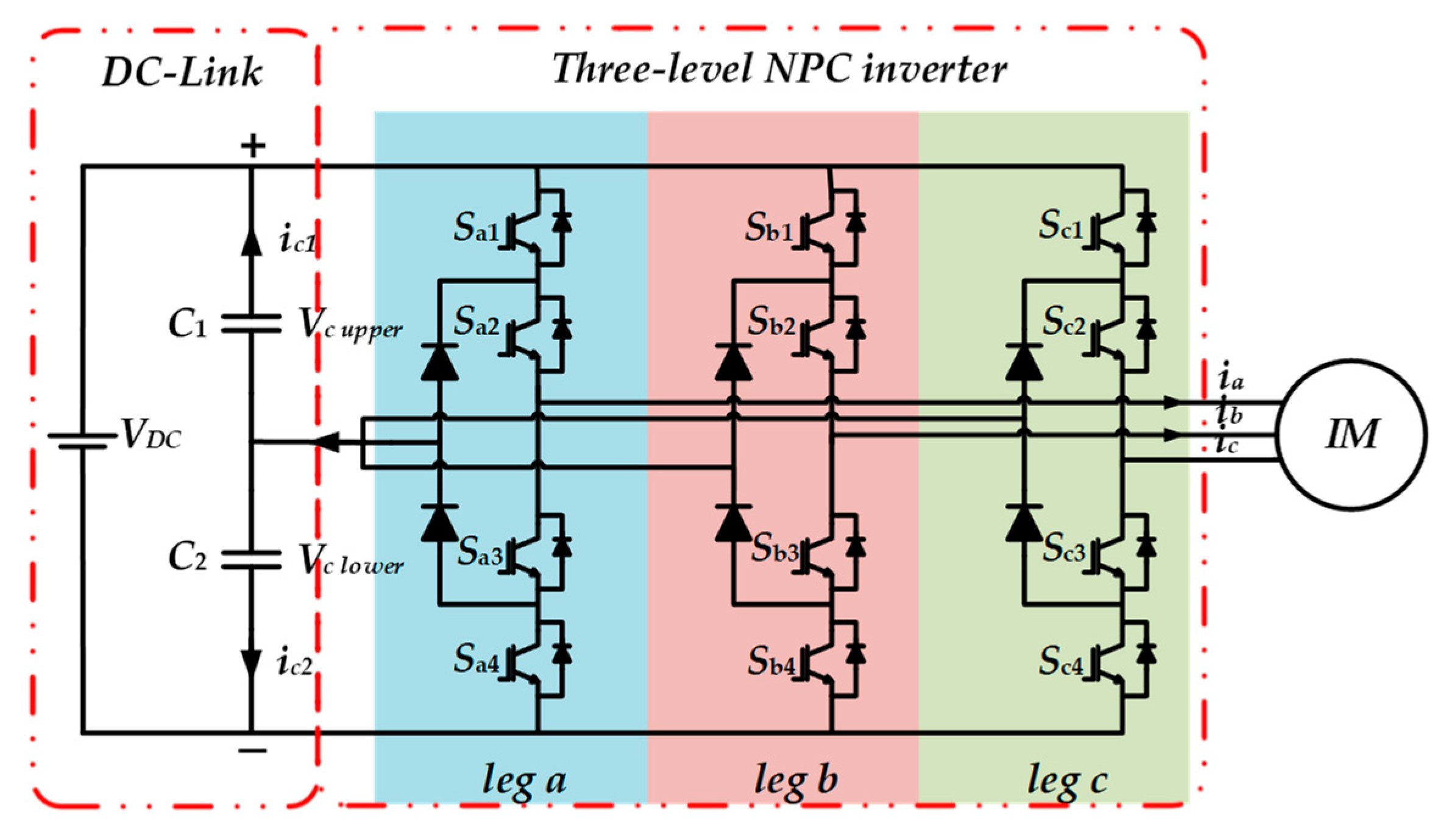
3. Three-Level Neutral-Point-Clamped Inverter for DTC of IM
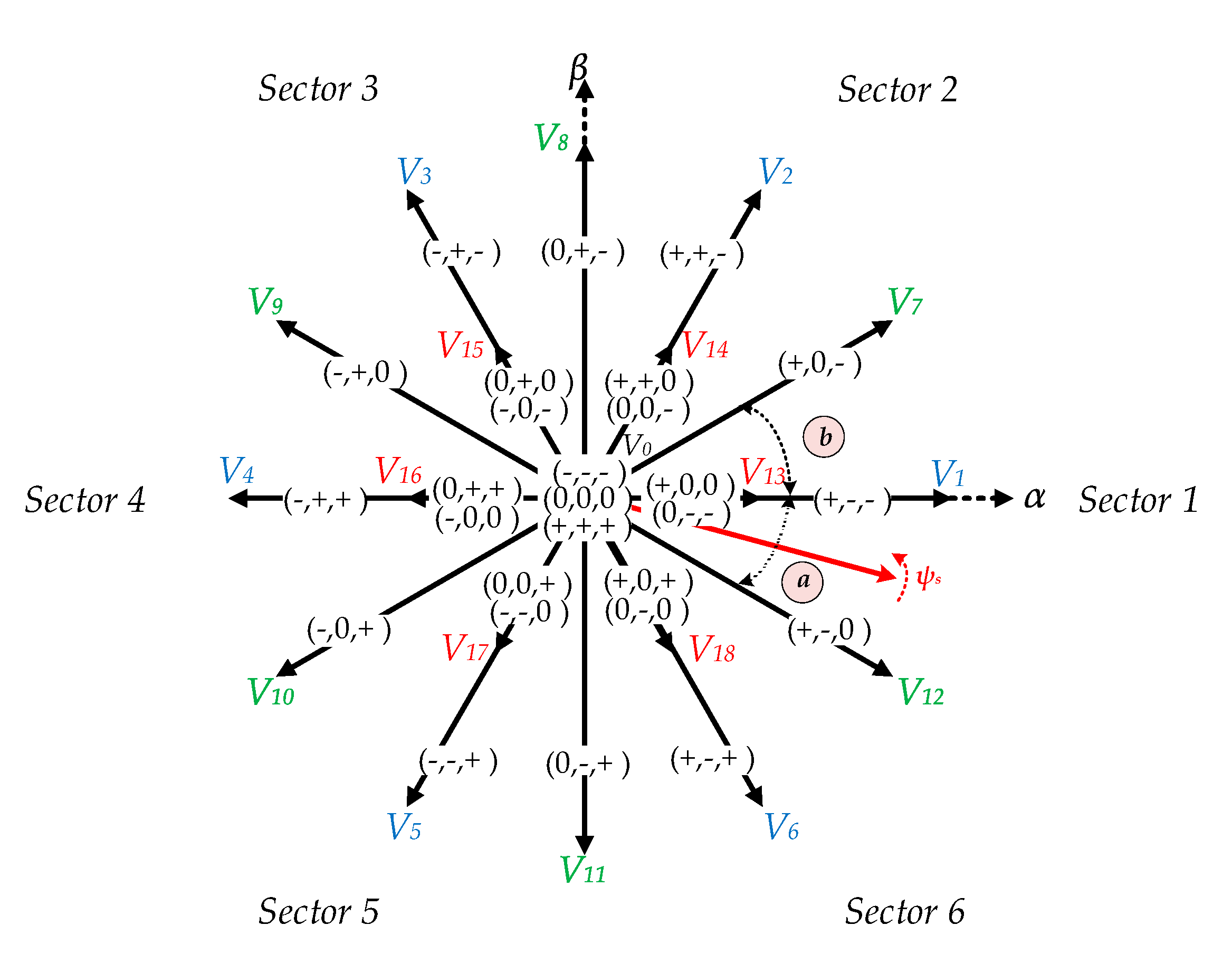
4. Classical DTC of IM and Its Limitations at Low-Speed Regions
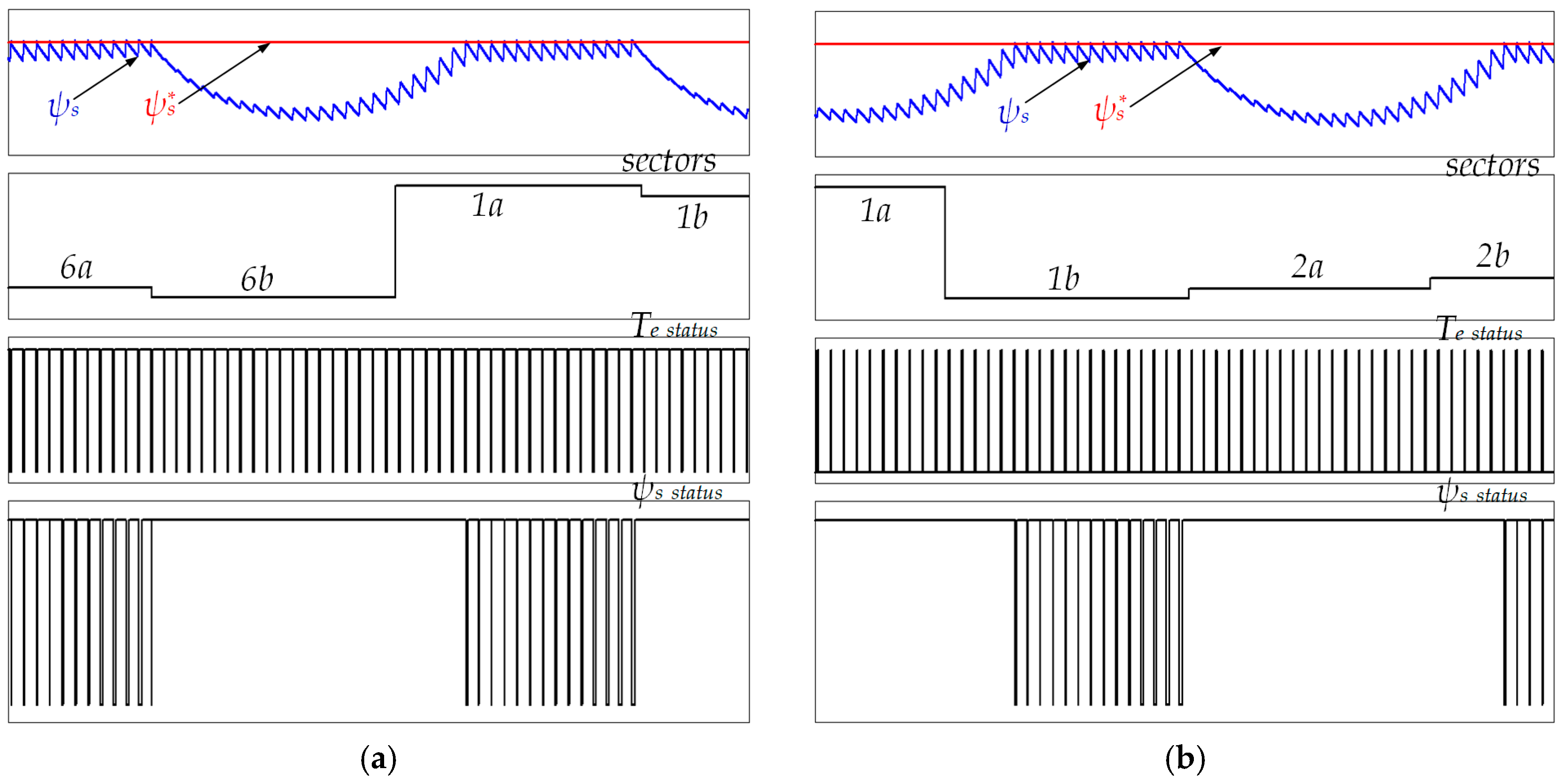
5. Low-Speed Performance Improvement
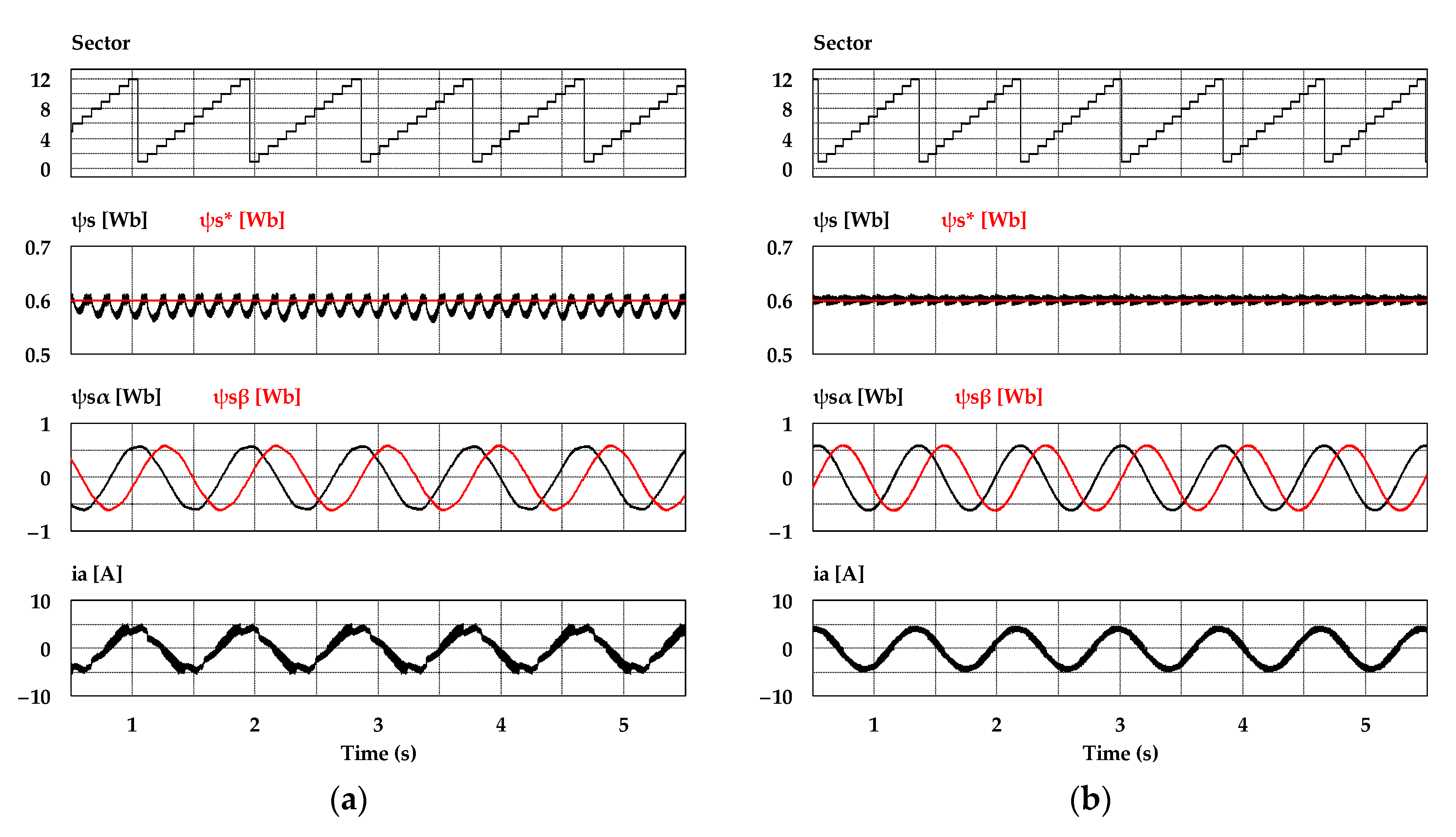
6. Simulation Results
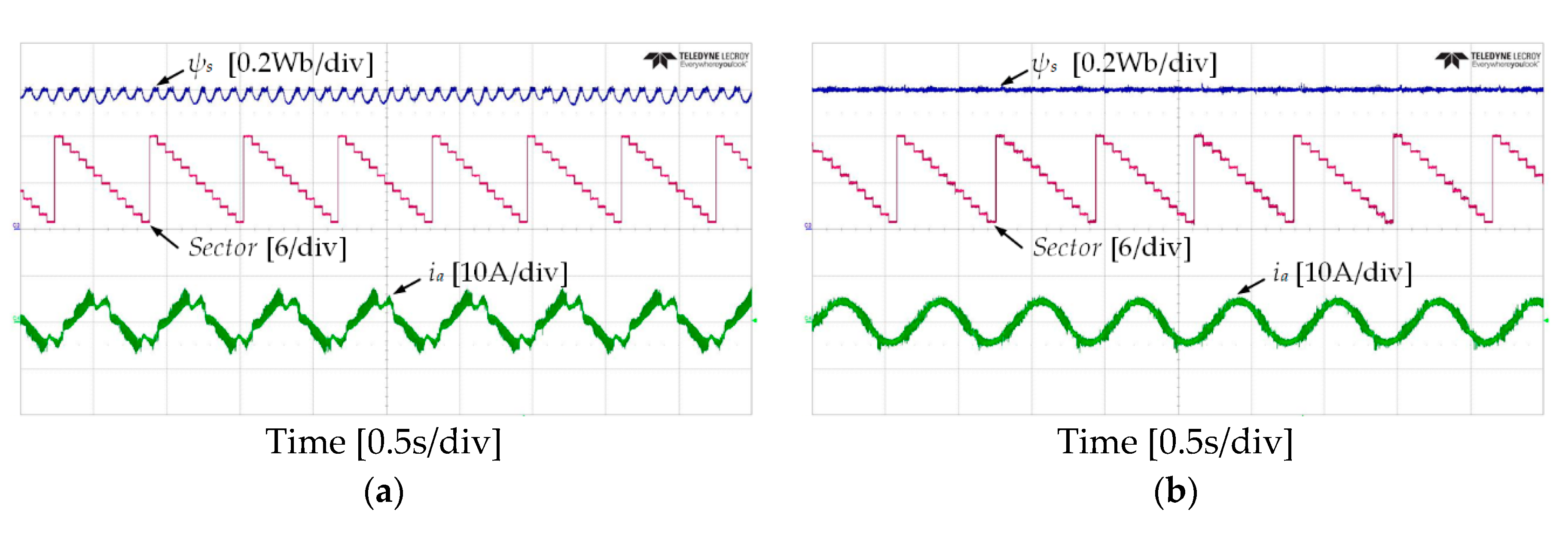
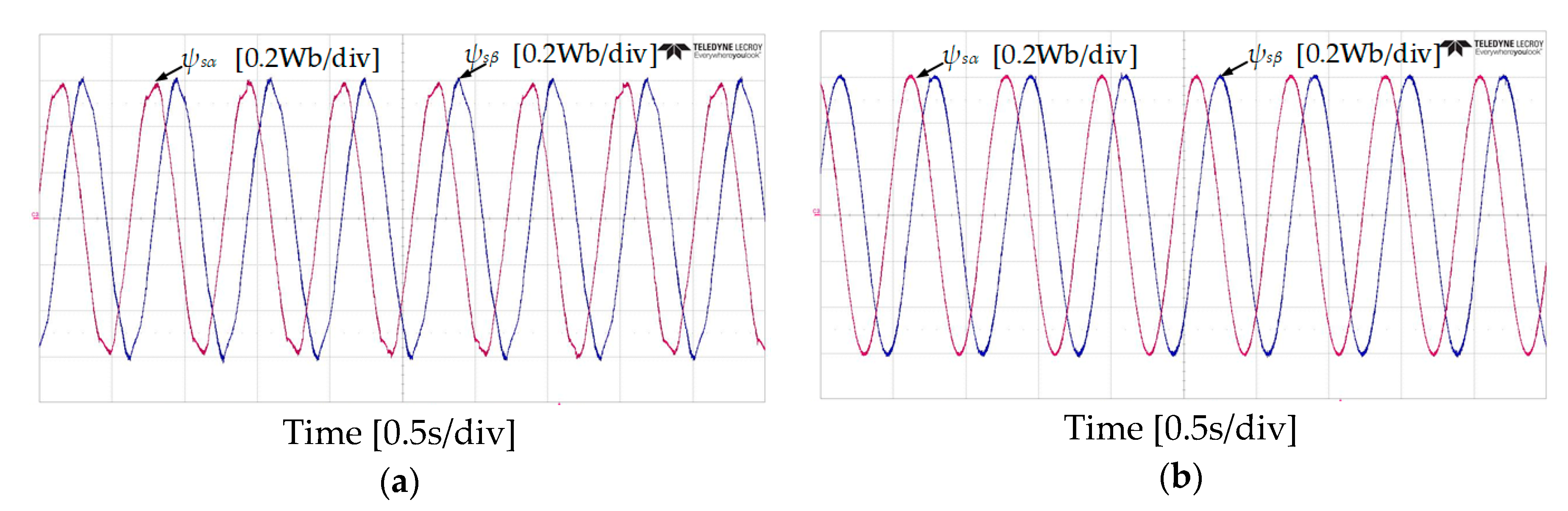
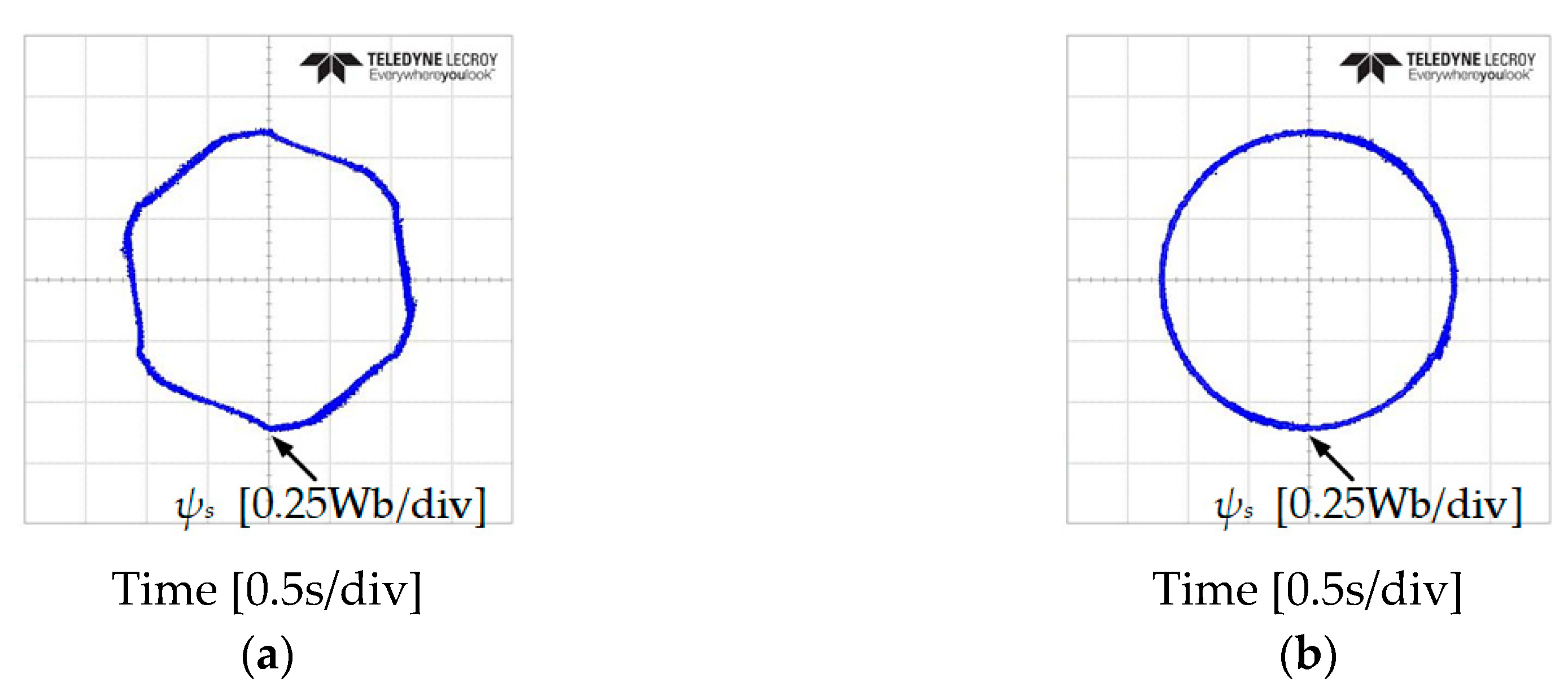
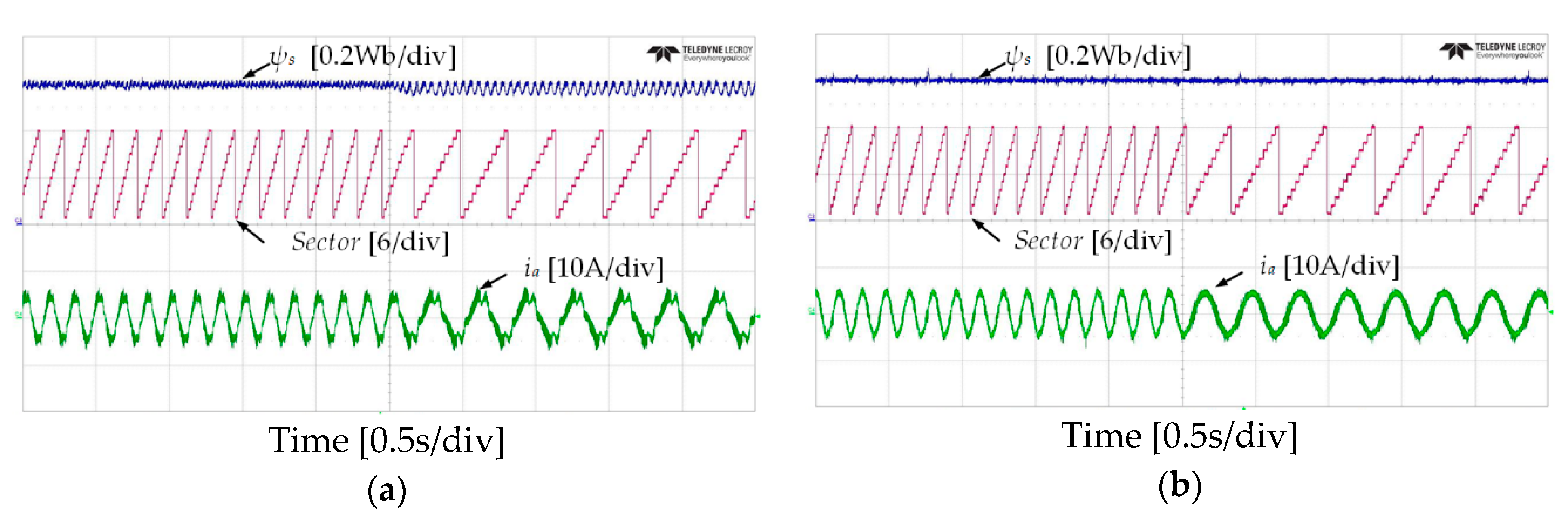
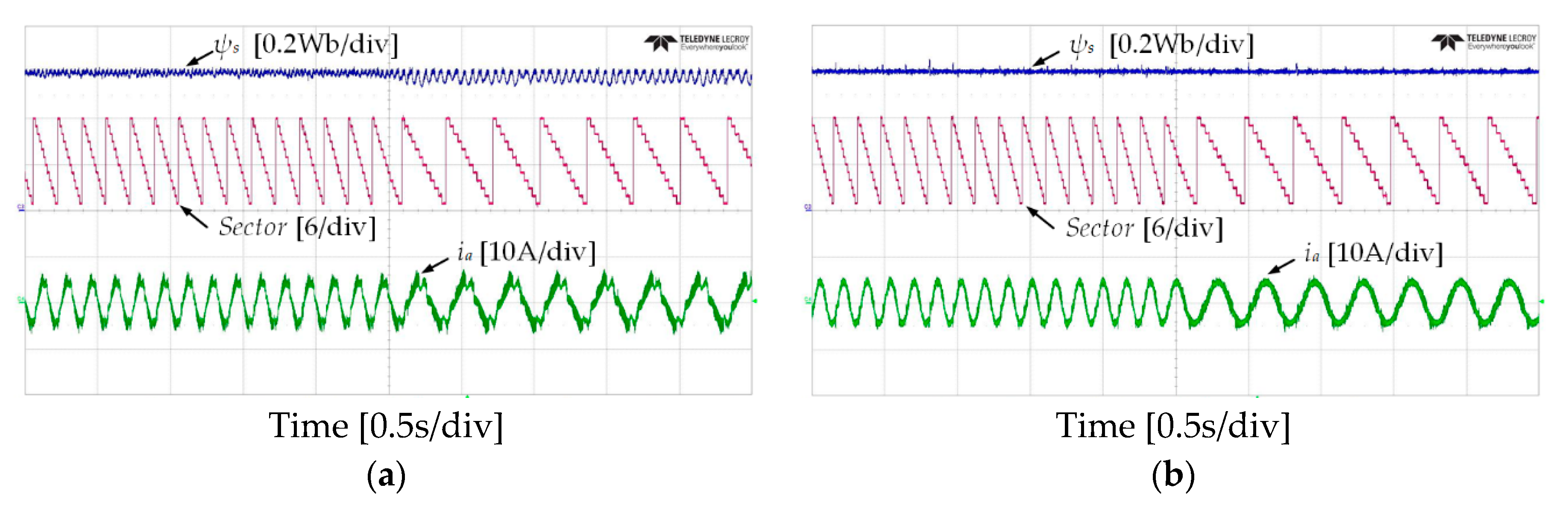
7. Experimental Results
7.1. Steady-State Operation
7.2. Transient-State Operation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chan, T.-F.; Shi, K. Applied Intelligent Control of Induction Motor Drives; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hannan, M.A.; Ali, J.A.; Jern, K.P.; Mohamed, A.; Lipu, M.S.H.; Hussain, A. Switching techniques and intelligent controllers for induction motor drive: Issues and recommendations. IEEE Access 2018, 6, 47489–47510. [Google Scholar] [CrossRef]
- Takahashi, I.; Noguchi, T. A new quick-response and high efficiency control strategy of an induction motor. IEEE Trans. Ind. Appl 1986, IA–22, 820–827. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Kim, K.Y.; Lee, S.S.; Lee, K.-B. A Modified Flux Regulation Method to Minimize Switching Frequency and Improve DTC-Hysteresis-Based Induction Machines in Low-Speed Regions. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2346–2355. [Google Scholar] [CrossRef]
- Lee, K.-B.; Song, J.H.; Choy, I.; You, J.Y. Improvement of low-speed operation performance of DTC for three-level inverter-fed induction motors. IEEE Trans. Ind. Electron. 2001, 48, 1006–1014. [Google Scholar]
- Yuan, T.; Wang, D. Performance Improvement for PMSM DTC System through Composite Active Vectors Modulation. Electronics 2018, 7, 263. [Google Scholar] [CrossRef]
- Lee, K.-B.; Blaabjerg, F. An improved DTC-SVM method for sensorless matrix converter drives using an overmodulation strategy and a simple nonlinearity compensation. IEEE Trans. Ind. Electron. 2007, 54, 3155–3166. [Google Scholar] [CrossRef]
- Lee, J.S.; Choi, C.-H.; Seok, J.-K.; Lorenz, R.D. Deadbeat–direct torque and flux control of interior permanent magnet synchronous machines with discrete time stator current and stator flux linkage observer. IEEE Trans. Ind. Appl. 2011, 47, 1749–1758. [Google Scholar] [CrossRef]
- Lascu, C.; Trzynadlowski, A.M. Combining the principles of sliding mode, direct torque control, and space-vector modulation in a high-performance sensorless AC drive. IEEE Trans. Ind. Appl. 2004, 40, 170–177. [Google Scholar] [CrossRef]
- Lee, H.; Nguyen, H.M.; Chun, T. Implementation of Direct Torque Control Method using Matrix Converter Fed Induction Motor. J. Power Electron. 2008, 8, 74–80. [Google Scholar]
- Liu, G.; Yang, Y.; Chen, Q. Virtual Signal Injected MTPA Control for DTC Five-Phase IPMSM Drives. J. Power Electron. 2019, 19, 956–967. [Google Scholar]
- Deng, Y.; Liang, Z.; Xia, P.; Zuo, X. Improved Speed Sensorless Vector Control Algorithm of Induction Motor Based on Long Cable. J. Electr. Eng. Technol. 2019, 14, 219–229. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Idris, N.R.N.; Lee, K.-B. Impact of Observability and Multi-objective Optimization on the Performance of Extended Kalman Filter for DTC of AC Machines. J. Electr. Eng. Technol. 2019, 14, 231–242. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the Art of Finite Control Set Model Predictive Control in Power Electronics. IEEE Trans. Ind. Inform. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Du, M.; Tian, Y.; Wang, W.; Ouyang, Z.; Wei, K. A Novel Finite-Control-Set Model Predictive Directive Torque Control Strategy of Permanent Magnet Synchronous Motor with Extended Output. Electronics 2019, 8, 388. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Wang, Q.; Li, G.; Zhang, M. Fast FCS-MPC-Based SVPWM Method to Reduce Switching States of Multilevel Cascaded H-Bridge STATCOMs. J. Power Electron. 2019, 19, 244–253. [Google Scholar]
- Bak, Y.; Jang, Y.; Lee, K.-B. Torque Predictive Control for Permanent Magnet Synchronous Motor Drives Using Indirect Matrix Converter. J. Power Electron. 2019, 19, 1536–1543. [Google Scholar]
- Zhou, Y.; Li, H.; Zhang, H.; Mao, J.; Huang, J. Model Free Deadbeat Predictive Speed Control of Surface-Mounted Permanent Magnet Synchronous Motor Drive system. J. Electr. Eng. Technol. 2019, 14, 265–274. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Hu, H. Predictive control of torque and flux of induction motor drives. In Proceedings of the 2005 International Conference on Power Electronics and Drives Systems (PEDS), Kuala Lumpur, Malaysia, 28 November–1 December 2005; pp. 67–71. [Google Scholar]
- Wang, F.; Zhang, Z.; Davari, S.A.; Fotouhi, R.; Khaburi, D.A.; Rodríguez, J.; Kennel, R. An Encoderless Predictive Torque Control for an Induction Machine with a Revised Prediction Model and EFOSMO. IEEE Trans. Ind. Electron. 2014, 61, 6635–6644. [Google Scholar] [CrossRef]
- Habibullah, M.; Lu, D.D.-C. A Speed-Sensorless FS-PTC of Induction Motors Using Extended Kalman Filters. IEEE Trans. Ind. Electron. 2015, 62, 6765–6778. [Google Scholar] [CrossRef]
- Cho, Y.; Bak, Y.; Lee, K.-B. Torque-Ripple Reduction and Fast Torque Response Strategy for Predictive Torque Control of Induction Motors. IEEE Trans. Power Electron. 2018, 33, 2458–2470. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, Y.; Zhou, Z.; Yan, Y.; Xia, C. Torque Ripple Reduction in Three-Level Inverter-Fed Permanent Magnet Synchronous Motor Drives by Duty-Cycle Direct Torque Control Using an Evaluation Table. J. Power Electron. 2017, 17, 368–379. [Google Scholar] [CrossRef]
- Vafaie, M.H.; Dehkordi, B.M.; Moallem, P.; Kiyoumarsi, A. Minimizing Torque and Flux Ripples and Improving Dynamic Response of PMSM Using a Voltage Vector With Optimal Parameters. IEEE Trans. Ind. Electron. 2016, 63, 3876–3888. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, K.-B.; Song, J.-H.; Lee, Y. -I. Torque-ripple minimization and fast dynamic scheme for torque predictive control of permanent-magnet synchronous motors. IEEE Trans. Power Electron. 2015, 30, 2182–2190. [Google Scholar] [CrossRef]
- Mohan, D.; Zhang, X.; Foo, G.H.B. Three-Level Inverter-Fed Direct Torque Control of IPMSM with Constant Switching Frequency and Torque Ripple Reduction. IEEE Trans. Ind. Electron. 2016, 63, 7908–7918. [Google Scholar] [CrossRef]
- Naganathan, P.; Srinivas, S.; Ittamveettil, H. Five-level torque controller-based DTC method for a cascaded three-level inverter fed induction motor drive. IET Power Electron. 2017, 10, 1223–1230. [Google Scholar] [CrossRef]
- Lee, K.-B.; Lee, J.S. Reliability Improvement Technology for Power Converters; Springer: Singapore, 2017. [Google Scholar]
- Lee, K.-B.; Song, J.-H.; Choy, I.; Yoo, J.Y. Torque ripple reduction in DTC of induction motor driven by three-level inverter with low switching frequency. IEEE Trans. Power Electron. 2002, 17, 255–264. [Google Scholar]
- Alsofyani, I.M.; Bak, Y.; Lee, K.-B. Fast Torque Control and Minimized Sector-Flux Droop for Constant Frequency Torque Controller based-DTC of Induction Machines. IEEE Trans. Power Electron. 2019, 34, 12141–12153. [Google Scholar] [CrossRef]
- Hakami, S.S.; Alsofyani, I.M.; Lee, K.-B. Improved Constant Switching Frequency Torque Regulator based DTC of IM Fed by 3L-NPC Inverter for Wide Speed Region. In Proceedings of the 2019 IEEE Conference on Energy Conversion (CENCON), Yogyakarta, Indonesia, 16–17 October 2019; pp. 42–46. [Google Scholar]









| ψs Status | Te Status | Sec 1a | Sec 1b | Sec 2a | Sec 2b | Sec 3a | Sec 3b | Sec 4a | Sec 4b | Sec 5a | Sec 5b | Sec 6a | Sec 6b |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| +2 | V8 | V3 | V9 | V4 | V10 | V5 | V11 | V6 | V12 | V1 | V7 | V2 | |
| +1 | V14 | V15 | V15 | V16 | V16 | V17 | V17 | V18 | V18 | V13 | V13 | V14 | |
| 1 | 0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 |
| −1 | V17 | V18 | V18 | V13 | V13 | V14 | V14 | V15 | V15 | V16 | V16 | V17 | |
| −2 | V5 | V11 | V6 | V12 | V1 | V7 | V2 | V8 | V3 | V9 | V4 | V10 | |
| +2 | V7 | V2 | V8 | V3 | V9 | V4 | V10 | V5 | V11 | V6 | V12 | V1 | |
| +1 | V13 | V14 | V14 | V15 | V15 | V16 | V16 | V17 | V17 | V18 | V18 | V13 | |
| 0 | 0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 | V0 |
| −1 | V18 | V13 | V13 | V14 | V14 | V15 | V15 | V16 | V16 | V17 | V17 | V18 | |
| −2 | V6 | V12 | V1 | V7 | V2 | V8 | V3 | V9 | V4 | V10 | V5 | V11 |
| Parameter | Value |
|---|---|
| Nominal power | 3.7 kW |
| Nominal torque | 20.36 Nm |
| Nominal speed | 1750 r/min |
| Nominal current | 8.28 A |
| Reference flux | 0.6 Wb |
| Number of pole-pairs | 2 |
| Rotor inductance | 146.2 mH |
| Rotor resistance | 1.225 Ω |
| Stator inductance | 146.2 mH |
| Stator resistance | 0.934 Ω |
| Mutual inductance | 139.52 mH |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakami, S.S.; Mohd Alsofyani, I.; Lee, K.-B. Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter. Electronics 2020, 9, 77. https://doi.org/10.3390/electronics9010077
Hakami SS, Mohd Alsofyani I, Lee K-B. Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter. Electronics. 2020; 9(1):77. https://doi.org/10.3390/electronics9010077
Chicago/Turabian StyleHakami, Samer Saleh, Ibrahim Mohd Alsofyani, and Kyo-Beum Lee. 2020. "Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter" Electronics 9, no. 1: 77. https://doi.org/10.3390/electronics9010077
APA StyleHakami, S. S., Mohd Alsofyani, I., & Lee, K.-B. (2020). Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter. Electronics, 9(1), 77. https://doi.org/10.3390/electronics9010077







