Novel Prediction Framework for Path Delay Variation Based on Learning Method
Abstract
1. Introduction
- Regarding the single corner, it not only eliminates the characterization effort for the timing library of each cell, but also performs better than AOCV.
- Concerning the multi-corner, the single model setting can be easily expanded to multi-corner, which is not possible in traditional AOCV and MC methods and have less error compared to existing works.
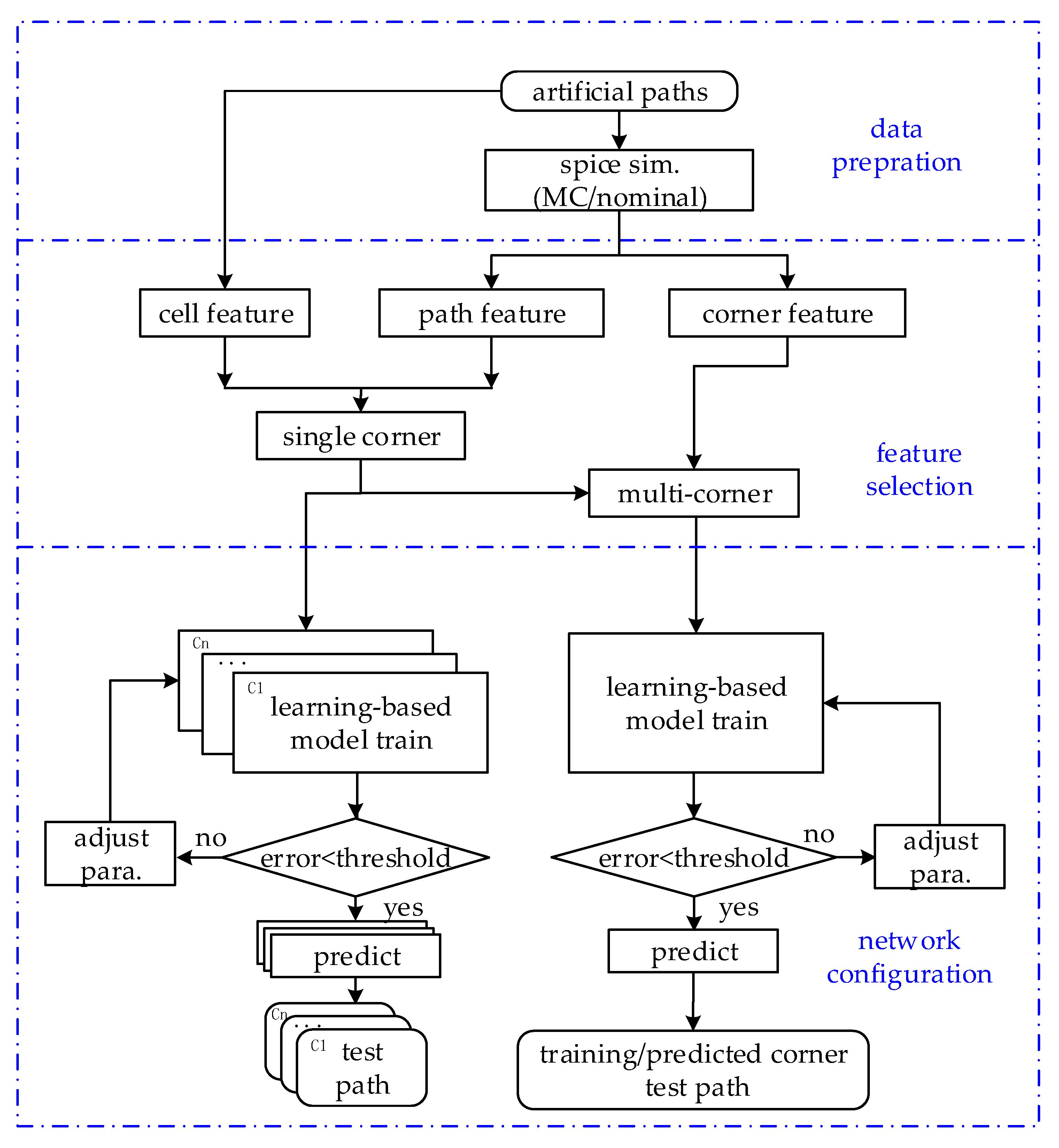
2. Proposed Prediction Framework for Path Delay Variation-Based Learning Method
2.1. Data Preparation
2.2. Feature Selection
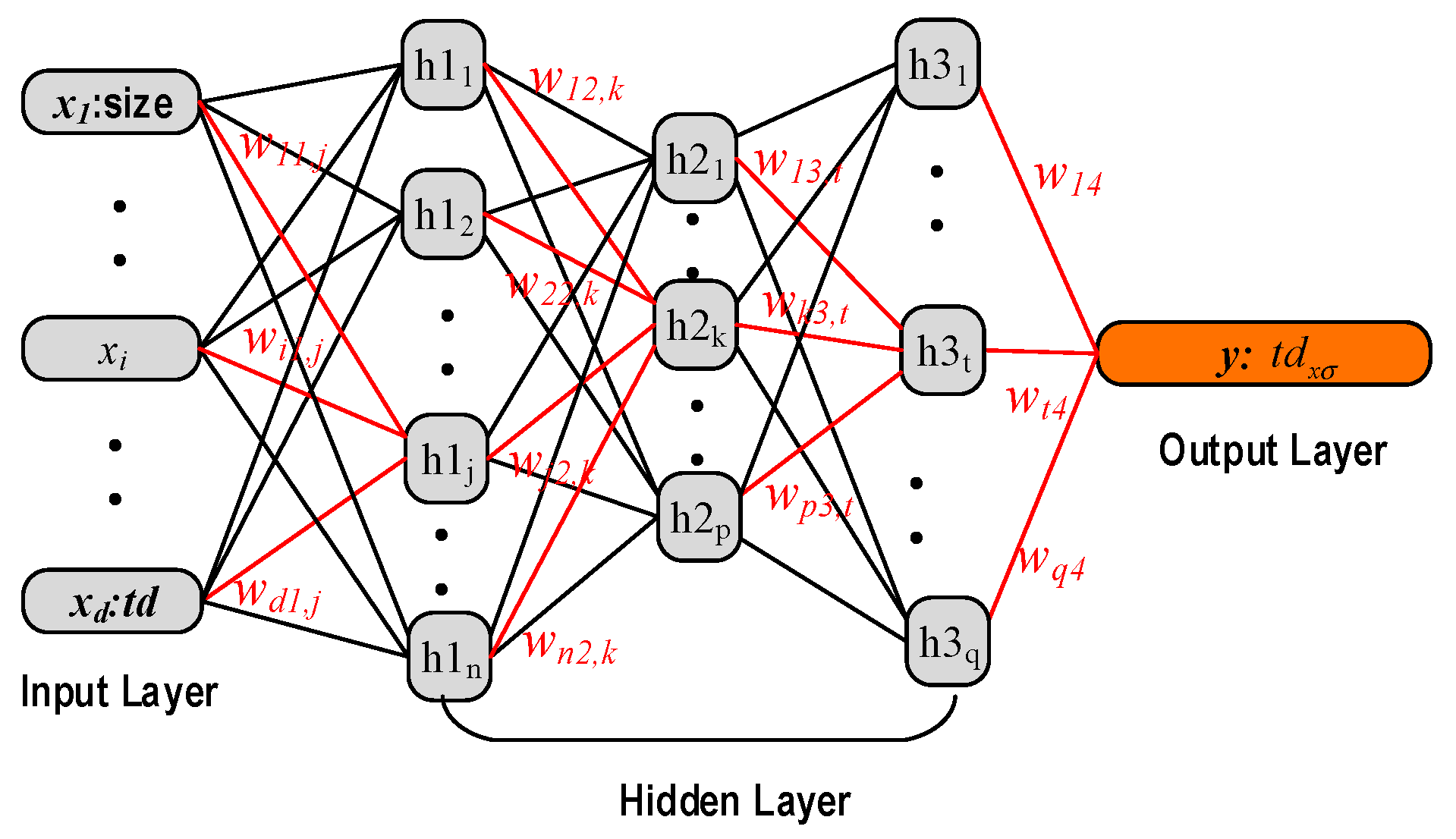
2.3. Network and Configuration
3. Experimental Results and Discussions
3.1. Path Delay Variation Prediction at a Single Corner
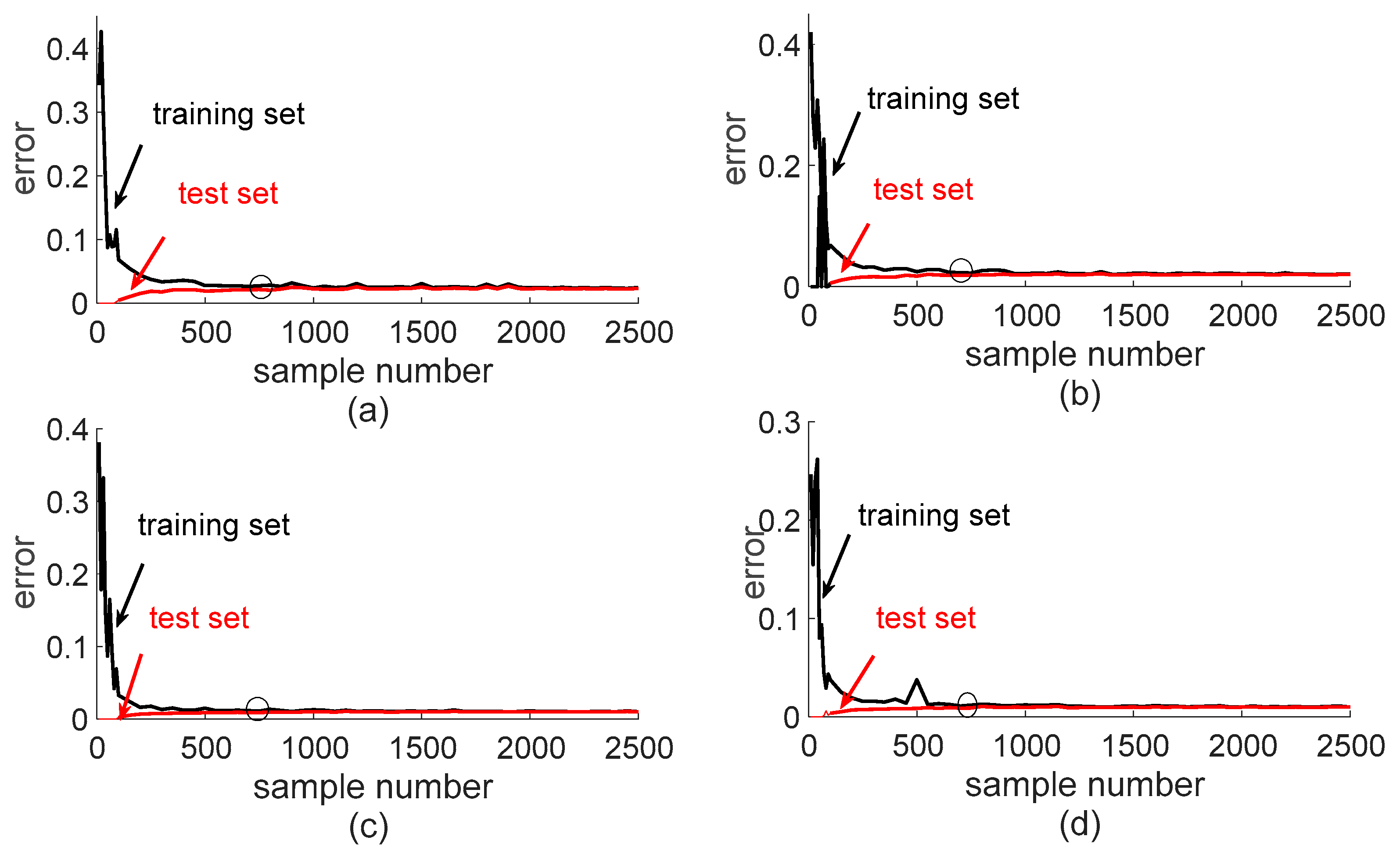
3.1.1. The Selection of Sample Number
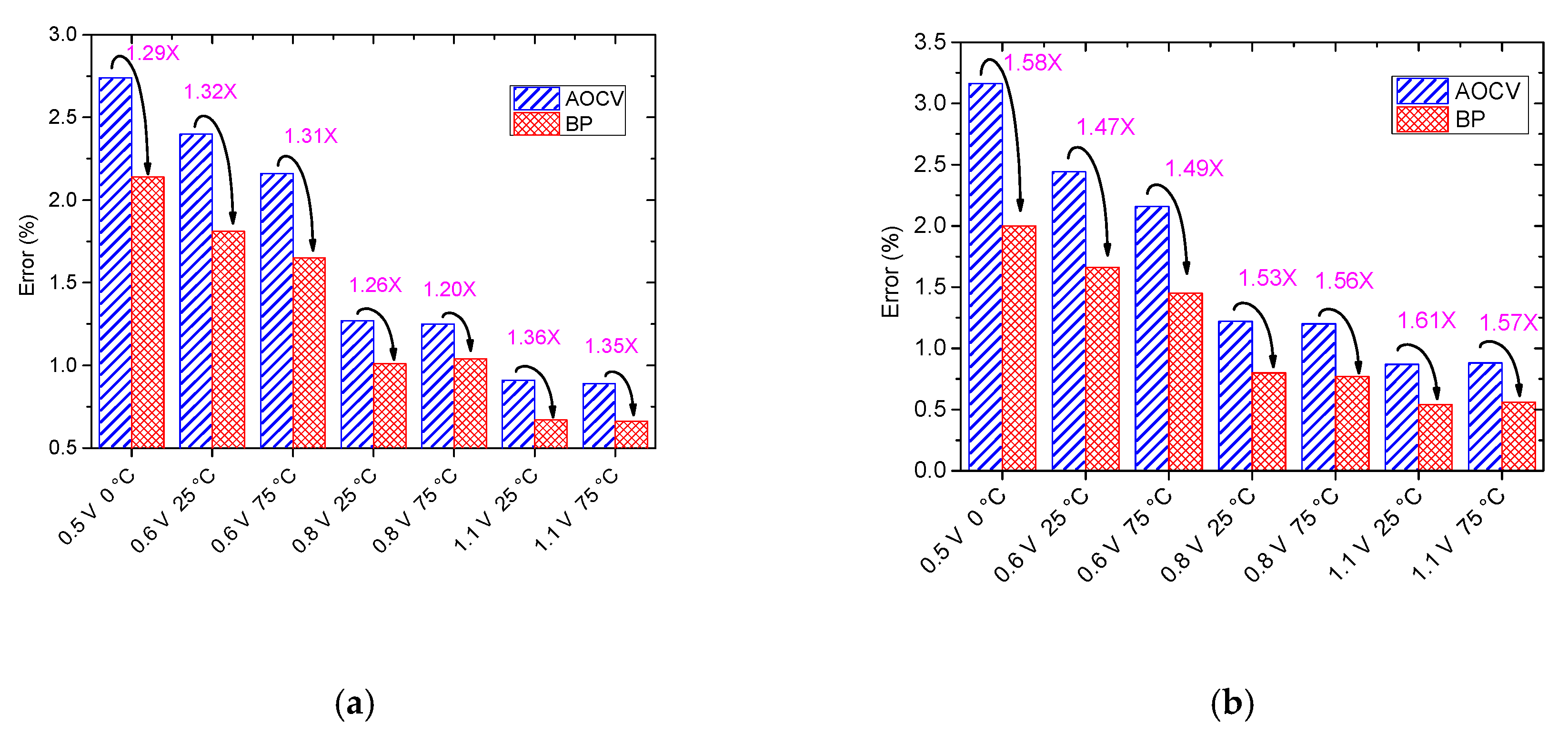
3.1.2. Path Delay Variation Prediction at Single Corner
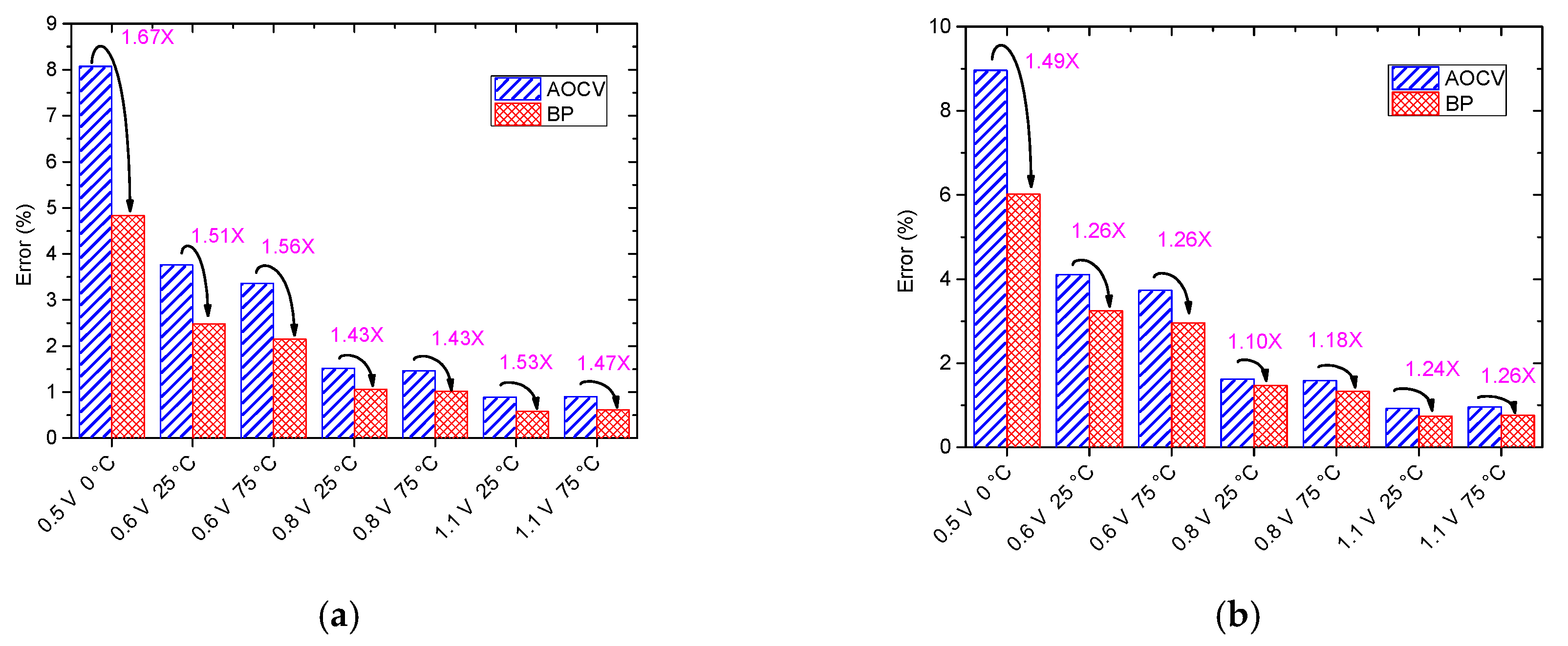
3.2. Path Delay Variation Prediction at Multi-Corner
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McConaghy, T.; Breen, K.; Dyck, J.; Gupta, A. Variation-Aware Design of Custom Integrated Circuits: A Hands-On Field Guide; Springer Science and Business Media: New York, NY, USA, 2012. [Google Scholar]
- Abu-Rahma, M.H.; Anis, M. A statistical design-oriented delay variation model accounting for within-die variations. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2008, 27, 1983–1995. [Google Scholar] [CrossRef]
- Corsonello, P.; Frustaci, F.; Lanuzza, M.; Perri, S. Over/undershooting effects in accurate buffer delay model for sub-threshold domain. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 1456–1464. [Google Scholar] [CrossRef]
- Tolbert, J.R.; Mukhopadhyay, S. Accurate buffer modeling with slew propagation in subthreshold circuits. In Proceedings of the International Symposium on Quality Electronic Design, San Jose, CA, USA, 16–18 March 2009; pp. 91–96. [Google Scholar]
- Takahashi, R.; Takata, H.; Yasufuku, T. Large within-die gate delay variations in sub-threshold logic circuits at low temperature. IEEE Trans. Circuits Syst. II Express Briefs 2012, 12, 918–921. [Google Scholar] [CrossRef]
- Harris, D.M.; Keller, B.; Karl, J.; Keller, S. A transregional model for near-threshold circuits with application to minimum-energy operation. In Proceedings of the International Conference on Microelectronics, Cairo, Egypt, 19–22 December 2011; pp. 64–67. [Google Scholar]
- Dreslinski, R.G.; Wieckowski, M.; Blaauw, D. Near-Threshold Computing: Reclaiming Moore’s Law Through Energy Efficient Integrated Circuits. Proc. IEEE 2010, 98, 253–266. [Google Scholar] [CrossRef]
- Kaul, H.; Anders, M.; Hsu, S.; Agarwal, A. Near-threshold voltage (NTV) design: Opportunities and challenges. In Proceedings of the 49th Annual Design Automation Conference, San Francisco, CA, USA, 3–7 June 2012; pp. 1153–1158. [Google Scholar]
- Markovic, D.; Wang, C.C.; Alarcon, L.P. Ultralow-Power Design in Near-Threshold Region. Proc. IEEE 2010, 98, 237–252. [Google Scholar] [CrossRef]
- Datta, B.; Burleson, W. Temperature effects on energy optimization in sub-threshold circuit design. In Proceedings of the International Symposium on Quality Electronic Design, San Jose, CA, USA, 16–18 March 2009; pp. 680–685. [Google Scholar]
- Kuhn, K.J.; Giles, M.D.; Becher, D.; Kolar, P.; Kornfeld, A.; Kotlyar, R.; Mudanai, S. Process technology variation. IEEE Trans. Electron Devices 2011, 58, 2197–2208. [Google Scholar] [CrossRef]
- Shoniker, M.; Oleynikov, O.; Cockburn, B.F.; Han, J.; Rana, M.; Pedrycz, W. Automatic Selection of Process Corner Simulations for Faster Design Verification. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 37, 1312–1316. [Google Scholar] [CrossRef]
- De Jonghe, D.; Maricau, E.; Gielen, G.; McConaghy, T.; Tasić, B.; Stratigopoulos, H. Advances in variation-aware modeling, verification, and testing of analog ICs. In Proceedings of the Conference on Design, Automation and Test in Europe, Dresden, Germany, 12–16 March 2012; pp. 1615–1620. [Google Scholar]
- Alioto, M. Ultra-low power VLSI circuit design demystified and explained: A tutorial. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 3–29. [Google Scholar] [CrossRef]
- Keller, S.; Harris, D.M.; Martin, A.J. A compact transregional model for digital CMOS circuits operating near threshold. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 2041–2053. [Google Scholar] [CrossRef]
- Rithe, R.; Gu, J.; Wang, A.; Datla, S.; Gammie, G.; Buss, D.; Chandrakasan, A. Non-linear operating point statistical analysis for local variations in logic timing at low voltage. In Proceedings of the Conference on Design, Automation and Test in Europe, Dresden, Germany, 8–12 March 2010; pp. 965–968. [Google Scholar]
- Zhang, Y.; Calhoun, B.H. Fast, accurate variation-aware path timing computation for sub-threshold circuits. In Proceedings of the Fifteenth International Symposium on Quality Electronic Design, Santa Clara, CA, USA, 3–5 March 2014; pp. 243–248. [Google Scholar]
- Shiomi, J.; Ishihara, T.; Onodera, H. Statistical Timing Modeling Based on a Lognormal Distribution Model for Near-Threshold Circuit Optimization. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2015, 98, 1455–1466. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, J.; Wang, M.; Nie, J.; Liu, X.; Ge, W.; Yang, J. Analytical inverter chain’s delay and its variation model for sub-threshold circuits. IEICE Electron. Express 2017, 14, 20170390. [Google Scholar] [CrossRef]
- Frustaci, F.; Corsonello, P.; Perri, S. Analytical delay model considering variability effects in subthreshold domain. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 168–172. [Google Scholar] [CrossRef]
- Zhang, G.; Li, B.; Liu, J.; Shi, Y.; Schlichtmann, U. Design-phase buffer allocation for post-silicon clock binning by iterative learning. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 37, 392–405. [Google Scholar] [CrossRef]
- Zhang, G.; Li, B.; Liu, J.; Schlichtmann, U. Sampling-based buffer insertion for post-silicon yield improvement under process variability. In Proceedings of the Design Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 14–18 March 2016; pp. 1457–1460. [Google Scholar]
- Orshansky, M.; Nassif, S.; Boning, D. Design for Manufacturability and Statistical Design: A Constructive Approach; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Khandelwal, V.; Srivastava, A. A quadratic modeling-based framework for accurate statistical timing analysis considering correlations. IEEE Trans. Very Large Scale Integr. Syst. 2007, 15, 206–215. [Google Scholar] [CrossRef]
- Li, B.; Chen, N.; Xu, Y.; Schlichtmann, U. On timing model extraction and hierarchical statistical timing analysis. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2013, 32, 367–380. [Google Scholar] [CrossRef][Green Version]
- Hong, J.; Huang, K.; Pong, P.; Pan, J.D.; Kang, J.; Wu, K.C. An LLC-OCV methodology for statistic timing analysis. In Proceedings of the IEEE International Symposium on VLSI Design, Automation and Test (VLSI-DAT), Hsinchu, Taiwan, 25–27 April 2007; pp. 1–4. [Google Scholar]
- Alioto, M.; Scotti, G.; Trifiletti, A. A novel framework to estimate the path delay variability on the back of an envelope via the fan-out-of-4 metric. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 2073–2085. [Google Scholar] [CrossRef]
- Cohen, E.; Malka, D.; Shemer, A.; Shahmoon, A.; Zalevsky, Z.; London, M. Neural networks within multi-core optic fibers. Sci. Rep. 2016, 6, 29080. [Google Scholar] [CrossRef]
- Malka, D.; Vegerhof, A.; Cohen, E.; Rayhshtat, M.; Libenson, A.; Aviv Shalev, M.; Zalevsky, Z. Improved Diagnostic Process of Multiple Sclerosis Using Automated Detection and Selection Process in Magnetic Resonance Imaging. Appl. Sci. 2017, 7, 831. [Google Scholar] [CrossRef]
- Malka, D.; Berke, B.A.; Tischler, Y.; Zalevsky, Z. Improving Raman spectra of pure silicon using super-resolved method. J. Opt. 2019, 21, 075801. [Google Scholar] [CrossRef]
- Das, B.P.; Amrutur, B.; Jamadagni, H.S.; Arvind, N.V.; Visvanathan, V. Voltage and temperature-aware SSTA using neural network delay model. IEEE Trans. Semicond. Manuf. 2011, 24, 533–544. [Google Scholar] [CrossRef]
- Kahng, A.B.; Luo, M.; Nath, S. SI for free: Machine learning of interconnect coupling delay and transition effects. In Proceedings of the ACM/IEEE International Workshop on System Level Interconnect Prediction (SLIP), San Francisco, CA, USA, 6 June 2015; pp. 1–8. [Google Scholar]
- Han, S.S.; Kahng, A.B.; Nath, S.; Vydyanathan, A.S. A deep learning methodology to proliferate golden signoff timing. In Proceedings of the conference on Design, Automation & Test in Europe, Dresden, Germany, 24–28 March 2014; p. 260. [Google Scholar]
- Yi, J.; Wang, Q.; Zhao, D.; Wen, J.T. BP neural network prediction-based variable-period sampling approach for networked control systems. Appl. Math. Comput. 2007, 185, 976–988. [Google Scholar] [CrossRef]
- Li, Y.; Fu, Y.; Li, H.; Zhang, S.W. The improved training algorithm of back propagation neural network with self-adaptive learning rate. IEEE Int. Conf. Comput. Intell. Nat. Comput. 2009, 1, 73–76. [Google Scholar]

| Category | Feature | Notation | Single Corner | Multi-Corner |
|---|---|---|---|---|
| cell | size | the drive strength of each gate | √ | √ |
| Nstack | the stack transistor number of each gate | √ | √ | |
| path | polar | rise of fall of each gate | √ | √ |
| load | the load capacitance of each stage | √ | √ | |
| td | the nominal delay of each path | √ | √ | |
| the variation delay of each path at xσ | √ | √ | ||
| corner | T | the temperature of the operation condition | - | √ |
| V | the voltage of the operation condition | - | √ |
| Function | ||
|---|---|---|
| Input | Output | |
| Hidden 1 layer | ||
| Hidden 2 layer | ||
| Hidden 3 layer | ||
| Output layer | ||
| V | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | |
|---|---|---|---|---|---|---|---|
| T (°C) | |||||||
| 0 | ▲ | ▲ | ★ | ▲ | |||
| 20 | ★ | ||||||
| 25 | ▲ | ▲ | ▲ | ||||
| 50 | ★ | ★ | ★ | ||||
| 75 | ▲ | ▲ | ▲ | ||||
| 100 | ★ | ★ | |||||
| 125 | ▲ | ▲ | ▲ | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Cao, P.; Sun, Z.; Xu, B.; Liu, Z.; Yang, J. Novel Prediction Framework for Path Delay Variation Based on Learning Method. Electronics 2020, 9, 157. https://doi.org/10.3390/electronics9010157
Guo J, Cao P, Sun Z, Xu B, Liu Z, Yang J. Novel Prediction Framework for Path Delay Variation Based on Learning Method. Electronics. 2020; 9(1):157. https://doi.org/10.3390/electronics9010157
Chicago/Turabian StyleGuo, Jingjing, Peng Cao, Zhaohao Sun, Bingqian Xu, Zhiyuan Liu, and Jun Yang. 2020. "Novel Prediction Framework for Path Delay Variation Based on Learning Method" Electronics 9, no. 1: 157. https://doi.org/10.3390/electronics9010157
APA StyleGuo, J., Cao, P., Sun, Z., Xu, B., Liu, Z., & Yang, J. (2020). Novel Prediction Framework for Path Delay Variation Based on Learning Method. Electronics, 9(1), 157. https://doi.org/10.3390/electronics9010157





