Calibration and Characterization of a Reduced Form-Factor High Accuracy Three-Axis Teslameter
Abstract
:1. Introduction
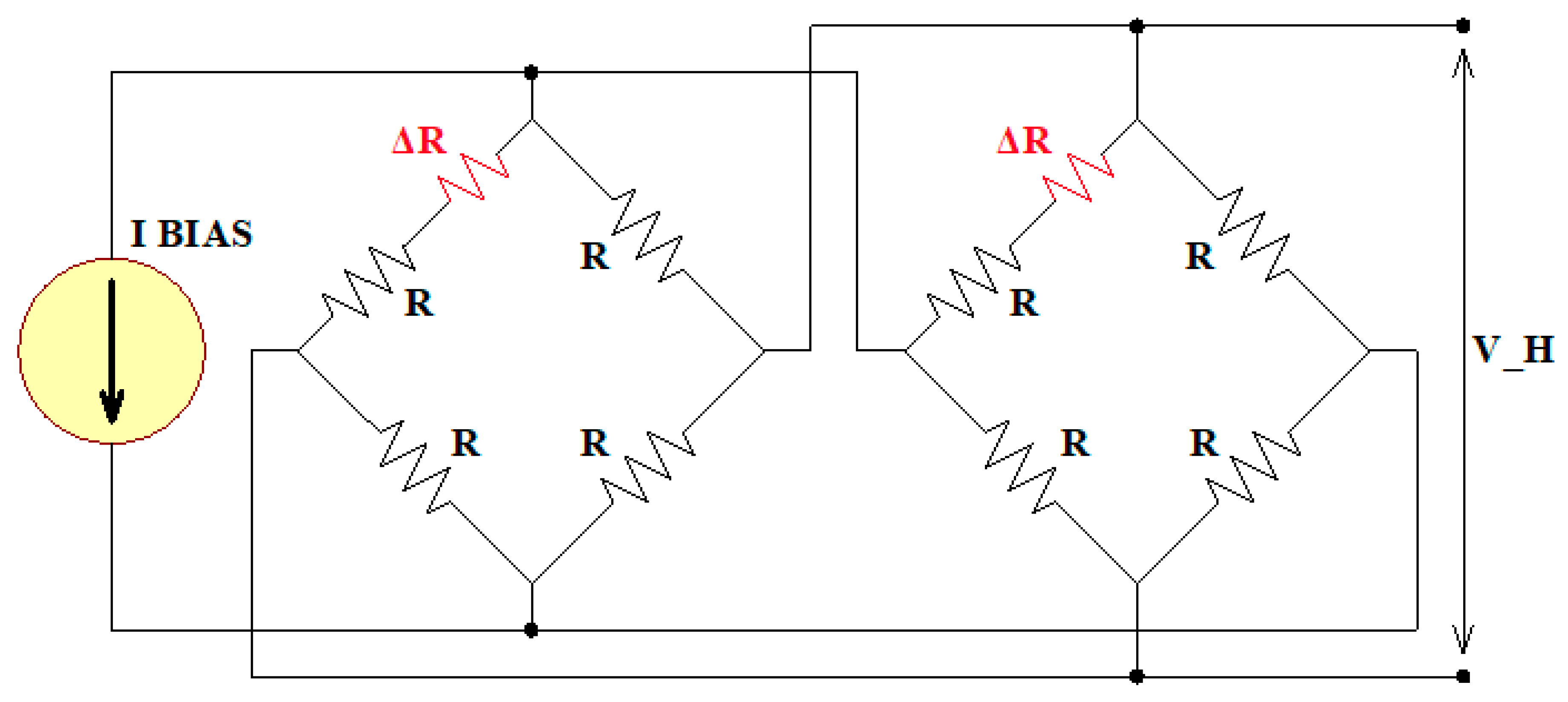
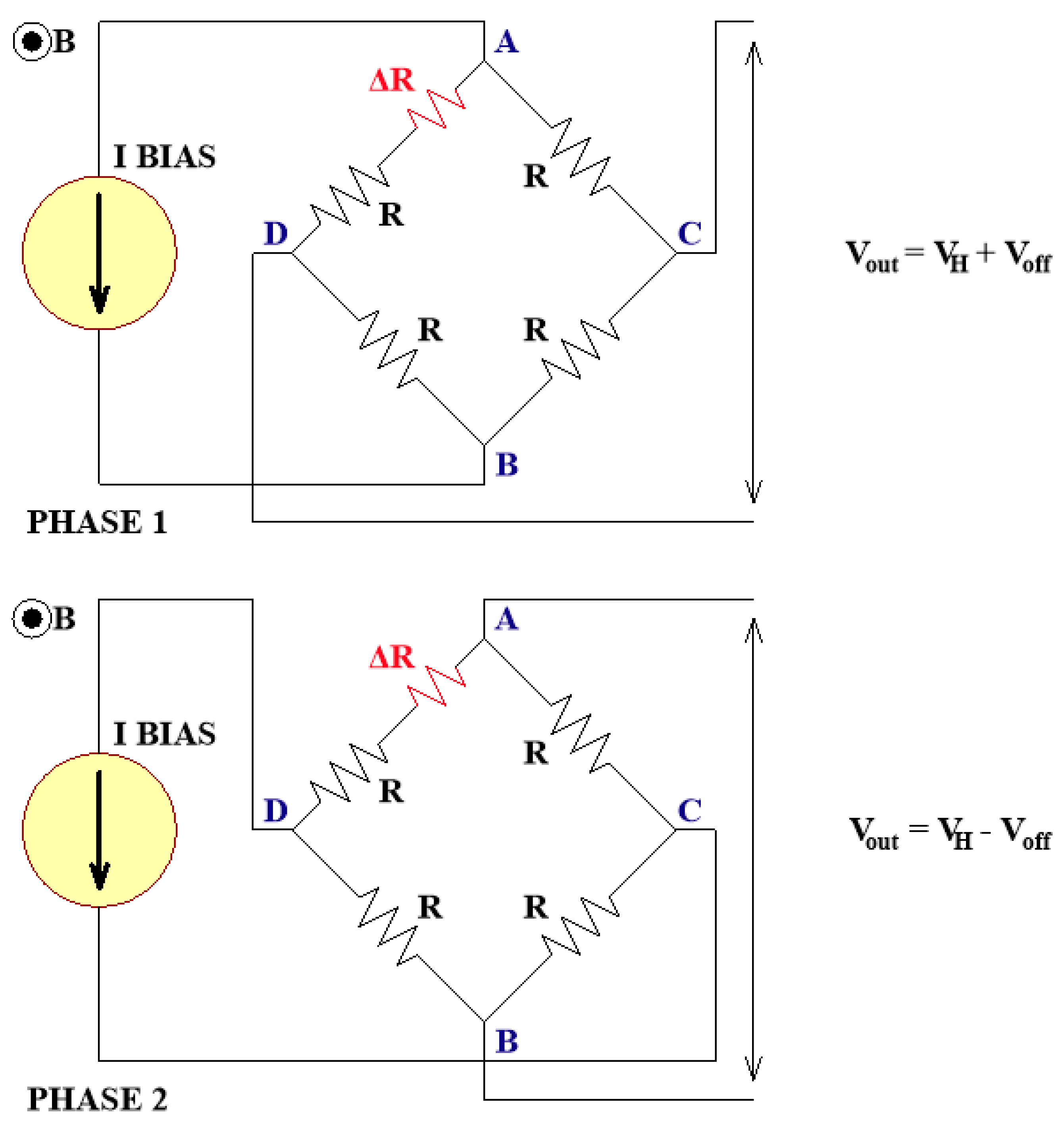
2. Spinning Current Modulation Technique
3. Architecture of the Teslameter
4. Instrument Calibration Overview
5. Calibration Procedure and Results
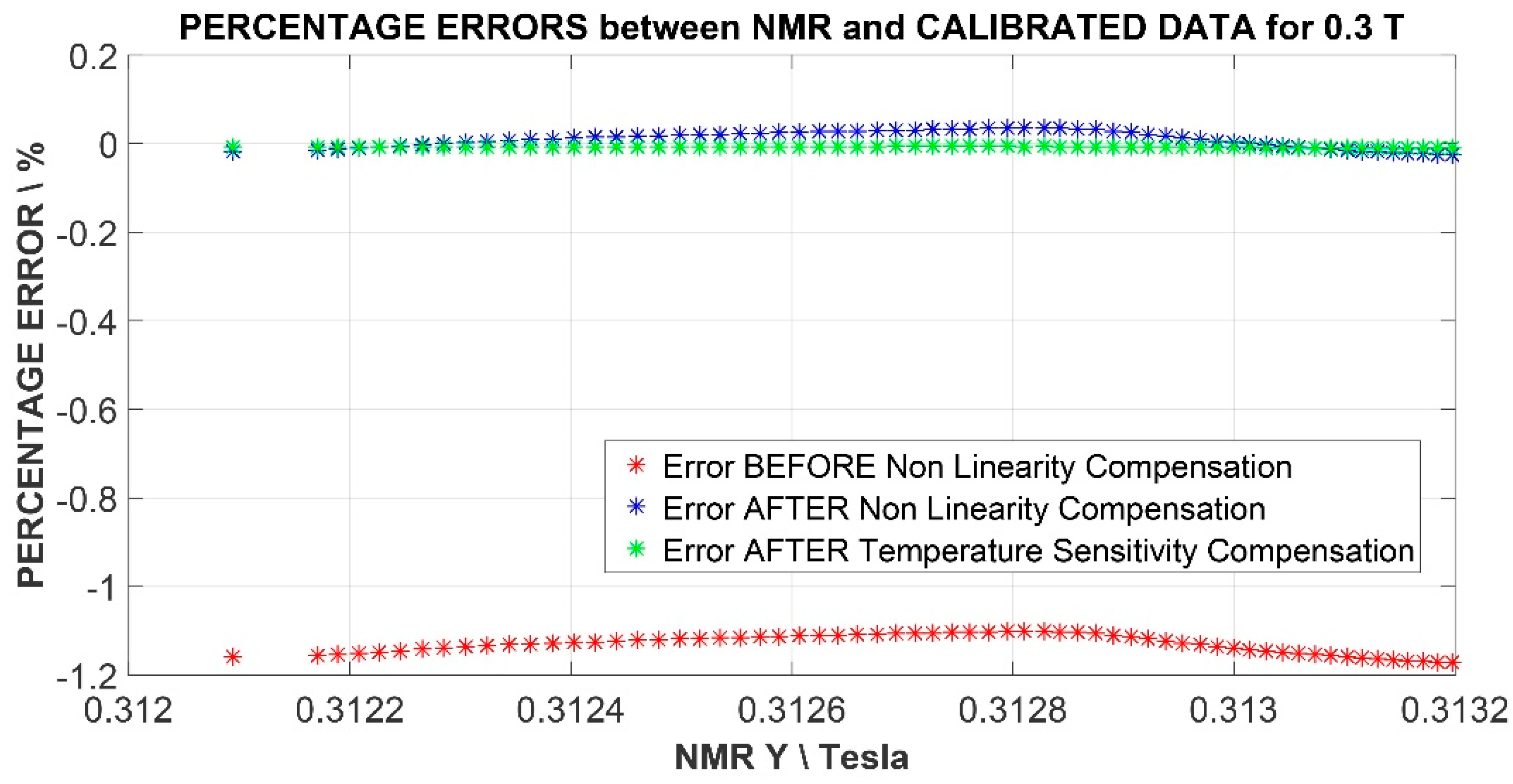
5.1. Correction of Nonlinearity
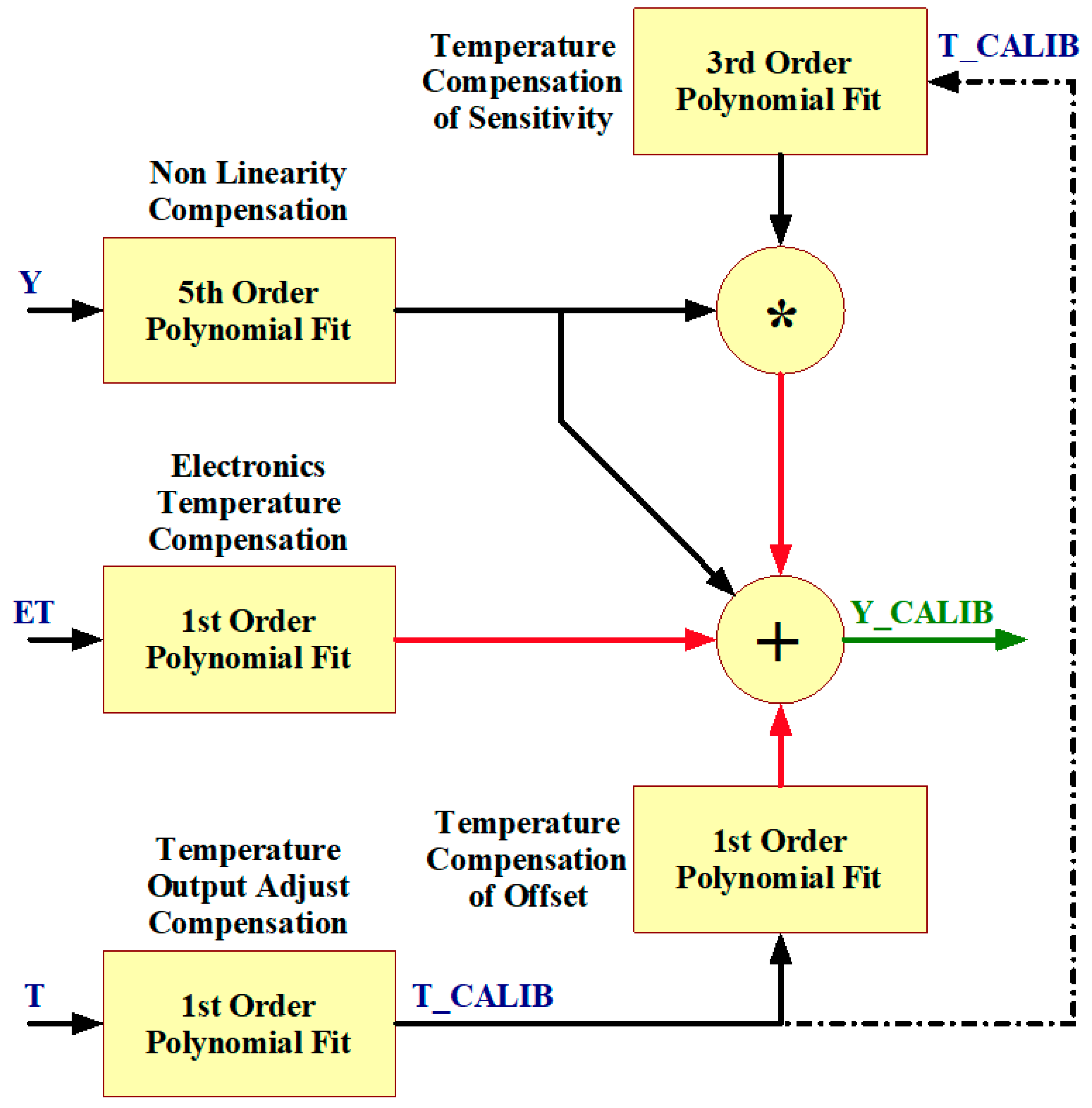
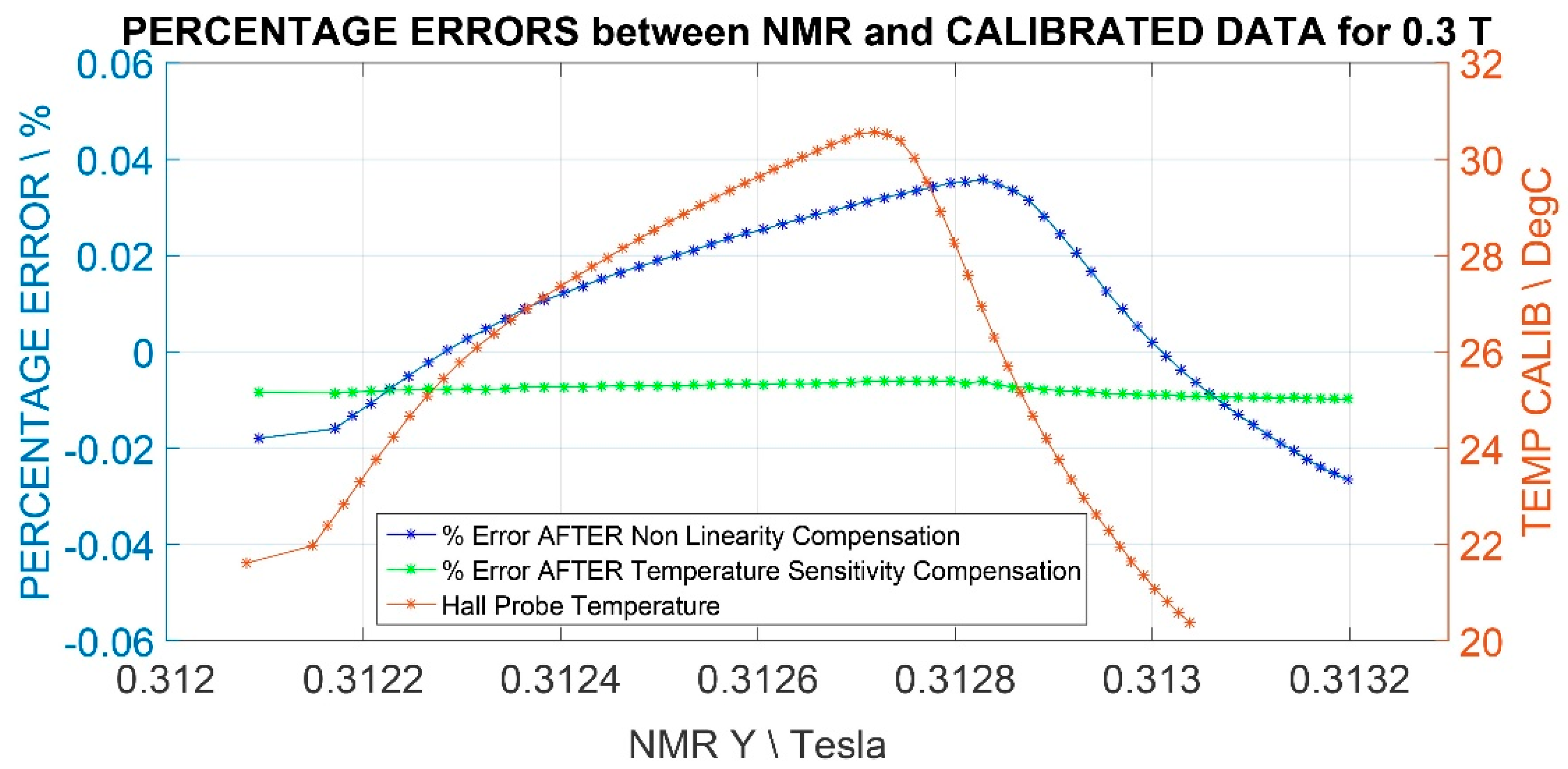
5.2. Correction of Temperature Influence
5.2.1. Temperature Output Adjust
5.2.2. Temperature Compensation of Offset
5.2.3. Temperature Compensation of Sensitivity
5.2.4. Electronics Temperature Compensation
6. Calibration Verification
7. Calibration of Angular Errors of the Hall Probe
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sanfilippo, S. Hall probes: Physics and application to magnetometry. In Presented at the Specialised Course on Magnets; Paul Scherrer Institut: Villigen, Switzerland, 2009; pp. 423–462. [Google Scholar]
- Popovic, D.R.; Dimitrijevic, S.; Blagojevic, M.; Kejik, P.; Schurig, E.; Popovic, R.S. Three-Axis Teslameter With Integrated Hall Probe. IEEE Trans. Instrum. Meas. 2007, 56, 1396–1402. [Google Scholar] [CrossRef]
- Popovic, R.S. High Resolution Hall Magnetic Sensors. In Proceedings of the 29th International Conference on Microelectronics, Belgrade, Serbia, 12–14 May 2014; pp. 69–74. [Google Scholar]
- Popovic, R.S. Hall Effect Devices, 2nd ed.; IOP Publishing: Philadelphia, PA, USA, 2004; Chapters 4 and 5. [Google Scholar]
- Mosser, V.; Matringe, N.; Haddab, Y. A Spinning Current Circuit for Hall Measurements down to the Nanotesla Range. IEEE Trans. Instrum. Meas. 2017, 66, 637–650. [Google Scholar] [CrossRef]
- Junfeng, J.; Wilko, K.; Kofi, M. A Continuous-Time Ripple Reduction Technique for Spinning-Current Hall Sensors. IEEE J. Solid-State Circuits 2014, 49, 1525–1534. [Google Scholar]
- Cassar, J.; Sammut, A.; Sammut, N.; Calvi, M.; Dimitrijevic, S.; Popovic, R.S. Design and Development of a Reduced Form-Factor High Accuracy Three-Axis Teslameter. J. Electron. 2019, 8, 368. [Google Scholar] [CrossRef] [Green Version]
- Cassar, J.; Sammut, A.; Sammut, N.; Calvi, M.; Spasic, S.; Renella, D.P. Performance Analysis of a Reduced Form-Factor High Accuracy Three-Axis Teslameter. J. Electron. 2019, 8, 1230. [Google Scholar] [CrossRef] [Green Version]
- Popovic, D.R.; Dimitrijevic, S.; Spasic, S.; Popovic, R.S. High-accuracy teslameter with thin high-resolution three-axis Hall probe. J. Int. Meas. Confed. 2015, 98, 407–413. [Google Scholar] [CrossRef]

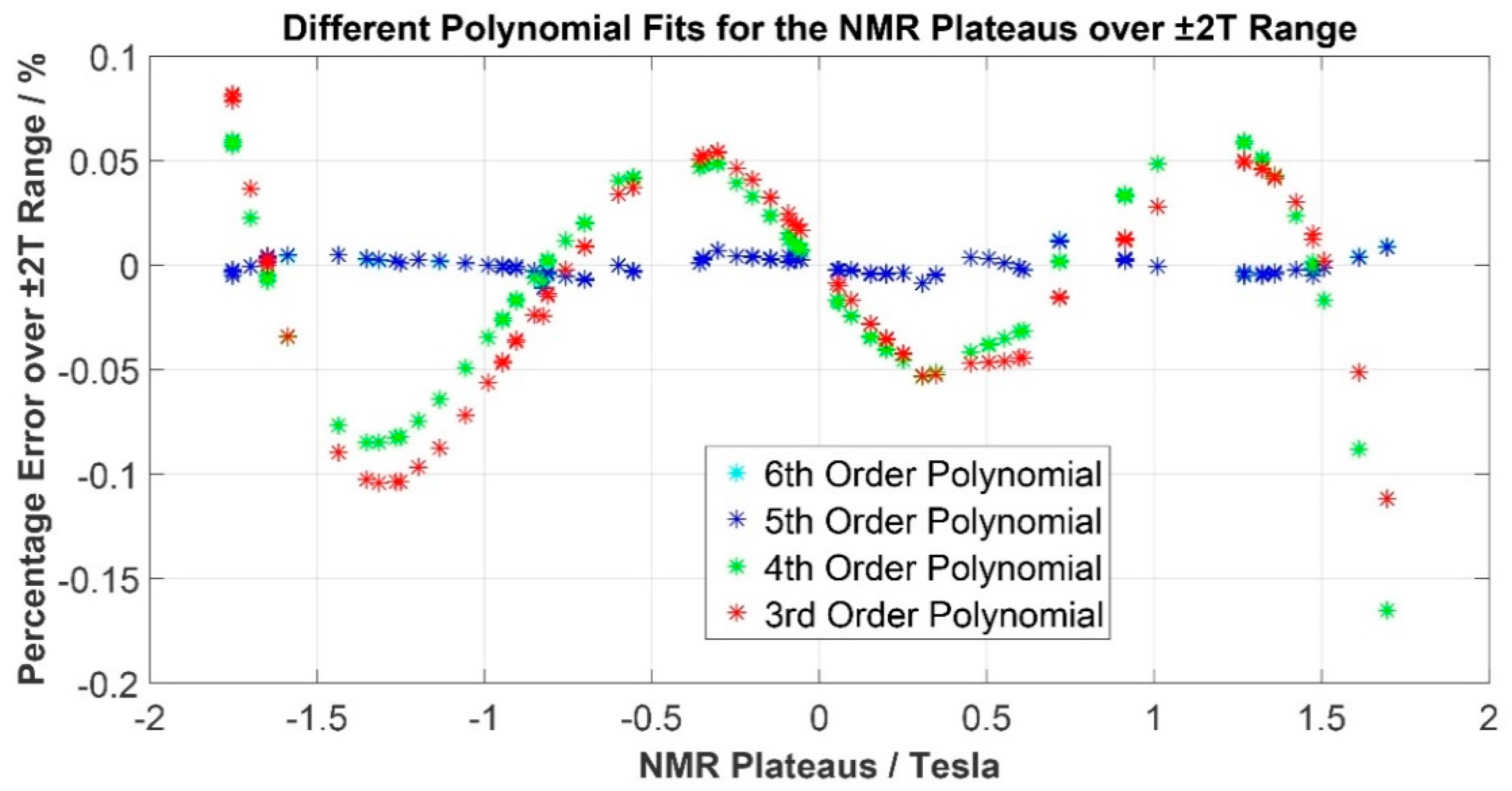
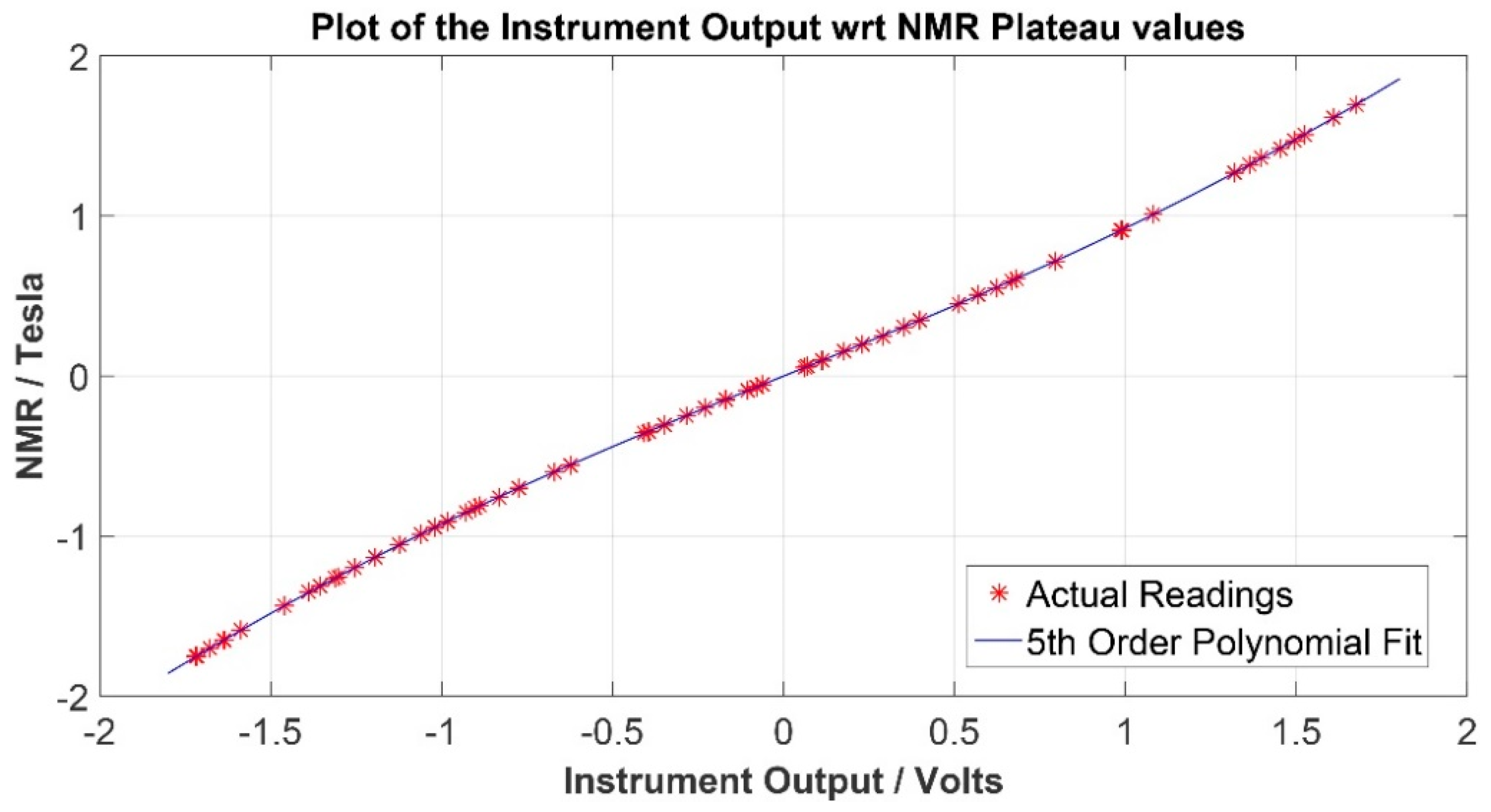
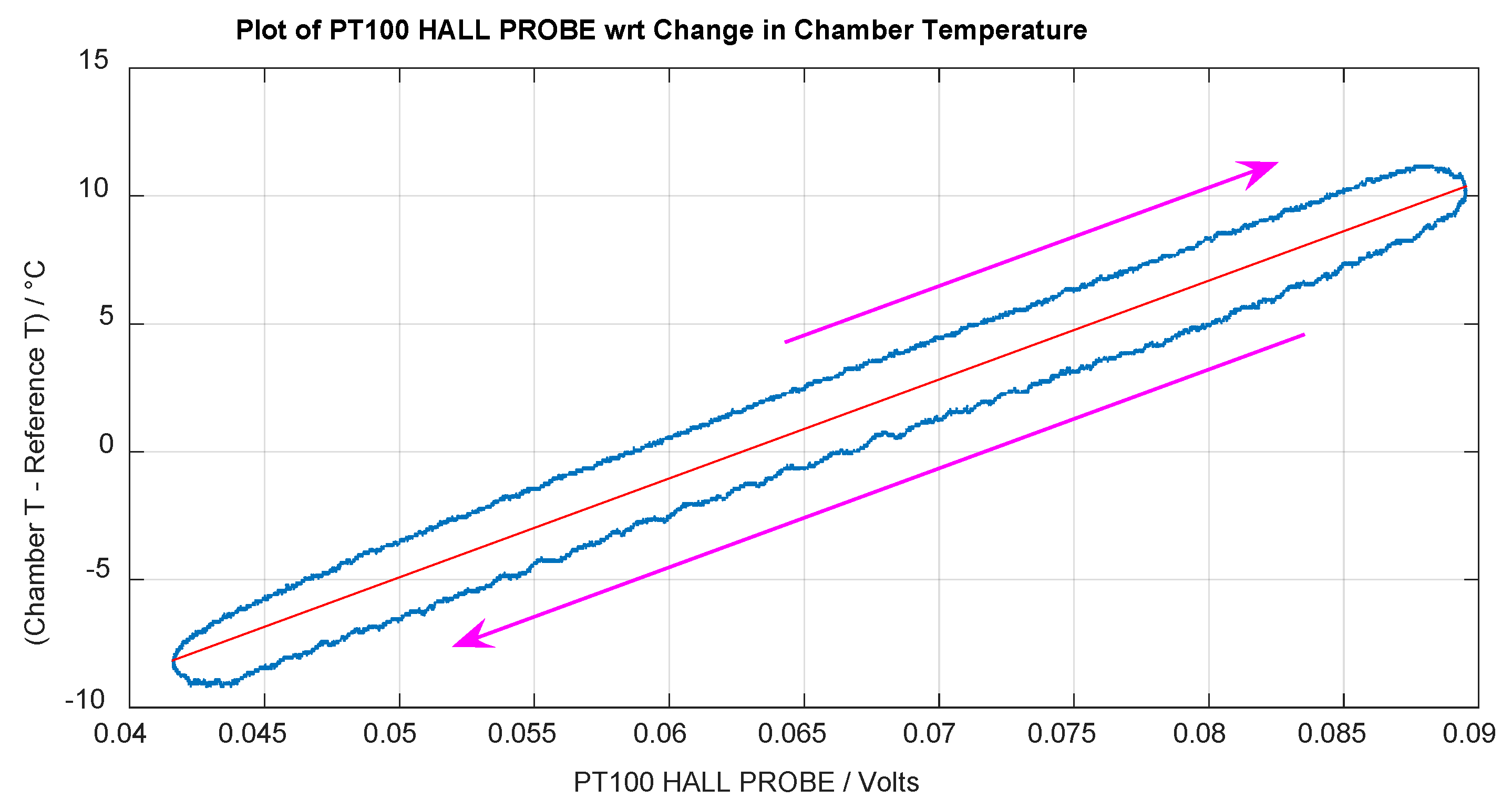
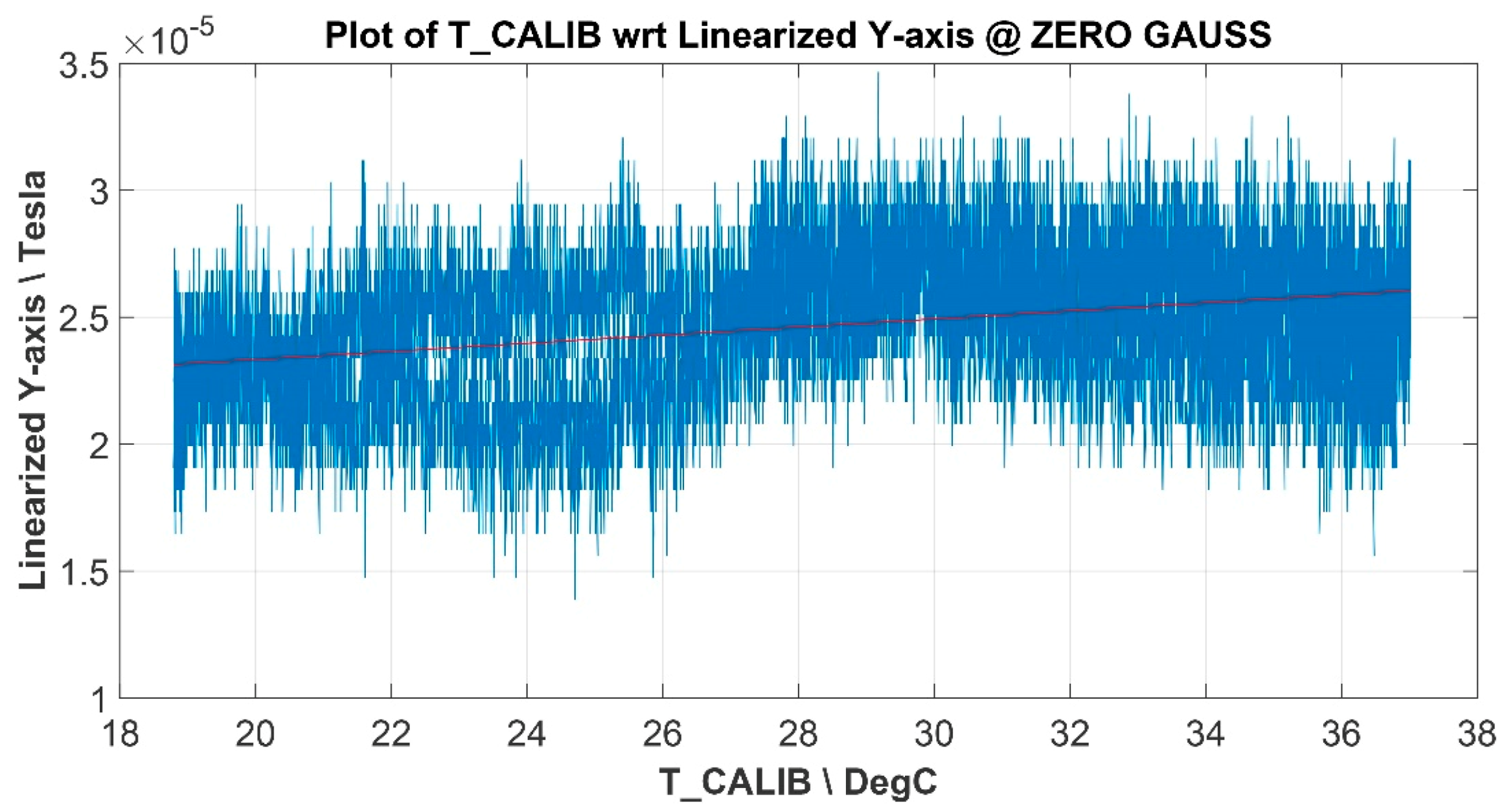

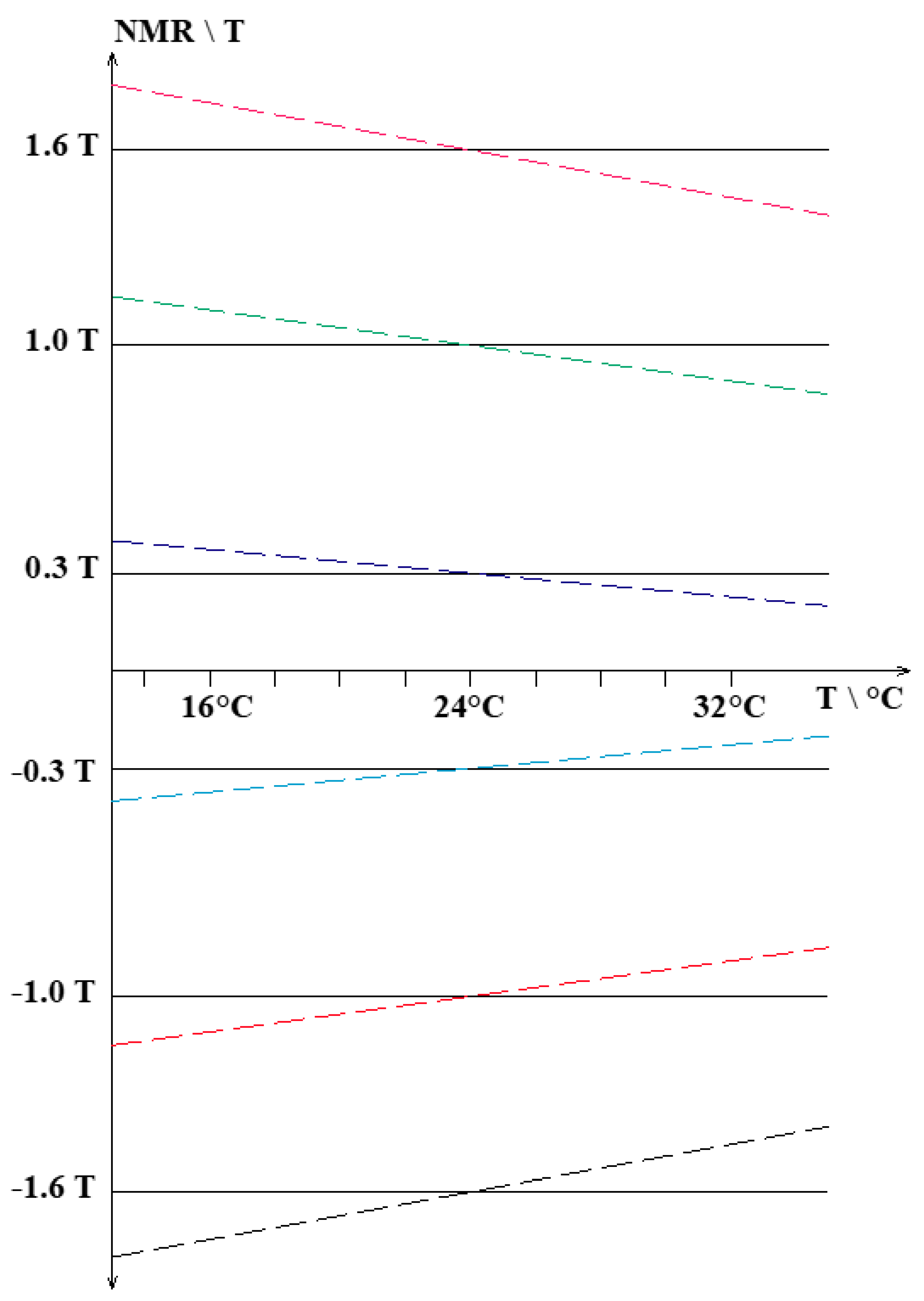
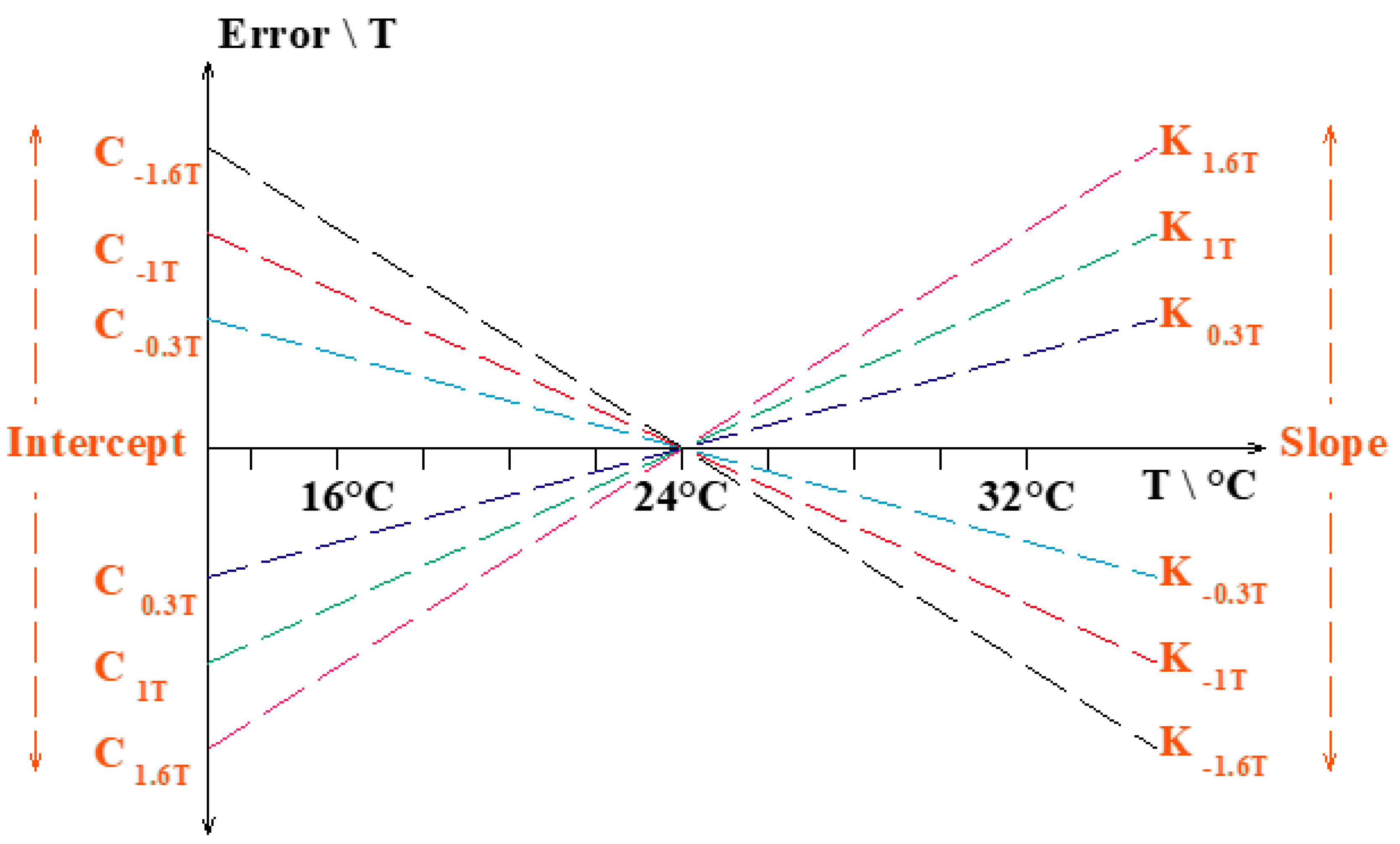
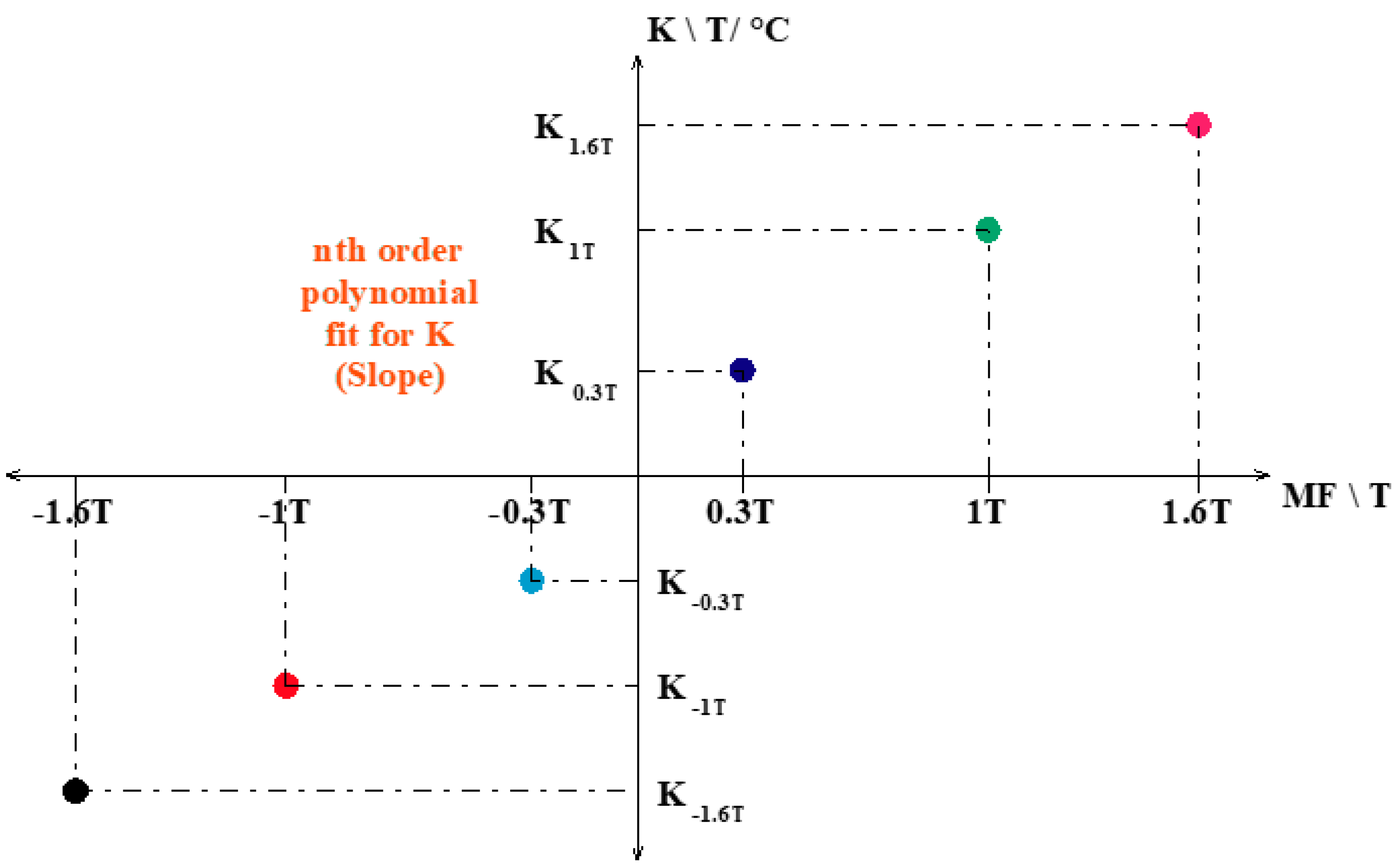
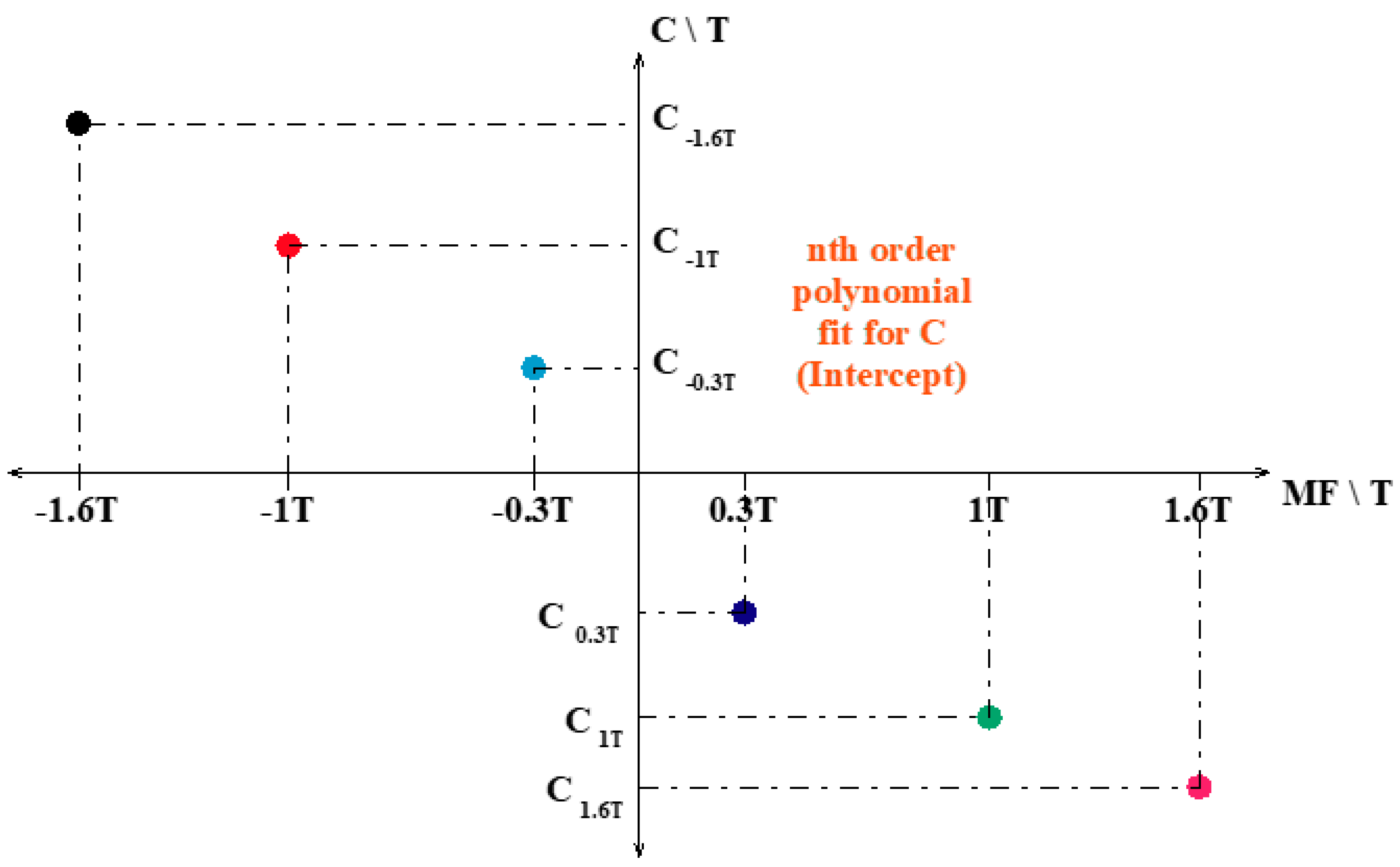
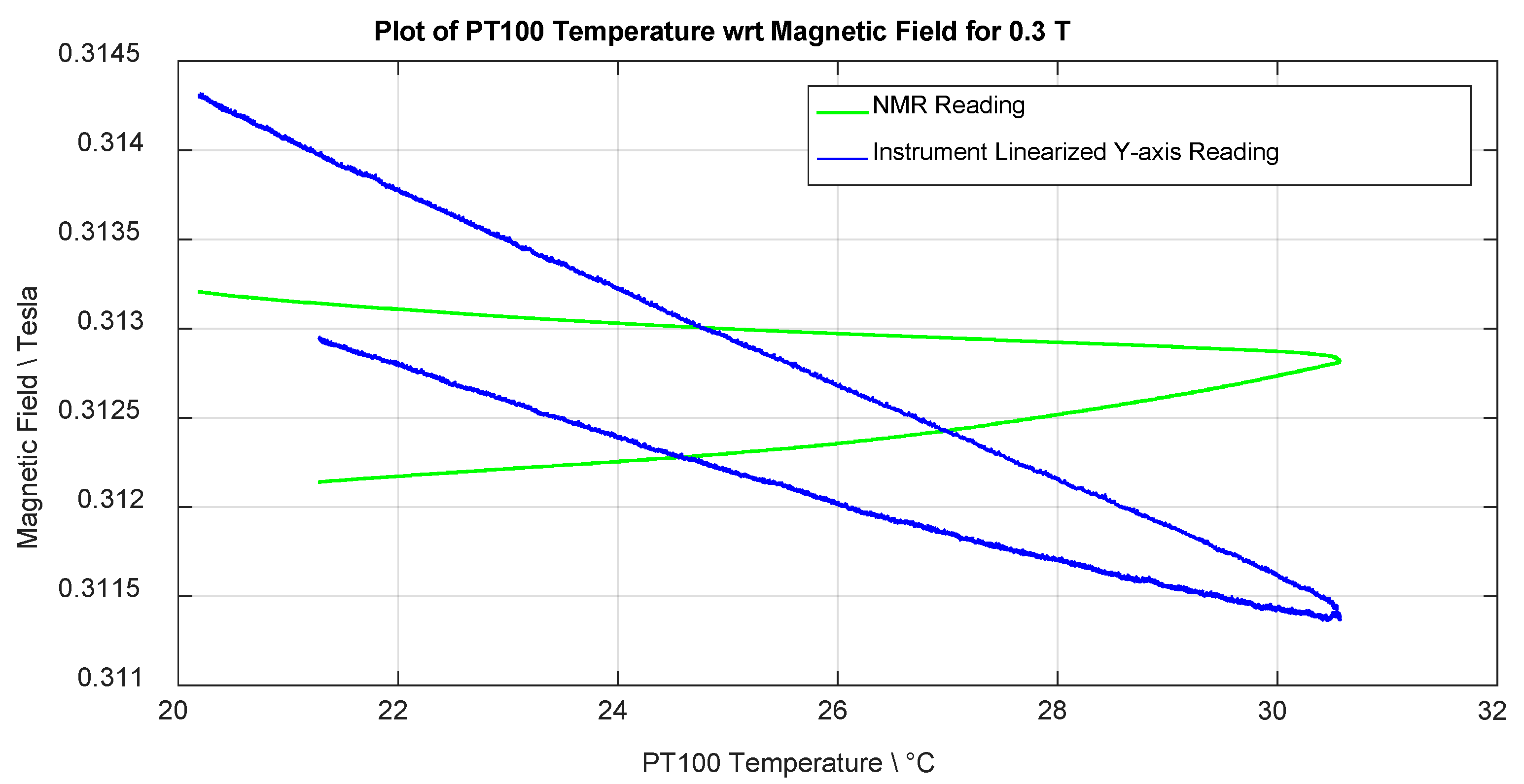
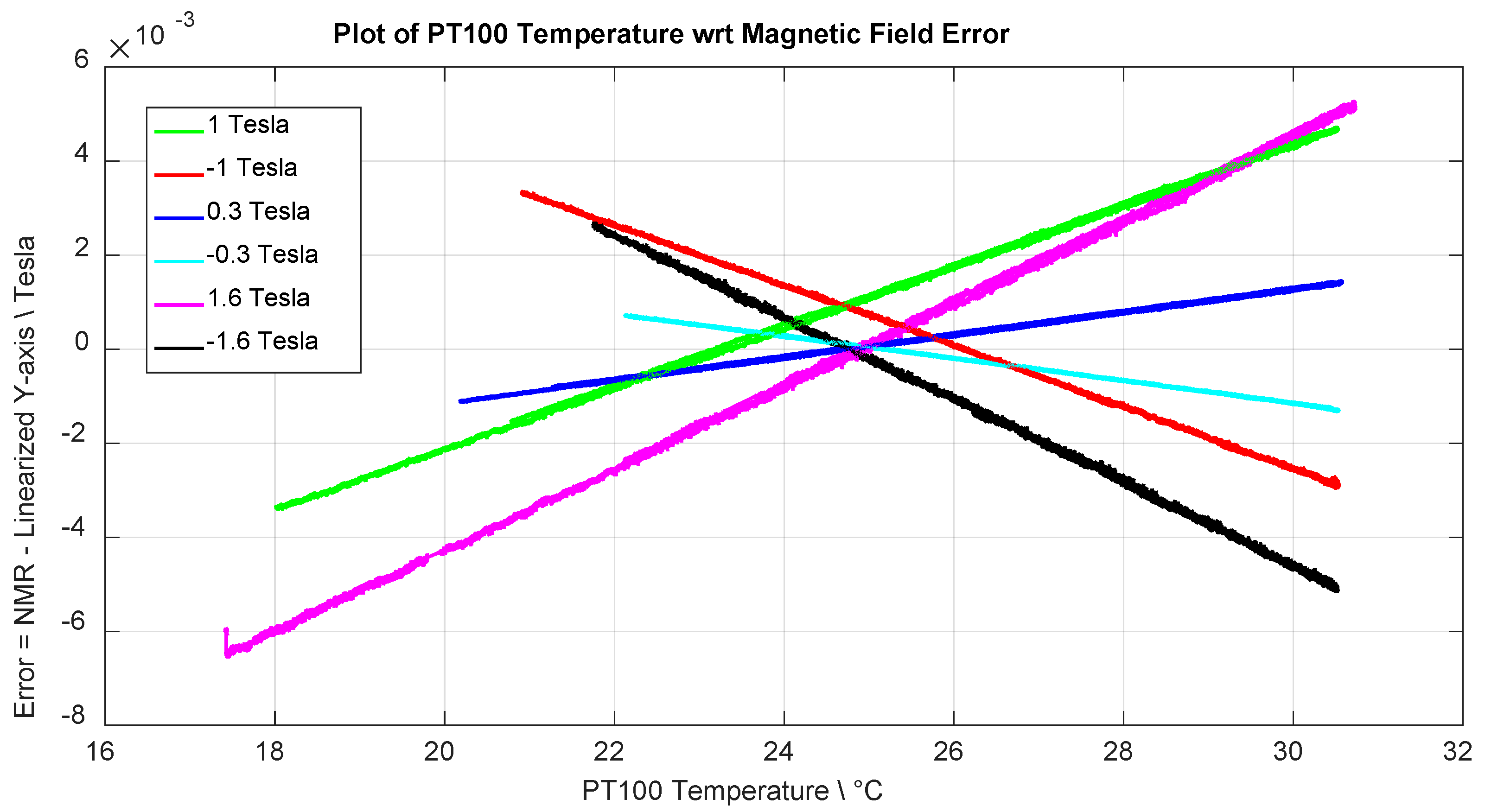
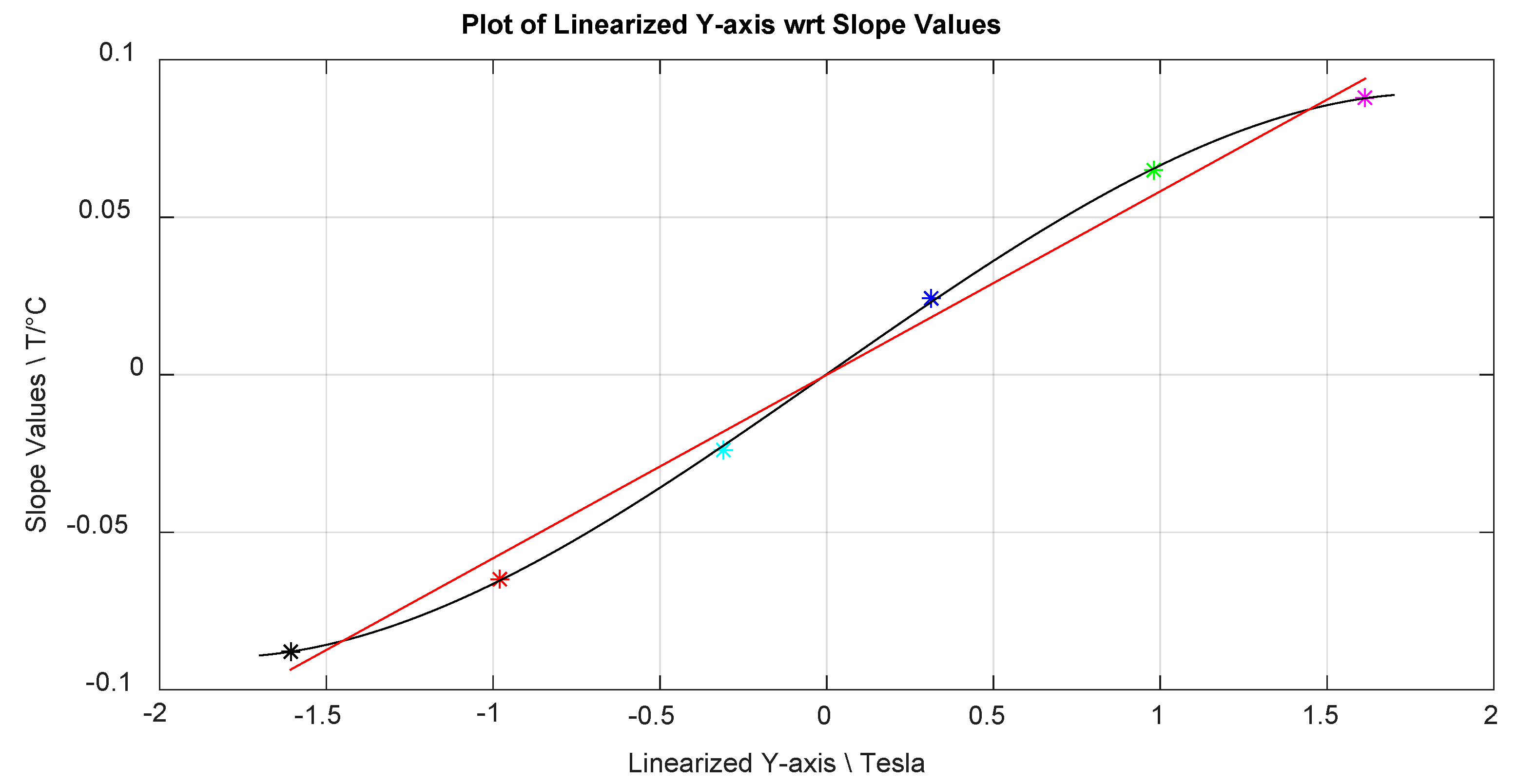

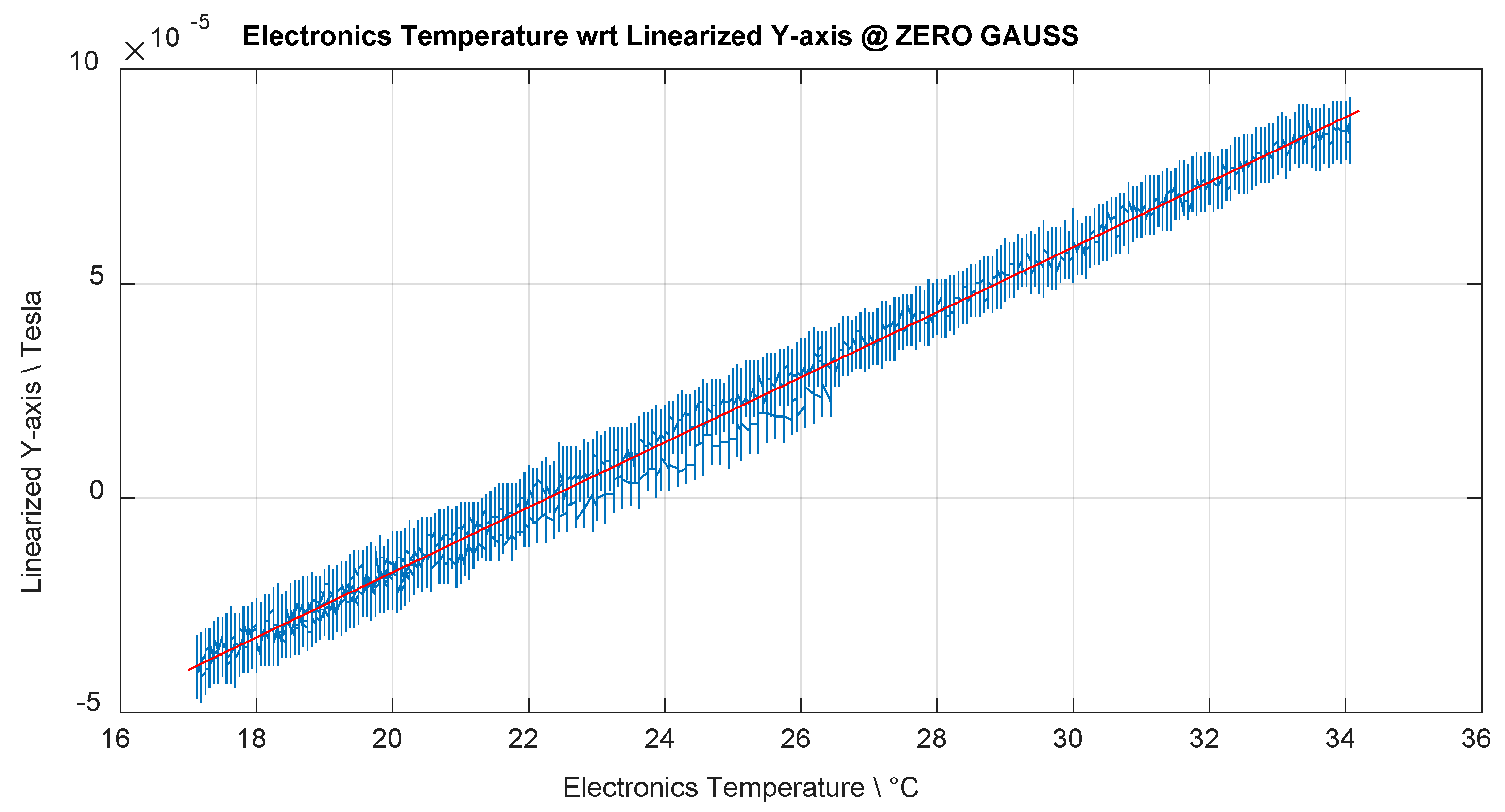
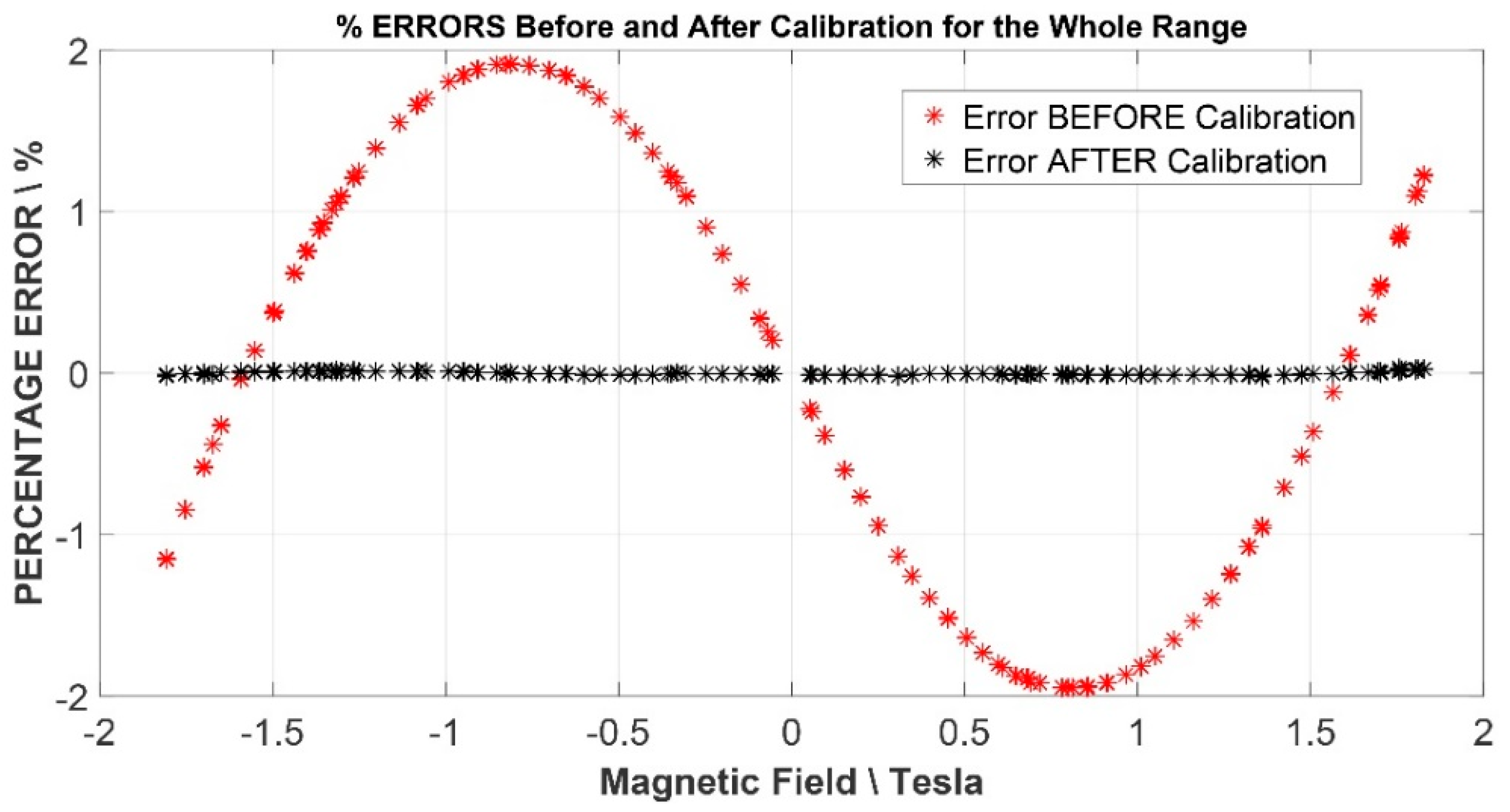
| Polynomial Fit Order | Y-Axis MAX Error/% |
|---|---|
| Before Compensation | 1.915818 |
| 1st Order Fit | 2.224081 |
| 2nd Order Fit | 2.857286 |
| 3rd Order Fit | 0.111724 |
| 4th Order Fit | 0.165389 |
| 5th Order Fit | 0.011999 |
| 6th Order Fit | 0.012135 |
| Output State | Mean Error/% | Polynomial Order | B/T |
|---|---|---|---|
| Uncalibrated | −1.129865 | NA | 0.3 |
| After Nonlinearity | 0.009666 | 5 | 0.3 |
| After Offset Comp | 0.009657 | 1 | 0.3 |
| After Sensitivity | −0.007776 | 1 | 0.3 |
| After Sensitivity | −0.005007 | 3 | 0.3 |
| Uncalibrated | 1.085900 | NA | −0.3 |
| After Nonlinearity | −0.011547 | 5 | −0.3 |
| After Offset Comp | −0.011559 | 1 | −0.3 |
| After Sensitivity | −0.008812 | 1 | −0.3 |
| After Sensitivity | −0.007351 | 3 | −0.3 |
| Uncalibrated | −1.824601 | NA | 1 |
| After Nonlinearity | 0.023719 | 5 | 1 |
| After Offset Comp | 0.023716 | 1 | 1 |
| After Sensitivity | 0.016652 | 1 | 1 |
| After Sensitivity | 0.015094 | 3 | 1 |
| Uncalibrated | 1.804986 | NA | −1 |
| After Nonlinearity | −0.006501 | 5 | −1 |
| After Offset Comp | −0.006511 | 1 | −1 |
| After Sensitivity | 0.001530 | 1 | −1 |
| After Sensitivity | 0.001016 | 3 | −1 |
| Uncalibrated | 0.105296 | NA | 1.6 |
| After Nonlinearity | −0.008425 | 5 | 1.6 |
| After Offset Comp | −0.008428 | 1 | 1.6 |
| After Sensitivity | −0.006905 | 1 | 1.6 |
| After Sensitivity | −0.006158 | 3 | 1.6 |
| Uncalibrated | −0.170719 | NA | −1.6 |
| After Nonlinearity | −0.048356 | 5 | −1.6 |
| After Offset Comp | −0.048368 | 1 | −1.6 |
| After Sensitivity | −0.009150 | 1 | −1.6 |
| After Sensitivity | −0.008985 | 3 | −1.6 |
| Output State | Mean Error/% | 1σ Error/% | Peak Error/% |
|---|---|---|---|
| X-Axis | |||
| Uncalibrated Output | −0.022588 | 1.278237 | 1.935724 |
| Calibrated Output | 0.003280 | 0.021758 | 0.141789 |
| Y-Axis | |||
| Uncalibrated Output | 0.085041 | 1.344989 | 1.948582 |
| Calibrated Output | 0.001234 | 0.005751 | 0.027175 |
| Z-Axis | |||
| Uncalibrated Output | −0.064033 | 1.276952 | 1.815720 |
| Calibrated Output | −0.002833 | 0.034240 | 0.065478 |
| Calibration Step | Number of Clock Cycles |
|---|---|
| Non-Linearity Compensation | 28 |
| Temperature Output Adjust Compensation | 7 |
| Electronics Temperature Compensation | 9 |
| Temperature Compensation of Offset | 5 |
| Temperature Compensation of Sensitivity | 30 |
| Merging of all individual Calibration steps | 9 |
| Total number of Clock Cycles | 88 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassar, J.; Sammut, A.; Sammut, N.; Calvi, M.; Mitrovic, Z.; Popovic, R.S. Calibration and Characterization of a Reduced Form-Factor High Accuracy Three-Axis Teslameter. Electronics 2020, 9, 151. https://doi.org/10.3390/electronics9010151
Cassar J, Sammut A, Sammut N, Calvi M, Mitrovic Z, Popovic RS. Calibration and Characterization of a Reduced Form-Factor High Accuracy Three-Axis Teslameter. Electronics. 2020; 9(1):151. https://doi.org/10.3390/electronics9010151
Chicago/Turabian StyleCassar, Johann, Andrew Sammut, Nicholas Sammut, Marco Calvi, Zarko Mitrovic, and Radivoje S. Popovic. 2020. "Calibration and Characterization of a Reduced Form-Factor High Accuracy Three-Axis Teslameter" Electronics 9, no. 1: 151. https://doi.org/10.3390/electronics9010151
APA StyleCassar, J., Sammut, A., Sammut, N., Calvi, M., Mitrovic, Z., & Popovic, R. S. (2020). Calibration and Characterization of a Reduced Form-Factor High Accuracy Three-Axis Teslameter. Electronics, 9(1), 151. https://doi.org/10.3390/electronics9010151







