A Review on Stochastic Approach for PHEV Integration Control in a Distribution System with an Optimized Battery Power Demand Model
Abstract
1. Introduction
- (1)
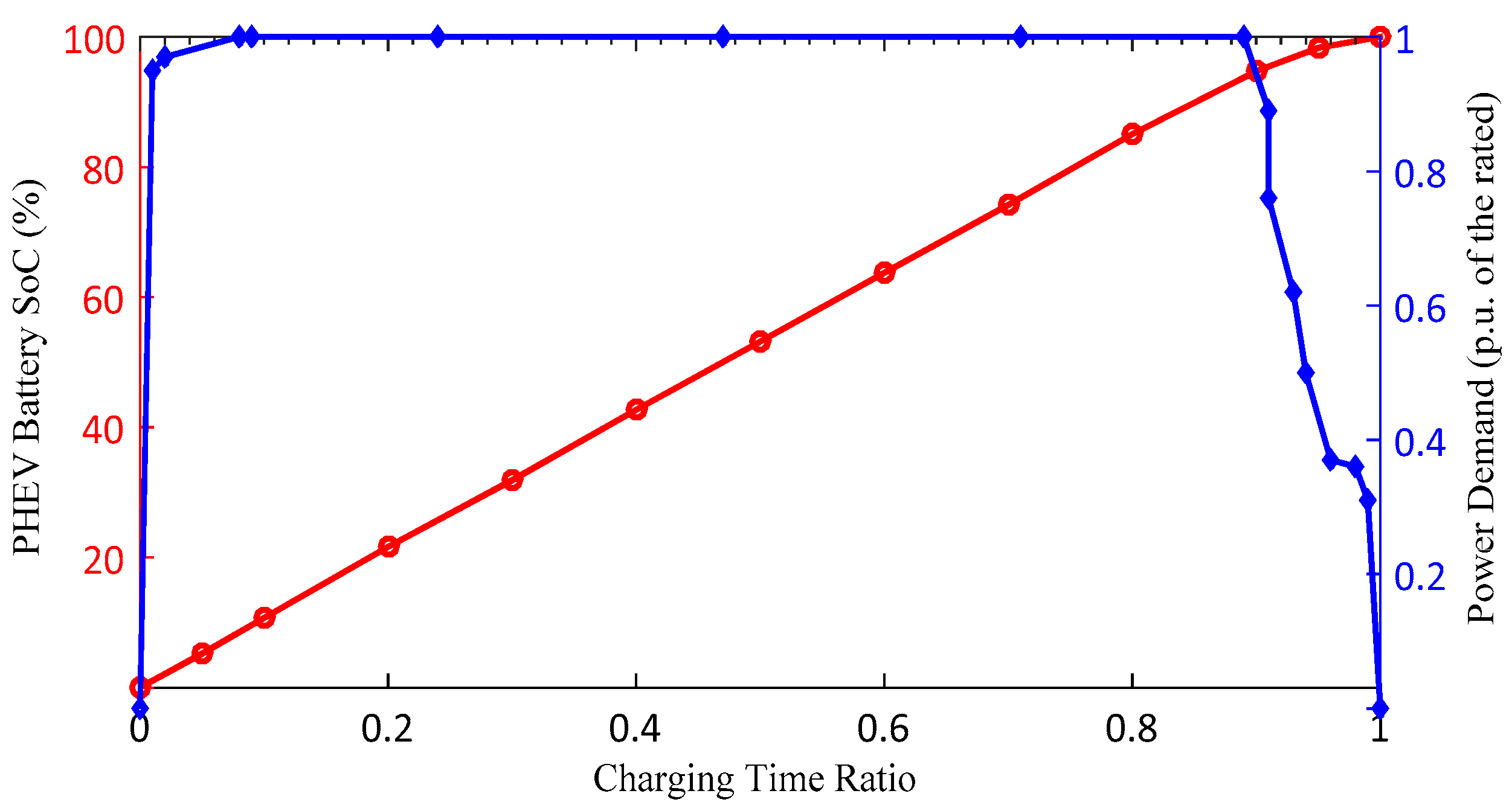
- A precise estimation of PHEV power demand during the charging process was overlooked in most previous works and if mentioned it was vaguely explained, in this paper the power demand is expressed in the function of battery SoC and the rated power of the charger.
- (2)
- The study in this paper focuses on the technical impacts (voltage deviation and power losses in the distribution grid).
- (3)
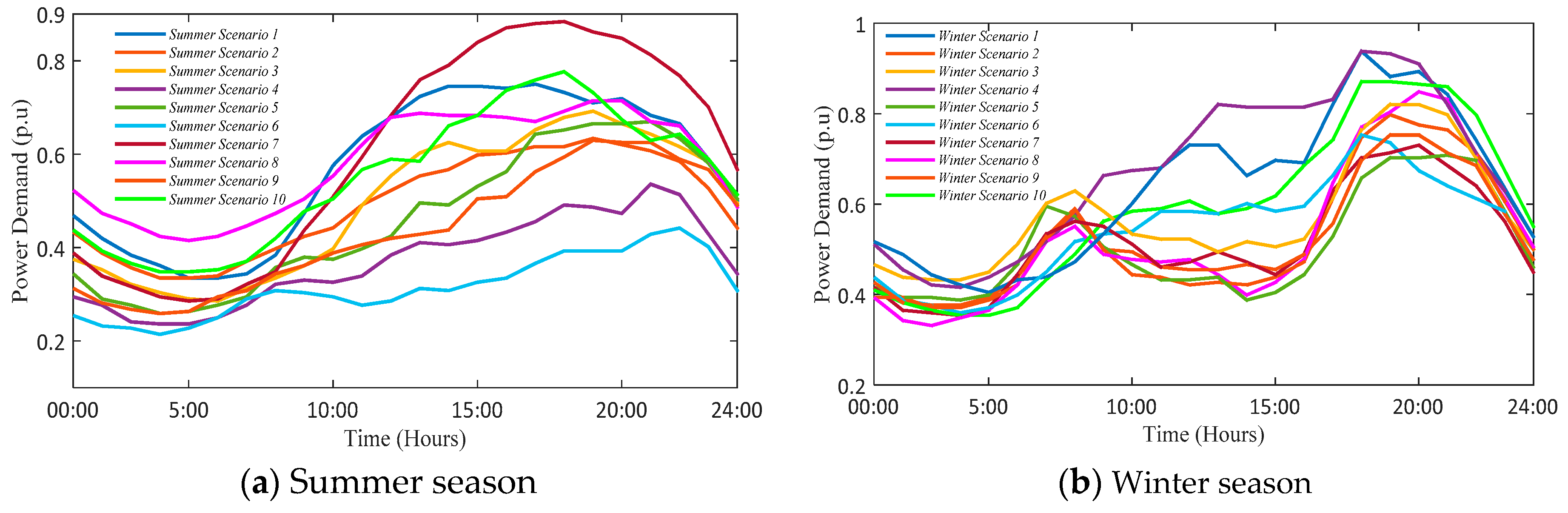
- The developed framework investigates the seasonal effect by taking two sets of daily residential power consumption for summer and winter as well, while ignoring the seasonal effect that can cause an underestimation or an overestimation of the effects.
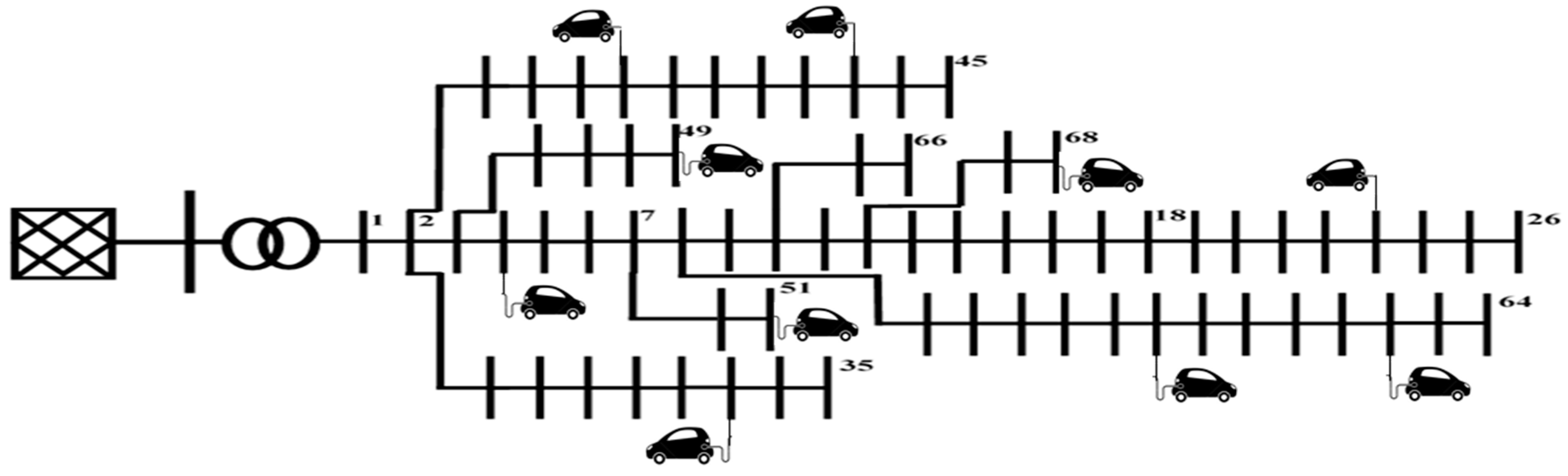
2. Framework Assumptions and Parameters
3. Stochastic Modeling for the PHEV’s Mobility and Charging Behaviors
3.1. PHEV Departure Time
3.2. PHEV Arrival Home Time
3.3. PHEV Daily Trip Length
3.4. PHEV Battery Charge Model
3.5. PHEV Battery Discharge Model
3.6. PHEV Battery Power Demand
4. Daily Residential Load Profiles
4.1. Measured Data for Fixed Daily Residential Load
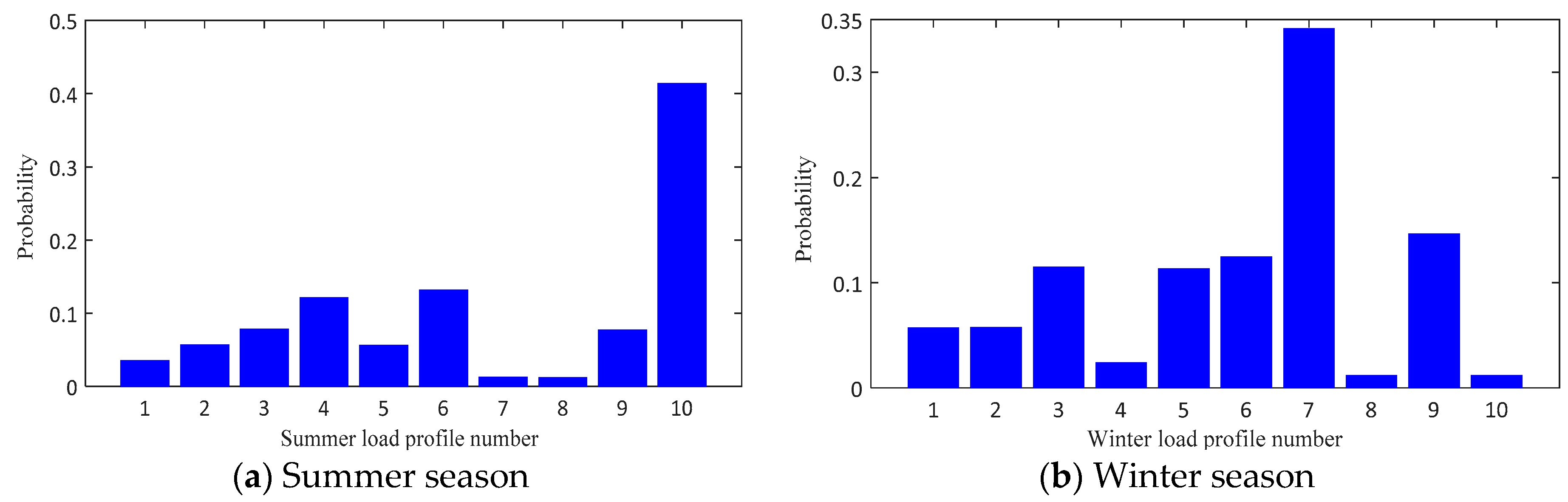
4.2. Scenario Reduction Algorithm
- 1)
- Determine the scenario ‘k’ to be eliminated from the original set, mathematically this scenario is determined as follows:
- 2)
- Update the remaining load profile set and calculate the distance between each pair of scenarios.
- 3)
- Update the probability of the nearest load profile Sn to the removed one Sk
4.3. Genetic Algorithm for Scenario Generation
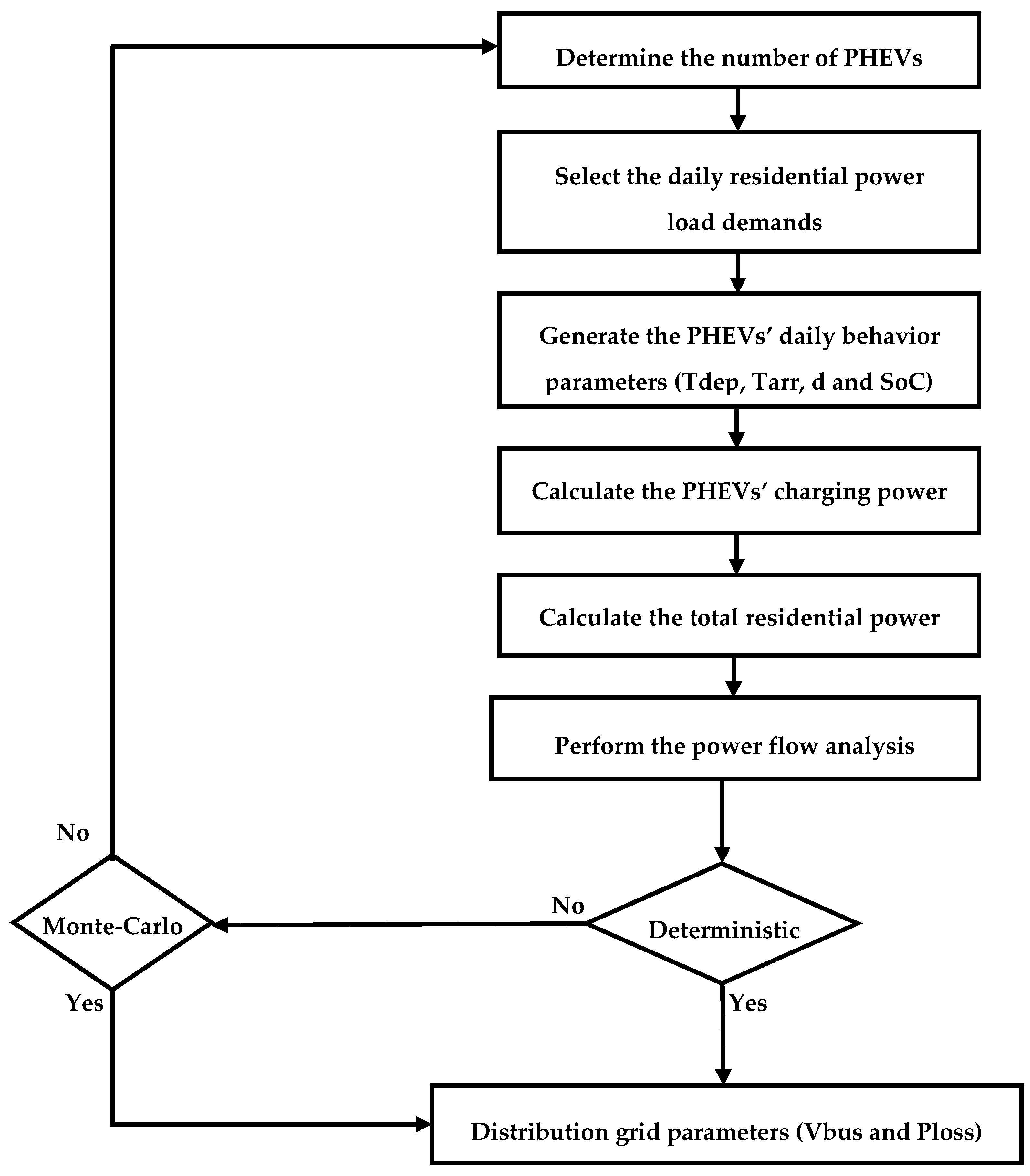
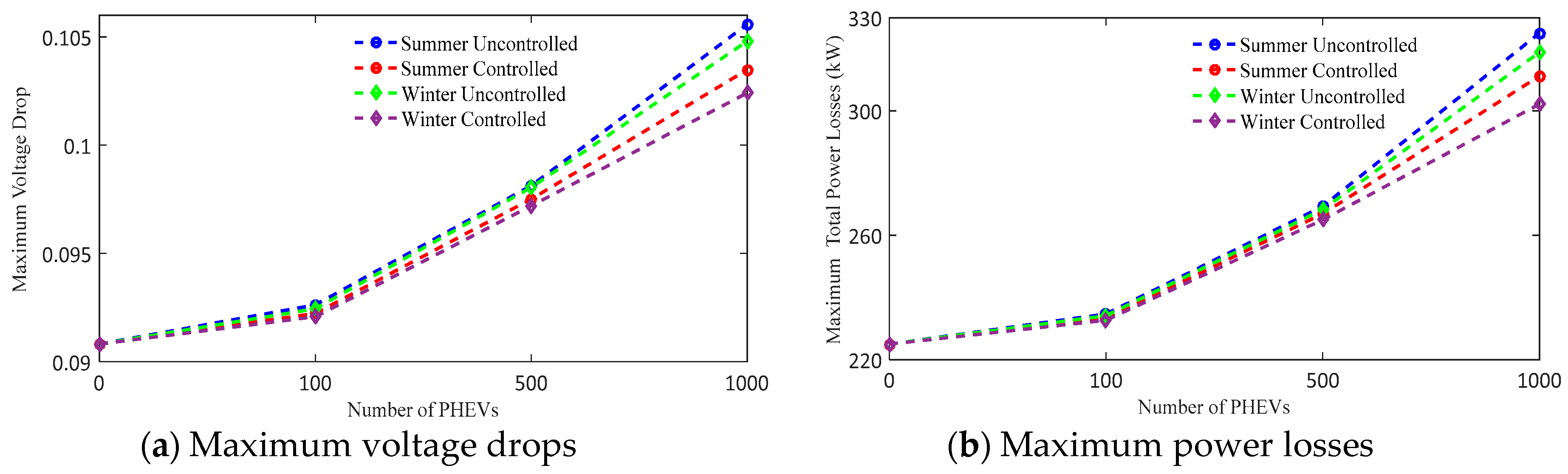
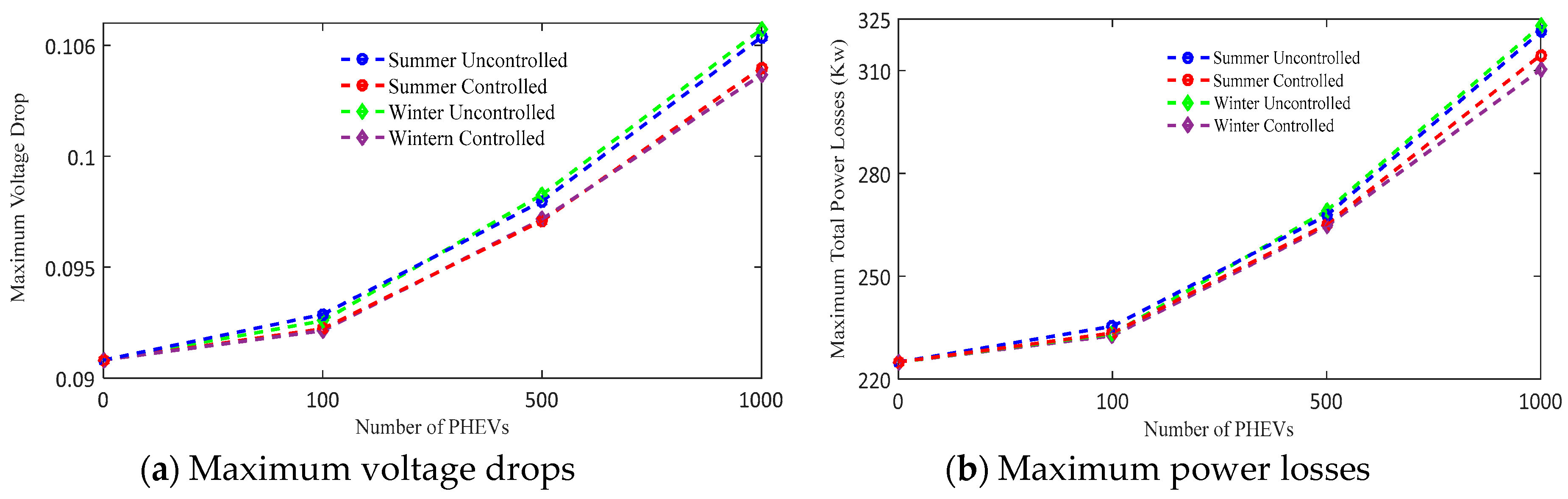
5. Methodology and Numerical Results
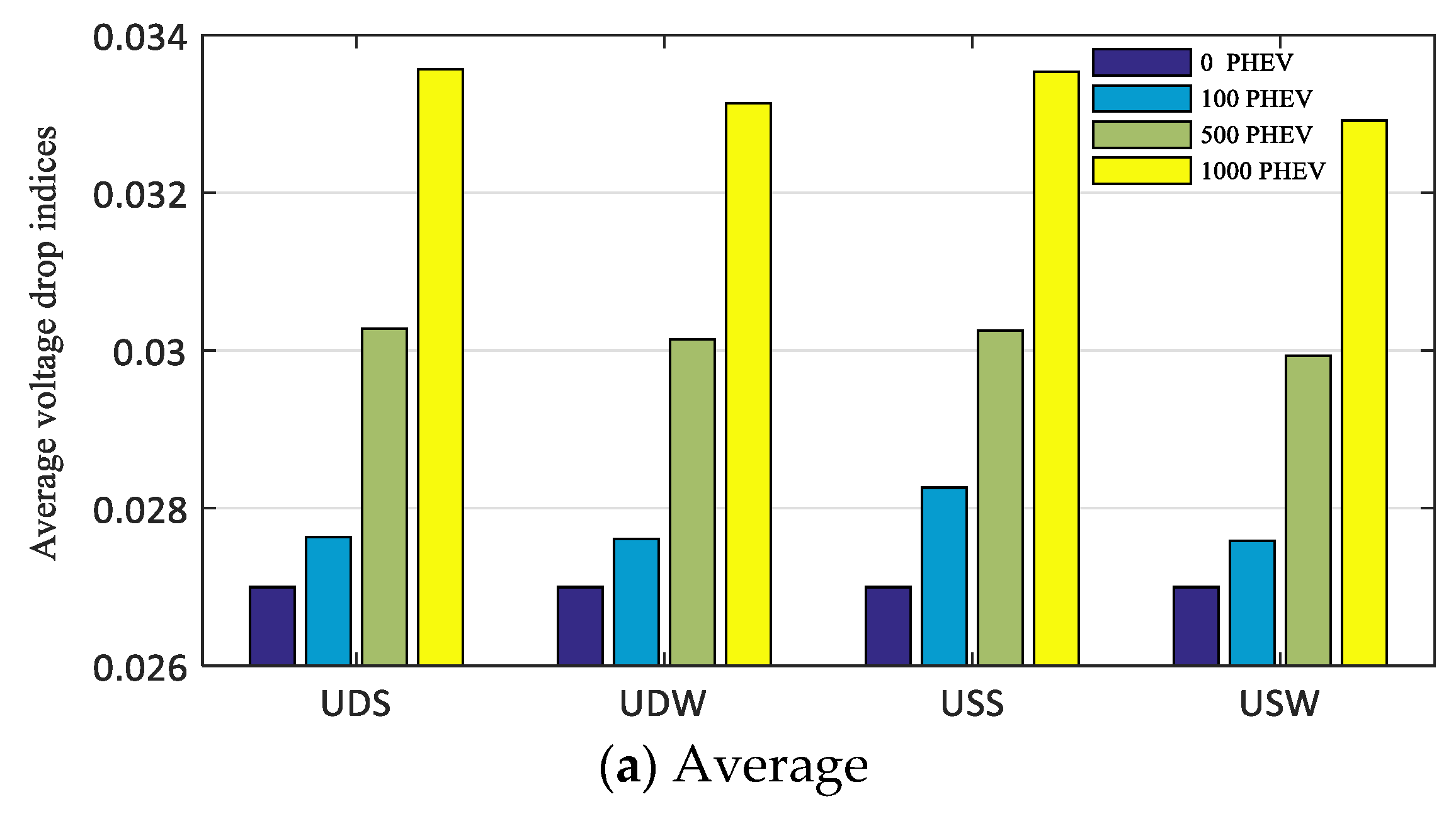
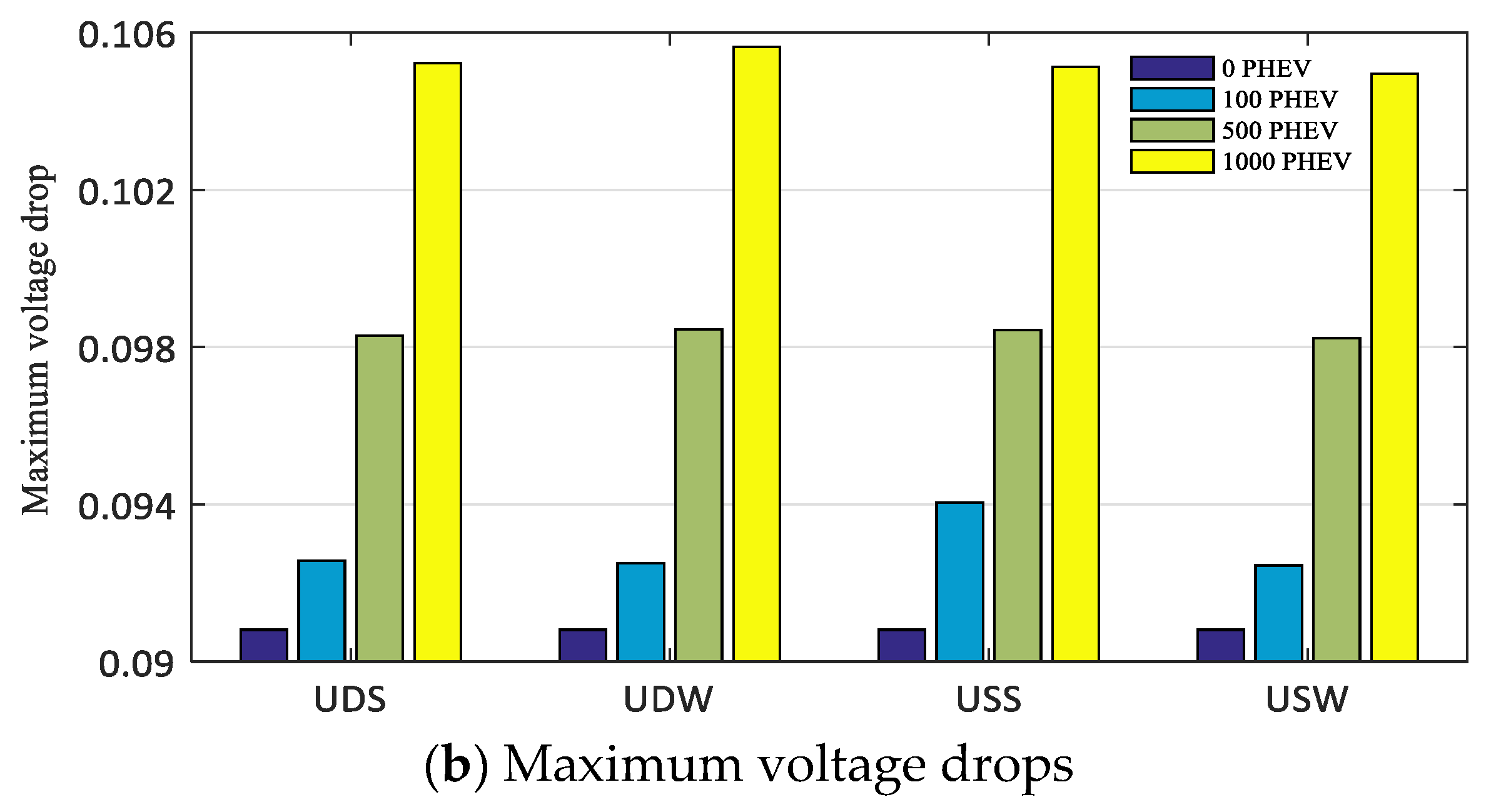
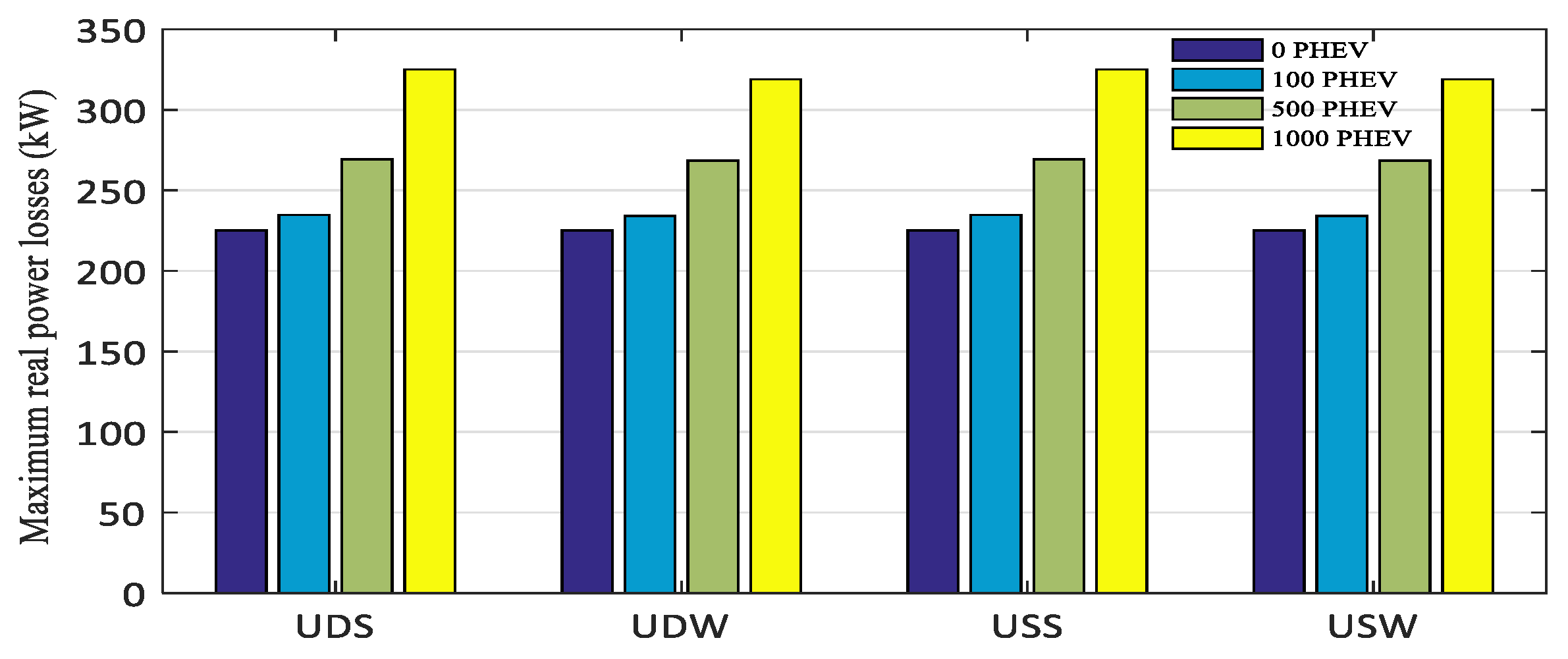
5.1. Case 1: “Uncontrolled Charging”
- 1-
- The Uncontrolled Deterministic Summer (UDS).
- 2-
- The Uncontrolled Deterministic Winter (UDW).
- 3-
- The Uncontrolled Stochastic Summer (USS).
- 4-
- The Uncontrolled Stochastic Winter (USW).
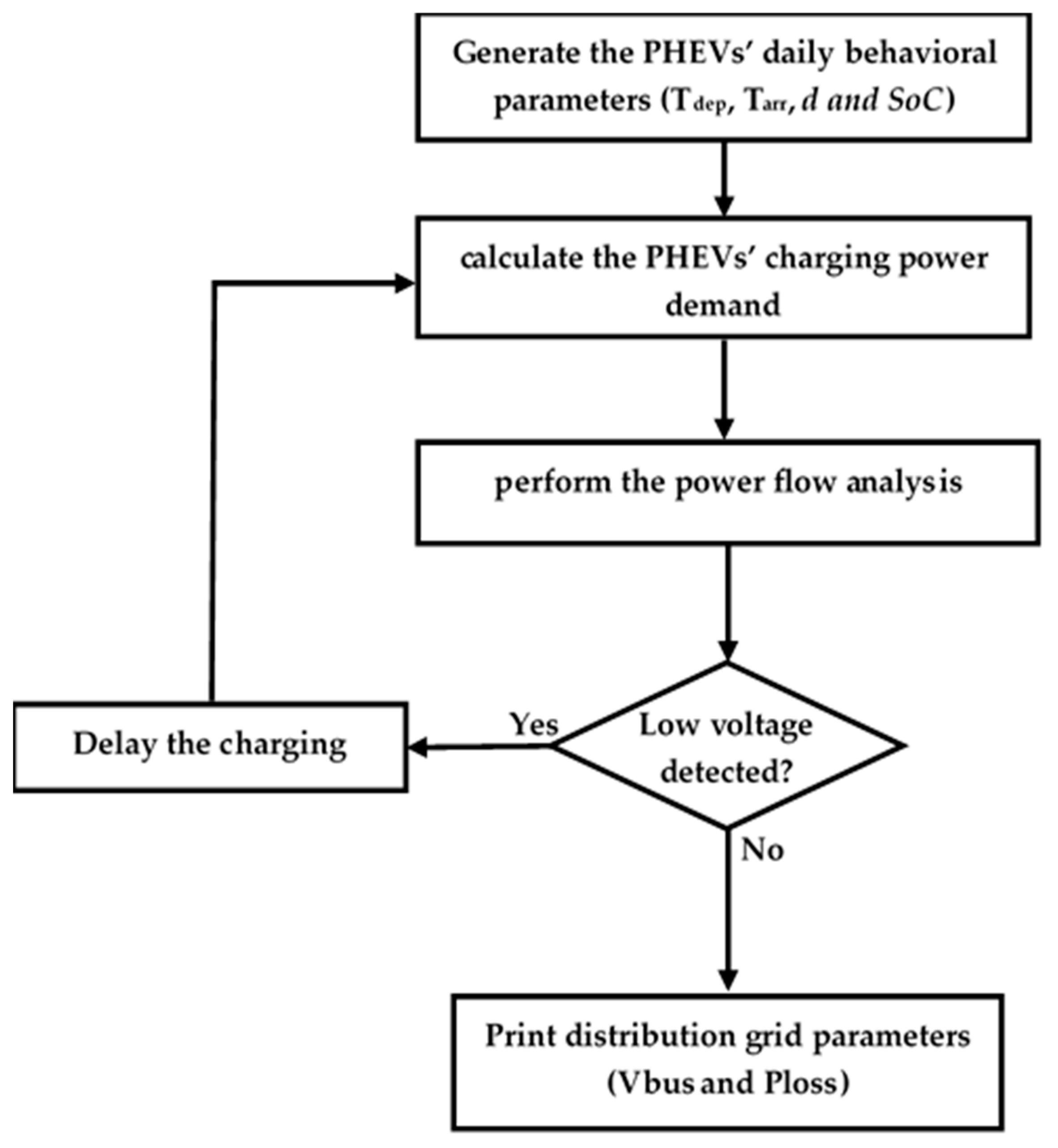
5.2. Case 2: ‘Controlled Charging’
- It estimates the total residential power demand (household demand and the power demand to charge the EVs) and runs the power flow analysis.
- Check for the state of charge of the electric vehicles and proceed to charge them following the rule “first came-first served”.
- Before the charging demand is approved, another power flow analysis is performed to ensure the voltage profile is still within the margin of voltage prior to the charging power request. Otherwise, the charging is delayed to the next time-frame (i.e. temporal load shifting).
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BEV | battery electrical vehicles |
| PHEV | Plug-in hybrid electric vehicles |
| FCEV | Fuel Cell Electric Vehicles |
| NHTS | National Household Travel Survey |
| AER | All-electric range |
| AVD | Average Voltage Drop |
| MVD | Maximum Voltage Drop |
| MDRPL | Maximum Daily Real Power Losses |
| UDS | The Uncontrolled Deterministic Summer case |
| UDW | The Uncontrolled Deterministic Winter case |
| USS | The Uncontrolled Stochastic Summer case |
| USW | The Uncontrolled Stochastic Winter case |
| Nomenclature | |
| tdep | Departure time |
| µdep | The mean value of the departure time PDF |
| σdep | The standard deviation of the departure time PDF |
| tarr | Arrival time |
| µarr | The mean value of the arrival time PDF |
| σarr | The standard deviation of the arrival time PDF |
| d | The daily travelled distance |
| µd | The mean value of daily travelled distance PDF |
| σd | The standard deviation of the daily travelled distance PDF |
| SoC | State of Charge |
| N | The number of hours required to fully charge the battery from an empty state |
| D | Traveled distance |
| SoCreg | SoC recharged from the regenerative braking |
| Dk | The Kantorovich distance between two scenarios |
| Si | The ith Scenario |
| K | the number of scenarios in the original set |
| Fk | fitness level to each member in the set |
| P(i) | the probability of ith representative load profile |
| Vref | The rated bus voltage |
| Vt,i | The node voltage at time t |
| Nb | The numbers of nodes in the power system |
| Nl | The numbers of branches in the power system |
| T | The number of time intervals |
References
- United Nations Framework Convention on Climate Change (UNFCCC). Paris Declaration on Electro-Mobility and Climate Change & Call to Action. December 2015. Available online: https://unfccc.int/media/521376/paris-electro-mobility-declaration.pdf (accessed on 30 June 2019).
- International Energy Agency. Global EV Outlook 2017. Available online: https://webstore.iea.org/download/direct/291?fileName=GlobalEVOutlook2017.pdf (accessed on 25 May 2019).
- International Organisation of Motor Vehicles Manifacturers. Climate Change and CO2. May 2008. Available online: http://oica.net/wp-content/uploads/climate-change-and-co2-brochure.pdf (accessed on 25 May 2019).
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Hong, B. Plug-in Hybrid Electric Vehicles (PHEVs); IEEE Emerging Technologies Portal: New York, NY, USA, 2012. [Google Scholar]
- U.S Department of Energy. Vehicle Technologies Program. October 2011. Available online: https://www.energy.gov/eere/electricvehicles/electric-vehicle-basics (accessed on 20 May 2019).
- Boudina, R.; Wang, J.; Benbouzid, M.; Khoucha, F.; Boudour, M. Impact evaluation of large scale integration of electric vehicles on power grid. Front. Energy 2018. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of electric vehicles in the electric power system. Proc. IEEE 2011, 99, 168–183. [Google Scholar] [CrossRef]
- Putrus, G.A.; Suwanapingkarl, P.; Johnston, D.; Bentley, E.C.; Narayana, M. Impact of electric vehicles on power distribution networks. In Proceedings of the Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009. [Google Scholar] [CrossRef]
- Jayaweera, D.; Islam, S. Risk of supply insecurity with weather condition-based operation of plug in hybrid electric vehicles. IET Gener. Transm. Distrib. 2014, 8, 2153–2162. [Google Scholar] [CrossRef]
- Haidar, A.M.A.; Muttaqi, K.M.; Haque, M.H. Multistage time-variant electric vehicle load modelling for capturing accurate electric vehicle behaviour and electric vehicle impact on electricity distribution grids. IET Gener. Transm. Distrib. 2015, 9, 2705–2716. [Google Scholar] [CrossRef]
- Kim, Y.; Kwak, J.; Chong, S. Dynamic pricing, scheduling, and energy management for profit maximization in PHEV charging stations. IEEE Trans. Veh. Technol. 2017, 66, 1011–1026. [Google Scholar] [CrossRef]
- Dong, Q.; Niyato, D.; Wang, P.; Han, Z. The PHEV charging scheduling and power supply optimization for charging stations. IEEE Trans. Veh. Technol. 2016, 65, 566–580. [Google Scholar] [CrossRef]
- Berthold, F.; Ravey, A.; Blunier, B.; Bouquain, D.; Williamson, S. Design and development of a smart control strategy for plug-in hybrid vehicles including vehicle-to-home functionality. IEEE Trans. Transp. Electrif. 2015, 1, 168–177. [Google Scholar] [CrossRef]
- Hu, J.; Si, C.; Lind, M.; Yu, R. Preventing distribution grid congestion by integrating indirect control in a hierarchical electric vehicles’ management system. IEEE Trans. Transp. Electrif. 2016, 2, 290–299. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Su, W.; Chow, M.-Y. Performance evaluation of an EDA-based large-scale plug-in hybrid electric vehicle charging algorithm. IEEE Trans. Smart Grid 2012, 3, 308–315. [Google Scholar] [CrossRef]
- Hajimiragha, A.; Canizares, C.A.; Fowler, M.W.; Elkamel, A. Optimal transition to plug-in hybrid electric vehicles in Ontario, Canada, considering the electricity-grid limitations. IEEE Trans. Ind. Electron. 2010, 57, 690–701. [Google Scholar] [CrossRef]
- Shafiee, S.; Fotuhi-Firuzabad, M.; Rastegar, M. Investigating the impacts of plug-in hybrid electric vehicles on power distribution systems. IEEE Trans. Smart Grid 2013, 4, 1351–1360. [Google Scholar]
- Rezaee, S.; Farjah, E.; Khorramdel, B. Probabilistic analysis of plug-in electric vehicles impact on electrical grid through homes and parking lots. IEEE Trans. Sustain. Energy 2013, 4, 1024–1033. [Google Scholar]
- Tan, J.; Wang, L. Integration of plug-in hybrid electric vehicles into residential distribution grid based on two-layer intelligent optimization. IEEE Trans. Smart Grid 2014, 5, 1774–1784. [Google Scholar] [CrossRef]
- Gray, M.K.; Morsi, W.G. Power quality assessment in distribution systems embedded with plug-in hybrid and battery electric vehicles. IEEE Trans. Power Syst. 2015, 30, 663–671. [Google Scholar] [CrossRef]
- Wang, X.; Karki, R. Exploiting PHEV to augment power system reliability. IEEE Trans. Smart Grid 2017, 8, 2100–2108. [Google Scholar] [CrossRef]
- Gao, S. Design, Analysis and Control of Vehicle-to-Grid Services. Ph.D. Thesis, The University of Hong Kong (HKU), Hong Kong, China, 2014. [Google Scholar]
- Marra, F.; Yang, G.Y.; Træholt, C.; Larsen, E.; Rasmussen, C.N.; You, S. Demand profile study of battery electric vehicle under different charging options. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Jiang, J.; Zhang, C. Fundamentals and Application of Lithium-Ion Batteries in Electric Drive Vehicles; John Wiley & Sons: Singapore, 2015; Volume 2015, pp. 19–20. [Google Scholar]
- Toyota Motor Sales. Toyota Prius Prime 2017 Hybrid Electric Car. Available online: https://www.toyota.com/priusprime/ (accessed on 25 October 2017).
- Santos, A. Summary of travel trends: 2009 national household travel survey. 2011. Available online: https://nhts.ornl.gov/2009/pub/stt.pdf (accessed on 10 March 2019).
- U.S. Department of Transportation Federal Highway Administration. National Household Travel Survey; U.S. Department of Transportation Federal Highway Administration: Washington, DC, USA, 2009. [Google Scholar]
- Leou, R.-C.; Su, C.-L.; Lu, C.-N. Stochastic analyses of electric vehicle charging impacts on distribution network. IEEE Trans. Power Syst. 2014, 29, 1055–1063. [Google Scholar] [CrossRef]
- Kromer, M.A. Electric Powertrains: Opportunities and Challenges in the US Light-Duty Vehicle Fleet. 2007. Massachusetts Institute of Technology. Available online: http://energy.mit.edu/wp-content/uploads/2007/05/MIT-LFEE-07-003-RP.pdf (accessed on 15 March 2019).
- Darabi, Z.; Ferdowsi, M. Aggregated Impact of Plug-in Hybrid Electric Vehicles on Electricity Demand Profile. IEEE Trans. Sustain. Energy 2011, 2, 501–508. [Google Scholar] [CrossRef]
- Hua, L.; Wang, J.; Zhou, C. Adaptive electric vehicle charging coordination on distribution network. IEEE Trans. Smart Grid 2014, 5, 2666–2675. [Google Scholar]
- National Grid US. National Grid Residential Load Data. Available online: https://www9.nationalgridus.com/masselectric/energy_supplier/index.asp (accessed on 7 October 2017).
- Kazarlis, S.A.; Bakirtzis, A.; Petridis, V. A genetic algorithm solution to the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Li, W. Reliability Assessment of Electric Power Systems Using Monte Carlo Methods; Springer Science & Business Media: New York, NY, USA, 1994; p. 51. [Google Scholar]
| Parameters | Value | Unit |
|---|---|---|
| Average battery capacity | 8.8 | kWh |
| All-electric range | 25 | Mile |
| Full Charging Time (Level 1) | 5.5 | Hour |
| Full Charging Time (Level 2) | 2.5 | Hour |
| Depletion Mode Energy Use (η) | 0.37 | kWh/mile |
| 1 | 2 | 3 | … | N | |
|---|---|---|---|---|---|
| 1 | 0 | 0.48877 | 0.61957 | … | 0.2168 |
| 2 | 0.48877 | 0 | 0.35714 | … | 0.6437 |
| 3 | 0.61957 | 0.34375 | 0 | … | 0.77604 |
| . | . | . | . | . | |
| N | 0.2168 | 0.6437 | 0.77604 | … | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudina, R.; Wang, J.; Benbouzid, M.; Yao, G.; Zhou, L. A Review on Stochastic Approach for PHEV Integration Control in a Distribution System with an Optimized Battery Power Demand Model. Electronics 2020, 9, 139. https://doi.org/10.3390/electronics9010139
Boudina R, Wang J, Benbouzid M, Yao G, Zhou L. A Review on Stochastic Approach for PHEV Integration Control in a Distribution System with an Optimized Battery Power Demand Model. Electronics. 2020; 9(1):139. https://doi.org/10.3390/electronics9010139
Chicago/Turabian StyleBoudina, Rabah, Jie Wang, Mohamed Benbouzid, Gang Yao, and Lidan Zhou. 2020. "A Review on Stochastic Approach for PHEV Integration Control in a Distribution System with an Optimized Battery Power Demand Model" Electronics 9, no. 1: 139. https://doi.org/10.3390/electronics9010139
APA StyleBoudina, R., Wang, J., Benbouzid, M., Yao, G., & Zhou, L. (2020). A Review on Stochastic Approach for PHEV Integration Control in a Distribution System with an Optimized Battery Power Demand Model. Electronics, 9(1), 139. https://doi.org/10.3390/electronics9010139







