Design, Analysis, and Modeling of an Isolated Constant-Current to Constant-Voltage Converter in Cabled Underwater Information Networks
Abstract
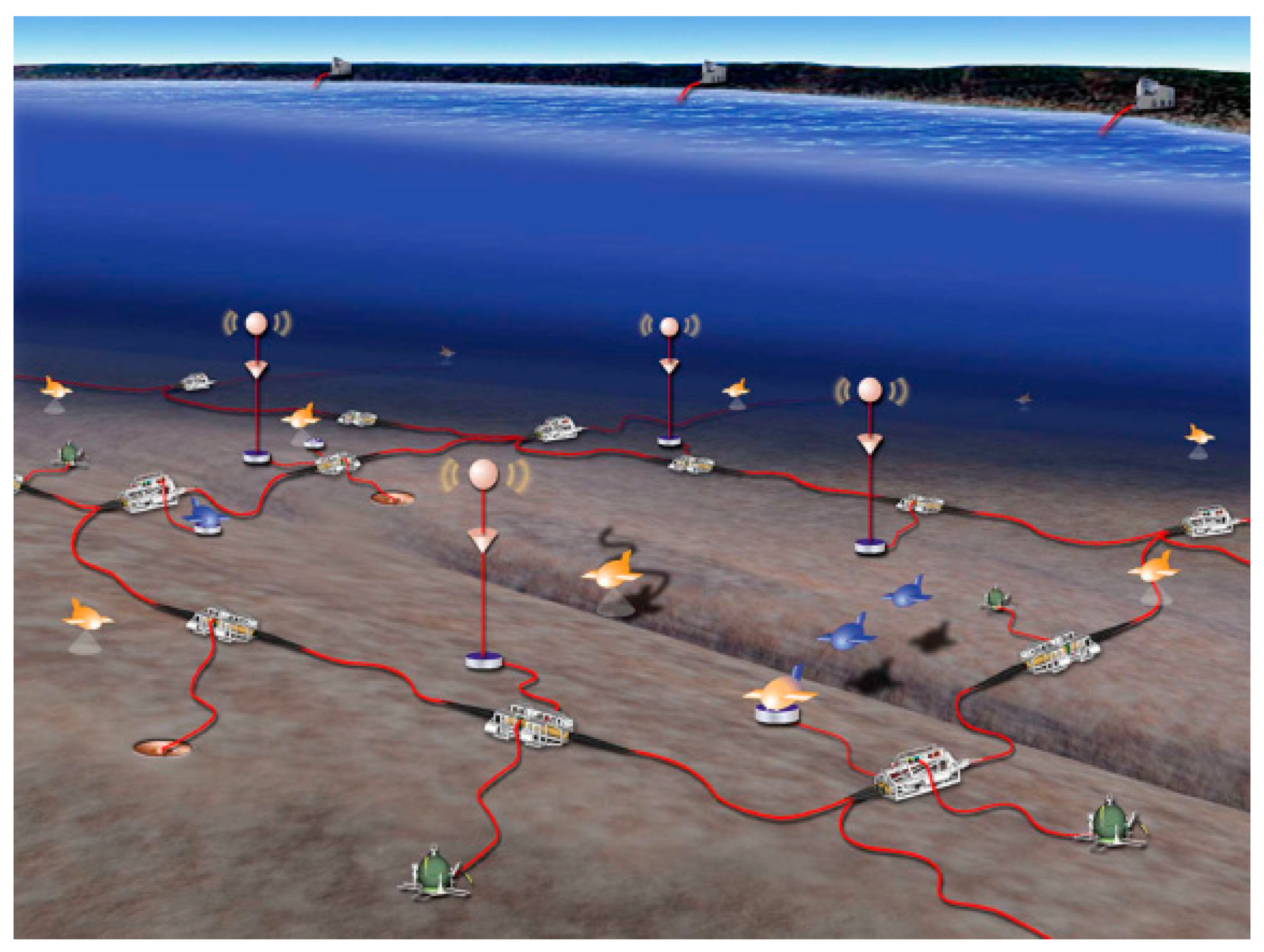
:1. Introduction
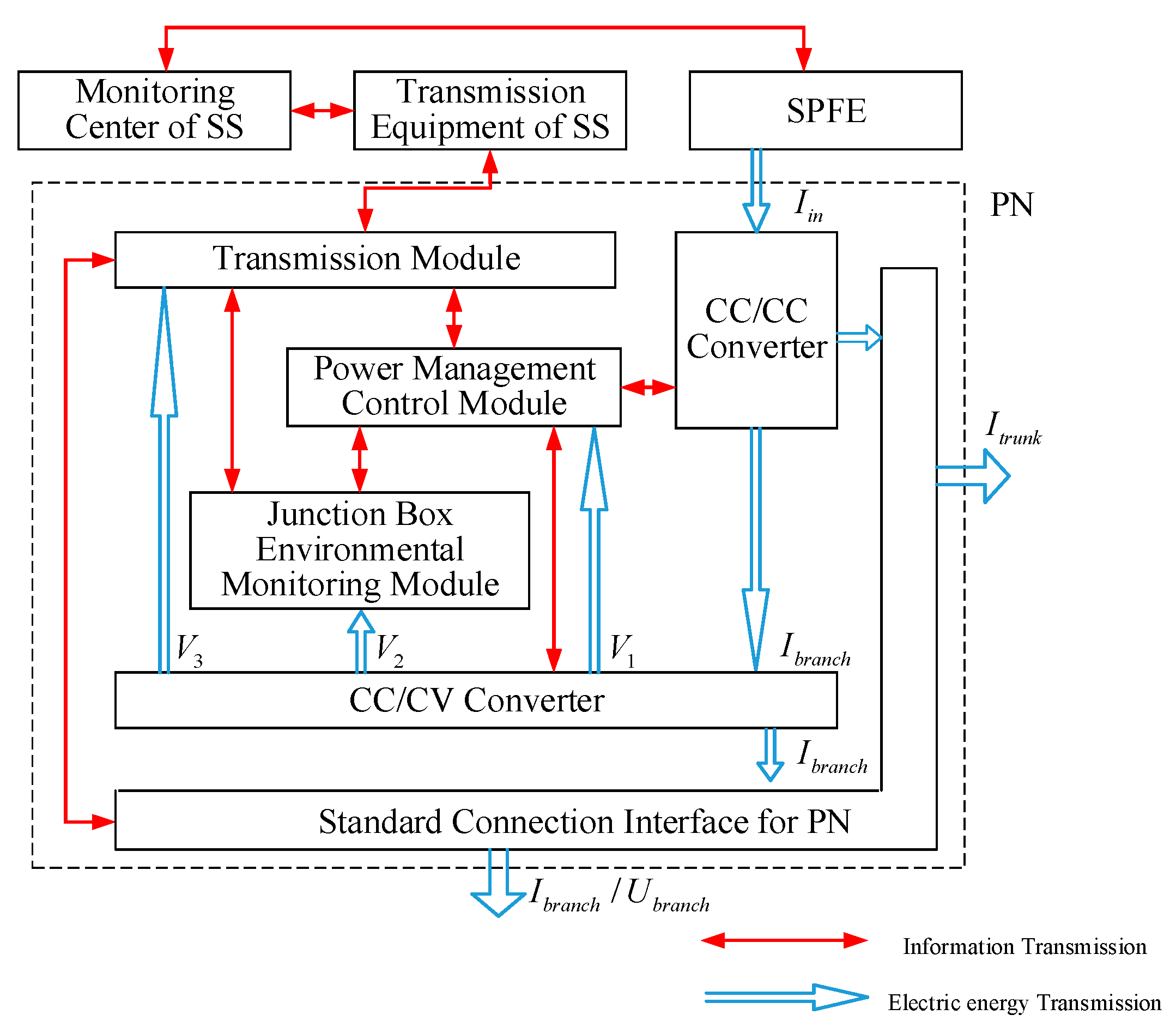
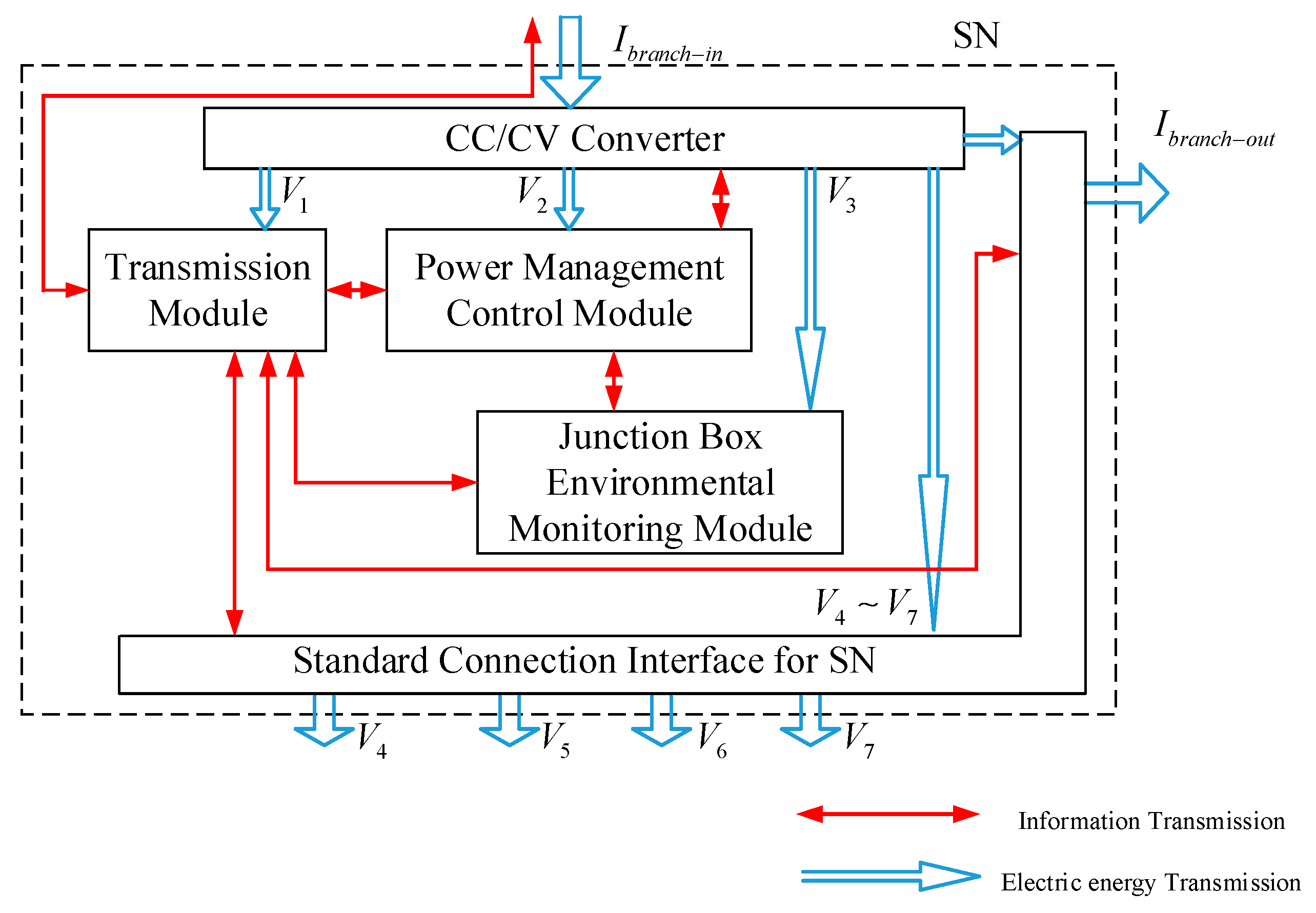
2. Design Concept of CC–CV Converter Circuit
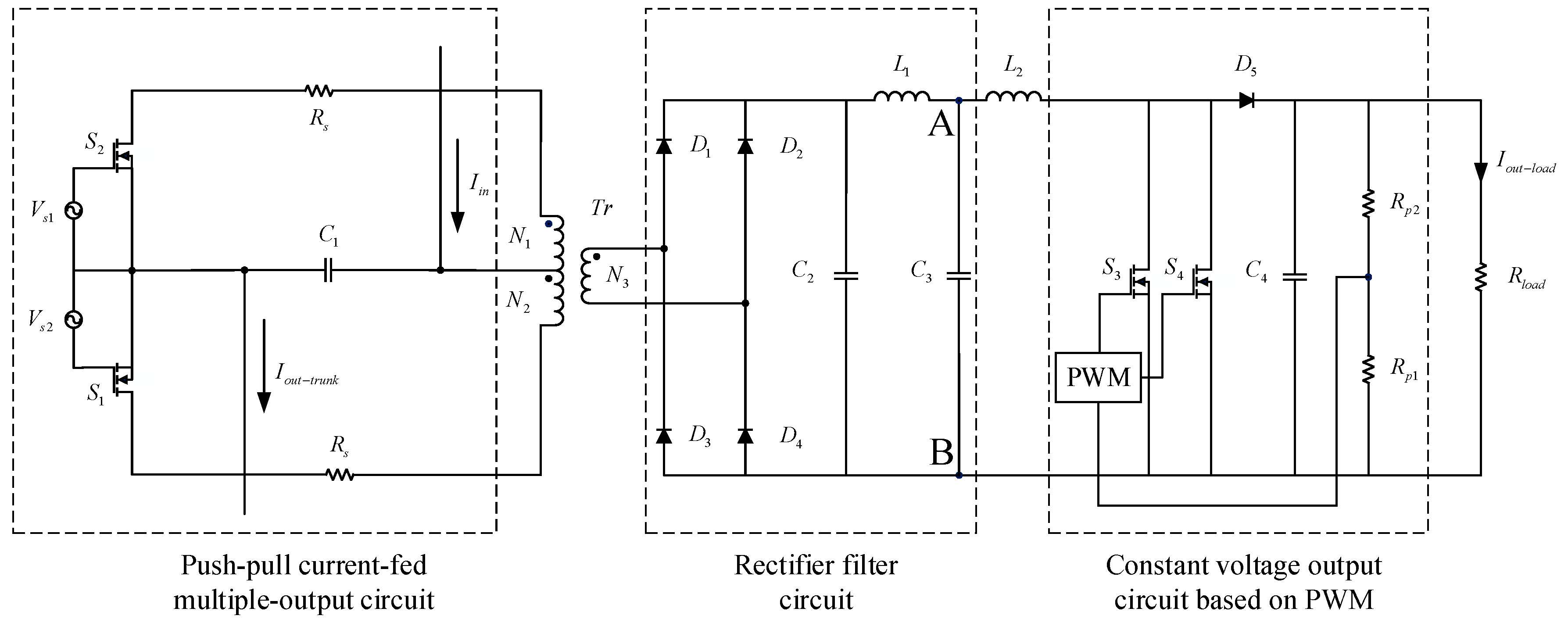
3. Characteristics Analysis of CC–CV Converter Circuit
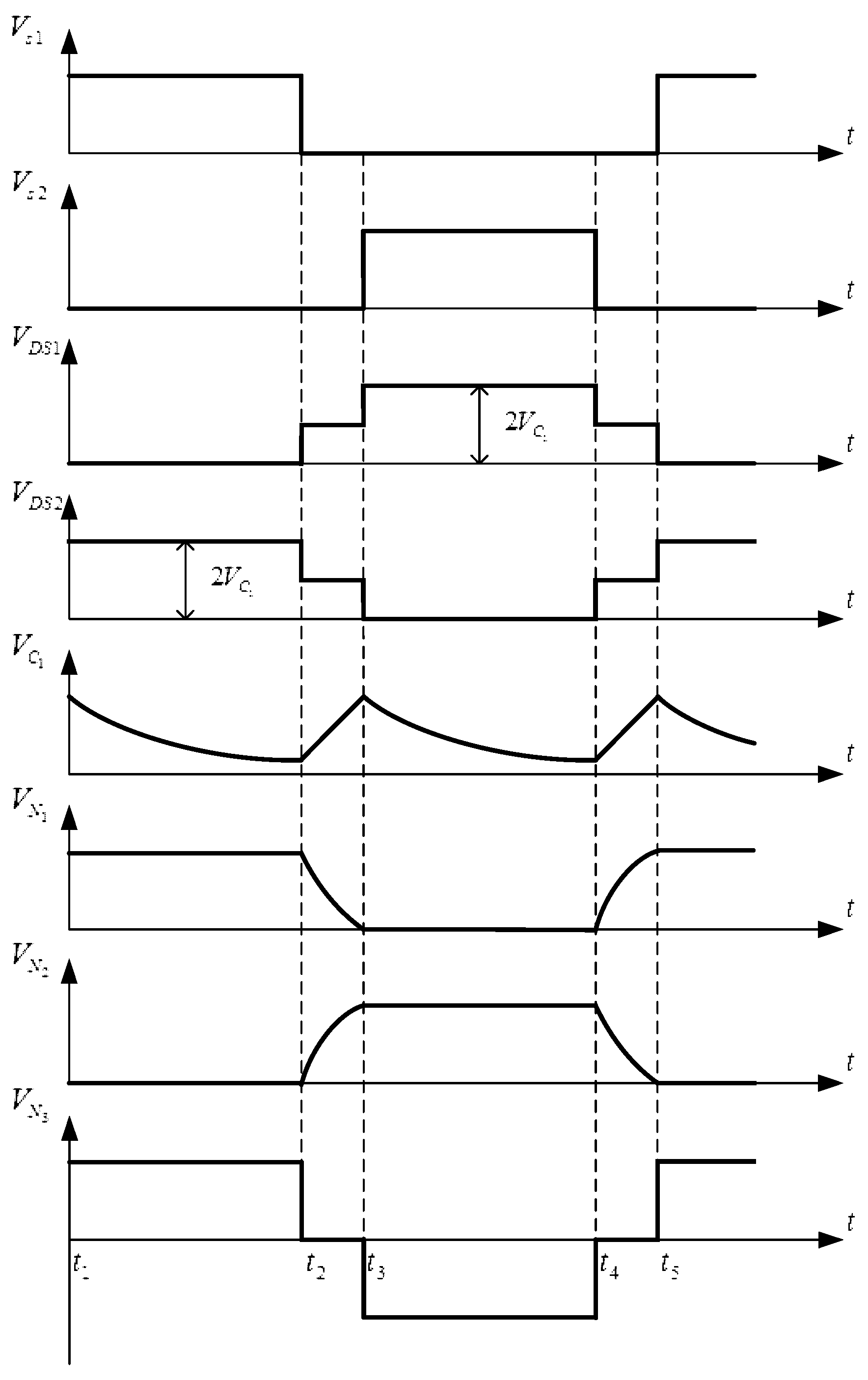
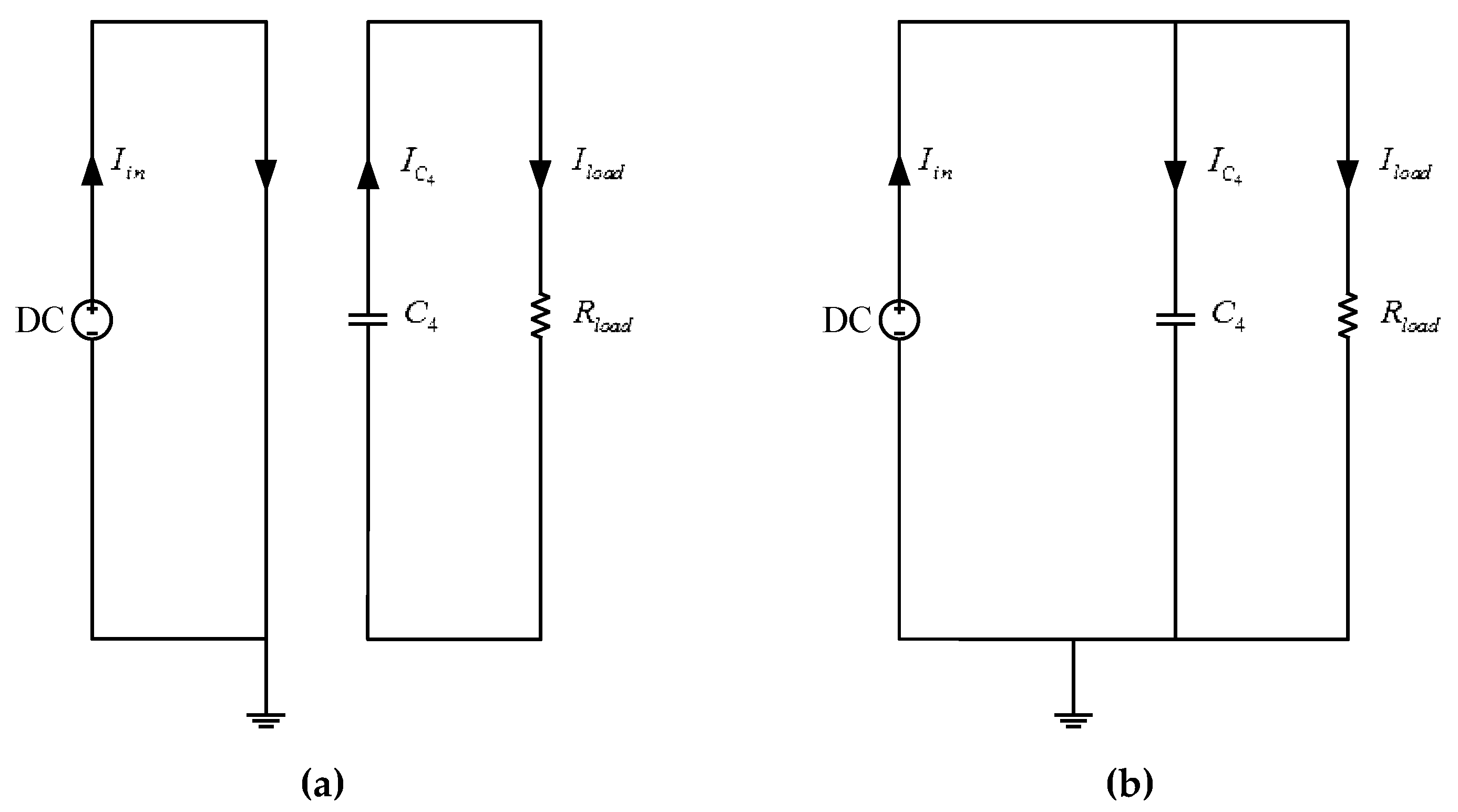
3.1. Principle and Characteristic Analysis of CC Isolation Circuit
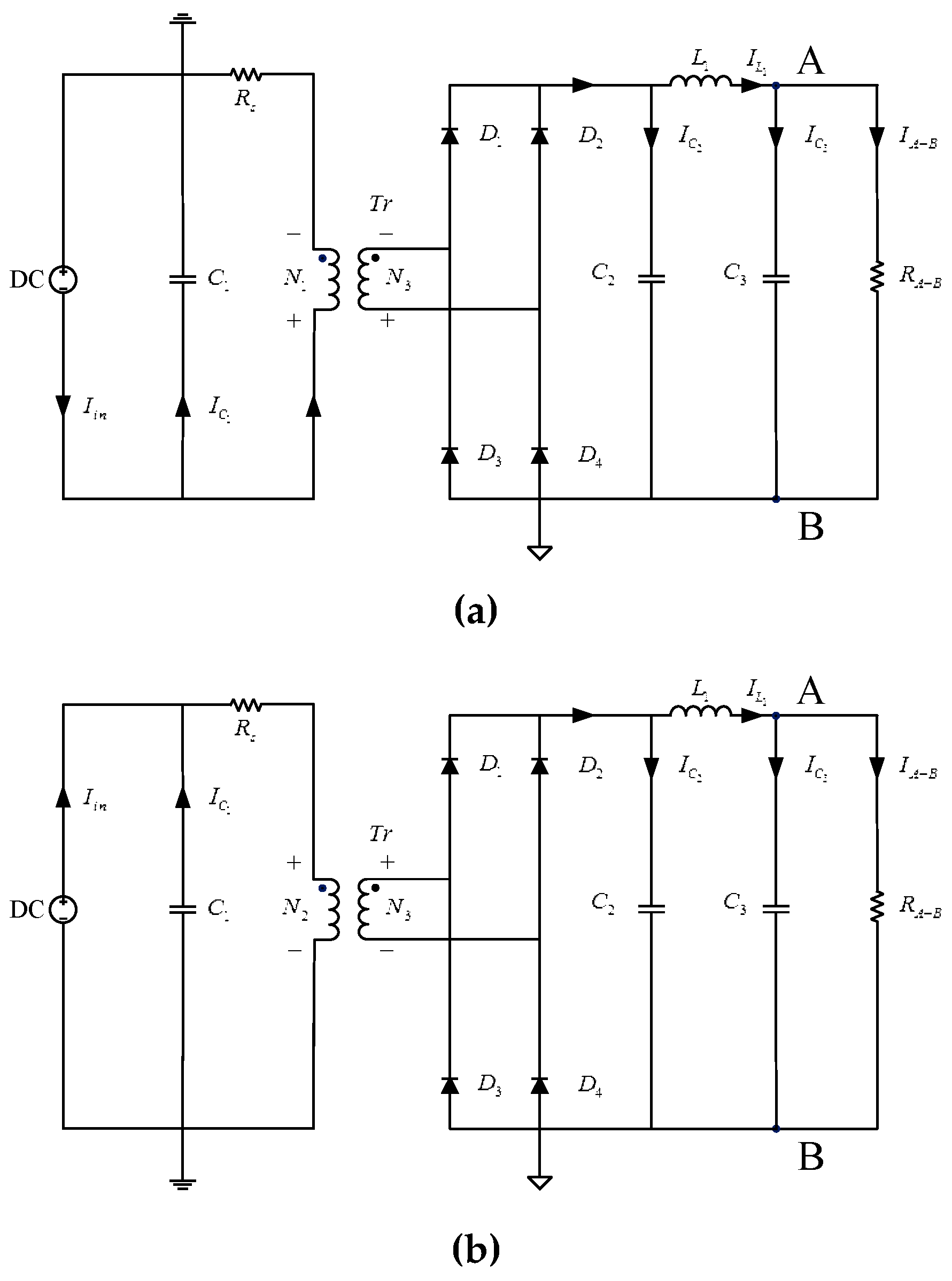
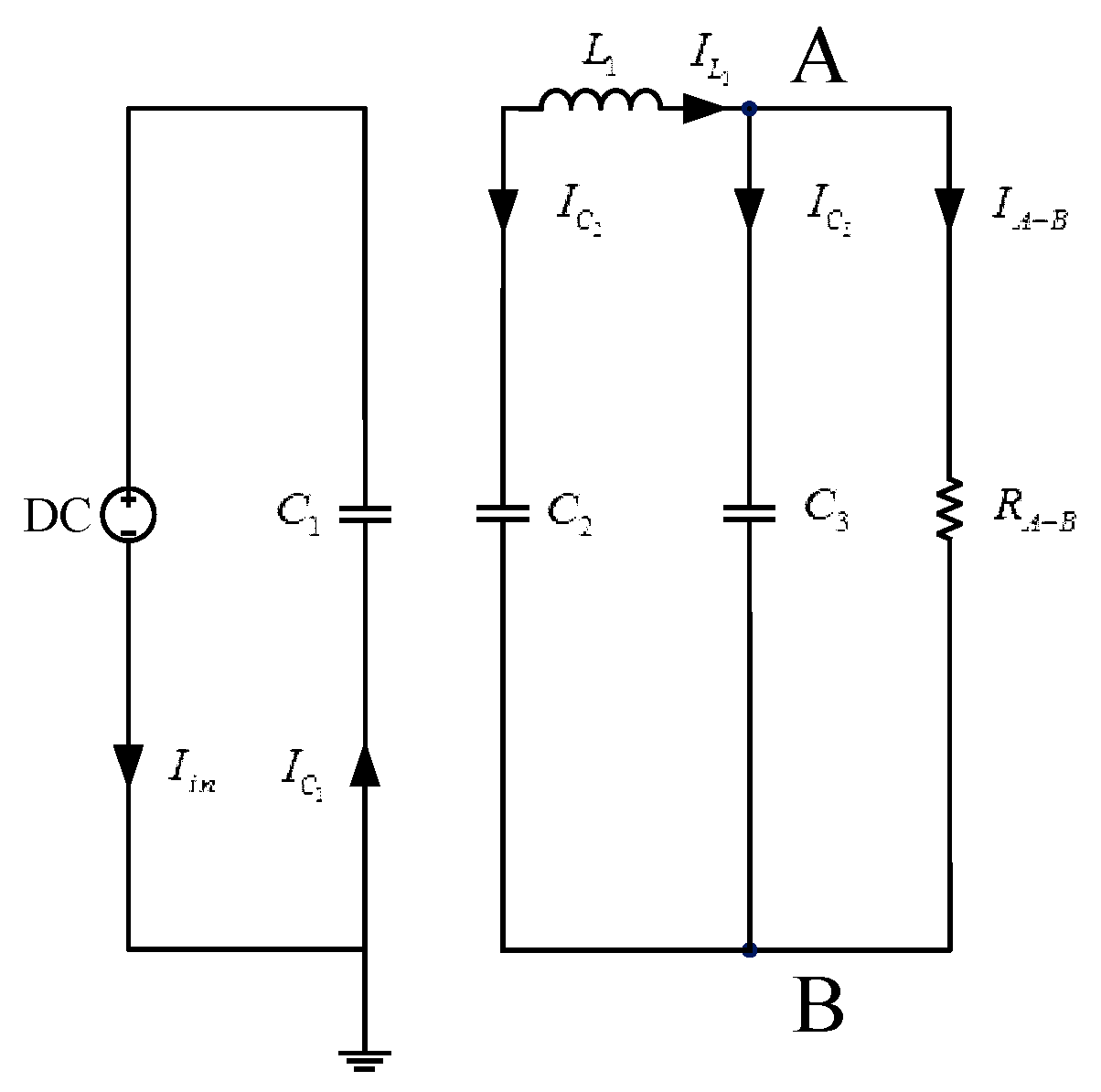
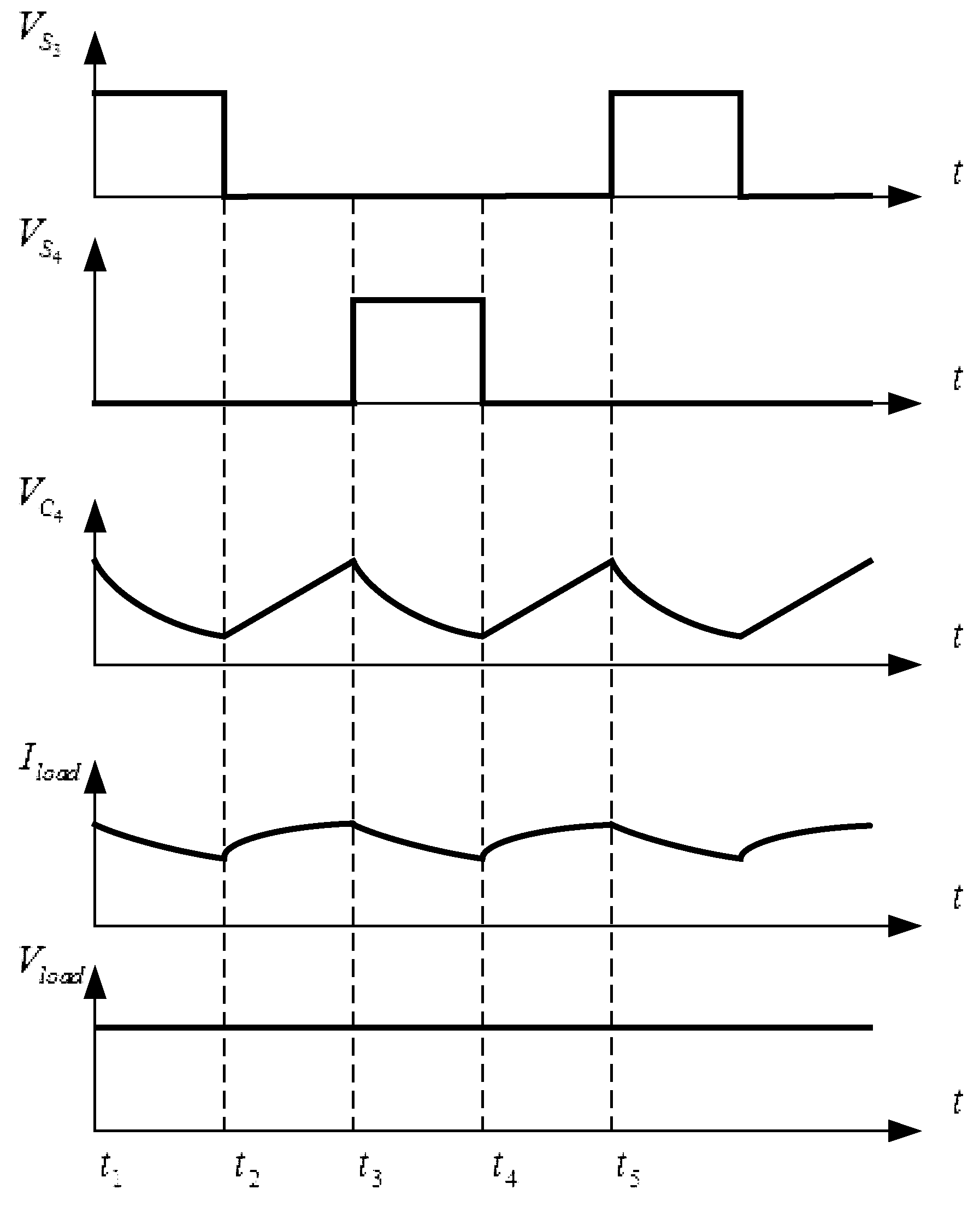
3.2. Principle and Characteristic Analysis of DC Constant Voltage Conversion Circuit
4. Analysis and Research of Modeling Simulation and Verification of Physical Prototype
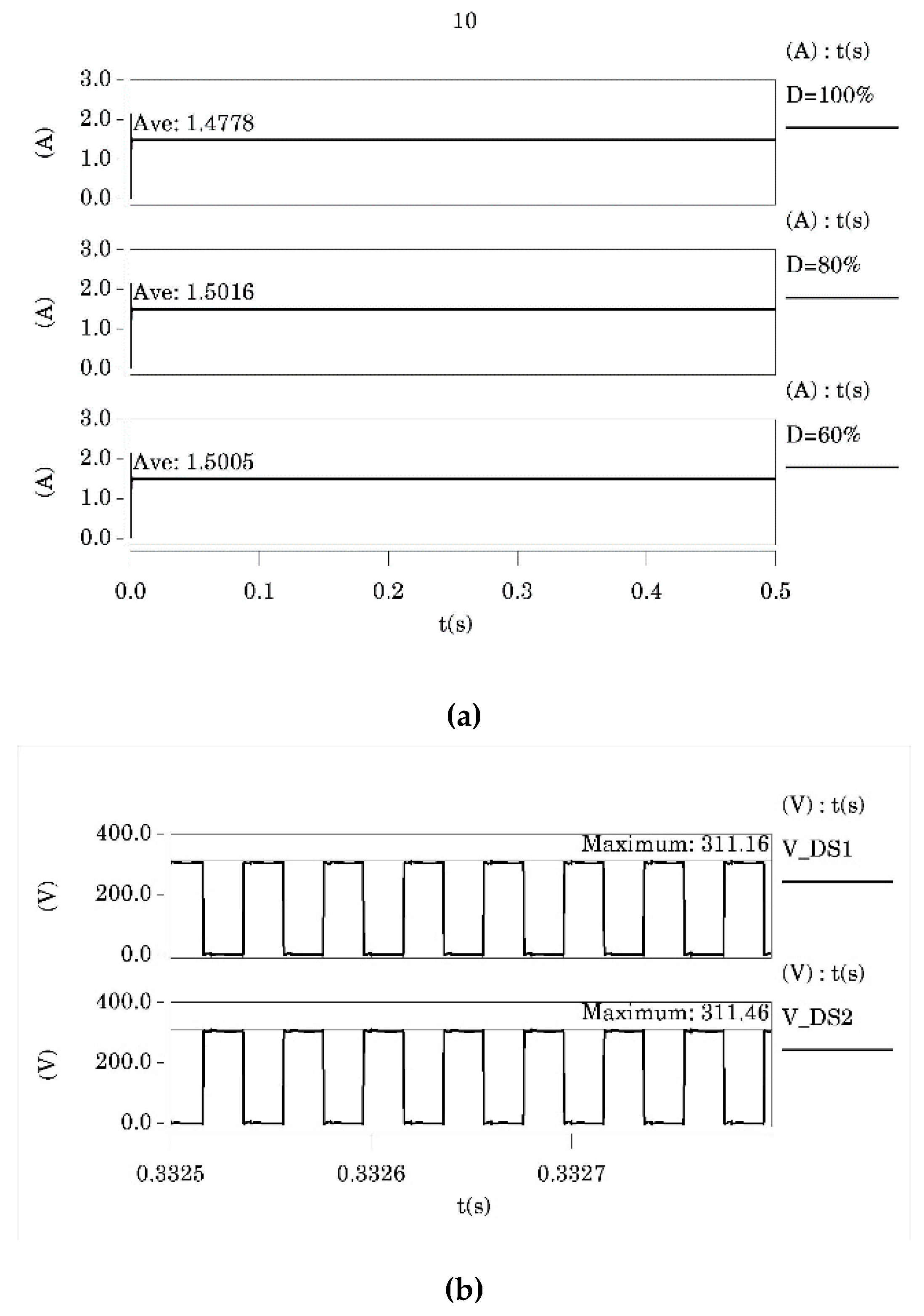
4.1. Modeling and Simulation Analysis of CC–CV Converter Circuit
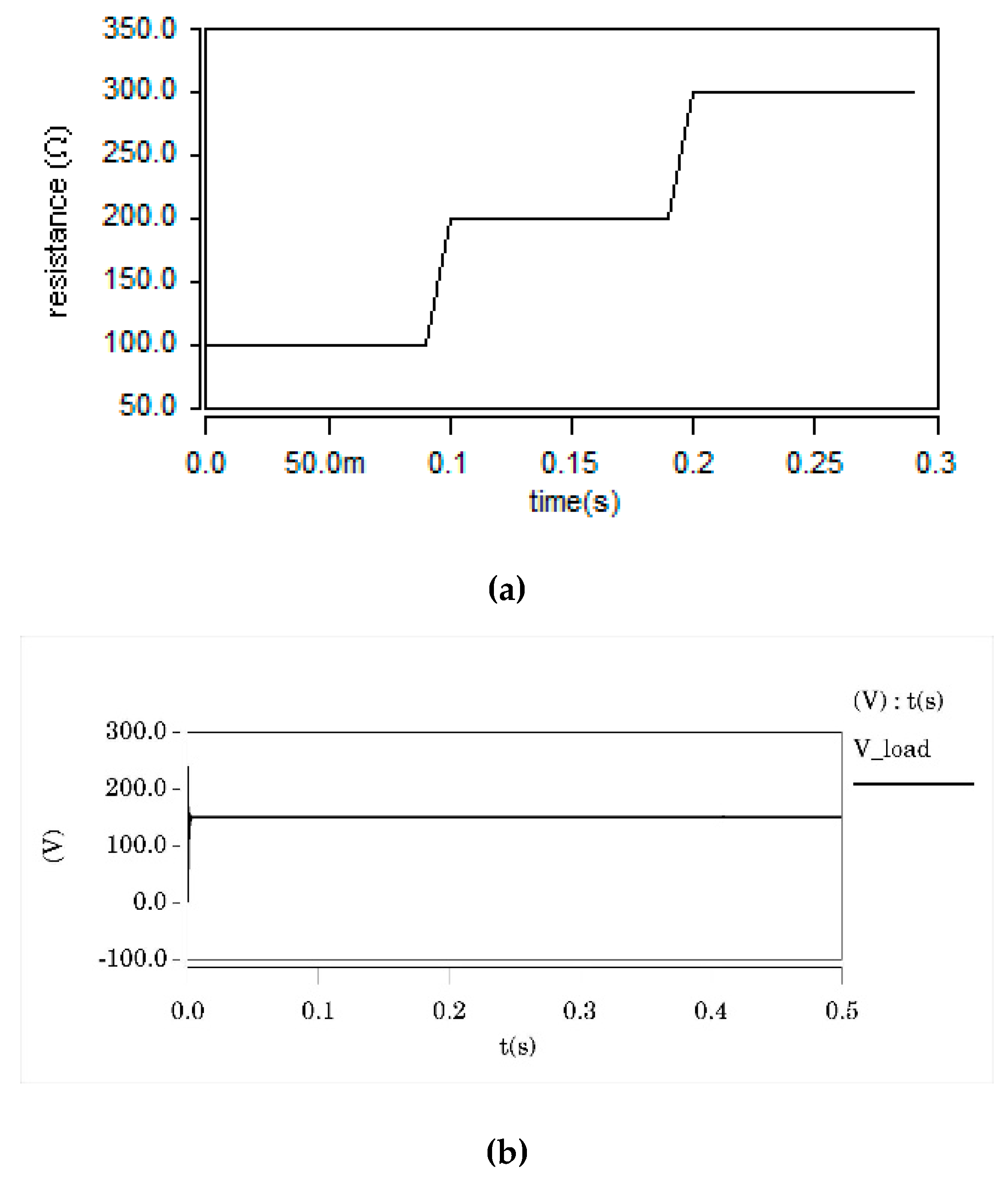
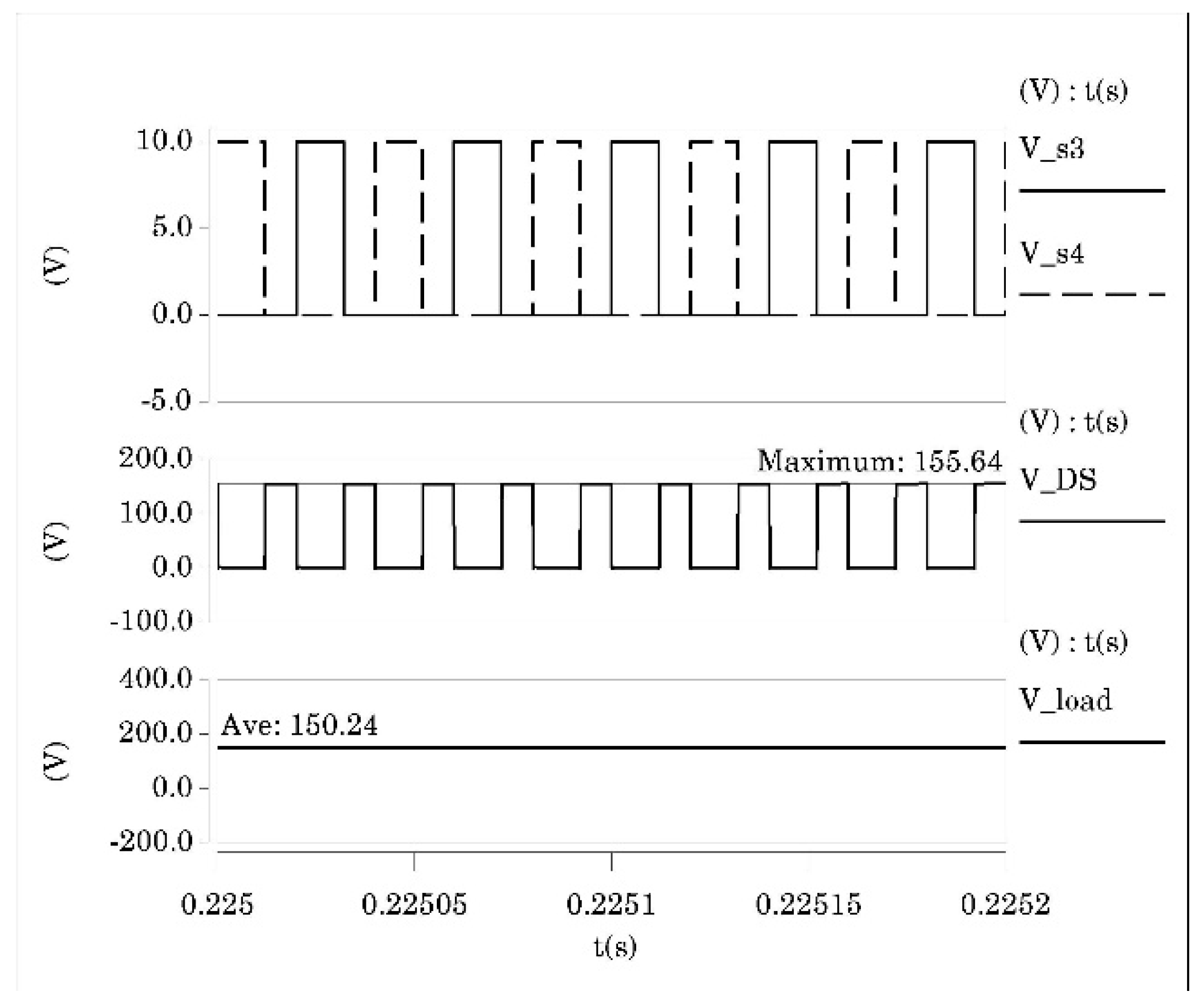
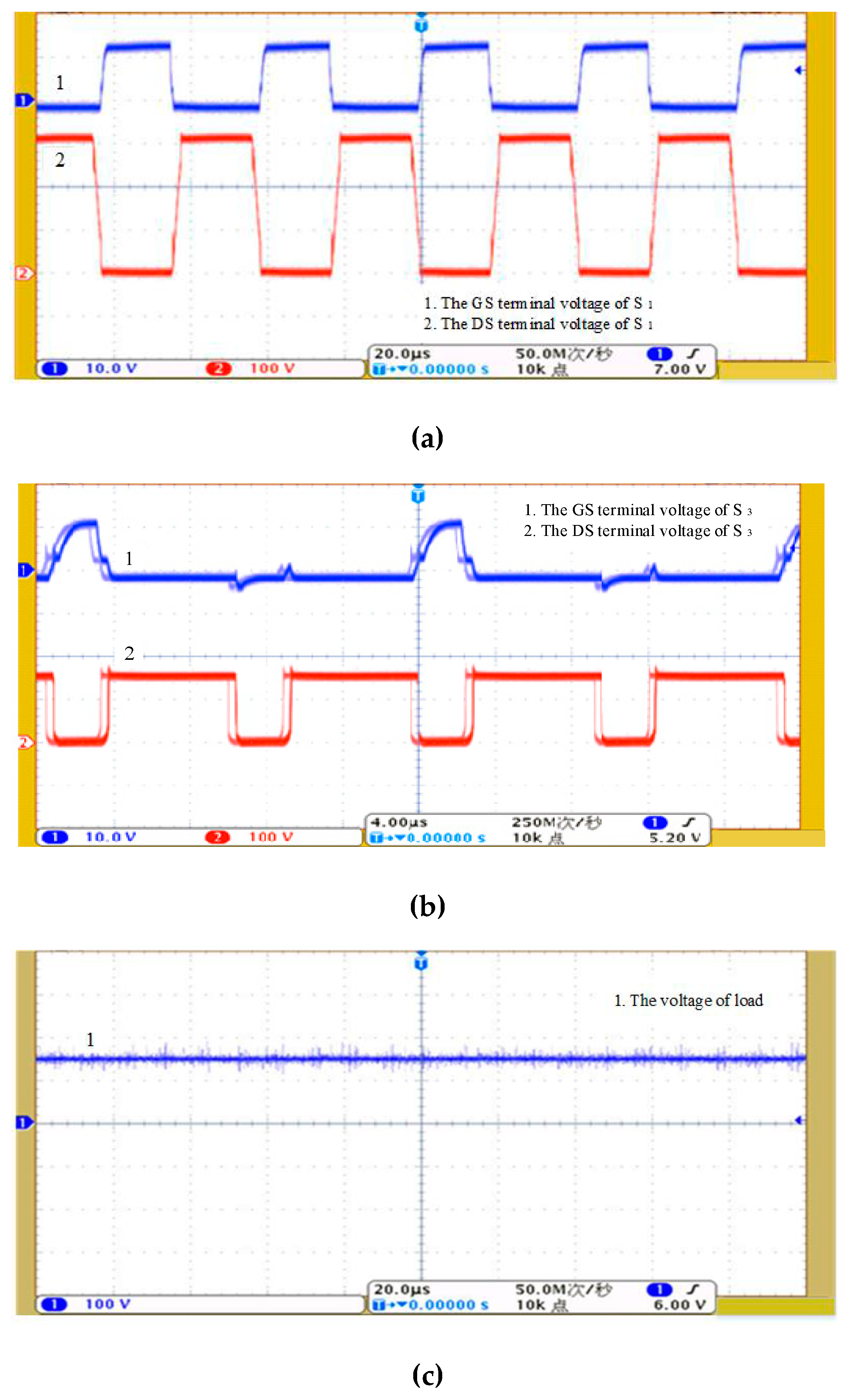
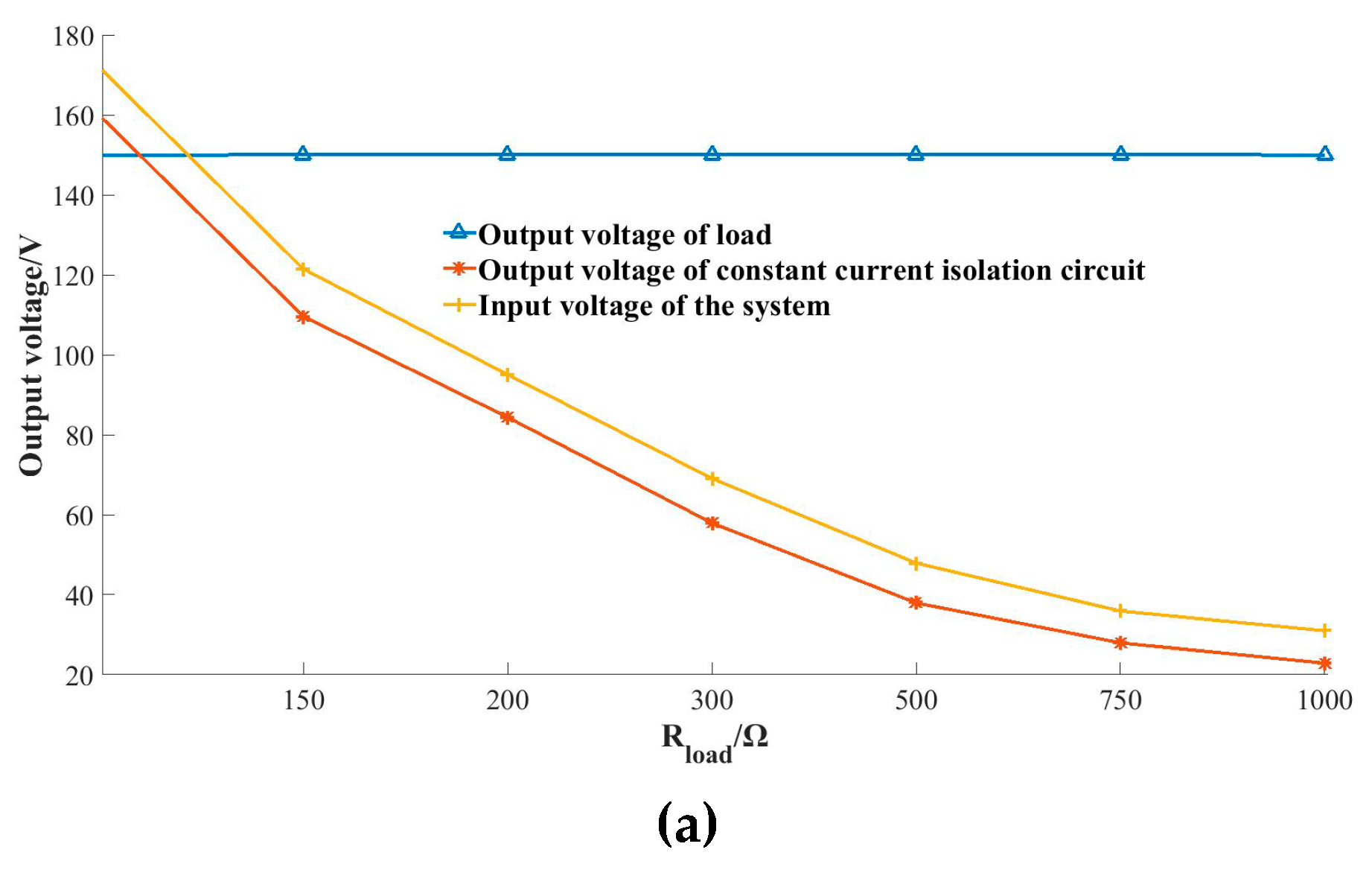
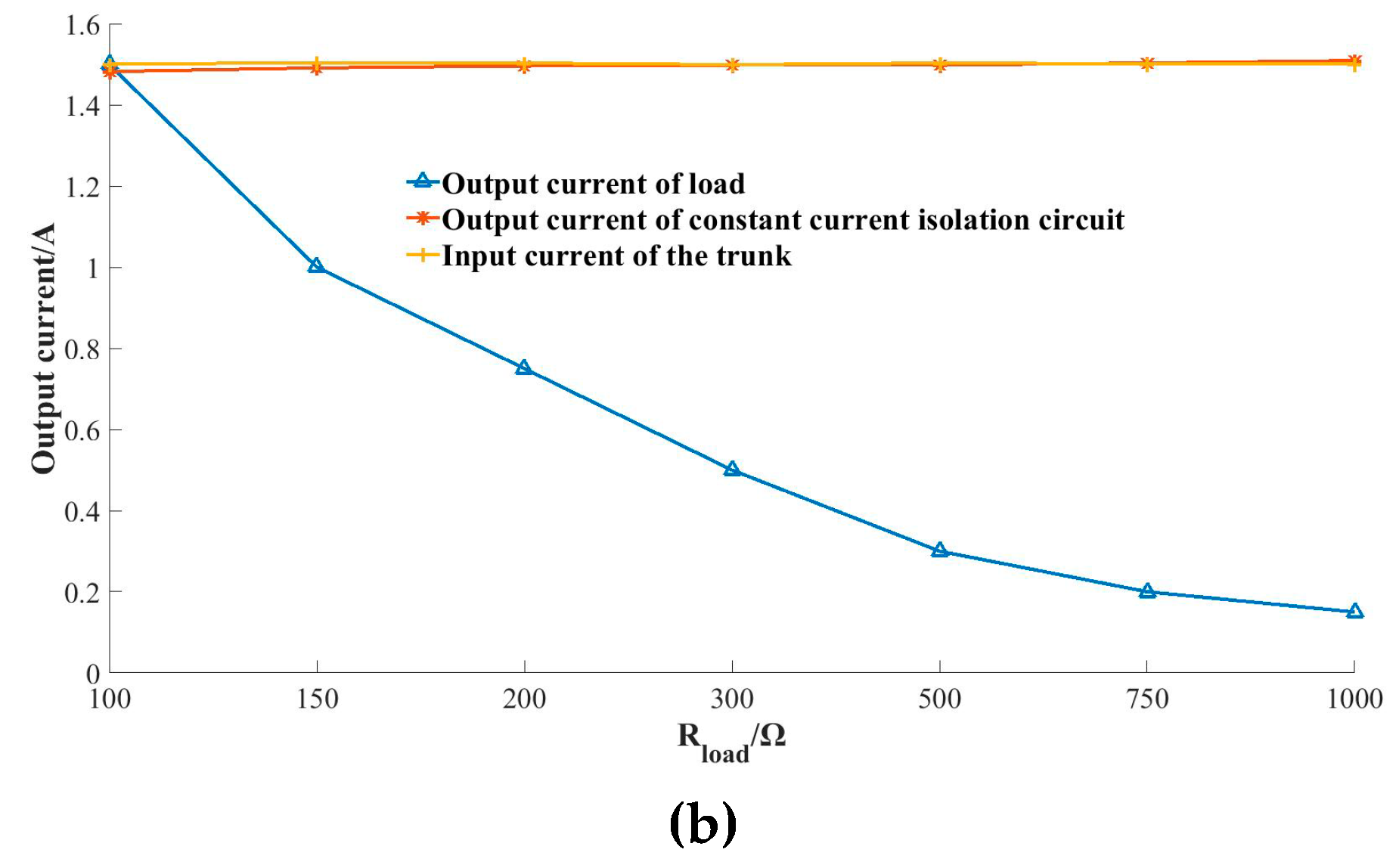
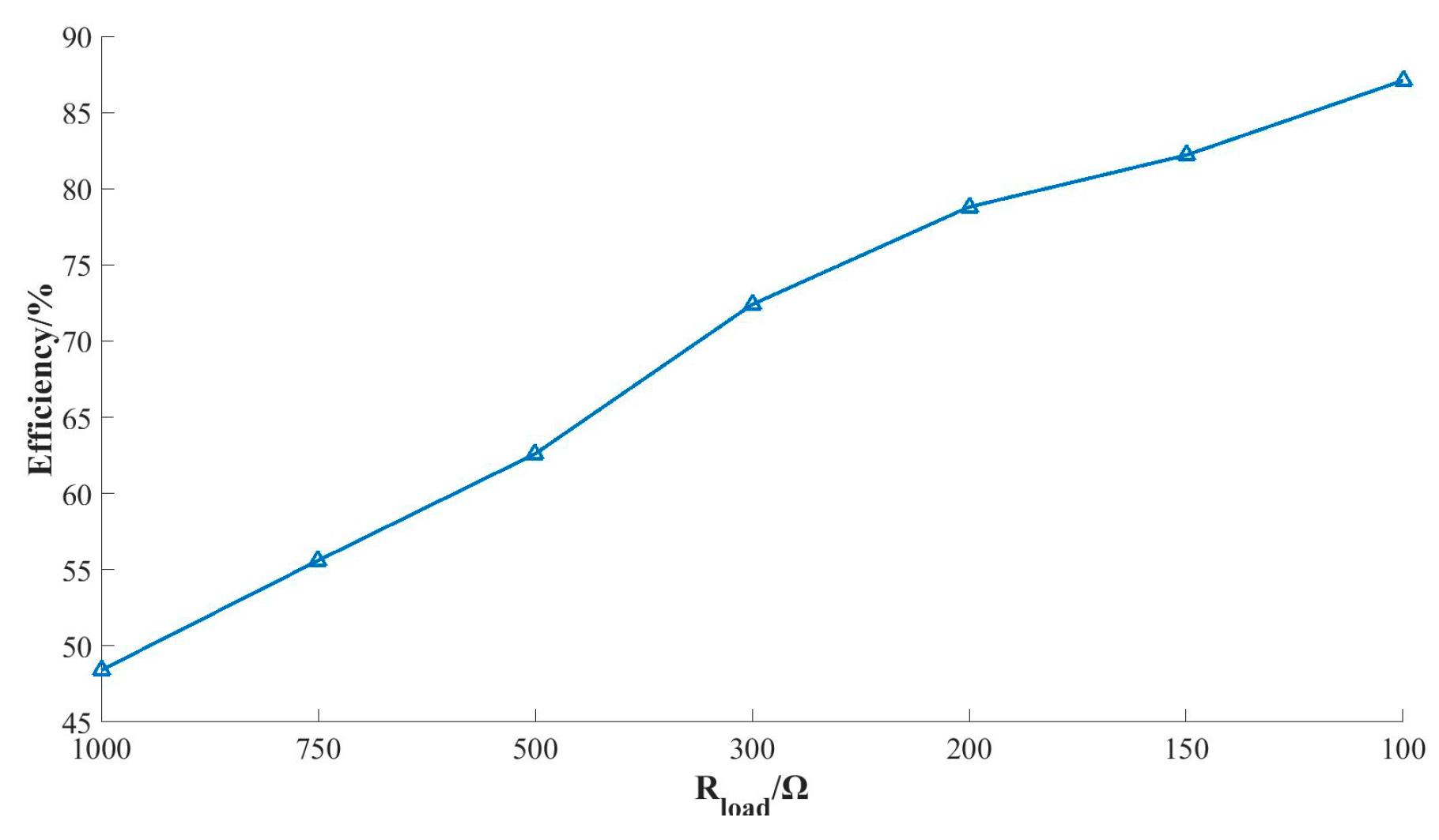
4.2. Research on Verification of Prototype of CC–CV Converter
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y. Ocean observation technology. In Fundamentals of Ocean Technology; Ocean Press: Beijing, China, 2018; Volume 6, pp. 227–235. [Google Scholar]
- Lu, F.; Zhou, H.; Peng, X. Technical preparation and prototype development for long-term cabled seafloor observatories in Chinese marginal seas. In Seafloor Observatories; Springer: Berlin/Heidelberg, Germany, 2015; Volume 19, pp. 503–529. [Google Scholar]
- Lionel, C. Environmental impacts. In Submarine Cables and the Oceans: Connecting the World; Lavenham Press: London, UK, 2009; Volume 5, pp. 29–37. [Google Scholar]
- Feng, L.; Huaiyang, Z. Progress of scientific cabled seafloor observatory networks. J. Eng. Stud. 2016, 8, 139–154. [Google Scholar]
- Qu, F.; Wang, Z.; Song, H.; Chen, Y.; Yang, L. A Study on a cabled seafloor observatory. IEEE Intell. Syst. 2015, 30, 66–69. [Google Scholar] [CrossRef]
- Garrett, L.D. Design of global submarine networks. J. Opt. Commun. Netw. 2018, 10, A185–A195. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, X.; Wang, X. Short-circuit fault diagnosis and interval location method for constant current remote supply system in cabled underwater information networks. J. Zhejiang Univ.-Eng. Sci. 2019, 53, 1190–1197. [Google Scholar]
- Zhou, X.; Fan, C.; Li, D.; Zhou, Y. Power scheme selecting method for constant current power system of cabled seafloor observatory network. Autom. Electr. Power Syst. 2015, 39, 126–131. [Google Scholar]
- Wang, X.-C.; Zhou, X.-J.; Hu, R.; Fan, C.; Miao, H. Reliability simulation of remote power feeding system. J. Shanghai Jiao Tong Univ.-Sci. 2013, 47, 428–433. [Google Scholar]
- Hua, C. Technologies of cabled submarine networking observation. In International Progress in Submarine Scientific Observation; Tongji University Press: Shanghai, China, 2017; Volume 9, pp. 139–154. [Google Scholar]
- Chen, Y. Research on the Key Technologies of Power Junction for Cabled Ocean Observatories System Based on Tree Topology; Zhejiang University: Hangzhou, China, 2012. [Google Scholar]
- Kawaguchi, K.; Kaneda, Y.; Araki, E. The DONET: A real-time seafloor research infrastructure for the precise earthquake and tsunami monitoring. In Proceedings of the OCEANS 2008, Kobe, Japan, 8–11 April 2008; pp. 1–4. [Google Scholar]
- Kawaguchi, K.; Araki, E.; Kaneda, Y. A design concept of seafloor observatory network for earthquakes and tsunamis. In Proceedings of the 2007 Symposium on Underwater Technology and Workshop on Scientific Use of Submarine Cables and Related Technologies, Tokyo, Japan, 17–20 April 2007; pp. 176–178. [Google Scholar]
- El Sharkawi, M.A.; Upadhye, A.; Lu, S.; Kirkham, H.; Howe, B.M.; McGinnis, T.; Lancaster, P. North east Pacific time-integrated undersea networked experiment (NEPTUNE): Cable switching and protection. IEEE J. Ocean. Eng. 2005, 30, 232–240. [Google Scholar] [CrossRef]
- Chan, T.; Liu, C.-C.; Howe, B.M.; Kirkham, H. Fault location for the NEPTUNE power system. IEEE Trans. Power Syst. 2007, 22, 522–531. [Google Scholar] [CrossRef]
- Barnes, C.R. Challenges, benefits, and opportunities in installing and operating cabled ocean observatories: Perspectives from NEPTUNE-Canada. IEEE J. Ocean. Eng. 2013, 38, 144–157. [Google Scholar] [CrossRef]
- Chesnoy, J. Terminal equipment. In Undersea Fiber Communication Systems, 2nd ed.; Academic Press: San Diego, CA, USA, 2016; Volume 10, pp. 237–260. [Google Scholar]
- Choi, J.K. Automated cable-laying system for thin optical-fiber submarine cable installation. IEEE J. Ocean. 2015, 40, 981–992. [Google Scholar] [CrossRef]
- Choi, J.K.; Yokobiki, T. ROV-based automated cable-laying system: Application to DONET2 installation. IEEE J. Ocean. Eng. 2017, 43, 665–676. [Google Scholar] [CrossRef]
- Asakawa, K.; Kojima, J.; Muramatsu, J.; Takada, T. Novel current to current converter for mesh-like scientific underwater cable network—Concept and preliminary test result. In Proceedings of the Oceans 2003, San Diego, CA, USA, 22–26 September 2003; pp. 1868–1873. [Google Scholar]
- Asakawa, K.; Kojima, J.; Muramatsu, J.; Takada, T.; Kawaguchi, K.; Mikada, H. Current-to-Current Converter for Scientific Underwater Cable Networks. IEEE J. Ocean. Eng. 2007, 32, 584–592. [Google Scholar] [CrossRef]
- Kawaguchi, K.; Araki, E.; Kogure, Y.; Takahashi, N.; Katayama, T.; Hishiki, K.; Fujiwara, N.; Iida, N.; Kaneda, Y. Development of DONET2—Off Kii chanel observatory network. In Proceedings of the 2013 IEEE International Underwater Technology Symposium, Tokyo, Japan, 5–8 March 2013; pp. 1–5. [Google Scholar]
- Yokobiki, T.; Choi, J.-K.; Nishida, S.; Matsumoto, H.; Araki, E.; Kawaguchi, K.; Takahashi, N.; Kodaira, S. Construction of DONET2. In Proceedings of the 2016 Techno-Ocean, Kobe, Japan, 6–8 October 2016; pp. 435–438. [Google Scholar]
- Miriem El, F.; Ziad, H. Detection of fault location, monitoring and control in underwater power system. In Proceedings of the 2013 48th International Universities’ Power Engineering Conference, Dublin, Ireland, 2–5 September 2013; pp. 1–6. [Google Scholar]
- Lv, F.; Zhou, H.; Yue, J.; He, B. Remote power monitoring and control system for cabled seafloor observatory networks. J. Tongji Univ. 2014, 42, 1725–1732. [Google Scholar]
- Zhu, J.; Lyu, F. Powering backbone devices of large-scale cabled seafloor observatories by current-to-voltage DC-DC converters. In Proceedings of the OCEANS 2018, Kobe, Japan, 28–31 May 2018; pp. 1–5. [Google Scholar]
- Feng, L.; Huaiyang, Z.; Jiguang, Y. Power system reliability of networks structure and cabled seafloor topology observatory. J. Tongji Univ. 2014, 42, 1604–1610. [Google Scholar]
- Zhu, J.; Lyu, F. A current-to-voltage DC-DC converter for powering backbone devices of scientific cabled seafloor observatories. Energies 2019, 12, 2261. [Google Scholar] [CrossRef]
- Bagchi, A.C.; Saha, T.; Kamineni, A.; Zane, R. Analysis and design of a wireless charger for underwater vehicles fed from a constant current distribution cable. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics, Padua, Italy, 25–28 June 2018; pp. 1–8. [Google Scholar]
- Wang, H.; Saha, T.; Zane, R. Design considerations for series resonant converters with constant current input. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition, Milwaukee, WI, USA, 18–22 September 2016; pp. 1–9. [Google Scholar]
- Wang, H.; Saha, T.; Riar, B.S.; Zane, R. Design considerations for current regulated series resonant converters with constant input current. IEEE Trans. Power Electr. 2018, 34, 141–150. [Google Scholar] [CrossRef]
- Orekan, T.; Zhang, P.; Shih, C. Analysis, design and maximum power efficiency tracking for undersea wireless power transfer. IEEE J. Emerg. Sel. Top. Power Electr. 2018, 6, 843–854. [Google Scholar] [CrossRef]
- Saha, T.; Wang, H.; Riar, B.; Zane, R. Analysis and design of a parallel resonant converter for constant current input to constant voltage output DC-DC converter over wide load range. In Proceedings of the 2018 International Power Electronics Conference, Niigata, Japan, 20–24 May 2018; pp. 4074–4079. [Google Scholar]
- Xuewei, P.; Rathore, A.K. Naturally clamped zero-current commutated soft-switching current-fed push–pull DC/DC converter: Analysis, design, and experimental results. IEEE Trans. Power Electr. 2015, 30, 1318–1327. [Google Scholar] [CrossRef]


| Advantages | Disadvantages | |
|---|---|---|
| Get power based on zener diode | Simple structure; easy to implement | Only suitable for small current systems; low power |
| Get power based on high-medium-low two-stage voltage transformation | Easy to implement; good research foundation; high voltage resistance; high power | Low reliability; poor standardization; poor self-healing |
| Get power based on CC–CV converters | Standardization; modularity; high reliability; self-healing; high power; easy to expand | Less research foundation; less reference prototype |
| /A | 1.500 | 1.504 | 1.503 | 1.499 | 1.503 | 1.501 | 1.500 |
| /A | 1.482 | 1.491 | 1.496 | 1.498 | 1.498 | 1.503 | 1.509 |
| /A | 1.499 | 0.998 | 0.748 | 0.509 | 0.303 | 0.199 | 0.149 |
| /V | 171.985 | 121.460 | 95.056 | 69.101 | 47.917 | 35.924 | 30.982 |
| /V | 160.013 | 109.631 | 84.373 | 57.948 | 37.952 | 27.964 | 22.868 |
| /V | 149.946 | 150.032 | 150.073 | 150.022 | 150.047 | 150.033 | 149.986 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhou, X.; Wang, X.; Wu, T. Design, Analysis, and Modeling of an Isolated Constant-Current to Constant-Voltage Converter in Cabled Underwater Information Networks. Electronics 2019, 8, 961. https://doi.org/10.3390/electronics8090961
Zhang Z, Zhou X, Wang X, Wu T. Design, Analysis, and Modeling of an Isolated Constant-Current to Constant-Voltage Converter in Cabled Underwater Information Networks. Electronics. 2019; 8(9):961. https://doi.org/10.3390/electronics8090961
Chicago/Turabian StyleZhang, Zheng, Xuejun Zhou, Xichen Wang, and Tianshu Wu. 2019. "Design, Analysis, and Modeling of an Isolated Constant-Current to Constant-Voltage Converter in Cabled Underwater Information Networks" Electronics 8, no. 9: 961. https://doi.org/10.3390/electronics8090961
APA StyleZhang, Z., Zhou, X., Wang, X., & Wu, T. (2019). Design, Analysis, and Modeling of an Isolated Constant-Current to Constant-Voltage Converter in Cabled Underwater Information Networks. Electronics, 8(9), 961. https://doi.org/10.3390/electronics8090961





