Toward a Comfortable Driving Experience for a Self-Driving Shuttle Bus
Abstract
:1. Introduction
2. Comfort Driving Criteria for Public Transit Vehicles
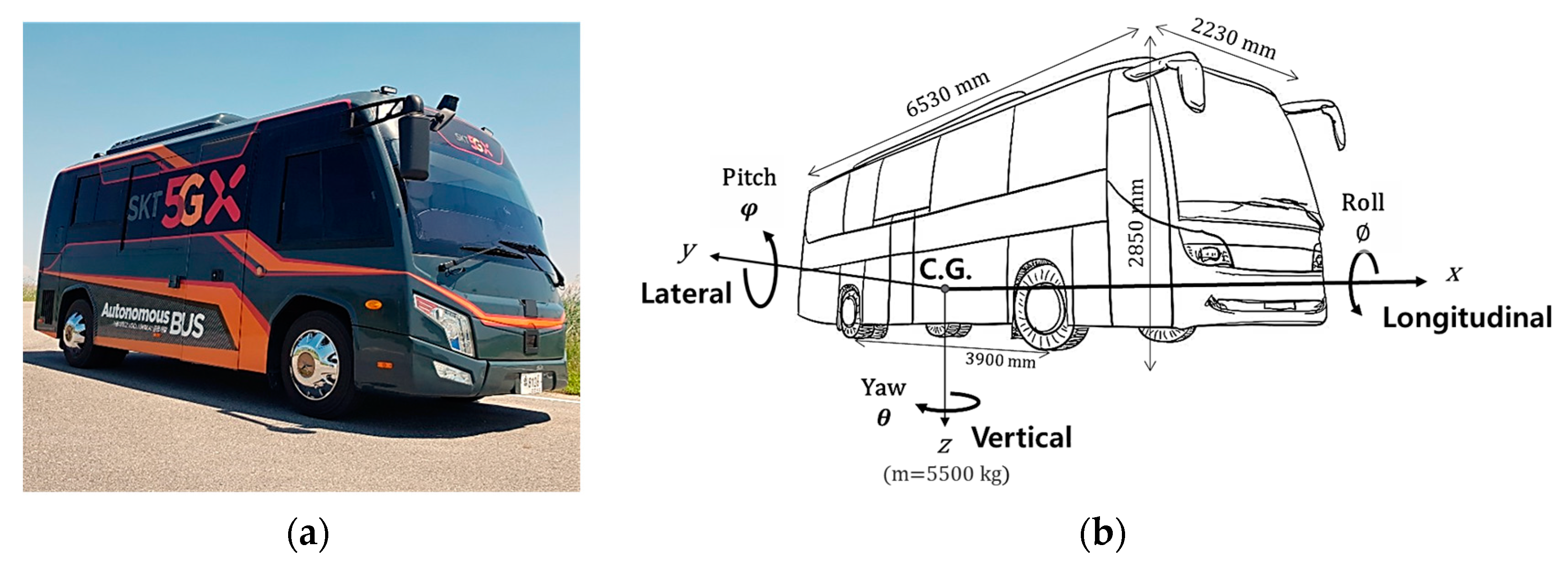
2.1. Vehicle Movements and Forces
2.2. Acceleration and Jerk Criteria for Public Transportation
3. Vehicle Kinematic Model and Controller
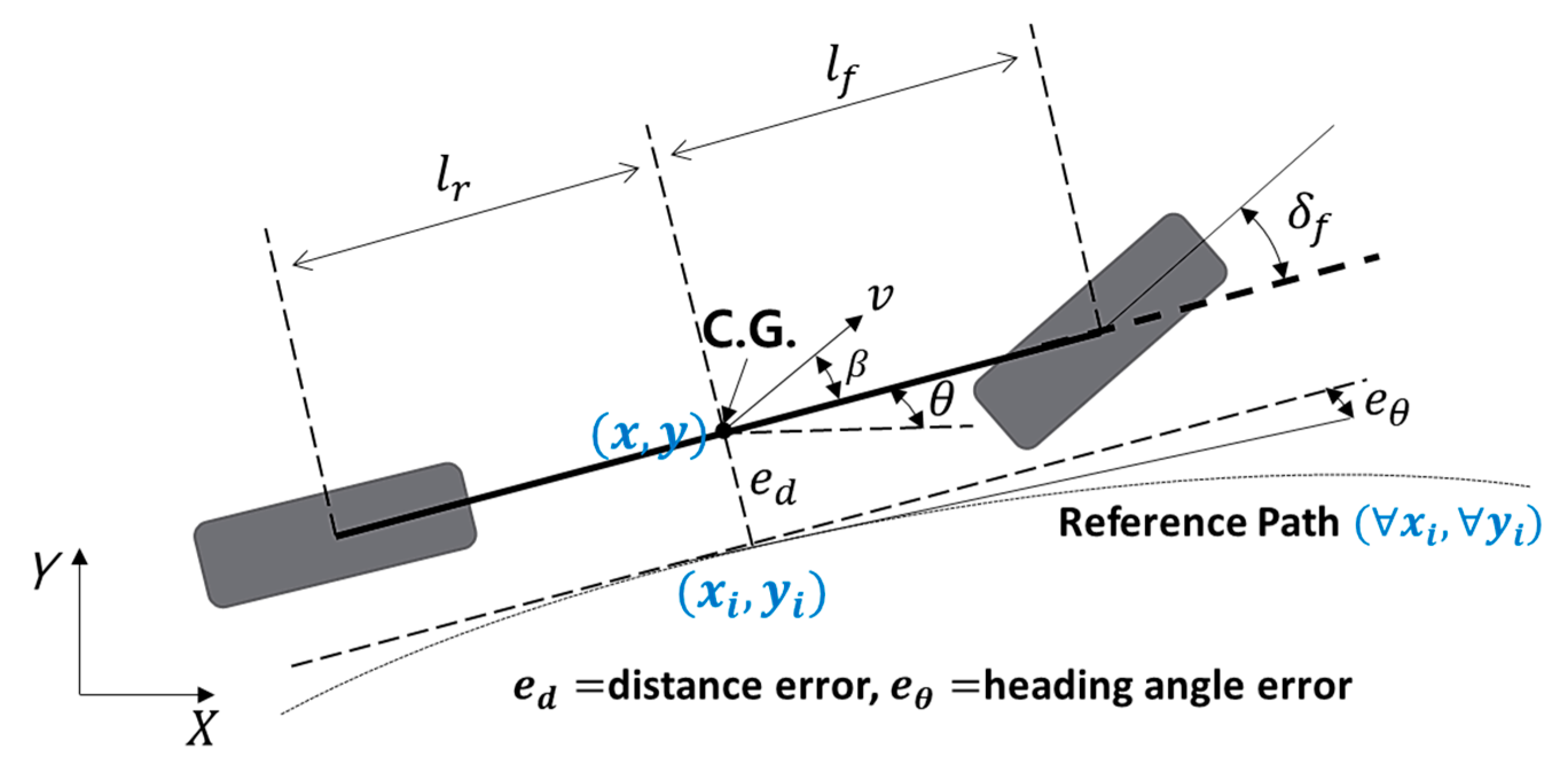
3.1. Bicycle Kinematic Model
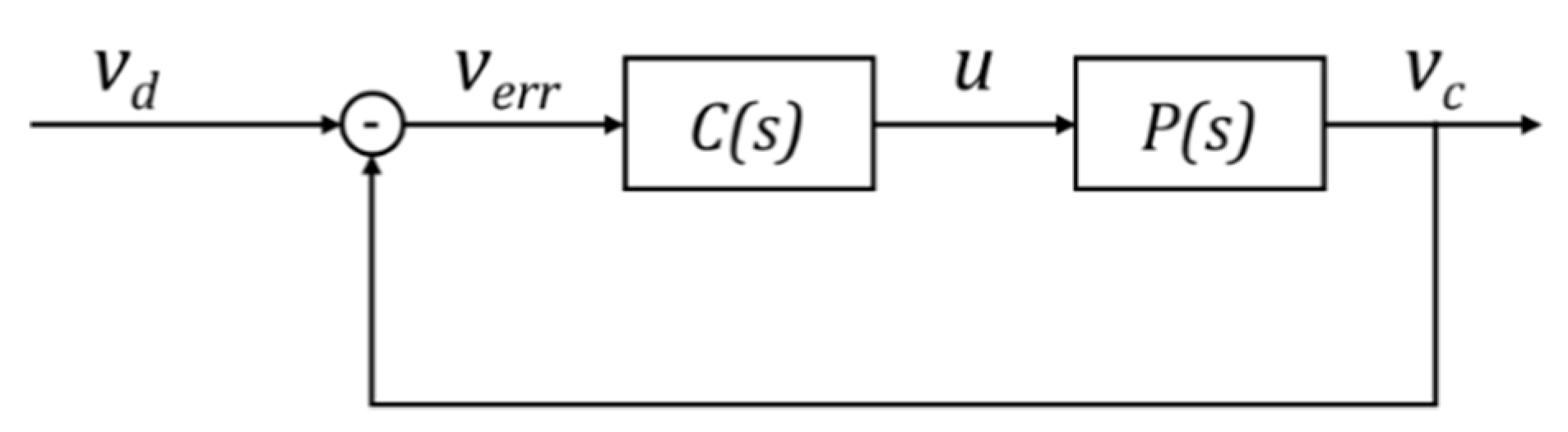
3.2. Lateral and Longitudinal Controller
4. Time-Optimal Velocity Planning for Comfort Driving
4.1. Conventional Velocity Planning Method
4.2. Proposed Velocity Optimization Method
5. Software-in-the-Loop (SIL) Simulations
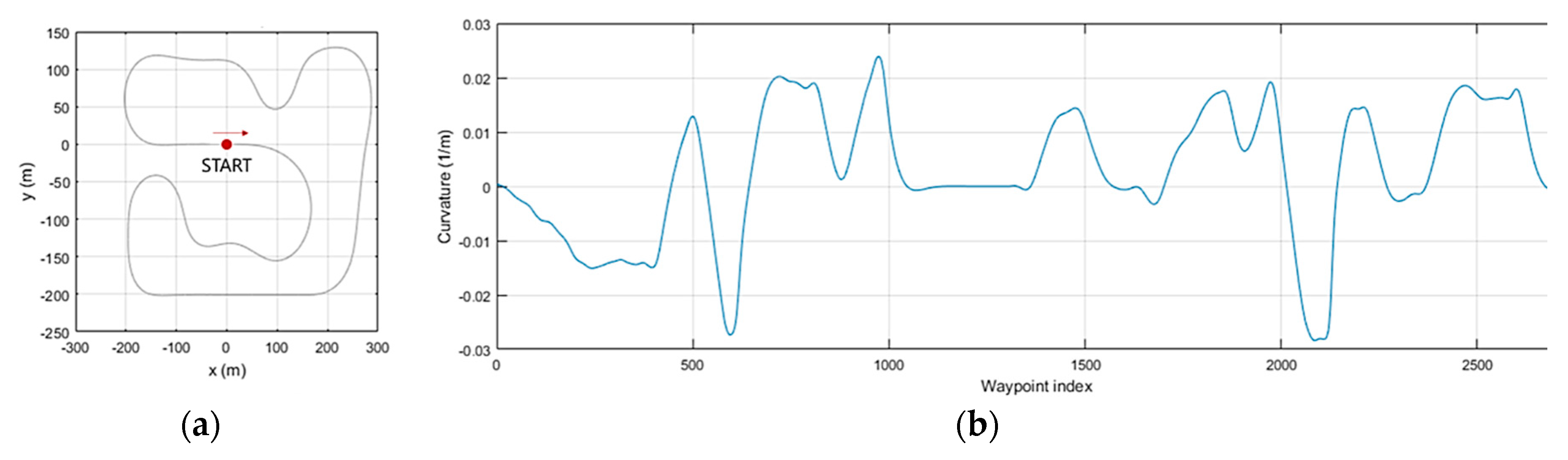
5.1. Simulation Environment
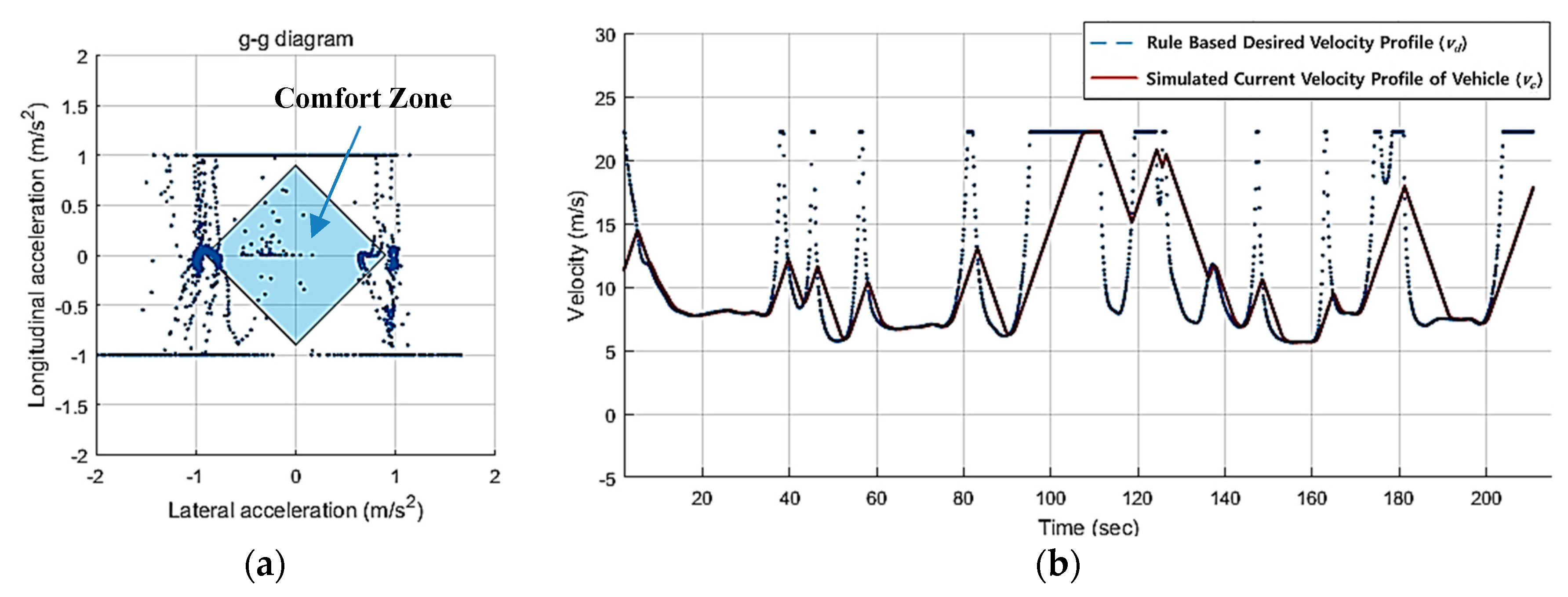
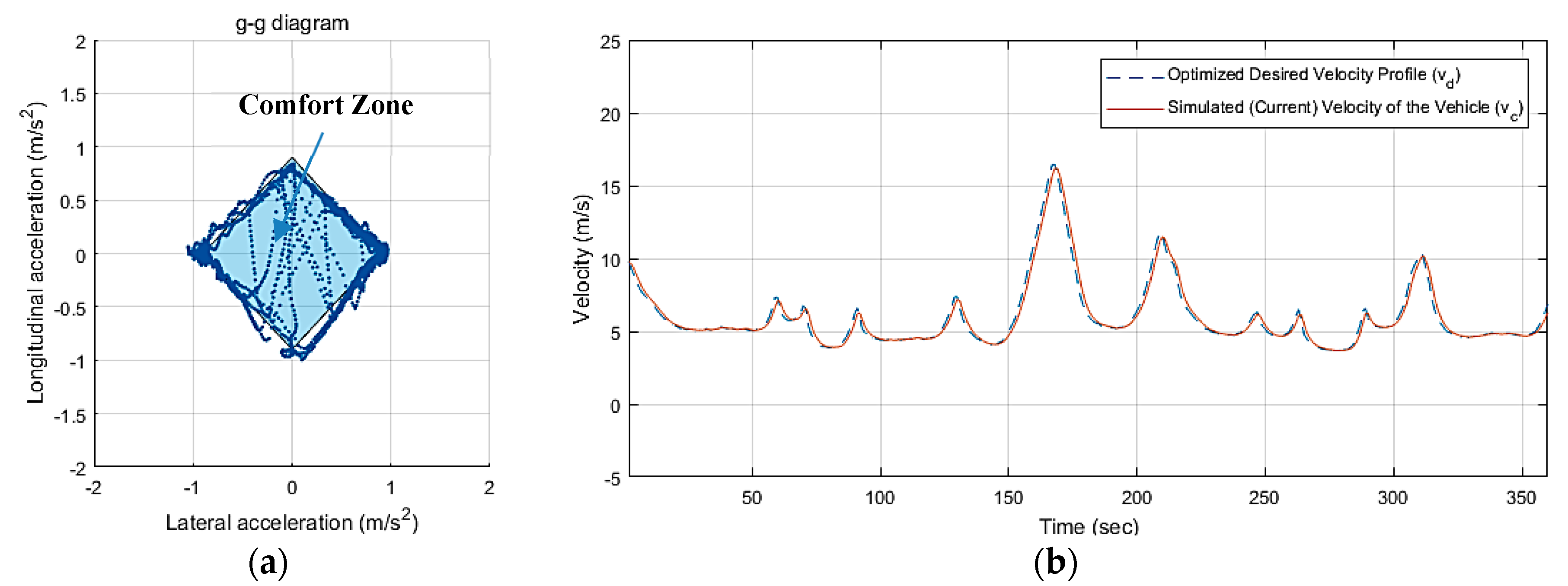
5.2. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Bojarski, M.; Del Testa, D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to end learning for self-driving cars. arXiv 2016, arXiv:1604.07316. [Google Scholar]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4, eaaw1975. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, K.W.; Yoo, W.S. Method to objectively evaluate subjective ratings of ride comfort. Int. J. Automot. Technol. 2011, 12, 831–837. [Google Scholar] [CrossRef]
- Kyriakidis, M.; de Winter, J.C.; Stanton, N.; Bellet, T.; van Arem, B.; Brookhuis, K.; Martens, M.H.; Bengler, K.; Andersson, J.; Merat, N.; et al. A human factors perspective on automated driving. Theor. Issues Ergon. Sci. 2019, 20, 223–249. [Google Scholar] [CrossRef]
- Hartwich, F.; Beggiato, M.; Krems, J.F. Driving comfort, enjoyment and acceptance of automated driving-effects of drivers’ age and driving style familiarity. Ergonomics 2018, 61, 1017–1032. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. In the Passenger Seat: Investigating Ride Comfort Measures in Autonomous Cars. IEEE Intell. Transp. Syst. Mag. 2015, 7, 4–17. [Google Scholar] [CrossRef]
- Salonen, A.; Haavisto, N. Towards Autonomous Transportation. Passengers’ Experiences, Perceptions and Feelings in a Driverless Shuttle Bus in Finland. Sustainability 2019, 11, 588. [Google Scholar] [CrossRef]
- Salonen, A.O. Passenger’s subjective traffic safety, in-vehicle security and emergency management in the driverless shuttle bus in Finland. Transp. Policy 2018, 61, 106–110. [Google Scholar] [CrossRef]
- Turner, M.; Griffin, M.J. Motion sickness in public road transport: The effect of driver, route and vehicle. Ergonomics 1999, 42, 1646–1664. [Google Scholar] [CrossRef]
- Svensson, L.; Eriksson, J. Tuning for ride quality in autonomous vehicle: Application to linear quadratic path planning algorithm. Dissertation, Uppsala University, Uppsala, Sweden, 2015. [Google Scholar]
- Diels, C. Will autonomous vehicles make us sick? In Contemporary Ergonomics and Human Factors 2014; CRC Press: Boca Raton, FL, USA, 2014; pp. 301–307. [Google Scholar]
- Park, Y.; Ha, H.-K. Analysis of the impact of high-speed railroad service on air transport demand. Transp. Res. Part E Logist. Transp. Rev. 2006, 42, 95–104. [Google Scholar] [CrossRef]
- Kilinç, A.S.; Baybura, T. Determination of minimum horizontal curve radius used in the design of transportation structures, depending on the limit value of comfort criterion lateral jerk. In Proceedings of the TS06G-Engineering Surveying, Machine Control and Guidance, Rome, Italy, 6–10 May 2012. [Google Scholar]
- Martin, D.; Litwhiler, D.H. An Investigation of acceleration and jerk profiles of public transportation vehicles. In Proceedings of the ASEE Annual Conference and Exposition, Pittsburgh, PA, USA, 22–25 June 2008. [Google Scholar]
- Fiero 2M4. Available online: http://ironduke7.tripod.com/corneringpower.htm (accessed on 1 July 2019).
- Sivak, M.; Schoettle, B. Motion Sickness in Self-Driving Vehicles; UMTRI: Ann Arbor, MI, USA, 2015. [Google Scholar]
- De Graaf, B.; Van Weperen, W. The Retention of Blance: An Exploratory Study into the Limits of Acceleration the Human Body Can Withstand without Losing Equilibrium. Hum. Factors J. Hum. Factors Ergon. Soc. 1997, 39, 111–118. [Google Scholar] [CrossRef]
- Bosetti, P.; Da Lio, M.; Saroldi, A. On the human control of vehicles: An experimental study of acceleration. Eur. Transp. Res. Rev. 2014, 6, 157–170. [Google Scholar] [CrossRef]
- Moon, S.; Yi, K. Human driving data-based design of a vehicle adaptive cruise control algorithm. Veh. Syst. Dyn. 2008, 46, 661–690. [Google Scholar] [CrossRef]
- Levison, W.H.; Campbell, J.L.; Kludt, K.; Bittner, A.C.; Potts, I.B.; Harwood, D.W.; Hutton, J.M.; Gilmore, D.K.; Howe, J.G.; Christos, J.P.; et al. Development of a Driver Vehicle Module (DVM) for the Interactive Highway Safety Design Model (IHSDM); United States Federal Highway Administration Office of Research and Technology Services: McLean, VA, USA, 2007.
- Kendall, J.; Solomon, K.A. Airbag deployment criteria: Institute of Risk & Safety Analyses. Forensic Exam. 2014. [Google Scholar]
- Sotelo, M.A. Lateral control strategy for autonomous steering of Ackerman-like vehicles. Robot. Auton. Syst. 2003, 45, 223–233. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking; Robotics Institute: Pittsburgh, PA, USA, 2009; CMU-RITR-09-08. [Google Scholar]
- Bae, I.; Kim, J.H.; Kim, S. Steering rate controller based on curvature of trajectory for autonomous driving vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gold Coast, Australia, 23–26 June 2013; pp. 1381–1386. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Jo, K.; Lee, M.; Kim, D.; Kim, J.; Jang, C.; Kim, E.; Kim, S.; Lee, D.; Kim, C.; Kim, S.; et al. Overall Reviews of Autonomous Vehicle A1—System Architecture and Algorithms. IFAC Proc. 2013, 46, 114–119. [Google Scholar] [CrossRef]
- Bae, I.; Moon, J.; Cha, J.; Kim, S. Integrated lateral and longitudinal control system for autonomous vehicles. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 406–411. [Google Scholar]
- Bosetti, P.; Da Lio, M.; Saroldi, A. On Curve Negotiation: From Driver Support to Automation. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2082–2093. [Google Scholar] [CrossRef]
- Heimer, L.R. The Common Optimization Interface for Operations Research: Promoting open-source software in the operations research community. IBM J. Res. Dev. 2003, 47, 57–66. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Fourer, R.; Gay, D.M.; Kernighan, B.W. AMPL. A Modeling Language for Mathematical Programming; Cengage: Boston, MA, USA, 2013. [Google Scholar]
- Chen, X.; Salem, M.; Das, T.; Chen, X. Real Time Software-in-the-Loop Simulation for Control Performance Validation. Simulation 2008, 84, 457–471. [Google Scholar] [CrossRef]
- Li, S.E.; Deng, K.; Li, K.; Ahn, C. Terminal sliding mode control of automated car-following system without reliance on longitudinal acceleration information. Mechatronics 2015, 30, 327–337. [Google Scholar] [CrossRef]
- Eboli, L.; Mazzulla, G.; Pungillo, G. Combining speed and acceleration to define car users’ safe or unsafe driving behaviour. Transp. Res. Part C Emerg. Technol. 2016, 68, 113–125. [Google Scholar] [CrossRef]



| Parameters | Notation | Value (Unit) |
|---|---|---|
| Initial state | 0 (km), 10 (m/s), 0 (m/s2) | |
| Terminal state | 2.4 (km), 10 (m/s), 0 (m/s2) | |
| Max. allowed speed of path | 80 (km/h) | |
| Front-C.G. distance | 2.0 (m) | |
| Rear-C.G. distance | 1.9 (m) | |
| Longitudinal acc. constraint | 0.9 (m/s2) | |
| Longitudinal de-acc. constraint | −0.9 (m/s2) | |
| Lateral acc. constraint | || | 0.9 (m/s2) |
| Longitudinal jerk constraint | || | 0.6 (m/s3) |
| Lateral jerk constraint | || | 0.6 (m/s3) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, I.; Moon, J.; Seo, J. Toward a Comfortable Driving Experience for a Self-Driving Shuttle Bus. Electronics 2019, 8, 943. https://doi.org/10.3390/electronics8090943
Bae I, Moon J, Seo J. Toward a Comfortable Driving Experience for a Self-Driving Shuttle Bus. Electronics. 2019; 8(9):943. https://doi.org/10.3390/electronics8090943
Chicago/Turabian StyleBae, Il, Jaeyoung Moon, and Jeongseok Seo. 2019. "Toward a Comfortable Driving Experience for a Self-Driving Shuttle Bus" Electronics 8, no. 9: 943. https://doi.org/10.3390/electronics8090943
APA StyleBae, I., Moon, J., & Seo, J. (2019). Toward a Comfortable Driving Experience for a Self-Driving Shuttle Bus. Electronics, 8(9), 943. https://doi.org/10.3390/electronics8090943




