ℓp-STFT: A Robust Parameter Estimator of a Frequency Hopping Signal for Impulsive Noise
Abstract
1. Introduction
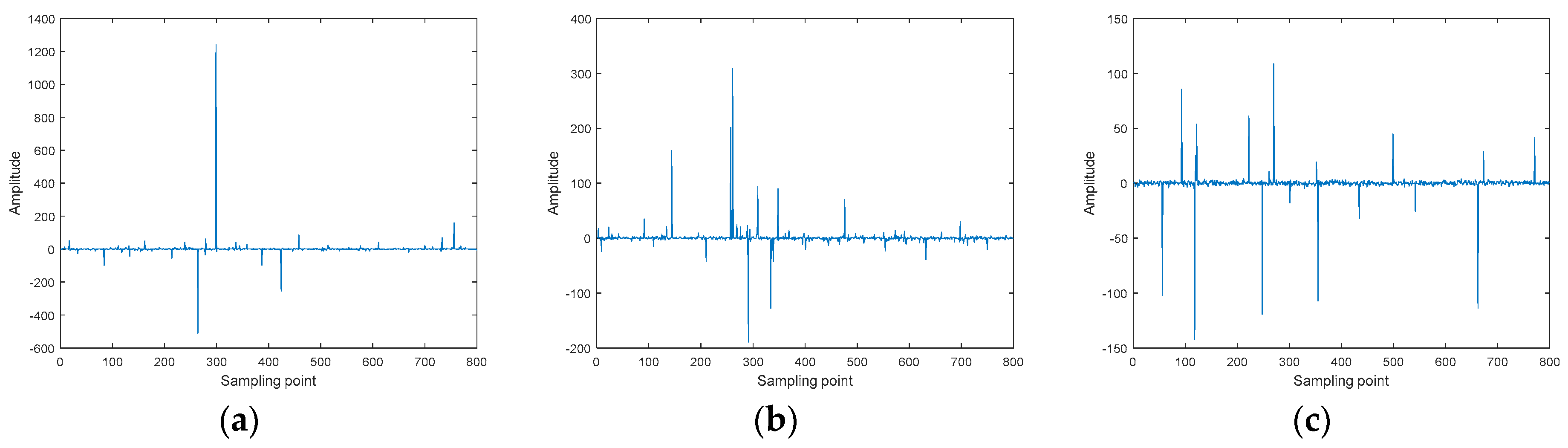
2. Impulsive Noise Distribution
3. Proposed Algorithm
3.1. Implementation of ℓp-STFT
| Algorithm 1: For ℓp-norm short-time Fourier transform (ℓp-STFT) |
| 1. Reconstruct the original signal into a signal matrix and build the STFT cost function. |
| 2. Simplify the matrix ℓp-norm optimization into sequential vector ℓp-norm optimization. |
| 3. Initialize the weighted matrix with and the estimated with . |
| 4. Compute the residual vector and use to reconstruct the weighting matrix . |
| 5. Update . |
| 6. Repeat steps 4 and 5 until to get the updated . If , stop the iteration; otherwise, go to step 4. |
| 7. Arrange the vectors into a time-frequency matrix in order. |
| 8. Construct time-frequency analysis algorithm using a ℓp-STFT spectrum matrix. |
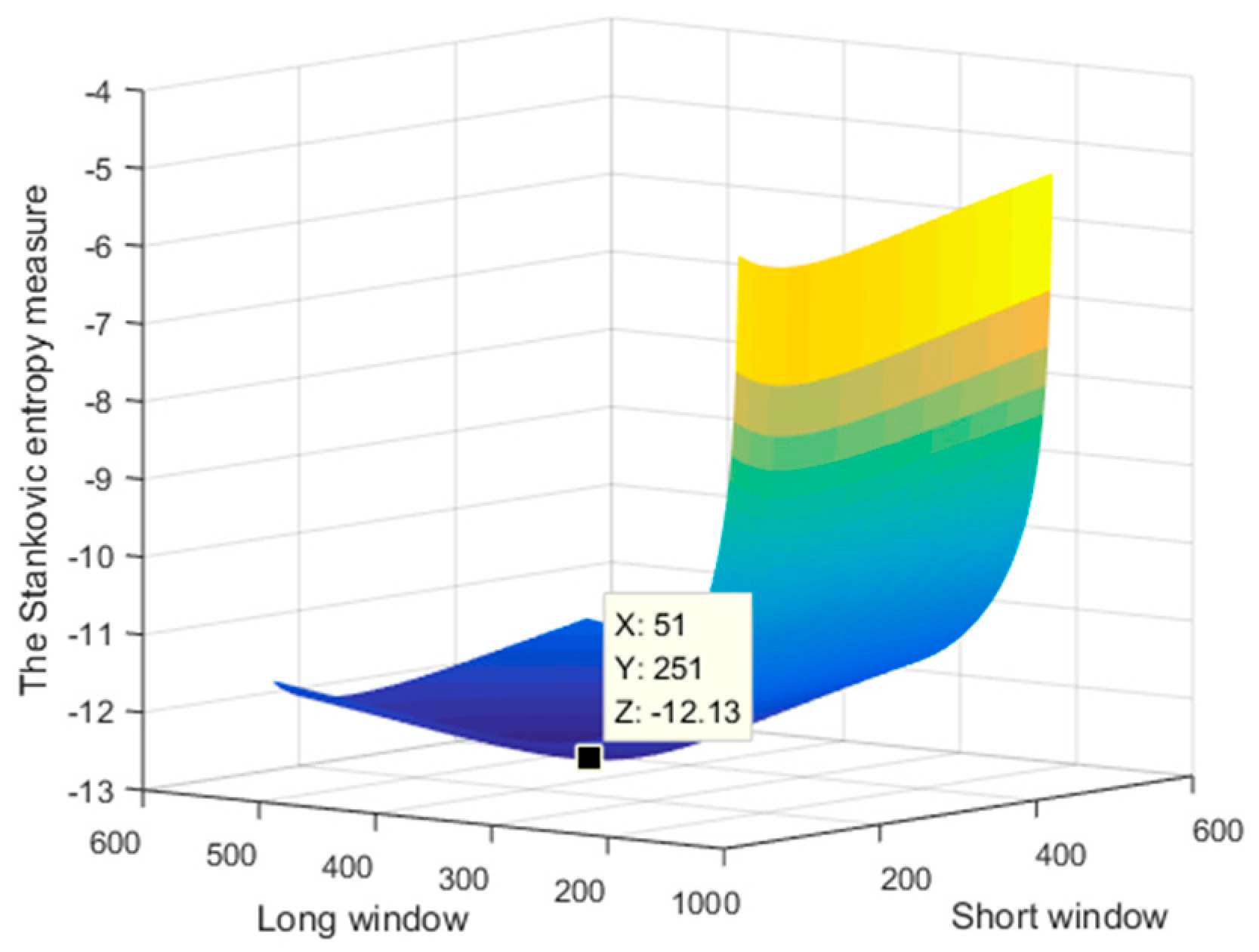
3.2. Parameter Estimation Based on ℓp-STFT
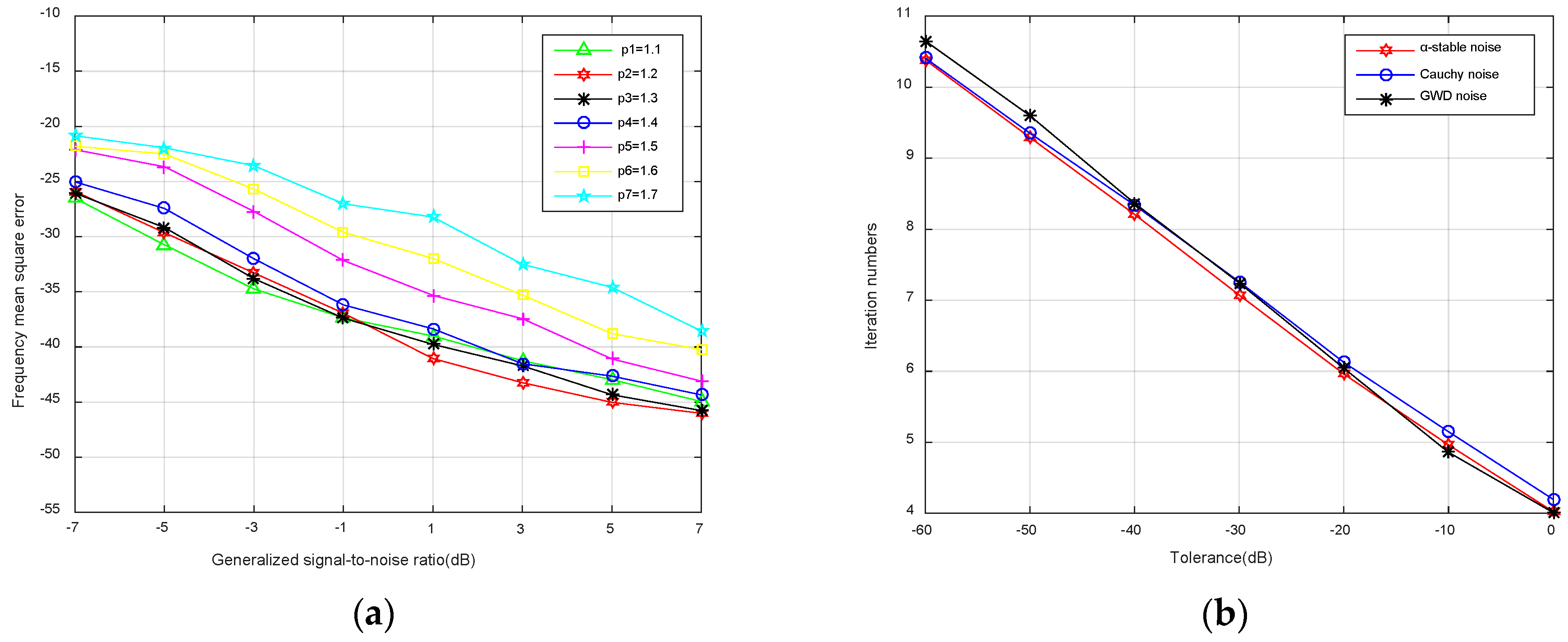
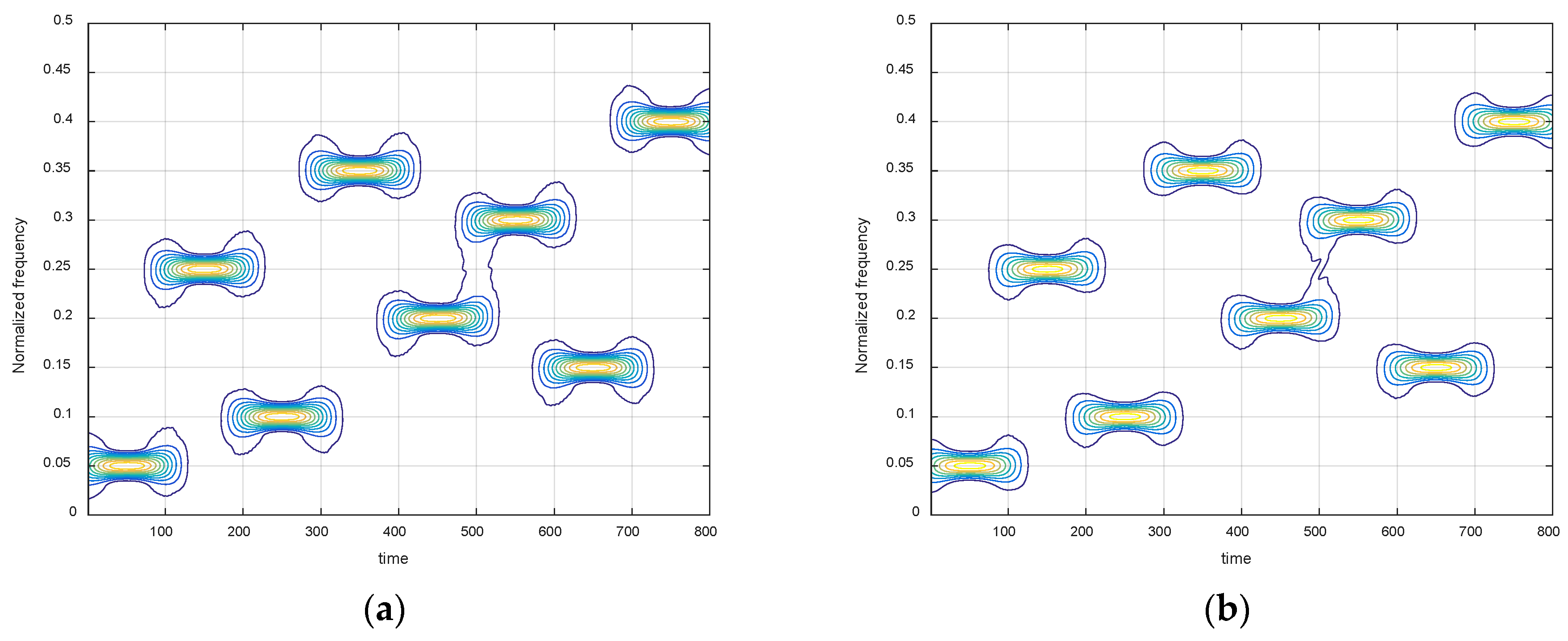
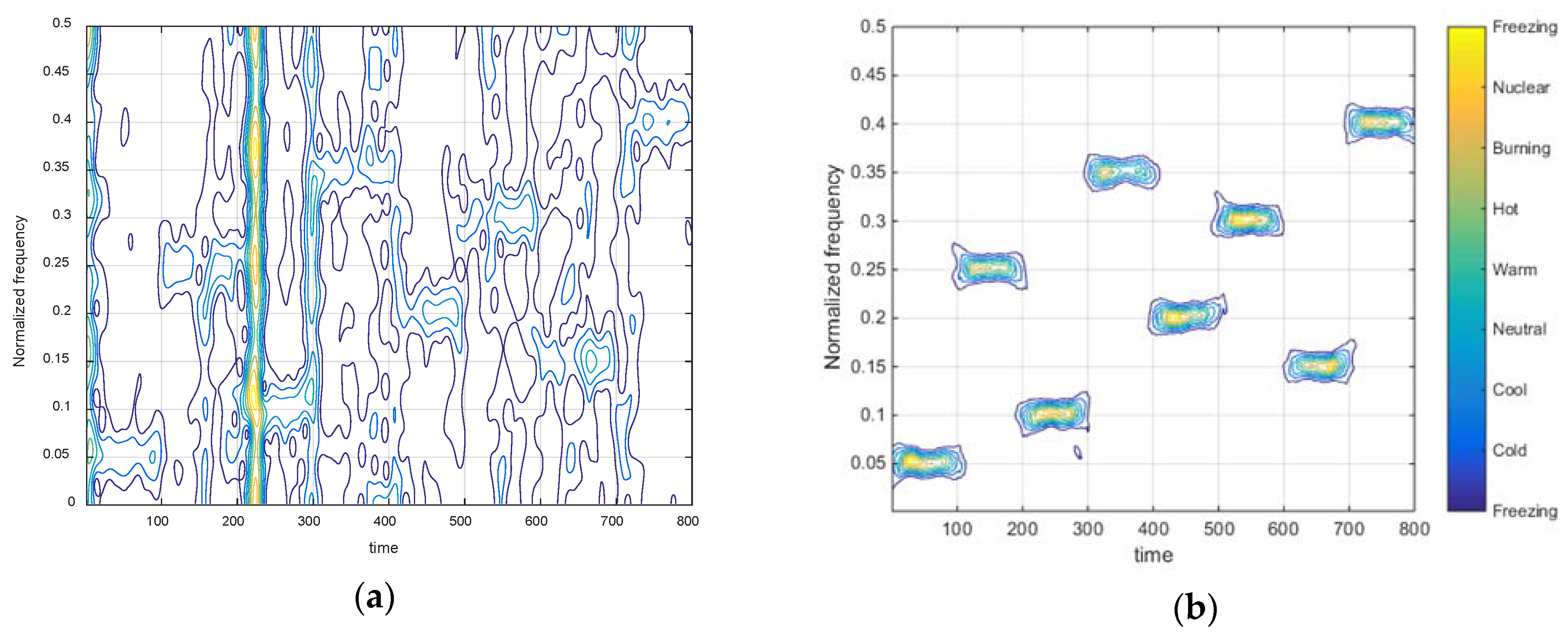
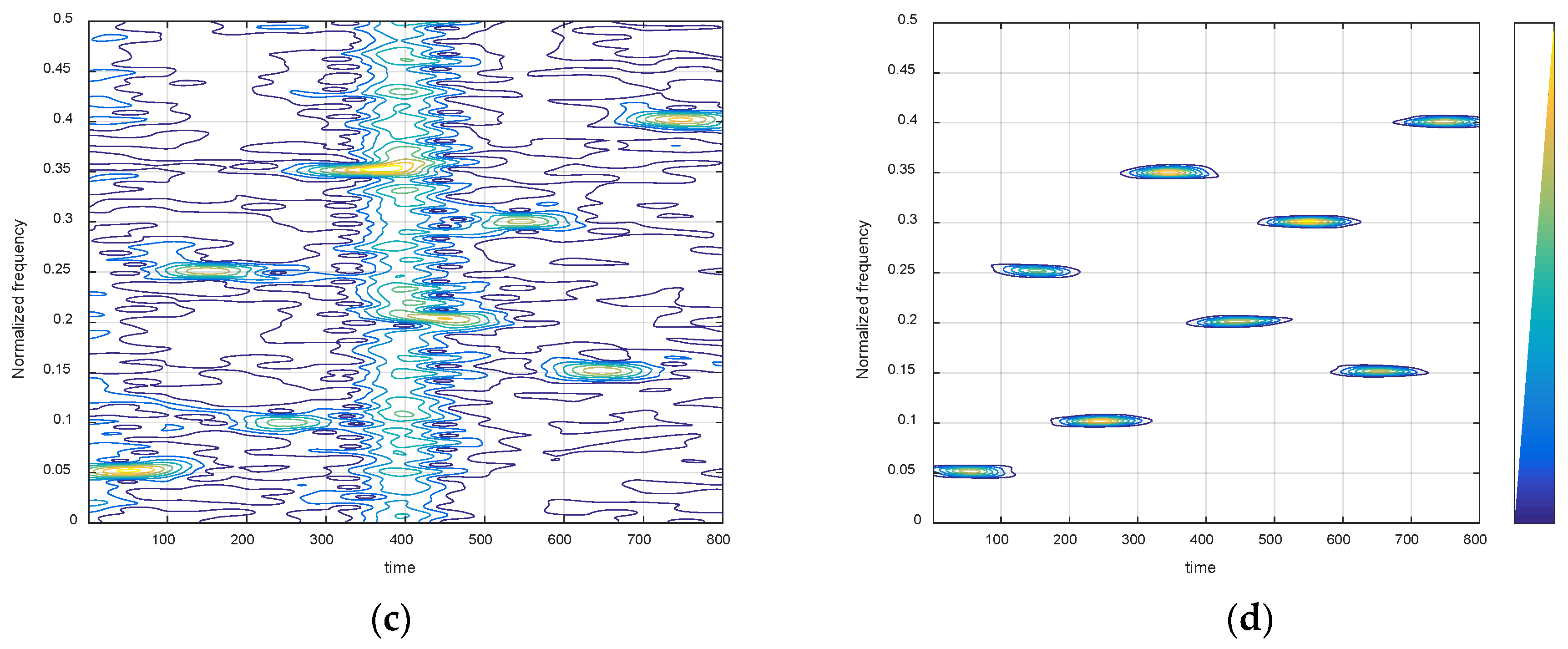
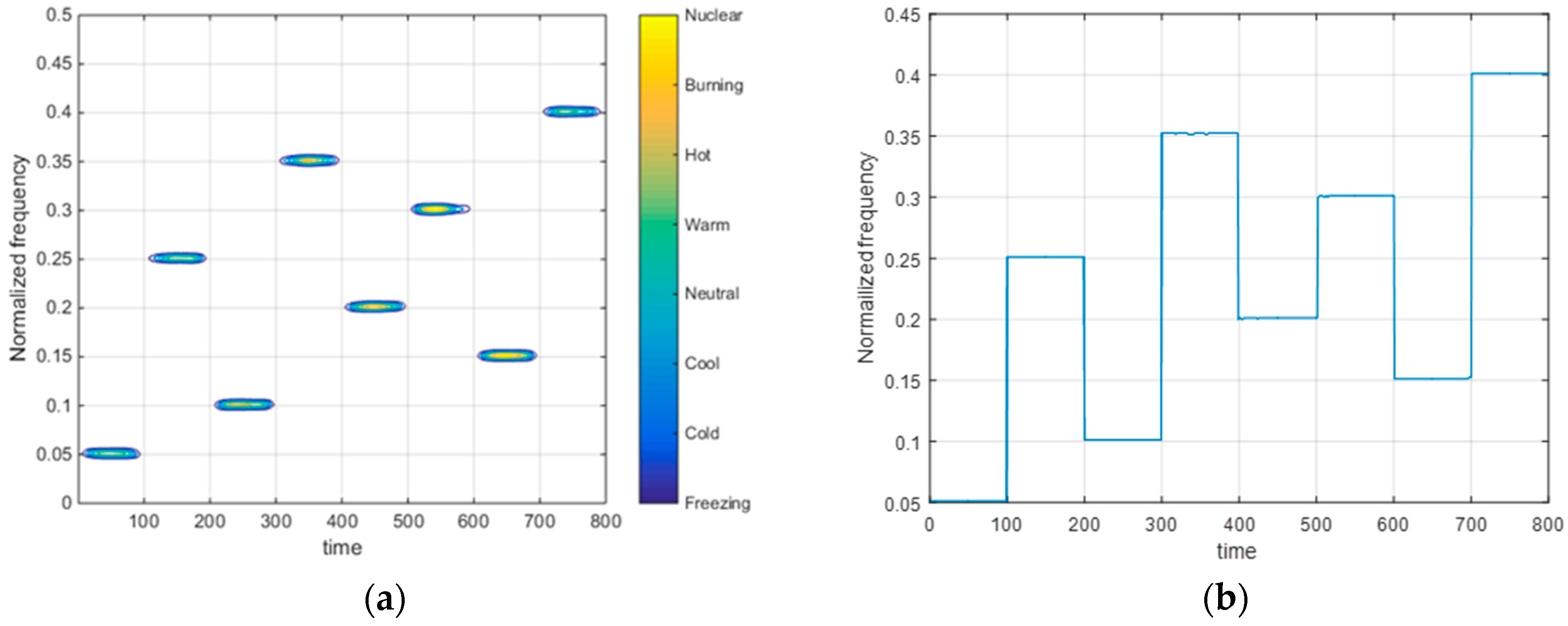
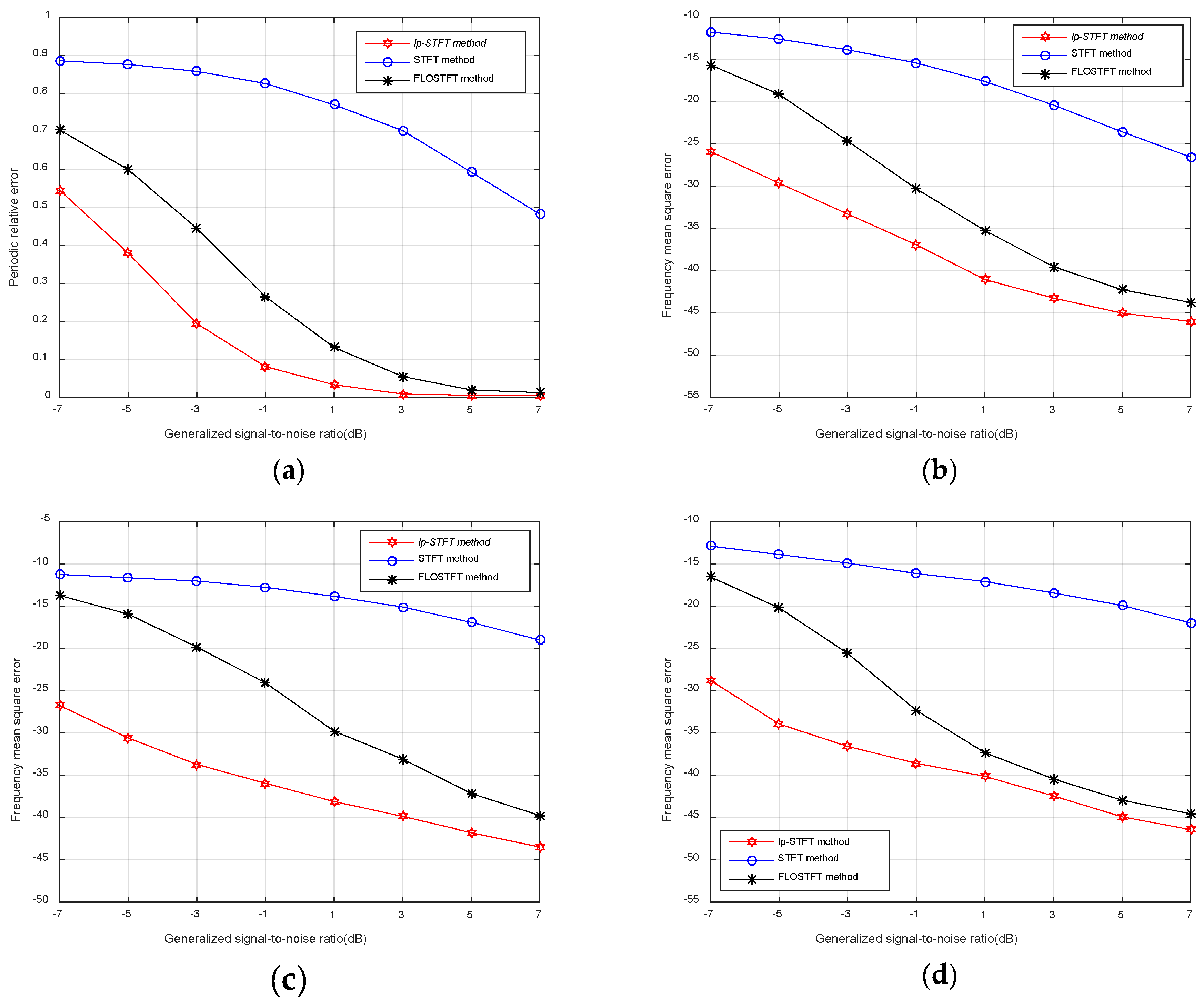
4. Simulation Result and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Jin, Y.; Liu, J. Parameter estimation of frequency hopping signals in alpha stable noise environment. In Proceedings of the International Conference on Signal Processing, Beijing, China, 21–25 October 2012; pp. 250–253. [Google Scholar]
- Fan, H.N.; Guo, Y.; Meng, Q.W. Blind parameter estimation of frequency-hopping signals based on atomic decomposition. In Proceedings of the 2009 First International Workshop on Education Technology and Computer Science, Wuhan, China, 7–8 March 2009. [Google Scholar]
- Chen, T.C. Joint signal parameter estimation of frequency-hopping communications. IET Commun. 2012, 6, 381–389. [Google Scholar] [CrossRef]
- Liu, S.H.; Zhang, Y.M. Structure-aware Bayesian compressive sensing for frequency-hopping spectrum estimation with missing observations. IEEE Trans. Signal Process. 2018, 66, 2153–2166. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, J. Parameter estimation of frequency hopping signals based on the robust S-transform algorithms in alpha stable noise environment. AEU-Int. J. Electron. Commun. 2016, 70, 611–616. [Google Scholar] [CrossRef]
- Yue, B.B.; Peng, Z.M.; He, Y.M. Impulsive noise suppression using fast Myriad filter in seismic signal processing. In Proceedings of the International Conference on Computational and Information Sciences, Shiyang, China, 21–23 June 2013. [Google Scholar]
- Amirshahi, P.; Navidpour, S.M.; Kavehrad, M. Performance analysis of uncoded and coded OFDM broadband transmission over low voltage power-line channels with impulsive noise. IEEE Trans. Power Deliv. 2006, 21, 1927–1934. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, Y.; Jian, Y. Structure-adaptive fuzzy estimation for random-valued impulse noise suppression. IEEE Trans. Circuits Syst. Video Technol. 2016, 28, 414–427. [Google Scholar]
- Tong, L.; Tang, Y.; Lv, J. Parameter estimation of FH signals based on STFT and music algorithm. In Proceedings of the International Conference on Computer Application and System Modeling, Taiyuan, China, 22–24 October 2010. [Google Scholar]
- He, Y.; Su, Y.; Chen, Y. Double window spectrogram difference method: A blind estimation of frequency-hopping signal for battlefield communication environment. In Proceedings of the Asia-Pacific Conference on Communications, Ningbo, China, 12–14 November 2018; pp. 439–443. [Google Scholar]
- Tsihrintzis, G.A.; Nikias, C.L. Performance of optimum and suboptimum receivers in the presence of impulsive noise modeled as an alpha-stable process. IEEE Trans. Commun. 1995, 43, 904–914. [Google Scholar] [CrossRef]
- Gu, G.D.; Zhang, Y.S.; Tian, B. Estimation of LFM signal’s time parameters under the alpha-stable distribution noise. In Proceedings of the IEEE Circuits and Systems International Conference on Testing and Diagnosis, Chengdu, China, 28–29 April 2009. [Google Scholar]
- Zhao, C.H.; Yang, W.C.; Cheng, B.Z. Parameter estimation of MPSK signals in alpha stable distribution noise environment. J. Shenyang Univ. Technol. 2013, 35, 194–199. [Google Scholar]
- Wierzchowski, W.; Pawełczyk, M. Median filtering approach for active control of impulsive noise. In Proceedings of the International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 2–5 September 2014. [Google Scholar]
- Ismaeil, M.; Pritamdas, K.; Devi, K.J.K. Performance analysis of new adaptive decision based median filter on FPGA for impulsive noise filtering. In Proceedings of the International Conference on Electronics, Materials Engineering and Nano-Technology, Kolkata, India, 28–29 April 2017. [Google Scholar]
- Kowalski, M. Sparse regression using mixed norms. Appl. Comput. Harmon. Anal. 2009, 27, 303–324. [Google Scholar] [CrossRef]
- Gardner, T.J.; Magnasco, M.O. Sparse time-frequency representations. Proc. Natl. Acad. Sci. USA 2006, 103, 6094–6099. [Google Scholar] [CrossRef] [PubMed]
- Ming, X.; Xu, L.; Jian, L. IAA spectral estimation: Fast implementation using the Gohberg–Semencul factorization. IEEE Trans. Signal Process. 2011, 59, 3251–3261. [Google Scholar] [CrossRef]
- Li, T.H. A nonlinear method for robust spectral analysis. IEEE Trans. Signal Process. 2010, 58, 2466–2474. [Google Scholar] [CrossRef]
- Chen, B.S.; Chen, J.M.; Shern, S.C. An ARMA robust system identification using a generalized ℓp-norm estimation algorithm. IEEE Trans. Signal Process. 1994, 42, 1063–1073. [Google Scholar] [CrossRef]
- Kuruoglu, E.E.; Fitzgerald, W.J.; Rayner, P.J.W. Nonlinear autoregressive modeling of non-Gaussian signals using l/sub p/-norm techniques. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 21–24 April 1997. [Google Scholar]
- Zhao, X.; Li, F. Sparse Bayesian compressed spectrum sensing under Gaussian mixture noise. IEEE Trans. Veh. Technol. 2018, 67, 6087–6097. [Google Scholar] [CrossRef]
- So, H.C.; Chan, Y.T.; Chen, Y. Simple formulas for bias and mean square error computation. IEEE Signal Process Mag. 2013, 30, 162–165. [Google Scholar]
- Lai, M.J.; Xu, Y.; Yin, W. Improved iteratively reweighted least squares for unconstrained smoothed ℓp minimization. Siam J. Numer. Anal. 2013, 51, 927–957. [Google Scholar] [CrossRef]
- Wen, F.; Liu, W. Iteratively reweighted optimum linear regression in the presence of generalized Gaussian noise. In Proceedings of the IEEE International Conference on Digital Signal Processing, Beijing, China, 16–18 October 2016. [Google Scholar]
- Zeng, W.J.; So, H.C.; Huang, L. ℓp-MUSIC: Robust direction-of-arrival estimator for impulsive noise environments. IEEE Trans. Signal Process. 2013, 61, 4296–4308. [Google Scholar] [CrossRef]
- Li, L.; Nicolas, H.; Shi, X.F. Joint Estimation of Doppler Stretch and Time Delay of Wideband Echoes for LFM Pulse Radar Based on Sigmoid-FRFT Transform under the Impulsive Noise Environment. Electronics 2019, 8, 121. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Wang, L.; Chen, Y.; Yang, X. ℓp-STFT: A Robust Parameter Estimator of a Frequency Hopping Signal for Impulsive Noise. Electronics 2019, 8, 1017. https://doi.org/10.3390/electronics8091017
Su Y, Wang L, Chen Y, Yang X. ℓp-STFT: A Robust Parameter Estimator of a Frequency Hopping Signal for Impulsive Noise. Electronics. 2019; 8(9):1017. https://doi.org/10.3390/electronics8091017
Chicago/Turabian StyleSu, Yang, Lina Wang, Yuan Chen, and Xiaolong Yang. 2019. "ℓp-STFT: A Robust Parameter Estimator of a Frequency Hopping Signal for Impulsive Noise" Electronics 8, no. 9: 1017. https://doi.org/10.3390/electronics8091017
APA StyleSu, Y., Wang, L., Chen, Y., & Yang, X. (2019). ℓp-STFT: A Robust Parameter Estimator of a Frequency Hopping Signal for Impulsive Noise. Electronics, 8(9), 1017. https://doi.org/10.3390/electronics8091017



