Energy Optimization for Software-Defined Data Center Networks Based on Flow Allocation Strategies
Abstract
1. Introduction
- We formulate SD-DCN energy consumption optimization problem as an Integer Linear Programming (ILP) model. Besides, we propose three different flow scheduling strategies to improve the QoS satisfaction ratio;
- We propose a strategy-based Minimum Energy Consumption (MEC) heuristic algorithm to ensure the QoS satisfaction ratio in the process of energy optimization;
- We evaluate and discuss the strategy-based heuristic algorithm in terms of effectiveness.
2. Related Work
3. Network Model and Problem Formulation
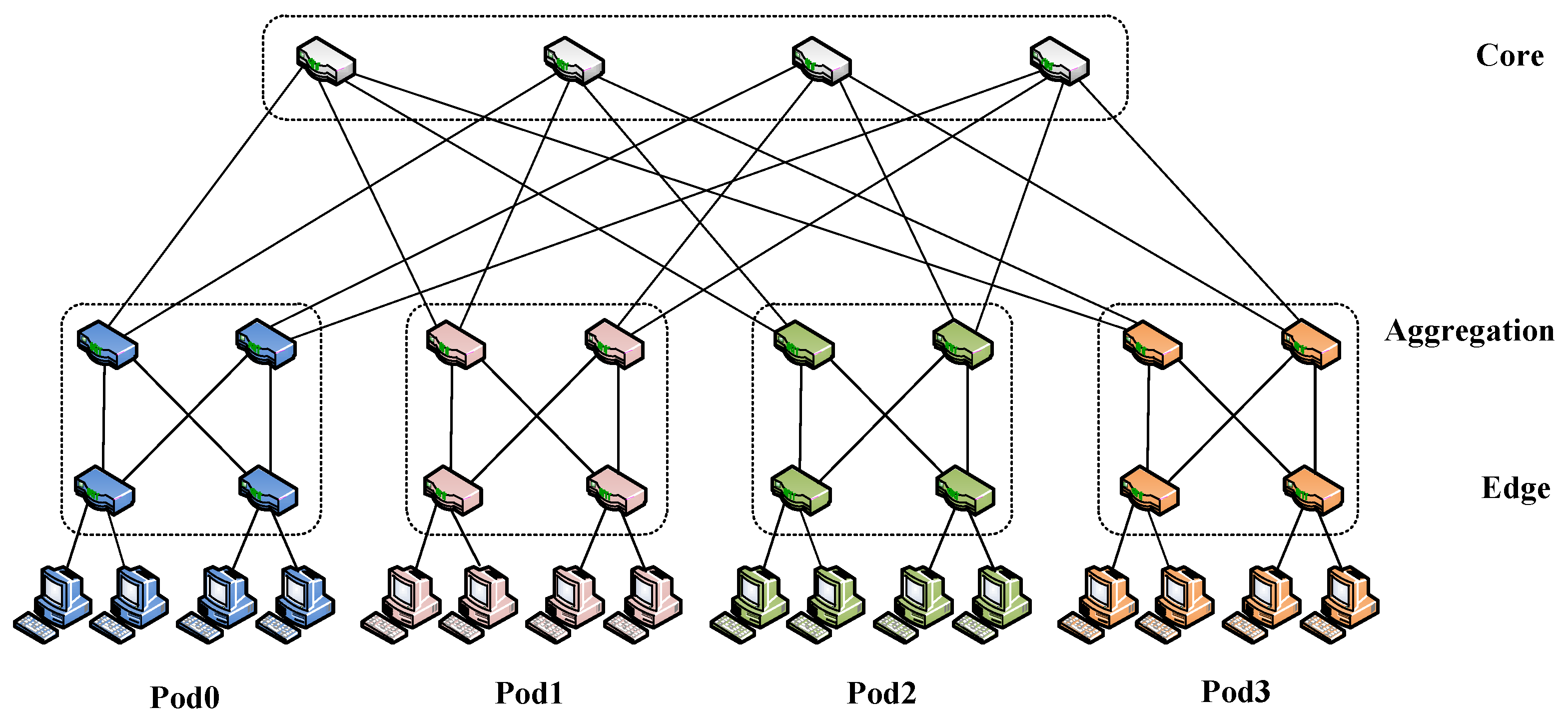
3.1. Network Model
3.2. Problem Formulation
4. Algorithm Design
| Algorithm 1 Strategy-based Minimum Energy Consumption Heuristic Algorithm | |
| Input: graph , TCAM size C, link capacity B, flow demand F | |
| Output: activated link set , activated switch set , flow path set | |
| 1: | Find candidate path information to candidatePath |
| 2: | Initialize: fPath = ∅, aSwitch= ∅, and aLink = ∅ |
| 3: | demand = sortFlowDemand(strategy, F) |
| 4: | for all in demand do |
| 5: | search the candidate path set pathX for from candidatePath |
| 6: | while do |
| 7: | for p in pathX do |
| 8: | |
| 9: | activePower[i] = getNewlyActivePower(G, p) |
| 10: | |
| 11: | end for |
| 12: | |
| 13: | |
| 14: | obtain path and path |
| 15: | if or then |
| 16: | candidatePath = candidatePath \ {path} |
| 17: | continue |
| 18: | end if |
| 19: | if then |
| 20: | |
| 21: | else |
| 22: | |
| 23: | end if |
| 24: | Let , , and update link capacity and TCAM size) |
| 25: | end while |
| 26: | end for |
5. Performance Evaluation
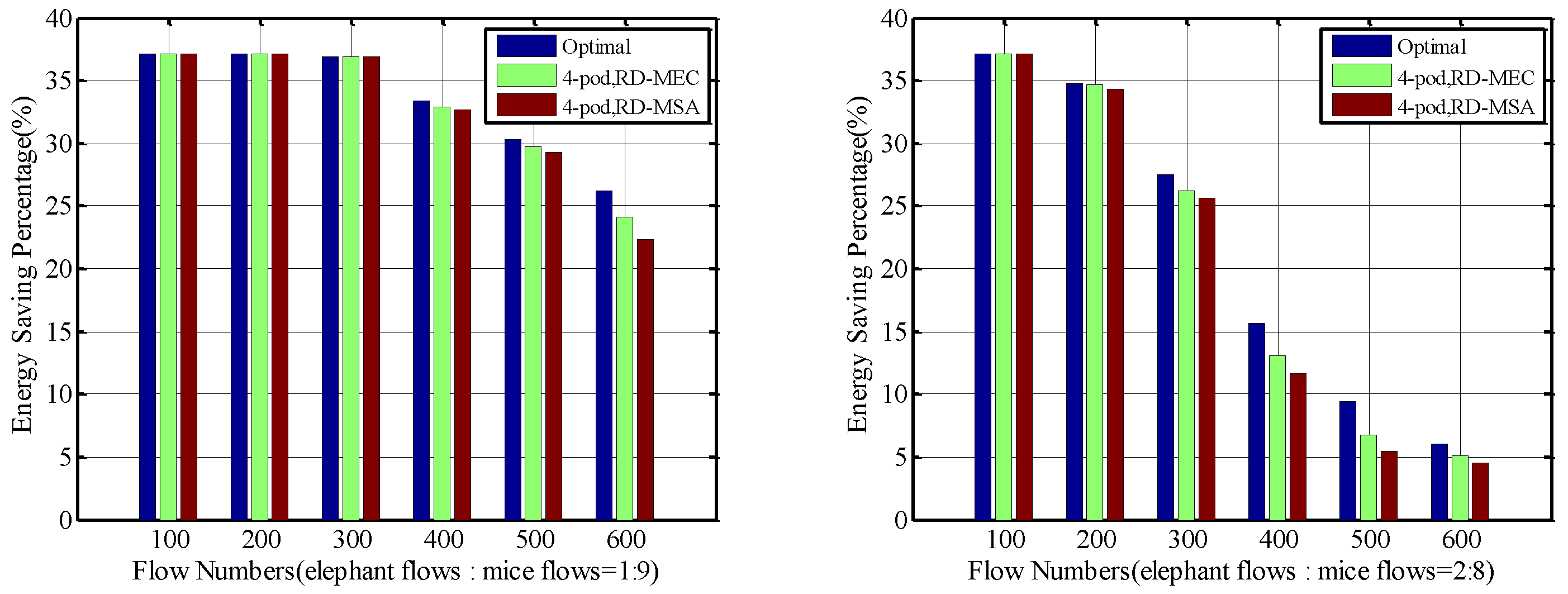
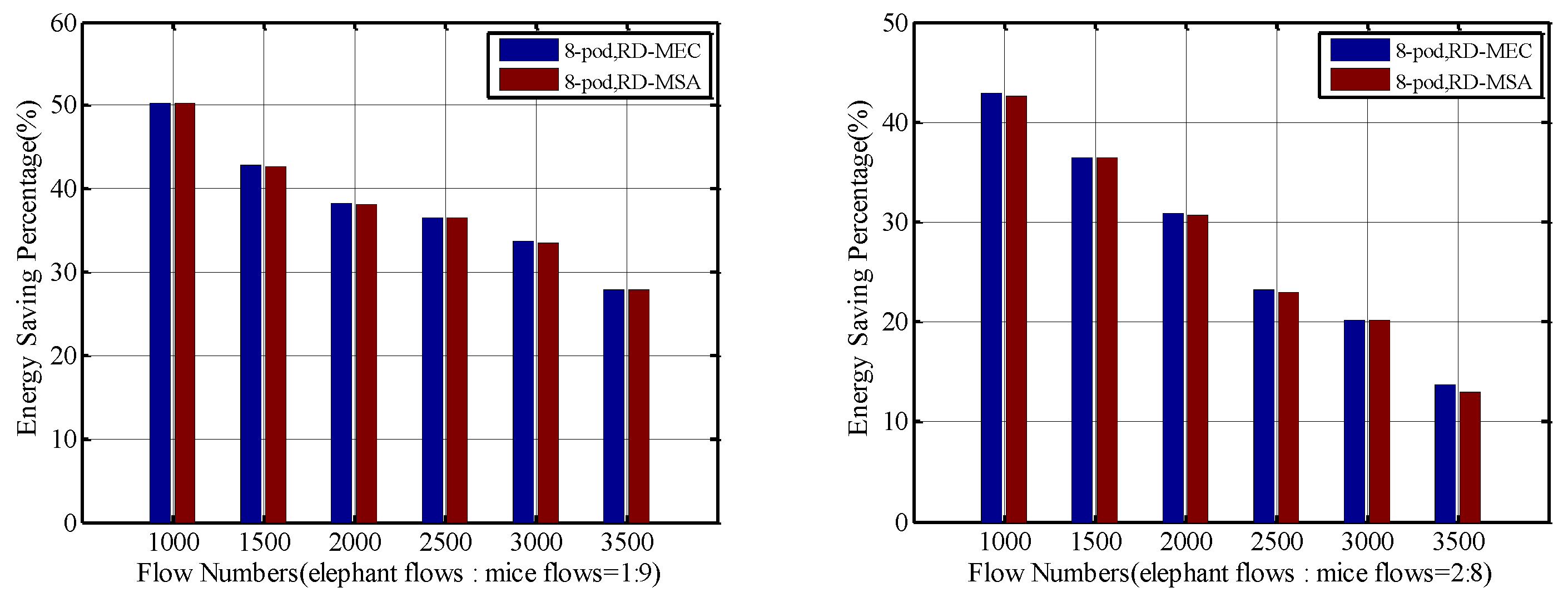
5.1. Energy Savings
5.2. QoS Satisfaction Ratio
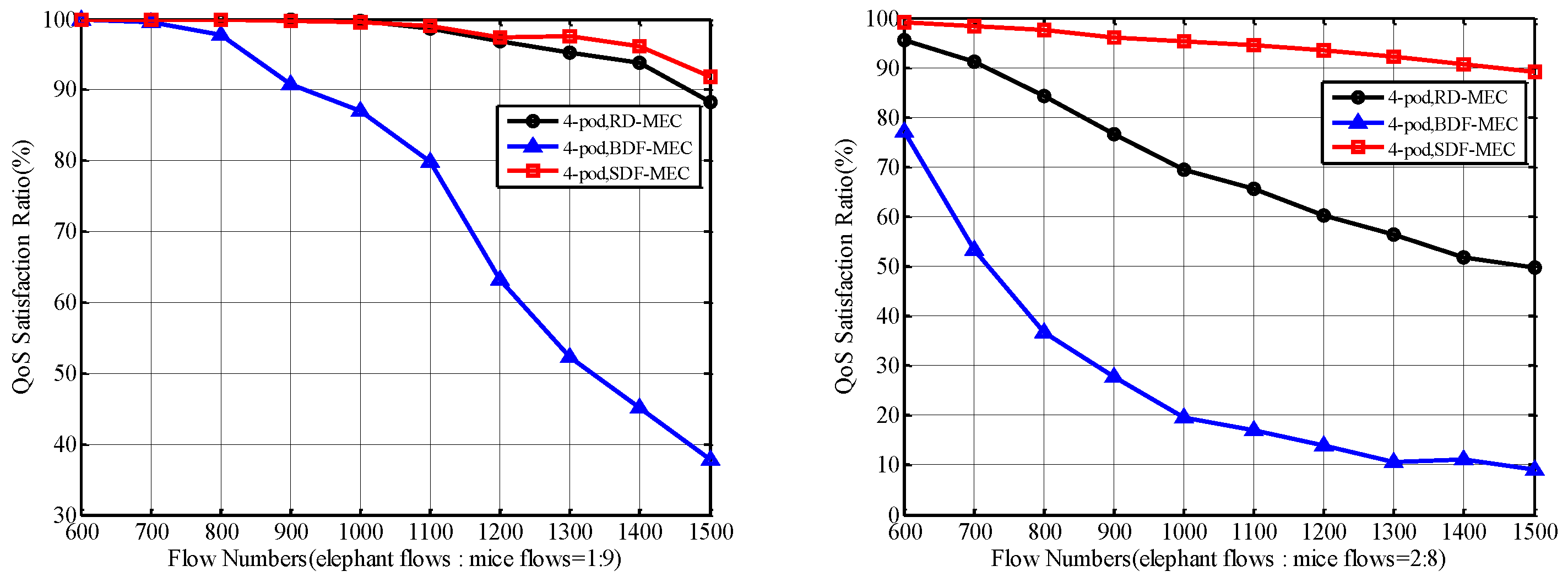
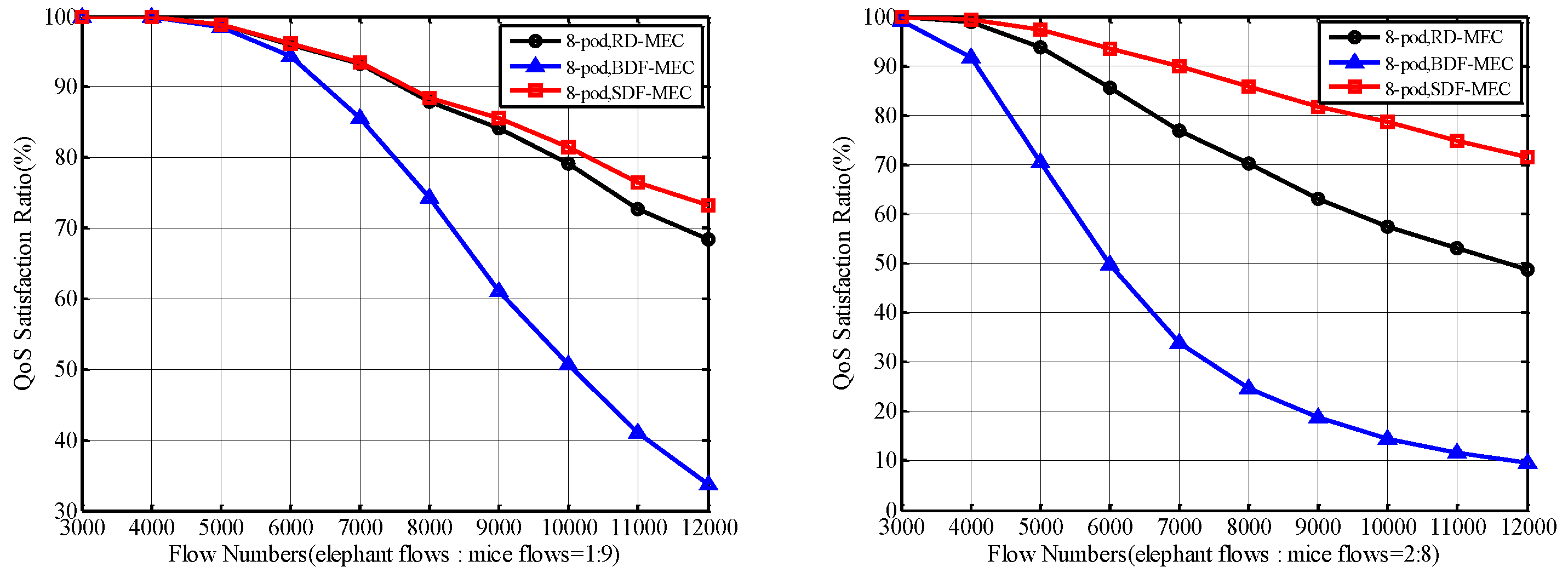
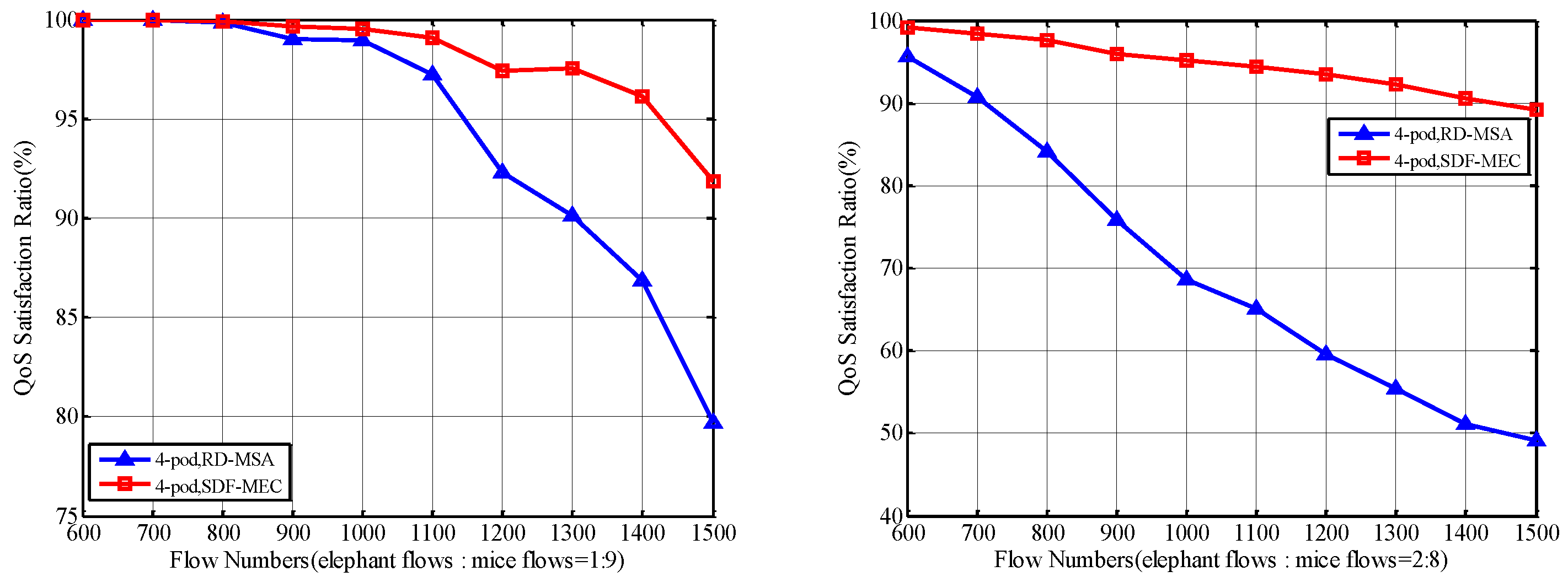
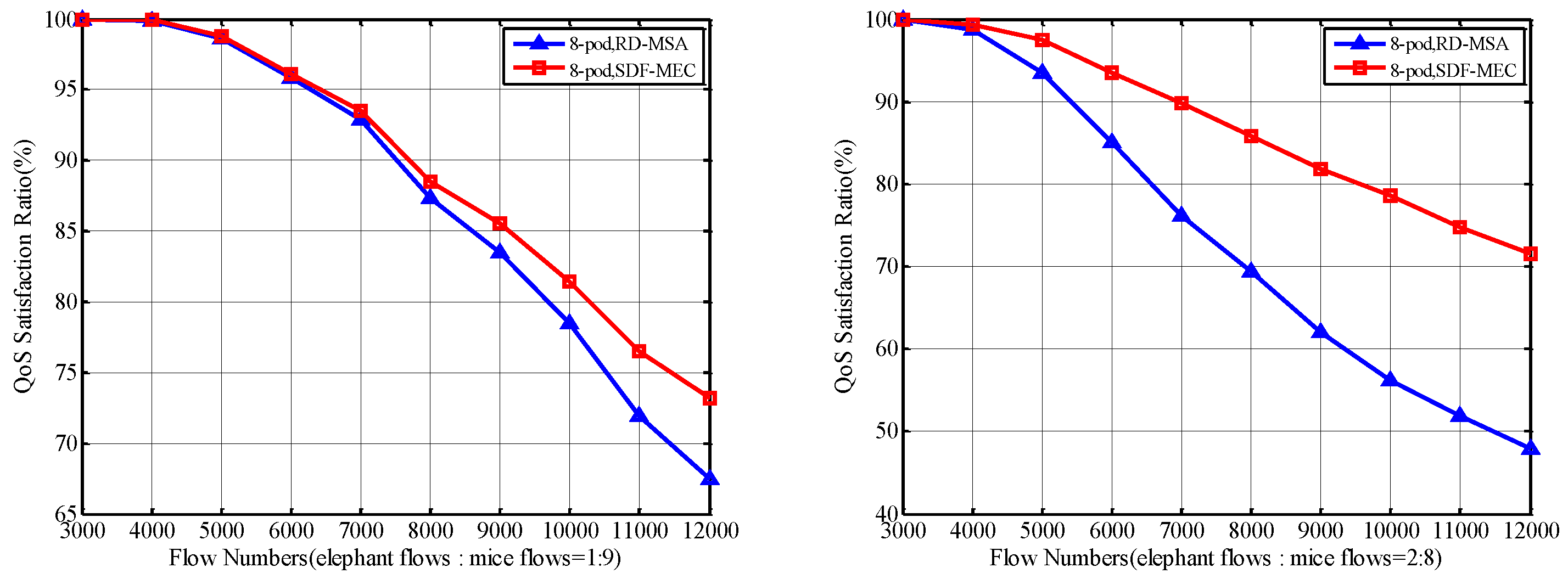
5.2.1. QoS Satisfaction Ratio of Total Flows
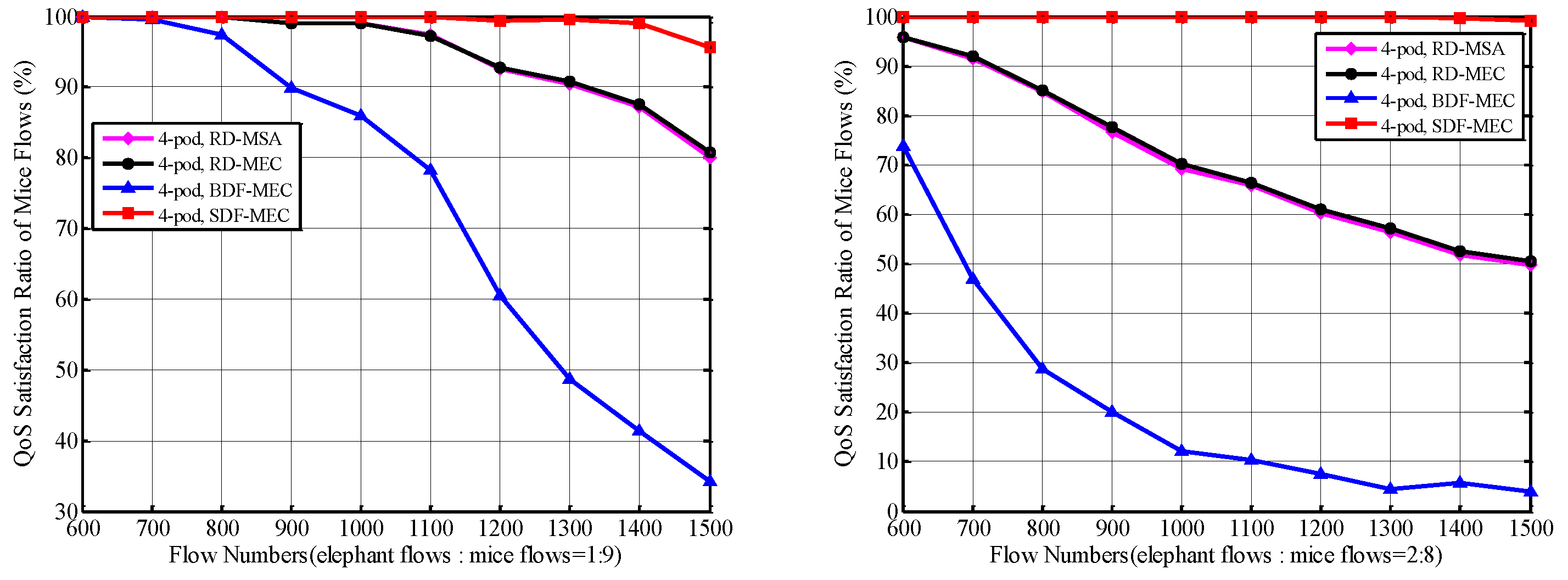
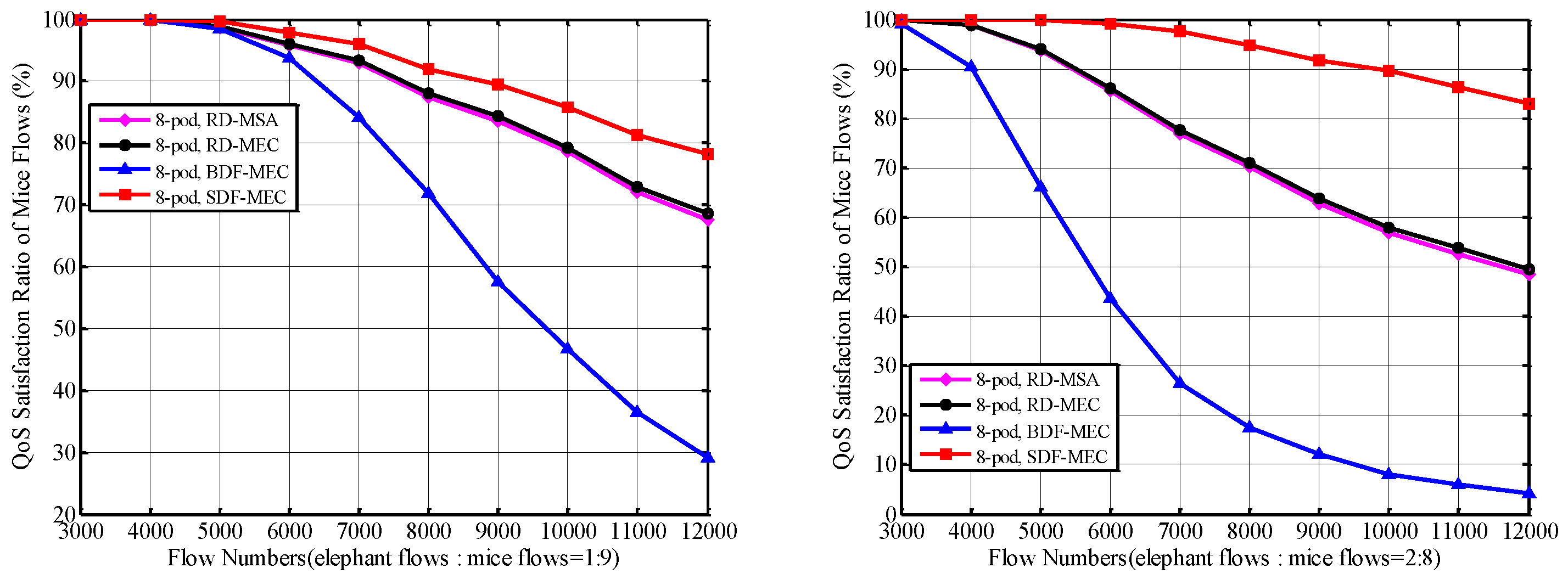
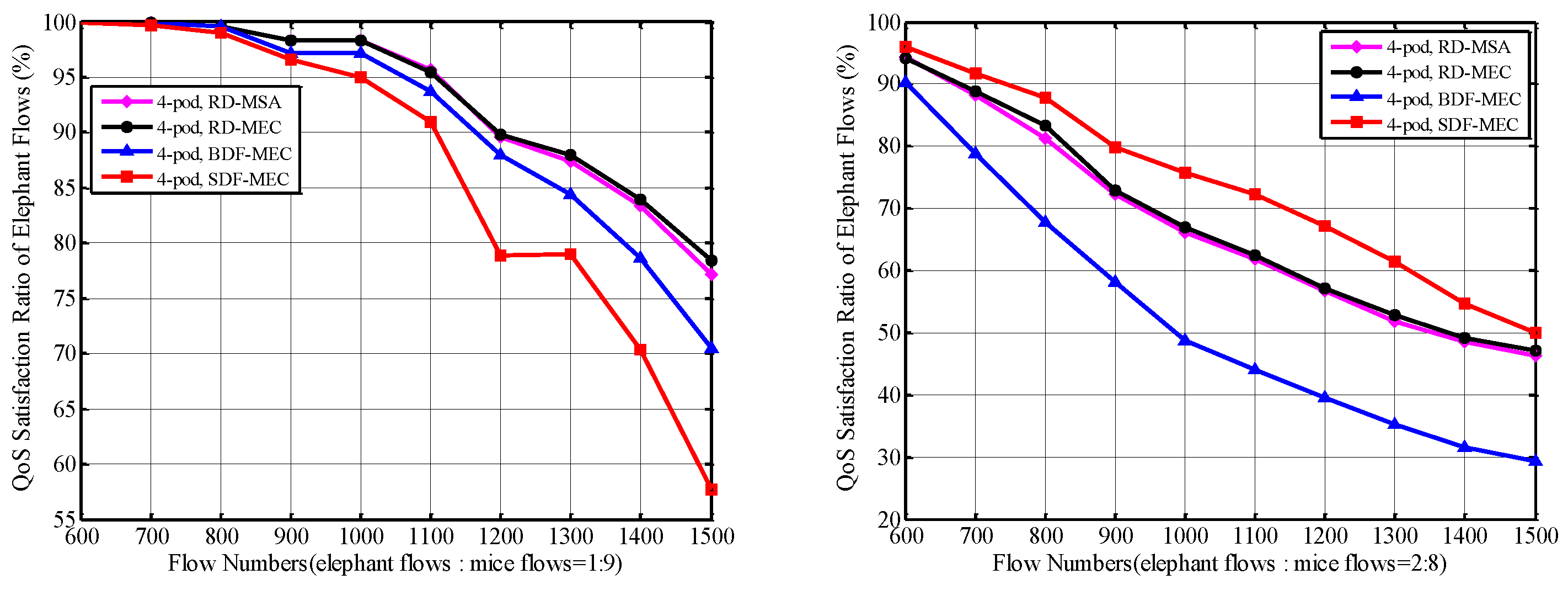
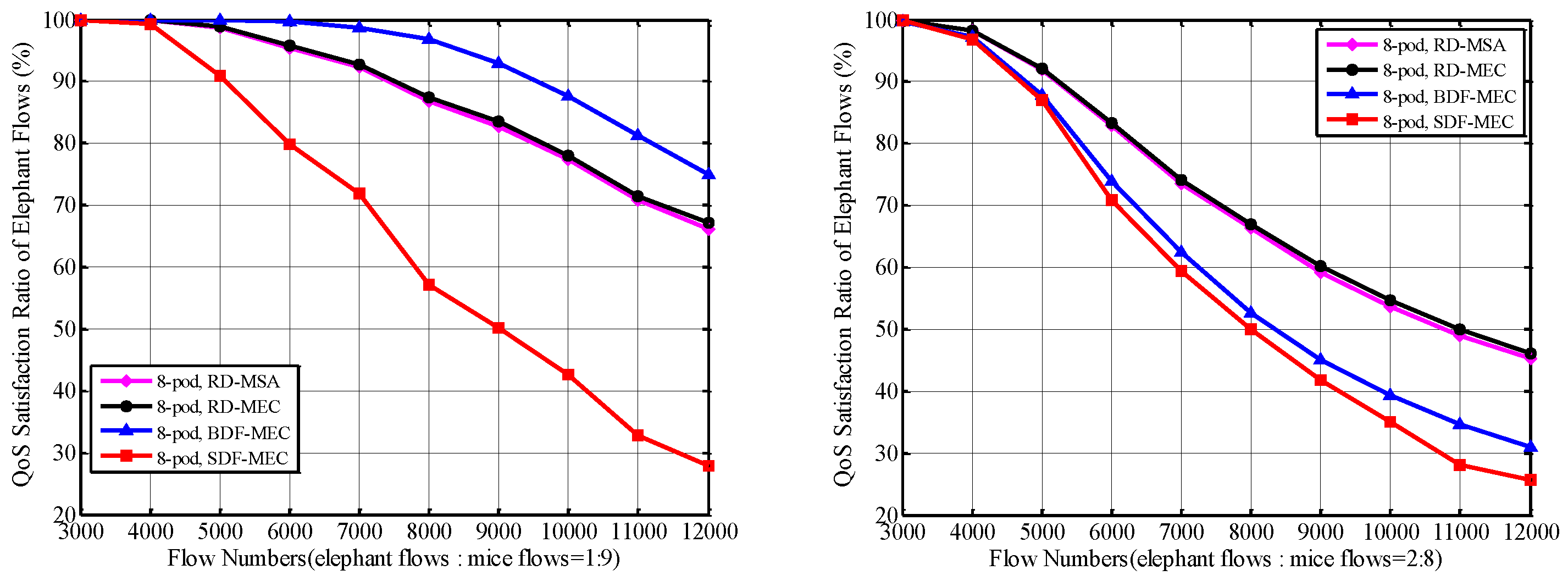
5.2.2. QoS Satisfaction Ratio of Mice Flows and Elephant Flows
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koomey, J. Growth in Data Center Electricity Use 2005 to 2010; Technical Report; Analytics Press: El Dorado Hills, CA, USA, 2011. [Google Scholar]
- Gao, P.X.; Curtis, A.R.; Wong, B.; Keshav, S. It’s not easy being green. ACM SIGCOMM Comput. Commun. Rev. 2012, 42, 211–222. [Google Scholar] [CrossRef]
- Abts, D.; Marty, M.R.; Wells, P.M.; Klausler, P.; Liu, H. Energy proportional datacenter networks. ACM SIGARCH Comput. Archit. News 2010, 38, 338–347. [Google Scholar] [CrossRef]
- Al-Fares, M.; Loukissas, A.; Vahdat, A. A scalable, commodity data center network architecture. ACM SIGCOMM Comput. Commun. Rev. 2008, 38, 63–74. [Google Scholar] [CrossRef]
- Greenberg, A.; Hamilton, J.R.; Jain, N.; Kandula, S.; Kim, C.; Lahiri, P.; Maltz, D.A.; Patel, P.; Sengupta, S. VL2: A scalable and flexible data center network. ACM SIGCOMM Comput. Commun. Rev. 2009, 39, 51–62. [Google Scholar] [CrossRef]
- Guo, C.; Wu, H.; Tan, K.; Shi, L.; Zhang, Y.; Lu, S. Dcell: A scalable and fault-tolerant network structure for data centers. ACM SIGCOMM Comput. Commun. Rev. 2008, 38, 75–86. [Google Scholar] [CrossRef]
- Guo, C.; Lu, G.; Li, D.; Wu, H.; Zhang, X.; Shi, Y.; Tian, C.; Zhang, Y.; Lu, S. BCube: A high performance, server-centric network architecture for modular data centers. ACM SIGCOMM Comput. Commun. Rev. 2009, 39, 63–74. [Google Scholar] [CrossRef]
- McKeown, N.; Anderson, T.; Balakrishnan, H.; Parulkar, G.; Peterson, L.; Rexford, J.; Shenker, S.; Turner, J. OpenFlow: Enabling innovation in campus networks. ACM SIGCOMM Comput. Commun. Rev. 2008, 38, 69–74. [Google Scholar] [CrossRef]
- Hu, C.; Yang, J.; Gong, Z.; Deng, S.; Zhao, H. DesktopDC: Setting all programmable data center networking testbed on desk. ACM SIGCOMM Comput. Commun. Rev. 2014, 44, 593–594. [Google Scholar] [CrossRef]
- Gao, X.; Xu, Z.; Wang, H.; Li, L.; Wang, X. Reduced Cooling Redundancy: A New Security Vulnerability in a Hot Data Center; NDSS: New York, NY, USA, 2018. [Google Scholar]
- Tu, R.; Wang, X.; Yang, Y. Energy-saving model for SDN data centers. J. Supercomput. 2014, 70, 1477–1495. [Google Scholar] [CrossRef]
- Yoon, M.S.; Kamal, A.E. Power minimization in fat-tree SDN datacenter operation. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–7. [Google Scholar]
- Wei, M.; Zhou, J.; Gao, Y. Energy efficient routing algorithm of software defined data center network. In Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou, China, 6–8 May 2017; pp. 171–176. [Google Scholar]
- Zeng, D.; Yang, G.; Gu, L.; Guo, S.; Yao, H. Joint optimization on switch activation and flow routing towards energy efficient software defined data center networks. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Lorenz, D.H.; Orda, A. Optimal partition of QoS requirements on unicast paths and multicast trees. IEEE/ACM Trans. Netw. 2002, 10, 102–114. [Google Scholar] [CrossRef]
- Korkmaz, T.; Krunz, M. A randomized algorithm for finding a path subject to multiple QoS requirements. Comput. Netw. 2001, 36, 251–268. [Google Scholar] [CrossRef]
- Chen, S.; Nahrstedt, K. Distributed quality-of-service routing in ad hoc networks. IEEE J. Sel. Areas Commun. 1999, 17, 1488–1505. [Google Scholar] [CrossRef]
- Gong, S.; Chen, J.; Kang, Q.; Meng, Q.; Zhu, Q.; Zhao, S. An efficient and coordinated mapping algorithm in virtualized SDN networks. Front. Inf. Technol. Electron. Eng. 2016, 17, 701–716. [Google Scholar] [CrossRef]
- Orda, A.; Sprintson, A. Precomputation schemes for QoS routing. IEEE/ACM Trans. Netw. 2003, 11, 578–591. [Google Scholar] [CrossRef]
- Lorenz, D.H.; Orda, A.; Raz, D. Optimal partition of QoS requirements for many-to-many connections. In Proceedings of the IEEE INFOCOM 2003 Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No. 03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 3, pp. 1670–1679. [Google Scholar]
- Lorenz, D.H.; Orda, A. QoS routing in networks with uncertain parameters. IEEE/ACM Trans. Netw. 1998, 6, 768–778. [Google Scholar] [CrossRef]
- Orda, A.; Sprintson, A. A scalable approach to the partition of QoS requirements in unicast and multicast. IEEE/ACM Trans. Netw. 2005, 13, 1146–1159. [Google Scholar] [CrossRef]
- Wang, Z.; Crowcroft, J. Quality-of-service routing for supporting multimedia applications. IEEE J. Sel. Areas Commun. 1996, 14, 1228–1234. [Google Scholar] [CrossRef]
- Xu, G.; Dai, B.; Huang, B.; Yang, J.; Wen, S. Bandwidth-aware energy efficient flow scheduling with SDN in data center networks. Future Gener. Comput. Syst. 2017, 68, 163–174. [Google Scholar] [CrossRef]
- Heller, B.; Seetharaman, S.; Mahadevan, P.; Yiakoumis, Y.; Sharma, P.; Banerjee, S.; McKeown, N. Elastictree: Saving energy in data center networks. In Proceedings of the 7th USENIX Symposium on Networked Systems Design and Implementation (NSDI), San Jose, CA, USA, 28–30 April 2010; Volume 10, pp. 249–264. [Google Scholar]
- Jiang, H.P.; Chuck, D.; Chen, W.M. Energy-aware data center networks. J. Netw. Comput. Appl. 2016, 68, 80–89. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zheng, K.; Yao, Y.; Cao, Q. Correlation-aware traffic consolidation for power optimization of data center networks. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 992–1006. [Google Scholar] [CrossRef]
- Li, D.; Shang, Y.; He, W.; Chen, C. EXR: Greening data center network with software defined exclusive routing. IEEE Trans. Comput. 2015, 64, 2534–2544. [Google Scholar] [CrossRef]
- Huang, H.; Li, P.; Guo, S.; Ye, B. The joint optimization of rules allocation and traffic engineering in software defined network. In Proceedings of the 2014 IEEE 22nd International Symposium of Quality of Service (IWQoS), Hong Kong, China, 26–27 May 2014; pp. 141–146. [Google Scholar]
- Wang, T.; Qin, B.; Su, Z.; Xia, Y.; Hamdi, M.; Foufou, S.; Hamila, R. Towards bandwidth guaranteed energy efficient data center networking. J. Cloud Comput. 2015, 4, 9. [Google Scholar] [CrossRef]
- Gao, X.; Gu, Z.; Kayaalp, M.; Pendarakis, D.; Wang, H. ContainerLeaks: Emerging security threats of information leakages in container clouds. In Proceedings of the 2017 47th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Denver, CO, USA, 26–29 June 2017; pp. 237–248. [Google Scholar]
- IBM ILOG CPLEX Optimization Studio. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 10 September 2019).
- Gurobi Optimizer Inc. Gurobi Optimizer Reference Manual. 2015. Available online: http://www.gurobi.com (accessed on 10 September 2019).
- Zhu, H.; Liao, X.; de Laat, C.; Grosso, P. Joint flow routing-scheduling for energy efficient software defined data center networks: A prototype of energy-aware network management platform. J. Netw. Comput. Appl. 2016, 63, 110–124. [Google Scholar] [CrossRef]
- Guo, L.; Matta, I. The war between mice and elephants. In Proceedings of the Ninth International Conference on Network Protocols, Riverside, CA, USA, 11–14 November 2001; pp. 180–188. [Google Scholar]
- Curtis, A.R.; Mogul, J.C.; Tourrilhes, J.; Yalagandula, P.; Sharma, P.; Banerjee, S. DevoFlow: Scaling flow management for high-performance networks. ACM SIGCOMM Comput. Commun. Rev. 2011, 41, 254–265. [Google Scholar] [CrossRef]
- Curtis, A.R.; Kim, W.; Yalagandula, P. Mahout: Low-overhead datacenter traffic management using end-host-based elephant detection. Infocom 2011, 11, 1629–1637. [Google Scholar]
- Liu, R.; Gu, H.; Yu, X.; Nian, X. Distributed flow scheduling in energy-aware data center networks. IEEE Commun. Lett. 2013, 17, 801–804. [Google Scholar] [CrossRef]
- Jiang, J.W.; Lan, T.; Ha, S.; Chen, M.; Chiang, M. Joint VM placement and routing for data center traffic engineering. In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 2876–2880. [Google Scholar]
- Wang, R.; Gao, S.; Yang, W.; Jiang, Z. Energy aware routing with link disjoint backup paths. Comput. Netw. 2017, 115, 42–53. [Google Scholar] [CrossRef]
| Type | QoS Requirements |
|---|---|
| bottleneck | bandwidth, CPU, and TCAM [17,18,19,20] |
| additive | delay, jitter, and loss rate [15,16,21,22,23] |
| Notation | Description |
|---|---|
| Undirected graph where N is the set of switches and hosts (i.e., servers) and E is the set of links | |
| S | Set of switches |
| H | Set of hosts |
| TCAM size of switch u | |
| Capacity of link | |
| Power consumption of link | |
| Power consumption of switch u | |
| K | Set of all traffic flows, each flow |
| Traffic demand by flow k from host to | |
| Binary variable indicating whether link is powered on | |
| Binary variable indicating whether switch u is powered on | |
| The amount of flow k that is routed through link | |
| Binary variable indicating whether flow k goes through switch u on outgoing link |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Lei, J.; He, Y.; Li, Z.; Deng, S.; Gao, X. Energy Optimization for Software-Defined Data Center Networks Based on Flow Allocation Strategies. Electronics 2019, 8, 1014. https://doi.org/10.3390/electronics8091014
Lu Z, Lei J, He Y, Li Z, Deng S, Gao X. Energy Optimization for Software-Defined Data Center Networks Based on Flow Allocation Strategies. Electronics. 2019; 8(9):1014. https://doi.org/10.3390/electronics8091014
Chicago/Turabian StyleLu, Zebin, Junru Lei, Yihao He, Zhengfa Li, Shuhua Deng, and Xieping Gao. 2019. "Energy Optimization for Software-Defined Data Center Networks Based on Flow Allocation Strategies" Electronics 8, no. 9: 1014. https://doi.org/10.3390/electronics8091014
APA StyleLu, Z., Lei, J., He, Y., Li, Z., Deng, S., & Gao, X. (2019). Energy Optimization for Software-Defined Data Center Networks Based on Flow Allocation Strategies. Electronics, 8(9), 1014. https://doi.org/10.3390/electronics8091014





