Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method
Abstract
1. Introduction
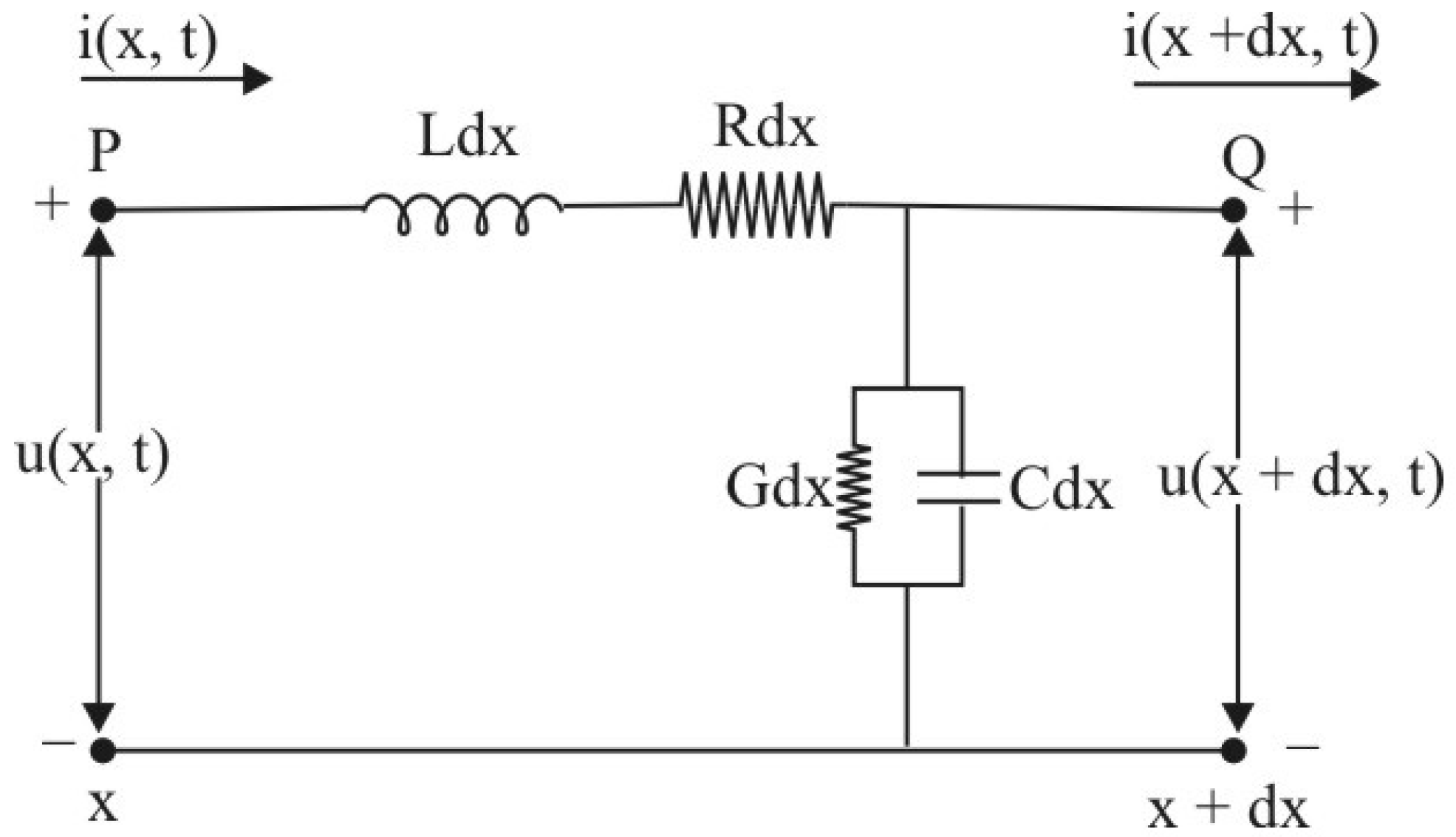
2. Mathematical Modeling
- capacitance to the ground,
- distance from the cable end,
- voltage at any time, on the cable,
- inductance of the cable
- current at any time, on the cable,
- inductance of the cable, and
- resistance of the cable.
3. Preliminaries
4. The Procedure of NTDM
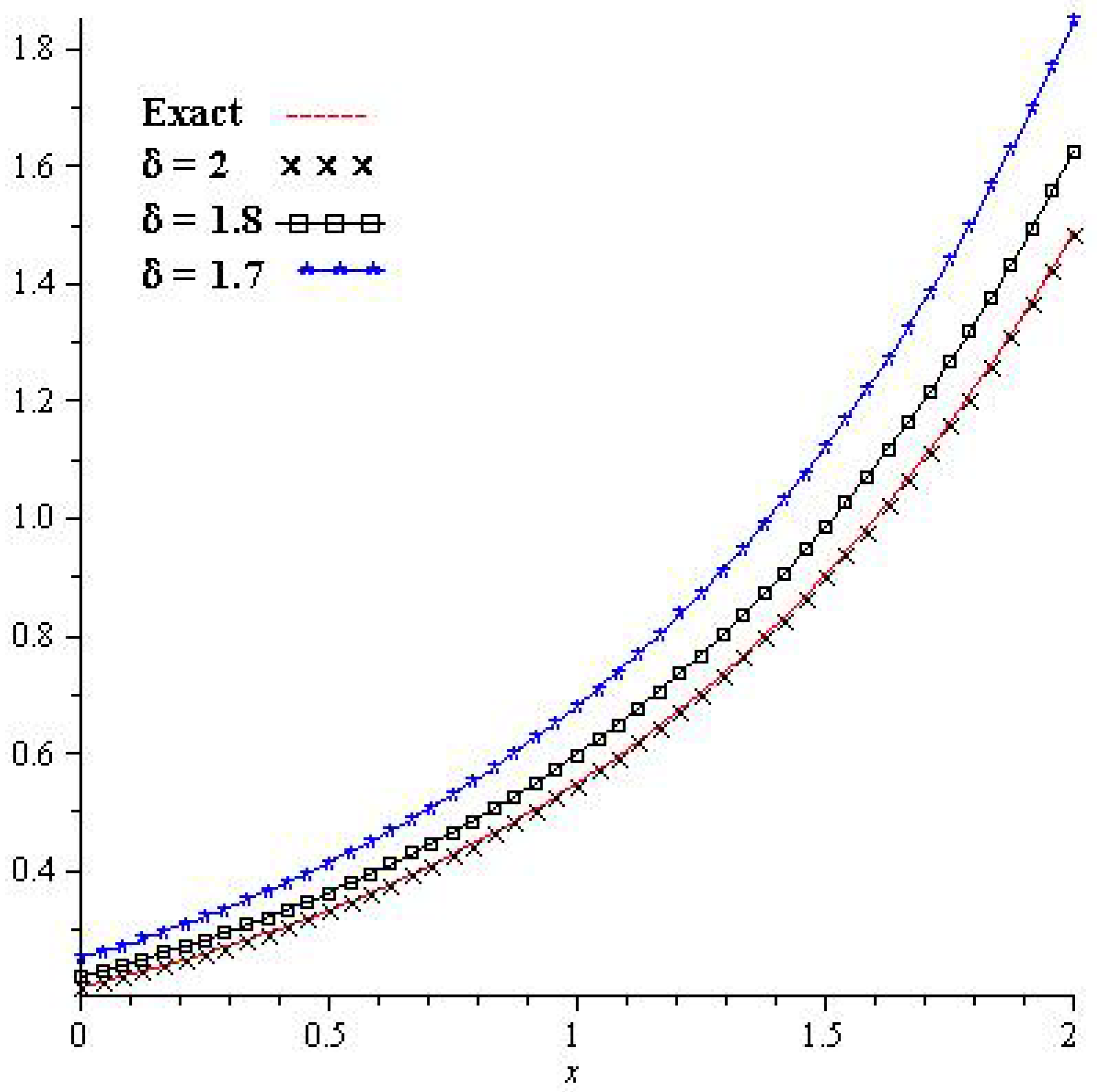
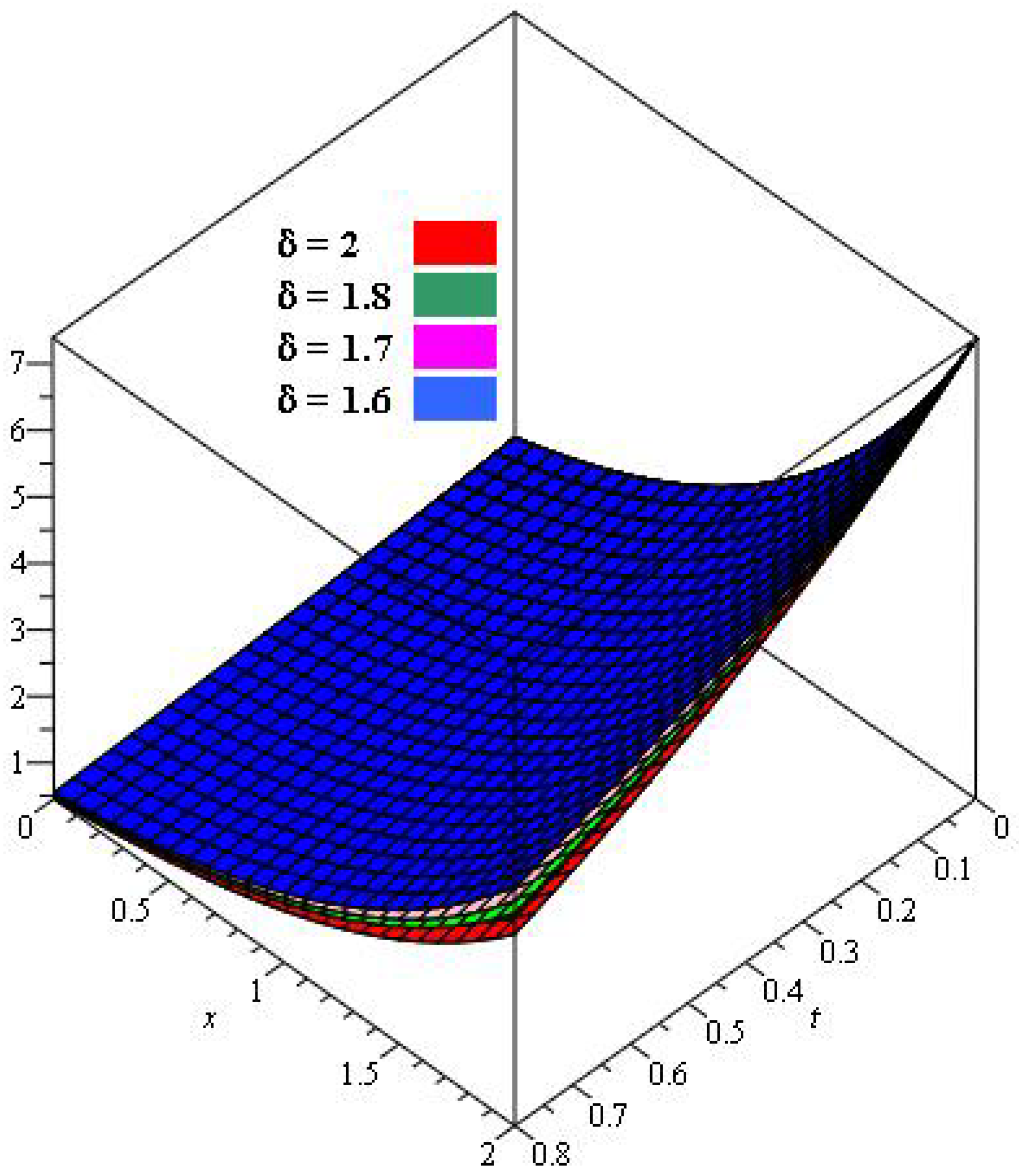
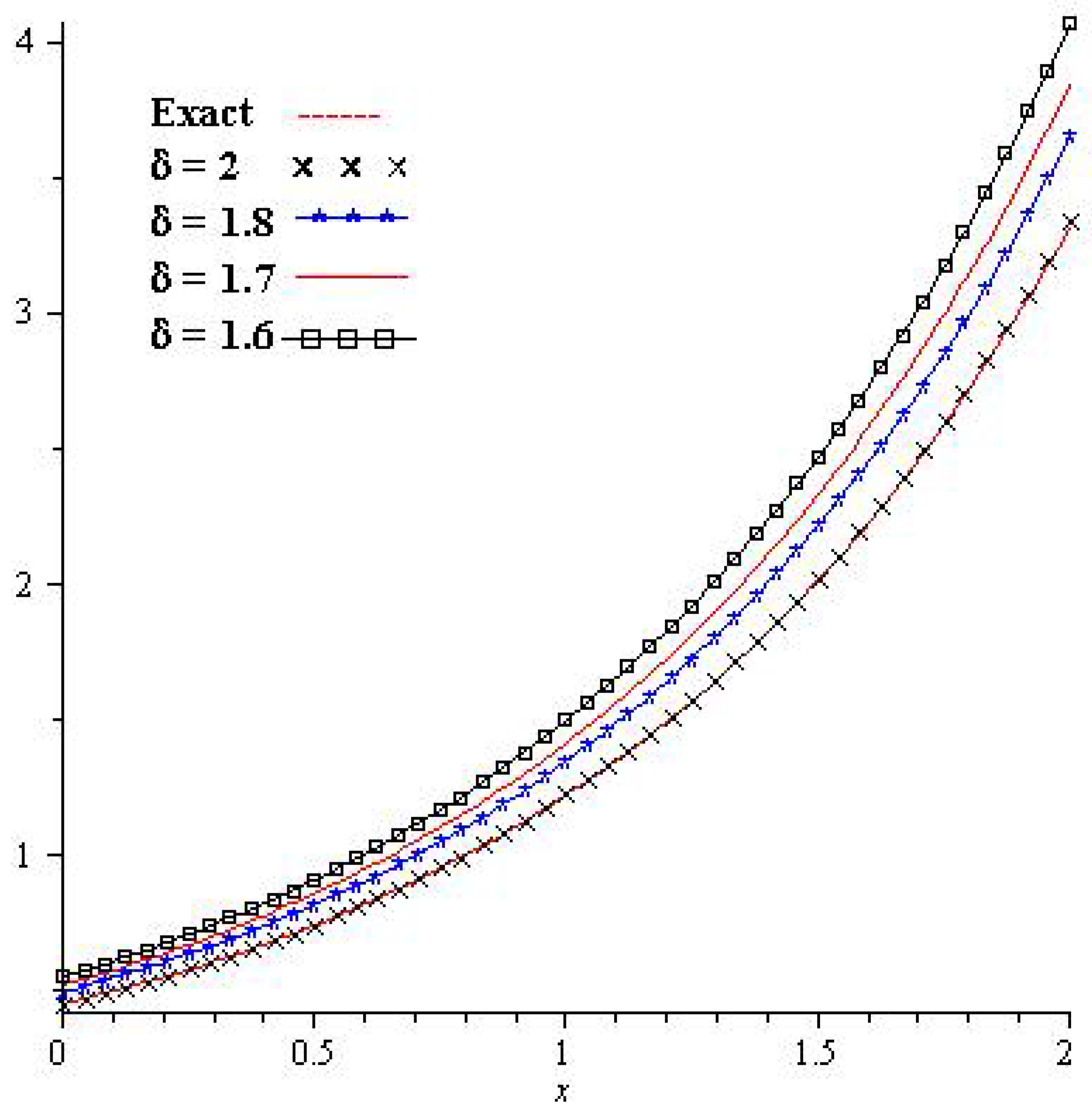
5. Results
6. Results and Discussion
7. Physical Implementation
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus AND Fractional Differential Equations, 1st ed.; Wiley: London, UK, 1993; p. 384. [Google Scholar]
- Srivastava, V.K.; Awasthi, M.K.; Tamsir, M. RDTM solution of Caputo time fractional-order hyperbolic telegraph equation. AIP Adv. 2013, 3, 032142. [Google Scholar] [CrossRef]
- Das, S.; Gupta, P.K. Homotopy analysis method for solving fractional hyperbolic partial differential equations. Int. J. Comput. Math. 2011, 88, 578–588. [Google Scholar] [CrossRef]
- Mollahasani, N.; Moghadam, M.M.M.; Afrooz, K. A new treatment based on hybrid functions to the solution of telegraph equations of fractional order. Appl. Math. Model. 2016, 40, 2804–2814. [Google Scholar] [CrossRef]
- Dehghan, M.; Shokri, A. A numerical method for solving the hyperbolic telegraph equation. Numer. Methods Partial. Differ. Equ.: Int. J. 2008, 24, 1080–1093. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. Numerical solution of hyperbolic telegraph equation using the Chebyshev tau method. Numer. Methods Partial. Differ. Equ.: Int. J. 2010, 26, 239–252. [Google Scholar] [CrossRef]
- Pirkhedri, A.; Javadi, H.H.S.; Navidi, H.R. Numerical algorithm based on Haar-Sinc collocation method for solving the hyperbolic PDEs. Sci. World J. 2014, 2014, 340752. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Momani, S. Analytic and approximate solutions of the space-and time-fractional telegraph equations. Appl. Math. Comput. 2005, 170, 1126–1134. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Baleanu, D.; Arif, M. An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations. Mathematics 2019, 7, 426. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Baleanu, D. Numerical approximation of higher-order time-fractional telegraph equation by using a combination of a geometric approach and method of line. J. Comput. Phys. 2016, 316, 10–20. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving coupled system of nonlinear PDE’s using the natural decomposition method. Int. J. Pure Appl. Math. 2014, 92, 757–776. [Google Scholar] [CrossRef]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional Telegraph Equation and Its Solution by Natural Transform Decomposition Method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M.; Baleanu, D. Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay. Mathematics 2019, 7, 532. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Abdel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedl-Rahim, H.R. Natural transform for solving fractional models. J. Appl. Math. Phys. 2015, 3, 1633. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy 2019, 21, 597. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Mustafa, S.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Diffusion Equations by Natural Transform Decomposition Method. Entropy 2019, 21, 557. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S. Analytic and approximate solutions of space-time fractional telegraph equations via Laplace transform. Walailak J. Sci. Technol. (WJST) 2013, 11, 711–728. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R. Advances in the natural transform. AIP Conf. Proc. 2012, 1493, 106–110. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics 2019, 8, 1015. https://doi.org/10.3390/electronics8091015
Khan H, Shah R, Baleanu D, Kumam P, Arif M. Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics. 2019; 8(9):1015. https://doi.org/10.3390/electronics8091015
Chicago/Turabian StyleKhan, Hassan, Rasool Shah, Dumitru Baleanu, Poom Kumam, and Muhammad Arif. 2019. "Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method" Electronics 8, no. 9: 1015. https://doi.org/10.3390/electronics8091015
APA StyleKhan, H., Shah, R., Baleanu, D., Kumam, P., & Arif, M. (2019). Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics, 8(9), 1015. https://doi.org/10.3390/electronics8091015







