1. Introduction
Buildings account for a major portion of both primary energy and electricity consumption, and previous investigations indicated that building electricity consumption can be reduced by up to 10%–15% using energy management [
1,
2]. The smart grid and its supporting home automation network can promote residents’ understanding of household appliance consumption and have the potential to be an effective means of energy management. To make household appliance consumption clear and understandable, each appliance requires a sensor, which can be achieved by modifying the existing appliances. This is associated with a low customer acceptance and thus is an obstacle in the promotion of the smart grid. Nonintrusive load monitoring (NILM), instead of placing a sensor on each appliance, reveals appliance usage at home from a single sensing point, which has been shown to increase customer acceptance of the home automation network [
3,
4,
5].
NILM was first proposed by Hart [
6] in the 1980s, in which the steady-state active power (P) and reactive power (Q) consumptions were used as load signatures. However, in certain situations, two appliances may consume the same amount of P and Q, which makes the two appliances indistinguishable [
7]. Therefore, researchers extract appliance signatures from electrical parameters in switch states [
8,
9,
10]. Nevertheless, transient signals require non-stop monitoring, which imposes data transmission and storage challenges. To observe the phase noise near 60 Hz, the current was measured 170 times per s in [
8]. Furthermore, some of the transient signal can be missed, while some of the non-transient signal can be mistaken as transient [
11]. In this paper, to tackle this problem, spurious emissions in the spectrum of each appliance are employed to identify different appliances. This technique is based on the fact that spurious emissions coupled into the power cord from various appliances are different due to their unique nonlinear components, such as the diode. The employment of spurious emissions can obviously reduce the amount of data storage and still guarantee identification accuracy.
To recognize the operating states of household appliances, the features of historical data are firstly extracted to establish a classifier model, and then, the operating states of home appliances are identified through real-time data. The issue of how to extract individual features from measured data is critical. In our study, the features of spurious emissions are extracted from the time–frequency distribution and their physical properties, respectively. The peak intensity of the fractional correlation is higher than the traditional correlation, and the correlation operation can be extended to any angle of the time–frequency plane by the fractional Fourier transform (FrFT) [
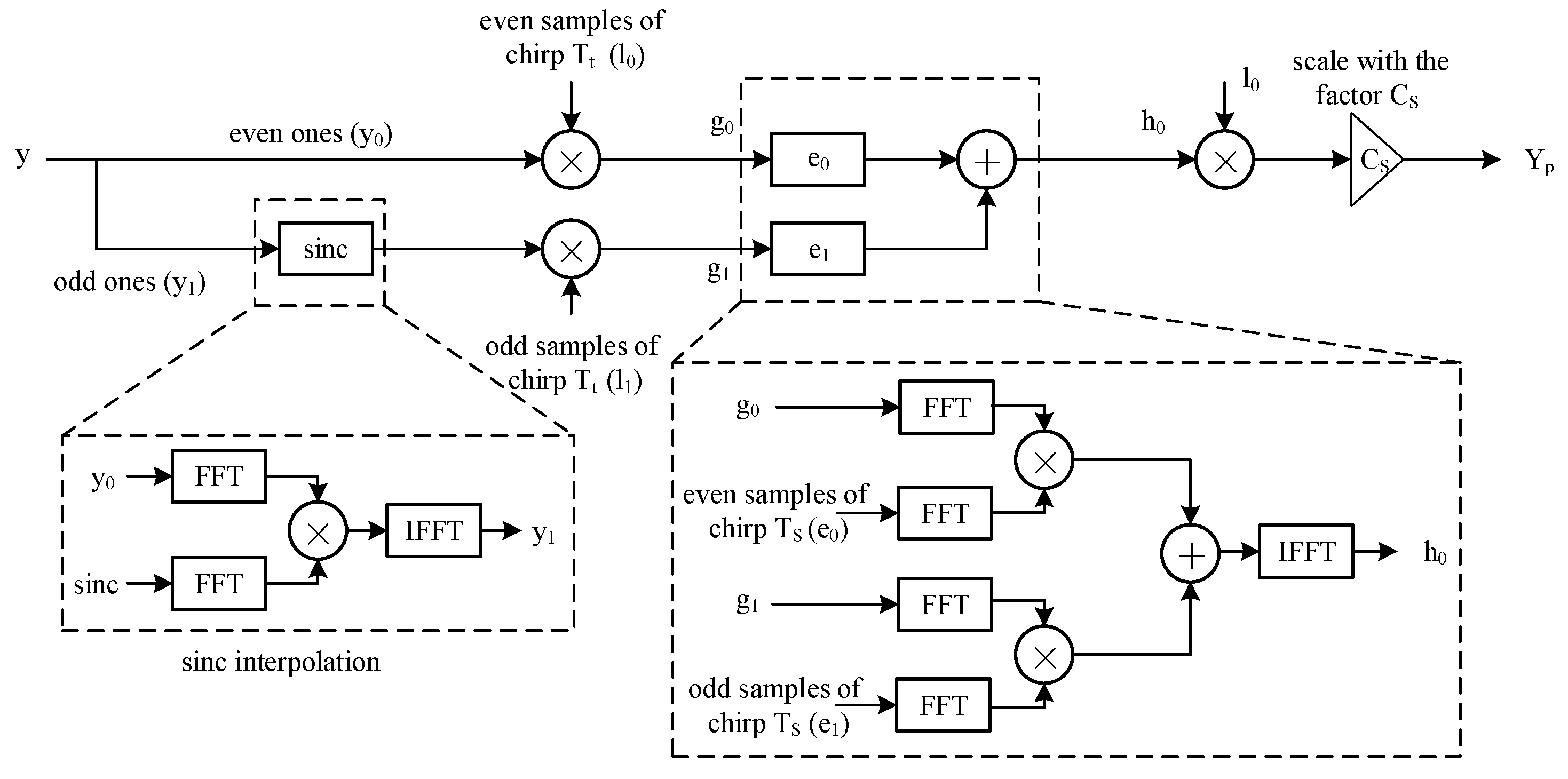
12]. Furthermore, electromagnetic emissions can be divided into different components based on physical characteristics, presented in the “basic emission waveform theory” [
13]. The signal can be accurately separated through B-spline curve fitting on the physical layer to obtain the statistical features of different components. Therefore, in this paper, the fractional correlation-based algorithm and B-spline curve fitting-based algorithm are proposed to extract two groups of complementary features, which show long-time stability and then are used in a classifier. There are various classification algorithms, such as an improved fuzzy clustering algorithm [
14], neural networks [
15,
16], and so on. However, considering the amount of training sample, a combining classifier is used. The combining classifier is based on support vector machine (SVM) and Dempster–Shafer (D-S) evidence theory, which shows the final identification results.
The main contributions in this paper are summarized as follows:
Different from previous studies, spurious emissions in the spectrum of each appliance are used to identify the operating states based on the nonlinear components, which can obviously reduce the amount of data storage and still guarantee identification accuracy;
Two groups of complementary features are extracted from the spurious emissions of household appliances. The fractional correlation-based algorithm exploits the correlation coefficient to evaluate the similarity between transformed sequences in the time–frequency plane, and the B-spline curve fitting-based algorithm obtains statistical features of different components on the physical layer.
The paper is organized as follows. In
Section 2, the feature extraction method is proposed based on the fractional correlation-based algorithm and the B-spline curve fitting-based algorithm.
Section 3 briefly introduces the combining classifier based on SVM and D-S evidence theory. The measurement system and experimental verification are presented in
Section 4. The conclusion comes in
Section 5.
3. Combining Classifier
The features extracted by different algorithms compose different feature spaces [
23]; some samples are in an overlapping region of one feature space, while they may be absent from the overlapping region of another feature space. Therefore, high-dimensional feature spaces, superimposed directly on low-dimensional feature spaces, may deteriorate the aggregation of samples belonging to the same class. To solve this problem, a combining classifier was introduced, and the combination of several complementary classifiers improved the performance of individual classifiers.
In this paper, considering the high cost of sample collection, the SVM was employed as the individual classifiers. Its core idea is that of using a kernel function to map a non-linearly-separable space to a linear separable high-dimensional space and then searching for the optimal separating hyperplane [
24]. For linearly-separable data, the decision function of SVM is defined as:
where
is the kernel function and
w and
b determine the hyperplane of the mapped space. For linear inseparable data, the decision function of SVM is defined as:
where
is the kernel function,
l is the number of training data,
is the
mode embedded dimension, and
is the
label. The classification problem is converted into a constrained optimization function, given by:
where
C is a penalty factor. By solving the optimization problem in Equation (
7),
and
b are sequentially obtained. The classifier model is established.
Furthermore, the combination of individual classifiers was based on D-S evidence theory [
25] in this study. By only using the recognition, substitution, and rejection rates of each individual classifier as the prior knowledge, the performance indexes of a classifier were well represented by testing the classifier with a test sample set. Firstly, the basic probability assignment (BPA) function of each classifier was determined. Suppose that the classification result of classifier
is
for an input feature vector
X,
;
means the classifier
does not recognize the input
X.
M is the total number of identified classes. The error of classifier
is described by its confusion matrix as follows:
where
denotes the number that the sample of class
i has been assigned a label
j by classifier
. The uncertainty of event
can be given by conditional probabilities expressed as:
The BPA function of classifier
is
, if
. While
, the focal elements are
,
,
, and the corresponding BPA functions can be calculated by the following formula:
,
, and
can be normalized to obtain
,
, and
. Then, considering the recognition performance of the classifier for different samples of the same class, the BPA functions are modified by the defined posterior probability function,
, where
is the output vector of the classifier
for the input
X and
is the average output vector of the classifier
for samples of class
i. The modified BPA functions are:
The different identification results of the individual classifiers can be combined by D-S evidence theory using Equation (
13), and the belief value
expresses the final beliefs with uncertainty on each
M mutually-exclusive propositions
; the higher the
, the more likely
is to be true. The identification result is determined by a threshold
,
in this deployment.
4. Experiment and Verification
In this section, we evaluate the identification performance of the proposed method through various numerical experiments. The measurement system is described in
Section 4.1. The distinguishability and time stability of the proposed features are discussed in
Section 4.2 and
Section 4.3, respectively. The identification performance by the combining classifier is verified in
Section 4.4.
4.1. Measurement System
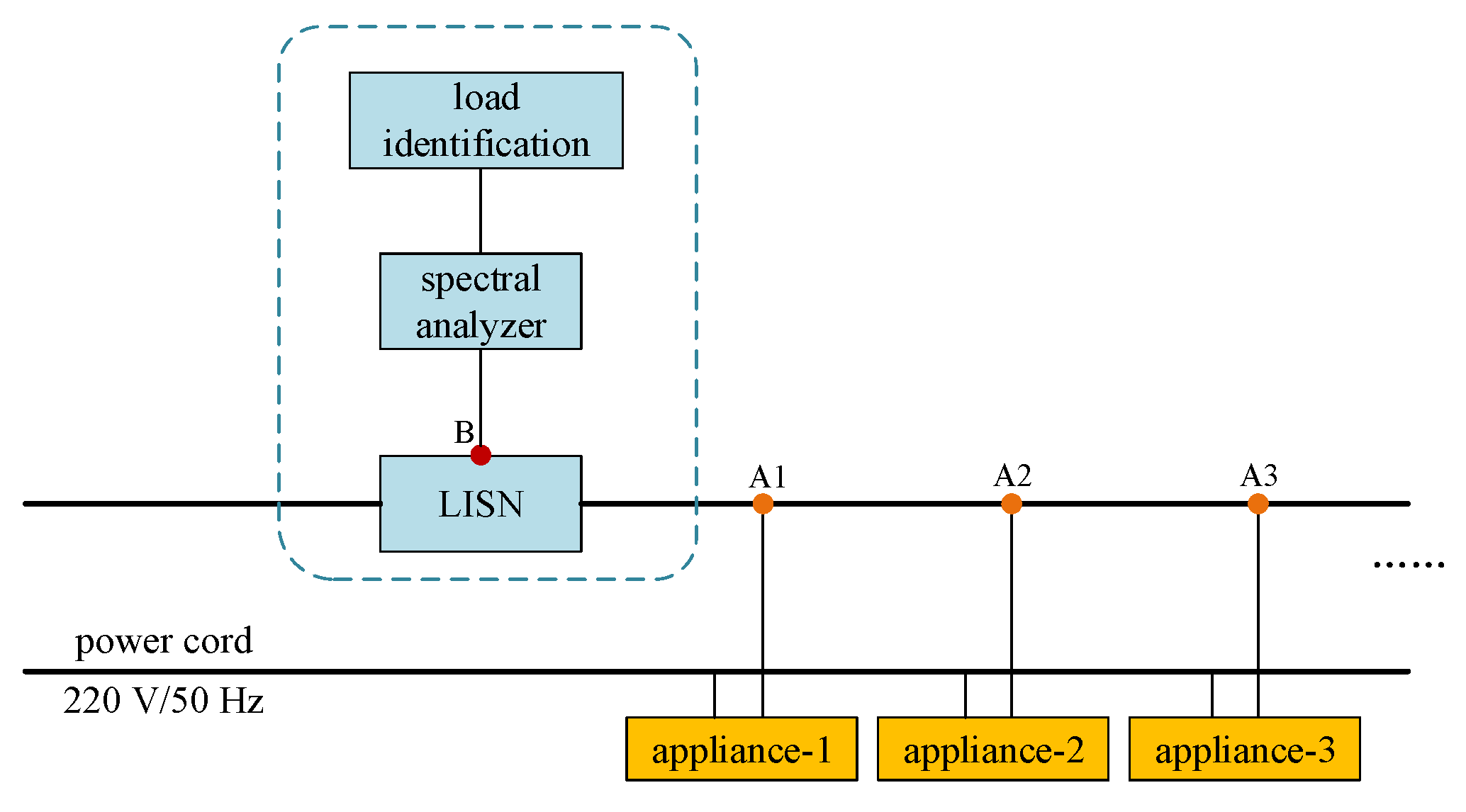
To validate the proposed method, some experiments were carried out in a shielded chamber, and the power of spurious emission was measured, which was different from the measurement of active power in [
4]. The measurement system, mimicking the usage of household appliances, is shown in
Figure 3, where a line impedance stabilization network (LISN, Schwarzbeck NNBL 8225) accessed the power cord, external noise was filtered out, and a spectral analyzer (CETC-41 AV4037MB) was used to provide the real-time spurious emission spectrum on the neutral or live line while the appliances were operating. Since the difference between a neutral and live line signal is not critical for identification, the access point of the spectral analyzer could be selected at either. Spectrum data were recorded with 1200 sample points per 15 s, to reduce data storage effectively [
8], in which an WCS2210 Hall sensor and an UNO R3 Arduino were used, as well as the current with a measurement interval of 1/170 s obtained. However, the phase information was missing during the spectrum measurement, leading to an increase in the number of training sample, which was discussed in
Section 4.2.
The actual access locations in the power cord of some household appliances were variable, that is the distance between Access Point A, marked as A1, A2, and A3 for Appliance-1, Appliance-2, and Appliance-3 as shown in
Figure 3, and Monitoring Point B, the location of LISN, was not fixed in the measurement system. Therefore, low-frequency spectra were recorded to ensure that the measurement results were not affected by the access location of the appliance. In addition, the frequency of the tested grid was 50 Hz; hence, the measuring spectral range was set from 30 kHz–150 kHz with a resolution of 200 Hz to obtain the spurious emissions from the power cord. To gather as much useful information as possible, both the maximum and minimum were recorded.
4.2. Different Appliances’ Measurement
In this subsection, the proposed method was verified using household appliances including a laptop, fluorescent table lamp, hair dryer, far infrared heater, and ultrasonic humidifier. The brand and model are shown in
Table 1. In the following, only 50 groups of measured data,
, 10 for each appliance, were used to demonstrate the results of our proposed methods for clear visualization. However, in our training procedure (discussed in
Section 4.4), 50 groups of measured data for each appliance were used to train the combined classifier.
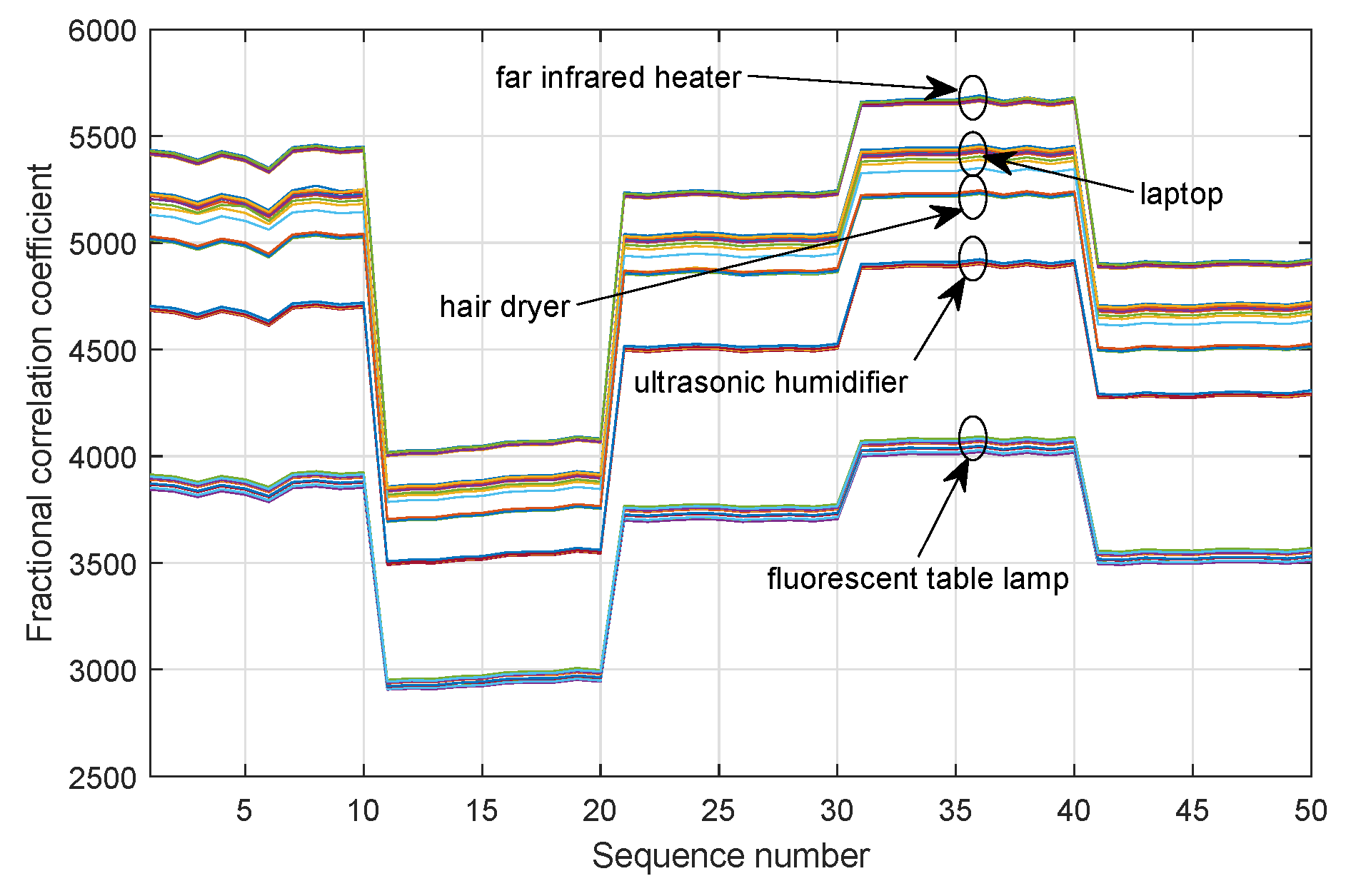
In the fractional correlation-based algorithm, 50 measured sequences were used as training sequences, thereby the dimension of feature vector
was 50 for each sequence, as shown in
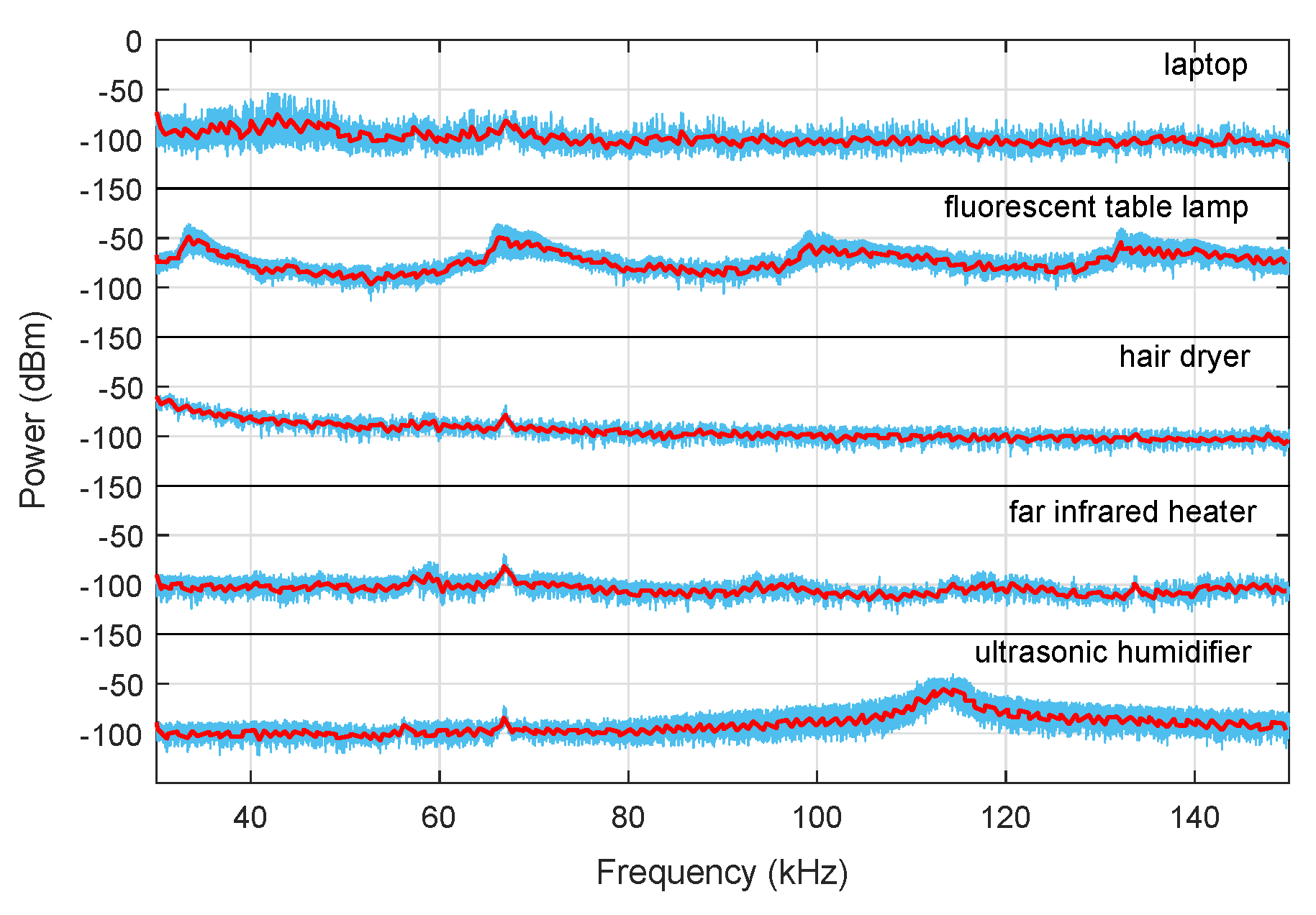
Figure 4. It can be seen that the correlation coefficients of 10 sequences were almost identical for the same appliance, while distinguishable from those of other appliances. In the B-spline curve fitting-based algorithm, the fitted broadband component of each appliance is shown in
Figure 5, which obviously showed differences in the peaks, the amplitude, and other features, which led to obvious differences in the statistical parameters used.
Measurements covering different operating states were taken. Since an additional circuit was developed during the “on” state for the laptop, some narrowband components were introduced, which could be removed using curve fitting, because in our study, broadband components were mainly considered. In addition, the oscillation frequency of the broadband component for the ultrasonic humidifier varied with the states due to different circuit parameters, which could be used for the identification of operating states.
The results in
Figure 4 and
Figure 5 show that most devices in isolation were identifiable by the extracted features. However, spurious emissions from the power cord involved, in practicality, multiple appliances in parallel and not a simple amplitude addition due to the phase [
26]. Therefore, further measurements were required for appliance combinations.
4.3. Long-Time Stability Measurement
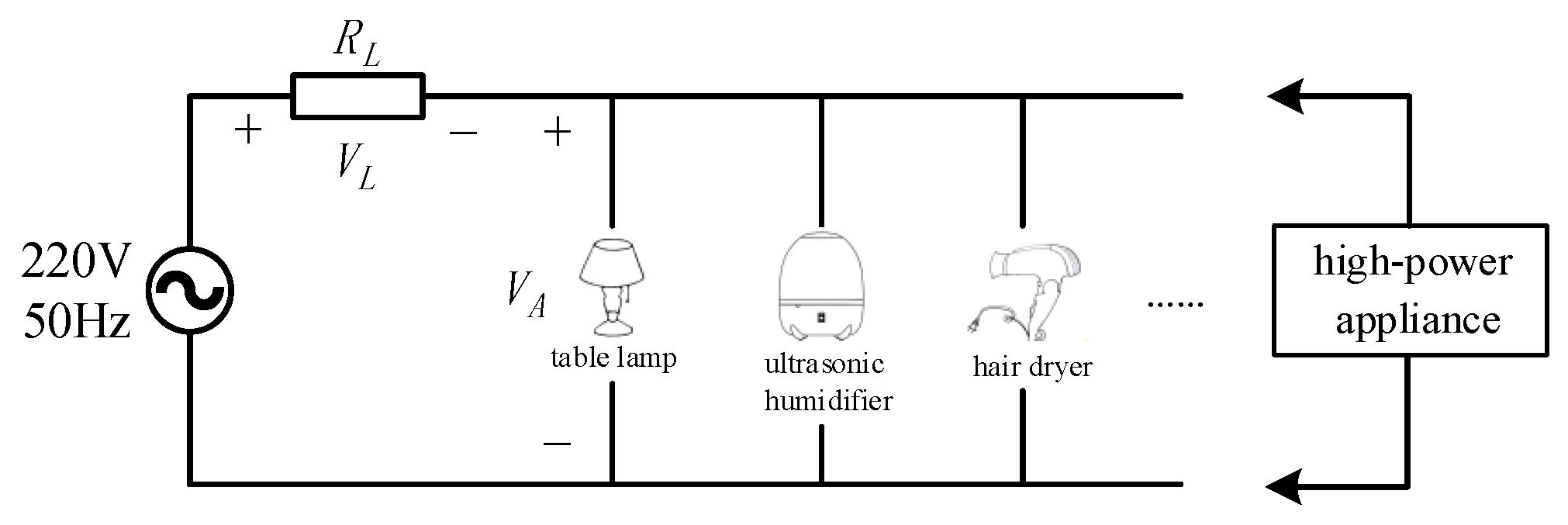
The power grid was not stable due to the access of high-power appliances and the power quality, which indicated that the measured spectra for each appliance may be different over time. Although the appliances were in parallel, the current on the power cord would increase when a high-power appliance was operating, which would increase the voltage
across the loss resistance
of the power cord and decrease the voltage
across the appliances, as shown in
Figure 6. Therefore, the stability of the features extracted for identifying various loads was required. In our study, the table lamp was taken as an example to validate the long-time stability of the extracted features.
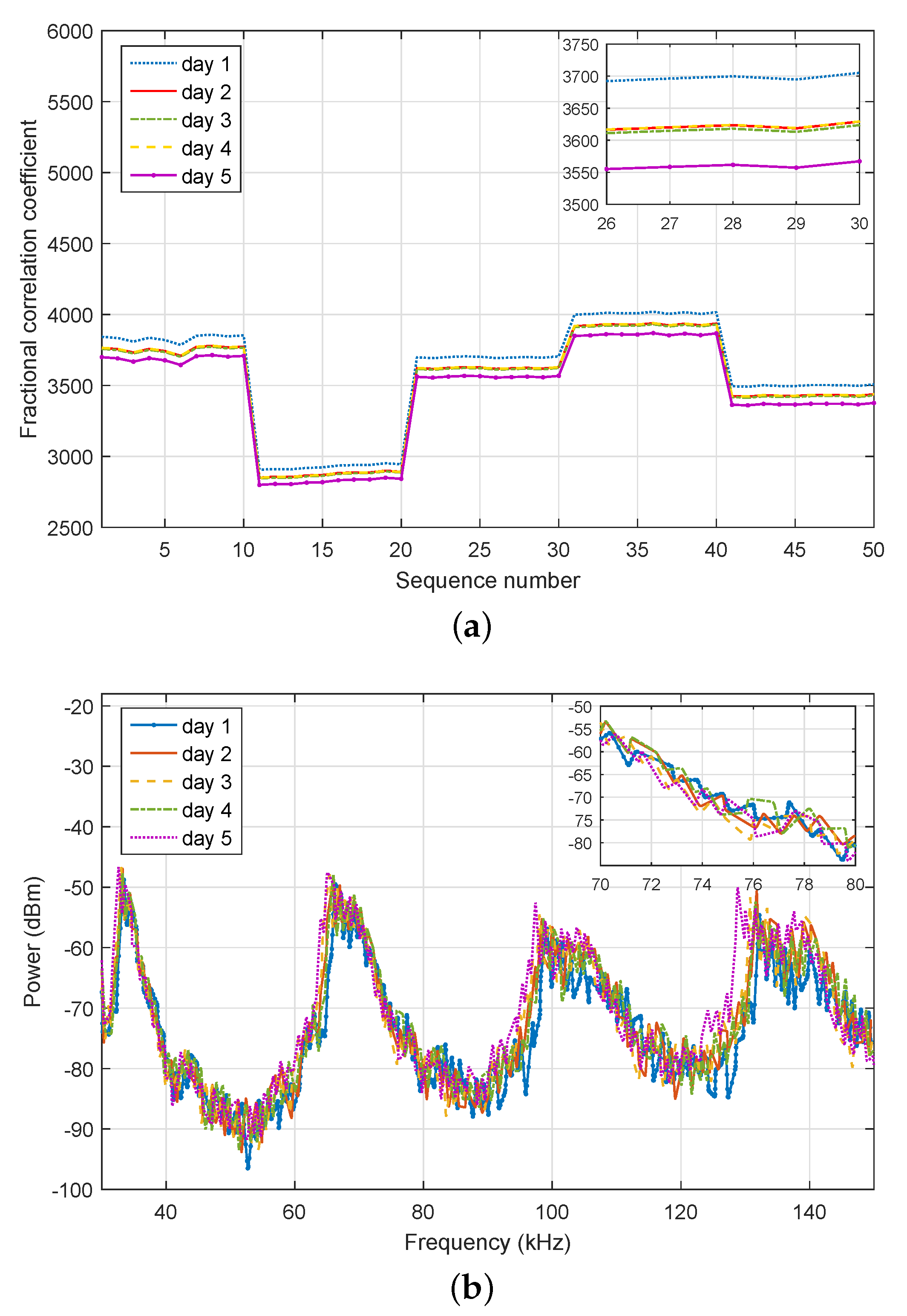
The spurious emissions of the table lamp were measured over five consecutive days, and the features were extracted using the proposed methods, as shown in
Figure 7.
Figure 7a demonstrates that the difference in correlation coefficients was limited to 150, and the coefficients over three days almost overlapped. In addition,
Figure 7b indicates that the broadband components of the spectra were consistent over time, although there was some variation around 130 kHz. However, this small variation was acceptable for a classifier.
4.4. Identification Accuracy
To evaluate the identification accuracy of the features extracted from the proposed method, the probability of correct identification was used as a performance measure. Three types of appliances were considered: the fluorescent table lamp, hair dryer, and ultrasonic humidifier. Fifty measured data groups for each appliance were used, and the total number of training sequences was , where K is the number of appliances, and in this subsection.
Different feature spaces were constructed by the fractional correlation-based algorithm and B-spline curve fitting-based algorithm. Two SVM classifiers were trained by those two feature spaces, respectively, and the results from the two classifiers were combined for high identification accuracy. Here, two SVM classifiers were first implemented where the Gaussian radial basis function (RBF) was selected as the kernel function [
27], then the combined results using D-S evidence theory were calculated. The accuracy was 85.5% for 800 test sequences, which were collected in different time periods over one day and covered all appliance combinations, showing better performance than individual classifiers.
Note that the household meter included a main switch, toilet switch, and kitchen switch, amongst others, which controlled the power cord of the apartment and the power cords of different rooms covering specific appliances. In our study, the power cord of the room was mainly considered, that is the number of measured appliances K and the total number of training sequences N were acceptable and would not cause an index explosion.
5. Conclusions
In this paper, a method to extract complementary spectrum features from spurious emissions was proposed for detecting the operating states of appliances, using the fractional correlation-based algorithm and B-spline curve fitting-based algorithm, which had the capacity to support NILM and home automation networks. Firstly, the spurious emissions in the spectrum coupled to the power cord were measured based on the existence of nonlinear components inside appliances. Then, two groups of complementary features were extracted using the similarity between transformed sequences in the time–frequency plane and the statistical features of different components on the physical layer. Finally, the feasibility and long-time stability of the proposed method were validated using several measurements, and the identification accuracy reached 85.5% using the combining classifier based on SVM and D-S evidence theory. It was found that the proposed feature extraction methods could be used to identify the appliances and showed good performance.
In future studies, further measurements should be performed for more household appliances in an actual home and the extracted features incorporated with other features to improve the identification accuracy. In addition, the identification results of appliance operating states would be applied to recover the energy consumption per appliance.