1. Introduction
Polar codes are the first error-correction codes proved to achieve a channel capacity with affordable encoding and decoding complexities [
1,
2,
3]. The polar codes employ channel polarization, which implies that bit channels are polarized into completely error-free and noisy channels as the code length increases. Based on channel polarization, (
N,
K) polar codes transmit useful information over the most reliable
K bit channels and fixed data over the least reliable
N-
K bit channels. The index set of the most reliable
K bit channels is called information set
A, and the index set of the least reliable
N-
K bit channels is called frozen set
. The classical methods to decode polar codes are the successive-cancellation (SC) [
4,
5,
6,
7] and belief-propagation (BP) [
8,
9,
10,
11,
12,
13,
14] decoding methods. SC [
4,
5,
6,
7] is widely employed for area-stringent applications owing to its serial nature, and BP is widely employed for throughput-demanding applications owing to its parallel nature [
8].
The conventional BP decoder passes reliable information over graphical models for performing inference until the maximum iteration number (
max-iteration) [
8]. In general, an early-termination technique [
15,
16,
17,
18] is widely adopted in BP decoders [
8] to improve the average throughput. Although previous early terminations including threshold-based [
15], information-BER-based [
16], and frozen-BER-based [
17] criteria succeeded in reducing decoding latency, they suffered from high hardware complexities to check the termination condition. Therefore, this letter presents an area-efficient early-termination method by simplifying the previous early-termination criterion. The proposed method achieves area-efficiency by using only part of the log-likelihood ratio (LLR) values on information bit channels rather than entire bit channels in [
15], and introduces no performance degradation incurred in References [
16,
17] by prohibiting the use of the windowing method. Experimental results show that the proposed method always provides the smallest hardware complexity, while maintaining error-correction capability and the average number of decoding iterations.
2. Belief-Propagation (BP) Decoder and Previous Early-Termination Techniques
The BP algorithm is one of the most efficient algorithms to decode polar codes, which iteratively propagates reliabilities over a factor graph [
8]. An
n-stage (
n = log
2N) factor graph is necessary for (
N,
K) polar codes, in which each stage consists of
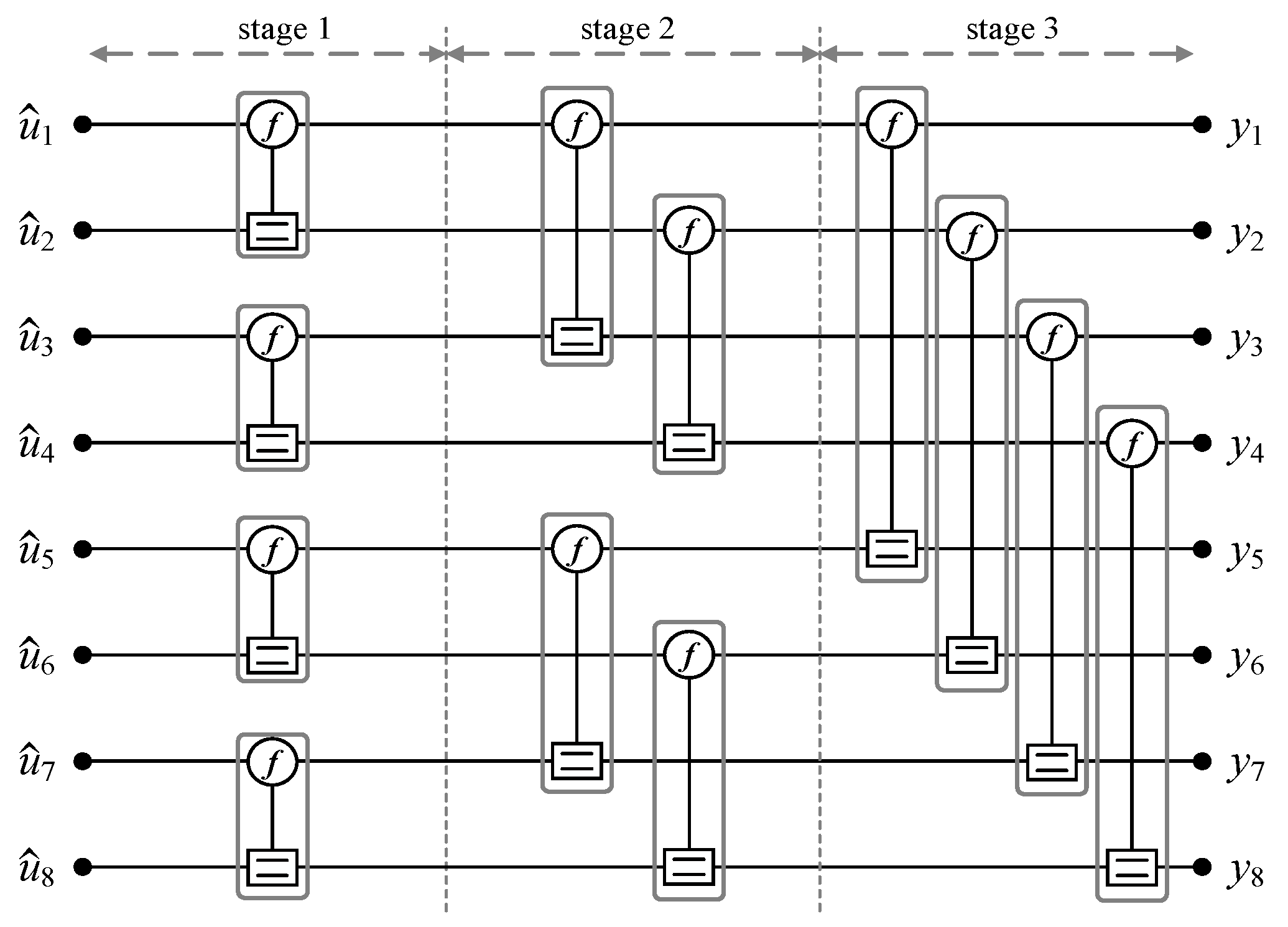
N/2 processing elements (PEs). For instance,
Figure 1 depicts the factor graph of (8, 4) polar codes with three decoding stages. Given received messages
yi (1 ≤
i ≤
N), the BP decoder computes estimated messages
(1 ≤
i ≤
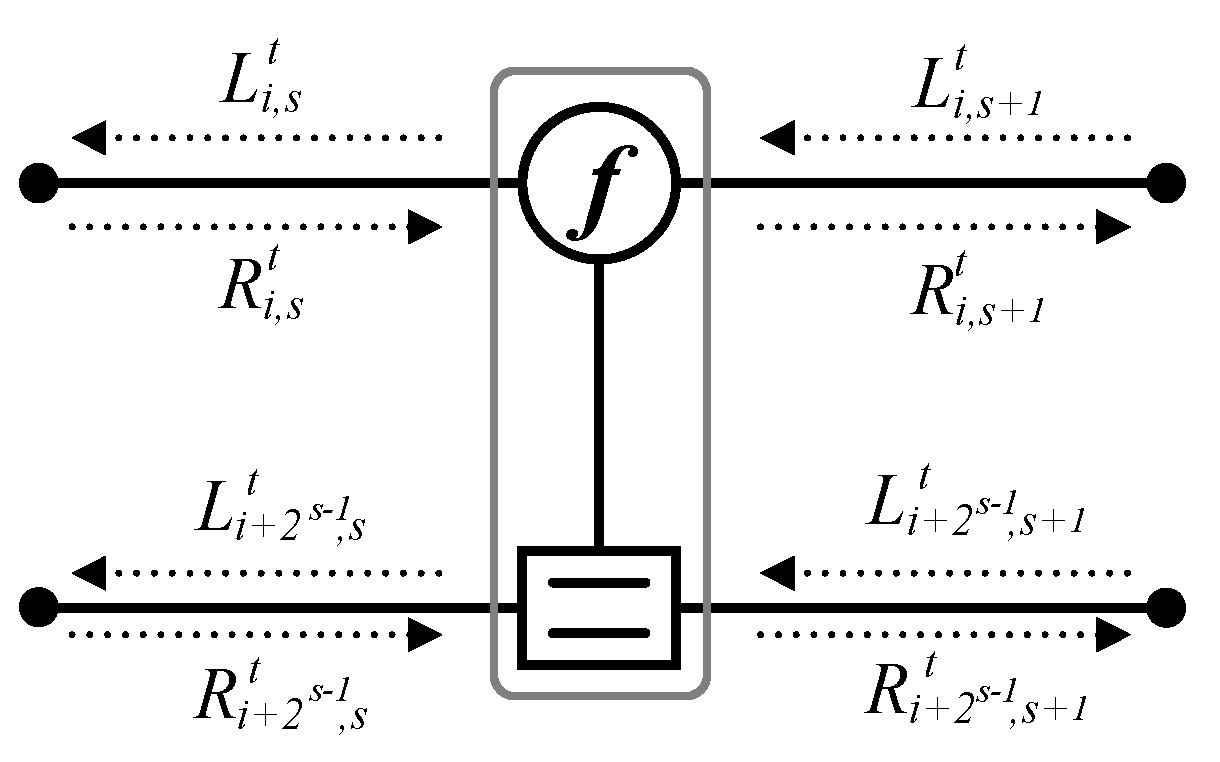
N). More precisely, one PE depicted in
Figure 2 passes LLRs using four left-LLRs (
) and four right-LLRs (
) along the right-to-left and left-to-right directions, respectively, where
i,
s, and
t respectively denote the node index (1≤
i ≤
N), stage index (1 ≤
s ≤
n+1), and iteration index (1 ≤
t ≤
T). As the BP algorithm iteratively propagates such LLR values, the initialization in a BP decoder is important to decode polar codes successfully [
8]. The right-most nodes at
s =
n + 1 are initialized as
and
based on the LLRs of the received messages. In addition, the left-most nodes at
s = 1 are initialized depending on the type of bit channels. For the information bit channels, the left-most nodes in set
A are initialized as
and for the frozen bit channels, the left-most nodes in set
are initialized as
The other nodes are initialized as zeros as there are no prior probabilities. After the initialization, all left-LLRs and right-LLRs are updated until the maximum number of iterations is reached as follows:
| Algorithm 1: Threshold-based [15] early-termination technique |
Initialization:
If (s == n+1) then = LLR (yi)
Else if (s ==1) & (i ∈) then = ∞
Else = = 0
Decoding iteration:
While t ≤ T
Update and based on (3) and (4)
If (β: threshold value) then Stop decoding iteration
t = t + 1 |
where
f(
a,
b) is the classical min-sum approximation calculated as
f(
a,
b) = sign(
a)·sign(
b)·min(|
a|, |
b|). After reaching the max iteration, the conventional BP decoder finally estimates the decoding result
by making a hard decision as sign (
) at the left-most node
s = 1.
Although the conventional BP decoder continues decoding iterations until the predetermined max iteration
T, the reliable estimations can in fact be obtained before the max iteration
T, especially for a high signal-to-noise ratio (SNR) channel condition. The early-termination method for BP polar decoders was first proposed in Reference [
15], which compares all the LLR values at the left-most nodes with a threshold value. When all the LLR values at the left-most nodes are larger than the predetermined threshold value, the decoding iteration is terminated even when the iteration number is less than
T. In the threshold-based method, decoding can be improved, but high additional hardware complexity is inevitable [
15]. The overall procedure of the threshold-based early-termination method [
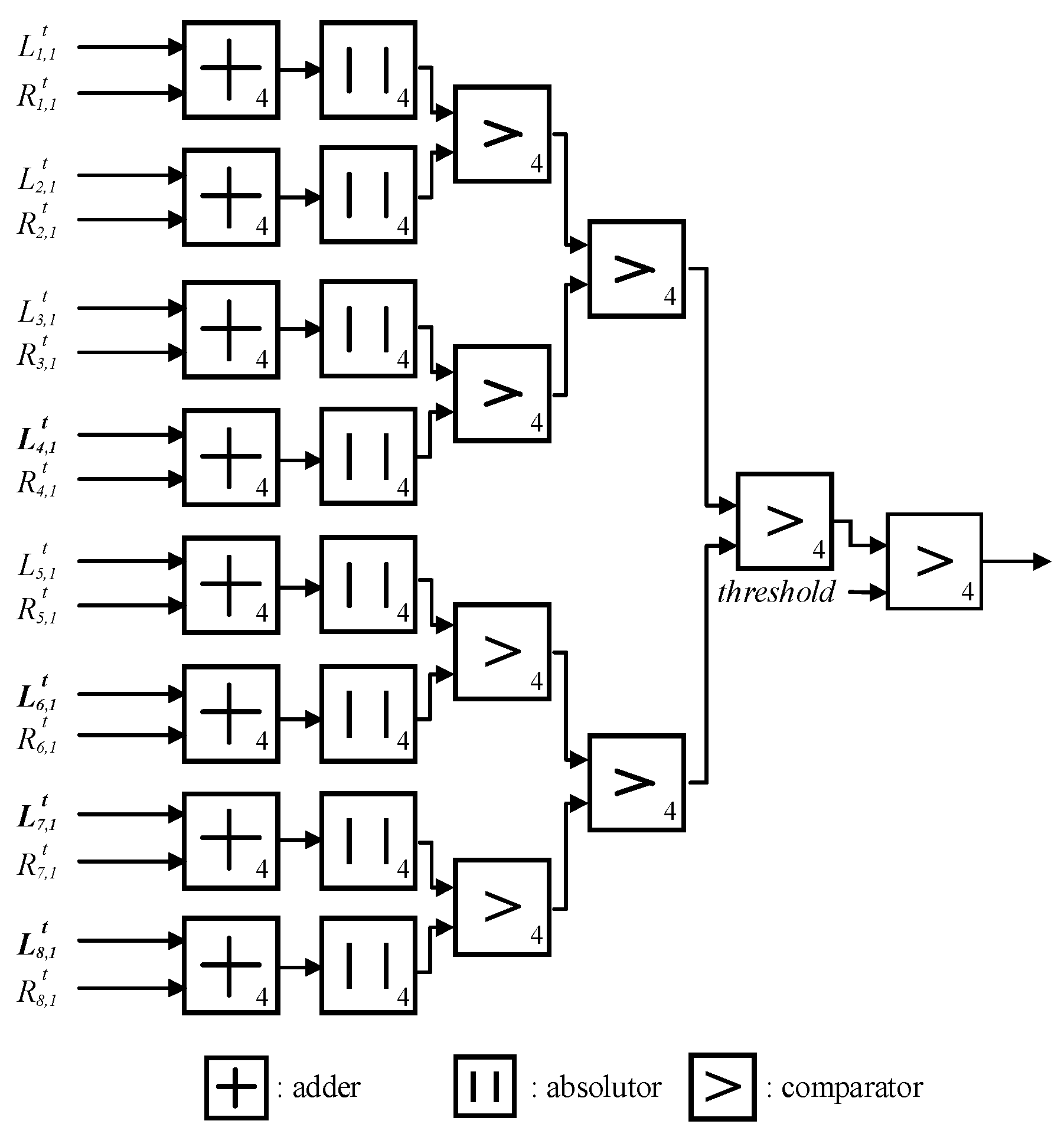
15] is explained in Algorithm 1, and
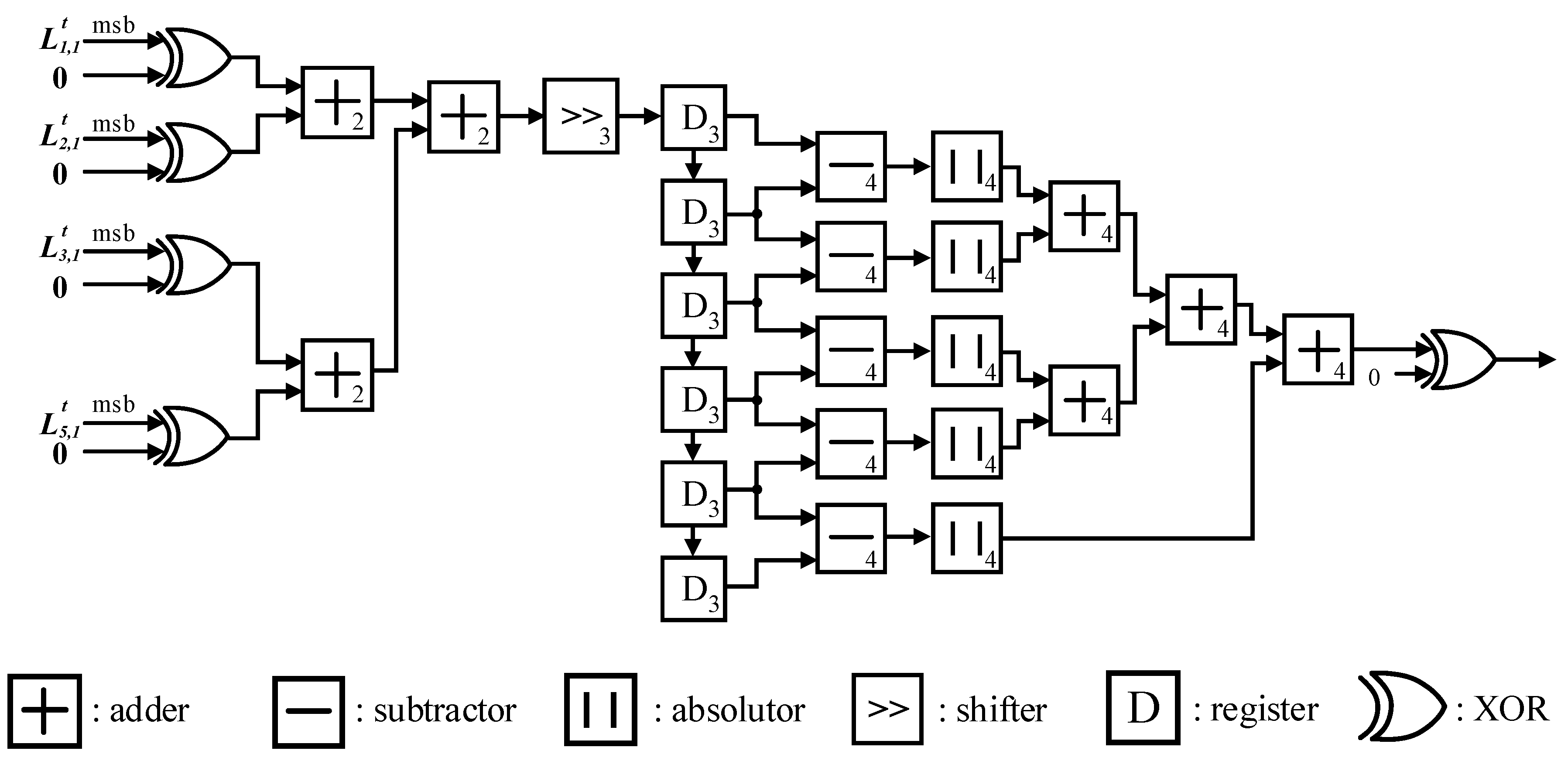
Figure 3 depicts the hardware architecture of the threshold-based early-termination method for (8, 4) polar codes. Note that the number inside the box represents the bit-width of the arithmetical operators. In
Figure 3, the threshold-based early-termination method requires 4-bit 8 adders, 8 abstractors, and 8 comparators for (8, 4) polar codes [
15].
In addition, References [
16,
17] propose area-efficient windowing methods that check the changes on the bit channels within the consecutive iteration numbers, known as the window size. Algorithm 2 and Algorithm 3 depict information-BER-based [
16] and frozen-BER-based [
17] early-termination processes, respectively. According to Algorithm 2 and Algorithm 3, information-BER-based [
16] and frozen-BER-based [
17] early-termination processes calculate the changes within the information set
A and the frozen set
during the window size
W. Although information-BER-based [
16] and frozen-BER-based [
17] early-terminations can save hardware resources significantly, they deteriorate the decoding throughput compared to the threshold-based method [
15].
Figure 4 and
Figure 5 show the hardware architecture of information-BER-based [
16] and frozen-BER-based [
17] for (8, 4) polar codes, respectively. Since we assumed that the information set
A is {4, 6, 7, 8} and the frozen set
is {1, 2, 3, 5}, information-BER-based [
16] and frozen-BER-based [
17] require only LLR values of information set
A and frozen set
, respectively. In this paper, we propose a new early-termination method that introduces no throughput or error-correcting degradations with the smallest hardware resources.
| Algorithm 2: Information-BER-based [16] early-termination technique |
Initialization:
If (s == n+1) then = LLR (yi)
Else if (s ==1) & (i ∈) then = ∞
Else = = 0
Decoding iteration:
While t ≤ T
Update and based on (3) and (4)
If then Stop decoding iteration
t = t + 1 |
| Algorithm 3: Frozen-BER-based [17] early-termination technique |
Initialization:
If (s == n+1) then = LLR (yi)
Else if (s ==1) & (i ∈) then = ∞
Else = = 0
Decoding iteration:
While t ≤ T
Update and based on (3) and (4)
If then Stop decoding iteration
t = t + 1 |
| Algorithm 4: Proposed early-termination technique |
Initialization:
If (s == n+1) then = LLR (yi)
Else if (s ==1) & (i ∈) then = ∞
Else = = 0
Decoding iteration:
While t ≤ T
Update and based on (3) and (4)
If i∈A & (β: threshold value) then Stop decoding iteration
t = t + 1 |
3. Proposed Method
For BP decoders, an internal LLR value is computed as
, which represents a statistical inference at each node [
8]. It is natural that the larger the absolute LLR values, the more reliable are the estimations expected. Using this LLR property, the previous threshold-based method presents a termination criterion to check whether all the magnitudes of
at the left-most nodes are larger than the predetermined threshold [
15]. As the comparison for each LLR value leads to
N comparisons, the threshold-based method first finds the minimum value, and then the minimum value is compared with the threshold value [
15]. Although the previous criterion [
15] succeeded in presenting an early-termination technique in a BP [
8] decoder for the first time, it needs optimization in terms of the hardware complexity. Especially, as the previous threshold-based method [
15] considers LLR values for every bit to check the early-termination criterion, the threshold-based method [
15] has a high hardware complexity. We first present two propositions to simplify the previous threshold-based early-termination technique [
15], and next describe a structure for the proposed early-termination technique. Lastly, we emphasize the advantages of the proposed technique by comparing it with information-BER-based [
16] and frozen-BER-based [
17] early-termination methods.
Proposition 1: .
According to (1) and (2), the right-LLR for the information set and frozen set at the left-most nodes are initialized as zero and infinity, respectively. Since the initial values of of the frozen set at the left-most nodes are infinity, the magnitude of in information set A is always less than the magnitude of in frozen set . As the minimum LLR value is important to check the termination condition, comparisons of the frozen set are no longer necessary.
Proposition 2: .
According to Equation (1), the right-LLR for information set A at the left-most nodes are initialized as zeroes so that directly becomes . Instead of finding the minimum among in information set A, the proposed method tries to find the minimum among demanding no additions. After finding the minimum value of left-LLR among the information set values, the minimum value can be compared to the pre-determined threshold value β.
Based on Propositions 1 and 2, we modified the threshold-based method [
15], resulting in the proposed early-termination algorithm as shown in Algorithm 4. The proposed early termination checks the condition if all the left-LLR
values for information set
A at the left-most nodes are larger than the threshold value. Note that no degradation is introduced compared to the threshold-based method [
15], as the same frame-error-rate performances are guaranteed according to Propositions 1 and 2 with the same number of decoding iterations compared with the threshold-based method [
15].
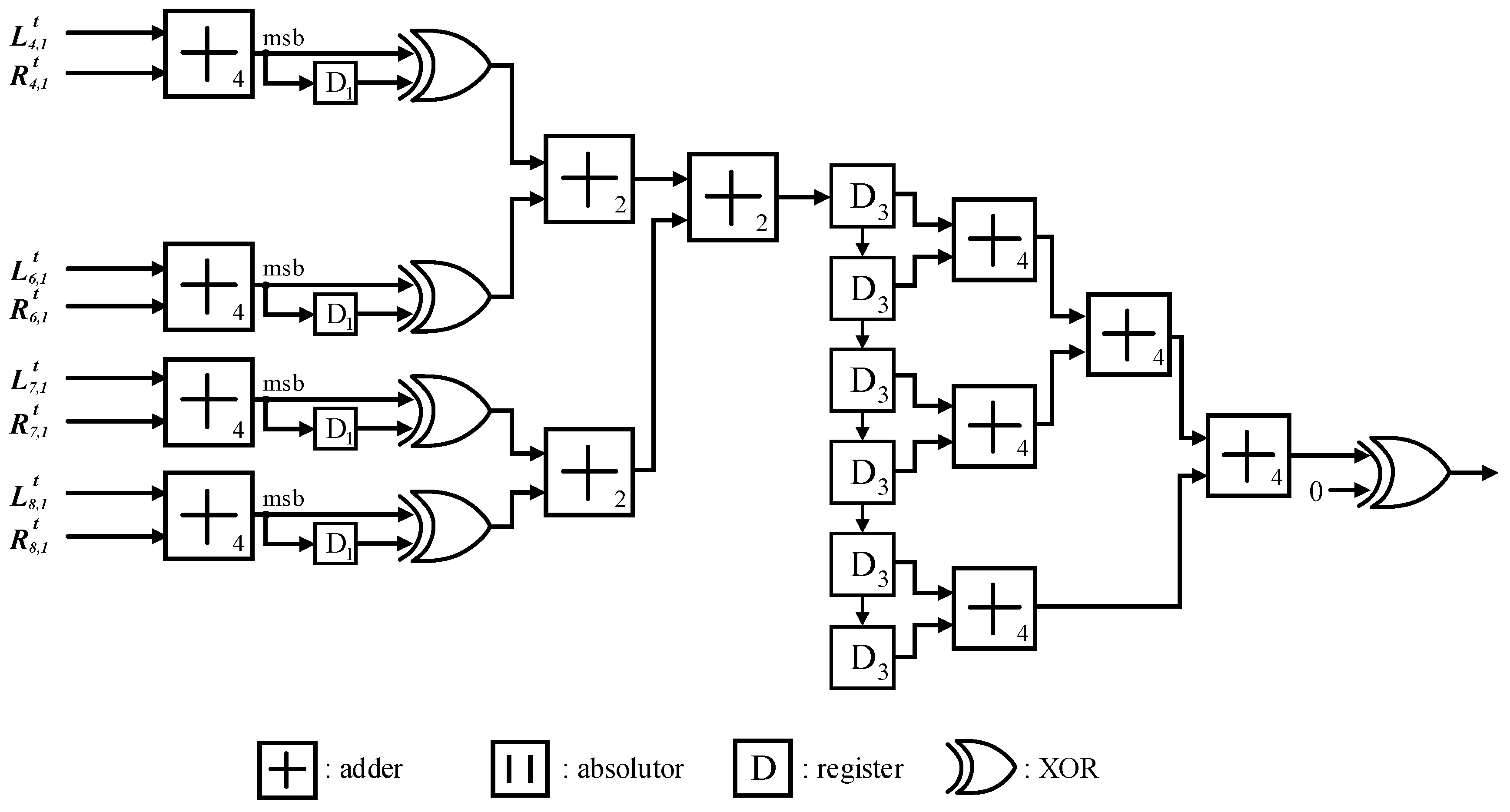
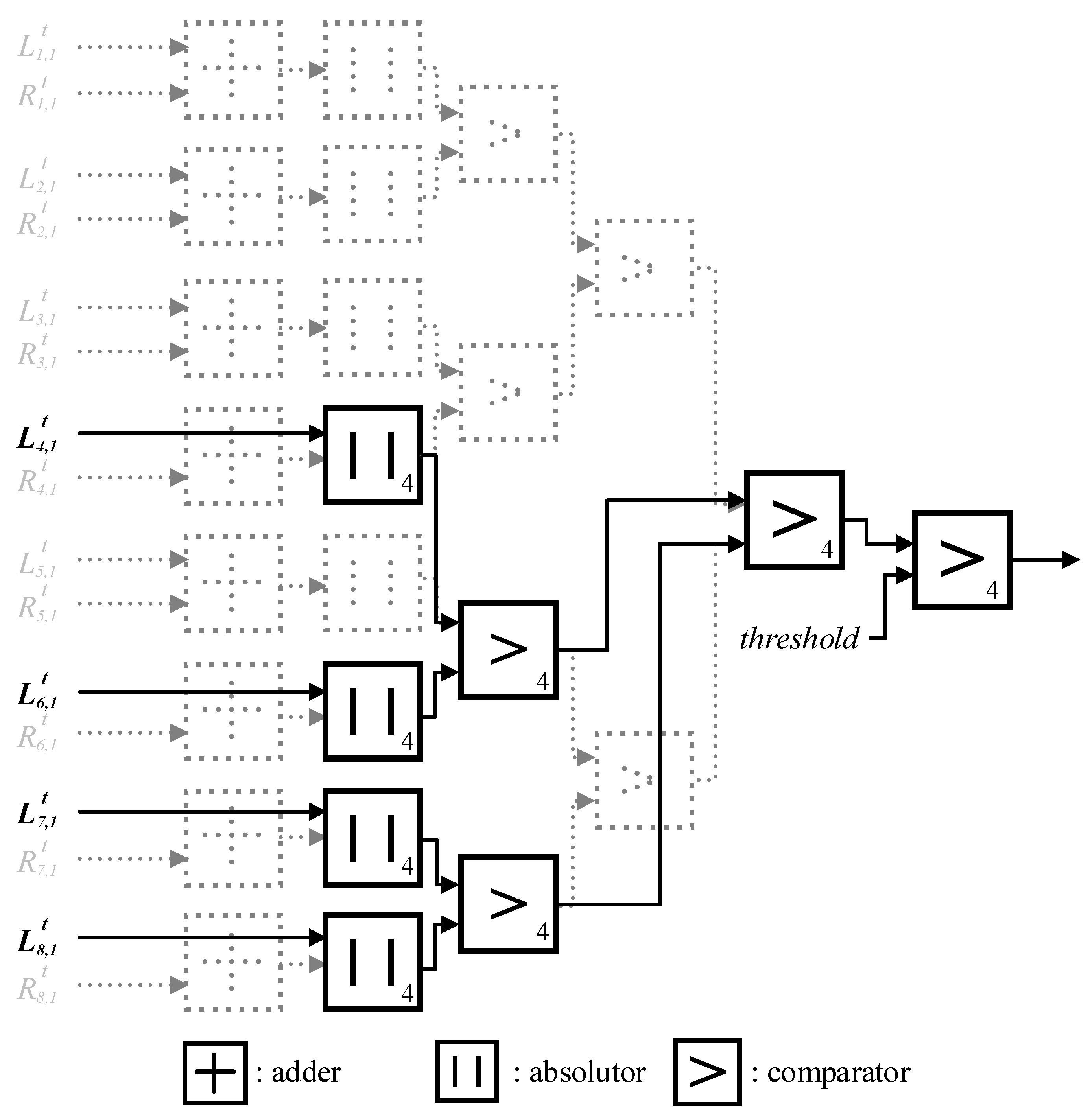
For instance,
Figure 6 represents the hardware architecture of the proposed early-termination technique for (8, 4) polar codes, where the dotted lines indicate the eliminated circuits from the previous threshold-based method [
15]. In
Figure 6, the proposed method requires a total of 4 absolute operators and 4 comparators, and the proposed method for (
N, K) polar codes requires
K absolute operators and
K comparators. We assumed the information set represented by
A to be {4, 6, 7, 8}, and the frozen set represented by
to be {1, 2, 3, 5} without loss of generality. As shown in
Figure 6, the circuitry for the frozen sets is completely eliminated, and the adders for the information set are also eliminated. Therefore, the proposed early termination provides an area-efficient solution without any degradation in system or error-correcting performance.
Furthermore, the proposed early-termination algorithm alleviates the disadvantages of information-BER-based [
16] and frozen-BER-based [
17] methods. Due to the use of the windowing approach, information-BER-based [
16] and frozen-BER-based [
17] methods terminate the decoding process when there are no changes on information or frozen bit channels within the window size, respectively. From the perspective of hardware complexity, information-BER-based [
16] and frozen-BER-based [
17] algorithms require several registers to store and check the current state within the window size, but the proposed method does not require any registers by not employing the windowing approach. From the perspective of system performance, information-BER-based [
16] and frozen-BER-based [
17] methods have a slight degradation on the decoding throughput compared with the proposed method, since an infinitely long window size is not feasible. For a more in-depth discussion, we will provide various practical experimental results in
Section 4.
4. Experimental Results
To compare various early-termination criteria, we simulated (1024, 512) polar decoding under different channel conditions. For a fair comparison, we carefully set the maximum decoding iteration
T at 40 and the threshold value at 3.5, obtained from a previous study [
15], to maintain the same level of error-correcting performance. Thus, the early-termination criteria [
15,
16,
17] did not affect the error-correcting performance but affected the average number of decoding iterations.
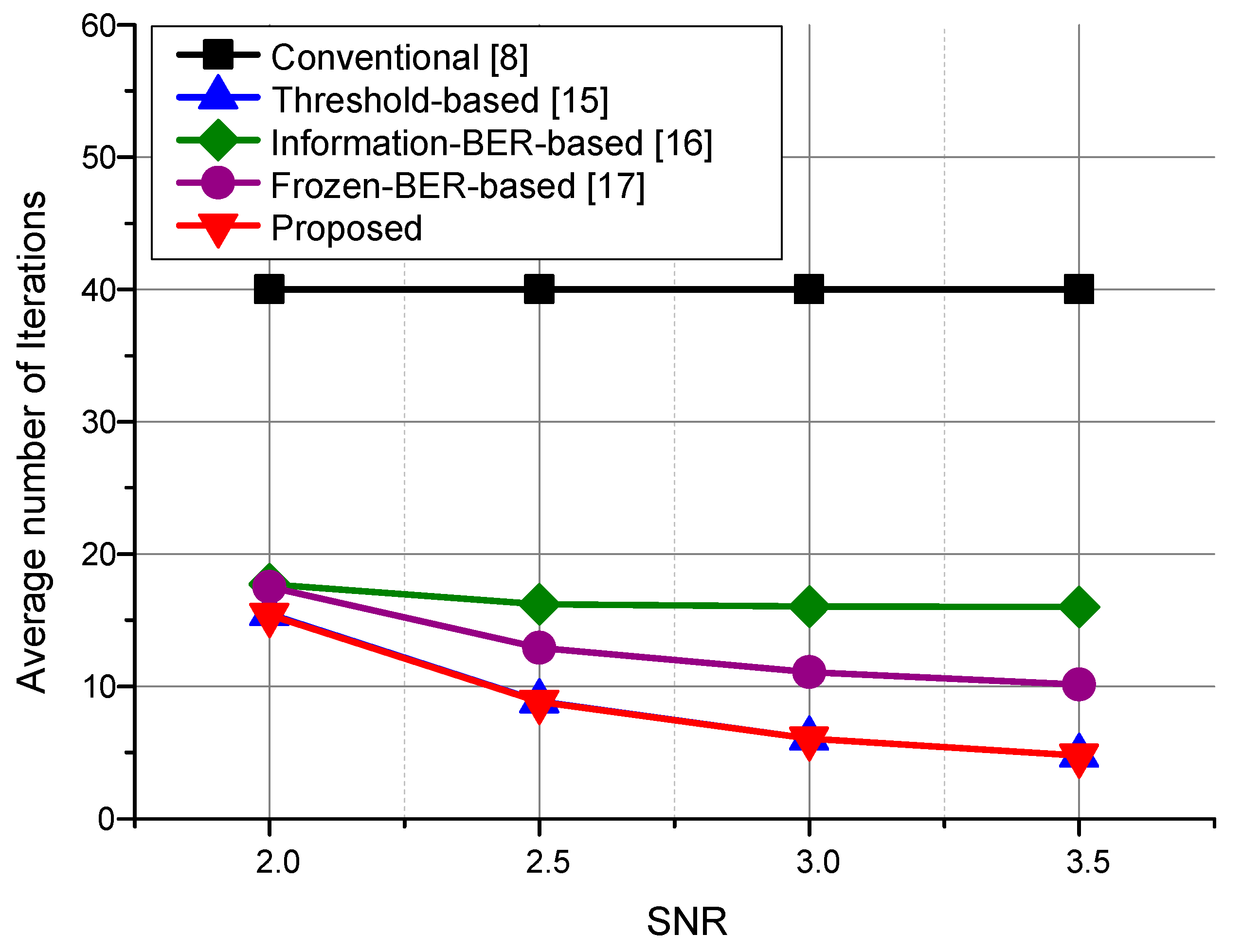
Figure 7 shows the average number of decoding iterations for the conventional [
8], threshold-based [
15], information-BER-based [
16], frozen-BER-based [
17], and proposed methods. In the conventional BP decoder with no early-termination technique, 40 decoding iterations were required regardless of the SNRs. The previous threshold-based [
15] and proposed early-termination methods [
15,
16,
17] have the same number of decoding iterations, as the proposed method simplifies circuitry checking without affecting the decoding performance. The information-BER-based [
16] and the frozen-BER-based [
17] methods require a slightly higher number of decoding iterations compared with the threshold-based [
15] and proposed methods.
For a complexity comparison, termination check circuitries for different methods were implemented using 65-nm CMOS (complementary metal-oxide-semiconductor) technology with an operating frequency of 200 MHz. All the internal LLR values are assumed as 4 bits.
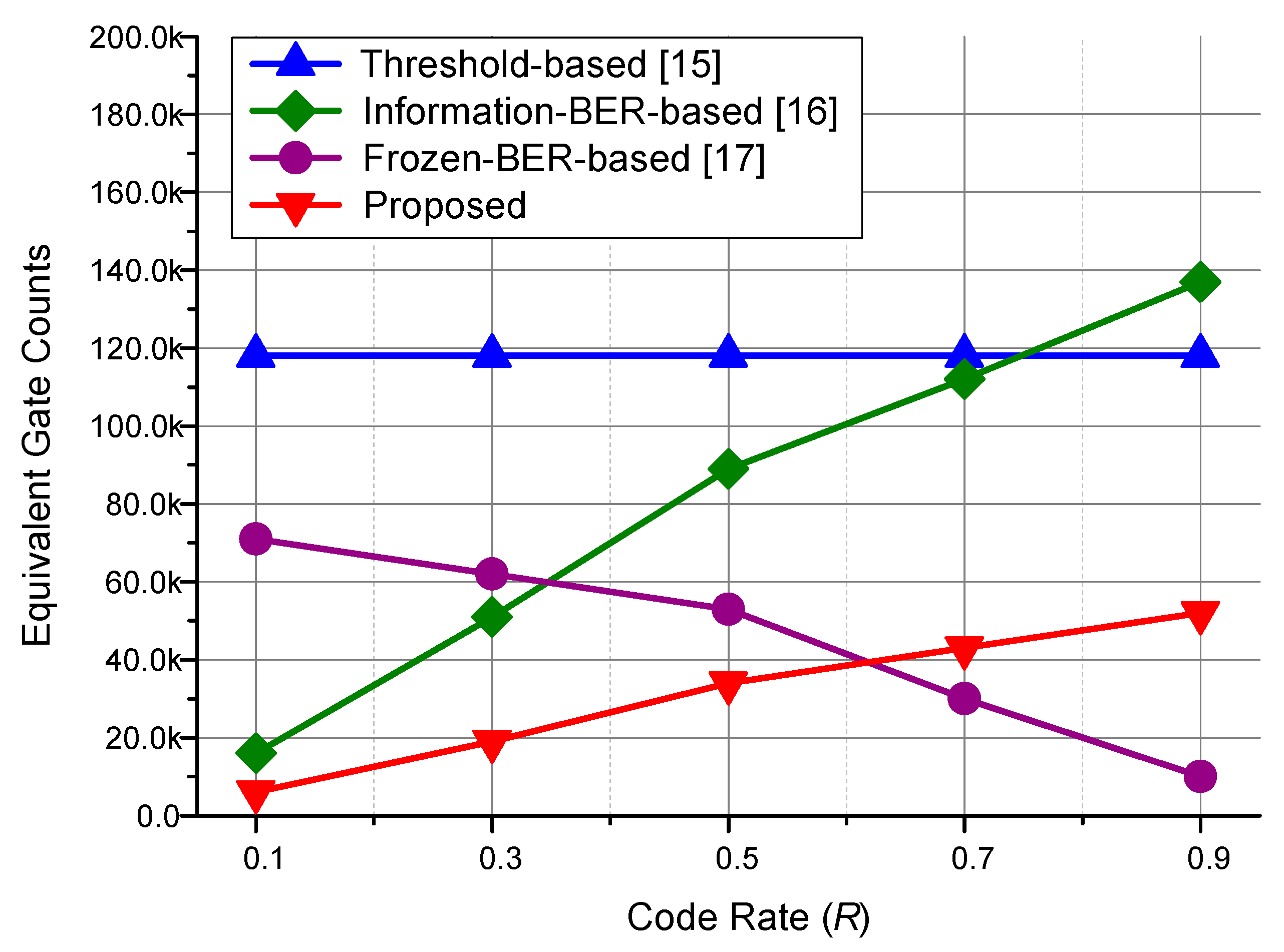
Figure 8 shows the equivalent gate counts for polar (1024,
K) according to the code rate
R =
K/
N. As the code rate increases, the equivalent gate count of the information-BER-based [
16] and proposed methods increases, and frozen-BER-based [
17] method decreases gradually. For code rate up to 0.6, the proposed algorithm requires the smallest equivalent gate counts, and the frozen-BER-based [
17] method has the smallest count when the code rate is higher.
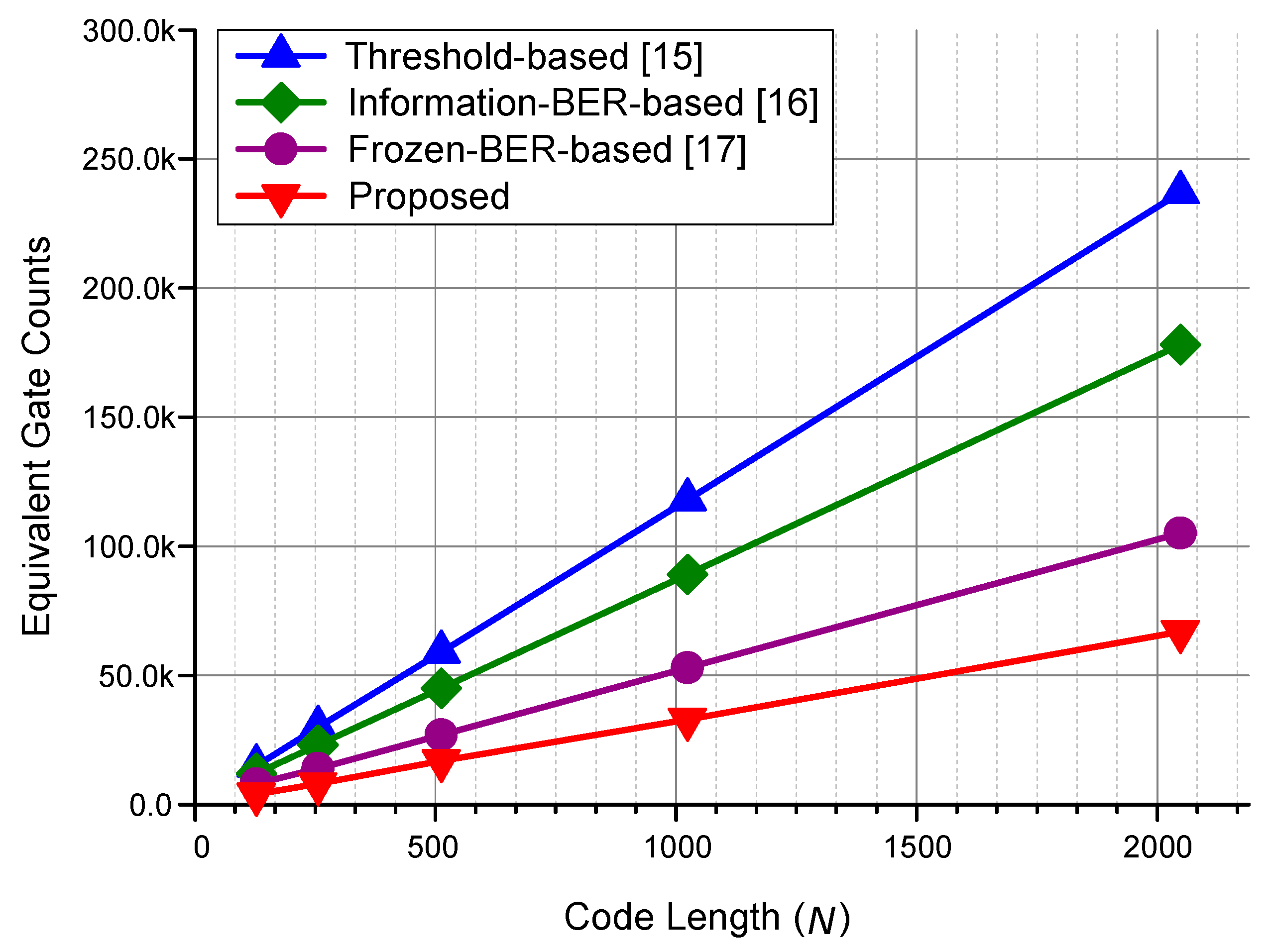
Figure 9, gate counts according for polar (
N,
N/2) to the code length with the code rate = 1/2. According to
Figure 8, as for (1024, 512) polar codes, the proposed method can reduce hardware complexities by 72.7%, 66.5%, and 59.7% compared to the previous threshold-based [
15], information-BER-based [
16], and frozen-BER-based [
17] methods, respectively.
To sum up,
Table 1 summarizes the additional hardware resources required to check the termination condition for different early-termination methods. For previous information-BER-based [
16] and frozen-BER-based [
17] methods, the single-bit or double-bit operators including adders and XORs are not taken into account so as to simplify the complexity comparison. The previous threshold-based method [
15] requires circuitry checks associated with both information and frozen bit channels; previous windowing methods, including information-BER-based [
16] and frozen-BER-based [
17] methods, require circuitry checks associated with either entire information bit channels or frozen bit channels. Whereas the windowing methods [
16,
17] inevitably demand registers to save intermediate values, the proposed method simplifies the threshold-based method [
15] based on Propositions 1 and 2, resulting in the smallest hardware complexity without any registers. Furthermore, many applications using polar codes adopt a polar code with a small code rate. For instance, 5G communication recently adopted polar codes as control channel error correction codes, and the 5G control channel uses a small polar code with a code rate (
K/
N) less than 1/2. Thus, the additional circuitry for a polar code with a small code rate becomes negligible compared to the previous methods.