1. Introduction
Visual servoing has been employed to increase the deftness and intelligence of industrial robots, especially in unstructured environments [
1,
2,
3,
4]. Based on how the image data are used to control the robot, visual servoing is classified into two categories: position-based visual servoing (PBVS) and image-based visual servoing (IBVS). A comprehensive analysis of the advantages and drawbacks of the aforementioned methods can be found in [
5]. This paper focuses on addressing some issues in IBVS.
Many studies have been conducted to overcome the weaknesses of IBVS and improve its efficiency [
6,
7,
8,
9]. However, the performance of most reported IBVS is not sufficiently high to meet the requirements of industrial applications [
10]. An efficient IBVS feasible for practical robotic operations requires a fast response with strong robustness to feature loss. One obvious way to increase the speed of IBVS is to increase the gain values in the control law. However, there is a limitation on the application of this strategy because the high gain in the IBVS controller tends to create shakiness and instability in the robotic system [
11]. Moreover, the stability of the traditional IBVS system is proven only in an area around the desired position [
5,
12]. Furthermore, when the initial feature configuration is distant from the desired one, the converging time is long, and possible image singularities may lead to IBVS failure. To address this issue, a switching scheme is proposed to switch the control signal between low-level visual servo controllers, i.e., homography-based controller [
13] and affine-approximation controller [
14]. In our previous work [
15,
16], the idea of switch control in IBVS was proposed to switch the controller between end-effector’s rotating and translational movements. Although it has been demonstrated that the switch control can improve the speed and tracking performance of IBVS and avoid some of its inherent drawbacks, feature loss caused by the camera’s limited FOV still prevents the method from being fully efficient and being applicable to real industrial robots.
The visual features contain much information such as the robots’ pose information, the tasks’ states, the influence of the environment, the disturbance to the robots, etc. The features are directly related to the motion screw of the end-effector of the robot. The completeness of the feature set during visual servoing is key to fulfilling the task successfully. Many features have been used in visual servoing such as feature points, image moments, lines, etc. The feature points are known for the ease of image processing and extraction. It is shown that at least three image points are needed for controlling a 6-DOF robot [
17]. Hence, four image points are usually used for visual servoing. However, the feature points tend to leave the FOV during the process of visual servoing. A strategy is needed to handle the situation where the features are lost.
There are two main approaches to handle feature loss and/or occlusion caused by the limited FOV of the camera [
18]. In the first approach, the controller is designed to avoid occlusion or feature loss, while in the second one, the controller is designed to handle the feature loss.
In the first approach, several techniques have been developed to avoid the feature loss or occlusion. In [
19], occlusion avoidance was considered as the second task besides the primary visual servoing task. In [
20], a reactive unified convex optimization-based controller was designed to avoid occlusion during teleoperation of a dual-arm robot. Some studies have been carried out in visual trajectory planning considering feature loss avoidance [
21,
22,
23]. Model predictive control methods have been adopted in visual servoing to prevent feature loss due to its ability to deal with constraints [
24,
25,
26,
27,
28]. In [
29], predictive control was employed to handle visibility, workspace, and actuator constraints. Despite the success of the studies on preventing feature loss, they suffered from the limited maneuvering workspace of the robot, due to the conservative design required to satisfy many constraints.
In the second approach, the controller tries to handle the feature loss instead of avoiding it. When the loss or occlusion of features occurs, if the remaining visible features are sufficient to generate the non-singular inverse of the image Jacobian matrix, the visual servoing task can still be carried out successfully. In this situation, the rank of the relative Jacobian matrix must be the same as the degrees of freedom [
30]. However, this method is no longer effective when the number of remaining visible features become too small to guarantee the full-rankness of the image Jacobian matrix. As studied in [
31], another solution is to foresee the position of the lost features and to continue the control process using the predicted features until they become visible again. This method allows partial or complete loss or occlusion of the features. In the second approach [
30,
31], the classical IBVS control is employed as the control method, which does not usually provide a fast response.
In this paper, an enhanced switch image-based visual servoing (ESIBVS) method is presented in which a Kalman filter-based feature prediction algorithm is proposed and is combined with our previous work [
15,
16] to make the switch IBVS control robust in reaction to feature loss. The feature prediction algorithm can predict the lost feature points based on the previously-estimated points. The switch control with the improved tracking performance along with the robustness to feature loss makes it more feasible for industrial robotic applications. To validate the proposed controller, extensive simulations and experiments have been conducted on a 6-DOF Denso robot with a monocular eye-in-hand vision system.
The structure of the paper is given as follows.
Section 2 gives a description of the problem. In
Section 3, the feature reconstruction algorithm is presented. In
Section 4, the controller design algorithm is developed. In
Section 5, the simulation results are given. Experimental results are presented in
Section 6, and finally, the concluding remarks are given in
Section 7.
2. Problem Statement
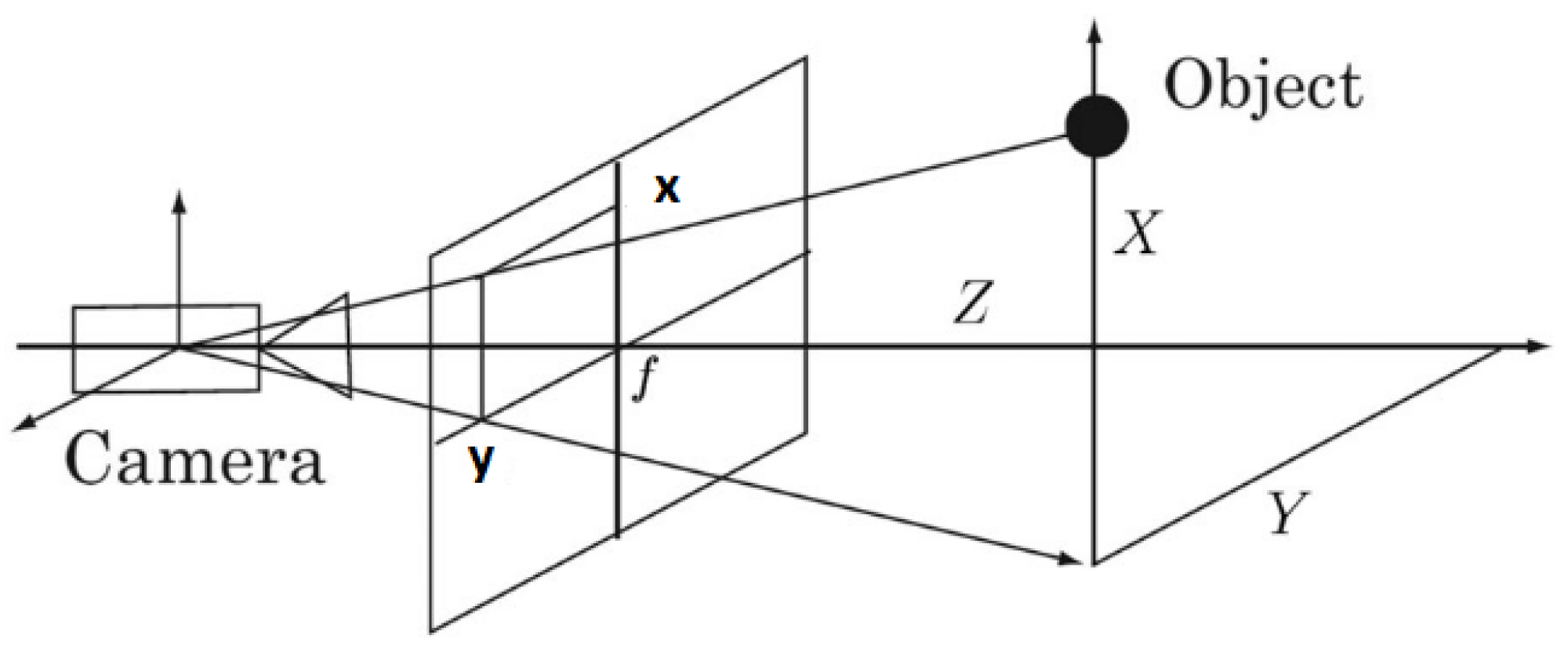
In IBVS, the object with
coordinates with respect to camera has the projected image coordinates
in the camera image (
Figure 1). The feature’s positions and the desired ones for the
feature in the image plane can be denoted by:
Thus, the vector of
s and
is defined as:
The goal of the IBVS task is to generate camera velocity commands such that the actual features and the desired ones are matched in the image plane. The velocity of the camera is defined as
. The camera and image feature velocities are related by:
where,
which is called the image Jacobian matrix and
are the depths of the features
. In this study, the system configuration is set as eye-in-hand, and the number of features is
. Furthermore, it is assumed that all the features share the same depth
Z. Considering these assumptions, the image Jacobian matrix for the
feature is given in [
17]:
where
f is the focal length of the camera.
The velocity of the camera can be calculated by manipulating (
3):
where
is the pseudo-inverse of the image Jacobian matrix. The error signal is defined as
. If we let
, the traditional IBVS control law may be designed as:
where
is the proportional gain.
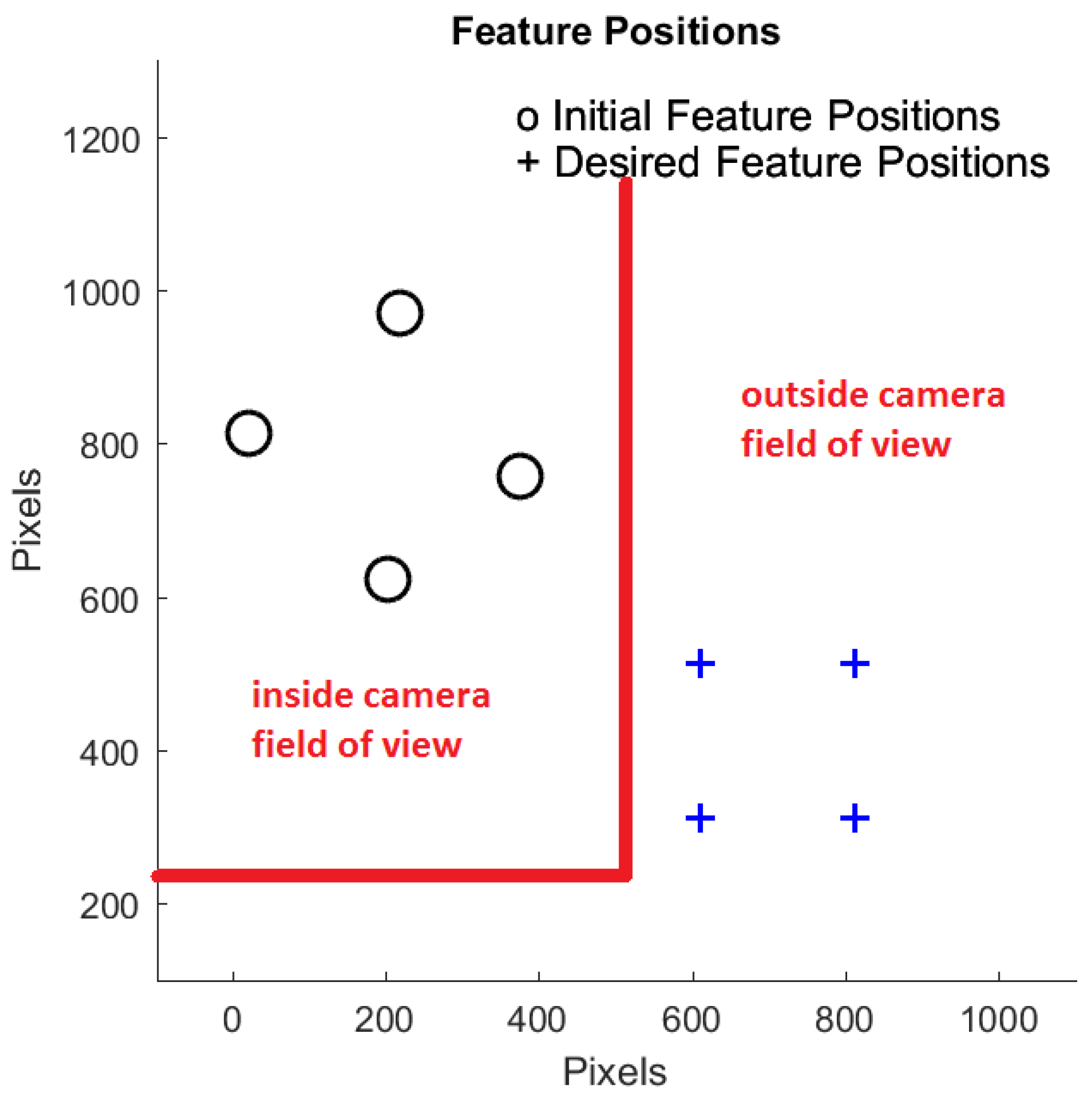
While guiding the robot end-effector to make the desired image features match the actual ones, some unexpected situations may occur in IBVS. The first case is feature loss: i.e., some or all of the image features may go beyond the camera’s FOV (
Figure 2). The second case is feature occlusion: i.e., some or all of the image features temporarily become invisible to the camera due to obstacles. The goal of this paper is to improve the performance of IBVS in terms of response time and tracking performance, while dealing with the feature loss situation. To reach this goal, the performance of the switch method in our previous work [
15,
16] is enhanced when it is combined with the proposed feature reconstruction algorithm.
3. Feature Reconstruction Algorithm
The velocity of the camera
can be divided into the translational velocity
and rotating velocity
. Therefore, it can be expressed as:
Furthermore, for the
feature
, the image Jacobian matrix in (
5) can be divided into the translational part
and the rotating part
:
where,
and:
where
and
are the feature coordinates in the image space.
In the design of the switch controller, the movement of the camera during the control task is divided into three different stages [
15,
16]. In the first stage, the camera has only pure rotation. In the second stage, the camera has only translational movement. Finally, in the third stage, both camera rotation and translation are used to carry out the fine-tuning.
Considering (
3), (
8), (
10) and (
11), the feature velocity in the image plane can be expressed as:
In the pure translational stage (first stage):
In the pure rotating stage (second stage):
and in the fine-tuning stage (third stage):
To remove the noise in the image processing and feature extraction, a feature state estimator is designed based on the Kalman filter algorithm.
In the formulations below,
k denotes the current time instant and
the next time instant, while
represents the sampling time. The estimated states are denoted by
notation. Considering four features, the feature state at the current instant (
sample) is defined as:
or with consideration of (
2):
where the elements of the vector can be obtained from (
12), (
13), or (
14). Furthermore, the measurement vector represents the vector of the image feature points’ coordinates extracted from the images of the camera:
First, the prediction equations are:
where
A is a
matrix whose diagonal elements equal one,
are equal to sampling time
, and the rest of the elements are zero,
represents the current prediction of the error covariance matrix, which gives a measure of the state estimate accuracy, while
is the previous error covariance matrix, and
represents the process noise covariance computed using the information of the time instant
.
Second, the Kalman filter gain
is:
where
is the previous measurement covariance matrix.
Third, the estimation update is given as follows:
When the features are out of the FOV of the camera (i.e.
,
,
), the feature reconstruction algorithm is proposed to provide the updated estimation vector under this circumstance. Since the features are out of FOV, the measurement vector will have some elements with zero values. This measurement vector will not lead to a satisfactory performance of switch IBVS. In order to improve the performance, instead of having zero values of the elements of
in (
17), it is reasonable to assume that the
feature that goes outside of FOV keeps its velocity at the moment (
) of leaving (
) during the period of feature loss. Hence, its position (i.e., point coordinates
]) can be generated by integrating the velocity over the time. This means that the elements of
can be represented by this formulation:
where
represents the number of time samples during the feature loss period,
is the sampling period, and
is an adjusting coefficient. Once the feature is visible to the camera again, the actual value of
provided by the camera is used to replace the state estimation (
21).
4. Controller Design
The IBVS controller was designed using the switch scheme. This method can set distinct gain values for the stages of the control law to achieve a fast response system while preserving the system stability.
In order to design the switch controller, the movement of the camera during the control task was divided into three different stages [
15,
16]. A criterion was needed for the switch condition between stages. In [
15], the norm of feature errors was defined as the switching criterion. In this paper, a more intuitive and effective criterion is used [
16]. As is shown in
Figure 3, the switch angle criterion
is introduced as the angle between actual features and the desired ones. As soon as the angle
meets the predefined value, the controller law switches to the next stage.
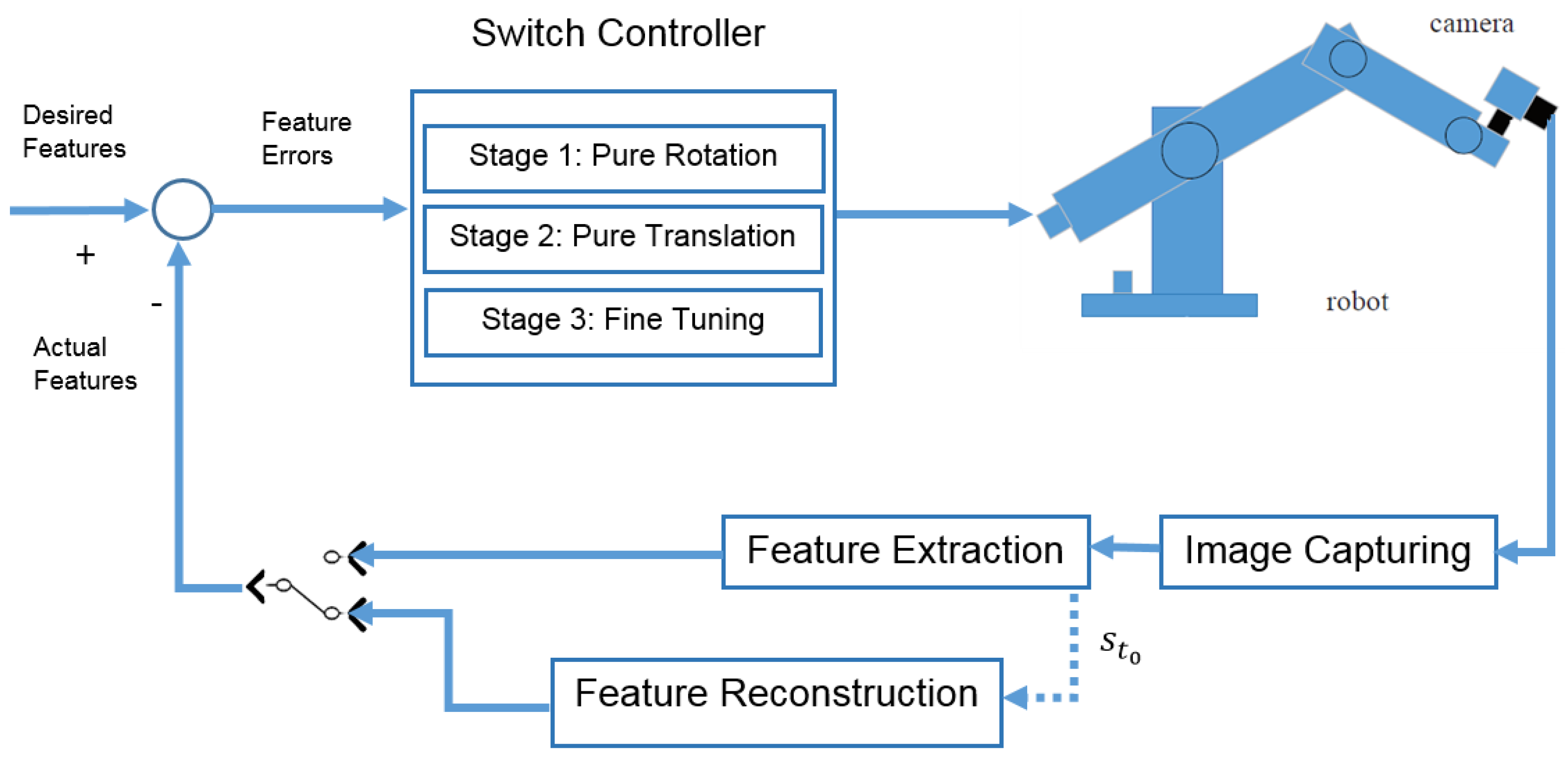
Based on this criterion, the switching control law is presented as follows:
where
(
) is the velocity of the camera in the
stage,
is the symmetric positive definite gain matrix at each stage, and
and
are two predefined thresholds for the control law to switch to the next stage. The block diagram of the proposed algorithm is shown in
Figure 4. Furthermore, the flowchart of the whole process of feature reconstruction and control is illustrated in
Figure 5.
It was expected that in comparison with switch IBVS, the proposed method would ensure the smooth transition of the visual servoing task in the case of the feature loss and provide a better convergence performance.
5. Simulation Results
To evaluate the performance of the proposed method, simulation tests were carried out by using MATLAB/SIMULINK software with the Vision and Robotic Toolbox. A 6-DOF DENSO robot with a camera installed in eye-in-hand configuration was simulated. The coordinates of the initial and desired features in the image space are given in
Table 1. The camera parameters are as shown in
Table 2.
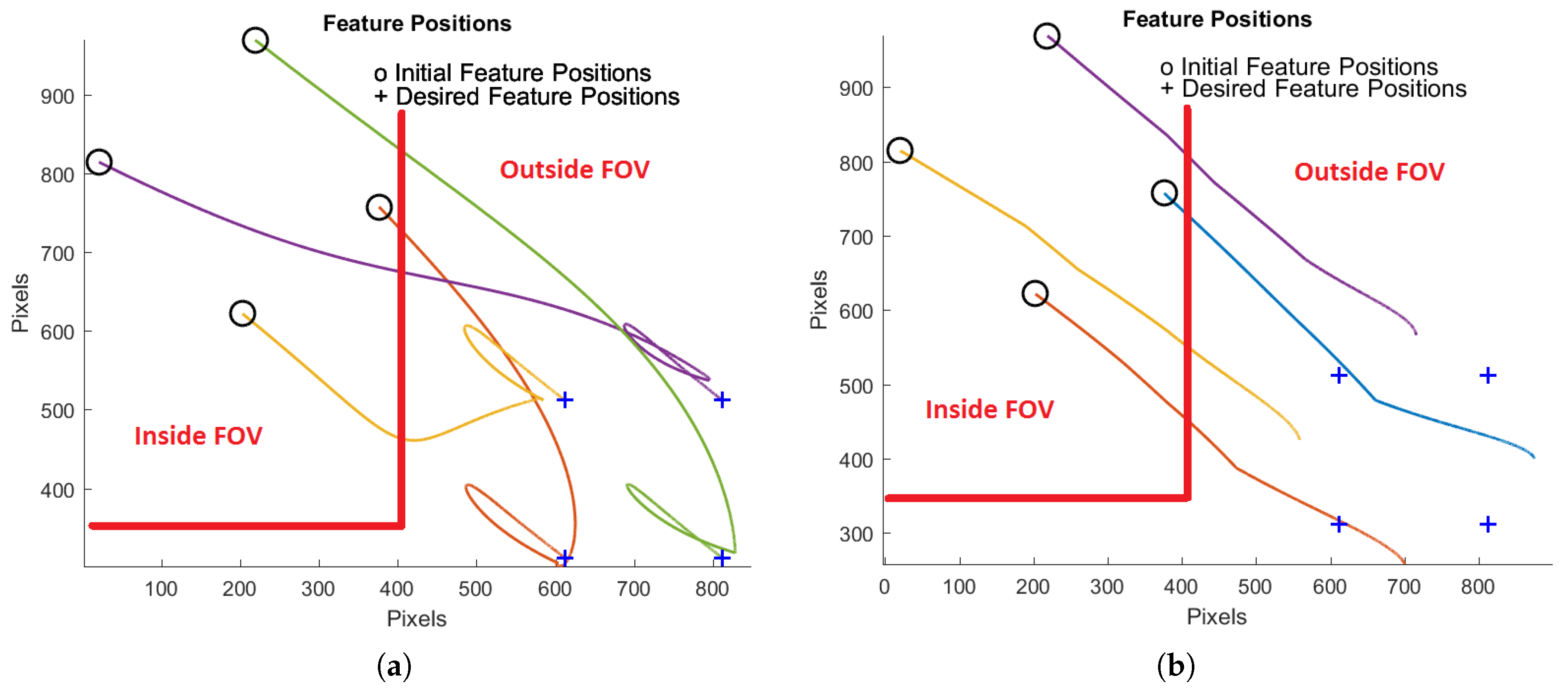
The task was to guide the end-effector to match the actual features with the desired ones in the camera image space. To simulate the condition where the features go outside FOV of the camera in real applications, the FOV of the camera was defined as the limited area shown in
Figure 6a,b. When the features were in the defined FOV, they had actual position coordinates, and when they went outside FOV, the position coordinates of the features were set to zero. In this case, the proposed feature reconstruction algorithm was activated, and an estimate of the feature positions was generated. The norm of feature errors (NFE) is defined as below,
where
and
are the
feature coordinates and
and
are the
desired feature coordinates in the image plane.
In the simulation test, we set the initial feature coordinates and the desired ones in a way that the image features were out of FOV.
Figure 6 and
Figure 7 demonstrate the performance comparison of the two methods. The paths of image features in the image space are given in
Figure 6a,b.
Figure 7a,b shows how the feature errors change with time in the proposed ESIBVSand switch method.
Figure 7c,d demonstrates the norm of the feature errors’ change with time in both methods. As shown in the figures, ESIBVS was able to reduce the norm of the errors to the preset threshold, while in the switch method, the norm of the errors did not converge. The summary of the simulation test is shown in
Table 3. The results demonstrate how the proposed method was able to handle the situation in which the features went outside of the camera’s FOV and completed the task successfully, while the switch method was unable to do so.
6. Experimental Results
In this section, to further verify the effectiveness of the proposed method, some experiments were carried out, and the results are presented. The experimental testbed included a 6-DOF DENSOrobot with a camera (specifications shown in
Table 2) installed on its end-effector (
Figure 8a). The camera model was a Logitech Webcam HD 720p, which captures the video with a resolution of
pixels.
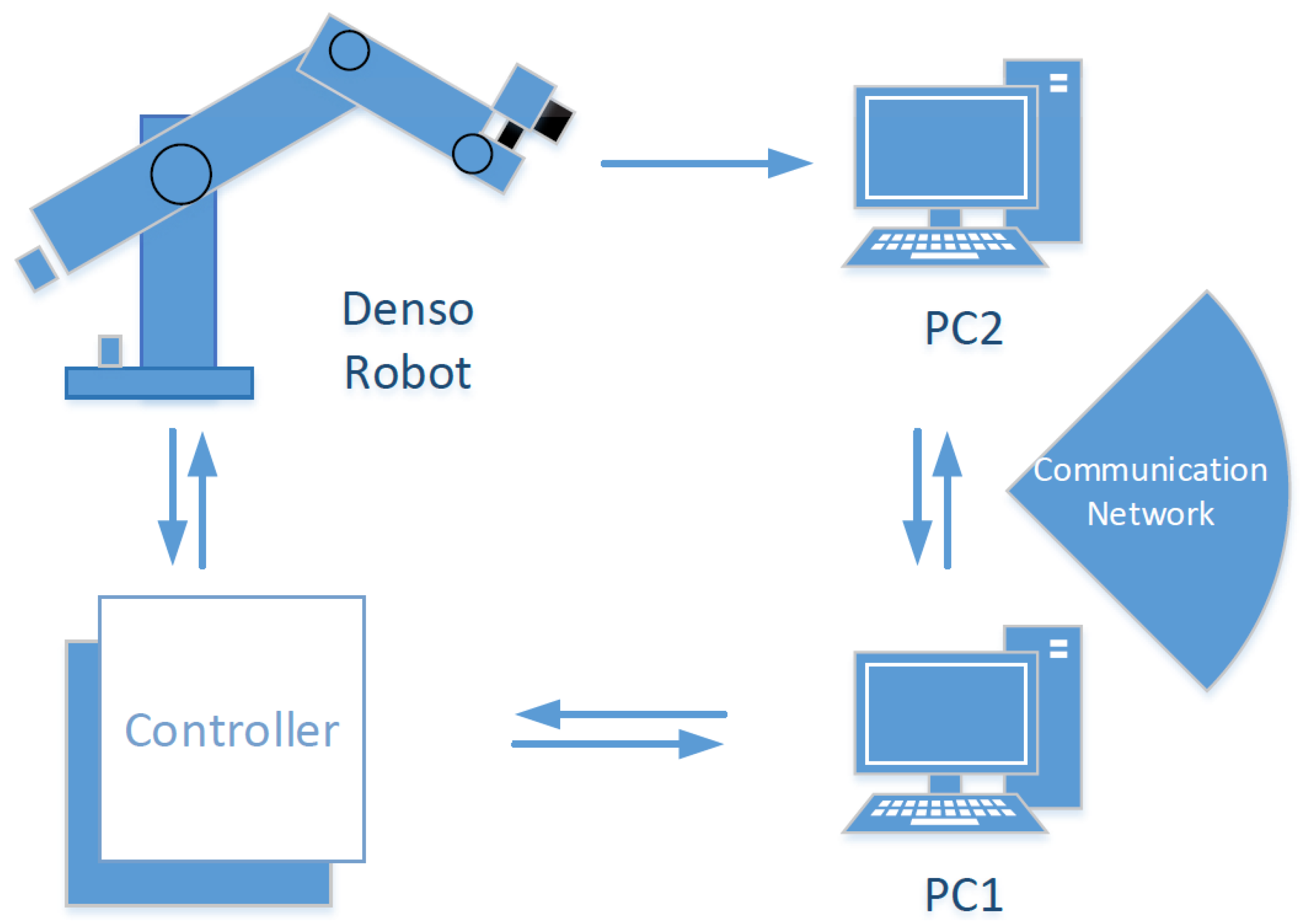
Two computers were used for the experimental tests. One computer carried out the image processing (PC2 in
Figure 9) and sent the extracted feature coordinates to the other computer (PC1 in
Figure 9), where the control algorithm was executed. Then, the control command (velocity of the end-effector) was sent to the robot controller. The image data taken by the camera were sent to an image processing program written by using the Computer Vision Toolbox of MATLAB. This program extracted the center coordinates of the features and sent them as feedback signals to the visual servoing controller in the sampling period of
s. Four feature points were used in the control task. The detailed information of the image processing and feature extraction algorithm can be seen in our previous work [
32]. The goal was to control the end-effector so that the actual features matched the desired ones (
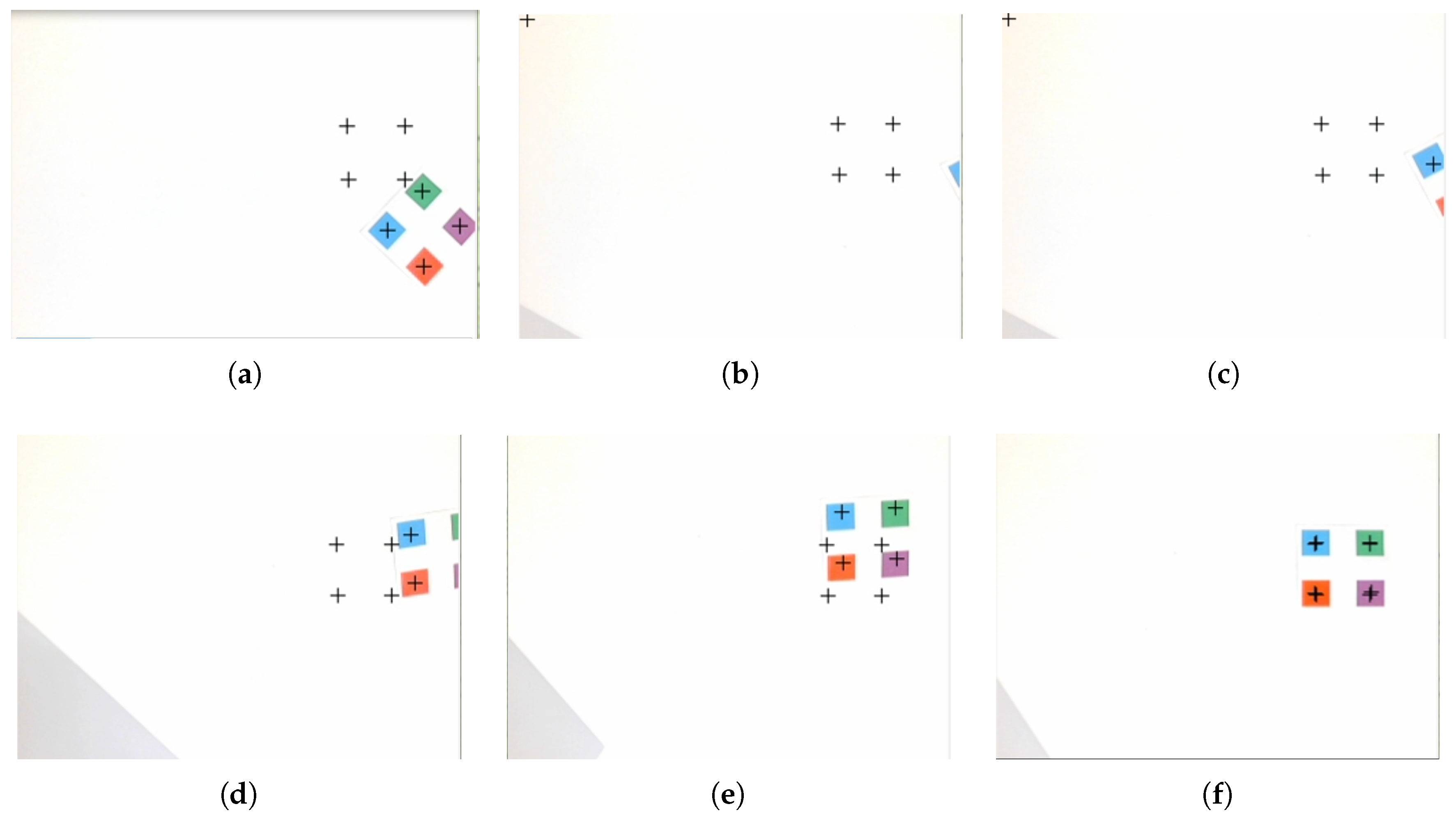
Figure 8b).
To evaluate the efficiency of ESIBVS, its performance was compared to that of the switch IBVS method. In all the tests, the threshold value of NFE was set to 0.005 (equivalent to four pixels). When NFE reached this value, the robot stopped, and the servoing task was fulfilled. The initial angle
between the actual and desired features (
Figure 3) was
.
,
, and
in (
22) were set to 1,
, and
, respectively.
Test 2: In this test (The video can be found in the
Supplementary Materials), the initial and desired features were set such that they went outside of the FOV of the camera during the test. The initial and desired feature coordinates in the test are given in
Table 4.
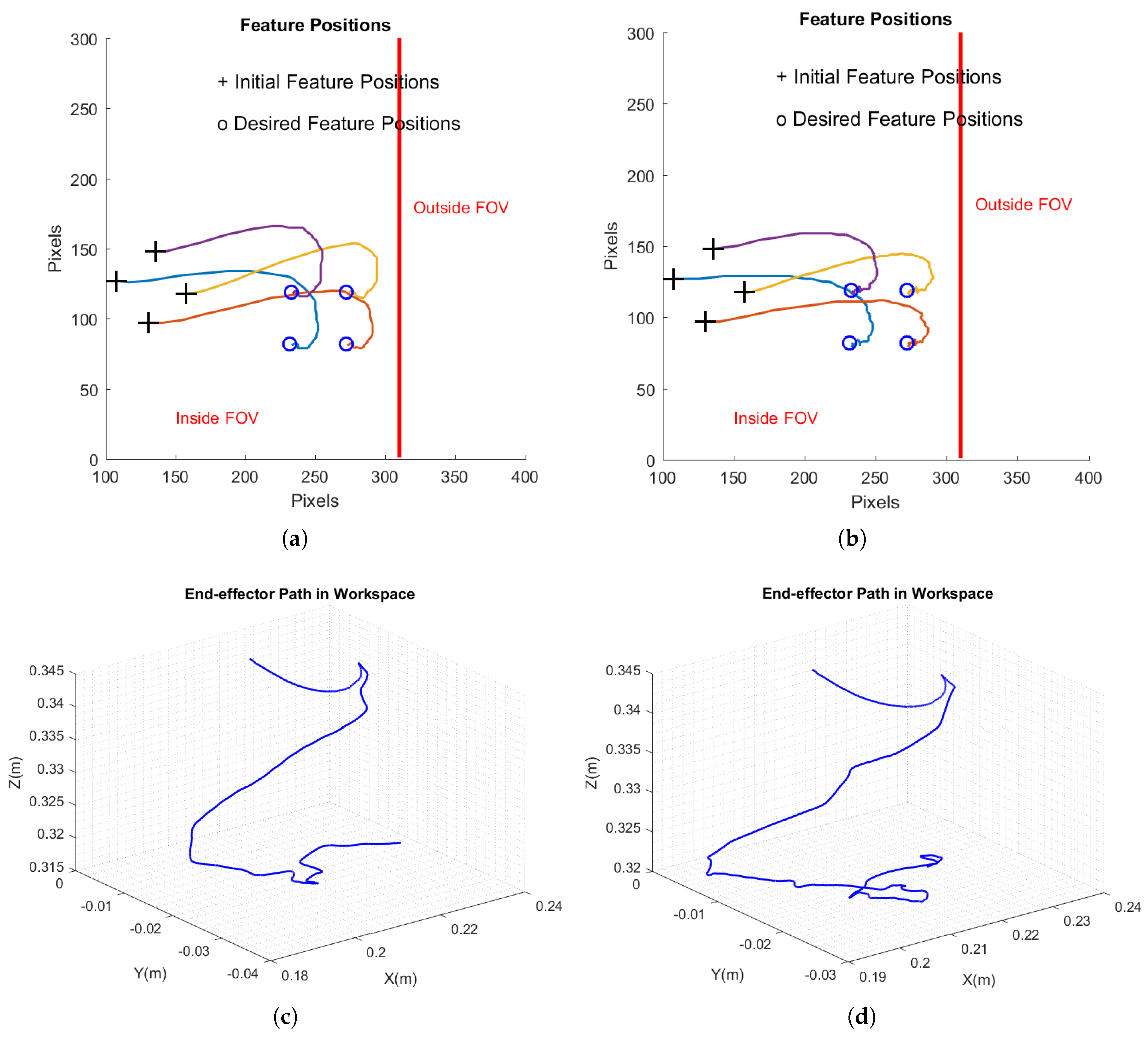
Figure 10 demonstrates the movement of actual features during the test of ESIBVS. It illustrates how the features went outside of FOV, then were reconstructed, went back to FOV, and finally matched the desired features.
Figure 11,
Figure 12 and
Figure 13 show the comparison results between ESIBVS and switch IBVS.
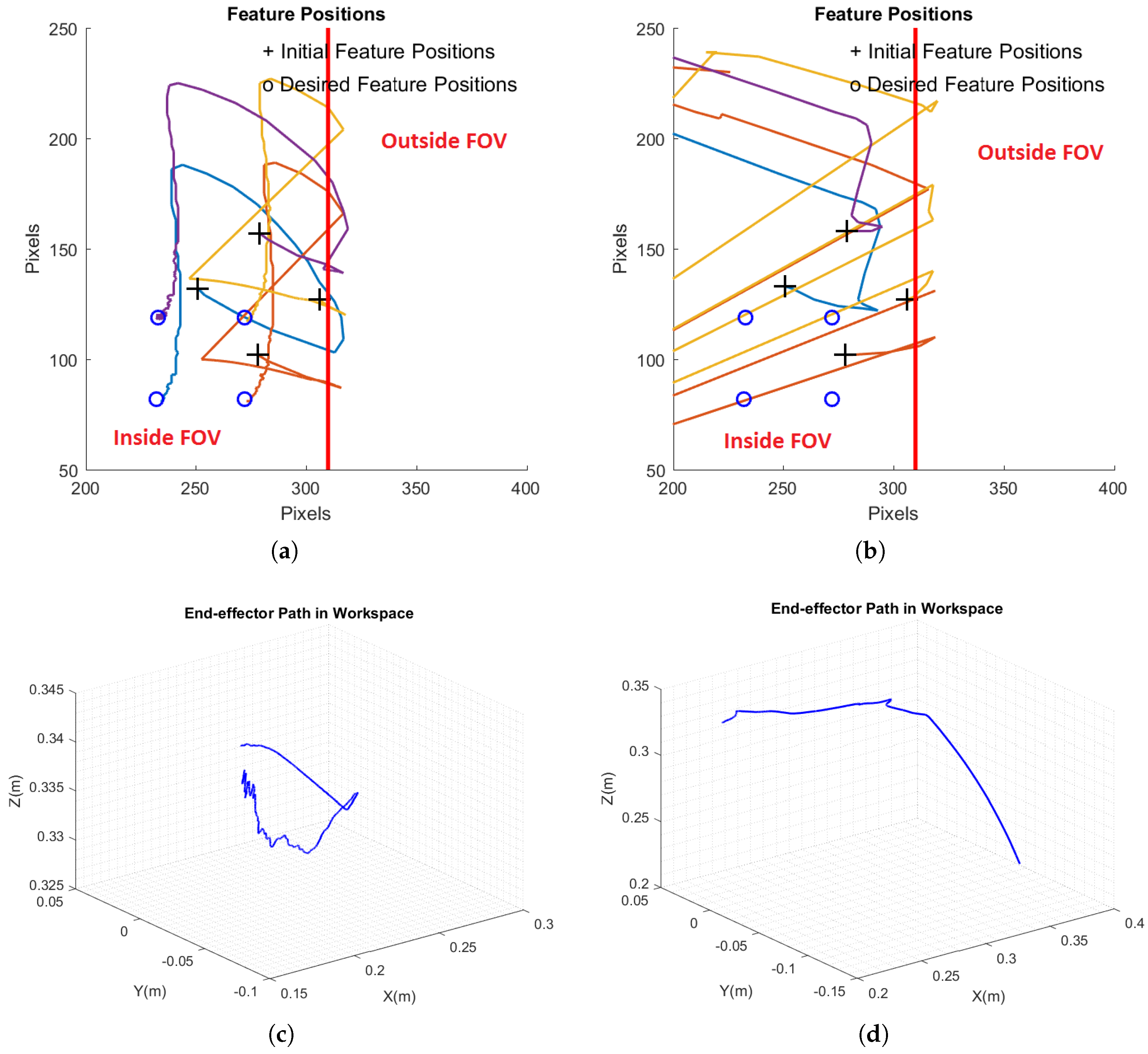
Figure 11 shows the paths of features in the image space from the initial positions to the desired ones, as well as the camera trajectory in Cartesian space. In the proposed method, the actual and desired features matched, while in switch IBVS, the actual features did not converge to the desired ones.
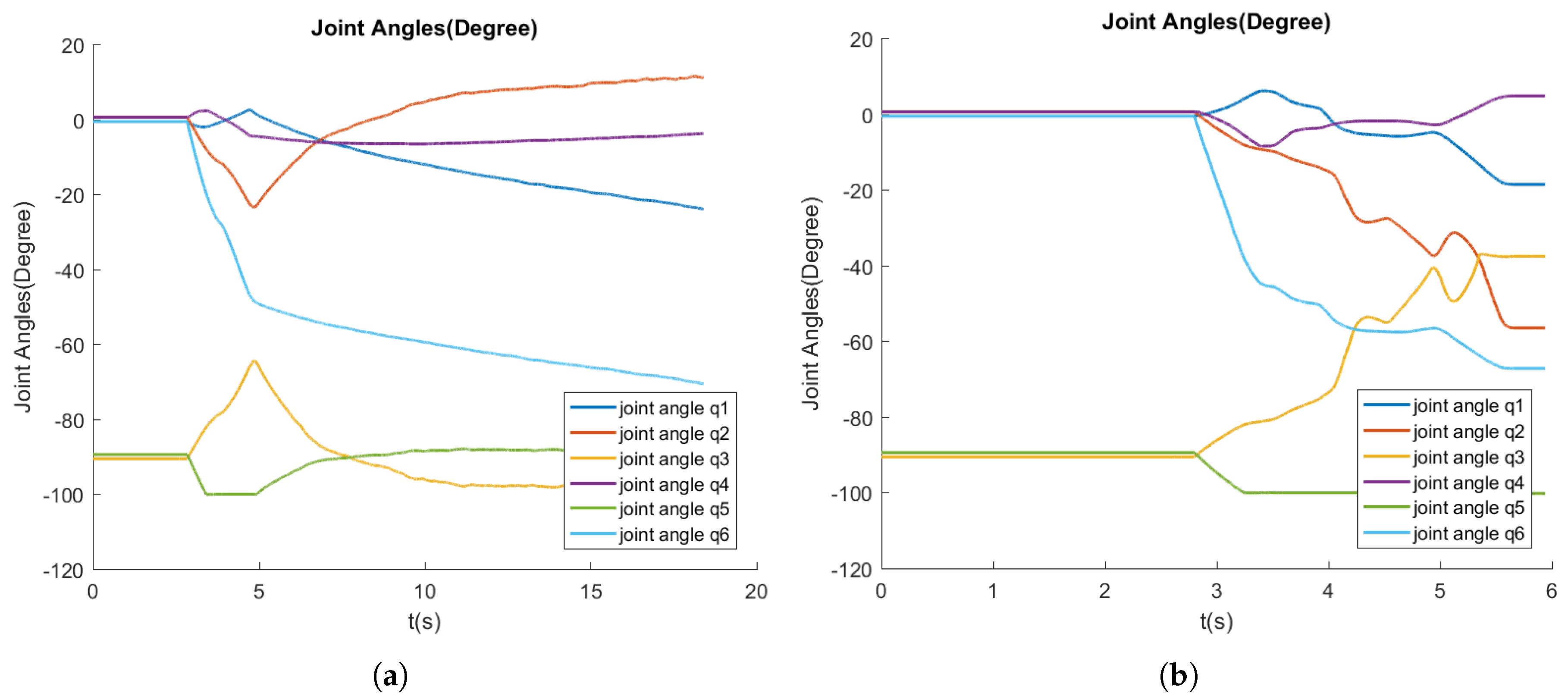
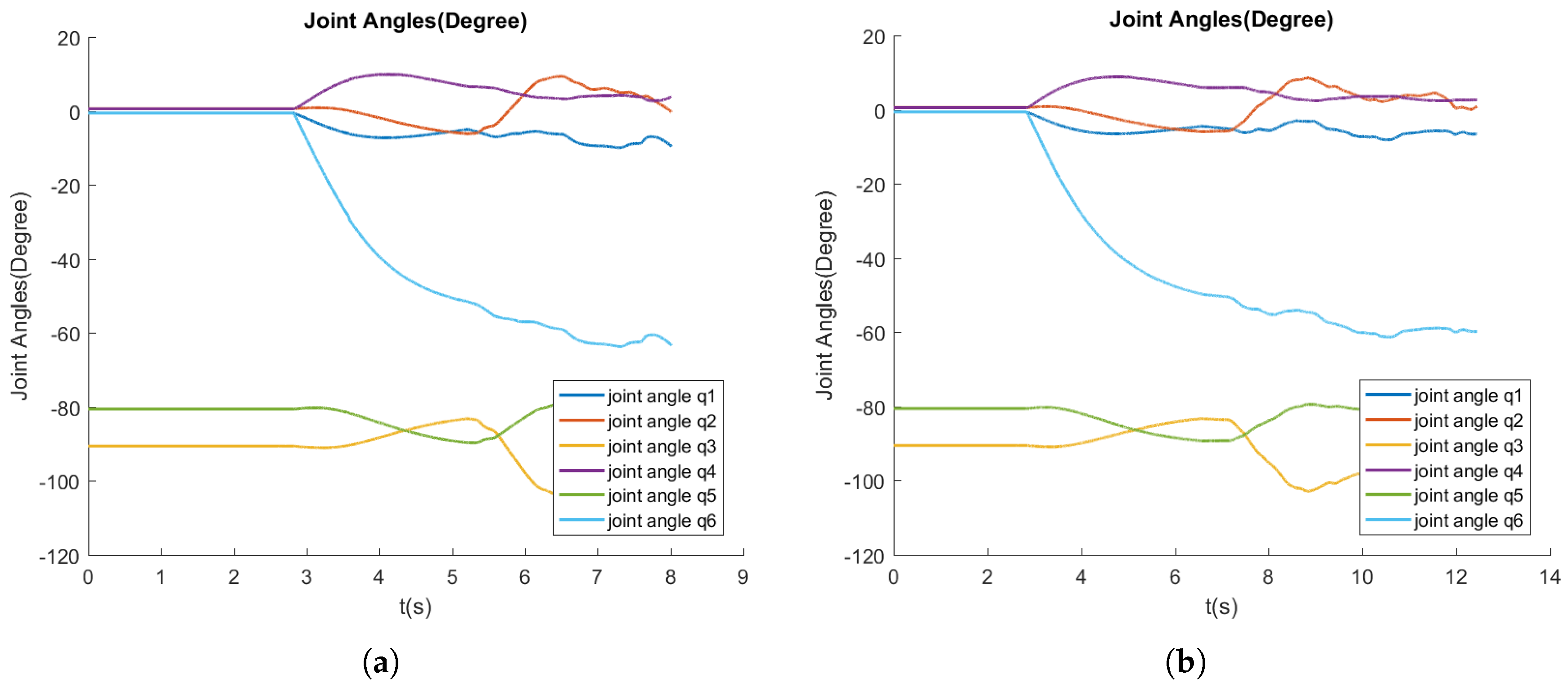
Figure 12 demonstrates the robot joint angles in ESIBVS and switch IBVS.
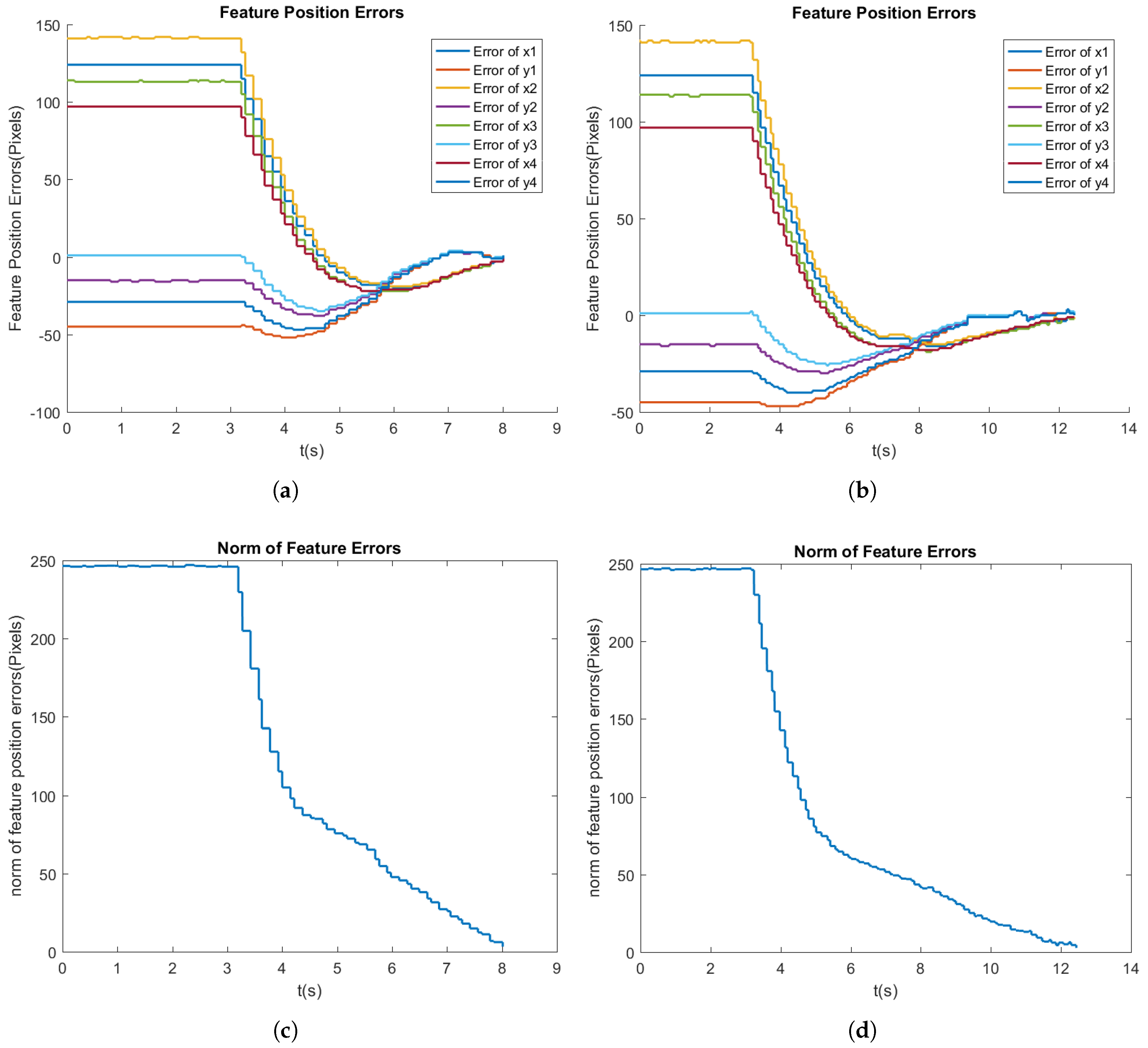
Figure 13 shows the comparison regarding the feature errors. The feature errors and the norm of feature errors in the proposed method successfully converged to the desired values (
Figure 13a,c), while in the switch IBVS, the task could not be completed, and thus, the feature errors did not converge (
Figure 13b,d).
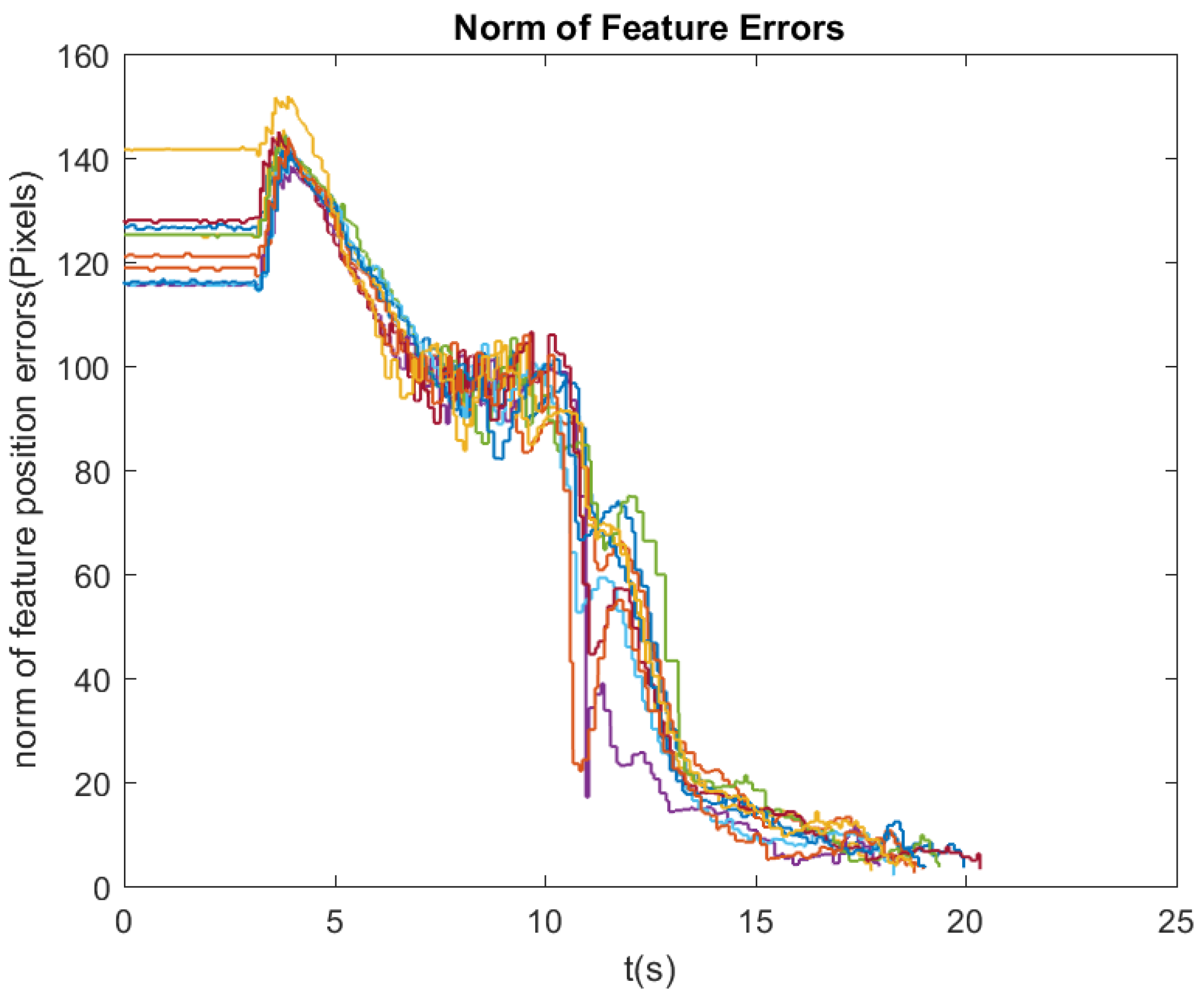
In order to further validate the performance of ESIBVS regarding the repeatability, the same test was repeated in 10 trials. The time of convergence and the final norms of feature error are shown in
Table 5. The variations of feature error norms with time in 10 trials of ESIBVS are illustrated in
Figure 14. As shown in the results, ESIBVS was able to overcome the feature loss and complete the task in each trial, while Switch IBVS was stuck in a point and did not converge.
Test 3: In this test, the performance of ESIBVS was compared with that of switch IBVS in the situation where the features did not leave the FOV of the camera. The initial and desired features were set in a way such that the features did not go outside of FOV (
Table 6). Similar to the previous tests, ESIBVS and switch IBVS were compared, and the results are shown in
Figure 15,
Figure 16 and
Figure 17 and
Table 7. As shown in the figures, ESIBVS had a
shorter convergence time than switch IBVS did, which was owed to the superior noise-filtering ability of the designed Kalman filter.
The experimental results showed the efficiency of ESIBVS in dealing with feature loss while keeping the superior performance of the switch IBVS over traditional IBVS. As already shown in our previous work [
15,
16], the switch method was proven to have a better performance in its response time and its tracking performance, making it more feasible for industrial applications in comparison with the conventional IBVS. However, it suffered the drawback of weakness in dealing with feature loss. The proposed ESIBVS solved this problem and made switch IBVS more robust by using the Kalman filter to reconstruct the lost features.