Dynamic Stress Measurement with Sensor Data Compensation
Abstract
:1. Introduction
2. Related Work
2.1. Sensor Data Compensation
2.2. Heuristic Algorithms for BP Neural Network
2.3. Stress Measurements of Parachutes
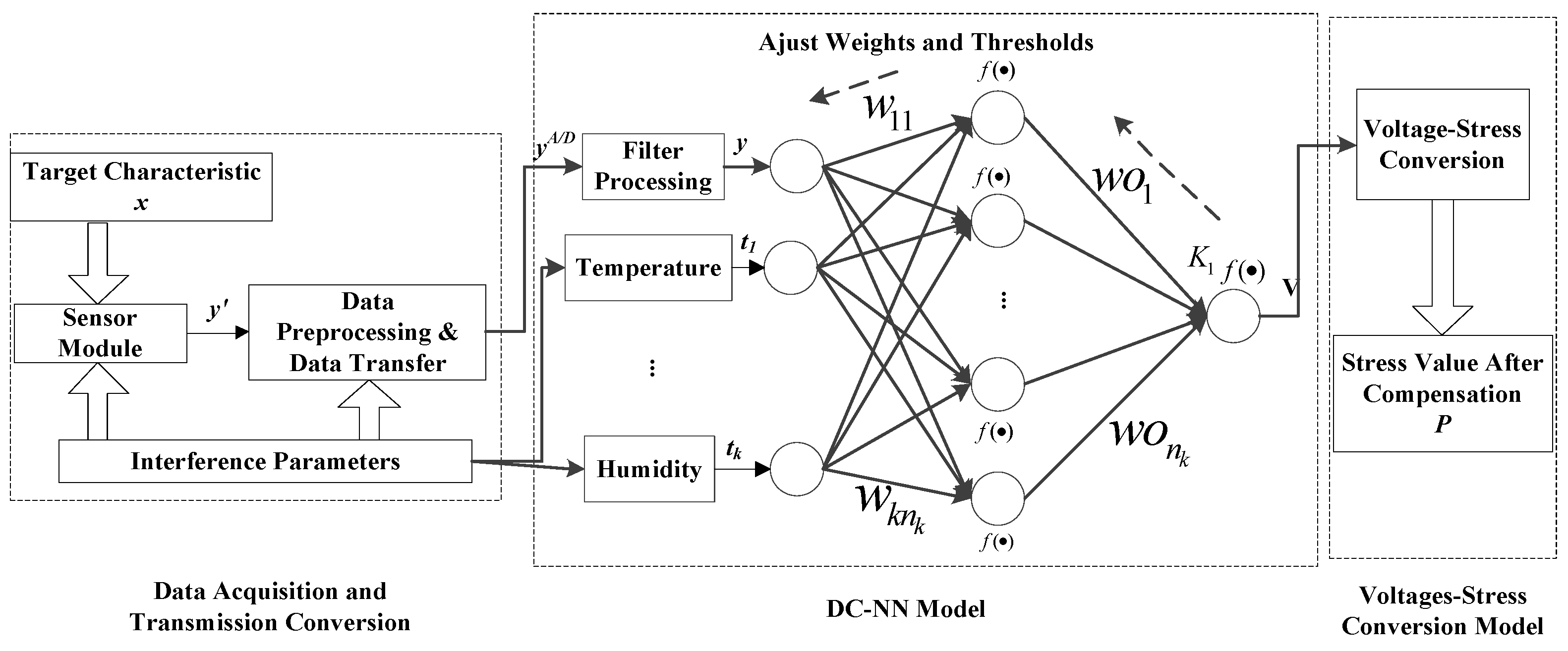
3. The Dynamic Measurement with Compensation System of Airdropped WSN
3.1. Network Structure and Deployment
3.2. DC-BPNN Model Establishment
3.3. Voltage-Stress Conversion Model
4. Adaptive Artificial Bee Colony Algorithm IN DC-BPNN Model
4.1. Adaptive ABC--Improvement of Path Search
4.2. Stability of AABC Algorithm in DC-BPNN Model
5. Experiments
5.1. Model Training in THMTT Machine
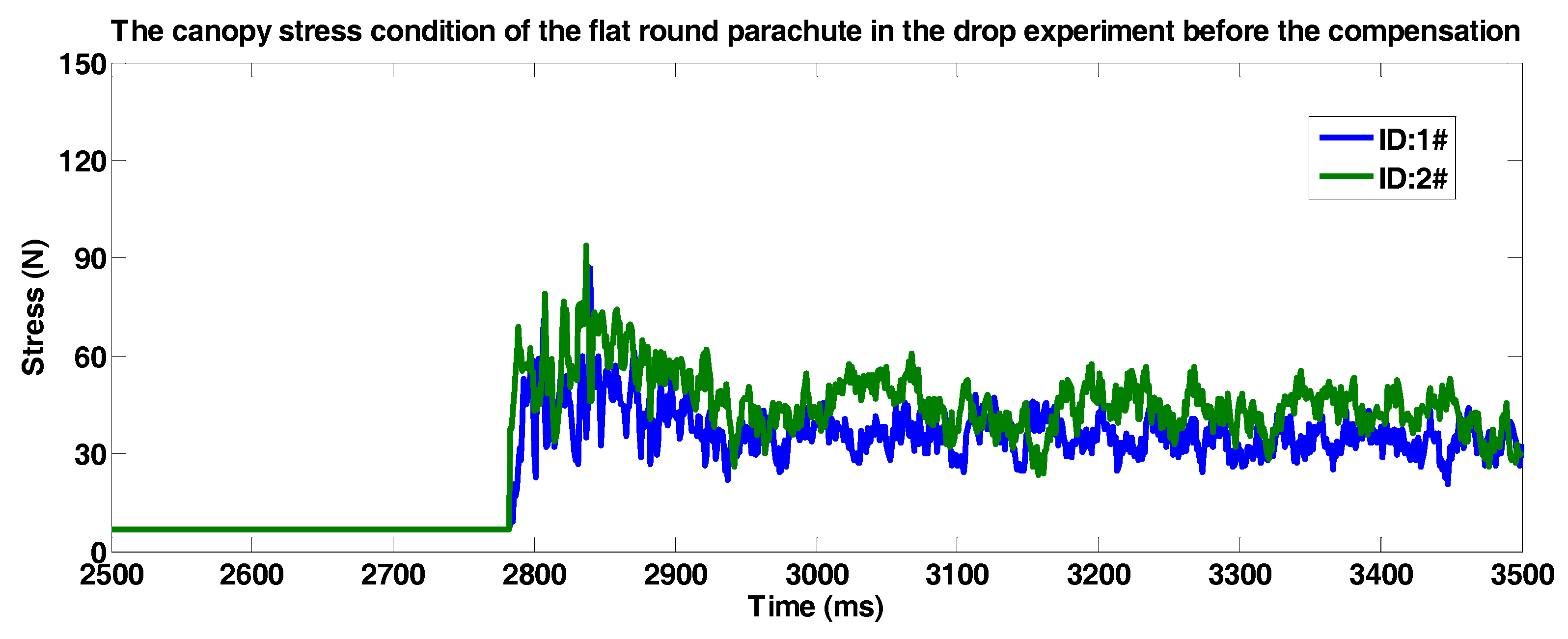
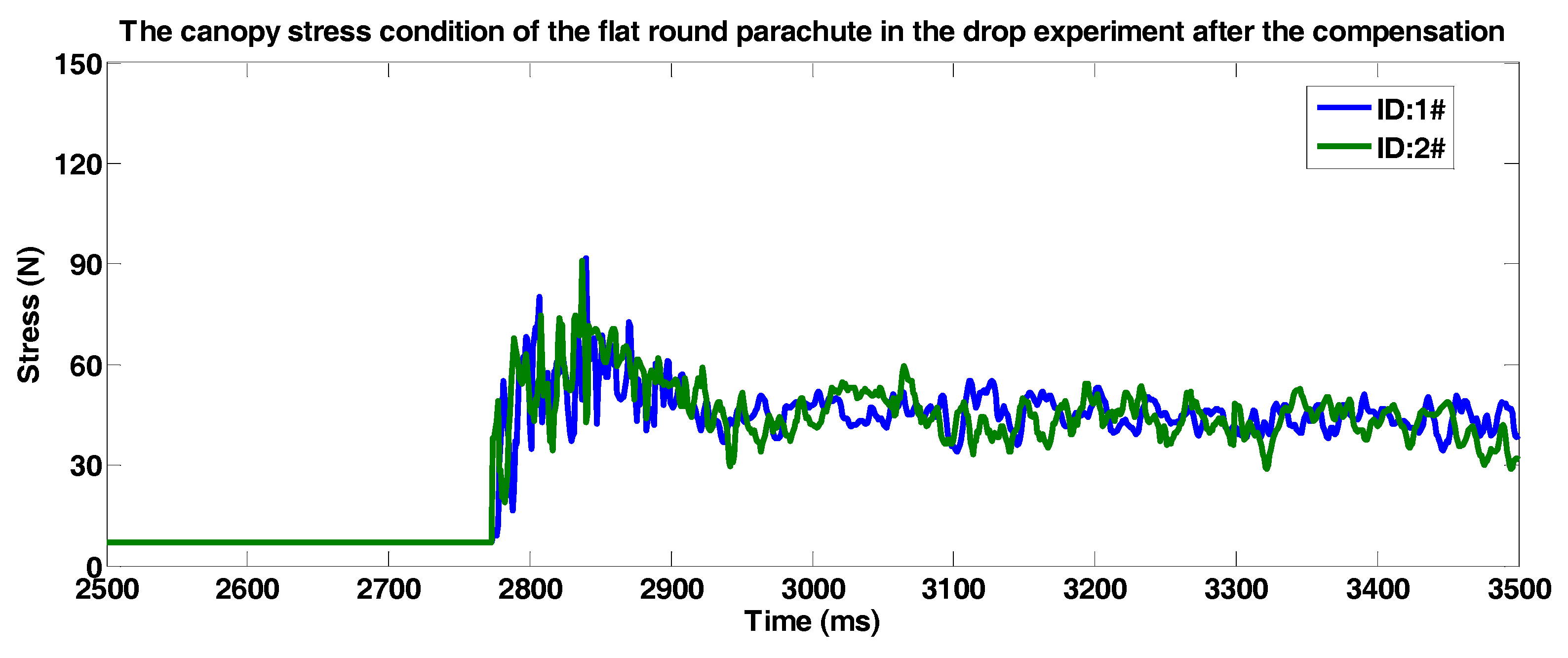
5.2. Airdropped Experiment
5.3. Effectiveness of AABC
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Wu, S.; Niu, J.; Chou, W.; Guizani, M. Delay-Aware Energy Optimization for Flooding in Duty-Cycled Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2016, 15, 8449–8462. [Google Scholar] [CrossRef]
- Xiao, Y.; Rayi, V.; Sun, B.; Du, X.; Hu, F.; Galloway, M. A Survey of Key Management Schemes in Wireless Sensor Networks. J. Comput. Commun. 2007, 30, 2314–2341. [Google Scholar] [CrossRef]
- Liu, G.J.; Tan, R.; Zhou, R.; Xing, G.L.; Song, W.Z.; Lees, J.M. Volcanic Earthquake Timing using Wireless Sensor Networks. In Proceedings of the 12th ACM/IEEE Conference on Information Processing in Sensor Networks (IPSN), Philadelphia, PA, USA, 8–11 April 2013; pp. 91–102. [Google Scholar]
- Du, X.; Xiao, Y.; Guizani, M.; Chen, H.H. An Effective Key Management Scheme for Heterogeneous Sensor Networks. Ad Hoc Netw. 2007, 5, 24–34. [Google Scholar] [CrossRef]
- Giggenbach, D.; Epple, B.; Horwath, J.; Moll, F. Optical Satellite Downlinks to Optical Ground Stations and High-Altitude Platforms. Lect. Notes Electr. Eng. 2008, 16, 331–349. [Google Scholar] [CrossRef]
- Zhao, J.; Zhuang, Y.; Gu, J.; Xu, Y.; Sun, J. Sensor Module Based on the Wireless Sensor Network for the Dynamic Stress on the Flexible Object with Large Deformation. J. Sens. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Motz, M.; Ausserlechner, U.; Holliber, M. Compensation of Mechanical Stress-Induced Drift of Bandgap References with On-Chip Stress Sensor. IEEE Sens. J. 2015, 15, 5115–5121. [Google Scholar] [CrossRef]
- Deng, C.; Mao, Y.; Ren, G. MEMS Inertial Sensors-Based Multi-Loop Control Enhanced by Disturbance Observation and Compensation for Fast Steering Mirror System. Sensors 2016, 16, 1920. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Weiss, R.; Weigel, R. Hysteresis Compensation Method for Magnetoresistive Sensors Based on Single Polar Controlled Magnetic Field Pulses. IEEE Trans. Ind. Electron. 2017, 64, 710–716. [Google Scholar] [CrossRef]
- Matko, V.; Milanović, M. High-Precision Hysteresis Sensing of the Quartz Crystal Inductance-to-Frequency Converter. Sensors 2016, 16, 995. [Google Scholar] [CrossRef]
- Matko, V. Next Generation AT-Cut Quartz Crystal Sensing Devices. Sensors 2011, 11, 4474–4482. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Han, T.; Lin, Z. Energy-Efficient Time Synchronization in Wireless Sensor Networks via Temperature-Aware Compensation. ACM Trans. Sens. Netw. 2016, 12, 1–29. [Google Scholar] [CrossRef]
- Verma, M.; Asmita, S.; Shukla, K. A Regularized Ensemble of Classifiers for Sensor Drift Compensation. IEEE Sens. J. 2016, 16, 1310–1318. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, X. BP artificial neural network based wave front correction for sensor-less free space optics communication. Opt. Commun. 2017, 385, 219–228. [Google Scholar] [CrossRef]
- Liu, S.; Hou, Z.; Yin, C. Data-Driven Modeling for UGI Gasification Processes via an Enhanced Genetic BP Neural Network with Link Switches. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, F.; Ren, H.; Zhang, Z.; Jiang, X. An Iterative Distortion Compensation Algorithm for Camera Calibration Based on Phase Target. Sensors 2017, 17, 1188. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Wu, J.; Yang, Y. Temperature compensation of eddy current sensor based on temperature-voltage model. In Proceedings of the 12th World Congress on Intelligent Control. and Automation (WCICA), Guilin, China, 12 June 2016; pp. 438–441. [Google Scholar]
- Bu, X.; Wu, X.; Wei, D.; Huang, J. Neural-approximation-based robust adaptive control of flexible air-breathing hypersonic vehicles with parametric uncertainties and control input constraints. Inf. Sci. 2016, 346, 29–43. [Google Scholar] [CrossRef]
- Wei, P.; Cheng, C.; Liu, T. A Photonic Transducer based Optical Current Sensor using Back-Propagation Neural Network. IEEE Photon. Technol. Lett. 2016, 28, 1513–1516. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, M.; Ruan, K. A Ranging Model Based on BP Neural Network. Intell. Autom. Soft Comput. 2016, 22, 325–329. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by Simulated Annealing. Read. Comput. Vis. 1987, 220, 606–615. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Birattrai, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2011; Volume 4, pp. 760–766. [Google Scholar]
- Chakrabarti, A. Mass-Spring-Damper System as the Mathematical Model for the Pattern of Sand Movement for an Eroding Beach Around Digha, West Bengal, India. J. Sediment. Res. 1977, 47, 311–330. [Google Scholar] [CrossRef]
- Meng, J.C.S.; Thomson, J.A.L. Numerical studies of some non-linear hydrodynamic problems by discrete vortex element methods. J. Fluid Mech. 1978, 84, 433–453. [Google Scholar] [CrossRef]
- Du, X.; Guizani, M.; Xiao, Y.; Chen, H.H. Transactions papers, A Routing-Driven Elliptic Curve Cryptography based Key Management Scheme for Heterogeneous Sensor Networks. IEEE Trans. Wirel. Commun. 2009, 8, 1223–1229. [Google Scholar] [CrossRef]
- Jalalifar, M.; Byun, G. A Wide Range CMOS Temperature Sensor with Process Variation Compensation for On-Chip Monitoring. IEEE Sens. J. 2016, 16, 5536–5542. [Google Scholar] [CrossRef]
- Gibbs, M.N.; Mackay, D.C. Variational Gaussian process classifiers. IEEE Trans. Neural Netw. 2002, 11, 1458–1464. [Google Scholar]
- Bousquet, O.; Elisseeff, A. Stability and generalization. J. Mach. Learn. Res. 2002, 2, 499–526. [Google Scholar]
- Hardt, M.; Recht, B.; Singer, Y. Train faster, generalize better: Stability of stochastic gradient descent. Int. Conf. Mach. Learn. 2016, Jun 11, 1225–1234. [Google Scholar]
- Shalev-Shwartz, S.; Shamir, O.; Srebro, N.; Sridharan, K. Learnability, stability and uniform convergence. J. Mach. Learn. Res. 2010, 11, 2635–2670. [Google Scholar]
- Budil, D.E.; Lee, S.; Saxena, S.; Freed, J.H. Nonlinear-Least-Squares Analysis of Slow-Motion EPR Spectra in One and Two Dimensions Using a Modified Levenberg–Marquardt Algorithm. J. Magn. Reson. Ser. A 1996, 120, 155–189. [Google Scholar] [CrossRef]




| Methods of Compensation | Main Idea | Disadvantages | Speed | Accuracy | |
|---|---|---|---|---|---|
| Hardware [5,6,7,8,9] | Use different complex circuits. | Costly, complex circuit, difficult to debug. | Fast | High | |
| Software | Interpolation [17] | The ranges are segmented into pieces, and each segment is expressed by a polynomial. | The higher the accuracy is, the more storage space it needs. | Low | Depend on number of segments. |
| LSPCF [18] | Find a matching function by minimizing the square of the error. | Ill-conditioned equations and long time-consumption caused by high order of fitted linear curves. | Medium | Medium | |
| BP-NN [19,20] | Minimize network error sum squares by feedback learning, with simpler implementation process. | Easy to fall into local optimal. | Fast | High | |
| AABC | DC-BPNN |
|---|---|
| Colony size | Solution quantity |
| Food source quality (Fitness) | MSE |
| Speed of searching the best food source | Speed of optimization |
| Best food source | Global optimal solution |
| Food source dimension | Neural network dimension |
| Methods | MSE | Time | |||
|---|---|---|---|---|---|
| Optimal Solution | Average Value | Variance | Average (s) | Variance | |
| LM | 2.13 × 10−9 | 2.31 × 10−8 | 2.56 × 10−8 | 2.49 | 0.0224 |
| ABC | 2.23 × 10−10 | 2.91 × 10−9 | 2.87 × 10−9 | 2.29 | 0.0337 |
| AABC | 4.79 × 10−13 | 4.17 × 10−12 | 2.35 × 10−12 | 2.11 | 0.0646 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, J.; Dong, Z.; Zhang, C.; Du, X.; Guizani, M. Dynamic Stress Measurement with Sensor Data Compensation. Electronics 2019, 8, 859. https://doi.org/10.3390/electronics8080859
Gu J, Dong Z, Zhang C, Du X, Guizani M. Dynamic Stress Measurement with Sensor Data Compensation. Electronics. 2019; 8(8):859. https://doi.org/10.3390/electronics8080859
Chicago/Turabian StyleGu, Jingjing, Zhiteng Dong, Cai Zhang, Xiaojiang Du, and Mohsen Guizani. 2019. "Dynamic Stress Measurement with Sensor Data Compensation" Electronics 8, no. 8: 859. https://doi.org/10.3390/electronics8080859
APA StyleGu, J., Dong, Z., Zhang, C., Du, X., & Guizani, M. (2019). Dynamic Stress Measurement with Sensor Data Compensation. Electronics, 8(8), 859. https://doi.org/10.3390/electronics8080859






