Effectiveness Assessment of a Nanocrystalline Sleeve Ferrite Core Compared with Ceramic Cores for Reducing Conducted EMI
Abstract
1. Introduction
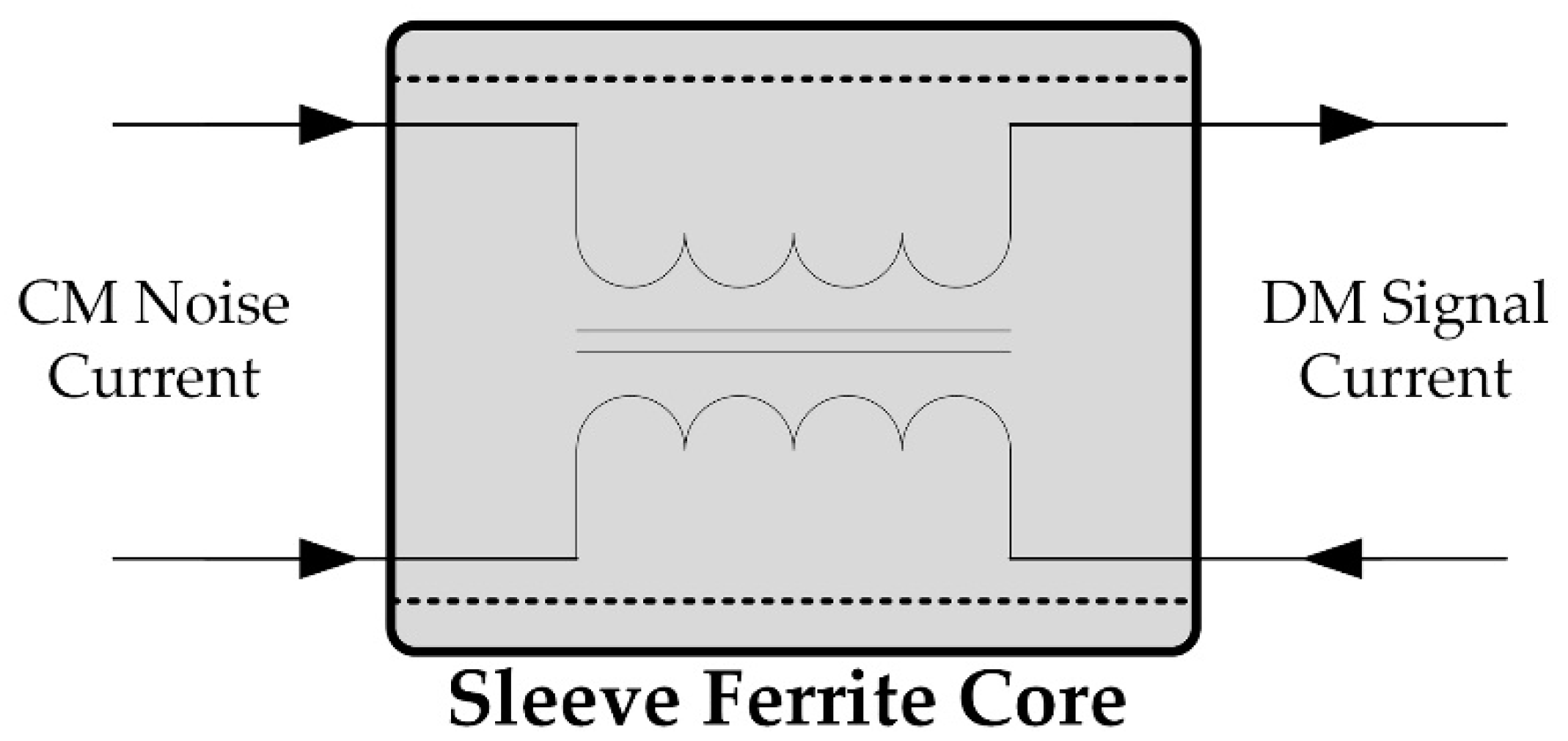
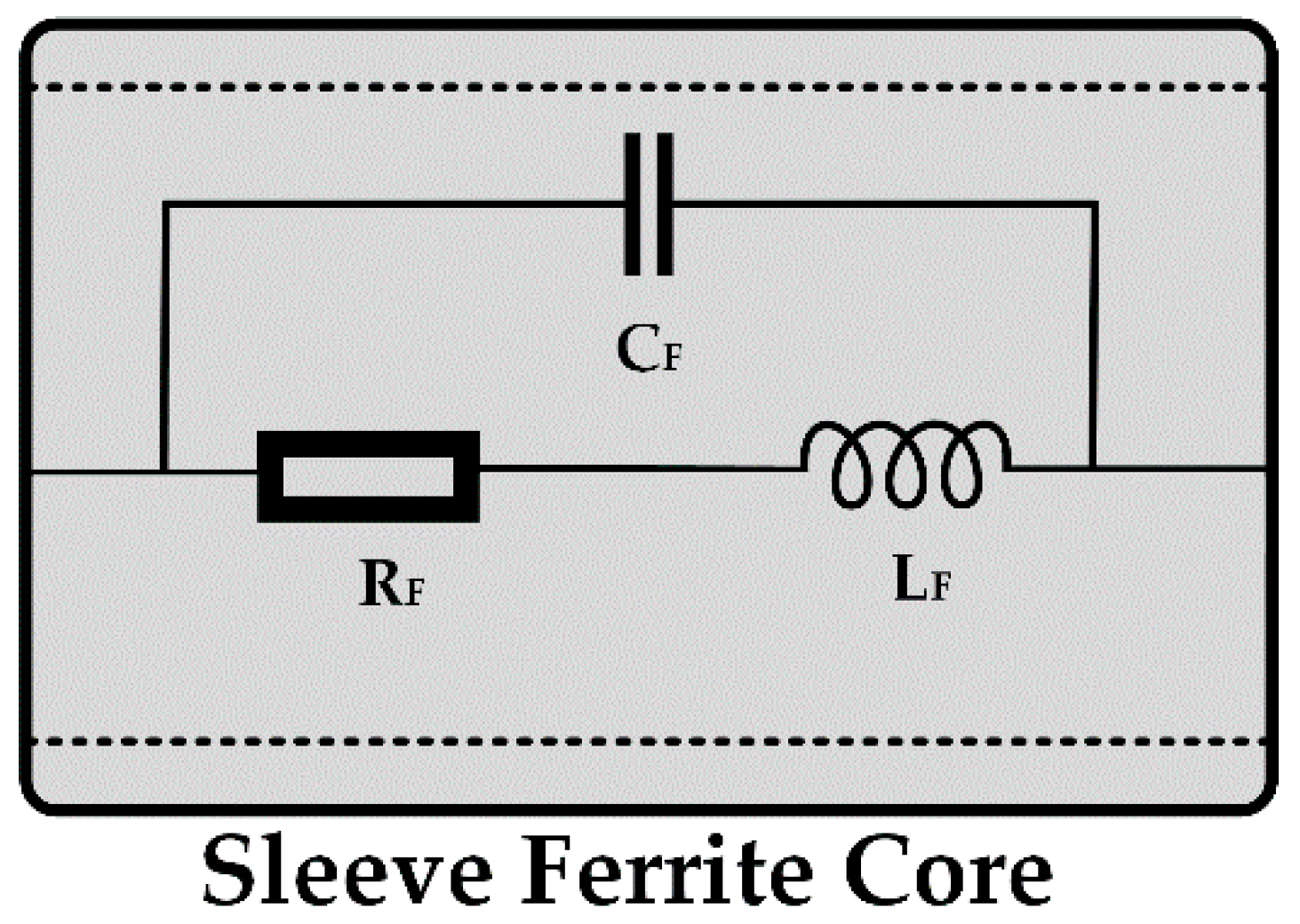
2. Sleeve Ferrite Core Characterization
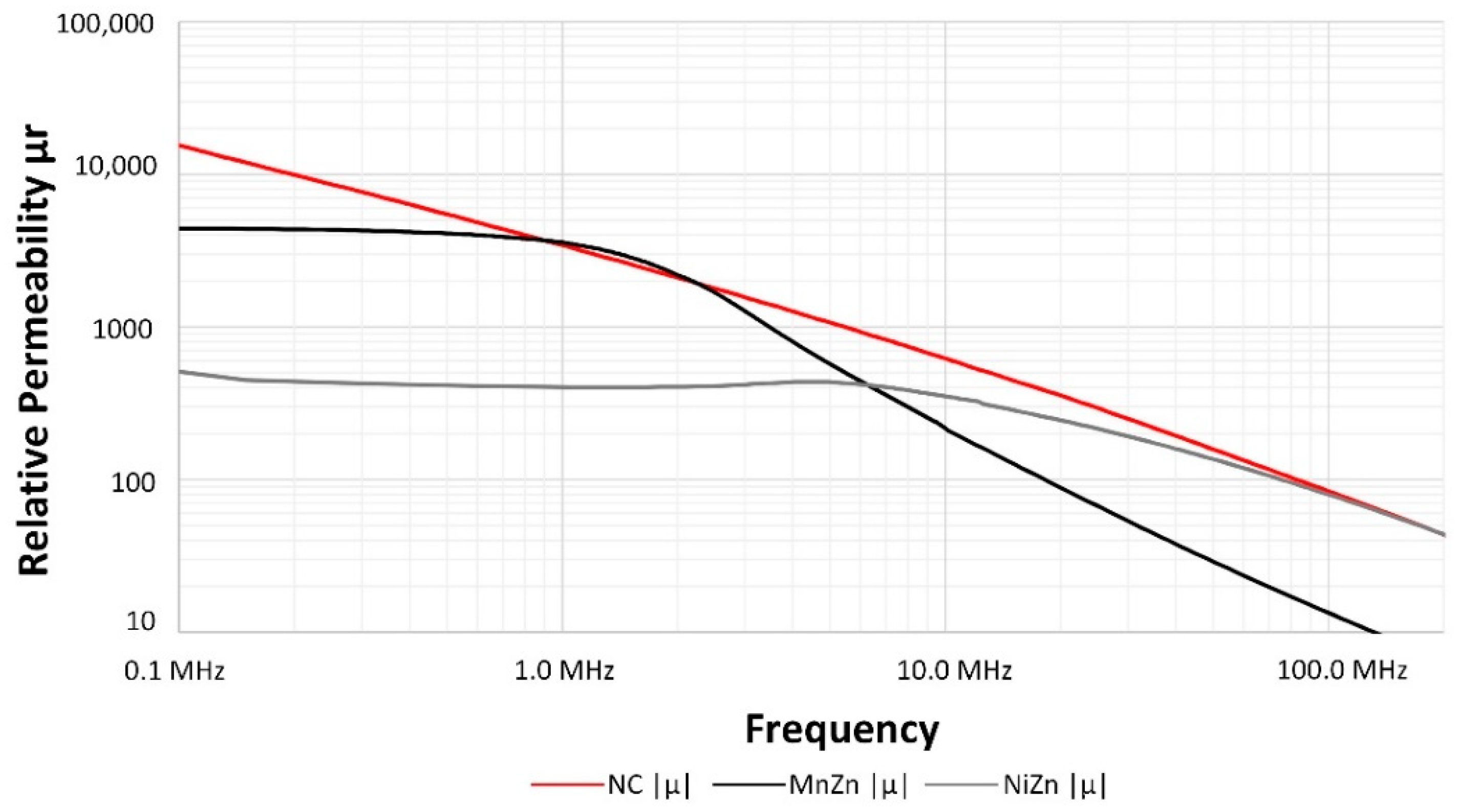
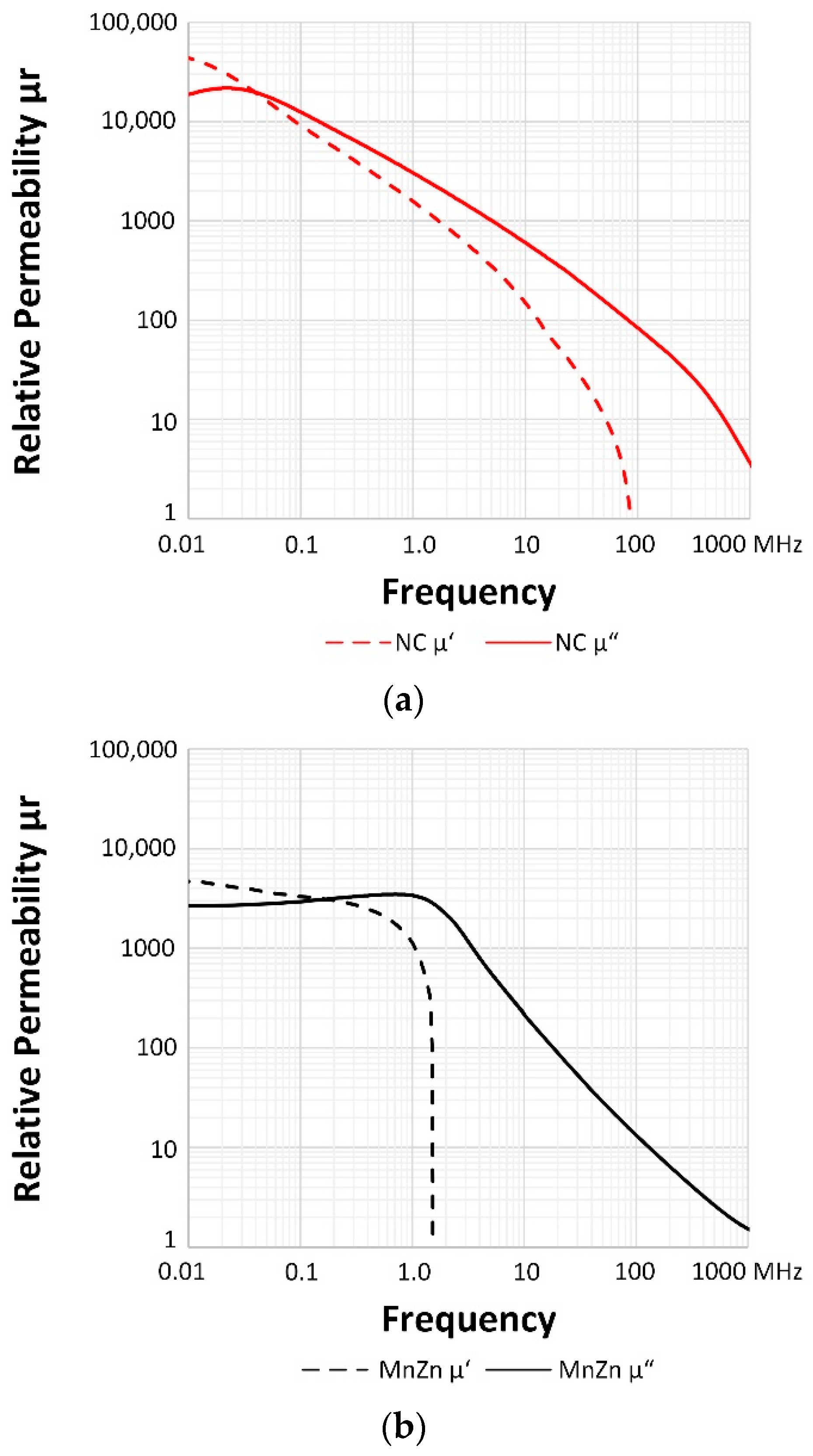
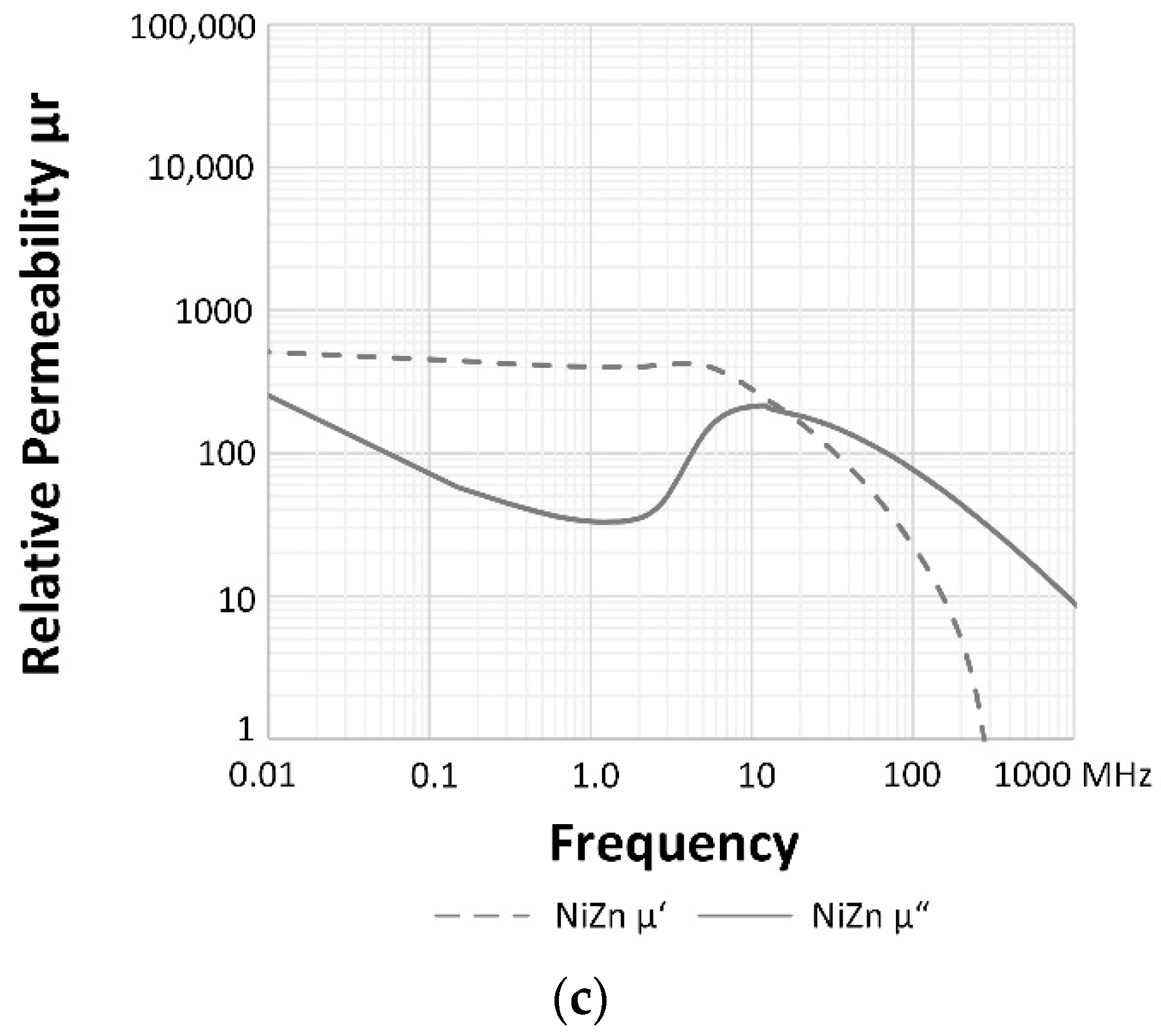
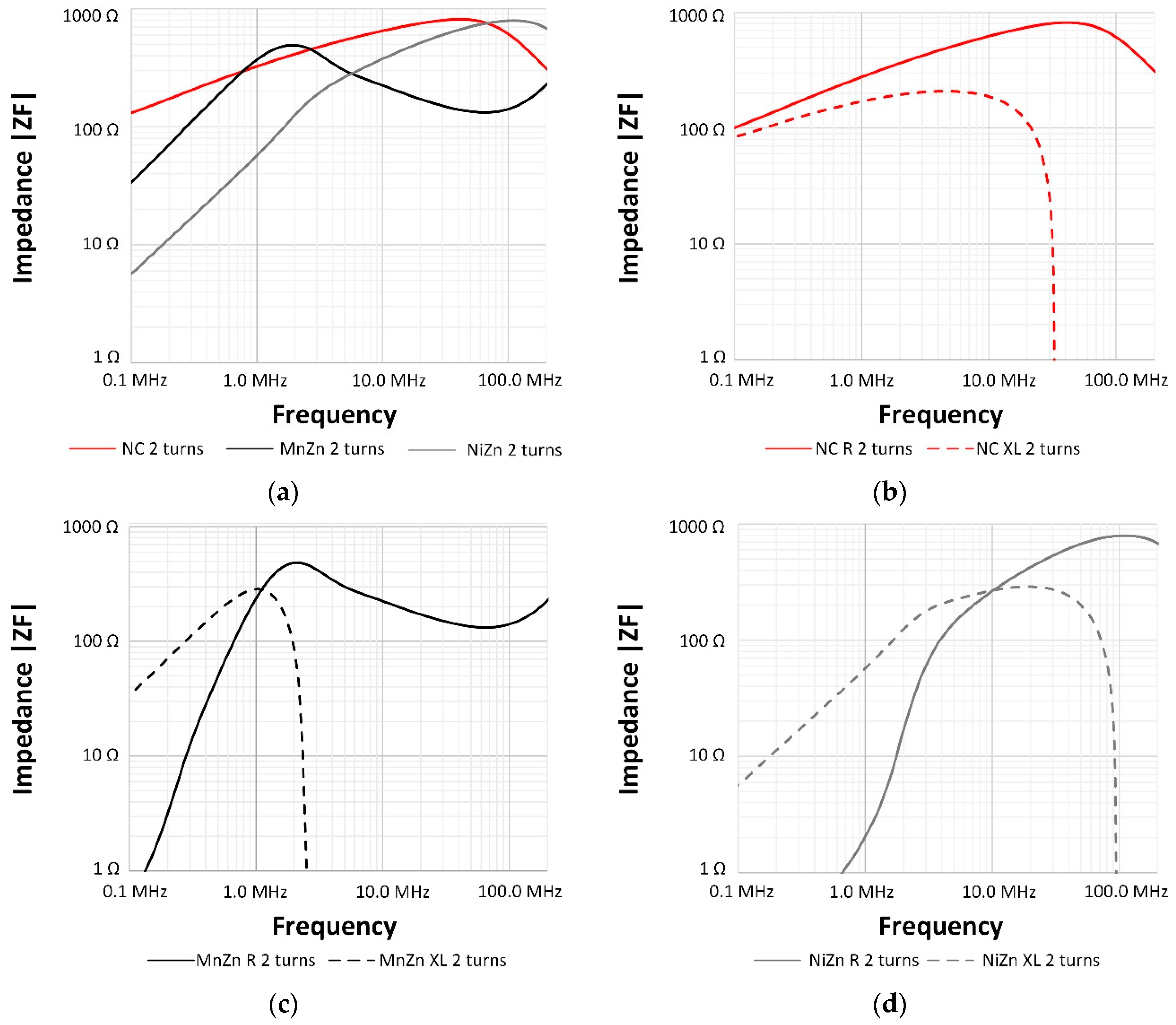
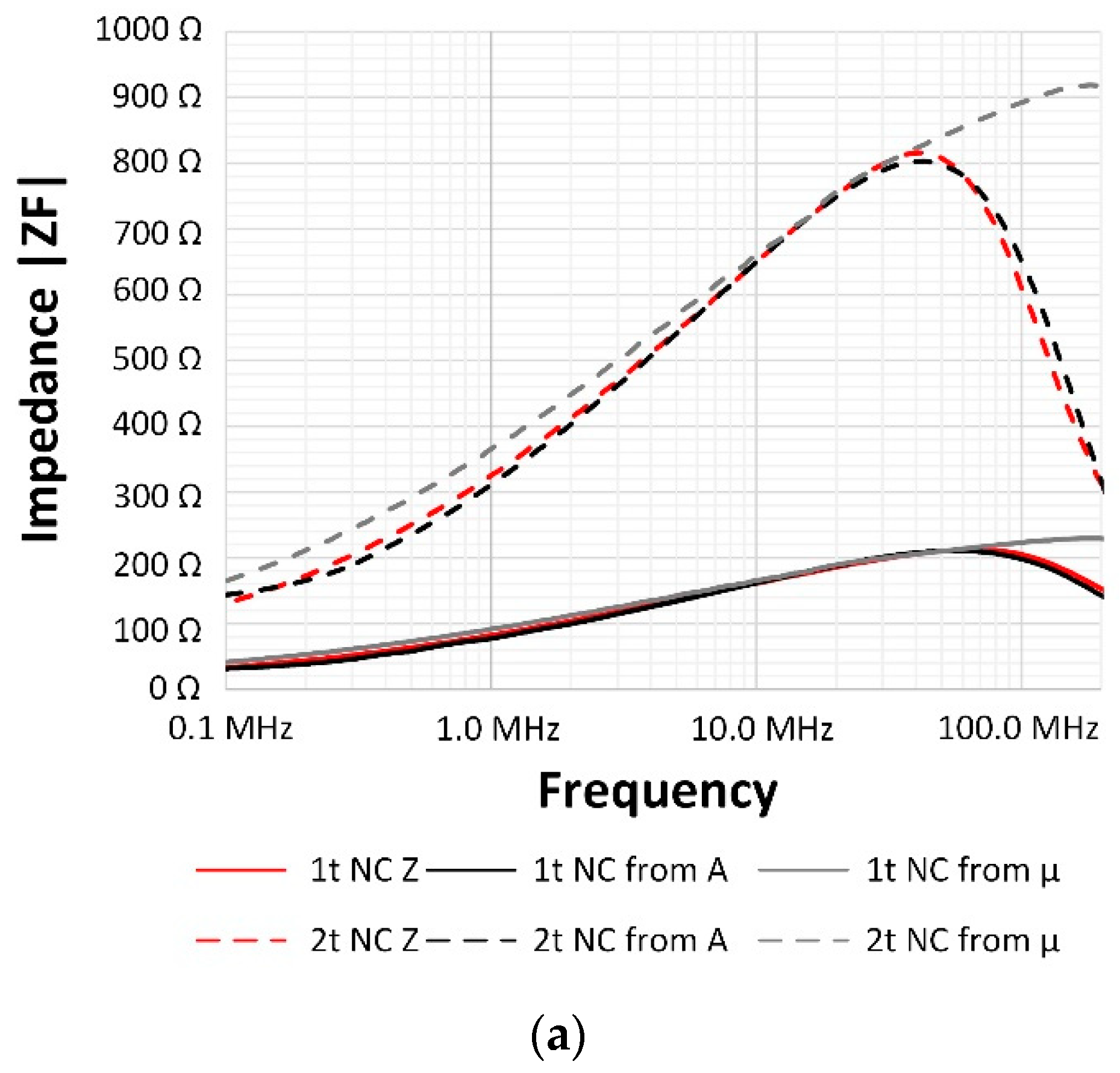
2.1. Magnetic Properties
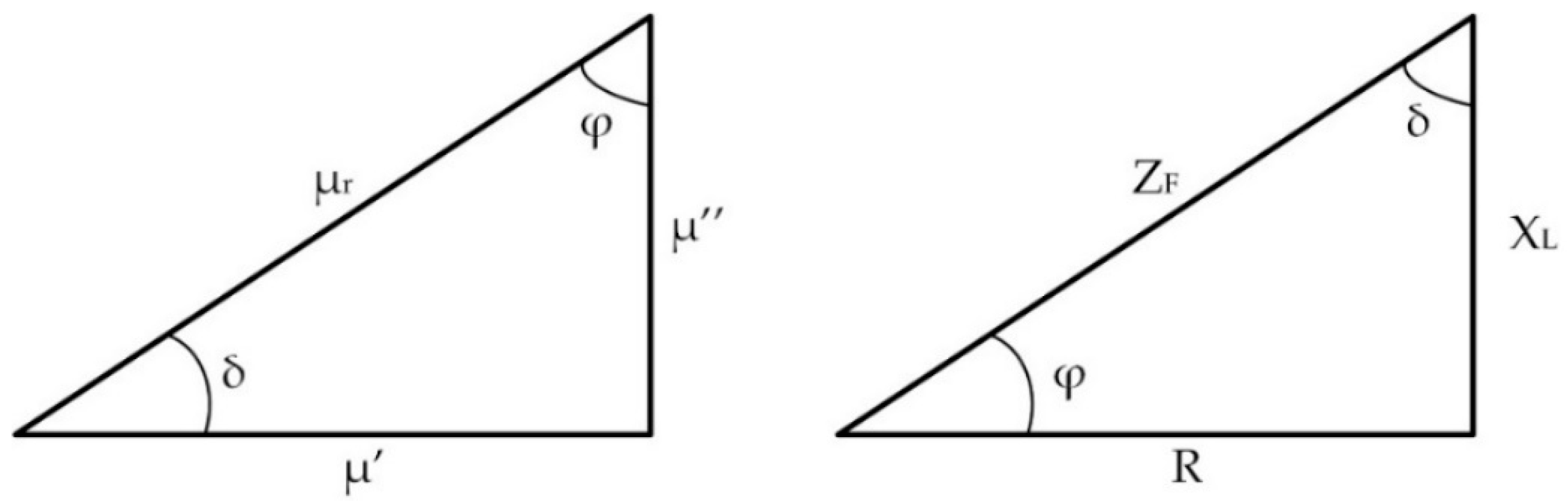
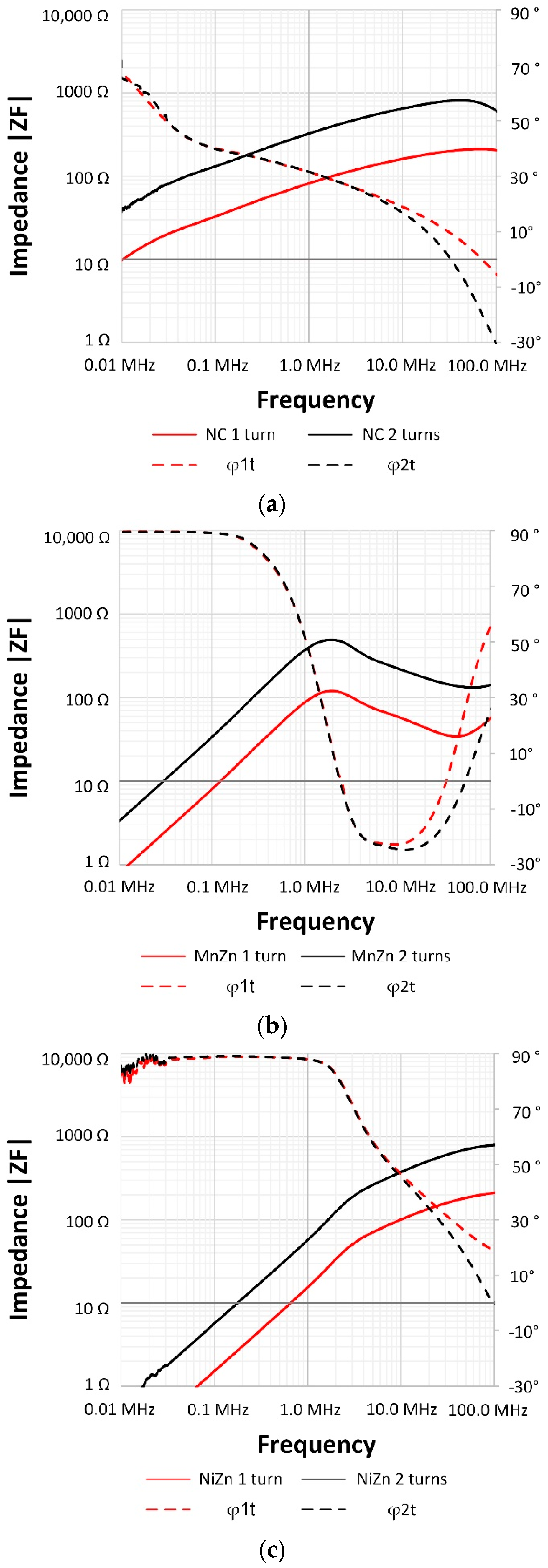
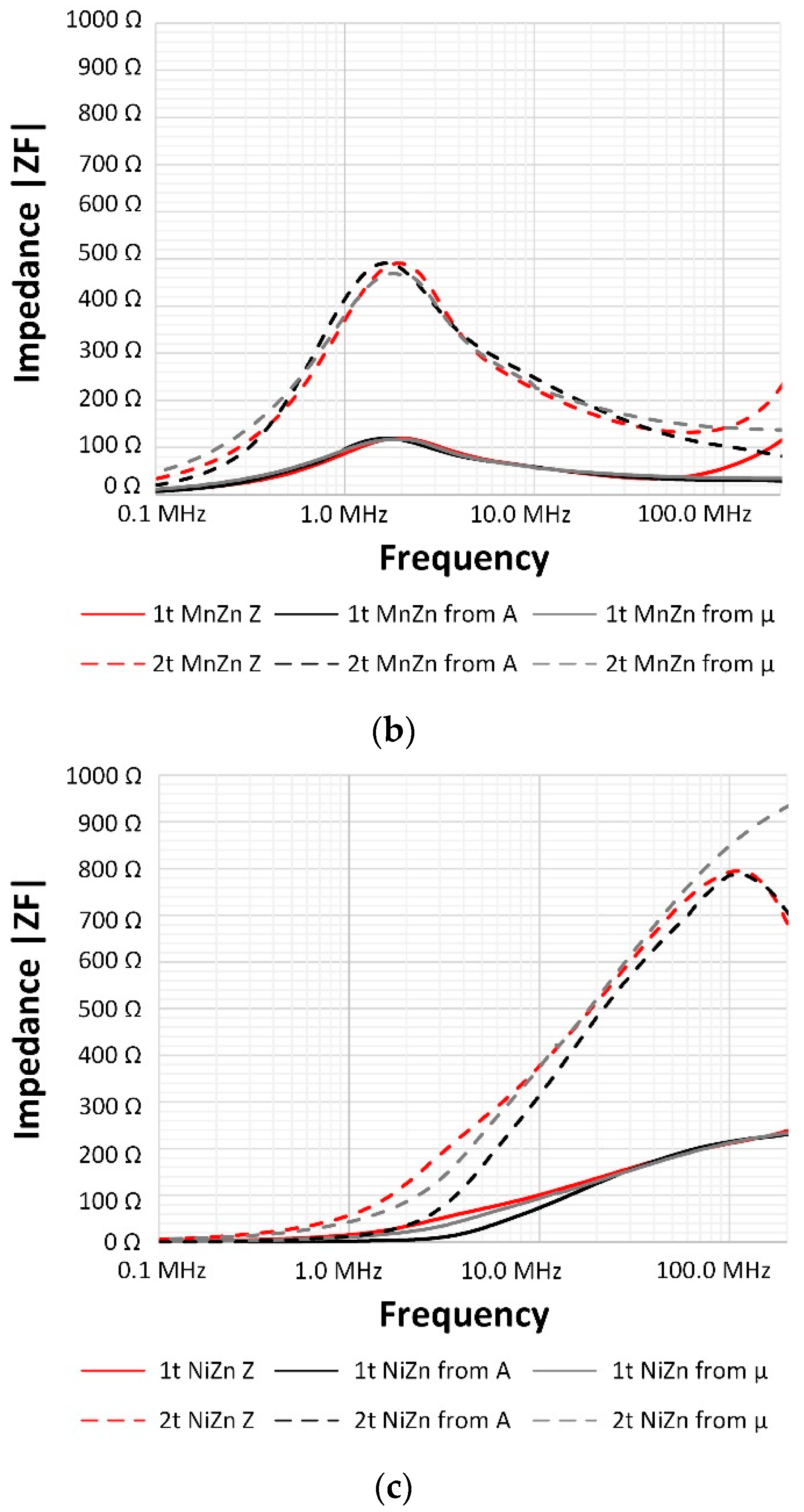
2.2. Impedance and Phase Description
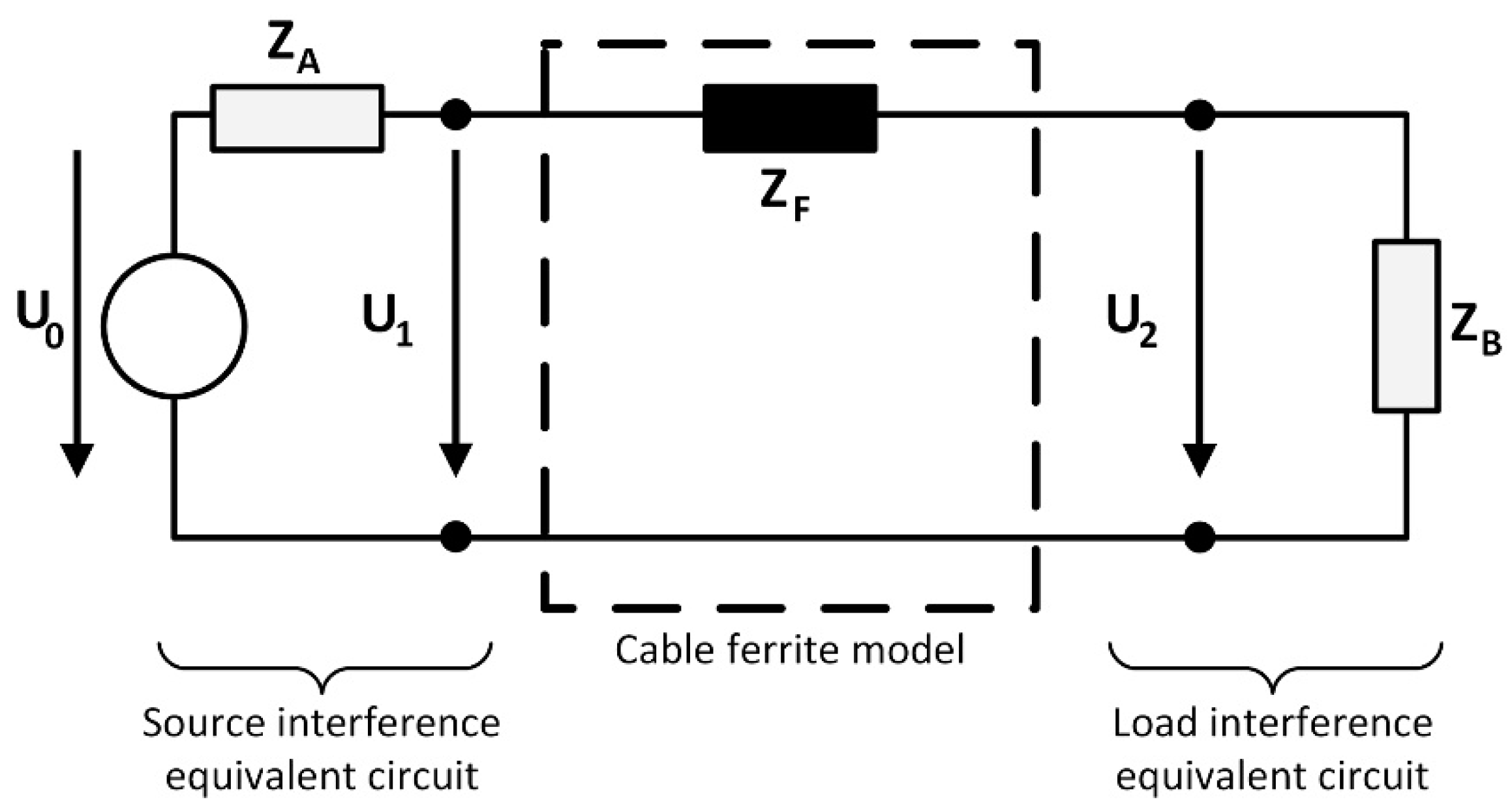
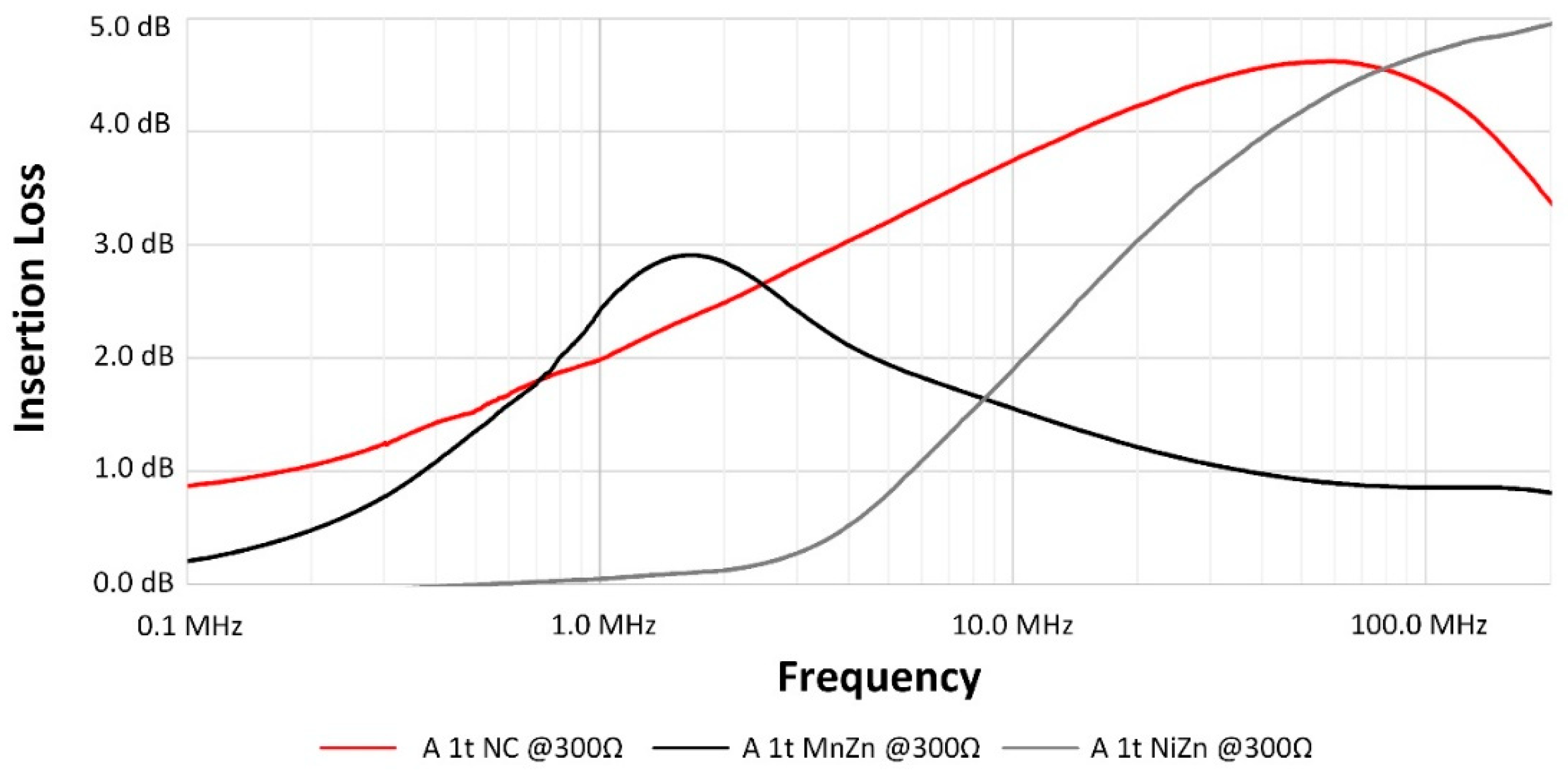
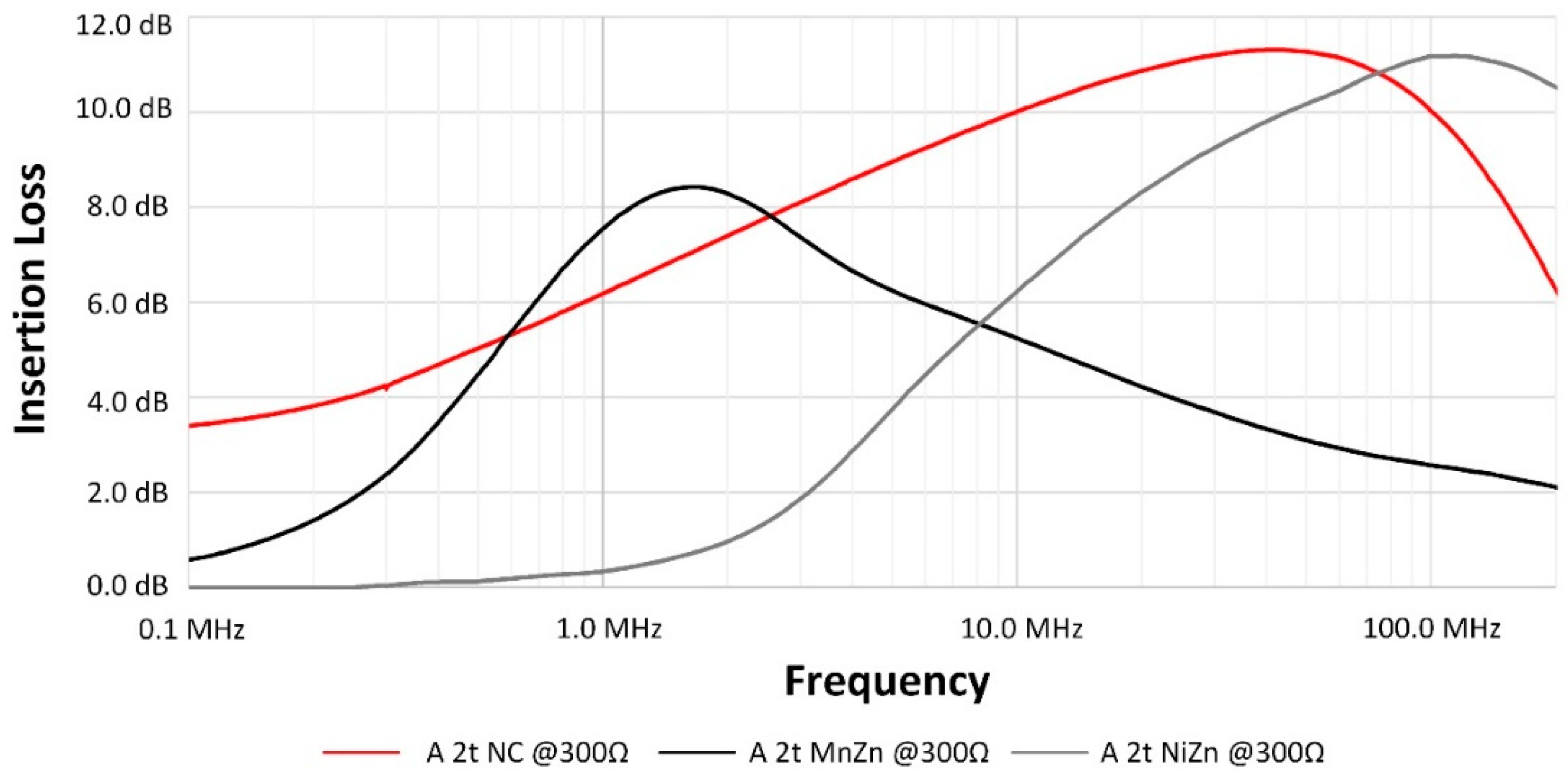
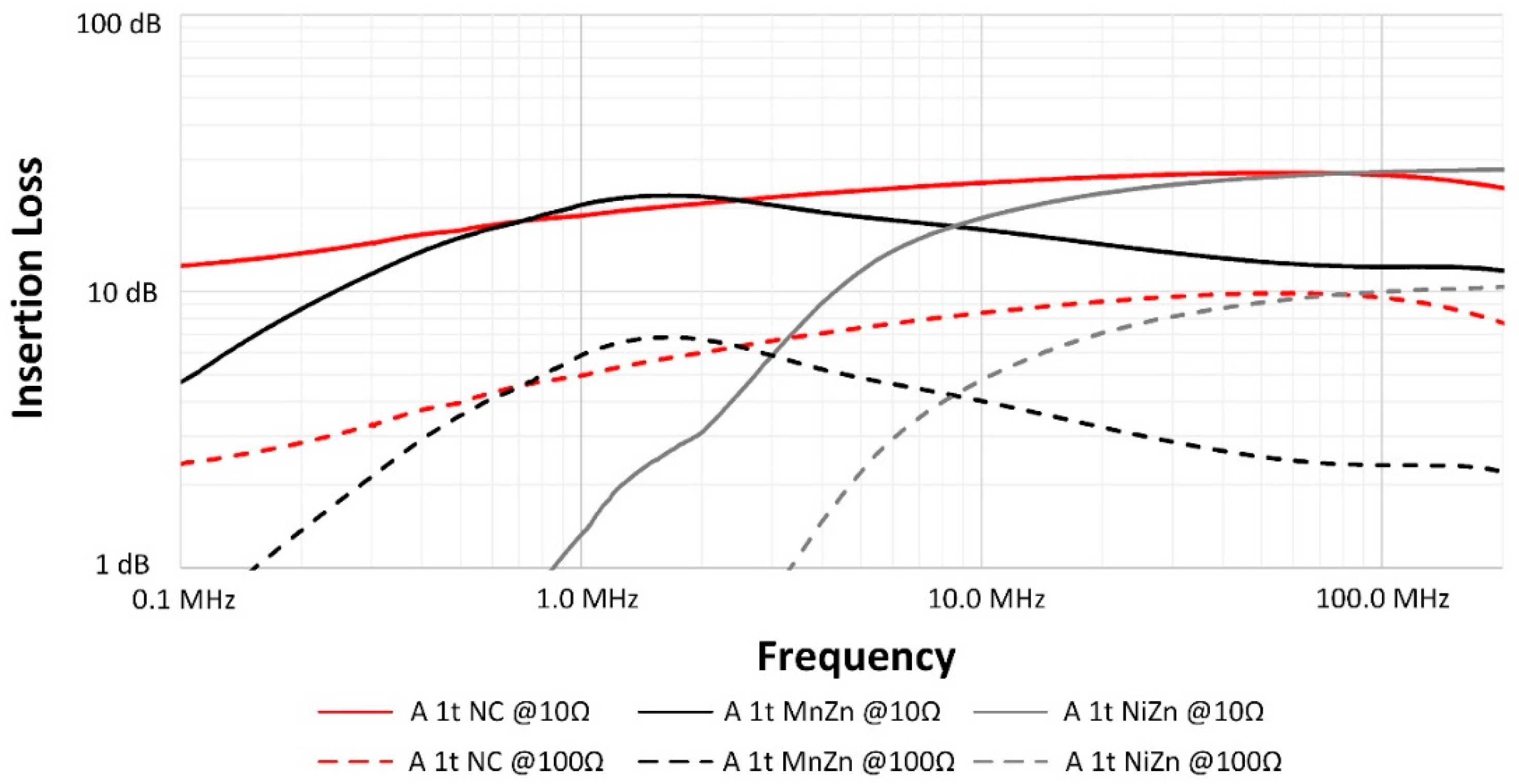
3. Insertion Loss
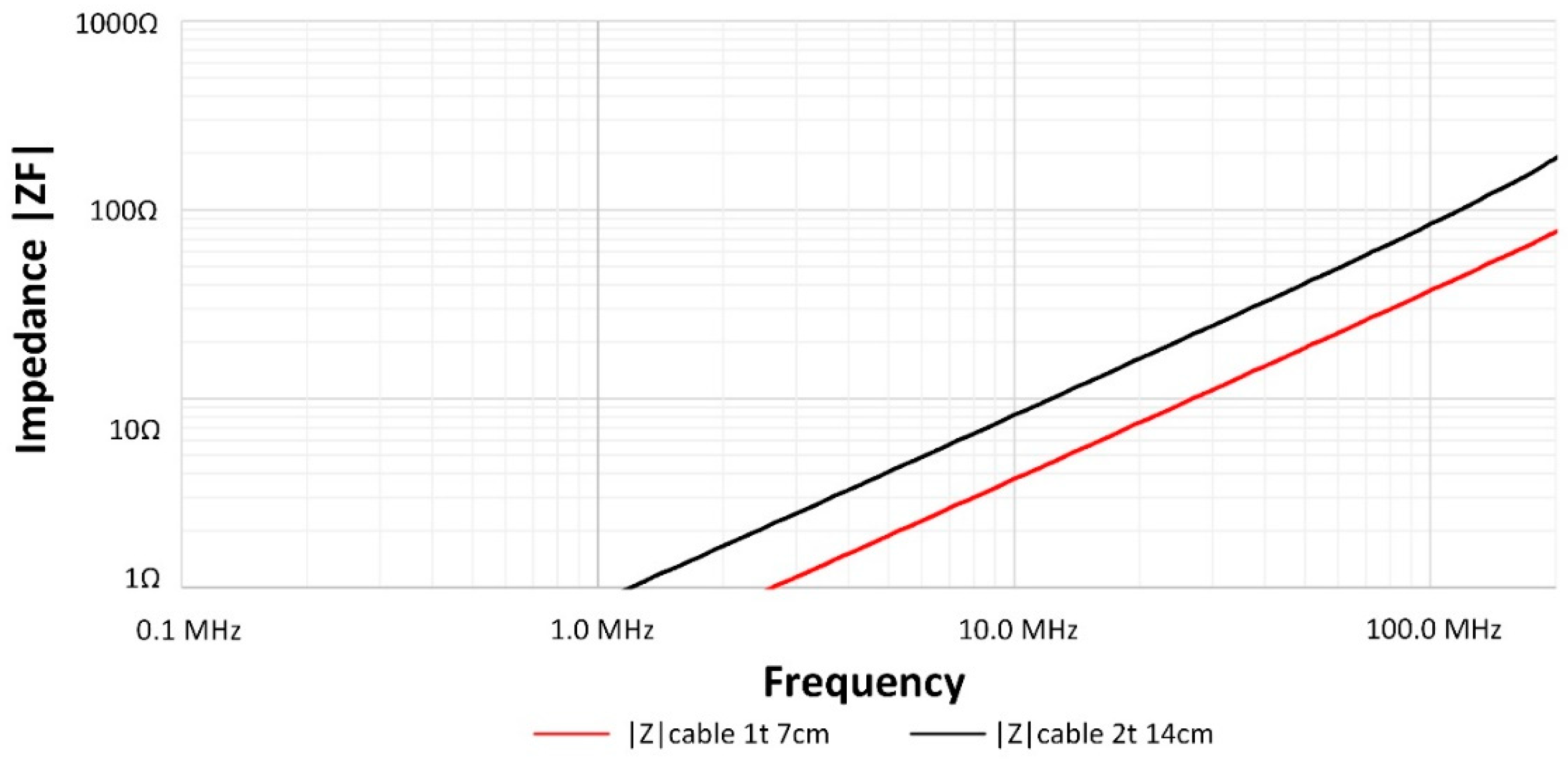
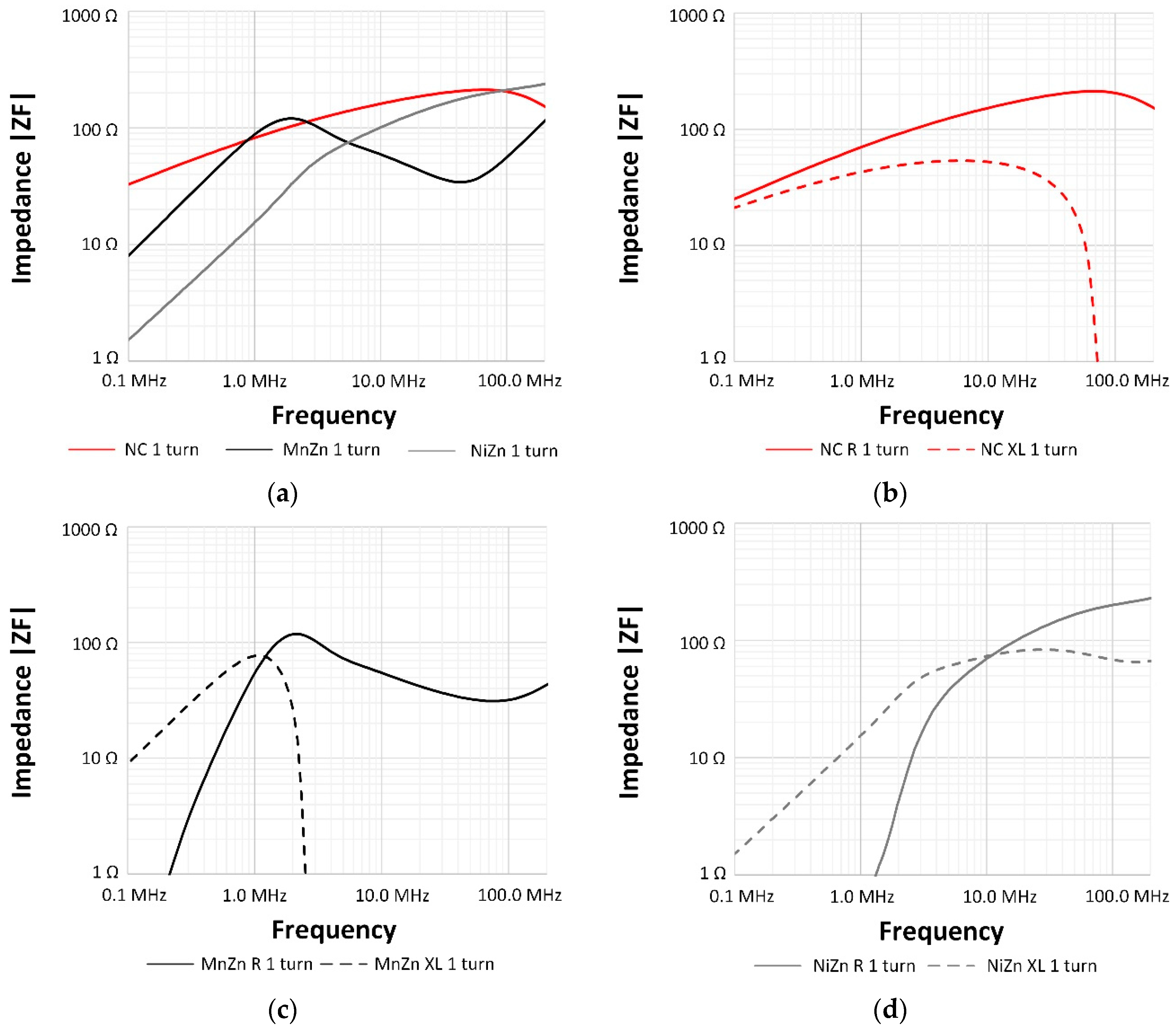
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Valenzuela, R. Novel Applications of Ferrites. Phys. Res. Int. 2012, 2012, 1–9. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Zhang, B.; Tang, W.K.; Halang, W.A. Suppressing electromagnetic interference in direct current converters. IEEE Circuits Syst. Mag. 2009, 9, 10–28. [Google Scholar] [CrossRef]
- Underwood, S.J. DC-DC converters suppress EMI: Minimizing EMI at its Source. Power Electron. Technol. 2002, 28, 14–21. [Google Scholar]
- Goldman, A. Modern Ferrite Technology, 2nd ed.; Springer Science & Business Media: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Ott, H.W. Electromagnetic Compatibility Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hegarty, T. An Overview of Conducted EMI Specifications for Power Supplies. Available online: http://www.ti.com/lit/wp/slyy136/slyy136.pdf (accessed on 31 May 2019).
- Mainali, K.; Oruganti, R. Conducted EMI Mitigation Techniques for Switch-Mode Power Converters: A Survey. IEEE Trans. Power Electron. 2010, 25, 2344–2356. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, D.; Zhang, X.; Qu, F. Reliability of Boost PFC Converters with Improved EMI Filters. Electronics 2018, 7, 413. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, T.; Cao, Y.; Yang, S.; Kavuma, S.; Feng, H. Conducted EMI Prediction and Mitigation Strategy Based on Transfer Function for a High-Low Voltage DC-DC Converter in Electric Vehicle. Energies 2018, 11, 1028. [Google Scholar] [CrossRef]
- Urabe, J.; Fujii, K.; Dowaki, Y.; Jito, Y.; Matsumoto, Y.; Sugiura, A. A Method for Measuring the Characteristics of an EMI Suppression Ferrite Core. IEEE Trans. Electromagn. Compat. 2006, 48, 774–780. [Google Scholar] [CrossRef]
- Hartmann, M.; Ertl, H.; Kolar, J.W. EMI Filter Design for a 1 MHz, 10 kW Three-Phase/Level PWM Rectifier. IEEE Trans. Power Electron. 2011, 26, 1192–1204. [Google Scholar] [CrossRef]
- Lukovic, M.D.; Nikolic, M.V.; Blaz, N.V.; Zivanov, L.D.; Aleksic, O.S.; Lukic, L.S. Mn-Zn Ferrite Round Cable EMI Suppressor with Deep Grooves and a Secondary Short Circuit for Different Frequency Ranges. IEEE Trans. Magn. 2013, 49, 1172–1177. [Google Scholar] [CrossRef]
- Cuellar, C.; Tan, W.; Margueron, X.; Benabou, A.; Idir, N. Measurement method of the complex magnetic permeability of ferrites in high frequency. In Proceedings of the Instrumentation and Measurement Technology Conference (I2MTC), Graz, Austria, 13–16 May 2012; pp. 63–68. [Google Scholar]
- University of York. Link PCP—EMC Aspects of Mobile Telecommunications Systems, Appendix G—Coupling of EMI to Cables: Theory and Models (Final Report). Available online: https://pdfs.semanticscholar.org/cd27/bdd7dab556ce1d0c8e1da41cf9a5605f3d4f.pdf (accessed on 30 November 2018).
- Urabe, J.; Fujii, K.; Harun, A.M.B.; Matsumoto, Y.; Sugiura, A. A study of EMI suppression characteristics of ferrite cores. In Proceedings of the 17th International Zurich Symposium on Electromagnetic Compatibility (EMC), Zurich, Switzerland, 27 February–3 March 2006; pp. 622–625. [Google Scholar]
- Damnjanovi, M.; Stojanovi, G.; Živanov, L.; Desnica, V. Comparison of different structures of ferrite EMI suppressors. Microelectron. Int. 2006, 23, 42–48. [Google Scholar] [CrossRef]
- Stojanović, G.; Lečić, N.; Damnjanović, M.; Živanov, L. Electrical and temperature characterization of NiZn ferrites. Int. J. Appl. Electromagn. Mech. 2011, 35, 165–176. [Google Scholar] [CrossRef]
- Saotome, H.; Sakaki, Y. Complex permeability of polycrystalline Mn-Zn and Ni-Zn ferrites. Electr. Eng. Jpn. 1998, 123, 1–7. [Google Scholar] [CrossRef]
- Suarez, A.; Victoria, J.; Alcarria, A.; Torres, J.; Martinez, P.A.; Martos, J.; Soret, J.; Garcia-Olcina, R.; Muetsch, S. Characterization of Different Cable Ferrite Materials to Reduce the Electromagnetic Noise in the 2–150 kHz Frequency Range. Materials 2018, 11, 174. [Google Scholar] [CrossRef] [PubMed]
- Herzer, G.; Vazquez, M.; Knobel, M.; Zhukov, A.; Reininger, T.; Davies, H.A.; Sanchez Ll, J.S. Round table discussion: Present and future applications of nanocrystalline magnetic materials. J. Magn. Magn. Mater. 2005, 294, 252–266. [Google Scholar] [CrossRef]
- Thierry, W.; Thierry, S.; Benoît, V.; Dominique, G. Strong volume reduction of common mode choke for RFI filters with the help of nanocrystalline cores design and experiments. J. Magn. Magn. Mater. 2006, 304, 847–849. [Google Scholar] [CrossRef]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]
- Liu, Y.; Han, Y.; Liu, S.; Lin, F. Pulse Magnetic Properties Measurement and Characterization of Fe-Based Nanocrystalline Cores for High-Voltage Pulse Magnetics Applications. IEEE Trans. Power Electron. 2015, 30, 6883–6896. [Google Scholar] [CrossRef]
- Naishadham, K. Closed-Form Design Formulas for the Equivalent Circuit Characterization of Ferrite Inductors. IEEE Trans. Electromagn. Compat. 2011, 53, 923–932. [Google Scholar] [CrossRef]
- Weinschrott, A.; Weinschrott, A. New measurement method for high frequency cable mounted ferrites. In Proceedings of the 2005 International Symposium on Electromagnetic Compatibility, Chicago, IL, USA, 8–12 August 2005; pp. 312–314. [Google Scholar]
- Schulze, S.; Al-Hamid, M.; Leone, M. Detailed study of different cable ferrite characterization methods using simulation and measurement. In Proceedings of the 2017 International Symposium on Electromagnetic Compatibility-EMC Europe, Angers, France, 4–7 September 2017; pp. 1–5. [Google Scholar]
- Brander, T.; Gerfer, A.; Rall, B.; Zenkner, H. Trilogy of Magnetics: Design Guide for EMI Filter Design, SMP & RF Circuits, 4th ed.; Swiridoff Verlag: Künzelsau, Germany, 2010. [Google Scholar]
- Saito, T.; Takemoto, S.; Iriyama, T. Resistivity and core size dependencies of eddy current loss for Fe-Si compressed cores. IEEE Trans. Magn. 2005, 41, 3301–3303. [Google Scholar] [CrossRef]
- Moongilan, D. Termination effects on attenuation properties of ferrites installed around cable conductors. In Proceedings of the 2013 International Symposium on Electromagnetic Compatibility, Denver, CO, USA, 5–9 August 2013; pp. 107–112. [Google Scholar]
- Suarez, A.; Victoria, J.; Alcarria, A.; Torres, J. Characterization of electromagnetic noise suppression sheet for aerospace applications. In Proceedings of the ESA Workshop on Aerospace EMC, Valencia, Spain, 23–25 May 2016; pp. 1–6. [Google Scholar]
- Victoria, J.; Suarez, A.; Torres, J.; Martinez, P.A.; Alcarria, A.; Martos, J.; Garcia-Olcina, R.; Soret, J.; Muetsch, S.; Gerfer, A. Transmission Attenuation Power Ratio Analysis of Flexible Electromagnetic Absorber Sheets Combined with a Metal Layer. Materials 2018, 11, 1612. [Google Scholar] [CrossRef]
- Hu, P.; Yang, H.B.; Pan, D.A.; Wang, H.; Tian, J.J.; Zhang, S.; Wang, X.; Volinsky, A.A. Heat treatment effects on microstructure and magnetic properties of Mn-Zn ferrite powders. J. Magn. Magn. Mater. 2010, 322, 173–177. [Google Scholar] [CrossRef]
- Beatrice, C.; Bottauscio, O.; Chiampi, M.; Fiorillo, F.; Manzin, A. Magnetic loss analysis in Mn-Zn ferrite cores. J. Magn. Magn. Mater. 2006, 304, e743–e745. [Google Scholar] [CrossRef]
- Sun, G.L.; Li, J.B.; Sun, J.J.; Yang, X.Z. The influences of Zn2+ and some rare-earth ions on the magnetic properties of nickel-zinc ferrites. J. Magn. Magn. Mater. 2004, 281, 173–177. [Google Scholar] [CrossRef]
- Costa, A.C.F.M.; Tortella, E.; Morelli, M.R.; Kiminami, R.H.G.A. Synthesis, microstructure and magnetic properties of Ni-Zn ferrites. J. Magn. Magn. Mater. 2003, 256, 174–182. [Google Scholar] [CrossRef]
- Snelling, E.C. Soft Ferrites, Properties and Applications, 2nd ed.; Butterworth: Boston, MA, USA, 1988. [Google Scholar]
- Reeve, W.D.; Hagen, T. Applying and Measuring Ferrite Beads: Part I Ferrite Bead Properties and Test Fixtures. Available online: http://www.reeve.com/Documents/Articles%20Papers/Ferrite%20Beads/Reeve-Hagen_FerriteBeads_P1.pdf (accessed on 30 November 2018).
- Paul, C.R. Introduction to Electromagnetic Compatibility, 2nd ed.; Wiley Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ott, H.W. Noise Reduction Techniques in Electronic Systems; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Keysight E5061B-3L3/3L4/3L5 LF-RF Network Analyzer with Option 005 Impedance Analysis Function. Available online: http://literature.cdn.keysight.com/litweb/pdf/5990-7033EN.pdf (accessed on 30 November 2018).

| Ferrite Part Number | Magnetic Material | External Diameter (OD) (mm) | Internal Diameter (ID) (mm) | Length (mm) |
|---|---|---|---|---|
| M-4304-02 | NC | 18.9 | 12.9 | 27.7 |
| 74277255 | MnZn | 18.6 | 10.2 | 28.5 |
| 74270055 | NiZn | 18.6 | 10.2 | 28.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suarez, A.; Victoria, J.; Torres, J.; Martinez, P.A.; Alcarria, A.; Martos, J.; Garcia-Olcina, R.; Soret, J.; Muetsch, S.; Gerfer, A. Effectiveness Assessment of a Nanocrystalline Sleeve Ferrite Core Compared with Ceramic Cores for Reducing Conducted EMI. Electronics 2019, 8, 800. https://doi.org/10.3390/electronics8070800
Suarez A, Victoria J, Torres J, Martinez PA, Alcarria A, Martos J, Garcia-Olcina R, Soret J, Muetsch S, Gerfer A. Effectiveness Assessment of a Nanocrystalline Sleeve Ferrite Core Compared with Ceramic Cores for Reducing Conducted EMI. Electronics. 2019; 8(7):800. https://doi.org/10.3390/electronics8070800
Chicago/Turabian StyleSuarez, Adrian, Jorge Victoria, Jose Torres, Pedro A. Martinez, Antonio Alcarria, Julio Martos, Raimundo Garcia-Olcina, Jesus Soret, Steffen Muetsch, and Alexander Gerfer. 2019. "Effectiveness Assessment of a Nanocrystalline Sleeve Ferrite Core Compared with Ceramic Cores for Reducing Conducted EMI" Electronics 8, no. 7: 800. https://doi.org/10.3390/electronics8070800
APA StyleSuarez, A., Victoria, J., Torres, J., Martinez, P. A., Alcarria, A., Martos, J., Garcia-Olcina, R., Soret, J., Muetsch, S., & Gerfer, A. (2019). Effectiveness Assessment of a Nanocrystalline Sleeve Ferrite Core Compared with Ceramic Cores for Reducing Conducted EMI. Electronics, 8(7), 800. https://doi.org/10.3390/electronics8070800






