Development of a Punch-O-Meter for Sport Karate Training
Abstract
1. Introduction
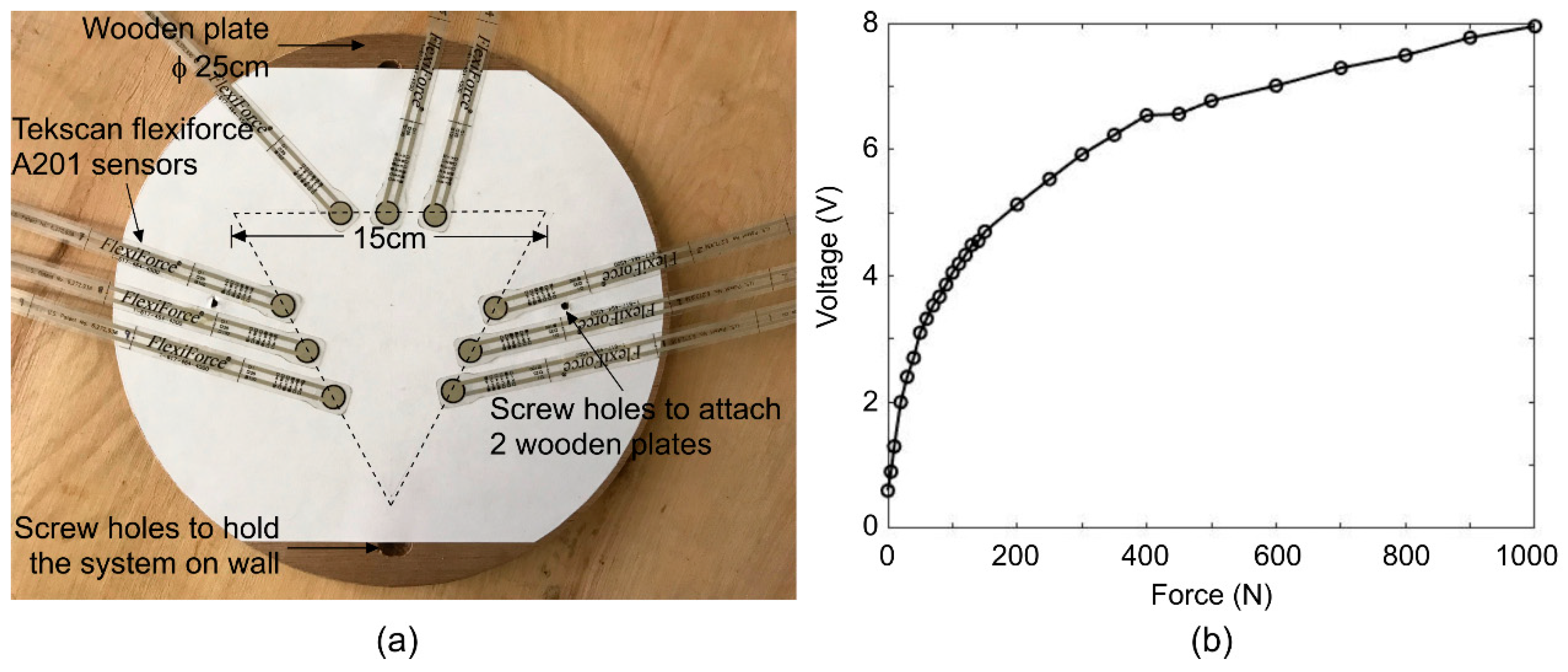
2. Materials and Methods
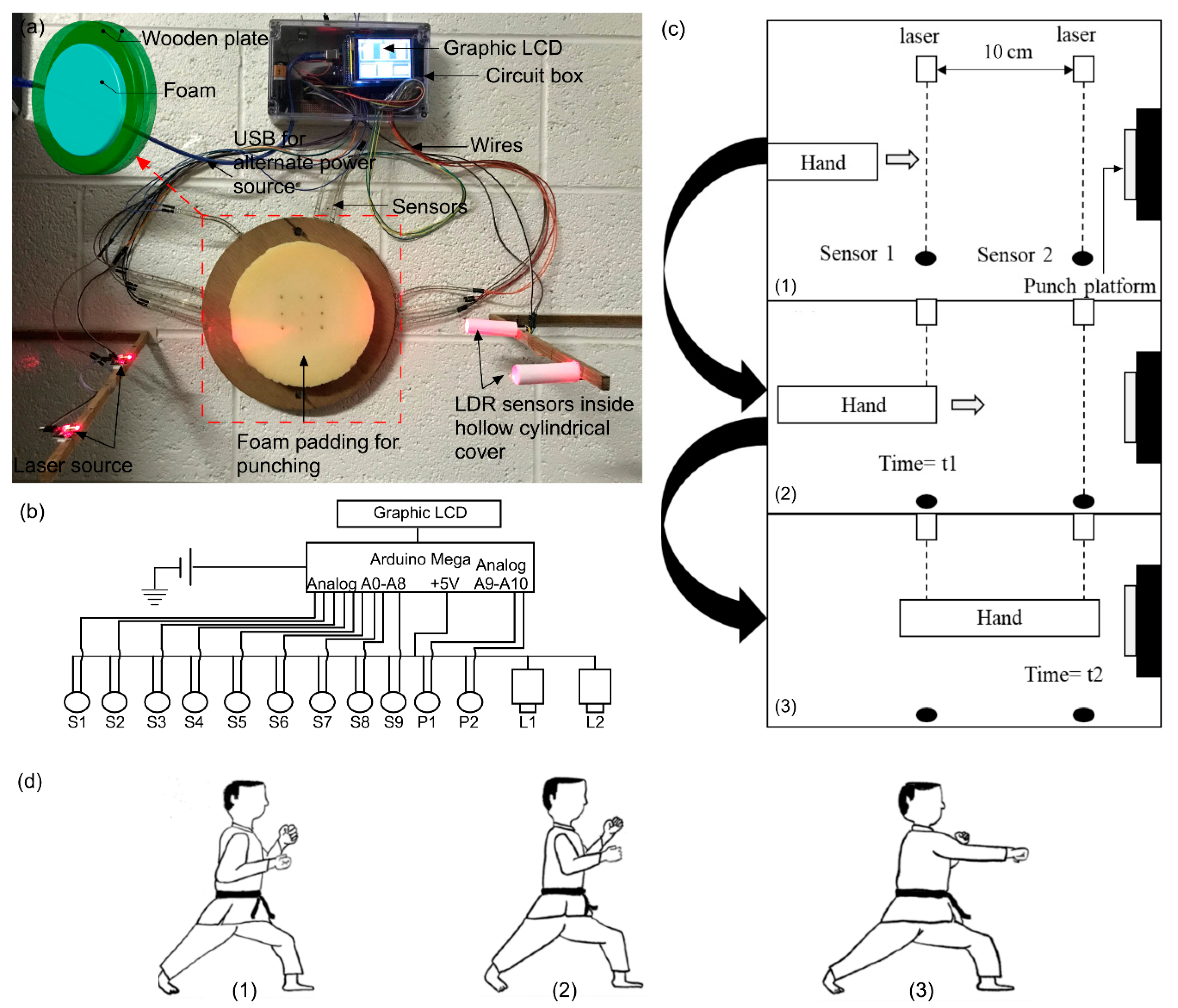
2.1. Punch Speed Detection Module
2.2. Other Components
2.3. System Specifications
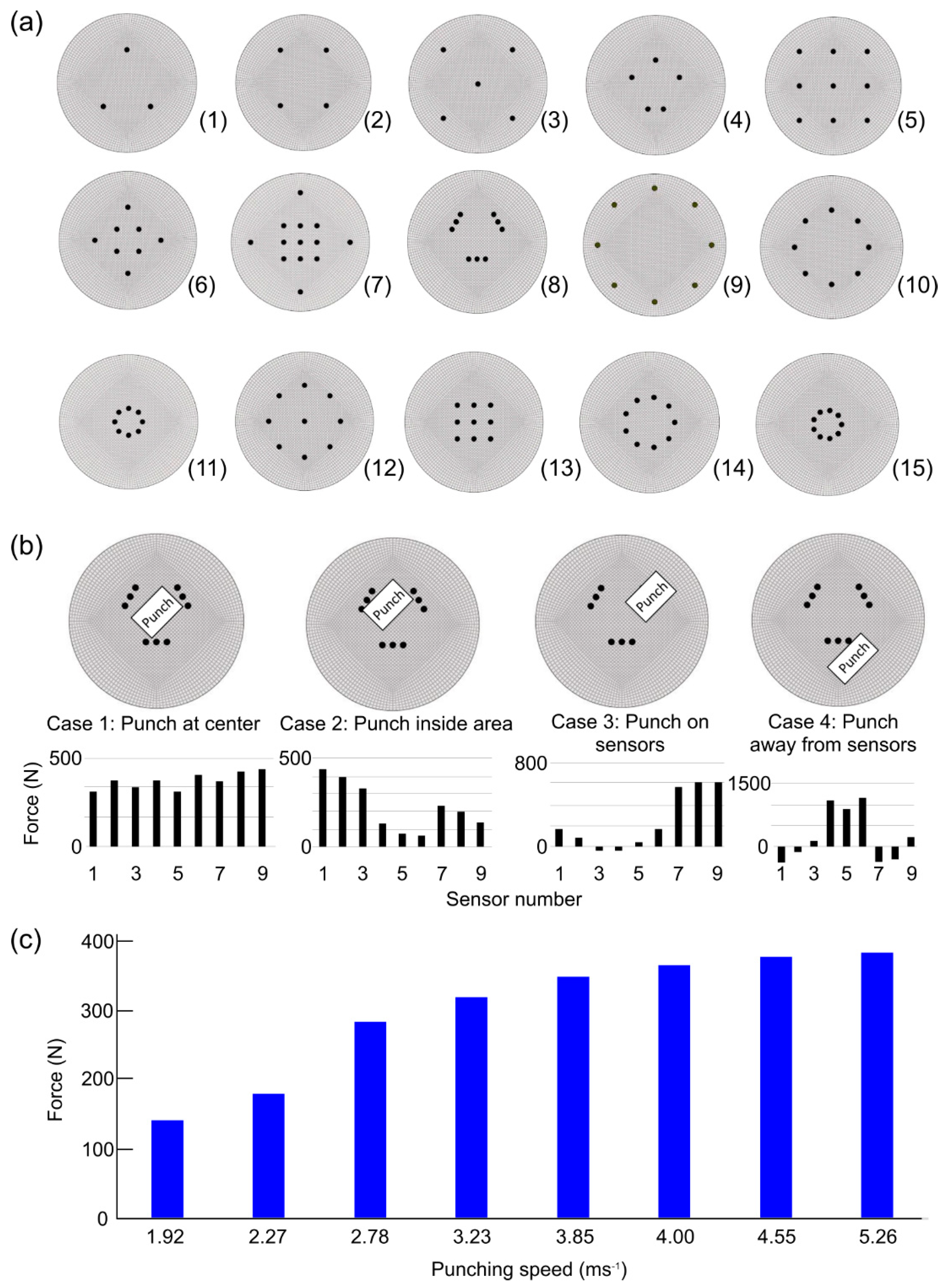
2.4. System Evaluation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Arus, E. Biomechanics of Human Motion: Applications in the Martial Arts; CRC Press: London, UK, 2012. [Google Scholar]
- Anupam, S. Analysis of Force, Time, Energy, Psychological Demand and Safety of Common Kicks in Martial Arts, in Industrial Engineering; Iowa State University: Ames, IA, USA, 2017. [Google Scholar]
- Ciubucciu-Ionete, G.; Mereuta, E. Biomechanics of Karate Techniques. Ann. Dunarea Jos Univ. Galati Fascicle XV 2008, 1454, 212–216. [Google Scholar]
- Rathee, N.K.; Magnes, J.; Davis, J. Kinematics of Board Breaking in Karate Using Video Analysis—A Dynamic Model of Applied Physics and Human Performance. Eur. Sci. J. 2014, 10, 1857–7881. [Google Scholar]
- Busko, K.; Staniak, Z.; Lach, P.; Mazur-Rożycka, J.; Michalski, R.; Gorski, M. Comparison of two boxing training simulators. Biomed. Hum. Kinet. 2014, 6. [Google Scholar] [CrossRef]
- Estevan, I.; Falco, C.; Jandacka, D. Mechanical analysis of the roundhouse kick according to the stance position. A Pilot Study. In Proceedings of the ISBS-Conference Proceedings Archive 2011, Porto, Portugal, 27 June–1 July 2011. [Google Scholar]
- Chadli, S.; Ababou, N.; Ababou, A. A new instrument for punch analysis in boxing. Procedia Eng. 2014, 72, 411–416. [Google Scholar] [CrossRef]
- Girodet, P.; Vaslin, P.; Dabonneville, M.; Lacouture, P. Two-dimensional kinematic and dynamic analysis of a karate straight punch. Comput. Methods Biomech. Biomed. Eng. 2005, 8, 117–118. [Google Scholar] [CrossRef]
- Estevan, I.; Alvarez, O.; Falco, C.; Castillo, I. Self-efficacy and performance of the roundhouse kick in taekwondo. Rev. Artes Marciales Asiaticas 2014, 9, 97–105. [Google Scholar] [CrossRef]
- Estevan, I.; Alvarez, O.C.T.A.V.I.O.; Falco, C.; Molina-García, J.; Castillo, I. Impact force and time analysis influenced by execution distance in a roundhouse kick to the head in taekwondo. J. Strength Cond. Res. 2011, 25, 2851–2856. [Google Scholar] [CrossRef]
- Estevan, I.; Falco, C.; Alvarez, O.; Molina-García, J. Effect of Olympic weight category on performance in the roundhouse kick to the head in taekwondo. J. Hum. Kinet. 2012, 31, 37–43. [Google Scholar] [CrossRef]
- Falco, C.; Alvarez, O.; Castillo, I.; Estevan, I.; Martos, J.; Mugarra, F.; Iradi, A. Influence of the distance in a roundhouse kick’s execution time and impact force in Taekwondo. J. Biomech. 2009, 42, 242–248. [Google Scholar] [CrossRef]
- Buśko, K.; Staniak, Z.; Szark-Eckardt, M.; Nikolaidis, P.T.; Mazur-Różycka, J.; Lach, P.; Górski, M. Measuring the force of punches and kicks among combat sport athletes using a modified punching bag with an embedded accelerometer. Acta Bioeng. Biomech. 2016, 18, 47–54. [Google Scholar]
- Smith, M.S.; Dyson, R.J.; Hale, T.; Janaway, L. Development of a boxing dynamometer and its punch force discrimination efficacy. J. Sports Sci. 2000, 18, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Walilko, T.J.; Viano, D.C.; Bir, C.A. Biomechanics of the head for Olympic boxer punches to the face. Br. J. Sports Med. 2005, 39, 710–719. [Google Scholar] [CrossRef] [PubMed]
- Karpiłowski, B.; Staniak, Z.; Nosarzewski, Z.; Ptak, C. Kontrola realizacji zadań treningowych przy pomocy trenażera bokserskiego, [Control of training task by means of a boxing simulator]. Trening 1997, 2, 159–164. [Google Scholar]
- Karpitowski, B.; Nosarzewski, Z.; Staniak, Z. A versatile boxing simulator. Biol. Sport 1994, 11, 133. [Google Scholar]
- Tekscan. FlexiForce A201 Sensor. 2016. Available online: https://www.tekscan.com/products-solutions/force-sensors/a201 (accessed on 21 June 2017).
- Shahbazi, M.M.; Sheikh, M.; Amini, A. Kinematic-kinetic comparisons of Tsuki technique in performing from waist and from midway in classic and individual styles. In Proceedings of the ISBS-Conference Proceedings Archive, Seoul, Korea, 14–18 July 2008. [Google Scholar]
- Gallaher, D.M. 3D Analysis of Punching Technique: Reverse vs. Lead (Gyaku tsuki vs. Oi tsuki). Master’s Thesis, California State University, Long Beach, CA, USA, 2014. [Google Scholar]
- Wąsik, J.; Da Silva, S.; Jonatas, F.; Franchini, E. Movement structure and kinetics of the traditional straight punch: Measurements in taekwon-do athletes. Ido Mov. Cult. 2013, 13, 42–47. [Google Scholar]
- Matko, V.; Milanović, M. Temperature-compensated capacitance–frequency converter with high resolution. Sens. Actuators A Phys. 2014, 220, 262–269. [Google Scholar] [CrossRef]
- Nasiriavanaki, M.; Xia, J.; Wan, H.; Bauer, A.Q.; Culver, J.P.; Wang, L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. USA 2014, 111, 21–26. [Google Scholar] [CrossRef]
- Turani, Z.; Fatemizadeh, E.; Blumetti, T.; Daveluy, S.; Moraes, A.F.; Chen, W.; Nasiriavanaki, M. Optical Radiomic Signatures Derived from Optical Coherence Tomography Images to Improve Identification of Melanoma. Cancer Res. 2019, 79, 2021–2030. [Google Scholar] [CrossRef]
- Mahmoodkalayeh, S.; Jooya, H.Z.; Hariri, A.; Zhou, Y.; Xu, Q.; Ansari, M.A.; Avanaki, M.R. Low Temperature-Mediated Enhancement of Photoacoustic Imaging Depth. Sci. Rep. 2018, 8, 4873. [Google Scholar] [CrossRef]
- Adabi, S.; Hosseinzadeh, M.; Noei, S.; Conforto, S.; Daveluy, S.; Clayton, A.; Nasiriavanaki, M. Universal in vivo textural model for human skin based on optical coherence tomograms. Sci. Rep. 2017, 7, 17912. [Google Scholar] [CrossRef]
- Zafar, M.; Kratkiewicz, K.; Manwar, R.; Avanaki, M. Development of Low-Cost Fast Photoacoustic Computed Tomography: System Characterization and Phantom Study. Appl. Sci. 2019, 9, 374. [Google Scholar] [CrossRef]
- De Souza, P.A., Jr.; Paulo, A.; Brasil, G. Hespanha, Assessing uncertainties in a simple and cheap experiment. Eur. J. Phys. 2009, 30, 615. [Google Scholar] [CrossRef]
| Configuration No. | Standard Deviation |
|---|---|
| 1 | 14.22 |
| 2 | 22.85 |
| 3 | 31.68 |
| 4 | 23.09 |
| 5 | 19.66 |
| 6 | 23.52 |
| 7 | 25.83 |
| 8 | 12.99 |
| 9 | 13.37 |
| 10 | 21.55 |
| 11 | 26.81 |
| 12 | 15.84 |
| 13 | 27.43 |
| 14 | 25.65 |
| 15 | 27.93 |
| Test No. | Normal gyaku tsuki |
|---|---|
| 1 | 5 |
| 2 | 5.56 |
| 3 | 5.26 |
| 4 | 5.26 |
| 5 | 5.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkatraman, J.; Manwar, R.; Avanaki, K. Development of a Punch-O-Meter for Sport Karate Training. Electronics 2019, 8, 782. https://doi.org/10.3390/electronics8070782
Venkatraman J, Manwar R, Avanaki K. Development of a Punch-O-Meter for Sport Karate Training. Electronics. 2019; 8(7):782. https://doi.org/10.3390/electronics8070782
Chicago/Turabian StyleVenkatraman, Jay, Rayyan Manwar, and Kamran (Mohammad) Avanaki. 2019. "Development of a Punch-O-Meter for Sport Karate Training" Electronics 8, no. 7: 782. https://doi.org/10.3390/electronics8070782
APA StyleVenkatraman, J., Manwar, R., & Avanaki, K. (2019). Development of a Punch-O-Meter for Sport Karate Training. Electronics, 8(7), 782. https://doi.org/10.3390/electronics8070782





