1. Introduction
Hypersonic vehicles have radial relative movement with ground telemetry and communication stations during high-speed flight, which brings Doppler frequency offset to the received signals. Moreover, maneuvering the flight of hypersonic vehicles can produce a Doppler change rate. When hypersonic vehicles fly at the speed of 10–25 Mach in the Ka communication frequency band, the produced Doppler frequency offset reaches 453 kHz–1.133 MHz and the Doppler change rate is as high as 100 kHz/s. Large dynamic Doppler brings a huge challenge to existing telemetry and communication systems, which makes correct demodulation of communication information extremely difficult and thereby causes failure of tasks.
The tracking speed in the traditional tracking loop is in contradiction with accuracy. Although the second-order phase-locked loop can accomplish accurate tracking of the Doppler frequency offset, it is inapplicable to the environment of large dynamic Doppler [
1,
2]. To address easy unlocking at sudden change of Doppler frequency offset in the second-order phase-locked loop, Li Zhe [
3] proposed an improved partial matched filtering (PMF)-FFT algorithm and a three-order phase-locked loop algorithm. Ma Ruofei [
4] proposed an FFT loop algorithm assisted by time–domain partial matching PLL and FLL. These algorithms can relock tracking more quickly than the traditional second-order phase-locked loop, but they still require secondary tracking upon unlocking fault, which prolongs telemetry and communication time to some extent. Zeng Chan [
5] introduced an Extended Kalman filter (EKF) to realize high dynamic tracking of GPS signals. EKF was composed of the third-order phase locked loop (PLL) assisted by frequency locked loop (FLL) and delay locked loop (DLL). Although EKF increased acquisition accuracy, it increased the structural complexity. Tu Zhiyong [
6] proposed a carrier tracking loop with high accuracy tracking performance based on Centerless Kalman filtering, which involved a feasible feedback way in the tracking loop so as to realize fast convergence of the algorithm and accurate tracking. This algorithm increased accuracy and stability at the cost of time. Zhang Zhaowei [
7] put forward a single-peak searching range correction (SRC) algorithm with simple closed expression and corrected the searching range of subsequent periods based on multiple combined periods. Later, the acquisition probability was further increased by overlaying the SRC algorithm and iterative SRC algorithm based on overlying SRC algorithm, but the complexity was very high. In short, acquisition and tracking method cannot meet demands for accuracy and speed in a large dynamic Doppler, due to the contradictory relation between acquisition and tracking speed and accuracy.
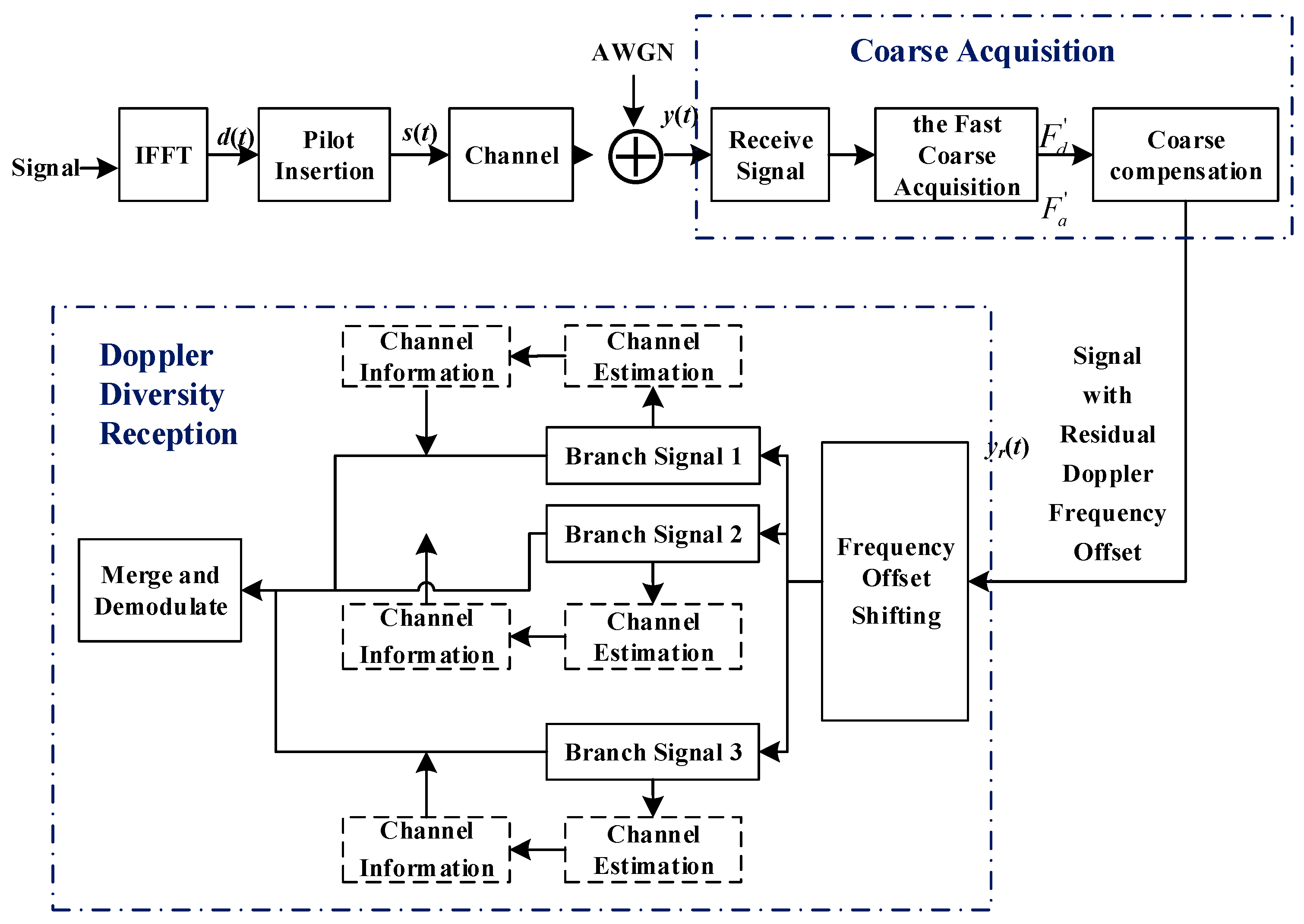
In this study, a telemetry and communication method based on the combination of Doppler diversity reception and fast coarse acquisition of Doppler frequency offset was proposed. The proposed method broke the above contradictions. Replacing accurate acquisition by coarse acquisition of Doppler frequency offset lowered the requirements on acquisition accuracy, thus saving acquisition time significantly. Replacing the real-time tracking of frequency and phase locked loop (FPLL) by Doppler diversity avoids unlocking fault caused by high complexity and dynamics variation of Doppler frequency offset in an ingenious way. The proposed method has flexible dynamic adjustment and it can adapt to the changing large dynamic Doppler environment.
The remainder of this paper is organized as follows:
Section 2 introduces the fast telemetry and communication method based on the Doppler diversity reception.
Section 3 introduces the simulation results and conclusions under typical large dynamic Doppler scenario.
Section 4 is the summary.
2. Fast Telemetry and Communication Method Based on Doppler Diversity Reception
In the traditional acquisition and tracking methods, the received signals have to be acquired and processed to make the residual Doppler frequency offset within the acquisition band of the narrow-band phase-locked tracking loop. Generally, residual Doppler has to be limited within 20 Hz. All of these propose very high requirements on signal acquisition. The Doppler capture search for hypersonic vehicles range from MHz to 10 Hz with spanning 105 orders of magnitude, which consumes a longer time and cannot meet the requirements of actual fast telemetry and communication.
From the perspective of communication, the large dynamic Doppler is a fast time-varying factor relative to the wireless channel and it is a disadvantageous factor against communication. Small Doppler can be adjusted through channel estimation and equalization, but large Doppler cannot be adjusted in the same method. Doppler diversity is a new diversity method that views Doppler frequency offset as an advantageous factor [
8,
9] and acquires gains through diversity processing in the Doppler domain [
10,
11,
12,
13,
14]. However, Doppler diversity has limited ability in processing frequency offset. Some studies have reported that the Doppler diversity is effective in the kHz level of mobile communication field. Doppler diversity might have poor adaptation to MHz large Doppler when it is applied to the communication of hypersonic vehicles directly. Therefore, it is still necessary to decrease Doppler frequency offset within the processing capacity range of diversity through compensation before using the Doppler diversity reception method. The main idea and specific implementation of the proposed communication scheme is shown in
Figure 1. Large Doppler frequency offsets and Doppler rate-of-change are estimated roughly through fast coarse acquisition. Meanwhile, the received signal is compensated and Doppler diversity treatment is performed to signals with residual Doppler frequency offset. The advantage of this communication scheme avoids the complicated refine acquisition and phase-locked tracking loop ingeniously, and it does not design complicated reliable mechanisms to guarantee secondary acquisition and tracking upon unlocking fault [
15,
16].
At the sending end, IFFT (Inverse Fast Fourier Transformation) is conducted to the modulated sending signal and the sending symbol
d(
t) is formed.
d(
t) is viewed as the frequency domain signals and pilot signals are inserted to form
s(
t) for sending.
h(
t) is the fading coefficient of time-varying channel. The received signal model at the reception end can be expressed as:
where
and
are the Doppler frequency offset and Doppler rate-of-change.
v(
t) denotes the additive white Gaussian noise.
Fast coarse acquisition of the received signals with large dynamic Doppler frequency offset is implemented. Suppose the rough estimations of Doppler frequency offset gained from coarse acquisition and its change rate are and, respectively. The received signals were compensated by the rough estimations, getting signals with residual Doppler frequency offset yr(t). yr(t) is shift by different frequency obtains branches and each branch channel state information is gained through channel estimation. All branches are combined by using channel state information in all branches, thus getting diversity gains. Finally, information is demodulated.
2.1. Fast Coarse Acquisition of Doppler Frequency Offset
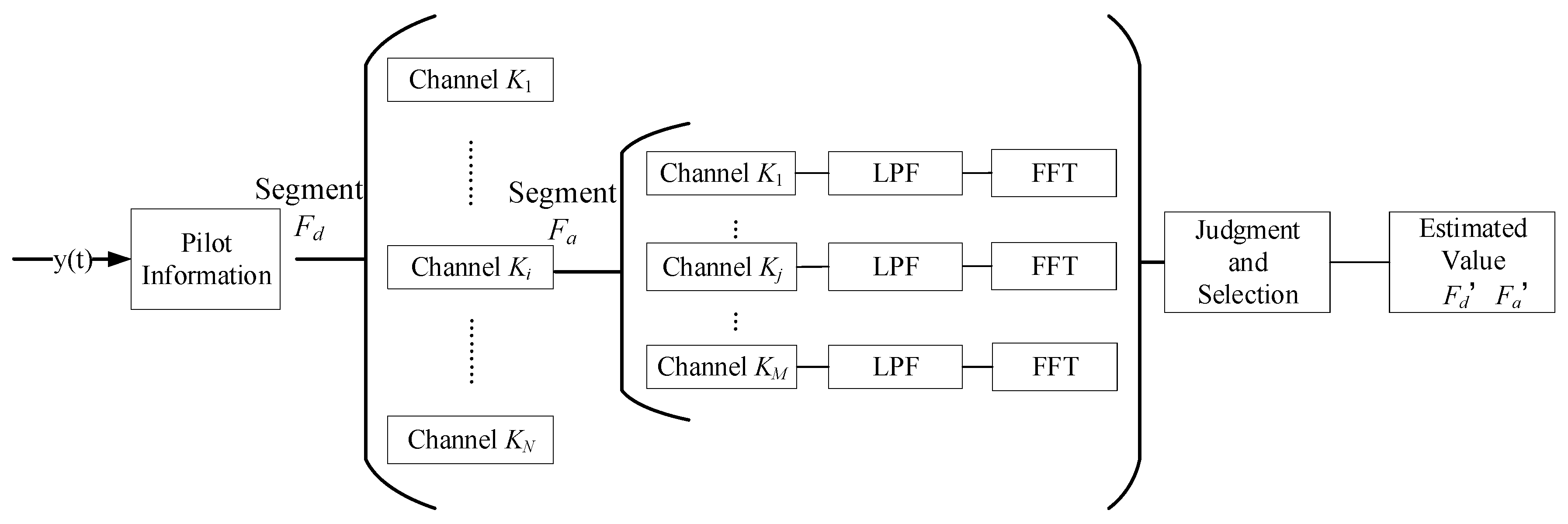
Doppler frequency offset in the hypersonic-speed flight environment can reach as high as 1.5 MHz. Doppler frequency offset changes in a large range. If Doppler frequency offset has to be precipitated at a time, tens of thousands of sample points have to be analyzed to assure spectral analysis accuracy, which consumes abundant analysis time [
17,
18]. To address this problem, the parallel fast coarse acquisition method is utilized, as shown in
Figure 2. The Doppler frequency offset range is divided into several channels to be processed simultaneously, which can reduce acquisition time significantly [
19,
20].
In
Figure 2,
Fd and Fa are the variation range of Doppler frequency offset [
fdmin,
fdmax] and range of Doppler rate-of-change [
famin,
famax]. The variation range of the whole Doppler frequency offset is divided into several sub-ranges at an equal interval and each sub-range is viewed as one channel. Different initial Doppler frequency offset is set for each channel at equal intervals. A large error between the acquired frequency offset and actual frequency offset caused by change rate of Doppler can lead to error of FFT analysis results. To prevent this error, Doppler rate-of-change in each channel is also divided into several sub-channels at an equal interval. Moreover, different initial Doppler rate-of-change is set with equal interval in each sub-channel.
Local carrier of the
Kj Doppler rate-of-change channel and the Ki Doppler frequency offset channel can be expressed as:
where
i = 1,2,…,
N;
j = 1,2,…,
M.
fdi is the Doppler frequency offset which set by the
Ki Doppler frequency offset channel.
faj is the change rate of Doppler which is set by the
Kj Doppler change rate channel.
In each sub-channel, the received signals are mixed with local frequency which is set by N × M channels parallel to relieve the effects of Doppler frequency offset in received signals. After high-frequency components are eliminated by a low-pass filter (LPF), FFT spectral analysis on signals in each sub-channel is carried out. Energy extreme point Vk (k = 1,2,…,N × M) is searched in the frequency domain. Size of energy extreme point in each sub-channel is compared to recognize the maximum value Vmax. fd and fa which are set by the channel where the maximum extreme point lies in are used as outcome of the current coarse acquisition, which are recorded as and . In this way, coarse acquisition of multiple Doppler frequencies and its rate-of-change is accomplished.
Based on coarse estimation, the received signals are then compensated and the compensated signal with residual Doppler
yr(
t) can be expressed as:
where
is the residual Doppler frequency offset after compensation and
t0 is the continuous time of data.
2.2. Doppler Diversity Reception Method Based on Artificial Frequency Shift
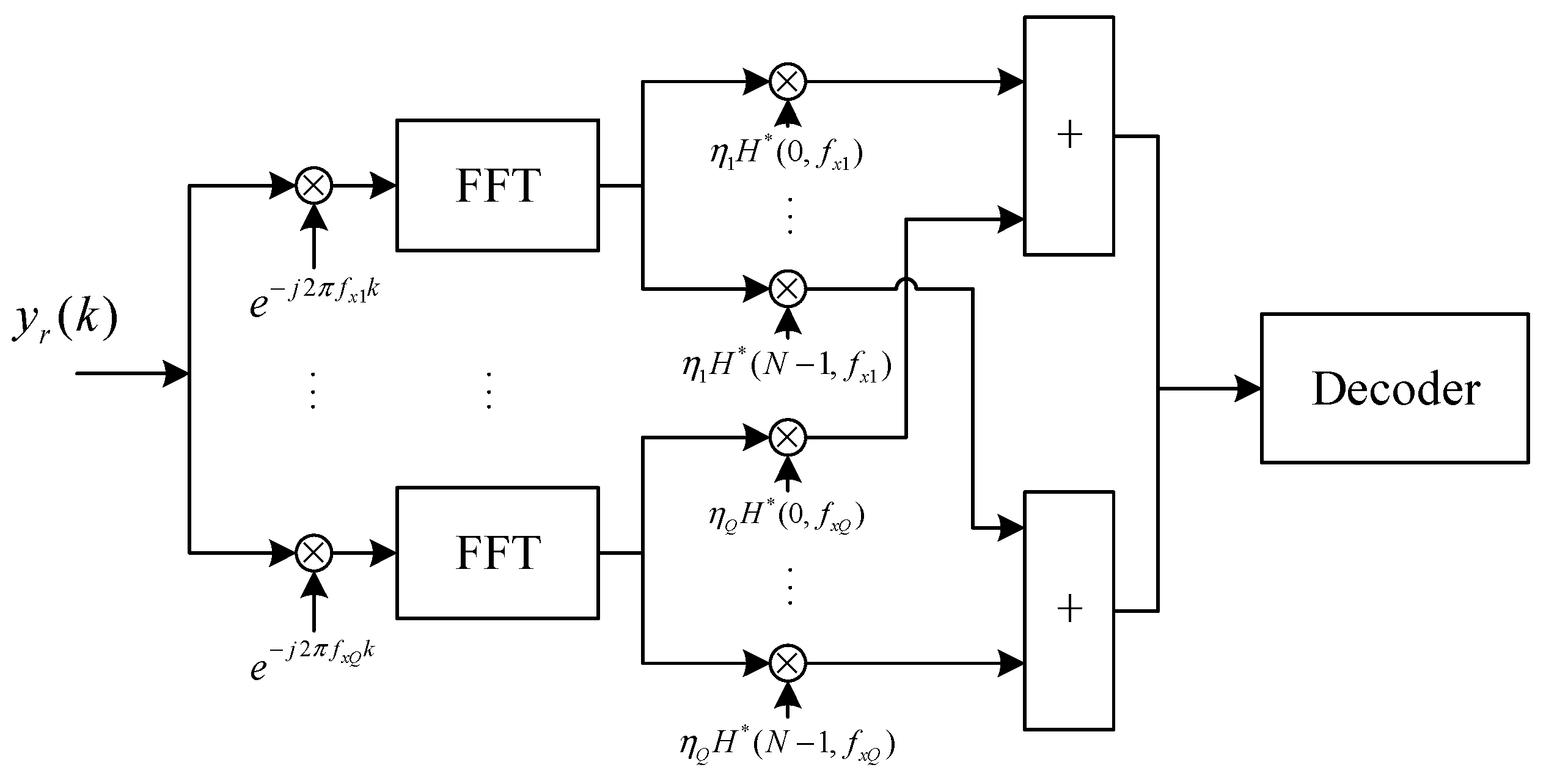
The Doppler diversity reception method based on artificial frequency shift is realized by shifting frequency offset differently through the received time–domain signal as well as generating and combining different signals of frequency shift branches. Interference signals of each branches after frequency shift are unrelated or weakly correlated. Different branches can be viewed as independently fading channels and diversity gains can be acquired from combining signals of branches. The reception framework is shown in
Figure 3.
Here, Q is the number of shifting branches. is the artificial shift frequency in different branches. k is the sequence number of signals after sampling. η is the weighting coefficient at combination of signals. H is the frequency domain channel response after time–frequency transformation. N is the number of data symbols in one FFT processing.
It can be seen from
Figure 1 that the discrete modulation signal
dn can be viewed as frequency–domain signal and it is transformed to time domain through IFFT. At this moment, transmitting signals in discrete domain can be expressed as:
Under this circumstance, channel can be equivalent to:
where
ap and
τp is the channel relative gain and time delay of the
pth multipath.
frp is the residual Doppler frequency offset on the pathway
p.
frp conforms to uniform distribution in the range of [−
FD].
FD is the maximum value residual Doppler frequency offset
fr and the continuous time of symbol is recorded as
T. Without loss of generality, the normalized Doppler frequency offset and normalized artificial shift frequency are applied to analyze system performance.
FDT is defined a normalized Doppler frequency offset and its value is in the range of [0, 1].
fxT is defined a normalized artificial shift frequency.
The equivalent signal after compensation in rapid coarse acquisition can be expressed as:
The equivalent signal is multiplied with
to shifting different artificial shift frequency
fx, thus generating several independent signals of shifting branches. On the shifting branch with a frequency offset of
fx, FFT of the
i receiving signal can be expressed as:
Finally, the combined output signal is:
where
is the combined weighted coefficient of the branch
q (
q = 1, 2,…
Q) and
is the gain coefficient of frequency–domain channel which is estimated within sub-channels. Finally, Z is demodulated.
For the selection of artificial shift frequency, the authors of [
8] decomposed Equation (7) into useful signals and interference signal. Correlation coefficient of interference signals between two branches is analyzed. It concludes that the correlation coefficient of interference signals of branches is almost 0 when the normalized Doppler frequency offset is higher than 0.25, the normalized artificial shift frequency within 0.75–0.8, and the signal to interference ratio increases with the increase of normalized Doppler frequency offset. Therefore, it is believed that the best normalized artificial shift frequency is in the interval of [0.75, 0.8].
3. Performance Evaluation
At present, the acquisition tracking technology is relatively mature, and it can accurately capture the carrier frequency with the residual frequency within 100 Hertz at low SNR easily. The compensated residual Doppler frequency offset might fully meet the requirements of Doppler diversity. It is well-known that contradiction exist between capture accuracy and speed, the lower the capture accuracy, the faster the capture speed, and the larger the residual Doppler offset of the Doppler diversity processed. This paper focuses on the ability of Doppler diversity and the selection of its parameters. At the same time, considering the strong ability of coarse capture, the simulation results of coarse capture are not given here.
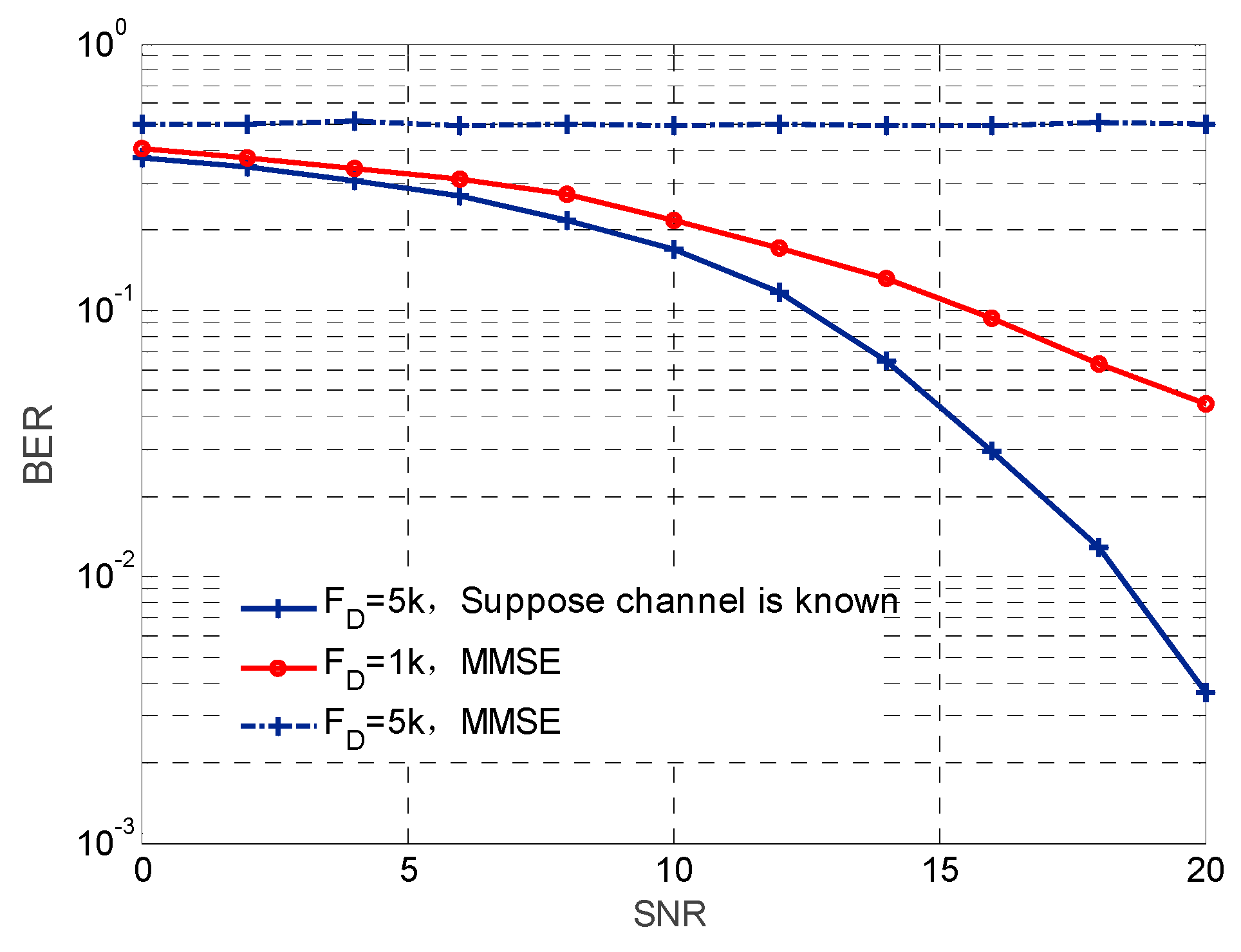
In the Doppler diversity module, the simulation system applies the BPSK (Binary Phase Shift Keying) modulation method and the shifting branches are
Q = 3. Artificial shift frequency
fxT = 0.75 according to the authors of [
8]. The bit error rate (BER) performance when
T = 10
−4,
FDT = 0.1 (
FD = 1 kHz) and
FDT = 0.5 (
FD = 5 kHz) is shown in
Figure 4. The BER performance is poor when
FDT = 0.1 and it has not reached 10
−2. When
FDT = 0.5, the ideal known channel state and MMSE (Minimum Mean Square Error) equilibrium are compared, which discovers mistakes of diversity combination due to inaccurate estimation of state information of channels, thus resulting in a high error rate of signal demodulation. This conforms to the conclusion drawn by the authors of [
11]. There is a trade-off relation between Doppler diversity and channel estimation error. With the increase of Doppler frequency offset, the fast time-varying performance of channel is strengthened, accompanied with increase of interference power and decrease of signal to interference ratio. All of these are disadvantageous to the communication system. Due to the estimation error of channel, the system performance drops dramatically. Therefore, the system performance cannot be improved whether or not the diversity reception method is adopted when
FDT > 0.1 (
FD > 1 kHz), thus failing to meet requirements on telemetry and communication.
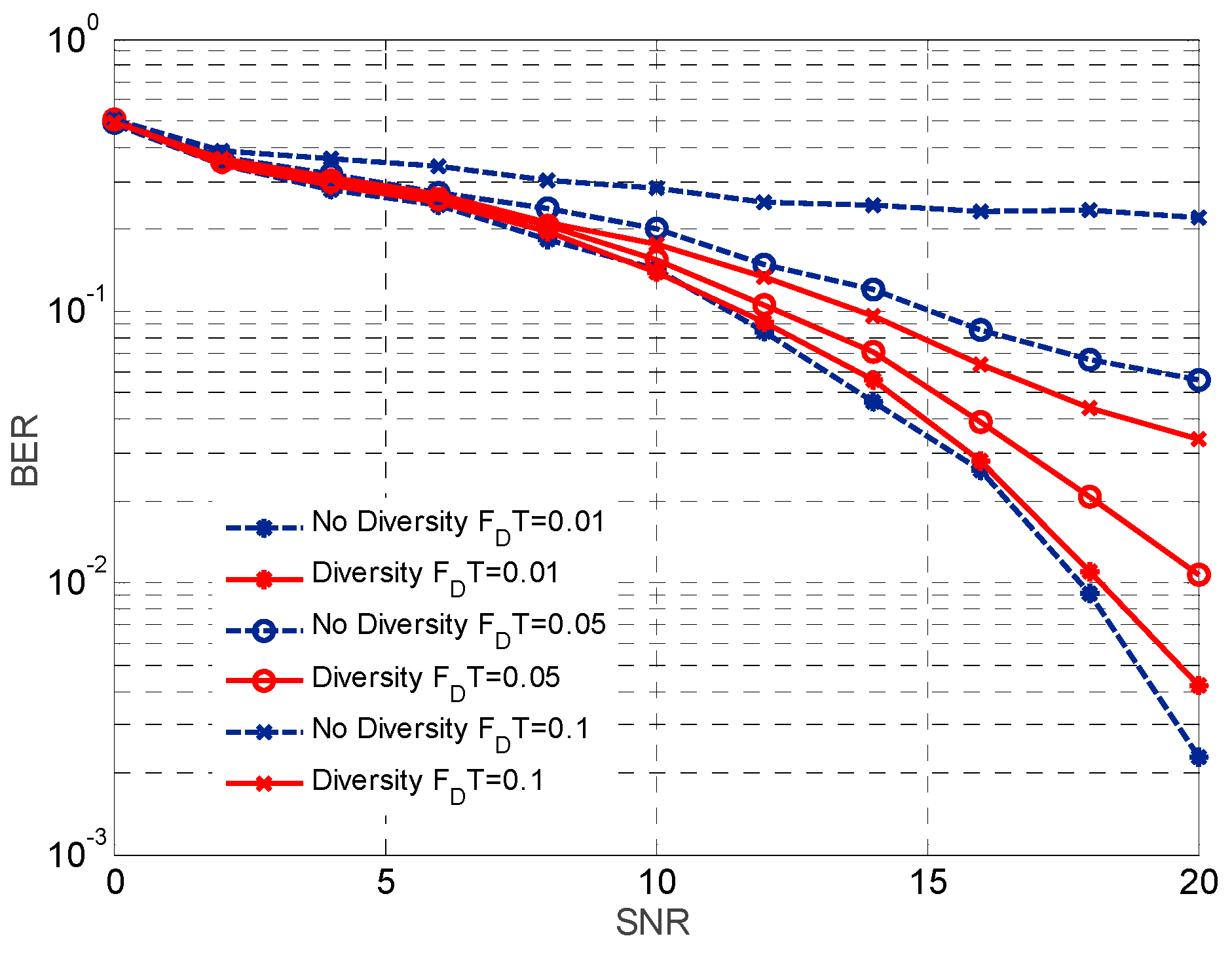
The BER performances with and without Doppler diversity when
FDT = 0.01, 0.05 and 0.1 under T = 10
−4 are shown in
Figure 5. The normalized Doppler frequency offset is decreased continuously. Generally, the system achieves good performance when
FDT < 0.1. When
FDT = 0.1 (
FD = 1 kHz), it is impossible to realize accurate demodulation when no Doppler diversity reception method is used. When
FDT = 0.05 (
FD = 500 Hz), BER performance under no Doppler diversity reception method is about 6 dB lower than that under the use of the Doppler diversity reception method. However, the BER performance under the use of diversity reception method is poorer than that without the diversity reception method when
FDT = 0.01 (
FD = 100 Hz). This shows that under a very small Doppler frequency offset, the system is slightly influenced by the Doppler offset, but the Doppler diversity reception method might strengthen interferences rather than offsetting interference signals mutually. It can be seen from
Figure 4 and
Figure 5 that when the residual Doppler frequency offset is too large, channel estimation is not accurate enough and the system performance is too poor, but conversely, the system cannot get evident gains when the diversity is too small. Hence, the diversity system might achieve the best performance when the residual Doppler frequency offset is around 1 kHz.
In a previous simulation analysis, the
fxT = 0.75 is determined according to [
8], when the normalized Doppler frequency offset is higher than 0.25. It can be seen from
Figure 4 and
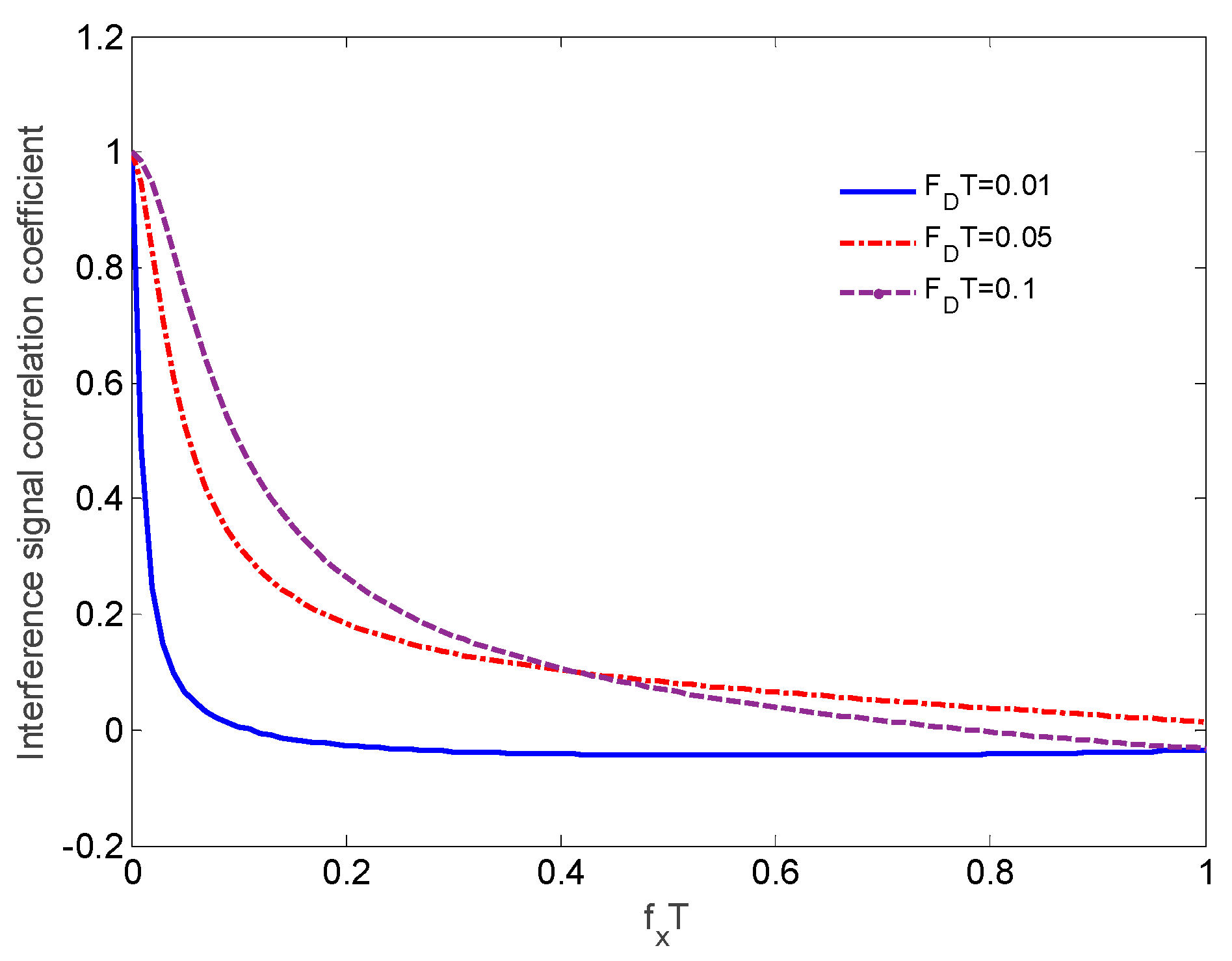
Figure 5 that the BER performances are not good when the normalized Doppler frequency offset is higher than 0.25. As a result, the selection of artificial shift frequency when the normalized Doppler is smaller than 0.1 has to be re-optimized. The variation trend of correlation coefficient of interference signals between two branches when
FDT < 0.1 is shown in
Figure 6. It is believed that when the correlation coefficient is lower than 0.2, two branches produce weak interference correlation and diversity can achieve good gains. The normalized artificial shift frequency range under different
FDT is shown in
Table 1. We are surprised that the artificial shift frequency under low normalized Doppler frequency offset has a larger range compared with [0.75, 0.8] which is introduced in previous studies. Consequently, the designed system proposes a looser requirement on parameter stability in practical applications and the system also has better fault tolerance.
In short, 1 kHz residual Doppler can achieve better Doppler diversity gain. When the normalized Doppler frequency offset is FDT = 0.01, the system has good BER performance and a larger selection range of artificial shift frequency. Under this condition, the normalized Doppler can be obtained 0.01 as long as the symbol period T is shortened to 10−5.
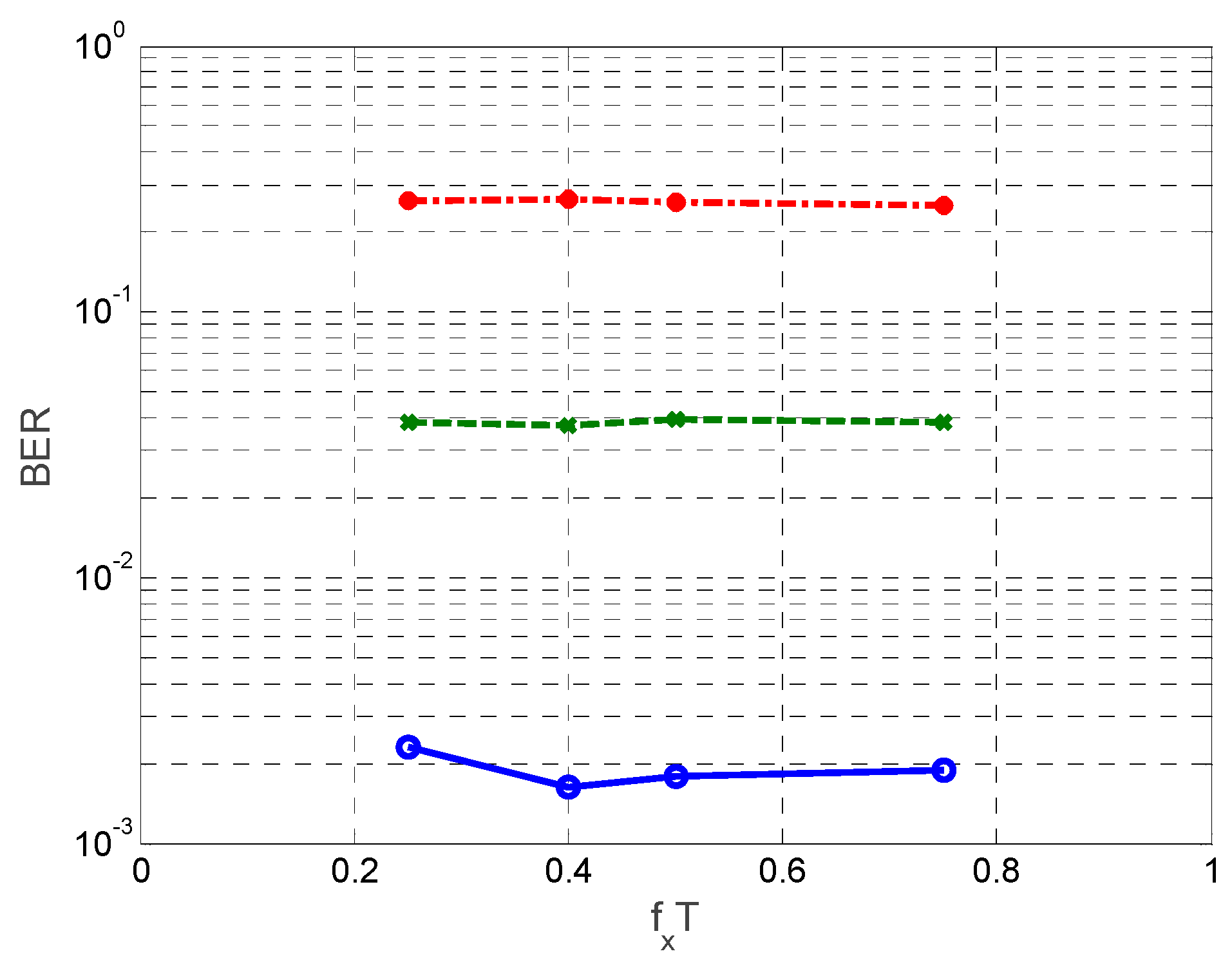
In order to discuss the influences of shortening symbol period
T, whether a good system performance can be achieved has to be discussed when the residual Doppler frequency offset shortened with
T = 10
−5. BER performance of different
FDT (0.01, 0.025 and 0.05) under
T = 10
−5 versus different normalized artificial shift frequency (0.25, 0.4, 0.5 and 0.75) are shown in
Figure 7 under signal-to-noise ratio = 20 dB. The BER curve when
FDT = 0.01 is close to 10
−3 and the best BER performance is achieved when the artificial shift frequency is 0.4, which is close to the curve when
FDT = 0.01 in
Figure 5. By observing two curves when
FDT = 0.05 in
Figure 7 and
Figure 5, the BER performance when
FD = 5 kHz is far poorer than that when
FD = 500 Hz. This reveals that when the actual residual Doppler frequency offset is too large, reducing normalized Doppler frequency offset by shortening the period
T cannot get similar BER performance. Therefore, it is recommended that the Doppler diversity system can be designed as residual Doppler frequency offset no higher than 1 kHz with normalized Doppler frequency offset 0.01, and normalized artificial shift frequency set to be 0.4.
4. Conclusions
To address difficulties in the fast telemetry and communication under large dynamic Doppler of hypersonic vehicles, a novel fast telemetry and communication method based on Doppler diversity reception for hypersonic vehicles is proposed in this study. Different from the acquisition and tracking ideas under traditional large dynamic Doppler, the proposed method does not use the complicated phase-locked tracking but Doppler diversity to processes demodulating signals directly. Moreover, an additional Doppler coarse acquisition is involved before diversity reception due to the limitation of diversity reception. In addition, the proposed scheme lowers requirements on acquisition accuracy and neglects the accurate tracking, thus enabling the shortening of acquisition time significantly. According to simulation results, the proposed method can achieve the best performance when the residual Doppler is no higher than 1 kHz, normalized Doppler frequency offset is 0.01 and normalized artificial shift frequency is 0.4.
In other words, the proposed scheme can accomplish fast telemetry and communication of hypersonic vehicles by controlling the residual Doppler within 1 kHz other than below 100 Hz in the traditional receiving scheme, which is easily accomplished by coarse acquisition module, and thus it has potential to realize fast telemetry and communication simply and effectively.